Evaluation of linear regression simultaneous myoelectric control using intramuscular EMG

Abstract

Goal

The objective of this study was to evaluate the ability of linear regression models to decode patterns of muscle co-activation from intramuscular EMG and provide simultaneous myoelectric control of a virtual three DOF wrist/hand system. Performance was compared to the simultaneous control of conventional myoelectric prosthesis methods using intramuscular EMG (parallel dual-site control) – an approach that requires users to independently modulate individual muscles in the residual limb, which can be challenging for amputees.

Methods

Linear regression control was evaluated in eight able-bodied subjects during a virtual Fitts’ law task, and was compared to performance of eight subjects using parallel dual-site control. An offline analysis also evaluated how different types of training data affected prediction accuracy of linear regression control.

Results

The two control systems demonstrated similar overall performance; however, the linear regression method demonstrated improved performance for targets requiring use of all three DOFs, whereas parallel dual-site control demonstrated improved performance for targets that required use of only one DOF. Subjects using linear regression control could more easily activate multiple DOFs simultaneously, but often experienced unintended movements when trying to isolate individual DOFs. Offline analyses also suggested that the method used to train linear regression systems may influence controllability.

Conclusion and Significance

Linear regression myoelectric control using intramuscular EMG provided an alternative to parallel dual-site control for 3-DOF simultaneous control at the wrist and hand. The two methods demonstrated different strengths in controllability, highlighting the tradeoff between providing simultaneous control and the ability to isolate individual DOFs when desired.

I. Introduction

Amputation of the upper extremity proximal to the wrist affects approximately 41,000 individuals in the United States [1]; the most common type of upper limb amputation occurs at the transradial level [2]. Myoelectric prostheses, which are typically controlled by surface electromyogram (EMG) signals from muscles in the amputated limb, have the potential to provide intuitive restoration of function for transradial amputees because EMG from physiologically appropriate muscles are available to control the prosthetic wrist and hand. However, clinically available myoelectric prostheses provide limited ability to control multiple degrees of freedom (DOFs) simultaneously, which if present would allow prosthesis movements that more closely mimic the coordinated multi-joint movements of intact limbs. Though simultaneous control of two DOFs is available for individuals with higher-level amputations after Targeted Muscle Reinnervation (TMR) surgery [3-5], transradial amputees using either traditional dual-site control methods [6] or the recently available pattern recognition control [7] are limited to sequential control DOFs. Simultaneous control of three or more DOFs is not clinically available for individuals with any level of upper limb amputation.

Recent studies have demonstrated the potential of providing simultaneous myoelectric control using intramuscular EMG, which provides the ability to record from deep muscles without crosstalk. Such approaches have included conventional myoelectric control methods [8, 9] and nonlinear regression methods [10]. Notably, intramuscular EMG obtained from Implantable Myoelectric Sensors (IMES^®) in the forearm were used to simultaneously control prosthetic wrist rotation and a 2-DOF hand [11, 12]. This approach used an extension of conventional dual-site methods, where EMG amplitudes from multiple physiologically-appropriate antagonistic muscle pairs controlled movement of the corresponding DOFs (parallel dual-site control). Simultaneous control of the wrist and hand using parallel dual-site control has demonstrated improved real-time performance metrics compared to sequential control in able-bodied subjects in a virtual task [8]. However, the success of this method depends on the ability of amputees to independently modulate muscles in the residual limb. Users must isolate individual muscle contractions to control only one DOF at a time. Difficulty in isolating residual limb muscles, which has been frequently documented in amputees [13, 14], may cause unintended movement of additional DOFs during parallel dual-site control [8, 9]. Thresholds on the EMG amplitudes are typically implemented to filter out as much unintended movement as possible [5, 9]; however, high thresholds may limit the ability of users to simultaneously engage multiple DOFs when desired. Though the IMES^® case study indicated that users may be able to learn to isolate muscle contractions, advanced control algorithms that are trained to decode patterns of muscle co-activation may allow for more intuitive simultaneous myoelectric control.

One method to learn the user’s natural co-activation patterns is to identify a linear mapping between EMG amplitude and intended prosthesis movement at each DOF (non-linear methods, including artificial neural networks, support vector regression, and kernel-ridge regression have also been evaluated [15-18]). Linear approaches have received substantial attention in the literature using surface EMG, and are frequently motivated by the motor control concept of muscle synergies [19, 20], where observed muscle activity during movement can be decomposed into a linear combination of a finite set of muscle co-activation patterns. Both linear regression [17, 21] and a semi-supervised implementation of non-negative matrix factorization (NMF) [19] have been previously used with surface EMG to map EMG amplitude to two wrist DOFs. Preliminary findings also suggest that use of intramuscular EMG allows linear regression methods to extend simultaneous control to two wrist DOFs and a hand grasp [22]. However, no previous studies have evaluated whether, when using the same set of EMG inputs, using linear regression methods to learn patterns of muscle co-activation provides a difference in real-time performance compared to parallel dual-site control.

To date, there also has not been a consensus on how linear regression myoelectric control systems should be configured or trained. Offline analysis for predicting two wrist DOFs suggested that providing training data for only single-DOF movements is equivalent to training with all possible movement combinations [17]. However, this has not been similarly demonstrated for a wrist/hand system, which requires additional use of EMG recordings from muscles originally spanning both the wrist and finger joints. Another issue that has not received substantial investigation is the training of the “rest state” (0% velocity output at a DOF). Many previous approaches for building linear models for simultaneous control, including NMF [21] and mixtures of linear experts [17], have trained the regression models using only EMG signals from corresponding contractions (e.g. the rotation models were trained using only data that included active supination or pronation), meaning that a DOF’s rest state is only trained with data collected when users are not actively contracting. Other linear methods [17, 21] have instead implemented a relabeling scheme, where the rest state is trained using any data where the DOF of interest was not active (e.g. the rest state for rotation was trained with true no motion, wrist flexion/extension, and hand open/close data, etc.). This relabeling approach has the potential to prevent unintended activation of additional DOFs by decreasing the weighting of EMG channels that are highly correlated to multiple different movements. To date, no previous studies have directly compared these two types of training data in linear myoelectric control systems that were otherwise equivalent.

The objective of this study was to evaluate the real-time performance of linear regression myoelectric control of a 3-DOF wrist/hand system using intramuscular EMG, and to compare its performance to the previously demonstrated parallel dual-site control. We hypothesized that EMG thresholds used for parallel dual-site control would allow for easier isolation of 1-DOF movements than linear regression control (previous studies using linear mappings demonstrated path efficiencies below 80% for tasks requiring use of only one DOF [19]). We also hypothesized that linear regression control would exhibit improved simultaneous control, because users do not need to independently activate muscles or intentionally exceed thresholds that were implemented to prevent simultaneous activity in multiple DOFs. An offline analysis was also performed to identify ideal training conditions for such systems, including the effects of using only single-DOF training and rest-state relabeling. Preliminary results were reported in conference proceedings [23].

II. Methods

This study was approved by the Northwestern University Institutional Review Board. Sixteen able-bodied subjects used fine-wire EMG to control a cursor in a virtual task controlling of three DOFs: wrist supination/pronation, wrist flexion/extension, and hand open/close. Subjects were randomly assigned to a control system; eight subjects used parallel dual-site and eight subjects used linear regression control. Subjects were experienced with sequential myoelectric control but naïve to simultaneous control of three DOFs.

A. Experimental Protocol

Fine-wire EMG electrodes (Motion Lab Systems, Inc.) were used to record intramuscular EMG from six forearm muscles: pronator teres, supinator, flexor carpi radialis, extensor carpi radialis longus, flexor digitorum profundus, and extensor digitorum. Insertion sites were guided by [24] and by palpation, and were confirmed by appropriate EMG activity during test contractions and/or by stimulation. Once the electrodes were inserted, subjects’ arms were placed in a custom forearm brace to enforce isometric contractions [8]. EMG signals were amplified 350x and band-pass filtered between 10 Hz and 2000 Hz using a Motion Lab Systems MA300 EMG system. Signals were sampled at 5 kHz by a 16-bit National Instruments data acquisition system. Signals were digitally high-pass filtered with a 3rd order Butterworth filter with a cut-off frequency of 20 Hz.

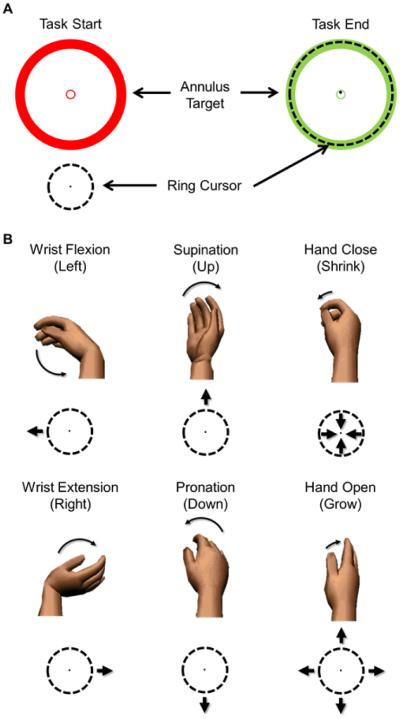
Subjects were randomly assigned to use either linear regression control or parallel dual-site control, which were configured as described in section IIB. Real-time performance was evaluated using a pseudo-three dimensional Fitts’ law task [8, 25] (Figure 1), similar to other implementations of Fitts’ Law for intramuscular myoelectric control evaluation [26]. Briefly, the output of the myoelectric control system controlled the velocity of a ring-shaped cursor by an easily-learned mapping: wrist flexion/extension controlled the speed of horizontal displacement, wrist rotation controlled the speed of vertical displacement, and hand open/close controlled the speed of change in cursor radius. Subjects were prompted to move the ring cursor into a variety of annulus-shaped targets as quickly as possible, and were neither encouraged nor discouraged from using simultaneous control. Successful trials required target acquisition within 30 s, with less than five overshoots (i.e., moving into and out of the target). Three levels of target complexity were presented with equal frequency: “1-DOF targets” required use of only one DOF, “2-DOF targets” required use of two DOFs, and “3-DOF targets” required use of three DOFs to successfully complete the trial. Fitts’ law trials were presented to subjects in six experimental blocks. All DOFs were available for the subjects to use during each target complexity; for example, the subjects had the ability to activate all three DOFs when acquiring a 1-DOF target, though using only one DOF would have been sufficient to accomplish the task. During each block, three targets were presented for each combination of target complexity and index of difficulty (Table I), resulting in 54 trials per block.

Figure 1.

Fitts’ law task [8, 28]. (A) Subjects were instructed to move a ring cursor into annulus-shaped targets. (B) Subjects used the system’s three DOFs (rotation, wrist flexion/extension, and hand open/close) to translate the cursor and make the radius of the cursor grow or shrink.

TABLE I.

Target conditions for the Fitts’ law task

Distance, D (normalized distance unit)	Thickness, W (normalized distance unit)	Index of Difficulty, ID (bits)
40	10	2.32
40	20	1.59
40	30	1.22
80	10	3.17
80	20	2.32
80	30	1.87

B. Myoelectric Control Systems

Both control systems used intramuscular EMG signals recorded from the six forearm muscles listed above. Mean absolute values (MAVs) from each channel, calculated from 250 ms windows with a frame increment of 50 ms, were used as inputs to the control systems [27].

Linear regression control used two linear regression models to predict the two directions of movement of a DOF (e.g., a supination model and a pronation model were used to predict intended wrist rotation) [17, 22]; thus six linear regression models were used to control three DOFs. Each regression model used MAVs from each of the six muscles listed above:

$${\mathrm{V}}_{\mathrm{i}}={{\mathbf{a}}_{\mathrm{i}}}^{\mathrm{T}}\mathbf{m}+{\mathrm{b}}_{\mathrm{i}}$$ (1)

where i was one of six movement types (supination, pronation, wrist flexion, wrist extension, hand open, hand closed), V_i was the predicted velocity for the movement as a percentage of maximum, a_i was the vector of multiplicative coefficients for each MAV, m was the vector of MAVs for each of the six muscles, and b_i was the constant offset.

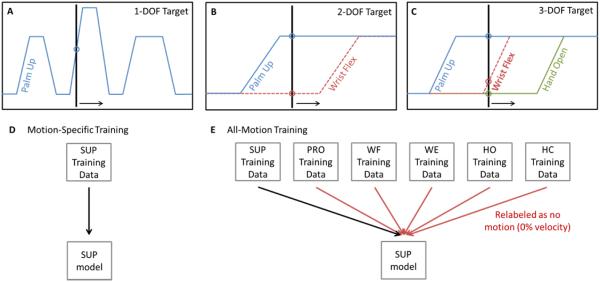
The regression models were trained using graded contractions in response to visual prompts (Figure 2A-C), where a cursor moved along a trajectory with ramps, prompting subjects to increase or decrease the intensity of their contraction accordingly. The middle level peak was mapped to 50% of maximum velocity, and the higher level peak was mapped to 75% of maximum velocity. The height of the visual prompt was used as the training label. Training prompts included all of the six motion types (1-DOF training data) and all possible combinations (2- and 3-DOF training data). Two different methods for training the models, and three different complexities of training data were evaluated. “Motion-specific training” (Figure 2D) used only EMG signals from corresponding contractions to train the regression models (e.g. the supination model was trained using only data that included active supination). “All-motion training” (Figure 2E) instead used the entire data set for each model; training data from sessions not corresponding to the model’s motion type were labelled as 0% velocity (i.e. rest-state relabeling). Both methods used least-squares regression. Training data complexities included (1) using only 1-DOF training data, (2) using 1- and 2-DOF training data, and (3) using 1-, 2-, and 3-DOF training data. The effect of training method and training data complexity was evaluated during offline analysis. For the online analysis, only all-motion training using 1, 2, and 3-DOF training data was used.

Figure 2.

Training protocols for linear regression control, (A-C): Visual prompts used to obtain training data for (A) each of the six 1-DOF movement types and (B) all possible 2-DOF combinations (C) and 3-DOF combinations. A cursor moved along a trajectory with three ramps, prompting subjects to increase or decrease the intensity of their contraction accordingly (arrow denotes direction of movement). Methods used to train regression models, (D-E): (D) Motion-specific training used data collected from only corresponding contractions (e.g. the supinator model was trained using data from when only supination was active). (E) All-motion training used all data as inputs into each regression model, where data not corresponding to the model’s motion type were labelled as 0% velocity (e.g. data from all motions were used to train the supinator model, but contractions where subjects were not actively supinating were labeled 0% supination velocity). SUP = supination, PRO = pronation, WF = wrist flexion, WE = wrist extension, HO = hand open, HC = hand closed.

For each regression model, predictions below 10% velocity were forced to 0% to reduce small unwanted movements. The movement direction and velocity output of the control system were determined by the difference between the two regression models that predicted movement of that DOF. A post-processing velocity ramp, originally developed for sequential pattern recognition control [28], was implemented to minimize abrupt changes in DOF activity. For each DOF, the ramp caused the output velocity to linearly increase to 100% of the intended velocity (calculated by Eq. 1) over 500 ms of continuous movement in the same direction.

Parallel dual-site control used a differential configuration [6] for each of the three DOFs [8]. MAVs from two physiologically appropriate antagonistic muscles were digitally amplified and thresholded, and the difference determined the velocity output at the DOF:

$${\mathrm{V}}_{\mathrm{j}}=\text{max}(0,{\mathrm{G}}_{\mathrm{j},1}{\mathrm{M}}_{\mathrm{j},1}-{\mathrm{T}}_{\mathrm{j},1})-\text{max}(0,{\mathrm{G}}_{\mathrm{j},2}{\mathrm{M}}_{\mathrm{j},2}-{\mathrm{T}}_{\mathrm{j},2})$$ (2)

where j is the DOF being controlled, V_j is the velocity output as a percentage of maximum, M_j,1 is the MAV of the first muscle in the antagonistic pair for DOF j, G_j,1 is the gain applied, and T_j,1, is the threshold. Similarly, M_j,2, G_j,2, and T_j,2 represent the MAV, gain, and threshold, respectively, for the second muscle for DOF j. Similar to clinical methods, gains and thresholds were manually configured to minimize unintended DOF activity and to maximize the dynamic range of velocities. The same post-processing ramp used for linear regression control was also implemented.

C. Real-Time and Offline Performance Evaluation

Real-time performance in the Fitts’ law task was quantified by throughput and path efficiency. Throughput was calculated by the mean of means method described by ISO 9241-9 [29], and path efficiency was calculated as the ratio of the shortest possible path length to the path length taken [30]. Throughput and path efficiency were calculated for each experimental block, to evaluate the effect of learning, and also averaged over the entire experiment. Subjects’ use of simultaneous control was also quantified over total and normalized fractions of trial duration. A DOF was considered to be active if the velocity output was greater than 5% of maximum output.

An offline analysis evaluated the effect of training method and training data complexity on prediction accuracy for linear regression control. Prediction accuracy was evaluated using random sub-sampling validation: accuracy was averaged over 100 repetitions of using a random sample of 90% of the data for training and the remaining for testing. Prediction accuracy was quantified by averaging the coefficient of determination (R²) calculated for each DOF. Accuracy was also quantified by the ability of the control system to predict the correct number of active DOFs, or whether the system predicted additional unintended movement, unintended no-movement, or incorrect movement at a DOF. Additionally, to evaluate which muscles’ EMG amplitudes were correlated with which motion types, R² values were calculated for univariate linear models that regressed activity in the six motion types onto each of the six muscles.

D. Statistical Analysis

Two-way analysis of variance (ANOVA) with interaction was used to evaluate the effects of control system and target complexity on throughput, path efficiency, and use of simultaneous control. Planned comparison two-sample t-tests were used to evaluate differences between control systems for 1-, 2-, and 3-DOF targets. Simultaneous control of 2-DOFs and 3-DOFs was evaluated individually using two ANOVAs. The presence of learning over consecutive experimental blocks was evaluated by t-tests on regression coefficients.

Three-way repeated measures ANOVA with interaction was used for the offline cross-validated linear regression analysis, to evaluate the effects of training method, training data complexity, and the complexity of the prompt on R² and DOF prediction accuracy. Means are reported as ± standard error. Error bars in figures represent standard error.

III. Results

A. Online Analysis

On average, subjects completed 99.7% ± 0.1% of all Fitts’ law trials within the time limit and without overshoot when using parallel dual-site control, and 98.5% ± 4.8% when using regression control. Mean completion time for each control scheme varied linearly with index of difficulty and target complexity (Figure 3A-B). The R² values for these Empirical Fitts’ law regression models ranged between 0.934 and 0.991, indicating that a Fitts’ law analysis was appropriate.

Figure 3.

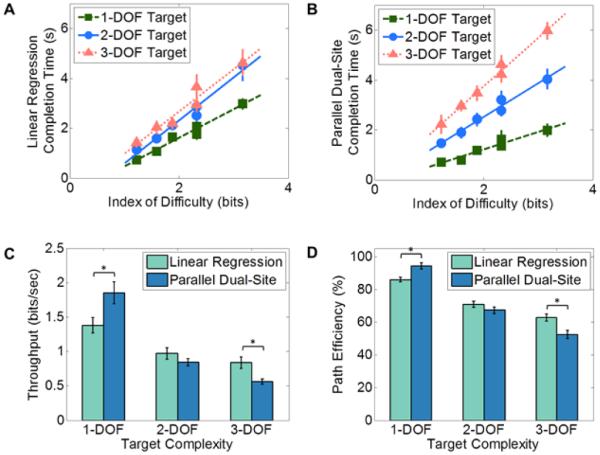
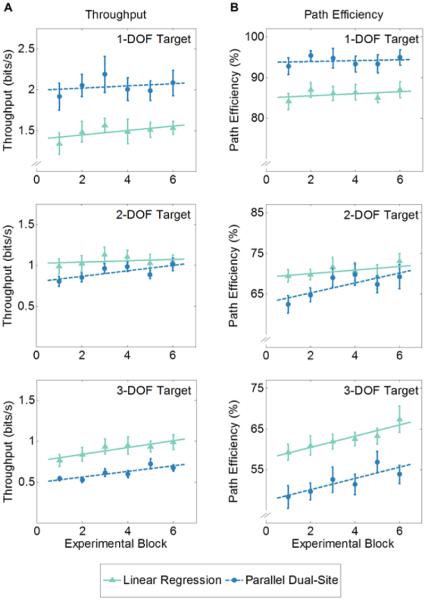
Fitts’ law performance. (A-B): Empirical Fitts’ law regression models, relationship between completion time and index of difficulty for the two control systems. (A) For linear regression control, R2 was 0.97, 0.97, and 0.95 for 1-, 2-, and 3-DOF targets, respectively. (B) For parallel dual-site control, R² was 0.94, 0.97, and 0.99 for 1-, 2-, and 3-DOF targets, respectively. (C-D): Fitts’ law performance metrics for the two control systems. Subjects exhibited higher values of throughput (C) and path efficiency (D) with linear regression control during 3-DOF targets, but lower values for 1-DOF targets. * p < 0.05

Fitts’ law results, averaged across all subjects for each control system and over all six of the experimental blocks, demonstrated no statistical difference between the two control systems when data from all three target complexities were combined (Table II; throughput, p = 0.782; path efficiency, p = 0.248). However, a significant interaction between the control method and the target complexity suggested that the two control systems differed when taking target complexity into account (Figure 3C-D; throughput, p = 0.001; path efficiency, p < 0.001). Subjects performed better on 1-DOF targets when using parallel dual-site control (throughput = 1.85 ± 0.16 bits/s; path efficiency = 94.1% ± 1.9%) compared to linear regression control (throughput = 1.38 ± 0.1 bits/s; path efficiency = 85.9% ± 1.5%). These differences were statistically significant (throughput, p = 0.035; path efficiency, p = 0.005). In contrast, subjects performed better on 3-DOF targets when using linear regression–based control (throughput = 0.84 ± 0.08 bits/s; path efficiency = 62.7% ± 2.0%) compared to parallel dual-site control (throughput = 0.56 ± 0.03 bits/s; path efficiency = 52.2% ± 2.5%). These differences were also statistically significant (throughput, p = 0.012; path efficiency, p = 0.007). For 2-DOF targets, no statistical difference was found between linear regression control (throughput = 0.97 ± 0.8 bits/s; path efficiency = 70.7% ± 1.8%) and parallel dual-site control (throughput = 0.84 ± 0.05 bits/s; path efficiency = 67.3% ± 2.1%).

TABLE II.

Fitts’ law results averaged over all three target complexities

Control System	Throughput	Path Efficiency
Linear Regression	1.06 ± 0.9 bits/s	73.1% ± 1.6%
Parallel Dual-Site	1.09 ± 0.8 bits/s	71.2 % ± 2.0%

Learning trends differed between the two control types (Figure 4), primarily for 2-DOF targets. For 1-DOF targets, no significant learning occurred for subjects using linear regression (throughput, p = 0.342; path efficiency, p = 0.571) or parallel dual-site control (throughput, p = 0.737; path efficiency, p = 0.840). For 2-DOF targets, subjects using linear regression control exhibited no significant learning (throughput, p = 0.728; path efficiency, p = 0.402), but subjects using parallel dual-site control did exhibit learning (throughput, p = 0.036; path efficiency, p = 0.044). For 3-DOF targets, subjects using linear regression control exhibited learning for 3-DOF targets, with significant improvements in path efficiency (p = 0.015) and a nearly significant improvement in throughput (p = 0.062). Subjects using parallel dual-site control also experienced significant improvements in throughput and path efficiency for 3-DOF targets (throughput, p = 0.003; path efficiency, p = 0.037).

Figure 4.

Learning trends over consecutive experimental blocks during the Fitts’ law trials. (A) Throughput: Subjects using linear regression control demonstrated no significant increase in performance over the course of the experiment for any target complexity, though a possible learning trend was present for 3-DOF targets (p = 0.062). In contrast, subjects using parallel dual-site control exhibited learning for 2- and 3-DOF targets (p = 0.036 and p = 0.003, respectively). (B) Path efficiency: Subjects using linear regression control exhibited learning for 3-DOF targets only (p = 0.015), whereas subjects using parallel dual-site control exhibited learning for both 2- and 3-DOF targets (p = 0.044 and p = 0.037, respectively). Note axis breaks.

Use of simultaneous control depended on the complexity of the target (Table III, p < 0.001). Subjects most often used two DOFs simultaneously when acquiring 2-DOF targets and most often used three DOFs simultaneously when acquiring 3-DOF targets. The control system also significantly influenced the amount of simultaneous control used (p < 0.001). When subjects used linear regression control, significantly more simultaneous DOF activity was present. This was true for 1-, 2-, and 3-DOF targets.

TABLE III.

Percentage of Trial Duration with at Least Two DOFs Simultaneously Active

	1-DOF Target		2-DOF Target		3-DOF Target
	Linear Regression	Parallel Dual-Site	Linear Regression	Parallel Dual-Site	Linear Regression	Parallel Dual-Site
2 DOFs simultaneously active *	25.6% (± 2.19%)	6.7% (± 2.2%)	48.7% (± 1.67%)	36.3% (± 2.8%)	38.8% (± 0.78%)	29.8% (± 2.5%)
3 DOFs simultaneously active*	2.8% (± 0.5%)	0.2% (± 0.2%)	12.3% (± 1.3%)	2.2% (± 1.1%)	26.4% (± 3.0%)	6.27% (± 1.9%)

^*Significant difference in amount of simultaneous activity between linear regression and parallel dual-site control (p < 0.001)

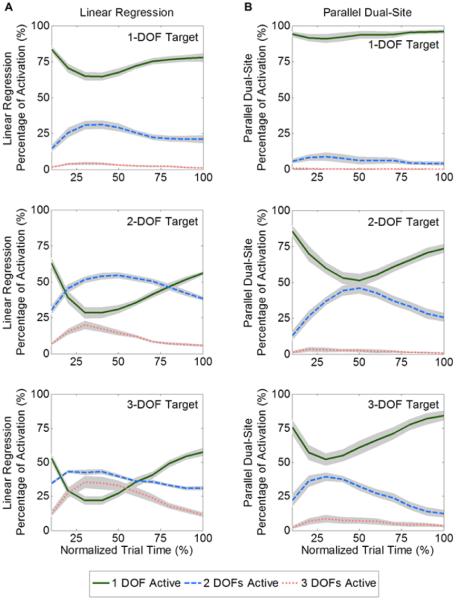
Figure 5 depicts profiles of simultaneous control use as a function of normalized trial time. The general strategy for using simultaneous control was similar between the two control methods, although linear regression control exhibited increased simultaneous activation of two or more DOFs for all target complexities. Use of simultaneous control peaked near the middle of the trial. Subjects used more 1-DOF movements at the end of the trial, typically for fine corrections.

Figure 5.

Distribution of how frequently subjects used one DOF at a time, two DOFs simultaneously, or three DOFs simultaneously as a function of normalized trial duration. (A) Linear regression control. (B) Parallel dual-site control. Both control systems exhibited similar overall strategies, with peak use of simultaneous control near the middle of the trial. Trials ended with greater use of sequential 1-DOF movements. Overall, more simultaneous control was present for all target complexities when using linear regression control compared to parallel dual-site control. Shaded region is standard error.

B. Offline Analysis

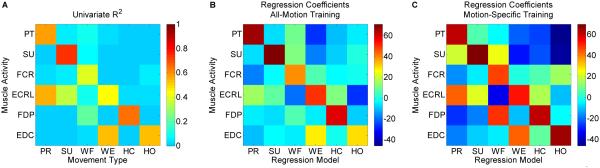
Figure 6 demonstrates how use of all-motion training affected the regression coefficients for each linear regression model in a representative subject. Univariate R² values highlighted individual muscles that were correlated with multiple intended movements (Figure 6A). Such muscles include extensor carpi radialis longus (correlated with pronation, supination, and wrist extension in this subject) and extensor digitorum communis (correlated with wrist extension and hand open in this subject). Of note, this univariate R² is different than the R² values calculated to evaluate offline prediction accuracy of the linear regression control method. Using all-motion training (Figure 6B) resulted in decreased regression coefficients for these muscles compared to motion-specific training (Figure 6C).

Figure 6.

Changes in regression model coefficients when using all-motion versus motion-specific training in a representative subject. (A) Univariate R² values highlighted individual muscles that were correlated with multiple intended movements in this subject, including extensor carpi radialis longus (correlated with pronation, supination, and wrist extension) and extensor digitorum communis (correlated with wrist extension and hand open).Using all-motion training (B) resulted in decreases in the weighting of these muscles in their respective regression models compared to when motion-specific training was used (C). Muscle activities: PT = pronator teres, SU = supinator, FCR = flexor carpi radialis, ECRL = extensor carpi radialis, FDP = flexor digitorum profundus, EDC = extensor digitorum communis. Movement types / regression models: PR = pronation, SU = supination, WF = wrist flexion, WE = wrist extension, HC = hand close, HO = hand open.

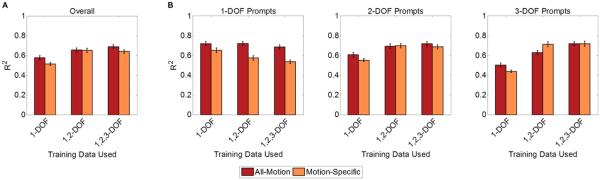
Using all-motion training instead of only motion-specific training resulted in significantly better prediction accuracy (R², Figure 7, p < 0.001). Regression models predicted 1-, 2-, and 3-DOF prompts with different levels of accuracy (p < 0.001), depending on whether 1-DOF training data, 1- and 2-DOF training data, or 1-, 2-, and 3-DOF training data were provided (p < 0.001). Prediction of 1-DOF prompts was most accurate when the system was trained with only 1-DOF data, whereas prediction of 3-DOF prompts was more accurate when 2- and 3-DOF training data were included. The relationship between training data complexity and prompt complexity was more pronounced when using motion-specific training (p < 0.001).

Figure 7.

Offline cross-validated prediction accuracies for the regression models. (A) Overall R2 value when all DOF complexities of prompt data (including 1-, 2-, and 3-DOF prompts) are predicted. Using all-motion training improved overall prediction accuracy compared to motion-specific training (p < 0.001). (B) Results broken down by DOF complexity of the prompt to be predicted. The training data complexity also significantly affected prediction accuracy for different prompt complexities (p < 0.001). 1-DOF prompts were predicted best by systems trained with only 1-DOF data, whereas 3-DOF prompts were predicted better by systems trained with 1-, 2-, and 3-DOF training data.

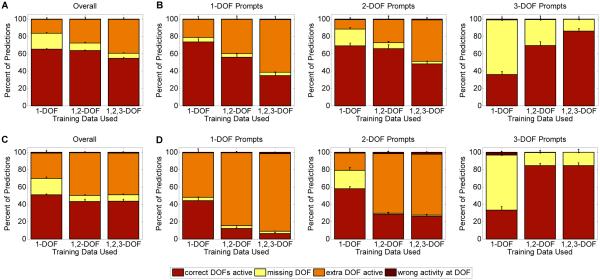
Error profiles in predicting activity of the correct DOFs are depicted in Figure 8. Using all-motion training resulted in a greater proportion of correct DOF activity (p < 0.001, ANOVA training method factor) and a significantly lower amount of unintended DOF activation (p < 0.001). Different training data complexities also affected the ability to accurately predict the correct DOF activity (p < 0.001). The effect of training data differed depending on the complexity of the prompt to be predicted (p < 0.001). Including 2- and 3-DOF training data resulted in more unintended DOF activation for 1-DOF prompts, but greater accuracy and fewer missed activations in 3-DOF prompts. The relationship between training data complexity and prompt complexity was more pronounced when using motion-specific training (p < 0.001).

Figure 8.

Offline cross-validated DOF-based prediction accuracy. (A,C) Overall DOF-prediction accuracy when all DOF complexities of prompt data (including 1-, 2-, and 3-DOF prompts) are predicted. Using all-motion training (A) results in greater proportion of correct DOF activity than motion-specific training (C) (p < 0.001). (B,D) DOF-prediction accuracy by separated by the DOF complexity of the prompt to be predicted. Using motion-specific training (D) resulted in more additional activation of unintended movements than using all-motion training (B) (p < 0.001), primarily in 1-DOF prompts.

IV. Discussion

The results of this study suggest that both linear regression and parallel duel site myoelectric control using intramuscular EMG have the potential to provide intuitive simultaneous control of three wrist/hand DOFs. Real time performance metrics using the linear regression approach provided a similar overall level of control as parallel dual-site control (Table II), which was previously demonstrated with implantable EMG recording devices [12] and has been shown to improve real-time performance metrics compared to sequential control [8]. Differences in the learning rates between the two control systems (Figure 4) demonstrated that simultaneous control provided by linear regression required less learning from the user. In the linear regression approach, subjects performed contractions to train the algorithm without feedback or constraints on how contractions should be executed; thus the training data contained subjects’ natural muscle co-activation patterns. This approach is foreseeably useful as amputees often have difficulty isolating contractions of individual residual limb muscles [13, 14]. In contrast, subjects using parallel dual-site control needed to isolate muscles for 1-DOF movements and learn how to independently combine them for simultaneous control of the DOFs. This need for learning was demonstrated in the simplest multi-DOF targets (2-DOF targets); subjects using linear regression started the experiment with a higher performance than those using parallel dual-site control and maintained this high performance during the experiment. In contrast, those using parallel dual-site control improved over the experiment, indicating that they learned the necessary techniques to implement this method of control. The increased complexity of 3-DOF targets elicited learning in both throughput and path efficiency for parallel dual-site control, but only statistically significant learning in path efficiency for linear regression control. Further work to characterize learning over multiple training sessions using these two systems is needed to elucidate these trends.

The results of the Fitts’ law analysis, when broken down by target complexity, indicated that linear regression and parallel dual-site control have different advantages. The gains and thresholds of parallel dual-site control were manually configured to minimize unintended movements, which allowed subjects to isolate individual DOFs with greater ease (Table III, Figure 5) and subsequently acquire 1-DOF targets with greater throughput and path efficiency than linear regression control (Figures 2C-D). Path efficiencies for 1-DOF targets acquired with parallel dual-site control were above 90%. However, such thresholds also made it more challenging to initiate and sustain simultaneous activation of multiple DOFs when desired. Consequently, subjects used less simultaneous activity for 2- and 3-DOF targets (Table III, Figure 5), resulting in overall poorer performance for 3-DOF targets (Figures 3C-D). In contrast, subjects using linear regression control, which did not use substantial thresholds on EMG activity, more easily activated all three DOFs simultaneously when attempting 3-DOF targets and resulted in improved throughput and path efficiency. However, this improved ease in activating multiple simultaneous DOFs also resulted in substantial additional unintended movement when trying to acquire 1-DOF targets, leading to poorer performance. For 2-DOF targets, the two systems demonstrated similar performance in the Fitts’ law task, likely reflecting a balance between the benefits of the two control systems: the improved ability to produce combined 2-DOF movements when desired (linear regression), and the improved ability to prevent unintended movement in the third DOF (parallel dual-site control).

The overall strategy in which subjects used simultaneous control was similar between the two control methods (Figure 5). In general, subjects’ peak use of simultaneous control occurred in the middle of the trial, with greater use of 1-DOF movements at the end. This is similar to previous reports suggesting that subjects tend to use simultaneous control more for gross movements and sequential control for fine positioning [8, 31, 32]. Subjects using linear regression control used fewer 1-DOF movements at the end of the trials than subjects using parallel dual-site control. However, it is unclear whether the subjects intentionally used more simultaneous control during fine positioning, or whether this simply reflected the greater prevalence of unintended simultaneous movement when using linear regression control.

The real-time tests used regression models that were trained using all-motion training with 1-, 2-, and 3-DOF data, because offline pilot analyses suggested that this setup would provide the highest overall prediction accuracy without substantial variation in accuracy between 1-, 2- or 3-DOF movements. The data in Figure 7 also demonstrate this. Offline analysis demonstrated that the training methods used for linear regression control have the potential to significantly influence control; therefore the real-time results of this study may have limited generalizability to linear regression systems trained with different methods or data. Based on our offline analysis, we expect that a linear regression model trained with only 1-DOF data would have performed similarly to parallel dual site control, i.e., with easier isolation of movements at the expense of simultaneous control of multiple DOFs. Future work should further evaluate the effect of training data complexity on real-time performance.

To date, many studies that have evaluated linear methods for simultaneous myoelectric control (including NMF-based methods [21] and mixtures of linear experts [17]) have used motion-specific or DOF-specific training methods, where the models are trained using only data for the corresponding movement type (e.g. a supination model is trained using only supination data) or using only data from within the same DOF (e.g. rotation models trained using both supination and pronation data). Some studies have also evaluated linear methods using all-motion training [17, 21], but to our knowledge no study has directly compared the difference in these two types of training for the same regression method. The results of the offline analysis highlight that using all available training data to train each linear regression model provides more robust prediction of intended prosthesis movement, and may explain why real-time path efficiencies for 1-DOF targets acquired with linear regression control were greater than efficiencies in previous studies using linear mappings trained by factorization (NMF) with DOF-specific data [21]. Training regression models with all available data allowed for minimized weighting of channels that were highly predictive of multiple prosthesis outputs, which occurred frequently when subjects co-activated muscles. In contrast, motion-specific training required channels that were highly correlated to multiple intended movements to be heavily weighted in multiple models, resulting in substantial unintended co-activation of the DOFs (Figure 8).

Though the real-time data suggest that the linearity assumption was satisfied sufficiently to provide an adequate control system, the dependence of cross-validated prediction accuracy on training data complexity (Figure 7) indicates that EMG amplitudes produced during 3-DOF training prompts were not exact linear combinations of the 1-DOF training EMG amplitudes. These results differ from previous reports for linear regression control of two DOFs at the wrist, where use of only 1-DOF training data did not significantly decrease overall R² (accuracies were not separated by DOF complexity in that study) [33]. Such differences may reflect the increased complexity of predicting hand movements in addition to wrist movements, which requires use of EMG signals from multiarticular muscles that cross both wrist and finger joints. Our offline analysis therefore suggests that use of non-linear methods may potentially improve performance, similar to previous studies [33]. Possible methods for introducing nonlinearities include use of nonlinear regression approaches [33], or probability-weighted linear regression [34]. Using such methods, which would likely require 2- and 3-DOF training data, is more burdensome than simply providing 1-DOF data. However, use of intramuscular EMG potentially makes such a system clinically feasible. Chronic implanted EMG recording devices would likely require less frequent retraining than surface EMG-based systems, such that more complex training regimens could be clinically acceptable. A hybrid approach between parallel dual-site control and linear regression control, where both linear mappings and empirically-tuned thresholds are used, may also provide an improved balance between ease of simultaneous control and the ability to isolate individual DOFs when desired.

Both the offline and online analyses highlight the importance of breaking down performance data for simultaneous control systems by the DOF-complexity of the movement being attempted. In this experiment, two control systems with similar overall performance had significantly different characteristics when generating isolated 1-DOF movements compared to simultaneously controlling multiple DOFs (Figures 5, 6). Because subjects tend to use both simultaneous and sequential control in tasks (simultaneous control more for gross movements and sequential control more for fine positioning [8, 31, 32]), it is important to evaluate performance of these two types of movement separately.

This study is limited by the use of subjects with intact limbs, and future work will extend investigations to persons with transradial amputations, using a prosthesis rather than a virtual task. Gains and thresholds used for parallel dual-site control were manually configured to minimize unintended movement but still allow subjects to simultaneously control DOFs, as has been done for previous implementations of parallel dual-site control [5, 9]. A sensitivity analysis on parallel dual-site parameters was not performed because of time constraints (each session required approximately 4-5 hours), and should be performed in a follow-up study. Future work should also evaluate the possible benefit of using nonlinear methods for simultaneously controlling the wrist and hand during a real-time task, and whether learning may allow subjects to improve their control by performing contractions for simultaneous DOFs that are more similar to linear combinations of single-DOF contractions.

V. Conclusion

Linear regression myoelectric control using intramuscular EMG provided an alternative to parallel dual-site control for 3-DOF simultaneous control at the wrist and hand. The two methods demonstrated different strengths in controllability, where linear regression control allowed for improved simultaneous control of multiple DOFs and parallel dual-site control allowed for improved single-DOF control. These results highlight the tradeoff between providing simultaneous control and the ability to isolate individual DOFs when desired. Differences in performance between the two methods likely resulted from differences in (1) whether significant thresholds on EMG activity were used and (2) whether activity from all available muscle signals were used as predictors for each DOF’s activity. The results of this study also demonstrate that training each linear regression model with exemplars of all available motion types is a more robust training method than using motion-specific data, as it significantly decreased the frequency at which the control system incorrectly predicted additional extraneous movements.

Biographies

Lauren H. Smith (S’13) received the BS and PhD degrees in biomedical engineering from Northwestern University, Evanston, IL, in 2008 and 2015. She is currently working toward the M.D. degree at Northwestern University, Chicago, IL. Her research interests include neural interfaces, bioelectric signal analysis, and clinical neurophysiology.

Todd A. Kuiken (M’99–SM’07) received his MD and Ph.D. in biomedical engineering from Northwestern University (1990) and completed his residency in Physical Medicine and Rehabilitation at the Rehabilitation Institute of Chicago (RIC, 1995). Dr. Kuiken is currently the Director of the Center for Bionic Medicine at the Rehabilitation Institute of Chicago. He is a Professor in the Departments of Physical Medicine and Rehabilitation, Biomedical Engineering and Surgery at Northwestern University.

Levi J. Hargrove (S’05-M’08) received his B.Sc. and M.Sc. and PhD degrees in electrical engineering from the University of New Brunswick (UNB), Fredericton, NB, Canada, in 2003 2005, and 2007 respectively. He joined the Center for Bionic Medicine at the Rehabilitation Institute of Chicago in 2008. His research interests include pattern recognition, biological signal processing, and myoelectric control of powered prostheses. Dr. Hargrove is a member of the Association of Professional Engineers and Geoscientists of New Brunswick. He is also an Assistant Professor in the Department of Physical Medicine and Rehabilitation (PM&R) and Biomedical Engineering, Northwestern University.