Abstract
This study developed a semi-mechanistic kidney model incorporating physiologically-relevant fluid reabsorption and transporter-mediated active reabsorption. The model was applied to data for the drug of abuse γ-hydroxybutyric acid (GHB), which exhibits monocarboxylate transporter (MCT1/SMCT1)-mediated renal reabsorption. The kidney model consists of various nephron segments – proximal tubules, Loop-of-Henle, distal tubules, and collecting ducts – where the segmental fluid flow rates, volumes, and sequential reabsorption were incorporated as functions of the glomerular filtration rate. The active renal reabsorption was modeled as vectorial transport across proximal tubule cells. In addition, the model included physiological blood, liver, and remainder compartments. The population pharmacokinetic modeling was performed using ADAPT5 for GHB blood concentration-time data and cumulative amount excreted unchanged into urine data (200–1000 mg/kg IV bolus doses) from rats (Felmlee et al (PMID: 20461486)). Simulations assessed the effects of inhibition (R=[I]/KI=0–100) of renal reabsorption on systemic exposure (AUC) and renal clearance of GHB. Visual predictive checks and other model diagnostic plots indicated that the model reasonably captured GHB concentrations. Simulations demonstrated that the inhibition of renal reabsorption significantly increased GHB renal clearance and decreased AUC. Model validation was performed using a separate dataset. Furthermore, our model successfully evaluated the pharmacokinetics of L-lactate using data obtained from Morse et al (PMID: 24854892). In conclusion, we developed a semi-mechanistic kidney model that can be used to evaluate transporter-mediated active renal reabsorption of drugs by the kidney.
Keywords: Semi-mechanistic kidney model, physiologically-relevant fluid reabsorption, transporter-mediated renal reabsorption, population pharmacokinetics, γ-hydroxybutyric acid (GHB), L-lactate, monocarboxylate transporters (MCTs)
Introduction
The kidneys play an essential role in maintaining physiological homeostasis by regulating the blood pressure and the acid-base balance, eliminating toxic endogenous and exogenous waste products, and conserving the essential nutrients such as electrolytes, amino acids, and glucose via active reabsorption. The interplay between the two important physiological processes, fluid filtration and reabsorption, facilitate these functions while continuously producing urine. The blood flow to the kidneys (QKI) is typically 25% of the cardiac output, the glomerular filtration rate (GFR) is about 10–15% of QKI, and urine flow is about 1–2% of GFR; therefore, the kidneys reabsorb about 98% of the glomerular filtrate and about 98–100% of essential solutes [1,2]. The nephron represents the functional unit of the kidneys and about 1 million nephrons are present in each adult human kidney. A nephron can be divided into several subsegments: namely, glomerulus, proximal tubules (PT), Loop-of-Henle (LOH), distal tubules (DT), and collecting ducts (CD). In humans, about 60–70% of glomerular filtrate is reabsorbed from the proximal tubules, about 15–20% from the descending thin Loop-of-Henle, and about 13–24% from the collecting ducts [1–3]. Proximal tubule epithelial cells (PTC) are further divided into three sub-segments, namely, S1, S2, and S3, owing to their unique cell morphology and differences in the density of PTC brush-border membrane (BBM) [3]. More than 400 transporters belonging to the ATP-binding cassette (ABC) and solute carrier (SLC) families are encoded by the human genome and numerous transporters belonging to these two super-families are expressed at the basolateral membrane (BLM) and the brush-border membrane, throughout the S1–S3 segments of the proximal tubule cells. These membrane transporters facilitate the reabsorptive and secretory functions of the nephrons [4–6].
Active reabsorption in the kidney is essential for the homeostasis of many endogenous compounds including glucose, amino acids, inorganic phosphate, inorganic sulfate, ascorbic acid, riboflavin, lactate, uric acid, and sodium, potassium and other electrolytes, to name a few. Few drugs are known to undergo transporter-mediated saturable renal reabsorption; but these include γ-hydroxybutyrate [7], oxypurinol [8], cefadroxil [9], perfluoroalkyl acids [10,11], and methotrexate [12], based on in vivo studies. In vitro substrates for the renal reabsorptive transporters include several drugs, namely, cephapirin and cephaloridine [13] pitavastatin (OATP1A2) [14], rosuvastatin (OATP1A2) [15], saquinavir (OATP1A2) [16], cephalexin (PEPT1) [17], amoxicillin (PEPT2) [18] and cefaclor (PEPT2) [18], among others; however their potential to undergo active renal reabsorption in vivo has not been validated. For substrates of renal reabsorptive transporters, it is important to consider the location, expression, and binding affinity of transporters in relation to the ongoing fluid reabsorption process, since these will determine concentrations of substrates available for the vectorial transport across the PTC. The volume of the filtrate present at the site of drug reabsorption along with the transporter kinetics will also play a vital role in elucidating the mechanistic basis for drug-drug and drug-transporter interactions. Moreover, these factors will determine therapeutic potential of inhibitors of the renal transporters.
Evidence for capacity-limited renal reabsorption was first reported for urea [19]. Theoretical, experimental, and mathematical aspects of renal clearance [20]. and effects of interplay of intrinsic and extrinsic factors [21], such as plasma protein binding [22], urine flow [23–25], urine pH [23], and osmotic diuresis [26], on the renal clearance of drugs have been extensively reported. Studies of nephron physiology have elucidated mechanisms of solute and water transport in proximal tubules [27–29], and described mathematical systems models of the urine concentrating mechanism in the rat renal medulla [30,31], and mathematical models of rat proximal tubule, loop of Henle and collecting ducts [32–34]. Although very extensive and insightful in terms of renal physiology, these models are not parsimonious and cannot readily be implemented using PK/PD model-fitting methods to evaluate transporter-mediated renal reabsorption and pharmacokinetics of drugs.
Over the past several decades, several pharmacokinetic models have been reported that incorporate capacity-limited renal tubular reabsorption of endogenous as well as exogenous compounds, including riboflavin [35], ascorbic acid [36], perfluoroalkylacids [10], and several sodium glucose transporter 1 and 2 inhibitors [37–39], to name a few. In our previous publication, we highlighted the scarcity and advantages of pharmacokinetic models incorporating more mechanistic kidney parameters available in the literature and potential pitfalls in data evaluation when mechanism-based models for active secretion and active reabsorption are not utilized when appropriate [40].
In light of this special issue in the honor of Dr. Gerhard Levy, we would like to acknowledge his extensive and significant contributions to the field of clinical pharmacokinetics, particularly in elucidating the mechanisms of renal elimination of numerous compounds including salicylates [41–44], ampicillin [45], riboflavin [35,46–48], theophylline [49], acetaminophen [50–52], pindolol [53], and inorganic sulfate [51,54,55], to name a few. Spanning over 50 publications, some of these significant contributions on renal drug elimination include evaluations of renal drug metabolism, renal drug-drug interactions, the role of protein binding in ADME of drugs, effects of pH, urine flow, and renal function on the pharmacokinetics of drugs, the renal elimination of drug metabolites such as various glucuronide conjugates, the pharmacokinetics of drugs in renal disease, and drug induced nephrotoxicity [35,41–67].
Given this extensive knowledge of mechanisms of renal clearance, the overall goal of the present study was to develop a semi-mechanistic kidney model incorporating the physiologically-relevant fluid reapportion and transporter-mediated active reabsorption. In development of our kidney model, we have used plasma and urine data for γ-hydroxybutyric acid (GHB), a naturally occurring short-chain fatty acid formed from γ-aminobutyric acid (GABA) [68]. Apart from the therapeutic use of GHB in the treatment of narcolepsy (Xyrem®, US) [69] and alcohol withdrawal (Europe) [70], GHB has been widely abused for recreation [71] and drug-induced sexual assault [72]. Nonlinear pharmacokinetics for GHB have been demonstrated in rats [73] and humans [74,75]. Saturable absorption [74,76], metabolism [74], and renal clearance [7] have been shown to contribute to the observed non-linearity in GHB pharmacokinetics. Renal clearance of GHB has been reported to contribute significantly to its total clearance at very high concentrations in overdose patients [77] and increase in a dose-dependent manner with increasing doses in rats [7]. Similar to GHB, L-lactate is also a substrate for renal proton-coupled monocarboxylate transporters MCT 1, 2, and 4 (SLC16A family) and sodium-dependent monocarboxylate transporter 1 (SMCT1, SLC5A8) [78,79]. We have also demonstrated the inhibition of active renal reabsorption of GHB by inhibitors of MCT1, L-lactate and AR-C155858, as potential treatment strategies in GHB overdose in rats [80–83] and in humans [84]. We previously published a semi-mechanistic pharmacokinetic model for GHB that included a kidney component with three compartments, namely a site for GHB reabsorption and two transit compartments to characterize the delayed appearance of GHB in urine [81,85]. A semi-mechanistic PK model for L-lactate was also developed in the previous modeling efforts [81].
A mathematical model incorporating mechanism-based drug disposition and a physiologically-relevant kidney component incorporating changes in flow and volume of renal filtrates as a result of fluid reabsorption and vectorial transport of drugs across the proximal tubule cells would provide enhanced utilitarian basis for evaluating drug-transporter interactions. The objectives of this study are to (1) develop a semi-mechanistic kidney model incorporating the physiologically-relevant fluid reapportion and transporter-mediated reabsorption (2) utilize this model to describe GHB pharmacokinetics in rats using a population analysis approach, incorporating MCT1/SMCT1-mediated reabsorption in the kidneys (3) perform clinically relevant simulations to evaluate the effects of inhibition of active reabsorption of GHB on its renal clearance (CLR) and systemic exposure (AUC), and (4) implement the developed model to evaluate the pharmacokinetics of L-lactate in rats.
Theoretical
Proposed semi-mechanistic PK model
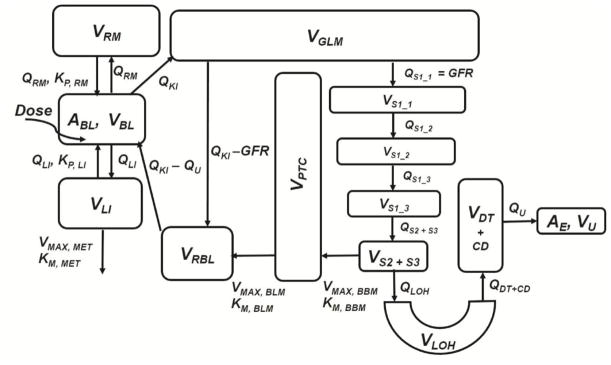
The proposed PK model, illustrated in Fig. 1, has three major components – (1) a semi-mechanistic kidney component incorporating physiologically-relevant fluid reabsorption and transporter-mediated active reabsorption and a GHB-specific components incorporating (2) non-linear renal transport kinetics (MCT1/SMCT1) and (3) systemic saturable metabolism and distribution of GHB.
Fig. 1.
Semi-mechanistic kidney model incorporating physiologically-relevant fluid reabsorption and MCT1/SMCT1-mediated renal reabsorption of GHB. Symbols are defined in Tables 1 and 2.
The semi-mechanistic kidney component was independently developed in an adaptive manner with a goal that it could be modified according to the transport kinetics of any compound. It consists of several compartments representing various lumen segments of the nephron containing the ultra-filtrate. These compartments do not represent physiological lumen space of nephron segments. The model also included blood, liver, and remainder (for mass and flow balance) compartments. A list of all fixed parameters including the values of physiological flows (Q) and volumes (V) are provided in Table 1.
Table 1.
List of fixed physiological flow and volume and in vitro/in vivo parameters utilized for the population PK model
| Parameter | Definition | Value |
|---|---|---|
| VBL (mL) | Volume of blood | 20.3 [97,98] |
| VPL (mL) | Volume of plasma | 12.5 [97,98] |
| VRM (mL) | Volume of remainder compartment | 264 [97,98] |
| VLI (mL) | Volume of liver | 12.4 [97,98] |
| QLI (mL/min) | Blood flow to liver | 11.6 [97,98] |
| QKI (mL/min) | Blood flow to kidneys | 10.5 [97,98] |
| QRM (mL/min) | Blood flow to remainder compartment | 27.1 [97,98] |
| KP, LI, KP, RM | Blood-to-tissue partition coefficients for liver and remainder compartments (unpublished in vivo data) | 0.4 |
| VGLM (mL) | Volume of glomerulus | 0.08 [99] |
| VPTC (mL) | Volume of proximal tubule epithelial cells | 1.03 [99] |
| VRBL (mL) | Volume of renal blood | 0.375 [99] |
| VRPL (mL) | Volume of renal plasma | 0.206 [99] |
| GFR (mL/min) | Glomerular filtration rate | 2.2 [100] |
| VS1_1 (mL), QS1_1 (mL/min) | Volume and flow of filtrate in lumen of 1stsub-segment of S1 segment of proximal tubule | GFR |
| VS1_2 (mL), QS1_2 (mL/min) | Volume and flow of filtrate in lumen of 2nd sub-segment of S1 segment of proximal tubule | 0.85 × GFR [1–3] |
| VS1_3 (mL), QS1_3 (mL/min) | Volume and flow of filtrate in lumen of 3rd sub-segment of S1 segment of proximal tubule | 0.70 × GFR [1–3] |
| VS2+S3 (mL), QS2+S3 (mL/min) | Volume and flow of filtrate in lumen of S2 and S3 segments of proximal tubule | 0.55 × GFR [1–3] |
| VLOH (mL), QLOH (mL/min) | Volume and flow of filtrate in lumen of Loop of Henle | 0.33 × GFR [1–3] |
| VDT+CD (mL), QDT+CD (mL/min) | Volume and flow of filtrate in lumen of distal tubules and collecting ducts | 0.18 × GFR [1–3] |
| VU (mL), QU (mL/min) | Volume and flow of urine | 0.02 × GFR [1–3] |
| In vitro Parameters for GHB | ||
| KM, MET (μg/mL) | Metabolic Michaelis-Menten affinity constant | 63 [7,101] |
| KM, BBM ((μg/mL) | Renal reabsorption Michaelis-Menten affinity constant at BBM | 480 [86] |
| KM, BLM ((μg/mL) | Renal reabsorption Michaelis-Menten affinity constant at BLM | 1092 [86] |
| In vitro/in vivo Parameters for L-lactate | ||
| KM, MET (μg/mL) | Metabolic Michaelis-Menten affinity constant (in vitro study) | 218 [92] |
| KLAC (μg/min) | Endogenous lactate production rate (in vivo study) | 4.97 [81] |
Physiological flow and volume parameters were obtained and optimized for an average rat of 300 g.
Blood compartment
The blood compartment (Eq. 1) is the depot for GHB input. From the blood (BL), GHB is distributed to the liver (LI), the kidneys (KI), and to the remainder of the body (RM). The model accounted for mass and flow balance. The initial condition (IC) for the blood compartment is the dose of GHB and is zero for all other compartments in the model.
| (1) |
Liver and remainder compartments
Since GHB is predominantly in the ionized form at physiological pH, its distribution into tissues requires MCT-mediated transport. GHB tissue distribution is dose-dependent and organ-specific (unpublished data). In the context of the present model, we have made two key assumptions: (1) since MCT1 is ubiquitously expressed, GHB distribution into the liver and the remainder compartments can be described by the respective blood-to-tissue partition coefficients (KP); the values of KP,LI and KP,RM were fixed to the observed KP values obtained from the tissue distribution study (Table 1), and (2) the liver is the major site for the saturable metabolism of GHB. Saturable tissue distribution of GHB was not observed for the doses of GHB studied (unpublished data). Eq. 2 and 3 describe the distribution of GHB into the liver and the remainder compartments, respectively, with IC=0. The saturable metabolism of GHB was incorporated as a single Michaelis-Menten equation:
| (2) |
| (3) |
Compartments incorporating physiologically-relevant fluid reabsorption and transporter-mediated renal reabsorption
The blood flow to the kidneys (QKI) carries GHB to the glomerulus (GLM), where a fraction of QKI becomes the GFR and the remaining fraction drains into the peritubular capillaries as:
| (4) |
The central principle for enacting this kidney component is – since fluid filtration and reabsorption across the nephrons are continuous processes, decreases in the volumes and flows of the filtrate across the nephron segments would be constant, proportional in degree, and equal in magnitude, both, spatially and temporally. In other words, the numerical values of the flows and the volumes of the filtrate at given nephron segments would be the same and can be described as fractions of GFR. The following assumptions were made in order to incorporate the fluid reabsorption process into the model. (1) Fractions of fluid reabsorption and urine pH across the nephrons are identical in all animals. (2) Fractions of fluid reabsorption at various segments are identical between rats and humans. (3) These fractions of fluid reabsorption are held constant and effects of concurrent solute reabsorption; changes in tonicity and osmolality of filtrate, effects of pH changes due to acid-base balance, and effects of changes in hydration status of animals are not considered in the present model. (4) The numerical value of flow exiting one segment is the numerical value of the volume of the next segment. The model assumes that about 67% of the total filtrate is reabsorbed from the proximal tubule [1–3]. The proximal tubule lumen segment was sub-divided into four lumen segments, which yielded three S1 segments (S1_1, S1_2, and S1_3) and a S2+S3 segment. This is physiologically relevant as the S1 segment contains a dense layer of BBM with many aquapores, which is more complex than S2 and S3 segments that have less dense BBM and similar cell morphology [3]. Moreover, about 2/3 of total fluid reabsorption from proximal tubules occurs from the S1 segment [3]; therefore, subdividing the S1 segment allows for incorporating the gradual process of fluid reabsorption across the PT. This also accounts for changes in drug concentration as a result of decrease in filtrate volume and concentration of drug available for transport in subsequent segments. The fraction of fluid reabsorption from each of the three subsegments of S1 is considered to be equal in magnitude. Fig. 1 and Table 1 detail the fractional decrease in flows and volumes of the filtrate, relative to GFR, with sequential fluid reabsorption. The fluid reabsorption from the three S1 segments is described as:
| (5) |
| (6) |
| (7) |
The remaining 1/3 of the total fluid reabsorption from proximal tubules occurs from the S2 and S3 segments (S2+S3) as described in Eq. 8, where LOH is the Loop of Henle.
| (8) |
Uptake of GHB has been reported to be pH- and sodium-dependent in BBM vesicles and pH-dependent in BLM vesicles in rats [86], suggesting the significance of SMCT1-mediated transport of GHB in BBM and MCT1- and MCT2-mediated transport at the BLM [86]. MCT1 is the most important transporter for the uptake of GHB in rat kidney BLM membrane vesicles [86] and in Human Kidney HK-2 cells [79]. MCT1/SMCT1-mediated reabsorption of GHB at the BBM was incorporated only from the S2 and S3 segments in our model, which is consistent with the observed predominant expression of SMCT1 at the S2 and S3 segments [87] and with the expression of MCT1 at the BBM [86].
The vectorial transport of GHB across the PTC is described in Eq. 9, where GHB is taken up into the PTC from the BBM and is transported to the renal blood (RBL) in the peritubular capillaries by MCT1 predominantly expressed at the BLM [86].
| (9) |
Renal blood in peritubular capillaries receives GHB that is (1) carried within the fraction of QKI (QKI-GFR) exiting the glomerulus and (2) entering the PTC across the BLM as described in Eq. 10. The renal blood then returns to the systemic circulation along with the reabsorbed GHB. The term QKI-QU accounts for the flow balance in the system: about 98% of fluid is reabsorbed every minute, where urine flow (QU) is ~1–2% of GFR [1–3].
| (10) |
After 67% of fluid reabsorption from the PT, about 33% of the total filtrate enters the Loop-of-Henle (LOH) (Table 1 and Fig. 1) as described in Eq. 11. Fluid reabsorption of about 15% results from this nephron segment [1–3].
| (11) |
The model assumes about 18% of the total filtrate enters the lumen of the distal nephrons consisting mainly of the distal tubules (DT) and the collecting ducts (CD) [1–3]. The lumens of distal tubules and the collecting ducts were combined into one compartment. Antidiuretic hormone (ADH)-mediated fluid reabsorption from late distal tubules and early collecting ducts was not considered in this model, and it was assumed that the hydration status of all animals was normal for the duration of this study [1,2,88]. Fluid reabsorption of about 16% was assumed to occur from this compartment (Eq. 12), which resulted in 2% of the filtrate as the urine flow (QU) and urine volume (VU) per minute as described in Eq. 13 [1–3]. Cumulative amount of GHB excreted unchanged into the urine (AE) is given by summation form:
| (12) |
| (13) |
| (14) |
The model outputs for the two PK endpoints of GHB are:
| (15) |
| (16) |
Methods
Pharmacokinetic data for GHB
Data for GHB plasma concentrations and cumulative amount of GHB excreted unchanged into the urine (AE) were obtained from Felmlee et al. [85]. Briefly, male Sprague-Dawley rats (Harlan, Indianapolis, Indiana) (280–320 g) were used for the study. GHB IV doses of 200, 400, 600, and 1000 mg/kg were administered to groups of 4–7 animals. GHB concentrations in plasma and urine were measured using a validated LC/MS/MS method [85]. Our laboratory has previously shown that MCT1 expressed on RBCs mediate linear partitioning of GHB from blood to plasma [89]. Since blood concentrations of GHB are more relevant in a clinical setting, blood concentrations were calculated from plasma concentrations using the GHB B/P partition ratio of 0.75 [89]. Blood concentration and cumulative amount excreted unchanged into the urine (AE) data were used in our model development and validation.
Population PK model development and validation
Population analysis was carried out for the following two reasons: (1) the mode of sampling was sparse, and (2) there was high inter-individual variability (IIV) in the urine data. Population analysis was performed using the maximum likelihood expectation minimization (MLEM) algorithm [90] in the ADAPT5 software (BMSR, Los Angeles, CA). No covariates were included in this model, since the only measured covariate, body weight (BW), had a narrow range and was statistically not significant.
GHB data for 200, 600, and 1000 mg/kg doses were used for the model development. Three parameters – maximal capacity of metabolism (VMAX, MET), maximal capacity of renal reabsorption at the PTC BBM (VMAX, BBM), and maximal capacity of renal reabsorption at the PTC BLM (VMAX, BLM) – and respective IIV were estimated. The three respective Michaelis-Menten affinity constant (KM) parameters were fixed to the observed in vitro values from our previous studies as listed in Table 1.
The VMAX parameter of a given metabolic or transport process is a function of protein expression of respective enzymes and transporters involved. The three VMAX parameters and IIV were estimated for the following reasons: (1) GHB is metabolized by several enzymes, namely, aldo-keto reductases 1A1 and 7A2, succinic semialdehyde reductase, and hydroxyacid-oxoacid transhydrogenase [91]; however, the protein, expression and relative contribution of these enzymes to the metabolism of GHB is not well-understood, (2) protein expression values of renal MCTs/SMCTs have not been characterized in rats or humans.
The residual variability was best described by a proportional error model (Eq. 17) for both PK endpoints:
| (17) |
Goodness-of-parameter estimation was evaluated using relative standard error (%RSE). The goodness-of-fit was evaluated using the visual predictive check (VPC) plots and other model diagnostic plots. VPC plots were generated by simulating 1000 subjects using the developed population model and SIM algorithm in ADAPT5 (BMSR, Los Angeles, CA). Medians, 90th, and 10th percentiles of the predicted values were calculated using MS Excel 2013 (Microsoft, Redmond, Washington). Other model diagnostic plots included: (a) observed vs. individual predicted data, (b) observed vs. population predicted data, which illustrated the predictive power of the model, (c) standard residuals vs. individual predicted data, and (d) standard residuals vs. population predicted data, which illustrated the appropriateness of the residual error model. Model validation was performed using the data for a dose of 400 mg/kg, which was an independent data set that was not used for model development. The 400 mg/kg dose is within the dose range that we have evaluated and therefore, is a reasonable validation set to evaluate the performance of this model. GHB does not demonstrate linear kinetics where, across a dose range, successful validation is almost always expected. Due to the complex dose-dependent kinetics of GHB, concentration predictions for different doses is not straight-forward, making independent data sets at other doses suitable as validation sets. Goodness-of-parameter estimation and goodness-of-fit was also evaluated for the validation set as described above.
Simulations
Clinically relevant simulations were performed using the SIM algorithm in ADAPT5 (BMSR, Los Angeles, CA) to evaluate the effects of the inhibition of active renal reabsorption of GHB on its systemic exposure (AUC) and renal clearance (CLR). Simulations were carried out for 200, 600, and 1000 mg/kg doses of GHB for up to six hours. Three mechanisms of inhibition – competitive (Eq. 18), uncompetitive (Eq. 19), and non-competitive (Eq. 20) – were evaluated, where R is the ratio of concentration of inhibitor administered at steady-state ([I]) and the inhibition constant (Ki).
| (18) |
| (19) |
| (20) |
Four sets of simulations were performed for each GHB dose and for each inhibition mechanism, where R = 0 (no inhibition), 1, 10, and 100. The AUC was calculated using the log-trapezoidal method and CLR was calculated using the ratio of AE, ∞ over AUC. 3D-surface plots were generated using SigmaPlot 11.0 (Systat Software, San Jose, CA) to elucidate the relationships among AUC or CLR, GHB doses, and R (0–100).
Evaluation of L-lactate pharmacokinetics
We evaluated active renal reabsorption of L-lactate using the developed model. Data for lactate plasma concentrations and cumulative amount of lactate excreted unchanged into the urine (AE) were obtained from Morse et al., [81]. Briefly, male Sprague-Dawley rats (Harlan, Indianapolis, Indiana) (270–330 g) were used for the study. Sodium L-lactate doses of 66 mg/kg+302.5 mg/kg/hr, 66 mg/kg+605 mg/kg/hr, and 198 mg/kg+1210 mg/kg/hr were administered to groups of 3–5 animals, and plasma and urine analyzed for L-lactate. The model was implemented with several modifications as described below. Plasma concentrations (not blood concentrations) of L-lactate were used in the modeling because experimental blood-to-plasma partitioning of L-lactate was not available. The model assumes that liver is the predominant site of L-lactate metabolism. Any extra-hepatic metabolism of L-lactate is not considered in this model under the assumption that extra-hepatic metabolism of L-lactate dose not contribute significantly to its observed PK over the dose range evaluated.
Plasma compartment
The plasma compartment is the depot for L-lactate input, where KLAC represents the endogenous lactate production rate as described by:
| (21) |
Active renal reabsorption of L-lactate
We previously demonstrated that SMCT1 plays a key role in the renal reabsorption of L-lactate and therefore, this process is considered to be rate-limiting [81]. SMCT1-mediated renal reabsorption of L-lactate was incorporated as a single Michaelis-Menten process occurring at the PTC BBM, where L-lactate is transported from PTC BBM of S2+S3 compartment into the renal plasma (RPL):
| (22) |
| (23) |
Transport across the PTCs and at the PTC BLM were not considered since BBB transport was assumed to represent the rate-limiting step. Since L-lactate is also a substrate for MCTs, distribution kinetics of L-lactate (pKa 3.86) was assumed to be the same as those of GHB. All other model components including the physiologically-relevant fractions of fluid reabsorption process were unchanged.
Pharmacokinetic analysis was performed using the maximum likelihood (ML) algorithm [90] under the individual parameter estimation program (ID) in ADAPT5 software (BMSR, Los Angeles, CA). Three parameters, maximal velocity for metabolism (VMAX, MET), maximal velocity for renal reabsorption at the PTC BBM (VMAX, BBM), and Michaelis-Menten affinity constant for renal reabsorption at the PTC BBM (KM, BBM) – were estimated. The respective Michaelis-Menten affinity constant of L-lactate metabolism (KM, MET) was fixed to the observed in vitro value of 218 μg/mL in human hepatocytes [92] (Table 1). The residual variability was best described by an additive error model for CPL and an additive plus a proportional error model for AE:
| (24) |
| (25) |
Results
PK model
The proposed model (Fig. 1) consisted of physiological blood, liver, remainder, glomerulus, proximal tubule cells, and renal tubular compartments. The sequential fluid reabsorption was incorporated using seven nephron segments, where flows and volumes of the filtrate in various segments were functions of GFR. It is important to note that the seven nephron segments do not represent physiological lumen space, as discussed previously. For GHB, single transporter kinetics was utilized at both the BBM and BLM. The vectorial reabsorption of GHB was best characterized by fixing the KM, BBM to 480 μg/mL and KM, BLM to 1092 μg/mL, which were in vitro observed KM values of GHB uptake in rat MCT1-MDA-MB231 cells (pH=6.0) and isolated rat kidney basolateral membrane vesicles (pH=5.5), respectively [86]. This suggested that MCT1 plays a role in GHB uptake at the BBM, but does not exclude the contribution of SMCT1.
Population GHB PK model performance
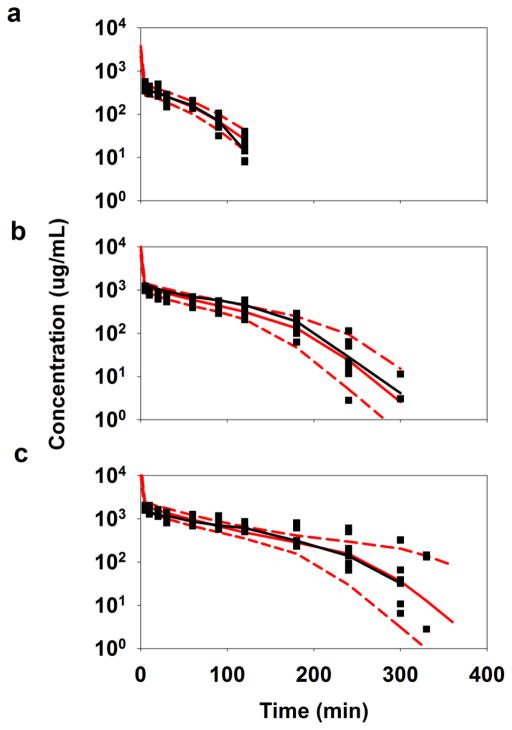
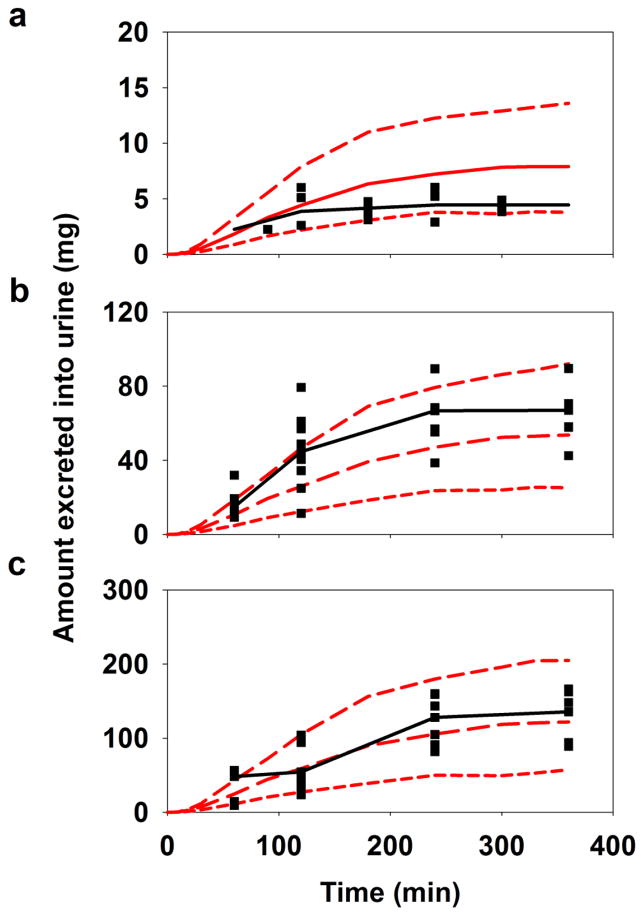
The VPC plots of GHB blood concentrations vs. time profiles are shown in Fig. 2. For all three doses, medians of the observed data were in very good agreement with the medians of the predicted data. On average, 10% of the observed data was outside the 90th and the 10th percentiles of the predicted values for CBL and AE profiles indicating the model performed well. The VPC plots of GHB AE vs. time profiles in Fig. 3 indicated the model somewhat over predicted and under predicted the data for GHB doses of 200 mg/kg (Fig. 3a) and 600 mg/kg (Fig. 3b), respectively. This can be attributed to the observed high variability in the data. However, medians of the observed and the predicted data were in fair agreement for the highest GHB dose of 1000 mg/kg as illustrated in Fig. 3c. Thus, VPC plots for both PK endpoints indicated the model adequately described GHB PK.
Fig. 2.
Population PK model predicted blood concentrations of GHB – VPC plots of (a) 200 mg/kg, (b) 600 mg/kg, and (c) 1000 mg/kg doses. The solid black squares and the line are the observed data and the median of the observed data, respectively. The solid red line is the median of the 1000 simulated subjects, and the top and the bottom dashed lines in red are 90th and 10th-percentiles, respectively, of 1000 simulated subjects.
Fig. 3.
Population PK model predicted cumulative amount of GHB excreted unchanged into the urine – VPC plots of (a) 200 mg/kg, (b) 600 mg/kg, and (c) 1000 mg/kg doses. Symbols and lines are as described in Fig. 2.
All three population parameter means and population %IIV were estimated with reasonable %RSE (<50%) as listed in Table 2. The VMAX, BLM had the highest %IIV of 31% and VMAX, BBM had an indeterminate %IIV of 18%, which was consistent with high IIV observed in the AE data. The estimated residual variability was higher for AE than for CBL (Table 2). The reason for this can be attributed to variability due to heterogeneous bladder emptying patterns of animals, collection of large volumes of urine over time and the potential for incomplete urine collections.
Table 2.
Estimated population PK parameters and inter-individual variability (IIV) for GHB; %RSE is relative standard error.
| Parameter | Definition | Estimate | %RSE | %IIV | %RSE |
|---|---|---|---|---|---|
| VMAX,MET (μg/min) | Maximal metabolic capacity | 670 | 4 | 11 | 40 |
| VMAX,BBM (μg/min) | Maximal renal reabsorption capacity at BBM | 1950 | 13 | 31 | 36 |
| VMAX,BLM (μg/min) | Maximal renal reabsorption capacity at BLM | 1101 | 10 | 18 | 41 |
| σ, Slope (CBL) | Slope of the residual variability of blood concentrations | 0.20 | 5 | ||
| σ, Slope (AE) | Slope of the residual variability of cumulative amount excreted into urine | 0.36 | 19 |
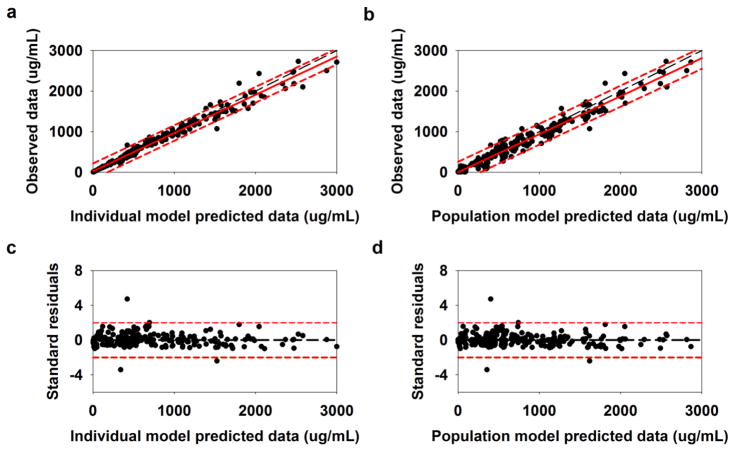
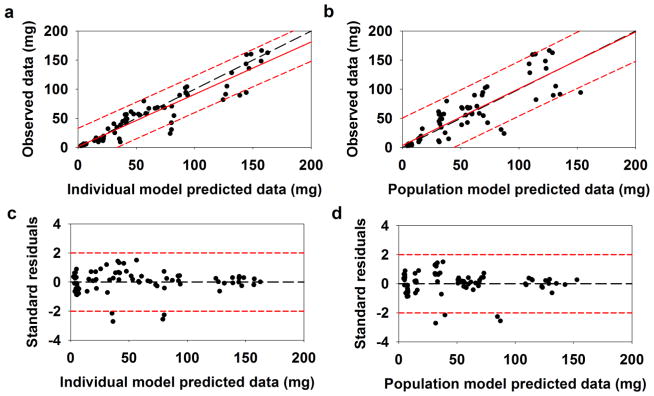
Model diagnostic plots for GHB CBL and AE are shown in Fig. 4 and Fig. 5. A very strong agreement was found between the observed vs. individual predicted data (Fig. 4a; R2 = 0.98) and the observed vs. population predicted data (Fig. 4b; R2 = 0.96), respectively, for GHB CBL. Moreover, the regression lines were in good agreement with the unity lines and the majority of the data points fell within the 95% prediction interval of the regression lines in both figures. The standard residuals vs. individual predicted data (Fig. 4c) and the standard residuals vs. population predicted data (Fig. 4d) were evenly distributed about the unity line and majority of the points fell within the 95% confidence interval of the standard residuals. There was fair agreement between the observed vs. individual predicted data (Fig. 5a; R2 = 0.89) and the observed vs. population predicted data (Fig. 5b; R2 = 0.78) for GHB AE. Moreover, Figs. 5c and 5d indicated that the majority of the data points were evenly distributed about the line of unity and were within the 95% confidence interval of the standard residuals. Thus, these figures demonstrate that the population PK model had strong quantitative power and that the residual error model was acceptable.
Fig. 4.
Model diagnostic plots for GHB blood concentrations: (a) observed vs. individual predicted data, (b) observed vs. population predicted data, (c) standard residuals vs. individual predicted data, and (d) standard residuals vs. population predicted data. In parts, a and b, the long-dashed line in black is the unity line, the solid line in red is the regression line, and the short-dashed lines in red are the 95% prediction intervals of the regression line. In parts c and d, the long-dashed line in black is the unity line and short-dashed lines in red are the 95% confidence intervals of the standard residuals
Fig. 5.
Model diagnostic plots for GHB AE: (a) observed vs. individual predicted data, (b) observed vs. population predicted data, (c) standard residuals vs. individual predicted data, and (d) standard residuals vs. population predicted data. Symbols and lines are as defined in Fig. 4.
The model was also validated using data for a GHB dose of 400 mg/kg as illustrated in Fig. 6. Medians of observed and predicted values for CBL and AE were in a very good agreement as shown in Fig. 6a and 6b. In other words, the model captured the centroid of the data very well. Taken together, VPC plots, the model diagnostic plots, and the validation results indicated that the population PK model was successfully developed and has a strong qualitative ability.
Fig. 6.
The VPC plots for our validation dataset for a 400 mg/kg dose of GHB, for (a) blood concentrations and (b) cumulative amount excreted unchanged into the urine. Symbols and lines are as defined in Fig. 2.
Clinically relevant simulations
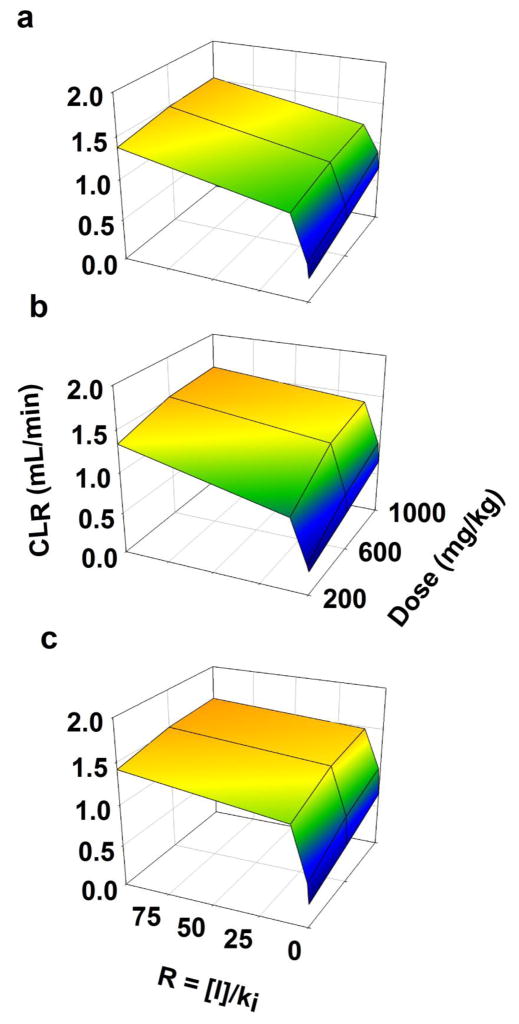
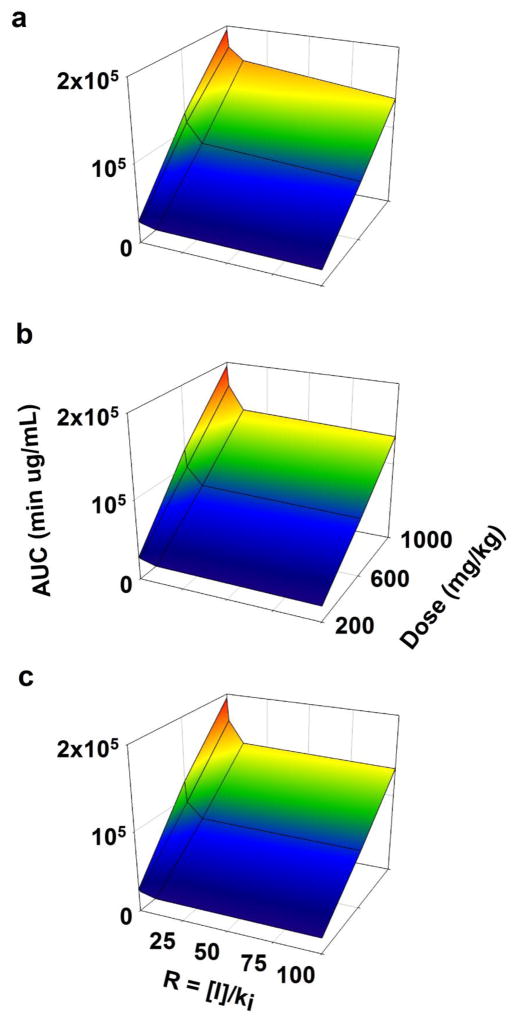
Simulations were performed to evaluate the effects of inhibition of active renal reabsorption of GHB from BBM and BLM on its CLR and AUC. With inhibition of renal reabsorption, CLR increased with increasing values of R (with no inhibition, R = 0) (Fig. 7). Although AUC increased with increasing dose (with no inhibition, R = 0), it statistically significantly decreased with increasing R (Fig. 8). The observed decrease in AUC was a result of an increase in with increasing R, regardless of the dose. Since R increases, CLR, values approach the GFR, effects observed at a lower dose (200 mg/kg) appear more substantial than at a higher dose (1000 mg/kg).
Fig. 7.
3D-surface plots illustrating changes in renal clearance (CLR) of GHB with (a) competitive, (b) uncompetitive, and (c) non-competitive inhibition of its active renal reabsorption.
Fig. 8.
3D-surface plots illustrating changes in AUC (systemic exposure) of GHB with (a) competitive, (b) uncompetitive, and (c) non-competitive inhibition of its active renal reabsorption.
Figures 7a, 7b, and 7c demonstrate the effects of competitive, uncompetitive, and non-competitive inhibition of renal reabsorption on CLR. The order of the observed increase in CLR with increasing R (in descending order) was non-competitive > uncompetitive > competitive (statistically significantly different using one-way ANOVA with Tukey’s test; not shown). Similarly, Figures 8a, 8b, and 8c showed the effects of competitive, uncompetitive, and non-competitive inhibition of renal reabsorption on AUC. The order of the observed decrease in CLR with increasing R (in descending order) was also non-competitive > uncompetitive > competitive (statistically significantly different using one-way ANOVA with Tukey’s test; not shown).
L-lactate pharmacokinetics
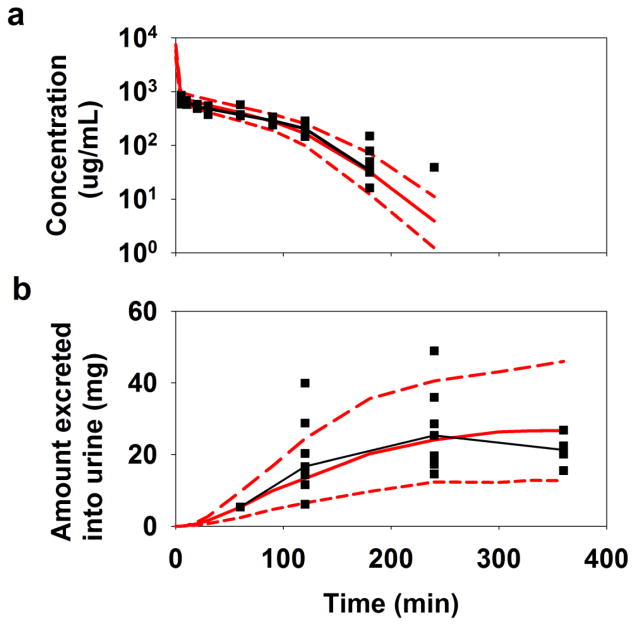
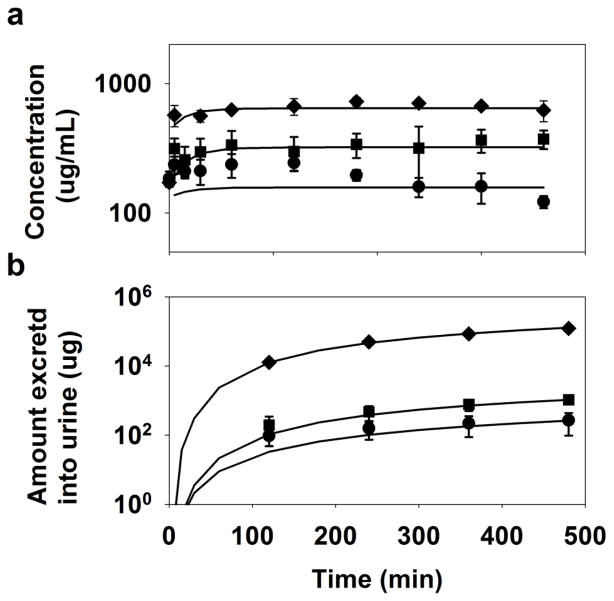
The model adequately described L-lactate concentrations in plasma and cumulative amount excreted unchanged into the urine as illustrated in Fig. 9. Although the plasma concentrations for the lowest dose of L-lactate were misfitted, the predicted CPL of the remaining two doses and AE of all three doses were in very good agreement with the observed data. All three parameters were estimated with low %CV as described in Table 3. The estimated value of KM, BBM of 2 μg/mL (22 μM) was significantly lower than the reported in vitro KM values of L-lactate transport by human SMCT1, ranging from 150–235 μM [93].
Fig. 9.
L-lactate pharmacokinetics: (a) plasma concentrations and (b) cumulative amount excreted into urine. Symbols, (●), (■), and (◆), respectively, represent means of the observed data for 66 mg/kg+302.5 mg/kg/hr, 66 mg/kg+605 mg/kg/hr, and 198 mg/kg+1210 mg/kg/hr doses of sodium L-lactate and the error bars are standard deviations (n = 3–5). The black lines are model-fitted values.
Table 3.
Estimated PK parameters and %CV for L-lactate; %CV is coefficient of variation.
| Parameter | Definition | Estimate | %CV |
|---|---|---|---|
| VMAX,MET (mg/min) | Maximal metabolic capacity | 13.8 | 15 |
| VMAX,BBM (μg/min) | Maximal renal reabsorption capacity at BBM | 963 | 7.2 |
| KM, BBM (μg/mL) | Renal reabsorption Michaelis-Menten affinity constant at BBM | 2.0 | 12 |
| σ, Intercept (CPL) | Intercept of the residual variability of plasma concentrations | 0.1 | 30 |
| σ, Slope (AE) | Slope of the residual variability of cumulative amount excreted into urine | 95 | 16 |
| σ, Intercept (AE) | Intercept of the residual variability of cumulative amount excreted into urine | 43 | 31 |
Discussion
A semi-mechanistic kidney model incorporating aspects of physiologically-relevant fluid reabsorption that allowed fitting of GHB and L-lactate PK data in rats. Generally, about 85% of the total glomerular filtrate is reabsorbed regardless of the body’s hydration status or the water balance. The remaining facultative fluid reabsorption occurs from the late distal tubules and early collecting ducts, which is regulated by ADH and is a function of the body’s hydration status [1,2,88]. With the assumptions that rats and humans have similar nephron segment-specific fluid reabsorption fractions and all rats had normal hydration status (not requiring ADH-mediated fluid reabsorption from the DT+CD compartment), the proposed model accounts for 67%, 15%, and 16% fluid reabsorption from the lumen of PT, LOH, and DT+CD, respectively, and QU is 2% of the total filtrate [1–3]. Moreover, about 2/3 of the total fluid reabsorption from the PT occurs from the S1 segment [3], where the three sub-segments account for 1/3 of the total reabsorption each from the S1 segment. The volumes of GLM, PTC, and RBL compartments were fixed to their physiological values as listed in Table 1 and the volumes of the nephron segments reflected the volumes of the filtrate in the respective segments. The model also assumed the numerical value of flow exiting one segment equals the numerical value of the volume of the next segment, reflecting the volume of the filtrate just prior to its respective fractional reabsorption in that segment. The fractional fluid reabsorption from each segment is characterized by a decrease in the flow exiting that segment.
It is important to note that the kidney component of the proposed model is enacted to account for changes in drug concentrations resulting from fluid reabsorption along nephron segments and vectorial transport of drugs across PTC. Values of fraction of fluid reabsorption used in the present study represent accepted and established values describing the general extent of fluid reabsorption in kidneys [1–3]. Under physiological conditions, the renal fluid reabsorption process represents a dynamic process, which is dependent on a complex set of conditions including, but not limited to, variable flow, pH, hydration status, osmolality, concurrent solute reabsorption, and effects of hormones on urine concentrating processes, that have been extensively reported in the literature [27–34,88]. We made several assumptions for parsimony and practical implementation of the proposed model. The current model illustrates a snapshot of very specific conditions of fluid reabsorption, governed by fixed values of fractions of fluid reabsorption as functions of GFR and is constructed with the sole purpose of evaluating drug-transporter interactions in a more mechanistic and potentially translational manner. However, the model does offer the flexibility in terms of allowing modifications to accommodate unique drug-transporter kinetics. While the model is not intended to represent the full complexity of renal physiology, it provides a semi-mechanistic and utilitarian basis for evaluating the active renal reabsorption of compounds.
We further applied this model using GHB, which undergoes MCT1/SMCT1-mediated active renal reabsorption. Compared with our previous publications [81,85], the present study has enabled us to further enhance the translational modeling framework of GHB PK by incorporating physiologically-relevant fluid reabsorption and its vectorial transport across the PTC. Moreover, the GHB-specific model component includes physiological tissue volumes and tissue blood flow values as well as the blood to tissue partitioning of GHB. The KM, BBM value of 460 μg/mL is similar to the GHB KM of 215 μg/mL in immortalized human kidney (HK-2) cells (pH=6.0 and lacking SMCT1) [79] and KM of 168 μg/mL in hSMCT1-transfected oocytes (pH=7.4) [93]. The KM value of GHB uptake in MDA-MB231 cells expressing MCT2 and MCT4 (pH=7.5) was 1830 μg/mL [94], and values were 288 μg/mL (pH=6.5) and 1768 μg/mL (pH=7.4) in rat erythrocytes where MCT1 as the sole MCT isoform [89]. These similarities of KM values of MCT isoforms across species further enhances the translational potential of the model.
The population model adequately captured GHB CBL and AE data. Population parameter means and %IIV were found with reasonable certainty. The model reflected the central tendency of CBL very well for all doses; however, moderate misfitting was evident for AE of 200 and 600 mg/kg doses, which can be attributed to the observed high IIV in the urine data. The model was able to adequately assess the AE,∞ of 600 and 1000 mg/kg doses. The model diagnostic plots for CBL and AE indicated very strong agreement between observed and individual model predicted and observed and population model predicted data. Moreover, the residual variability was reasonably explained with a proportional error model for both blood concentrations and cumulative amount eliminated in the urine and the model had a constant residual variance about the line of unity. Our population model was successfully validated as the predicated GHB PK was in very close agreement with the observed data for the 400 mg/kg dose.
The effects of competitive, uncompetitive and non-competitive inhibition of renal reabsorption on CLR and systemic AUC of GHB were examined. With increasing inhibition described by R= [I]/Ki, CLR increased and AUC decreased for the doses evaluated. It is important to note that non-competitive (alters VMAX) inhibition had the most pronounced effects on changes in CLR and AUC compared with competitive (alters KM) and uncompetitive (alters VMAX and KM) inhibition. This is consistent with our previous findings that the greatest changes in CLR and systemic AUC were observed with perturbations in VMAX of a given secretory or reabsorptive transporter, compared with perturbations in KM [40]. This indicates the importance of not only the dose and potency of the inhibitor, but also their mechanism of inhibition when screening for their therapeutic potential.
Our previous model consisted of a semi-mechanistic kidney component including a site for GHB reabsorption and two transit compartments. Moreover, two peripheral compartments with distributional clearances were incorporated to account for the nonlinear metabolism and distribution of GHB [81,85]. In a separate study, local sensitivity analysis of this model indicated that the model predictions were more sensitive to perturbations in the active reabsorption kinetics and metabolism kinetics than the distributional parameters (peripheral volumes and distributional clearances). [95] The greatest effects on GHB plasma concentrations and AE were observed with altering the VMAX of renal reabsorption parameter compared with any other parameters. As described above, perturbations in VMAX resulted in more pronounced effects than those in KM [40]. In the present study, the three VMAX parameters were estimated with reasonable certainty and all other parameters were fixed to either the physiological flow/volume values or observed in vitro or in vivo values, given in Table 1.
Pharmacokinetics of L-lactate were further evaluated using the developed model with several modifications specific to L-lactate. Although, L-lactate is a substrate for MCT1, 2 and 4 [78,94,96], SMCT1 plays the most significant role in the active renal reabsorption of L-lactate with in vitro KM values ranging 159–235 μM [81,93]. On the other hand, reported KM values of L-lactate uptake into MCT1-expressing tumor cells, MCT1-oocytes, MCT2-oocytes, and MCT4-oocytes are much higher, 4.5, 3.5, 0.74, and 28 mM, respectively [96]. The KM, BBM value for L-lactate (22 μM) was estimated and although it is was lower than the reported in vitro KM value, the parameter was estimated with reasonable certainty. Model fittings and parameter estimates indicated the model was able to reasonably characterize PK of L-Lactate. Therefore, this model can be used to evaluate PK of other drugs undergoing active renal reabsorption.
We previously demonstrated that MCT inhibition with L-lactate combined with osmotic diuresis presents an effective treatment strategy in human subjects since this increases renal clearance of GHB [84]. Our future modeling efforts will focus on translating this kidney model to humans in order to evaluate potential treatment strategies in GHB overdose. The following information will need be incorporated to achieve the translational potential of the proposed model: (1) since GHB is abused orally, a mechanistic PK model of GHB with non-linear absorption and first-pass elimination components will be needed [83,85], (2) scale-up of physiologically-relevant flow and volume parameters from rats to humans, and (3) estimation of all relevant VMAX parameters, while fixing the respective KM values to the observed in vitro data.
The three major advantages of this model are: (1) a semi-mechanistic kidney component can be independently used for any renal drug-drug and drug-transporter interactions, (2) nephron segments can be sub-divided into more segments or can be combined into fewer segments, as long as the fluid reabsorption is maintained, and (3) since the model incorporates the vectorial transport of a drug across the PTC, it can be potentially used to elucidate the effects of active secretion of compounds as well. In the context of GHB, the model offers a robust modeling framework to further evaluate GHB tissue distribution, GHB toxicodynamics, and treatment strategies in overdose.
In conclusion, a useful kidney model incorporating concurrent physiologically-relevant fluid reabsorption and membrane transport has been developed that provides a useful physiologically-based and semi-mechanistic modeling framework to evaluate the transporter-mediated active/facilitated reabsorption, as well as renal drug-transporter interactions. This model may be relevant for scale-up to humans for drugs with transporter-mediated renal reabsorption. Additionally, due to the vectorial transport across PTCs incorporated in the model, this renal model may be suitable for drugs eliminated by transporter-mediated active secretion.
Supplementary Material
Acknowledgments
This work was supported by the National Institutes of Health National Institute on Drug Abuse [grant R01DA023223]. We thank Robert S. Jones (University at Buffalo) for his suggestions and contributions to the kidney model.
Footnotes
Post-script
This manuscript is dedicated to Dr. Gerhard Levy, graduate mentor of Dr. Marilyn Morris and an inspiration in my life. His emphasis always on excellence and integrity has remained the corner stone of my career. I joined the Levy laboratory in the Fall of 1978 and became a member of the “sulfate group” consisting of myself and two postdoctoral fellows in the lab, Raymond Galinsky and Jiunn Lin. My PhD thesis focused on examining the importance of the cofactor inorganic sulfate in sulfate conjugation and characterizing its absorption and renal clearance, which involved renal reabsorption. I continued in the area of drug conjugation reactions in the laboratory of Dr. K. Sandy Pang at the University of Toronto, gaining additional modeling skills, and returning to Buffalo to become a colleague of Gerhard Levy’s in 1985. As an Assistant Professor, my initial research and my first NIH grant focused on inorganic sulfate homeostasis, evaluating the active reabsorption of inorganic sulfate in the kidney and focusing on the transporters involved in its renal reabsorption. Dr. Levy had extensive publications in renal clearance and reabsorption/secretion mechanisms in renal clearance (as described in the manuscript), including his seminal publication on “The effect of protein binding on the renal clearance of drugs” in 1980, that I still use in teaching in my lectures on renal clearance. However, in 1985 little was known regarding drug transporters in the kidney. Thirty years later, I am still focused on membrane transporters and currently on the monocarboxylate transporter-mediated renal reabsorption, as described for the drug GHB in this manuscript, which is in fact very similar in many aspects to the vectorial transport of inorganic sulfate in the renal proximal tubule. This research was performed with Rutwij Dave, a PhD student in my laboratory, and his research has focused on renal clearance mechanisms and modeling. Therefore, it seemed fitting to submit this manuscript on a physiologically-relevant approach to modeling of transporter-mediated renal reabsorption for publication in this issue of JPKPD dedicated to Dr. Levy.
References
- 1.Khurana I. Textbook of human physiology for dental students. 2. Elsevier Health Sciences APAC; 2014. Excretory system; pp. 280–281. [Google Scholar]
- 2.Lote CJ. Principles of renal physiology. 4. Kluwer Academic Publishers; 2000. Summary of the principal reabsorptive and secretory processes; pp. 161–162. [Google Scholar]
- 3.Lash LH. Principles and methods of renal toxicology. In: Hayes AW, editor. Principles and methods of toxicology. 5. Taylor & Francis; 2007. pp. 1513–1514. [Google Scholar]
- 4.Kusuhara H, Sekine T, Anzai N, Endou H. Drug transport in the kidney. In: You G, Morris ME, Wang B, editors. Drug transporters: Molecular characterization and role in drug disposition. Wiley; 2014. pp. 303–316. [Google Scholar]
- 5.Morrissey KM, Stocker SL, Wittwer MB, Xu L, Giacomini KM. Renal transporters in drug development. Annu Rev Pharmacol Toxicol. 2013;53:503–529. doi: 10.1146/annurev-pharmtox-011112-140317. [DOI] [PubMed] [Google Scholar]
- 6.Launay-Vacher V, Izzedine H, Karie S, Hulot JS, Baumelou A, Deray G. Renal tubular drug transporters. Nephron Physiol. 2006;103(3):p97–106. doi: 10.1159/000092212. [DOI] [PubMed] [Google Scholar]
- 7.Morris ME, Hu K, Wang Q. Renal clearance of gamma-hydroxybutyric acid in rats: Increasing renal elimination as a detoxification strategy. J Pharmacol Exp Ther. 2005;313(3):1194–1202. doi: 10.1124/jpet.105.083253. [DOI] [PubMed] [Google Scholar]
- 8.Iwanaga T, Kobayashi D, Hirayama M, Maeda T, Tamai I. Involvement of uric acid transporter in increased renal clearance of the xanthine oxidase inhibitor oxypurinol induced by a uricosuric agent, benzbromarone. Drug Metab Dispos. 2005;33(12):1791–1795. doi: 10.1124/dmd.105.006056. [DOI] [PubMed] [Google Scholar]
- 9.Shen H, Ocheltree SM, Hu Y, Keep RF, Smith DE. Impact of genetic knockout of pept2 on cefadroxil pharmacokinetics, renal tubular reabsorption, and brain penetration in mice. Drug Metab Dispos. 2007;35(7):1209–1216. doi: 10.1124/dmd.107.015263. [DOI] [PubMed] [Google Scholar]
- 10.Andersen ME, Clewell HJ, 3rd, Tan YM, Butenhoff JL, Olsen GW. Pharmacokinetic modeling of saturable, renal resorption of perfluoroalkylacids in monkeys--probing the determinants of long plasma half-lives. Toxicology. 2006;227(1–2):156–164. doi: 10.1016/j.tox.2006.08.004. [DOI] [PubMed] [Google Scholar]
- 11.Chang SC, Noker PE, Gorman GS, Gibson SJ, Hart JA, Ehresman DJ, Butenhoff JL. Comparative pharmacokinetics of perfluorooctanesulfonate (pfos) in rats, mice, and monkeys. Reprod Toxicol. 2012;33(4):428–440. doi: 10.1016/j.reprotox.2011.07.002. [DOI] [PubMed] [Google Scholar]
- 12.Hendel J, Nyfors A. Nonlinear renal elimination kinetics of methotrexate due to saturation of renal tubular reabsorption. Eur J Clin Pharmacol. 1984;26(1):121–124. doi: 10.1007/BF00546719. [DOI] [PubMed] [Google Scholar]
- 13.Arvidsson A, Borga O, Alvan G. Renal excretion of cephapirin and cephaloridine: Evidence for saturable tubular reabsorption. Clin Pharmacol Ther. 1979;25(6):870–876. doi: 10.1002/cpt1979256870. [DOI] [PubMed] [Google Scholar]
- 14.Fujino H, Saito T, Ogawa S, Kojima J. Transporter-mediated influx and efflux mechanisms of pitavastatin, a new inhibitor of hmg-coa reductase. J Pharm Pharmacol. 2005;57(10):1305–1311. doi: 10.1211/jpp.57.10.0009. [DOI] [PubMed] [Google Scholar]
- 15.Ho RH, Tirona RG, Leake BF, Glaeser H, Lee W, Lemke CJ, Wang Y, Kim RB. Drug and bile acid transporters in rosuvastatin hepatic uptake: Function, expression, and pharmacogenetics. Gastroenterology. 2006;130(6):1793–1806. doi: 10.1053/j.gastro.2006.02.034. [DOI] [PubMed] [Google Scholar]
- 16.Su Y, Zhang X, Sinko PJ. Human organic anion-transporting polypeptide oatp-a (slc21a3) acts in concert with p-glycoprotein and multidrug resistance protein 2 in the vectorial transport of saquinavir in hep g2 cells. Mol Pharm. 2004;1(1):49–56. doi: 10.1021/mp0340136. [DOI] [PubMed] [Google Scholar]
- 17.Watanabe K, Jinriki T, Sato J. Effects of progesterone and norethisterone on cephalexin uptake in the human intestinal cell line caco-2. Biol Pharm Bull. 2004;27(4):559–563. doi: 10.1248/bpb.27.559. [DOI] [PubMed] [Google Scholar]
- 18.Li M, Anderson GD, Phillips BR, Kong W, Shen DD, Wang J. Interactions of amoxicillin and cefaclor with human renal organic anion and peptide transporters. Drug Metab Dispos. 2006;34(4):547–555. doi: 10.1124/dmd.105.006791. [DOI] [PubMed] [Google Scholar]
- 19.Wesson LG., Jr A theoretical analysis of urea excretion by the mammalian kidney. Am J Physiol. 1954;179(2):364–371. doi: 10.1152/ajplegacy.1954.179.2.364. [DOI] [PubMed] [Google Scholar]
- 20.Tucker GT. Measurement of the renal clearance of drugs. Br J Clin Pharmacol. 1981;12(6):761–770. doi: 10.1111/j.1365-2125.1981.tb01304.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hall S, Rowland M. Relationship between renal clearance, protein binding and urine flow for digitoxin, a compound of low clearance in the isolated perfused rat kidney. J Pharmacol Exp Ther. 1984;228(1):174–179. [PubMed] [Google Scholar]
- 22.Levy G. Effect of plasma protein binding on renal clearance of drugs. J Pharm Sci. 1980;69(4):482–483. doi: 10.1002/jps.2600690437. [DOI] [PubMed] [Google Scholar]
- 23.Sand TE, Jacobsen S. Effect of urine ph and flow on renal clearance of methotrexate. Eur J Clin Pharmacol. 1981;19(6):453–456. doi: 10.1007/BF00548590. [DOI] [PubMed] [Google Scholar]
- 24.Tang-Liu DD, Tozer TN, Riegelman S. Dependence of renal clearance on urine flow: A mathematical model and its application. J Pharm Sci. 1983;72(2):154–158. doi: 10.1002/jps.2600720215. [DOI] [PubMed] [Google Scholar]
- 25.Romano G, Favret G, Damato R, Bartoli E. Proximal reabsorption with changing tubular fluid inflow in rat nephrons. Exp Physiol. 1998;83(1):35–48. doi: 10.1113/expphysiol.1998.sp004090. [DOI] [PubMed] [Google Scholar]
- 26.Lang F. Osmotic diuresis. Ren Physiol. 1987;10(3–4):160–173. doi: 10.1159/000173127. [DOI] [PubMed] [Google Scholar]
- 27.Liu FY, Cogan MG. Axial heterogeneity in the rat proximal convoluted tubule. I. Bicarbonate, chloride, and water transport. Am J Physiol. 1984;247(5 Pt 2):F816–821. doi: 10.1152/ajprenal.1984.247.5.F816. [DOI] [PubMed] [Google Scholar]
- 28.Liu FY, Cogan MG. Axial heterogeneity of bicarbonate, chloride, and water transport in the rat proximal convoluted tubule. Effects of change in luminal flow rate and of alkalemia. J Clin Invest. 1986;78(6):1547–1557. doi: 10.1172/JCI112747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Maddox DA, Gennari FJ. The early proximal tubule: A high-capacity delivery-responsive reabsorptive site. Am J Physiol. 1987;252(4 Pt 2):F573–584. doi: 10.1152/ajprenal.1987.252.4.F573. [DOI] [PubMed] [Google Scholar]
- 30.Layton AT. A mathematical model of the urine concentrating mechanism in the rat renal medulla. I. Formulation and base-case results. Am J Physiol Renal Physiol. 2011;300(2):F356–371. doi: 10.1152/ajprenal.00203.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Layton AT. A mathematical model of the urine concentrating mechanism in the rat renal medulla. Ii. Functional implications of three-dimensional architecture. Am J Physiol Renal Physiol. 2011;300(2):F372–384. doi: 10.1152/ajprenal.00204.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Weinstein AM. A mathematical model of the rat nephron: Glucose transport. Am J Physiol Renal Physiol. 2015;308(10):F1098–1118. doi: 10.1152/ajprenal.00505.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Weinstein AM. A mathematical model of rat proximal tubule and loop of henle. Am J Physiol Renal Physiol. 2015;308(10):F1076–1097. doi: 10.1152/ajprenal.00504.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Weinstein AM. A mathematical model of rat cortical collecting duct: Determinants of the transtubular potassium gradient. Am J Physiol Renal Physiol. 2001;280(6):F1072–1092. doi: 10.1152/ajprenal.2001.280.6.F1072. [DOI] [PubMed] [Google Scholar]
- 35.Jusko WJ, Levy G. Pharmacokinetic evidence for saturable renal tubular reabsorption of riboflavin. J Pharm Sci. 1970;59(6):765–772. doi: 10.1002/jps.2600590608. [DOI] [PubMed] [Google Scholar]
- 36.Blanchard J, Tozer TN, Rowland M. Pharmacokinetic perspectives on megadoses of ascorbic acid. Am J Clin Nutr. 1997;66(5):1165–1171. doi: 10.1093/ajcn/66.5.1165. [DOI] [PubMed] [Google Scholar]
- 37.Yamaguchi K, Kato M, Suzuki M, Asanuma K, Aso Y, Ikeda S, Ishigai M. Pharmacokinetic and pharmacodynamic modeling of the effect of an sodium-glucose cotransporter inhibitor, phlorizin, on renal glucose transport in rats. Drug Metab Dispos. 2011;39(10):1801–1807. doi: 10.1124/dmd.111.040048. [DOI] [PubMed] [Google Scholar]
- 38.Lu Y, Griffen SC, Boulton DW, Leil TA. Use of systems pharmacology modeling to elucidate the operating characteristics of sglt1 and sglt2 in renal glucose reabsorption in humans. Front Pharmacol. 2014;5:274. doi: 10.3389/fphar.2014.00274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Demin O, Jr, Yakovleva T, Kolobkov D, Demin O. Analysis of the efficacy of sglt2 inhibitors using semi-mechanistic model. Front Pharmacol. 2014;5:218. doi: 10.3389/fphar.2014.00218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Felmlee MA, Dave RA, Morris ME. Mechanistic models describing active renal reabsorption and secretion: A simulation-based study. AAPS J. 2013;15(1):278–287. doi: 10.1208/s12248-012-9437-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Levy G. Salicylurate formation demonstration of michaelis-menten kinetics in man. J Pharm Sci. 1965;54:496. doi: 10.1002/jps.2600540348. [DOI] [PubMed] [Google Scholar]
- 42.Nelson E, Hanano M, Levy G. Comparative pharmacokinetics of salicylate elimination in man and rats. J Pharmacol Exp Ther. 1966;153(1):159–166. [PubMed] [Google Scholar]
- 43.Levy G, Weintraub L, Matsuzawa T, Oles SR. Absorption, metabolism and excretion of salicylic phenolic glucuronide in rats. J Pharm Sci. 1966;55(11):1319–1320. doi: 10.1002/jps.2600551135. [DOI] [PubMed] [Google Scholar]
- 44.Levy G, Tsuchiya T. Salicylate accumulation kinetics in man. N Engl J Med. 1972;287(9):430–432. doi: 10.1056/NEJM197208312870903. [DOI] [PubMed] [Google Scholar]
- 45.Levy G. Effect of probenecid on blood levels and urinary recovery of ampicillin. Am J Med Sci. 1965;250:174–176. doi: 10.1097/00000441-196508000-00008. [DOI] [PubMed] [Google Scholar]
- 46.Levy G, Jusko WJ. Apparent renal tubular secretion of riboflavin in man. J Pharm Sci. 1966;55(11):1322. doi: 10.1002/jps.2600551137. [DOI] [PubMed] [Google Scholar]
- 47.Jusko WJ, Levy G. Effect of probenecid on riboflavin absorption and excretion in man. J Pharm Sci. 1967;56(9):1145–1149. doi: 10.1002/jps.2600560920. [DOI] [PubMed] [Google Scholar]
- 48.Jusko WJ, Levy G, Yaffe SJ, Gorodischer R. Effect of probenecid on renal clearance of riboflavin in man. J Pharm Sci. 1970;59(4):473–477. doi: 10.1002/jps.2600590407. [DOI] [PubMed] [Google Scholar]
- 49.Levy G, Koysooko R. Renal clearance of theophylline in man. J Clin Pharmacol. 1976;16(7):329–332. doi: 10.1002/j.1552-4604.1976.tb01528.x. [DOI] [PubMed] [Google Scholar]
- 50.Lowenthal DT, Oie S, Van Stone JC, Briggs WA, Levy G. Pharmacokinetics of acetaminophen elimination by anephric patients. J Pharmacol Exp Ther. 1976;196(3):570–578. [PubMed] [Google Scholar]
- 51.Lin JH, Levy G. Renal clearance of inorganic sulfate in rats: Effect of acetaminophen-induced depletion of endogenous sulfate. J Pharm Sci. 1983;72(3):213–217. doi: 10.1002/jps.2600720303. [DOI] [PubMed] [Google Scholar]
- 52.Morris ME, Levy G. Renal clearance and serum protein binding of acetaminophen and its major conjugates in humans. J Pharm Sci. 1984;73(8):1038–1041. doi: 10.1002/jps.2600730806. [DOI] [PubMed] [Google Scholar]
- 53.Oie S, Levy G. Relationship between renal function and elimination kinetics of pindolol in man. Eur J Clin Pharmacol. 1975;9(2–3):115–116. doi: 10.1007/BF00614006. [DOI] [PubMed] [Google Scholar]
- 54.Morris ME, Levy G. Serum concentration and renal excretion by normal adults of inorganic sulfate after acetaminophen, ascorbic acid, or sodium sulfate. Clin Pharmacol Ther. 1983;33(4):529–536. doi: 10.1038/clpt.1983.72. [DOI] [PubMed] [Google Scholar]
- 55.Galinsky RE, Slattery JT, Levy G. Effect of sodium sulfate on acetaminophen elimination by rats. J Pharm Sci. 1979;68(6):803–805. doi: 10.1002/jps.2600680642. [DOI] [PubMed] [Google Scholar]
- 56.Levy G, Calesnick B, Wase A. Relationship between hg-203 excretion rate and diuretic response following hg-203 mercaptomerin sodium administration. J Nucl Med. 1964;5:302–303. [PubMed] [Google Scholar]
- 57.Cummings AJ, Martin BK, Renton R. The elimination of salicylic acid in man: Serum concentrations and urinary excretion rates. Br J Pharmacol Chemother. 1966;26(2):461–467. doi: 10.1111/j.1476-5381.1966.tb01926.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Levy G. Clinical pharmacokinetics of salicylates: A re-assessment. Br J Clin Pharmacol. 1980;10(Suppl 2):285S–290S. doi: 10.1111/j.1365-2125.1980.tb01811.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Oie S, Lowenthal DT, Briggs WA, Levy G. Effect of hemodialysis on kinetics of acetaminophen elimination by anephric patients. Clin Pharmacol Ther. 1975;18(06):680–686. doi: 10.1002/cpt1975186680. [DOI] [PubMed] [Google Scholar]
- 60.Levy G, Procknal J. Letter: Determination of salicylate and its metabolites in urine. Clin Chem. 1976;22(3):395. [PubMed] [Google Scholar]
- 61.Levy G, Leonards JR. Urine ph and salicylate therapy. JAMA. 1971;217(1):81. doi: 10.1001/jama.217.1.81c. [DOI] [PubMed] [Google Scholar]
- 62.Levy G. Pharmacokinetics in renal disease. Am J Med. 1977;62(4):461–465. doi: 10.1016/0002-9343(77)90397-7. [DOI] [PubMed] [Google Scholar]
- 63.Yacobi A, Levy G. Intraindividual relationships between serum protein binding of drugs in normal human subjects, patients with impaired renal function, and rats. J Pharm Sci. 1977;66(9):1285–1288. doi: 10.1002/jps.2600660920. [DOI] [PubMed] [Google Scholar]
- 64.Jusko WJ, Levy G. Absorption, metabolism, and excretion of riboflavin-5′-phosphate in man. J Pharm Sci. 1967;56(1):58–62. doi: 10.1002/jps.2600560112. [DOI] [PubMed] [Google Scholar]
- 65.Jusko WJ, Levy G. Plasma protein binding of riboflavin and riboflavin-5′-phosphate in man. J Pharm Sci. 1969;58(1):58–62. doi: 10.1002/jps.2600580110. [DOI] [PubMed] [Google Scholar]
- 66.Jusko WJ, Rennick BR, Levy G. Renal exretion of riboflavin in the dog. Am J Physiol. 1970;218(4):1046–1053. doi: 10.1152/ajplegacy.1970.218.4.1046. [DOI] [PubMed] [Google Scholar]
- 67.Jusko WJ, Khanna N, Levy G, Stern L, Yaffe SJ. Riboflavin absorption and excretion in the neonate. Pediatrics. 1970;45(6):945–949. [PubMed] [Google Scholar]
- 68.Maitre M. The gamma-hydroxybutyrate signalling system in brain: Organization and functional implications. Prog Neurobiol. 1997;51(3):337–361. doi: 10.1016/s0301-0082(96)00064-0. S0301-0082(96)00064-0 [pii] [DOI] [PubMed] [Google Scholar]
- 69.Mamelak M, Scharf MB, Woods M. Treatment of narcolepsy with gamma-hydroxybutyrate. A review of clinical and sleep laboratory findings. Sleep. 1986;9(1 Pt 2):285–289. doi: 10.1093/sleep/9.1.285. [DOI] [PubMed] [Google Scholar]
- 70.Gallimberti L, Spella MR, Soncini CA, Gessa GL. Gamma-hydroxybutyric acid in the treatment of alcohol and heroin dependence. Alcohol. 2000;20(3):257–262. doi: 10.1016/s0741-8329(99)00089-0. S0741832999000890 [pii] [DOI] [PubMed] [Google Scholar]
- 71.Wong CG, Gibson KM, Snead OC., 3rd From the street to the brain: Neurobiology of the recreational drug gamma-hydroxybutyric acid. Trends Pharmacol Sci. 2004;25(1):29–34. doi: 10.1016/j.tips.2003.11.001. S0165614703003341 [pii] [DOI] [PubMed] [Google Scholar]
- 72.Schwartz RH, Milteer R, LeBeau MA. Drug-facilitated sexual assault (‘date rape’) South Med J. 2000;93(6):558–561. [PubMed] [Google Scholar]
- 73.Lettieri JT, Fung HL. Dose-dependent pharmacokinetics and hypnotic effects of sodium gamma-hydroxybutyrate in the rat. J Pharmacol Exp Ther. 1979;208(1):7–11. [PubMed] [Google Scholar]
- 74.Palatini P, Tedeschi L, Frison G, Padrini R, Zordan R, Orlando R, Gallimberti L, Gessa GL, Ferrara SD. Dose-dependent absorption and elimination of gamma-hydroxybutyric acid in healthy volunteers. Eur J Clin Pharmacol. 1993;45(4):353–356. doi: 10.1007/BF00265954. [DOI] [PubMed] [Google Scholar]
- 75.Scharf MB, Lai AA, Branigan B, Stover R, Berkowitz DB. Pharmacokinetics of gammahydroxybutyrate (ghb) in narcoleptic patients. Sleep. 1998;21(5):507–514. doi: 10.1093/sleep/21.5.507. [DOI] [PubMed] [Google Scholar]
- 76.Arena C, Fung HL. Absorption of sodium gamma-hydroxybutyrate and its prodrug gamma-butyrolactone: Relationship between in vitro transport and in vivo absorption. J Pharm Sci. 1980;69(3):356–358. doi: 10.1002/jps.2600690331. [DOI] [PubMed] [Google Scholar]
- 77.Sporer KA, Chin RL, Dyer JE, Lamb R. Gamma-hydroxybutyrate serum levels and clinical syndrome after severe overdose. Ann Emerg Med. 2003;42(1):3–8. doi: 10.1067/mem.2003.2530196064403003391. [pii] [DOI] [PubMed] [Google Scholar]
- 78.Cui D, Morris ME. The drug of abuse gamma-hydroxybutyrate is a substrate for sodium-coupled monocarboxylate transporter (smct) 1 (slc5a8): Characterization of smct-mediated uptake and inhibition. Drug Metab Dispos. 2009;37(7):1404–1410. doi: 10.1124/dmd.109.027169. dmd.109.027169 [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Wang Q, Lu Y, Morris ME. Monocarboxylate transporter (mct) mediates the transport of gamma-hydroxybutyrate in human kidney hk-2 cells. Pharm Res. 2007;24(6):1067–1078. doi: 10.1007/s11095-006-9228-6. [DOI] [PubMed] [Google Scholar]
- 80.Wang Q, Wang X, Morris ME. Effects of l-lactate and d-mannitol on gamma-hydroxybutyrate toxicokinetics and toxicodynamics in rats. Drug Metab Dispos. 2008;36(11):2244–2251. doi: 10.1124/dmd.108.022996. dmd.108.022996 [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Morse BL, Vijay N, Morris ME. Mechanistic modeling of monocarboxylate transporter-mediated toxicokinetic/toxicodynamic interactions between gamma-hydroxybutyrate and l-lactate. AAPS J. 2014;16(4):756–770. doi: 10.1208/s12248-014-9593-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Vijay N, Morse BL, Morris ME. A novel monocarboxylate transporter inhibitor as a potential treatment strategy for gamma-hydroxybutyric acid overdose. Pharm Res. 2015;32(6):1894–1906. doi: 10.1007/s11095-014-1583-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Morse BL, Morris ME. Effects of monocarboxylate transporter inhibition on the oral toxicokinetics/toxicodynamics of gamma-hydroxybutyrate and gamma-butyrolactone. J Pharmacol Exp Ther. 2013;345(1):102–110. doi: 10.1124/jpet.112.202796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Morris ME, Morse BL, Baciewicz GJ, Tessena MM, Acquisto NM, Hutchinson DJ, Dicenzo R. Monocarboxylate transporter inhibition with osmotic diuresis increases gamma-hydroxybutyrate renal elimination in humans: A proof-of-concept study. J Clin Toxicol. 2011;1(2):1000105. doi: 10.4172/2161-0495.1000105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Felmlee MA, Wang Q, Cui D, Roiko SA, Morris ME. Mechanistic toxicokinetic model for gamma-hydroxybutyric acid: Inhibition of active renal reabsorption as a potential therapeutic strategy. AAPS J. 2010;12(3):407–416. doi: 10.1208/s12248-010-9197-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Wang Q, Darling IM, Morris ME. Transport of gamma-hydroxybutyrate in rat kidney membrane vesicles: Role of monocarboxylate transporters. J Pharmacol Exp Ther. 2006;318(2):751–761. doi: 10.1124/jpet.106.105965. [DOI] [PubMed] [Google Scholar]
- 87.Yanase H, Takebe K, Nio-Kobayashi J, Takahashi-Iwanaga H, Iwanaga T. Cellular expression of a sodium-dependent monocarboxylate transporter (slc5a8) and the mct family in the mouse kidney. Histochem Cell Biol. 2008;130(5):957–966. doi: 10.1007/s00418-008-0490-z. [DOI] [PubMed] [Google Scholar]
- 88.Woodhall PB, Tisher CC. Response of the distal tubule and cortical collecting duct to vasopressin in the rat. J Clin Invest. 1973;52(12):3095–3108. doi: 10.1172/JCI107509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Morse BL, Felmlee MA, Morris ME. Gamma-hydroxybutyrate blood/plasma partitioning: Effect of physiologic ph on transport by monocarboxylate transporters. Drug Metab Dispos. 2012;40(1):64–69. doi: 10.1124/dmd.111.041285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.D’Argenio DZ, Schumitzky A, Wang X. Adapt 5 user’s guide: Pharmacokinetic/pharmacodynamic systems analysis software. 4. Biomedical Simulations Resource; Los Angeles, CA: 2009. [Google Scholar]
- 91.Lyon RC, Johnston SM, Panopoulos A, Alzeer S, McGarvie G, Ellis EM. Enzymes involved in the metabolism of gamma-hydroxybutyrate in sh-sy5y cells: Identification of an iron-dependent alcohol dehydrogenase adhfe1. Chem Biol Interact. 2009;178(1–3):283–287. doi: 10.1016/j.cbi.2008.10.025. [DOI] [PubMed] [Google Scholar]
- 92.Edlund GL, Halestrap AP. The kinetics of transport of lactate and pyruvate into rat hepatocytes. Evidence for the presence of a specific carrier similar to that in erythrocytes. Biochem J. 1988;249(1):117–126. doi: 10.1042/bj2490117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Ganapathy V, Thangaraju M, Gopal E, Martin PM, Itagaki S, Miyauchi S, Prasad PD. Sodium-coupled monocarboxylate transporters in normal tissues and in cancer. AAPS J. 2008;10(1):193–199. doi: 10.1208/s12248-008-9022-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Wang Q, Morris ME. The role of monocarboxylate transporter 2 and 4 in the transport of gamma-hydroxybutyric acid in mammalian cells. Drug Metab Dispos. 2007;35(8):1393–1399. doi: 10.1124/dmd.107.014852. [DOI] [PubMed] [Google Scholar]
- 95.Felmlee MA, Krzyzanski W, Morse BL, Morris ME. Use of a local sensitivity analysis to inform study design based on a mechanistic toxicokinetic model for gamma-hydroxybutyric acid. AAPS J. 2011;13(2):240–254. doi: 10.1208/s12248-011-9264-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Halestrap AP. The monocarboxylate transporter family--structure and functional characterization. IUBMB Life. 2012;64(1):1–9. doi: 10.1002/iub.573. [DOI] [PubMed] [Google Scholar]
- 97.Meno-Tetang GM, Li H, Mis S, Pyszczynski N, Heining P, Lowe P, Jusko WJ. Physiologically based pharmacokinetic modeling of fty720 (2-amino-2[2-(-4-octylphenyl)ethyl]propane-1,3-diol hydrochloride) in rats after oral and intravenous doses. Drug Metab Dispos. 2006;34(9):1480–1487. doi: 10.1124/dmd.105.009001. [DOI] [PubMed] [Google Scholar]
- 98.Peters SA. Physiologically-based pharmacokinetic (pbpk) modeling and simulations: Principles, methods, and applications in the pharmaceutical industry. Wiley; 2012. Appendices; p. 407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Niederalt C, Wendl T, Kuepfer L, Claassen K, Loosen R, Willmann S, Lippert J, Schultze-Mosgau M, Winkler J, Burghaus R, Brautigam M, Pietsch H, Lengsfeld P. Development of a physiologically based computational kidney model to describe the renal excretion of hydrophilic agents in rats. Front Physiol. 2012;3:494. doi: 10.3389/fphys.2012.00494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Jobin J, Bonjour JP. Measurement of glomerular filtration rate in conscious unrestrained rats with inulin infused by implanted osmotic pumps. Am J Physiol. 1985;248(5 Pt 2):F734–738. doi: 10.1152/ajprenal.1985.248.5.F734. [DOI] [PubMed] [Google Scholar]
- 101.Wang X, Wang Q, Morris ME. Pharmacokinetic interaction between the flavonoid luteolin and gamma-hydroxybutyrate in rats: Potential involvement of monocarboxylate transporters. AAPS J. 2008;10(1):47–55. doi: 10.1208/s12248-007-9001-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.