A random change point model for assessing variability in repeated measures of cognitive function

SUMMARY

Some cognitive functions undergo transitions in old age, which motivates the use of a change point model for the individual trajectory. The age when the change occurs varies between individuals and is treated as random. We illustrate the properties of a random change point model and use it for data from a Swedish study of change in cognitive function in old age. Variance estimates are obtained from Markov chain Monte Carlo simulation using Gibbs sampling. The random change point model is compared with models within the family of linear random effects models. The focus is on the ability to capture variability in measures of cognitive function. The models make different assumptions about the variance over the age span, and we demonstrate that the random change point model has the most reasonable structure.

1. INTRODUCTION

The development of cognitive function in old age is often nonlinear. Several studies have shown that some cognitive functions remain stable into old age, with more marked decline an indication of impending death within a few years [1, 2]. This phenomenon is referred to as terminal drop [3] and can potentially be captured by a random change point model incorporating the individual-specific age when a change occurs. In this paper we investigate the properties of a random change point model with two linear phases for each individual. The model allows the two trends and the age at transition from the first to the second phase to be individual-specific.

Random change point models have previously been used in several medical applications. These include studies of progression of HIV infection using CD4 T-Cell numbers [4-6] and development of prostate-specific antigen levels as a marker for prostate cancer [7]. Cognitive function in old age has also been studied using random change point models [8, 9]. In these studies, the focus has been on the mean trajectory of cognitive function in the pre-dementia phase.

In this paper we investigate an aspect of modeling cognitive function based on random change point models which has previously not been addressed, namely the ability to explain variability in cognitive function. We illustrate the approach using data from the Swedish Adoption/Twin Study of Aging (SATSA) [10], which is a longitudinal study based on a group of twins.

Although heritability estimates for cognitive functions are also high in the older ages, relatively little is known about the dynamics of cognitive decline in the old, and how genes and lifestyle factors affect the dynamics of the decline. This may be in part a result of the current longitudinal models for longitudinally measured cognition being too simplistic in the way they capture the variability over age. It is known that linear random effects models often used for longitudinal data [11] imply very specific assumptions about the marginal variance [12].

In this paper we present a random change point model that is flexible in its way of capturing both the average behavior of cognitive function over age and the variance over age. The model may further be used to predict the ages at which change points occur, as well as other parameters of the model. These individual-specific parameters may be used as outcomes in genetic association studies using measured genotypic data as predictors. The variances of these random parameters may also be further used in estimating heritability of characteristics of cognitive function in twin and family studies.

The random change point model is compared with the linear and the quadratic random effects models, which previously have been used for analyzing cognitive data from SATSA [13, 14]. Comparisons focus on the models’ ability to explain trait variability and their goodness of fit as measured by the deviance information criterion (DIC) [15].

We adopt a sampling-based Bayesian procedure, where numerical integration is avoided by taking repeated samples from the conditional posterior distributions for each parameter (or subset of parameters) in turn. We use a Markov chain Monte Carlo (MCMC) simulation through Gibbs sampling [16], which involves the construction of a Markov chain that has the posterior distribution of interest as the stationary distribution. In a small simulation study, we investigate the performance of the MCMC algorithm.

In Section 2 we describe the data on cognitive function analyzed in the paper. In Section 3 we describe the models considered and the procedures used for model fitting and model comparison. We present a simulation study in Section 4 and analyses of empirical data on cognitive function in Section 5. The methods and results are discussed in Section 6.

2. SATSA

We analyze data on cognitive function, measured by the symbol digit test, which tests the ability to quickly and accurately compare numbers and symbols [10]. Scores range from 0 to 100, with high scores corresponding to good cognitive function. The assessment of cognitive function is part of SATSA, a longitudinal study of aging that includes both questionnaire assessments and in-person testings of cognitive and functional capabilities, personality, and health. SATSA has been described in detail elsewhere [17]. The first in-person testing took place in 1986–1988 and follow-up data were obtained after 3, 6, 13, and 16 years.

Results from the symbol digit test from at least one of the five test occasions are available for 853 individuals (415 full twin pairs and 23 singletons). To avoid the issue of clustered sampling in this illustration, we include singletons and one twin from each twin pair (drawn at random). In this sample of 438 individuals, 60 per cent are women and 40 per cent are men. Individuals are measured at very different ages with mean age 62 years (range 37–88 years) at the first test (in 1986–1988).

Because some participants have a late entry into the study, have intermittent missing observations, or are lost to followup, only 98 of the 438 individuals have scores from all five tests. Further, 58 have scores from four tests, 106 from three tests, 102 from two tests, while 74 only from one single test. The mechanisms underlying the late entry into the study and intermittent missing data are reasonably assumed to be ‘ignorable’ in the sense of Little and Rubin [18]. It implies that data are missing at random, i.e. the fact that a measurement on cognitive function is missing is assumed to depend on age and observed measurements, but not on the missing observation itself. The mechanism behind dropout from the study is also assumed to be ignorable. Although this assumption may be relaxed, we do not expect non-ignorable missingness to play a major role for this application.

Figure 1 shows score trajectories for 10 randomly selected individuals with five repeated scores from the symbol digit test. The figure indicates high within- and between-individual variability, but besides an overall decrease in test scores with age, no particular functional form is suggested for the population curve.

Figure 1.

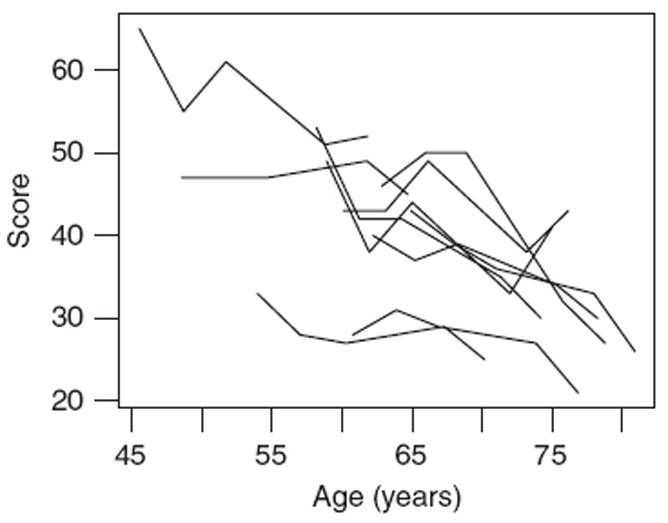
Symbol digit scores for 10 randomly selected participants in SATSA with five repeated measures of cognitive function.

3. STATISTICAL METHODS

3.1. Random change point model

We consider a random change point model with two linear phases, involving four individual-specific random effects. In order to minimize the correlation between estimated model parameters, the model is formulated as

$$y_{ij}=b_{0i}+b_{1i}({\mathrm{age}}_{ij}-b_{3i})+b_{2i}({\mathrm{age}}_{ij}-b_{3i})\mathrm{sign}({\mathrm{age}}_{ij}-b_{3i})+e_{ij}$$ (1)

where y_ij denotes the jth measurement of cognitive function for the ith individual and sign(z) = − 1 if z <0, sign(z) = 0 if z = 0, and sign(z) = +1 if z>0. The residual errors are denoted by e_ij. Under this parametrization, the slope is equal to b_1i − b_2i before the change point (b_3i) and equal to b_1i + b_2i after the change point. For individual i, b_0i is the expected value at the change point, b_1i is the average of the two slopes, and b_2i is half the difference between the two slopes.

In vector notation, b_i = (b_0i, b_1i, b_2i, b_3i)^T ~MVN (β, Σ), where β = (β₀, β₁, β₂, β₃)^T is the vector of population mean parameters and Σ is the 4×4 covariance matrix. In principle Σ can be unstructured. In our application to cognitive decline (Section 5), however, we include a non-zero correlation between b_0i and b_2i but set all other correlations to zero leading to a block-diagonal structure of Σ.

The residual errors in (1) are assumed to be independent of each other and of the random effects, and normally distributed with mean zero and constant variance ${\sigma }_{\mathrm{e}}^2$.

3.2. Linear and quadratic random effects models

Repeated measures of cognitive function from SATSA have previously been analyzed based on linear and quadratic random effects models [13, 14]. Here we compare the random change point model with the linear and the quadratic random effects models and investigate if the former improves our understanding of these data.

Using age as the time scale, the linear model is

$$y_{ij}=b_{0i}+b_{1i}{\mathrm{age}}_{ij}+e_{ij}$$ (2)

with b_i = (b_0i, b_1i)^T ~MVN (β, Σ) the vector of individual random effects. We assume that the individuals are independent and that the residual errors e_ij are uncorrelated with each other and with b_i and age_ij.

The quadratic model takes the corresponding form

$$y_{ij}=b_{0i}+b_{1i}{\mathrm{age}}_{ij}+b_{2i}{\mathrm{age}}_{\mathit{ij}}^2+e_{ij}$$ (3)

with b = (b_0i, b_1i, b_2i)^T ~MVN (β, Σ). In (2) and (3) the covariance matrix Σ is left unstructured.

3.3. Baysian approach based on MCMC

We perform MCMC simulations to approximate the posterior distribution of the parameters in models (1)–(3). MCMC simulation involves constructing a Markov chain with the required posterior distribution as its stationary distribution. We use a Gibbs sampler [16, 19] to construct the Markov chains, as implemented in the WinBUGS software [20]. After a burn-in to reach convergence, samples from the required distribution can be assembled.

We express the models defined in Sections 3.1 and 3.2 in the general form

$$\begin{array}{c}{\mathbf{y}}_i\mid {\mathbf{age}}_i,{\mathbf{b}}_i,{\sigma }_e^2\sim \mathrm{MVN}(\mathbf{f}({\mathbf{age}}_i,{\mathbf{b}}_i),{\sigma }_e^2{\mathbf{I}}_i)\\ {\mathbf{b}}_i\mid \mathbf{\beta },\mathbf{\sum }\sim \mathrm{MVN}(\mathbf{\beta },\mathbf{\sum })\end{array}$$

where ${\sigma }_{\mathrm{e}}^2$ is the residual error variance, I_i is the identity matrix, and Σ is the covariance matrix for the random effects. We use the following prior distributions:

$$\begin{array}{c}\mathbf{\beta }\sim \mathrm{MVN}({\mathbf{\beta }}^{\ast }\mathbf{,}\mathbf{H})\\ \mathbf{\sum }\sim \mathrm{invWishart}({\mathbf{\sum }}^{\ast },\rho )\\ {\sigma }_e^2\sim \mathrm{invGamma}({\lambda }_1,{\lambda }_2)\end{array}$$ (4)

where Σ~invWishart(Σ*, ρ) means that Σ⁻¹ has the Wishart distribution and ${\sigma }_{\mathrm{e}}^2$~invGamma (λ₁, λ₂) means that $1/{\sigma }_{\mathrm{e}}^2$ has the Gamma distribution with mean λ₁/λ₂ and variance ${\lambda }_1/{\lambda }_2^2$. These priors are proper conjugate distributions, with the desired property of leading to posterior distributions of known form [21]. Specific values used for the hyperparameters β*, H, Σ*, ρ, λ₁, and λ₂ are given in Section 5.

The parametrization in (1) aims at minimizing the correlation between model parameters when drawing from the conditional posterior distributions. In our applications, we assume independence between all individual-specific effects except for the level at change point (b_0i) and the difference in the two slopes (b_2i). For effects that are assumed to be independent of other effects, we use an inverse-gamma distribution for the variance parameter as priors.

3.4. Model comparison

We compare the linear, the quadratic, and the change point models based on the DIC [15], as well as by studying their ability to predict the mean and the variance of cognitive function over time. DIC is a Bayesian equivalent to the AIC [22]and consists of two components, a term that measures goodness of fit D̄ and a penalty term for increasing model complexity p_D: DIC = D̄ + p_D. D̄ is defined as the posterior expectation of the deviance. Hence, the better the model fits the data, the smaller is the value of D̄. The second component p_D measures the complexity of the model by the effective number of parameters and is defined as the difference between the posterior mean of the deviance and the deviance evaluated at the posterior mean of the parameters. It can be interpreted as the expected reduction in uncertainty due to estimation. The interpretation of DIC is similar to that of the AIC, as a summary of the relative fit between the model and the ‘true model’ generating the data. The smaller the DIC, the better the fit. DIC seeks to balance model complexity with the information available in the data, that is, a simpler model tends to be preferable for a smaller data set, whereas a larger data set may support a more complex model.

The primary goal of this study is to assess the variability in cognitive function, and in particular the variability as a function of age. We visually compare the models’ ability to predict variability in a plot of observed and predicted variance. Plots of the predicted mean are also included to contrast the different models. The predicted mean and the predicted variance are obtained by first predicting the random effects for each individual by the posterior mean. The predicted trajectories of repeated measurements are obtained from the predicted random effects and are then used to calculate the predicted mean and predicted variance using a moving window over age. In the calculation of the predicted variance, the residual error variance needs to be accounted for.

4. SIMULATION STUDY

In a small simulation study, we investigate the performance of the MCMC approach for fitting the random change point model. The main aim is to understand the data requirements for this rather complex model specification. The parameters in the simulations approximately mimic the cognitive data in SATSA. For simplicity, we use a balanced data design and a diagonal covariance matrix Σ for the random effects. Four scenarios are considered, which differ in the number of repeated measurements and the variance of individual-specific change points ( ${\sigma }_3^2$, Table I).

Table I.

Repeated measures time points and variance of individual-specific change points ( ${\sigma }_3^2$) used in simulation study.

Scenario	Time points	${\sigma }_3^2$
1	−6, −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, 6	4
2	−6, −3, 0, 3, 6	4
3	−6, −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, 6	25
4	−6, −3, 0, 3, 6	25

Scenario 1 in Table I is ideal in the sense that all individual-specific change points are within the observed age range, and the 13 repeated measures are centered around the mean change point. Scenario 2 is similar, except that the data are reduced to five repeated measurements. In Scenario 3 the variance of the individual-specific change points is increased to 25 years. With age points centered around zero, and individuals observed once a year between years −6 and 6, a standard error of 5 means that on average only 31 per cent have their change point inside the observed age range. Scenario 4 is the worst case with a large variability in change points and only five repeated measures for each individual.

For each scenario, 20 data sets were generated with 500 subjects each. The parameter values used for generating the simulated data are given in Table II. The prior distributions for the model parameters were chosen to be vague:

$$\begin{array}{c}{\beta }_0\sim \mathrm{N}(40,0.01)\\ {\beta }_1,{\beta }_2,\mathrm{and}{\beta }_3\sim N(0,0.01)\\ {\sigma }_0^2,{\sigma }_1^2,{\sigma }_2^2,{\sigma }_3^2,\mathrm{and}{\sigma }_e^2\sim \mathrm{invGamma}(0.001,0.001)\end{array}$$

Table II.

Simulation study on random change point model.

	True	Scenario 1			Scenario 2			Scenario 3			Scenario 4
		Mean	SEest	SEemp	Mean	SEest	SEemp	Mean	SEest	SEemp	Mean	SEest	SEemp
β0	45	45.01	0.40	0.56	44.99	0.40	0.42	44.82	0.47	0.40	45.12	0.46	0.34
β1	−0.5	−0.51	0.03	0.02	−0.51	0.03	0.03	−0.50	0.03	0.04	−0.49	0.03	0.03
β2	−0.3	−0.29	0.03	0.03	−0.30	0.03	0.04	−0.29	0.03	0.03	−0.30	0.04	0.05
β3	0	−0.06	0.16	0.15	0.04	0.20	0.18	−0.03	0.45	0.45	−0.10	0.48	0.47
${\sigma }_0^2$	75	75.56	4.94	4.21	75.31	4.99	4.99	77.25	5.70	4.65	75.17	5.68	6.50
${\sigma }_1^2$	0.3	0.30	0.02	0.02	0.29	0.02	0.03	0.32	0.03	0.03	0.29	0.03	0.04
${\sigma }_2^2$	0.3	0.30	0.02	0.02	0.30	0.03	0.02	0.30	0.03	0.03	0.30	0.03	0.03
${\sigma }_3^2$	4	3.89	0.61	0.68	4.21	0.88	0.82	22.90	3.36	3.39	26.49	4.67	5.71
${\sigma }_{\mathrm{e}}^2$	1	1.00	0.02	0.02	1.00	0.05	0.05	1.00	0.02	0.02	1.01	0.05	0.04

The prior mean of β₀ was set to a value fairly close to the true value to reduce the number of iterations needed to reach convergence and keep the running time at a reasonable level.

The simulation results given in Table II suggest that the Gibbs sampler performs well for all four scenarios. The means of the 20 medians of posterior parameter distributions are all close to the true parameter values. As expected, the variability in the 20 posterior medians for the mean β₃ and variance ( ${\sigma }_3^2$) of the change point increases as the variability in change points increases.

5. ANALYSIS OF COGNITIVE FUNCTION IN SATSA

We fit the change point, the linear, and the quadratic models to repeated measures of cognitive function as measured by the symbol digit test using the Bayesian approach described in Section 3.3. Age is centered at 65 years.

In initial analyses based on the change point model (1) with unrestricted covariance structure between all random effects convergence was not reached for some parameters. One possible explanation to this problem is overparameterization. The analyses also suggested a large correlation between the difference between the two slopes (b_2i) and the level at the change point (b_0i). We therefore restrict the model by explicitly including this correlation and setting all other random effects to be independent of each other. This leads to a block-diagonal structure for Σ, and the priors become

$$\begin{array}{c}{\mathbf{\beta }}_{02}\sim \mathrm{MVN}({\mathbf{\beta }}_{02}^{\ast },H_{02})\\ {\beta }_1\sim \mathrm{N}({\beta }_1^{\ast },H_1)\\ {\beta }_3\sim \mathrm{N}({\beta }_3^{\ast },H_3)\\ {\mathbf{\sum }}_{02}\sim \mathrm{invWishart}({\mathbf{\sum }}_{02}^{\ast },2)\\ {\sigma }_1^2\sim \mathrm{invGamma}({\lambda }_{11},{\lambda }_{12})\\ {\sigma }_3^2\sim \mathrm{invGamma}({\lambda }_{31},{\lambda }_{32})\\ {\sigma }_{\mathrm{e}}^2\sim \mathrm{invGamma}({\lambda }_1,{\lambda }_2)\end{array}$$

where H₀₂ is the covariance matrix for β₀₂ = (β₀, β₂), and H₁ and H₃ are the variances for β₁ and β₃, respectively. We consider three different sets of hyperparameters (Table III) to investigate the sensitivity of the results to the specific choice of prior distribution. We run two independent parallel chains of the Gibbs sampler, with different starting values. After thinning the sequences with a factor of 5, and removing the first 2000 iterations (burn-in), we use the 20 000 following iterations to obtain posterior distributions for the model parameters (β and Σ) and individual-specific random effects (b) by mixing the two sequences. Although the method is computationally demanding (it took 47 min to run on a computer with a Pentium Mobile processor running at 1.6 GHz with 512 MB of RAM), it can easily be done using the WinBUGS software (the WinBUGS code is given in Appendix A).

Table III.

Hyperparameters used for random change point model in analysis of cognitive function.

Hyperparameter	Prior 1	Prior 2	Prior 3
${\beta }_{02}^{\ast }$	(40, 0)	(20, −1)	(30,1)
${\beta }_1^{\ast }$	0	−1	1
${\beta }_3^{\ast }$	5	7	9
H02	$\left(\begin{array}{cc}100& 0\\ 0& 100\end{array}\right)$	$\left(\begin{array}{cc}10& 0\\ 0& 10\end{array}\right)$	$\left(\begin{array}{cc}100& 0\\ 0& 100\end{array}\right)$
H1	100	10	100
H3	10	10	100
${\sum }_{02}^{\ast }$	$\left(\begin{array}{cc}200& 0\\ 0& 1\end{array}\right)$	$\left(\begin{array}{cc}200& 0\\ 0& 1\end{array}\right)$	$\left(\begin{array}{cc}20& 0\\ 0& 0.1\end{array}\right)$
ρ	2	2	2
λ11	0.1	0.01	0.001
λ12	0.1	0.01	0.001
λ31	0.1	0.01	0.001
λ32	0.1	0.01	0.001
λ1	0.1	0.01	0.001
λ2	0.1	0.01	0.001

A summary of the posterior distributions of the model parameters is given in Table IV. We found that the choice of hyperparameters had little influence on the marginal posterior distributions, with an exception for the change point mean and variance parameters. In the presentation below we use the results from priors 3, which show the lowest value of DIC. Trace plots of the MCMC samples were used for checks of convergence, and an investigation of the residual errors confirmed that they follow a normal distribution.

Table IV.

Posterior means (and 95 per cent posterior intervals) for parameters in the change point model.

Parameter	Prior 1	Prior 2	Prior 3	Change point fixed
β0	35.3 (32.5, 38.7)	32.3 (30.0, 34.7)	34.3 (31.3, 37.6)	34.0 (31.3, 36.2)
β1	−0.81 (−0.89, −0.74)	−0.85 (−0.93, −0.77)	−0.82 (−0.89, −0.75)	−0.82 (−0.89, −0.75)
β2	−0.16 (−0.27, −0.06)	−0.14 (−0.25, −0.03)	−0.17 (−0.27, −0.07)	−0.13 (−0.22, −0.05)
β3	6.4 (2.9, 9.4)	9.3 (6.9, 11.8)	7.8 (4.3, 11.0)	7.6 (5.2, 10.6)
${\sigma }_0^2$	105 (75, 132)	111 (86, 138)	96 (64, 128)	110 (90, 133)
${\sigma }_1^2$	0.037 (0.016, 0.069)	0.014 (0.003, 0.037)	0.012 (0.001, 0.043)	0.027 (0.001, 0.075)
${\sigma }_2^2$	0.151 (0.087, 0.232)	0.160 (0.098, 0.239)	0.106 (0.049, 0.181)	0.090 (0.038, 0.166)
${\sigma }_3^2$	14.2 (0.2, 49.1)	18.5 (2.6, 43.7)	42.6 (10.3, 79.7)	—
${\sigma }_{02}^2$	−2.71 (−4.11, −1.45)	−3.04 (−4.40, −1.85)	−2.65 (−4.05, −1.42)	−2.27 (−3.48, −1.23)
${\sigma }_{\mathrm{e}}^{02}$	22.8 (20.5, 25.4)	23.0 (20.6, 25.6)	23.5 (21.1, 26.2)	24.1 (21.5, 26.9)

The estimates of the fixed effects (β₀, β₁, β₂, and β₃) reflect a general decline in cognitive function. The mean age for the change point is 73 years, and the mean slope is −0.65 points/year before the change point and −0.99 points/year after the change point. The correlation between an individual’s level at the change point and the difference in slopes before and after the change point is equal to −0.83. The negative correlation suggests that individuals with a high level at the change point have a larger (negative) difference in slope for the two phases.

Because the variance of the change point ( ${\sigma }_3^2$) appears to be difficult to estimate, we also consider a model where the age when a change occurs is the same for all individuals and treated as a fixed effect. A summary of the posterior distribution for the parameters in this model is also included in Table IV.

The results of the change point models were compared with the linear and the quadratic random effect models based on DIC (Table V). The results suggest that the random change point model is preferable compared with both the linear and the quadratic models. The model where all individuals have the same change point also has a larger value of DIC, suggesting that it is not a useful description of the data.

Table V.

Comparison of model goodness of fit using DIC.

Model	DIC	pD	D̄
Linear	8400.53	478.05	7922.48
Quadratic	8409.95	428.14	7981.80
Change point 1	8326.95	467.55	7859.40
Change point 2	8325.05	456.15	7868.90
Change point 3	8303.04	401.86	7901.18
Change point fixed	8387.31	457.57	7929.73

As discussed earlier, in the analysis of cognitive function in SATSA, there is a special interest in the predicted mean and variance as a function of age. Figure 2 displays the observed mean score for the SATSA sample as a function of age (moving average over 50 observations) together with the predicted mean based on the linear, the quadratic, and the change point models. The predicted means are based on the predicted outcomes from the posterior distribution of the individual-specific random effects. From Figure 2 it is clear that the observed overall trend is close to linear and the predicted mean curves are all close to the observed mean curve.

Figure 2.

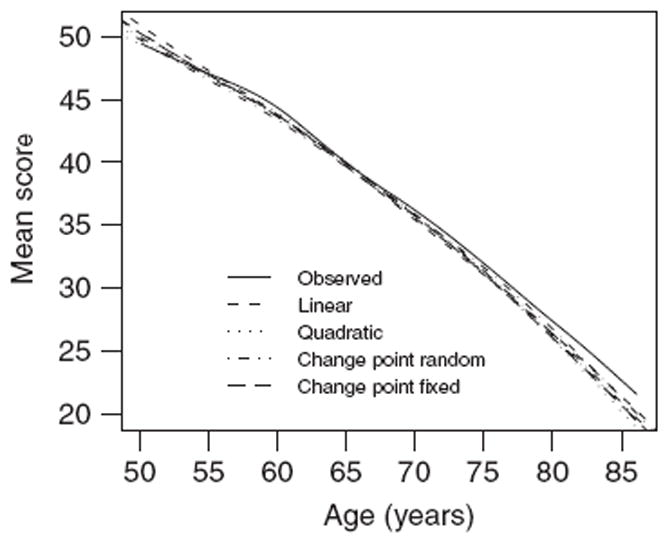
Observed and predicted mean curves for cognitive function.

Figure 3 displays the observed variance curve together with model-induced variance curves. The variance is calculated in a similar way as the mean curve, here using both the predicted outcomes and the predicted residual variance. The plot indicates that the variability in observed test scores increases in the range 60–70 years. Apparently, all the models considered imply very different assumptions about the variability, although the mean curves in Figure 2 are similar. The variance curve predicted from the random change point model approximately follows the observed variance curve, although the variance is somewhat underestimated in the beginning and in the end of the age span considered (where the least data are available). This is the case also for the change point model where the change point is treated as a fixed effect. In contrast, both the linear and the quadratic variance curves are far from the empirical variance curve.

Figure 3.

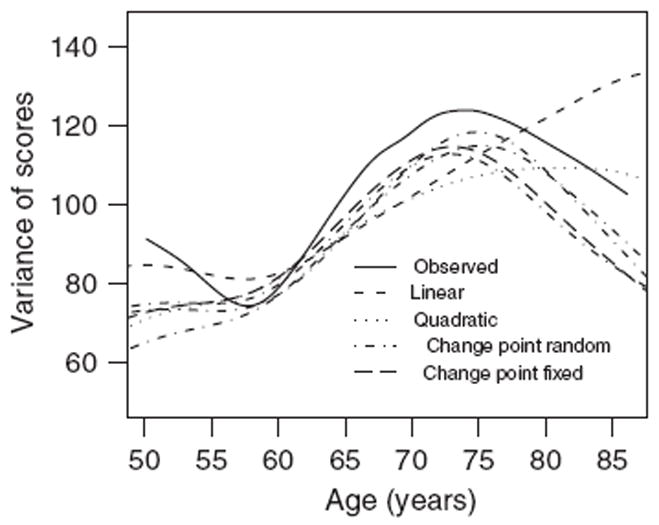
Observed and predicted variance curves for cognitive function.

6. DISCUSSION

We have demonstrated the use of random change point models for modeling variability in longitudinal data. Although neglected in many applications of linear random effects models, it is well known that the form of the random effects model has implications for the variance structure [12]. This is especially problematic in applications where the primary interest is in the variance, which is the case in family studies. On the basis of an empirical study of cognitive function in old age, we showed that in contrast to the linear and the quadratic models, the random change point model is flexible in capturing variability as a function of age.

We used a Bayesian approach and MCMC simulation to fit all models. The linear and the quadratic random effects models belong to the family of linear random effects models, and thus they can easily be estimated using maximum likelihood methods. We used a Bayesian approach here to simplify comparisons based on DIC, which is a summary measure of goodness of fit. We also judge the models’ ability to predict the variance as a function of age.

The reason for the greater flexibility in predicting variance is not obvious but supposedly in part related to the fact that the change point model includes more parameters than the linear and the quadratic models. For the linear and the quadratic models, which both belong to the family of linear random effects models, it is possible to derive an analytic expression for the variance as a function of the model parameters and age. For example, the variance curve for the linear model is a quadratic function of age. For the random change point model, however, it is not possible to derive such an expression for the variance and it is therefore difficult to identify exactly how the increased number of parameters improves the flexibility of the model.

MCMC simulation based on Gibbs sampling was shown to be a useful tool for estimating the random change point model. This approach is conceptually straightforward, albeit computationally demanding. In a small simulation study the approach performed well also in situations with as little as five repeated measures and a large variability in the change point. Both the simulation study and the analysis of empirical data suggest that the largest difficulty lies in the estimation of the change point itself.

Some issues regarding this Bayesian approach merit further attention. For example, it is not yet clear how prior distributions for the variance–covariance parameters should be chosen to be non-informative. It has been suggested that the inverse-gamma distribution, often used as non-informative for a variance parameter, may have problems [23]. Instead, a uniform prior on the hierarchical standard deviation is recommended. The generalization to priors for a multivariate nonlinear hierarchical model, such as the random change point model, merits further investigation.

In spite of the fairly complex structure of the random change point model, it may still not capture all features of cognitive evolution. For example, censored change points are not explicitly modelled. In studies of cognition in old age, loss to followup is also a reality. If the dropout is ‘non-ignorable’ it has to be accounted for explicitly to avoid selection bias. Jacqmin-Gadda et al. [9]adapted a random change point model for cognitive decline tied to a survival model for dementia to address this issue.

Other potential extensions of the model include the extension to several change points, which would be possible with data containing enough measurement time points. The model could also be extended by including covariates, and by relaxing the assumption of constant residual variance to allow for heterogeneity in residual errors [24].

APPENDIX A: IMPLEMENTATION USING WinBUGS

The following code was used to fit the random change point model (with priors 3):

model {
 for (i in 1:N) {
  y [i] ~ dnorm(mu[i],e.tau)
   mu [i] <- b[id[i],1] + b1 [id[i]] * (age[i]-b3 [id[i]]) +
    b[id[i],2] * (age[i] -b3 [id[i]]) * (2*step (age[i] - b3 [id[i]])-1)
 }
 for(j in 1:M) {
  b[j,1:2] ~ dmnorm (b.mu [1:2] ,b.tau[1:2,1:2])
  b1 [j]  ~ dnorm(b1.mu, b1.tau)
  b3[j] ~ dnorm(b3.mu, b3.tau)
 }
 b.mu [1:2] ~ dmnorm(b.mean [1:2], b.prec [1:2,1:2])
 b1.mu ~ dnorm (1,0.001)
 b3.mu ~ dnorm (9,0.001)
 b1.tau ~ dgamma (0.001,0.001)
 b3.tau ~ dgamma(0.001,0.001)
 b.tau[1:2,1:2] ~ dwish (R[1:2, 1:2] ,2)
 e.tau ~ dgamma (0.001,0.001)
 }
list (b.mean = c(30, 1), b.prec = structure (.Data=c (0.01, 0, 0,
0.01), .Dim = c(2, 2)), R = structure (.Data=c (20, 0, 0, 0.1), .Dim =
c(2, 2)))