Mechanical Stress is Associated with Right Ventricular Response to Pulmonary Valve Replacement in Patients with Repaired Tetralogy of Fallot

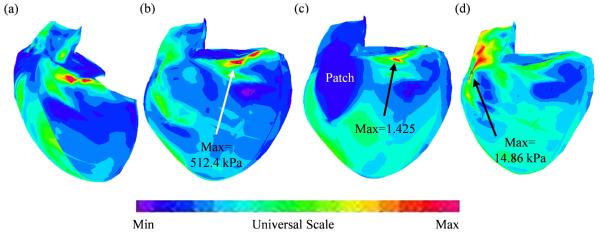
Abstract

Background

Patients with repaired tetralogy of Fallot (TOF) account for a substantial proportion of cases with late-onset right ventricular (RV) failure. The current surgical approach, which includes pulmonary valve replacement/insertion (PVR), has yielded mixed results. Therefore, it may be clinically useful to identify parameters that can potentially be used to predict RV function response to PVR.

Methods and Results

Cardiac magnetic resonance (CMR) data before and 6-month after PVR were obtained from 16 patients with repaired TOF (8 m, 8 f, median age 42.75). RV ejection fraction (EF) change from pre- to post-PVR was used as the outcome. The patients were divided into Group 1 (n=8, better outcome) and Group 2 (n=8, worst outcome). CMR-based patient-specific computational RV/LV models were constructed and RV mechanical stress and strain, wall thickness (WT), curvature, and volumes were obtained for analysis. Our results indicated that RV wall stress was the best single predictor for post-PRV outcome with an area under the receiver operating characteristic curve of 0.819. Mean values of stress, strain, WT, and longitudinal curvature differed significantly between the two groups with RV wall stress showing the largest difference. Mean RV stress from Group 2 was 103% higher than that from Group 1.

Conclusion

Computational modeling and RV stress may be used as a potential tool to identify RV function response to PVR. Large-scale clinical studies are needed to validate these preliminary findings.

Introduction

Survival of patients with tetralogy of Fallot (TOF) has steadily increased since the introduction of open-heart surgery, with operative mortality currently <2% [1]. Survival past the first two decades of life has also improved with recent reports showing a 30-year survival rate nearing 90% [2]. Since this operation was first performed in the mid 1950s, a conservative estimate projects that the number of survivors of TOF repair in the United States exceeds 100,000 and increases by 3,000-4,000 patients every year [3]. As a result of the surgical reconstruction of the right ventricular (RV) outflow tract and other operative sequelae, patients are exposed to chronic pulmonary regurgitation that leads to progressive RV dilatation and dysfunction. The current surgical approach to address chronic pulmonary regurgitation includes pulmonary valve replacement/insertion (PVR) with or without RV remodeling. However, while most patients demonstrate a variable degree of decrease in RV size, many do not experience an improvement in RV function and some show a decline after PVR [3-9]. Facilitated by the advent of cardiac magnetic resonance imaging (CMR) imaging [8,10], data from the INDICATOR cohort has demonstrated that preoperative RV ejection fraction (EF) is an independent predictor of death and sustained ventricular tachycardia in this population [11].

Recent advances in computational modeling, methods, and computer technology have facilitated the use of computer-simulated procedures to aid clinical decision-making, potentially replacing empirical and often risky clinical experimentation to examine the efficiency and suitability of various reconstructive cardiac procedures. Recent reviews of the modeling development, especially CMR-based ventricle modeling could be found in [12-14]. In our previous papers, patient-specific CMR-based computational RV and left ventricular (LV) models with fluid-structure interactions were introduced to assess outcomes of various RV reconstruction techniques with different scar tissue trimming and patch sizes [15-18]. These investigations on TOF patients undergoing PVR have focused on surgical remodeling of RVOT in order to improve functional recovery of the RV by removing or reducing the non-contracting tissue (scar and patch) in the outflow tract free wall [19]. In our previously reported randomized clinical trial of surgical remodeling of the RVOT in 64 patients with repaired TOF undergoing PVR, we found no significant difference between groups in change in RV EF from pre- to 6 months post PVR [19]. However, it has remained unclear why some patients had experienced an improvement in RV EF whereas in others RV function had deteriorated.

In this study, 3D computational RV/LV models were constructed for 16 ToF patients based on their patient-specific pre-PVR CMR data, material parameters chosen to match CMR data and catheter-measure pressure conditions. RV stress, strain, volume, ventricular wall thickness, longitudinal- and circumferential curvatures were obtained and used to identify morphologic or mechanical stress/strain markers that may be associated with improved RV function after PVR.

Methods

Patients

The Boston Children’s Hospital Committee on Clinical Investigation approved the study. CMR data before and 6 months after PVR were obtained from 16 ToF patients (8 male, median age 42.75, see Table 1, online) who were previously enrolled in our RV surgical remodeling trial [19]. For this analysis, we selected the 8 best (Group 1) and 8 worst (group 2) responders based on their change in RV EF from pre- to post-PVR. RV EF was chosen due to its strong association with adverse clinical outcomes in patients with repaired TOF. Demographic information, RV volumes, pressure conditions, and EF before and after PVR are summarized in Table 1 (online).

Table 1.

Demographic and CMR data before and after PVR

			Pre-PVR					Post-PVR
Pt. #	S e x	Age (y)	Begin- Filling P	Begin- Ejection P	RV EDV (cm3)	RV ESV (cm3)	RV EF (%)	RV EDV (cm3)	RV ESV (cm3)	RV EF (%)	ΔEF (%)
Group 1
P1	M	22.5	21.6	31.4	406.9	254.5	37.5	188.3	115.0	38.9	1.4
P2	F	38.5	6	28	328.8	196.0	40.4	168.3	106.0	37.0	−3.4
P3	M	47.7	2	31	408.8	254.8	37.7	327.2	212.3	35.1	−2.6
P4	M	50.0	3	33	364.6	239.5	34.3	220.0	150.9	31.4	−2.9
P5	F	42.0	10	45	323.3	177.8	45.0	222.2	113.3	49.0	4.0
P6	F	14.3	3	29	204.0	104.3	48.8	136.5	62.3	54.4	5.6
P7	F	15.3	2	15	193.7	105.1	45.7	177.9	84.8	52.3	6.6
P8	M	17.0	3	27	188.3	108.3	42.5	135.5	75.2	44.5	2.0
Mean ± SD		30.9 ±15.2	3.90 ±2.79	29.9 ±8.24	302.3. ±93.9	180.0 ±67.0	41.5 ±4.9	197.0 ±61.9	115.0 ±48.0	42.8 ±8.5	1.4 ±3.9
Group 2
P9	F	56.9	5	41	385.1	184.6	52.1	216.4	142.6	34.1	−18.0
P10	M	11.6	10	36	204.2	121.3	40.6	156.3	106.0	32.2	−8.4
P11	M	43.5	17	65	665.1	464.0	30.2	391.0	332.4	15.0	−15.2
P12	M	54.1	4	63	334.8	170.8	49.0	306.2	177.6	41.0	−7.0
P13	F	49.5	12	52	277.2	151.3	45.4	244.8	145.9	40.4	−5.0
P14	M	17.8	2	30	365.0	178.0	51.2	292.1	170.2	41.7	−9.5
P15	F	44.6	11	50	299.0	186.0	37.8	218.7	163.0	25.5	−12.3
P16	F	45.3	9	49	571.1	371.3	35.0	398.7	312.6	21.6	−13.4
Mean ± SD		40.4 ±16.6	8.75 ±4.89	48.3 ±12.3	387.7 ±154.8	228.4 ±121.3	42.7 ±8.0	278.0 ±85.8	193.8 ±82.6	31.4 ±9.9	−11.1 ±4.4
P- value*		0.25	0.02	0.003	0.20	0.34	0.73	0.05	0.03	0.027	<0.001

^*P-value comparing Group 1 with Group 2.

Abbreviations: F, Female; M, male; EDV, end-diastolic volume; ESV, end-systolic volume; EF, ejection fraction.

Data acquisition and modeling

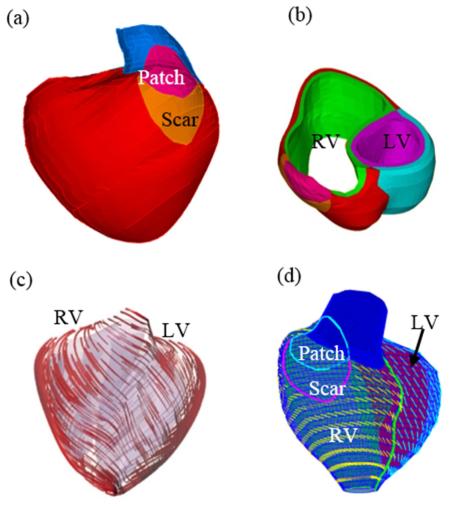
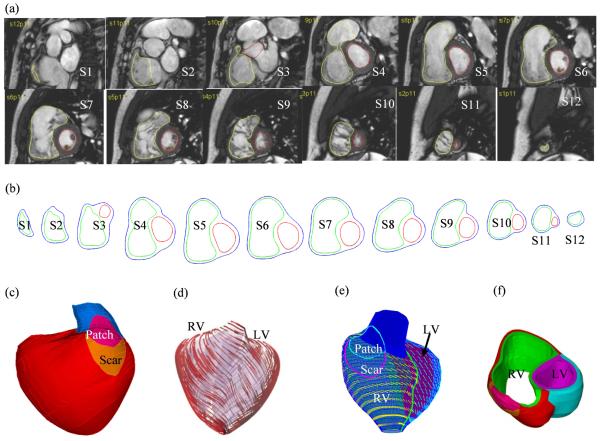
Data acquisition and modeling procedures were described in [12,15-17] and details are omitted here to avoid repetition. Some key points are summarized below. CMR studies were performed with 1.5 Tesla scanners (GE Medical Systems, Milwaukee, Wisconsin, and Philips Healthcare, Best, the Netherlands). For each cine MR acquisition, 30 frames per cardiac cycle were reconstructed. The location and extent of the Right Ventricular Outflow Tract (RVOT) patch was determined based on cine imaging and delayed enhancement CMR and was subsequently confirmed by surgical inspection at the time of PVR. 3D RV/LV geometry and computational meshes were constructed as previously described (Fig. 1) [15-17].

Figure 1.

CMR-based model construction process. (a) CMR image of a patient, end of systole; (b) segmented contours; (c) reconstructed 3D geometry; (d)-(e) fiber orientation; (g) two-layer construction.

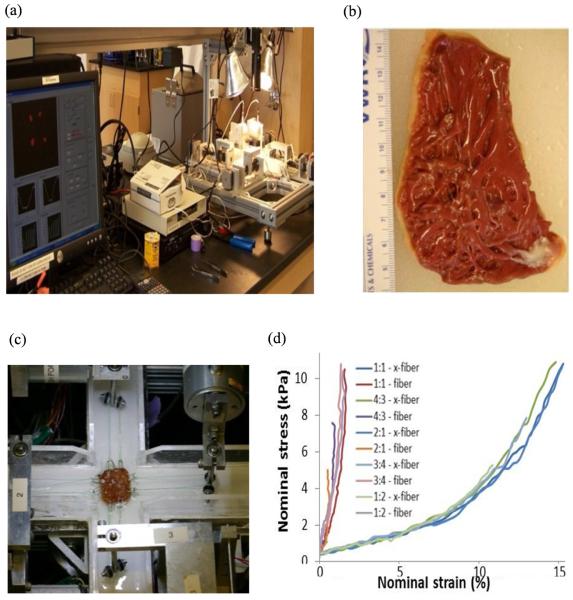
Because tissue mechanical properties are essential for computational ventricular modeling, based on the methods of Sacks and Chuong [20], Billard and Sacks [21], and Humphrey [22], we generated the first complete biaxial mechanical data set for ventricular tissues using a cadaveric normal human heart sample (Fig 2, online). Detailed description of the custom biaxial testing device and method has been previously described [20-21]. We were able to choose parameter values in our modified Mooney-Rivlin model to fit our direct measurement of biaxial stress-strain data. It should be noted that the ex vivo biaxial testing data was used to support the choice of our material model, i.e., the modified anisotropic Mooney-Rivlin model (equations are given later) is able to represent ventricle tissue anisotropic material properties. The parameter values in the material model for each patient was determined using CMR-measured RV volume data.

Figure 2 (online).

Biaxial mechanical testing and initial results. (a) The biaxial testing apparatus; (b) human right ventricle tissue sample; (c) tissue sample mounted for biaxial test; (d) anisotropic data from the human right ventricle sample.

The governing equations for all material models were:

$$\rho {\mathrm{V}}_{i,\mathrm{tt}}={\sigma }_{\mathrm{ij},j},\mathrm{i},\mathrm{j}=1,2,3;\mathrm{sum}\mathrm{over}\mathrm{j},$$ (1)

$${\epsilon }_{\mathrm{ij}}=({\mathrm{v}}_{i,j}+{\mathrm{v}}_{j,i}+{\mathrm{v}}_{\alpha ,i}{\mathrm{v}}_{\alpha ,j})∕2,i,j,\alpha =1,2,3,$$ (2)

where σ is the stress tensor, ε is the strain tensor, v is displacement, and ρ is material density. The normal stress was assumed to be zero on the outer (epicardial) RV/LV surface and equal to the pressure conditions imposed on the inner (endocardial) RV/LV surfaces. Structure-only RV/LV models were used to optimize model computing time. These models provided RV volume, ejection fractions, and RV stress/strain values for analysis. RV pressure was obtained from pre-PVR cardiac catheterization.

The RV and LV materials were assumed to be hyperelastic, anisotropic, and nearly incompressible. The patch and scar materials were assumed to be hyperelastic, isotropic and nearly incompressible. The nonlinear Mooney-Rivlin model was used to describe the nonlinear anisotropic and isotropic material properties. The strain energy function for the isotropic modified Mooney-Rivlin model is given by [15-17]:

$$\mathrm{W}={\mathrm{c}}_1({\mathrm{I}}_1-3)+{\mathrm{c}}_2({\mathrm{I}}_2-3)+{\mathrm{D}}_1[\exp \left({\mathrm{D}}_2({\mathrm{I}}_1-3)\right)-1],$$ (3)

where I₁ and I₂ are the first and second strain invariants given by,

$${\mathrm{I}}_1=\sum C_{ii},{\mathrm{I}}_2=1∕2[{{\mathrm{I}}_1}^2-{\mathrm{C}}_{\mathrm{ij}}\mathrm{C}\mathrm{ij}],$$ (4)

C = [C_ij] = X^TX is the right Cauchy-Green deformation tensor, X = [X_ij] = [∂x_i/∂a_j], (x_i) is the current position, (a_i) is the original position, c_i and D_i are material parameters chosen to match experimental measurements [15,22]. The parameter values are: Scar, c₁= 19.23 kPa, c₂= 0, D₁= 19.23 kPa, D₂= 9.0; Patch, c₁= 38.45 kPa, c₂= 0, D₁= 38.45 kPa, D₂= 9.0.

The strain energy function for the anisotropic modified Mooney-Rivlin model anisotropic model was obtained by adding an additional anisotropic term in Eq. (4) [16-17]:

$$\mathrm{W}={\mathrm{c}}_1({\mathrm{I}}_1-3)+{\mathrm{c}}_2({\mathrm{I}}_2-3)+{\mathrm{D}}_1[\exp \left({\mathrm{D}}_2({\mathrm{I}}_1-3)\right)-1]+{\mathrm{K}}_1∕\left(2\mathrm{K}2\right)\exp [{\mathrm{K}}_2{({\mathrm{I}}_4-1)}^2-1],$$ (5)

where I ₄ = C_ij (n_f)_i (n_f)_j, C_ij is the Cauchy-Green deformation tensor, n_f is the fiber direction, K₁ and K₂ are material constants. Choosing c₁ = 0.35 kPa, c₂ = 0, D₁ = 0.063 kPa, D₂ = 5.3, K₁ = 1.91 kPa, K₂ = 6.00, it was shown that stress-strain curves derived from Eq. (5) agreed very well with the stress-strain curves from the anisotropic (transversely isotropic) strain-energy function with respect to the local fiber direction given in McCulloch et al. [13].

$$\mathrm{W}=\frac{C}{2}({\mathrm{e}}^{\mathrm{Q}}-1),$$ (6)

$$\mathrm{Q}=b_1{E}_{ff}^2+b_2(E_{cc}^2+E_{rr}^2+E_{cr}^2+E_{rc}^2)+b_3(E_{fc}^2+E_{cf}^2+E_{fr}^2+E_{rf}^2),$$ (7)

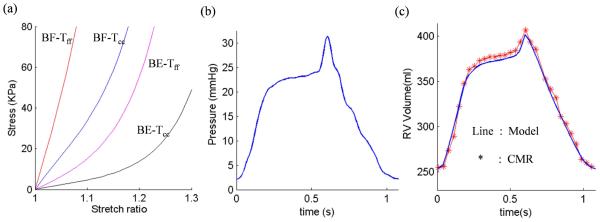
where E_ff is fiber strain, E_cc is cross-fiber in-plane strain, E_rr is radial strain, and E_cr, E_fr and E_fc are the shear components in their respective coordinate planes, C, b₁, b₂, and b₃ are parameters to be chosen to fit patient data. Time-dependent parameter values (c₁(t), D₁(t)) and C(t) in (5)-(6) were chosen to fit the CMR-measured RV volume data for each patient to get patient-specific material models (Fig. 3, online). Active contraction and expansion of myocardium were modeled by material stiffening and softening in our model reflected in the change of (c₁(t), D₁(t)) and C(t) values in (5)-(6) .

Figure 3 (online).

Material Stress-Stretch curves, pressure conditions used in the paper and computational RV volume curve matching CMR-measured data. (a) Stress-Stretch curves from Mooney-Rivlin anisotropic RV tissue models used in this paper. Model parameter values in Eq. (6)-(7) for a patient: beginning-filling (BF): C=72.16 kPa, b₁=8.7875; b₂=1.7005; b₃=0.7743; beginning-ejection (BE): C=9.922 kPa, b₁=8.7875; b₂=1.7005; b₃=0.7743. T_ff: Stress in the fiber direction; Tcc: Stress in fiber circumferential direction. (b) Imposed inner RV pressure; (c) Model validation: computational RV volume from the FSI model matching CMR-measured RV volume Data $(\mathrm{error}=\frac{\mid CMR\left(i\right)-num\left(i\right)\mid }{\sum \mid CMR\left(i\right)\mid }=0.0167.gt2\%)$.

Because patient-specific fiber orientation data was not available, we chose to construct a 2-layer RV/LV model and set fiber orientation angles using the fiber angles published by Hunter et al. (Fig. 1) and available human data [14,23]. Figure 1 shows epicardial and endocardial fiber layers from human and a pig hearts and how the 2-layer RV/LV model was constructed [15-17].

Solution methods and simulation procedures

The anisotropic RV/LV computational models were constructed for the 16 patients and the models were solved by ADINA (ADINA R&D, Watertown, MA, USA) using unstructured finite elements and the Newton-Raphson iteration method. Stress/strain distributions were computed. Because stress and strain are tensors, for simplicity, maximum principal stress (Stress-P₁) and strain (Strain-P₁) were used and referred to as stress and strain in this paper. Figure 4 (online) shows stress/strain plots from a cut-surface of an RV model, illustrating stress/strain distribution patterns at the beginning-of-ejection and beginning-of-filling phases.

Figure 4 (online).

Selected cut-surface, maximum principal stress (Stress-P₁) and strain (Strain-P₁) corresponding to end-of-diastole and end-of-systole pressure conditions. (a) Position of the cut surface; (b) Stress-P₁, end-of-diastole; (c) Strain-P₁, end-of-diastole; (d) Stress-P₁, end-of-systole.

Wall thickness and curvature calculations

In each CMR data set, every slice was divided into 4 quarters, each with equal inner wall circumferential length. Ventricular wall thickness (WT), circumferential curvature (C-curvature), longitudinal curvature (L-curvature), and stress/strain were calculated at all nodal points (100 points per slice, 25 points per quarter). Averaging their quantities over the 25 points in each quarter provided the “quarter” values of these parameters.

C-curvature (κ_c) at each point on an RV inner contour was calculated using:

$${\kappa }_c=\frac{x^{\prime }{y^{\prime }}^{\prime }-{x^{\prime }}^{\prime }{y}^{\prime }}{{({x^{\prime }}^2+{y^{\prime }}^2)}^{3∕2}}$$ (8)

where the contour was a planar curve, x,y are treated as an arc function, and the derivatives were evaluated using neighboring points on the contour. L-curvature (κ) at each point on an RV inner contour was calculated using:

$$\kappa =\frac{\sqrt{{({z^{\prime }}^{\prime }\left(t\right)y^{\prime }\left(t\right)-{y^{\prime }}^{\prime }\left(t\right)z^{\prime }\left(t\right))}^2+{({x^{\prime }}^{\prime }\left(t\right)z^{\prime }\left(t\right)-{z^{\prime }}^{\prime }\left(t\right)x^{\prime }\left(t\right))}^2+{({y^{\prime }}^{\prime }\left(t\right)x^{\prime }\left(t\right)-{x^{\prime }}^{\prime }\left(t\right)y^{\prime }\left(t\right))}^2}}{{({x^{\prime }}^2\left(t\right)+({y^{\prime }}^2\left(t\right)+\left({z^{\prime }}^2\left(t\right)\right)}^{3∕2}}$$ (9)

where the longitudinal curve is given by X = (x(t), y(t), z(t)). The derivatives were evaluated using points from neighboring slices vertically below and above the point being considered. Interpolations were used to obtain vertical neighboring points from adjacent slices. One-sided formulas were used for the top and bottom slices.

Statistical analysis

Continuous variables (RV volumes, WT, C- and L-curvatures, and stress and strain values) were summarized as mean ± SD or median (range) and compared between the outcome groups using an unpaired Student t-test. Associations between pre-PVR RV parameters and the outcome (change in RV EF) were explored using Pearson correlation analysis. Logistic regression analysis was used to identify pre-PVR parameters that best predicted the primary outcome—RV EF response to PVR. The sensitivity and specificity of these parameters and their area under the receiver operating characteristic curve (AUC) were determined.

To examine the validity of the logistic regression model, a 2-fold cross-validation procedure was used for model-fitting and prediction procedure. Specifically, we randomly selected 8 out of 16 patients as training data to fit a model that reached the best agreement between predictors’ values and the binary group outcome (optimal versus suboptimal RV EF response to PVR). The data of the remaining patients (test data) were then fed into the model to calculate the probabilities of their outcome group status. The training and test data were then interchanged and the same procedure was followed to complete a 2-fold cross-validation. In order to stabilize the result, we repeated the 2-fold cross-validation 100 times (each with a random partition of training and testing groups). The probabilities of group assignments from all cross-validation procedures were then combined to calculate the final prediction values.

All statistical tests were 2-sided and results were considered statistically significant if P<0.05. Data analysis was performed using R package [24].

Results

Agreement between CMR Data and Computational Modeling

The stress-stretch curves and parameter values of the RV/LV tissues at the beginning of ejection (BE) and beginning of filling (BF) in a representative model are shown in Fig. 3a (online). The imposed RV pressure conditions and computational RV volume data used in the same model are presented in Fig. 3b (online). Good agreement between computational and CMR-measured volume data was found (error < 2%) as exemplified in Fig. 3c (online).

RV EF change (ΔEF) correlated negatively with RV stress and volume

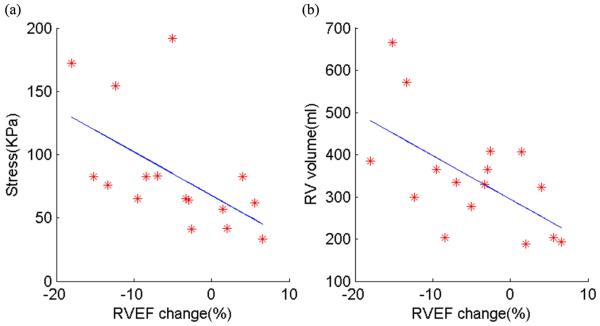
Table 2 summarizes the RV size, geometric parameters, and stress/strain data in the study patients. Correlation analyses were performed to determine whether changes in RV EF from pre- to post-PVR were associated with RV size (volumes and WT), geometry (C- and L-curvatures), or stress/strain data. In this cohort, RV EF change correlated negatively with stress (r= −0.56, P=0.025, see Fig. 5a, online) and with pre-PVR RV end-diastole volume (r= −0.60, P= 0.015, see Fig. 5b, online), but did not correlate with WT, C-curvature, L-curvature, or strain.

Table 2.

Summary of geometric and stress/strain parameters averaged in each patient at onset of ejection and their correlations with RVEF change.

	ΔEF (%)	WT (cm)	C-Cur (1/cm)	L-Cur (1/cm)	RV EDV (mL)	Stress (kPa)	Strain
Group 1
	1.4	0.39	0.47	1.24	406.9	56.9	0.29
	−3.4	0.34	0.39	0.77	328.8	65.3	0.43
	−2.6	0.65	0.37	1.01	408.8	41.0	0.33
	−2.9	0.49	0.54	1.54	364.6	64.1	0.36
	4.0	0.47	0.43	0.96	323.3	82.4	0.44
	5.6	0.48	0.50	1.20	204.0	61.9	0.48
	6.6	0.42	0.53	1.84	193.7	33.5	0.46
	2.0	0.51	0.53	1.85	188.3	42.0	0.40
Mean ± SD	1.34 ±3.9	0.47 ±0.09	0.47 ±0.07	1.3 ±0.4	302.3 ±93.9	55.9 ±16.1	0.40 ±0.07
Group 2
	−18.0	0.48	0.42	0.91	385.1	172.1	0.66
	−8.4	0.41	1.34	1.32	204.2	82.9	0.49
	−15.2	0.80	0.36	0.59	665.1	82.4	0.23
	−7.0	0.71	0.44	0.72	334.8	83.1	0.42
	−5.0	0.45	0.46	0.97	277.2	191.7	0.66
	−9.5	0.43	0.65	1.60	365.0	65.4	0.44
	−12.3	0.46	0.44	1.23	299.0	154.3	0.51
	−13.4	0.59	0.33	1.25	571.1	76.2	0.34
Mean ± SD	−11.1 ±4.4	0.54 ±0.14	0.56 ±0.33	1.07 ±0.34	387.7 ±154.8	113.5 ±50.4	0.47 ±015
*R-value		−0.35	0.01	0.41	−0.60	−0.56	−0.11
*P-value		0.18	0.97	0.11	0.015	0.025	0.68

R- and P-values are for the correlations between change in RV EF and geometric and stress/strain data. Abbreviations: WT, wall thickness; C-Cur, circumferential curvature; L-Cur, longitudinal curvature; RV, right ventricle.

Figure 5 (online).

RVEF change correlated negatively with stress (r= − 0.56, p=0.025) and with pre-PVR RV volume (r= − 0.60, p= 0.015). (a) Stress vs. EF change; (b) pre-PVR RV volume vs. EF change.

3.3 Group comparison: RV stress was much higher in Group 2 than that of Group 1

Table 3 summarizes the comparison of RV WT, C-curvature, L-curvature, volume, and stress and strain values between the outcome groups at the onsets of ejection and filling. At the onset of ejection (maximal volume and pressure), mean RV stress was 103% higher in Group 2 as compared with Group 1 (113.5±50.4 vs. 55.9±16.12 kPa; P=0.008). Furthermore, stress was the only parameter that showed significant differences between the two groups. Similar findings were noted at onset of filling with substantially lower values (Table 3).

Table 3.

Comparison of RV volumes, geometric parameters, and stress/strain between Group 1 and Group 2 at onset of emptying and onset of filling.

	Beginning of Ejection (Maximal Volume and Pressure)			Beginning of Filling (Minimal Volume and Pressure)
	Group 1	Group 2	P-value	Group 1	Group 2	P-value
RV volume (mL)	302.3±93.9	387.7±154.	0.20	180.0±67.0	228.4±121.3	0.34
WT (cm)	0.46±0.09	0.54±0.14	0.25	0.51±0.10	0.61±0.17	0.21
C-Cur (1/cm)	0.47±0.07	0.55±0.33	0.50	0.59±0.10	0.67±0.35	0.55
L-Cur (1/cm)	1.30±0.40	1.07±0.34	0.24	1.35±0.53	1.08±0.31	0.24
Stress (kPa)	55.9±16.1	113.5±50.4	0.008	4.15±3.24	10.49±5.81	0.017
Strain	0.40±0.07	0.47±0.14	0.25	0.04±0.04	0.08±0.06	0.20

Data is based on quarter mean values (see Methods for details). Values are expressed as mean ± standard deviation. Abbreviations as in Table 2.

RV stress is the best predictor for the outcome group category using median as threshold

Using the medians of the parameters shown in Table 3 as threshold values, we examined whether the pre-operative measurements in each patient predicted their group category. For example, the median RV stress at onset of ejection for the 16 patients was 70.8 kPa. If a patient’s pre- operative mean stress value was lower, the patient was predicted to belong to Group 1 and if the measurement was higher, the patient was predicted to belong to Group 2. If the prediction matches the actual group assignment, the prediction was considered “True.” Otherwise, the prediction was considered “False.” The results of the analysis are shown in Table 4. Using the values noted in the example above, group assignments based on the median value of RV stress were correct in 14 of the 16 cases (87.5%, 95% confidence interval 62.5%, 100%). Other parameters showed lower rates of correct group assignment.

Table 4.

True-or-false prediction results using the mean parameter values to predict patient’s group.

Patient	RV EDV (mL)	WT (cm)	C-Cur (1/cm)	L-Cur (1/cm)	Stress	Strain
P1	406.9 F	0.39 T	0.47 T	1.24 T	56.9 T	0.29 T
P2	328.8 T	0.34 T	0.39 F	0.77 F	65.3 T	0.43 T
P3	408.8 F	0.65 F	0.37 F	1.01 F	41.0 T	0.33 T
P4	364.6 F	0.49 F	0.54 T	1.54 T	64.1 T	0.36 T
P5	323.3 T	0.47 T	0.43 F	0.96 F	82.4 F	0.44 F
P6	204.0 T	0.48 F	0.50 T	1.20 F	61.9 T	0.48 F
P7	193.7 T	0.43 T	0.53 T	1.84 T	33.5 T	0.46 F
P8	188.3 T	0.51 F	0.53 T	1.85 T	42.0 T	0.40 T
P9	385.1 T	0.48 T	0.42 T	0.91 T	172.1 T	0.66 T
P10	204.2 F	0.41 F	1.34 F	1.32 F	82.9 T	0.49 T
P11	665.1 T	0.80 T	0.36 T	0.59 T	82.4 T	0.23 F
P12	334.8 T	0.71 T	0.44 T	0.72 T	83.1 T	0.42 F
P13	277.2 F	0.46 F	0.46 F	0.97 T	191.7 T	0.66 T
P14	365.0 T	0.43 F	0.65 F	1.60 F	65.4 F	0.44 T
P15	299.0 F	0.46 F	0.44 T	1.24 F	154.3 T	0.51 T
P16	571.1 T	0.59 T	0.33 T	1.25 F	76.2 T	0.34 F
Median	331.8	0.47	0.45	1.21	70.8	0.43
True Prediction	62.5%	50%	62.5%	50%	87.5%	62.5%
Confidence Interval	(37.5%, 87.5%)	(37.5%, 87.5%)	(12.5%, 75%)	(37.5%, 87.5%)	(62.5%, 100%)	(37.5%, 87.5%)

The median values were used as the thresholds for group assignments. Abbreviations as in Table 2.

RV stress has the best prediction accuracy among the 6 parameters using the logistic regression model

The logistic regression method was applied to all 63 possible combinations of the 6 candidate predictors WT, Ccur, Lcur, RV volume, stress, and strain to calculate their prediction accuracy for patient’s group category. Table 5 shows the 6 best combinations (out of 63) of RV parameters that correctly assigned patients to their ultimate outcome group. Pre-PVR RV stress was the best single predictor among the 6 individual parameters with an area under the ROC curve of 0.819. The second best single predictor was strain with an area under the ROC curve of 0.544. The best combination of parameters included WT + C-cur + RV volume + Strain an area under the ROC curve of 0.848. Among all combinations of parameters, stress was the best predictor based on sensitivity and specificity.

Table 5.

Prediction sensitivity, specificity, and AUC values RV parameters for outcome group prediction by the Logistic regression method.

Parameter	Probability CutOffs	Sensitivity	Specificity	Sensi+ Speci−	AUC	AUC Average	95% Confidence Interval		Rank
WT+C-cur+ Vol+Strain	1.000	0.75	0.78	1.53	0.840	0.848	0.838	0.850	1
Stress	0.626	0.80	0.85	1.65	0.822	0.819	0.818	0.822	2
Ccur+Vol+ Stress	1.000	0.78	0.74	1.51	0.802	0.806	0.803	0.811	3
WT+C-cur+ Stress	0.632	0.86	0.60	1.46	0.753	0.796	0.791	0.808	4
WT+C-cur+ Vol+Stress	0.001	0.89	0.56	1.45	0.743	0.794	0.792	0.802	5
WT+L-cur+ Stress	0.073	0.71	0.68	1.39	0.735	0.775	0.770	0.778	6
Strain	0.494	0.64	0.55	1.19	0.542	0.544	0.538	0.558
Volume	0.276	0.96	0.14	1.10	0.487	0.513	0.506	0.519
L-cur	0.849	0.19	0.94	1.13	0.558	0.508	0.504	0.515
WT	0.444	0.78	0.25	1.03	0.407	0.489	0.478	0.499
C-cur	0.459	0.84	0.24	1.08	0.408	0.410	0.407	0.416

AUC average and 95% confidence interval are based on 200 rounds of 10 repeats. Abbreviations as in Table 2.

Discussion

This study provides proof-of-concept that computational modeling based on patient-specific cardiac magnetic resonance image data can be used to predict RV response to PVR in patients with repaired TOF. While computational modeling has been employed in selecting congenital cardiac anomalies such as the Fontan circulation and repaired coarctation [25-26], it has not been used to evaluate the RV in patients with congenital heart disease affecting the right heart such as repaired TOF. Using patient-specific CMR image data, we developed 2-layer anisotropic models of right and left ventricles with material properties of the RV myocardium derived from in-vitro biaxial testing. These complex computational models have provided new insights into RV morphology (volumes and wall thickness), geometry (circumferential and longitudinal curvatures), and mechanics (RV stress and strain) in repaired TOF.

With the rapidly increasing number of late survivors of TOF repair, surgical management of patients with RV dysfunction has become a major clinical challenge. The wide variability in clinical status, variations of RV morphology, regurgitation at both tricuspid and pulmonary valves, extent of RV dilatation, scarring, and dysfunction at the time of presentation has resulted in disparate surgical results with pulmonary valve insertion.¹ To our knowledge, this is the first report providing evidence that RV stress before PVR may be used as a predictor of RV functional response to pulmonary valve implantation.

The current study adds computational modeling as a new investigative tool and stress/strain as new potential predictors for postoperative functional outcomes after PVR. It should be noted that stress/strain calculations depend heavily on data available and model assumptions. However, comparative studies can still provide meaningful results as long as the same data and modeling standard were applied to all patients. The results of this computational analysis study are intriguing. Specifically, RV stress stands out as the best predictor of RV function response to PVR among the 6 parameters examined. From a pathophysiologic perspective, these findings are plausible given that stress more accurately reflects the functional status of the myocardium as compared with EF, which is a global parameter of pump function influenced by loading conditions. From a clinical perspective, most published criteria for PVR have focused on RV volume-based parameters and ejection fraction. However, the results of this study suggest that RV stress may be more helpful in identifying the likelihood of functional recovery of the RV, thus informing the decision to recommend PVR better than relying on RV volumes alone. We recognize that our preliminary findings and their potential clinical implications require validation by large-scale studies. It is worth noting, however, that construction of patient-specific 2-layer models with fiber orientation is very labor-intensive and that with current state of computer technology it takes approximately 1 month to generate each model. Refinement of the model-building technique and advances in computer science will be essential for making the process less labor intensive and clinically applicable.

Several limitations of this study are worth noting. The small sample size, which reflects the proof-of-concept nature of this study, results in limited statistical power. Furthermore, the patients included in this study may not reflect the general population of patients with repaired TOF as they were drawn from a larger sample of individuals undergoing PVR. Another reason for the small sample size is the extensive amount of time required for constructing each computational model (approximately 1 month). As noted above, future work will aim at improving the model-building process in order to make it more clinically applicable.

Several improvements can enhance our models in the future for better accuracy and applicability, including: (a) The addition of valve mechanics to the model may improve accuracy with regard to timing of valve opening and closure and allow incorporation of tricuspid and pulmonary valve regurgitation; (b) The addition of fluid-structure interaction can be helpful to obtain both flow and structural stress/strain information for a more comprehensive mechanical analysis. Fluid-structure interaction (FSI) models could provide flow information which are important for RV remodeling and tissue regeneration process; (c) The addition of regional tissue mechanical properties and patient-specific fiber orientations will be a desirable addition for improved accuracy of our models; (d) Development of methods to model active contraction by adding active stress and techniques for adjusting zero-stress fiber length; and (e) Development of multi-scale models including organ, cell, and gene investigations. The latter will allow mechanical conditions obtained at the organ level to be integrated with information from the cellular and genetic levels to explore mechanisms of right heart failure and its treatment.

Conclusions

In this proof-of-concept study of 16 patients with repaired TOF undergoing PVR, computational modeling based on patient-specific CMR images demonstrated that among several morphologic, geometric, and RV mechanics parameters, stress was the best predictor of RV response to pulmonary valve implantation. These findings provide a basis for future studies aimed at validation of these results in larger groups of patients and further refinements of the computational modeling technique to improve its accuracy and practicality.

Ultramini-Abstract.

A multi-patient study was performed using CMR-based ventricle models to identify potential predictors for post PVR outcome. Initial results indicated that RV stress was the best individual predictor among the six morphological and mechanical parameters examined and may be used as a potential tool to identify RV function response.

Abbreviations

AUC

Area under the receiver operating characteristic curve

CMR

Cardiac magnetic resonance

C-cur

Circumferential curvature

EF

Ejection fraction

EDV

End-diastole volume

ESV

End-systole volume

LV

Left ventricle

L-cur

Longitudinal curvature

Strain-P₁

Maximum principal strain

Stress-P₁

Maximum principal stress

PVR

Pulmonary Valve Replacement

RV

Right ventricle

RVOT

Right Ventricular Outflow Tract

RVEF

RV ejection fraction

ΔEF

RV EF change

TOF

Tetralogy of Fallot

WT

Wall thickness