Three-Dimensional Stiffness of the Carpal Arch

Abstract

The carpal arch of the wrist is formed by irregularly shaped carpal bones interconnected by numerous ligaments, resulting in complex structural mechanics. The purpose of this study was to determine the three-dimensional stiffness characteristics of the carpal arch using displacement perturbations. It was hypothesized that the carpal arch would exhibit an anisotropic stiffness behavior with principal directions that are oblique to the conventional anatomical axes. Eight (n = 8) cadavers were used in this study. For each specimen, the hamate was fixed to a custom stationary apparatus. An instrumented robot arm applied three-dimensional displacement perturbations to the ridge of trapezium and corresponding reaction forces were collected. The displacement-force data were used to determine a three-dimensional stiffness matrix using least squares fitting. Eigendecomposition of the stiffness matrix was used to identify the magnitudes and directions of the principal stiffness components. The carpal arch structure exhibited anisotropic stiffness behaviors with a maximum principal stiffness of 16.4 ± 4.6 N/mm that was significantly larger than the other principal components of 3.1 ± 0.9 and 2.6 ± 0.5 N/mm (p < 0.001). The principal direction of the maximum stiffness was pronated within the cross section of the carpal tunnel which is accounted for by the stiff transverse ligaments that tightly bind distal carpal arch. The minimal principal stiffness is attributed to the less constraining articulation between the trapezium and scaphoid. This study provides advanced characterization of the wrist's three-dimensional structural stiffness for improved insight into wrist biomechanics, stability, and function.

2 Introduction

The structure of the wrist is formed by eight irregularly shaped carpal bones interconnected by numerous intercarpal ligaments. The carpal bones are arranged to form a bony arch in the dorsal, radial and ulnar aspects of the wrist. The hamate and trapezium situate at the distal arch, and the pisiform and scaphoid serve for the proximal arch endpoints. The transverse carpal ligament attaches to the volar aspects of these four carpal bones. The structural composition of the wrist culminates in complex mechanical characteristics that influence wrist stability and function (Crisco et al., 2011; Garcia-Elias, 2013; Garcia-Elias et al., 1989a; Garcia-Elias et al., 1992).

Wrist function is critically dependent on the biomechanical properties of the carpal tunnel structure and its constituents. For example, the structural mechanics enables wrist motion (Fischli et al., 2009; Majors and Wayne, 2011), provides stability to the carpal tunnel (Garcia-Elias et al., 1989a), and allows for force transmission between the hand and forearm during hand use, e.g. grasping (Horii et al., 1990; Marquez-Florez et al., 2015; Matsuki et al., 2009; Schuind et al., 1995). The intercarpal ligaments stabilize the wrist and facilitate the force transmission by preventing excessive carpal bone movement (Garcia-Elias, 2013); the loss of a single ligament can alter the mechanical balance of the wrist (Garcia-Elias et al., 1989a; Garcia-Elias et al., 1992; Gartsman et al., 1986). A disruption in the mechanical balance results in wrist instability (Garcia-Elias, 2013) that hinders the complex carpal movements required for daily hand activities (Crisco et al., 2011; Garcia-Elias, 2013).

The structural biomechanics of the wrist has been studied experimentally and computationally. Experimental studies have investigated the uniaxial stiffness characteristics of the wrist in the medial-lateral (Fuss and Wagner, 1996; Xiu et al., 2010) and dorsal-palmar directions (Garcia-Elias et al., 1989a). The two-dimensional mechanics of the wrist have also been investigated with respect to the compliance of the carpal tunnel (Tung et al., 2010), force transmission across wrist (Garcia-Elias et al., 1989b; Schuind et al., 1995), and manipulation of the carpal tunnel's cross-sectional area (Li et al., 2013; Li et al., 2011; Li et al., 2009). Three-dimensional studies of the wrist structure have been mainly studied with computational modeling with a particular focus on force transmission across the carpus (Fischli et al., 2009; Guo et al., 2009; Majima et al., 2008; Majors and Wayne, 2011; Marquez-Florez et al., 2015; Matsuki et al., 2009). However, there is a lack of experimental studies investigating the three-dimensional biomechanics of the wrist structure.

The purpose of this study was to determine the three-dimensional stiffness characteristics of the carpal arch; this was achieved using applied displacement perturbations together with perturbation induced reaction forces. It was hypothesized that the carpal arch would exhibit an anisotropic stiffness behavior. We further hypothesized that the principal stiffness component directions are oblique to the conventional anatomical axes (i.e. medial-lateral, proximal-distal, and dorsal-volar).

3 Methods

Experimental Setup

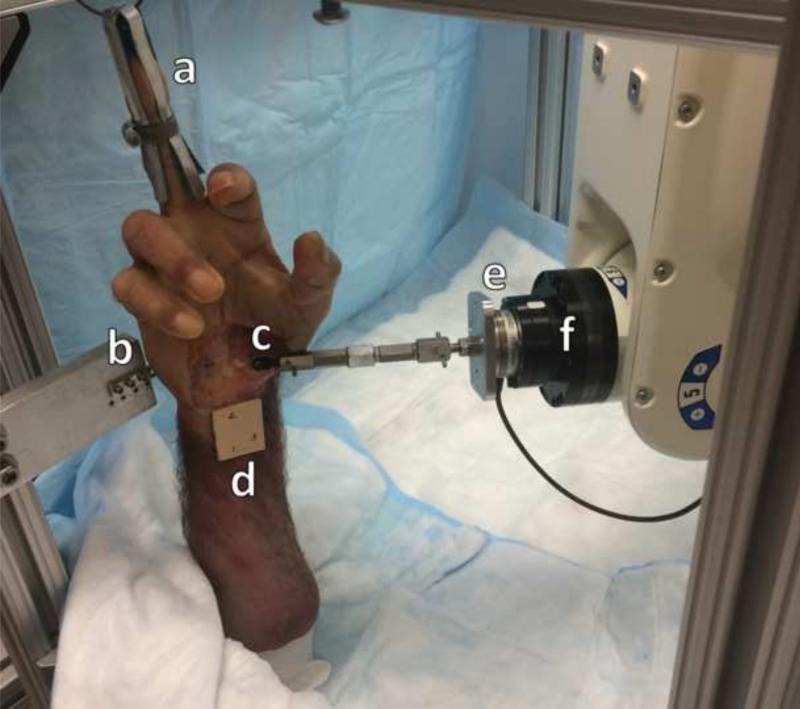
A custom apparatus was used to hold each hand specimen in a neutral and vertical posture (Figure 1). The apparatus was also used to rigidly fix the medial side of the carpal arch at the hamate. The lateral side of the carpal arch, i.e. ridge of the trapezium, was manipulated in three-dimensions with the assistance of a six-degree-of-freedom robot arm (Denso Corp., Kariya, Aichi, Japan) that was controlled with a custom LabVIEW program (National Instruments, Austin, TX). Attached to the end effector of the robot was a six-degree-of-freedom force transducer (Mini40, ATI Industrial Automation, Apex NC).

Figure 1.

Volar view of experimental setup for applying displacement perturbations to the trapezium with the fingertrap (a), bone plate (b), ball-joint (c), radius marker cluster (d), force transducer (e), and robot end-effector (f).

Preparation of Cadaveric Specimens

Eleven fresh frozen male cadaveric specimens (50.2 ± 6.3 years; 7 right and 4 left; BMI: 24.9 ± 3.5 kg/m²) were used for this study. The specimens had no documented history of injury or degenerative musculoskeletal disorders of the wrist. Each hand specimen was dissected volarly to expose the TCL and its attachment sites at the hook of the hamate and the ridge of the trapezium. A screw was used to secure a ball joint (2-56 Swivel Ball Link, Du-Bro Products, Wauconda, IL) to the ridge of the trapezium (Figure 1). A marker cluster was also attached to the volar aspect of the forearm. Dorsally, the hamate was exposed while keeping the intercarpal ligaments intact. A bone plate was then secured to the dorsal aspect of the hamate with two cortical screws. To maximize rigid fixation, glue (Gorilla Glue, Gorilla Glue, Inc., Cincinnati, OH) was applied to the metal interfaces with the trapezium and hamate. A specimen was then placed in the custom apparatus in a vertical position with the hand supported by a fingertrap attached to the third digit, and the specimen was fixed to the apparatus via the bone plate. Subsequently, the robot arm was positioned on the lateral aspect of the specimen and the ball joint was attached to the force transducer, allowing the robot to apply translational displacement perturbations to the ridge of the trapezium with free rotation and no torque constraints.

Experimental Procedures

Transformation Matrices

Prior to experimentation, transformation matrices between the coordinate frames of the robot, force transducer, hamate, and the hand specimen (i.e. anatomical) were established with the use of a digitizer (Microscribe, San Jose, CA, USA). The transformation matrices relating the force transducer coordinate system to the others was determined using a method in our previous study (Marquardt and Li, 2013). The local coordinate frame on the hamate was used to determine the actual displacements of the trapezium, relative to the hamate. This was done using three indented landmarks on the hamate, including one at the hook of hamate, that were also marked with ink. The anatomical coordinate frame of the hand specimens was defined using the marker cluster attached to volar forearm (Figure 1). The anatomical axes were the medial-lateral, proximal-distal, and volar-dorsal axes (x, y, and z axes respectively).

Displacement Perturbations, Preconditioning, and Testing

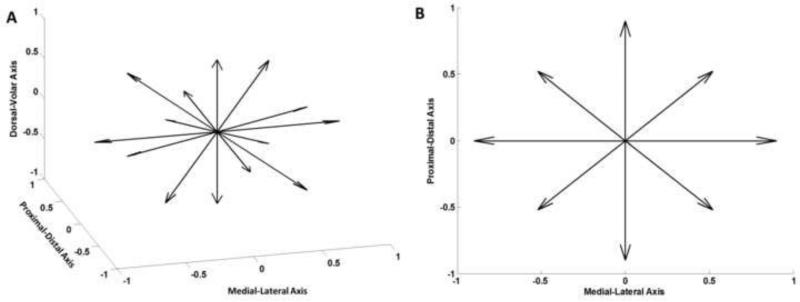
The ridge of the trapezium was displaced in 14 directions relative to its initial reference position (Figure 2). Six displacement directions were along the positive and negative directions of the anatomic axes. The remaining eight directions were distributed in the individual octants; each was oriented such that its three direction cosines were equal. In each direction, the robot displaced the trapezium by 0.5, 1.0, 1.5, and 2.0 mm. The initial reference position of the trapezium was its position when the ball joint was connected to the robot end effector. Prior to experimentation, each specimen was preconditioned by displacing the ridge of the trapezium by 2 mm in a set of the 14 directions; the order of the 14 directions was randomized within a set, and the preconditioning was repeated for 10 sets. A preconditioning magnitude of 2 mm was chosen because it is the largest displacement magnitude used for testing and the carpal arch remains relatively elastic within this amount of displacement (Gabra et al., 2012; Li et al., 2013; Xiu et al., 2010).

Figure 2.

Directions of the displacement perturbations in an isometric view (A) and volar view (B).

For experimentation, 56 displacements (i.e. 14 directions × 4 magnitudes) were applied to the ridge of the trapezium in a randomized order. During experimentation, force and position data were recorded at the initial and final positions of each displacement perturbation. More specifically, at the initial position 20 ms of force data was sampled and the average forces were determined. Then, the locations of ridge of trapezium, hook of hamate, force-transducer, and the remaining hamate landmarks (i.e. for defining the local coordinate system) were each digitized three times and averaged. The robot then performed displacement perturbations. For each perturbation, the force data at the end position was measured, and the end positions of the landmarks were digitized again. The actual displacement of the trapezium, relative to the hamate, might not necessarily correspond to the prescribed robot movement magnitude due to possible motions of the hamate. Digitization aided in determining the actual displacements of the trapezium relative to the hamate. The robot then moved back to the original position and the process was repeated for the next displacement perturbation.

Data Analysis

The three-dimensional displacement-force relationship was assumed to be linear with a constant stiffness matrix (Eq. 1). Furthermore, the stiffness matrix was constrained to be symmetric (Griffis and Duffy, 1993; Kovecses and Angeles, 2007; Logan, 2011).

$$\left\{\begin{array}{c}\hfill d{F}_x\hfill \\ \hfill d{F}_y\hfill \\ \hfill d{F}_z\hfill \end{array}\right\}=-\begin{array}{c}d\overline{F}=-Kd\overline{D}\hfill \\ \left[\begin{array}{ccc}\hfill K_{xx}\hfill & \hfill K_{xy}\hfill & \hfill K_{xz}\hfill \\ \hfill K_{yx}\hfill & \hfill K_{yy}\hfill & \hfill K_{yz}\hfill \\ \hfill K_{zx}\hfill & \hfill K_{zy}\hfill & \hfill K_{zz}\hfill \end{array}\right]\hfill \end{array}\left\{\begin{array}{c}\hfill dX\hfill \\ \hfill dY\hfill \\ \hfill dZ\hfill \end{array}\right\}$$ (1)

The experimental displacement and force data was used to determine the components of the stiffness matrix using a least squares regression technique. The principal components of the stiffness matrix and respective principal directions were determined with eigendecomposition. In addition, the determinant of the stiffness matrix (i.e. product of the three eigenvalues) was calculated to provide a scalar quantity of the overall stiffness value. The ratios between the principal stiffness components indicated the level of anisotropy that the carpal arch structure exhibited. The principal directions were converted into spherical coordinates (azimuth angle, elevation angle). The azimuth angle is the angle of the direction vector relative to the transverse plane (i.e. lateral-volar, XZ, plane), and the elevation angle, i.e. pronation angle, is the angle of the direction vector with respect to the frontal plane (i.e. lateral-distal, XY, plane).

Methods Verification

The experimental setup, testing, and analyses were verified by comparing a physical system of springs to a modeled, “theoretic”, equivalent spring system. The physical spring system was built of a number of springs with varying stiffness values attached to a shared center node where a ball joint was secured. This physical system was then recreated in ABAQUS (Dassault Systems, Waltham, MA, USA). In both systems, three-dimensional displacements up to 2 mm were applied to the center node and the resultant forces were determined. For the physical system, the displacement-force data were determined using the instrumented robot. The stiffness matrices were then calculated from the respective displacement-force relationships of the two systems. The physical system was tested during 3 separate trials and the average stiffness matrix among the trials was calculated and compared to the stiffness matrix of the theoretic system. The stiffness matrices derived by analytical and experimental methods were [0.7, 0.1, 0.1; 0.1, 1.0, −0.4; 0.1, −0.4, 0.7] N/mm and [0.7 ± 0.0, 0.1 ± 0.0, 0.1 ± 0.0; 0.1 ± 0.0, 0.9 ± 0.1, −0.3 ± 0.0; 0.1 ± 0.0, −0.3 ± 0.0, 0.7 ± 0.0] N/mm, respectively. The goodness of fit for the experimentally derived matrix is 0.989 ± 0.002. The principal stiffness components of both systems were in agreement with a normalized root mean squared error of 7.1%; normalization was with respect to the maximum principal component.

Statistical Analysis

A one-way repeated measures ANOVA was used to determine if the principal component stiffness magnitudes were different from each other. A post-hoc Tukey test was used for pairwise comparisons. All statistical tests had an alpha level of 0.05. The average principal directions among the specimens were determined using circular statistical analyses (Zar, 1984).

4 Results

The results are based on eight (n = 8; 49.6 ± 7.4 years; 6 right and 2 left; BMI: 25.4 ± 3.4 kg/m²) of the 11 specimens; two specimens fractured during preparation/experimentation, and the third specimen was excluded because the data acquisition system malfunctioned during experimentation. The least squares regression procedure to determine the stiffness matrix resulted in a goodness of fit of R² = 0.8360 ± 0.0661. The stiffness matrix was:

$$K=\left[\begin{array}{ccc}\hfill 11.8\pm 3.9\hfill & \hfill -0.5\pm 0.8\hfill & \hfill 6.3\pm 1.9\hfill \\ \hfill -0.5\pm 0.8\hfill & \hfill 2.9\pm 0.8\hfill & \hfill -0.2\pm 0.7\hfill \\ \hfill 6.3\pm 1.9\hfill & \hfill -0.2\pm 0.7\hfill & \hfill 7.4\pm 1.2\hfill \end{array}\right]\mathrm{N}∕\mathrm{mm}$$

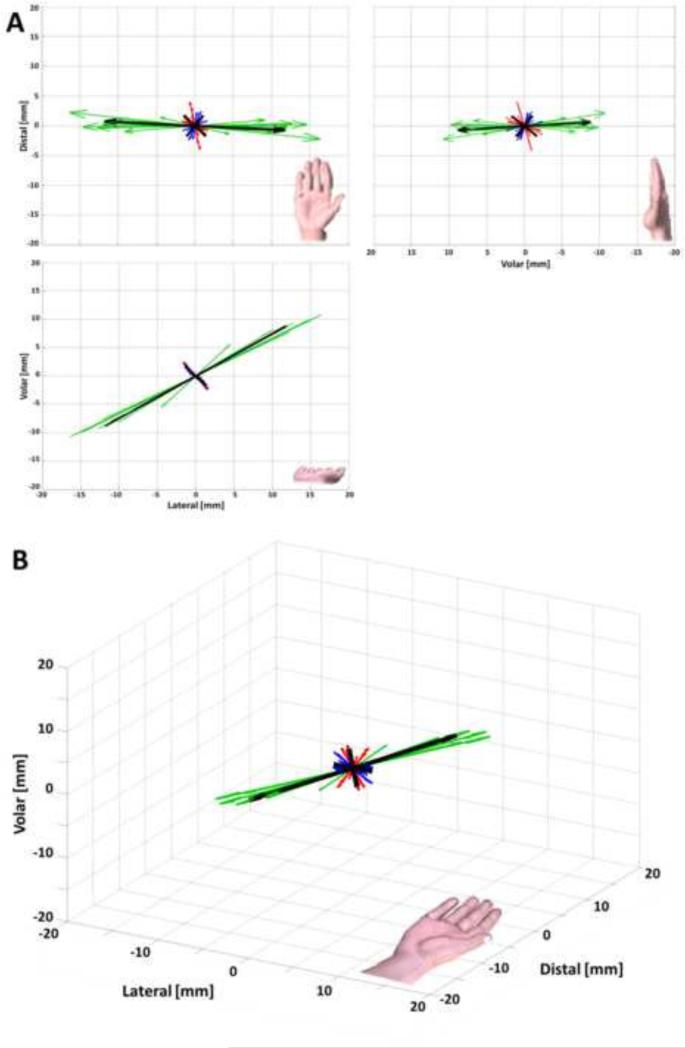
Eigendecomposition of the stiffness matrix resulted in the three principal components of 16.4 ± 4.6, 3.1 ± 0.9, and 2.6 ± 0.5 N/mm (Table 1). The corresponding principal directions, expressed as (azimuth, elevation) angles, are (−3.4° ± 6.7°, 36.6° ± 5.3°), (−50.0° ± 23.5°, −36.8° ± 16.3°), and (58.5° ± 22.6°, −27.3° ± 17.7°) (Figure 3). There was a significant difference in stiffness magnitudes among the principal components (p < 0.001). More specifically, the 1^st principal component stiffness was significantly larger than the 2^nd and 3^rd principal component stiffnesses (p < 0.001). There was no significant difference between the 2^nd and 3^rd principal component stiffnesses (p = 0.903). The ratios among the first, second, and third principal stiffness components were 6.3 ± 1.3 : 1.2 ± 0.1 : 1. The determinant of the stiffness matrix was 148.1 ± 89.0 N³/mm³.

Table 1.

Specimen Specific Principal Components of K

	Specimen	1	2	3	4	5	6	7	8
1st Principal Component	Stiffness [N/mm]	20.8	17.5	12.7	16.0	14.5	22.0	19.6	8.1
	Azimuth [deg]	−4.1	1.9	6.0	−0.9	−5.8	−7.8	0.7	−17.1
	Elevation [deg]	33.0	36.2	35.9	32.4	38.8	33.1	33.9	49.7
2nd Principal Component	Stiffness [N/mm]	3.6	3.1	3.2	3.5	2.2	2.7	4.7	1.9
	Azimuth [deg]	−44.2	−23.0	−24.7	−82.4	−73.6	−34.0	−80.4	−39.2
	Elevation [deg]	−49.6	−51.0	−49.9	−13.1	−25.2	−54.0	−12.9	−38.1
3rd Principal Component	Stiffness [N/mm]	3.0	2.6	2.5	2.9	2.1	2.5	3.3	1.8
	Azimuth [deg]	71.9	82.7	84.5	26.6	40.3	73.9	27.2	59.6
	Elevation [deg]	−20.5	−12.3	−15.4	−54.5	−40.7	−12.6	−53.1	−11.0

Figure 3.

Orthogonal (A) and isometric (B) views of the specimen specific principal stiffness components for the wrist structure. The 1^st, 2^nd, 3^rd, and averaged principal components are shown (green, red, blue, and black respectively) with length corresponding to stiffness magnitude. Note: the hands shown are for orientation purposes and are not to scale.

5 Discussion

The three-dimensional stiffness of the carpal arch was determined from displacement perturbations with the assistance of an instrumented robot arm. The resultant forces of each displacement were recorded with a custom program. The displacement-force data were fitted to a stiffness matrix with a linear relationship in the three-dimensional space, revealing the intrinsic stiffness characteristics of the wrist's carpal arch structure. It was found that the carpal arch had principal stiffness components that were oblique to the conventional anatomical axes and differed in magnitude from each other.

The carpal arch's maximal principal stiffness was oriented within the transverse plane and pronated with an elevation angle of 37 degrees. This orientation of the maximal principal stiffness axis was similar to that of the carpal tunnel geometrical major axis (Gabra et al., 2015; Mogk and Keir, 2008; Pacek et al., 2010). The carpal tunnel has an elliptical shape within the transverse plane with a major axis that is oblique to the conventional anatomical axes (Gabra et al., 2015; Mogk and Keir, 2008; Pacek et al., 2010). Gabra and Li (2015) quantified the orientation angle of the carpal tunnel's distal cross section and reported that its geometrical major axis was pronated by 16 degrees relative to an axis connecting the hook of hamate and ridge of trapezium. The hook of hamate is generally more dorsal than the ridge of the trapezium, indicating that the major axis is even more pronated (>16 degrees) relative to the conventional anatomical axes defined in the current study. A previous study also made an observation that the carpal tunnel's cross section had a major axis that was pronated approximately 30 degrees from the medial-lateral axis in the transverse plane (Mogk and Keir, 2008). Therefore, the orientation of the maximum principal stiffness direction is in agreement with that of the major axis for the carpal tunnel's cross section. This is consistent with principles of structural mechanics that an elliptical structure tends to be stiffest along its major axis. Such stiffness characteristics may be a mechanism for the stability of the carpal tunnel's bony structure in order to protect its contents from external forces (Garcia-Elias et al., 1989a).

The maximum principal stiffness alignment with the transverse plane is likely due to ligamentous constraints. Some of the stiffest intercarpal ligaments of the carpal arch are aligned with the transverse plane (Garcia-Elias, 1997; Garcia-Elias et al., 1989a). These transverse intercarpal ligaments play a major role with respect to the wrist's structural stability, and this results in a highly stable structure within the transverse plane (Garcia-Elias et al., 1989a). Carpal bone movement in/out of the transverse plane would be perpendicular to the ligamentous lines of action of the stiff transverse ligaments, diminishing their constraints. Therefore, the ligamentous constraints of the wrist play a larger role for carpal movements within the transverse plane.

Interestingly, the direction of the maximum principal stiffness is also associated with functional wrist kinematics related to dart throwing motion (Capener, 1956; Fisk, 1981; Garcia-Elias, 2013; Li, 2005; Moritomo et al., 2007; Palmer et al., 1985; Werner et al., 2004). Dart throwing motion refers to the most common wrist motion, from radial-extension to ulnar-flexion, that occurs during various functional tasks of the hand such as swinging a hammer (Capener, 1956; Fisk, 1981; Garcia-Elias, 2013; Li, 2005; Moritomo et al., 2007; Palmer et al., 1985; Werner et al., 2004). The maximum principal stiffness direction is aligned with the rotational axis of dart throwing motion. The carpal arch is structurally less stiff in a plane that is perpendicular to the maximum stiffness axis, i.e. rotational axis of dart throwing motion. This may explain why the wrist has the tendency to follow such a path of dart throwing motion during daily hand activities.

The minimal stiffness axis of the carpal arch was oblique to the conventional anatomic axes with a direction that is positioned 59° from the medial-lateral axis and dorsally elevated by 27°. The oblique orientation of minimal stiffness axis may be associated with the less constraining articulations of the midcarpal joint, i.e. between the proximal and distal levels of the wrist. More specifically, the orientation of minimal stiffness axis is likely due to the articulation between the trapezium and the highly mobile scaphoid (Kobayashi et al., 1997). A trapezium displacement directing along the volar aspect of the minimal stiffness axis would axially load the scaphoid and therefore cause the scaphoid to flex (Cooney et al., 1989; Garcia-Elias, 1997; Moritomo et al., 2000). This would also be true for a dorsally directed displacement of the trapezium along the minimal stiffness axis; the trapezium displacement would pull the scaphoid into extension via the scapho-trapezial-trapezoidal ligament (Garcia-Elias, 2013; Moritomo et al., 2000). This mobility of the scaphoid would accommodate for the trapezium's displacement and the resultant force of the displacement would be small, i.e. encounter minimal stiffness.

The carpal arch structure exhibited an anisotropic stiffness behavior with a maximum principal stiffness that was more than six times that of the minimum stiffness. The difference in principal stiffness magnitudes, particularly between the maximum principal stiffness component and to the other two components, is associated with the anisotropic geometry, e.g. elliptical, of the carpal tunnel. The anisotropic stiffness behavior can also be linked to the directionally dependent anatomical constraints of the wrist such as ligamentous connections and bone congruence (Gabra et al., 2012). The wrist is a complex joint composed of many obscurely shaped bones interconnected by numerous ligaments with multiple articulations. For example, the wrist has strong and stiff transverse ligaments, specifically those that tightly bind the distal carpal arch (de Lange et al., 1985; Garcia-Elias et al., 1989a; Moritomo et al., 2000; Ruby et al., 1988); the stiff ligaments contribute towards the magnitude of the maximum principal stiffness. In contrast, the constraints of the transverse ligaments are diminished in the longitudinal (i.e. proximal-distal) direction. The proximal carpal arch is also more mobile than the distal arch. The intercarpal articulations, especially between proximal and distal carpal arches, do not provide additional resistance, i.e. stiffness, to a structural deformation. Our findings that the second and third components have comparable magnitudes and less consistent directions (i.e. large variations in azimuth and elevation angles) indicate that the stiffness behavior of the carpal arch is relatively isotropic in the plane perpendicular to the major principal direction. The first principal component with much greater magnitude and consistent direction is likely associated with the major role played by the transverse ligaments in the structural stiffness. Functional mobility of the wrist are facilitated by the remaining principal components with lower stiffness magnitudes and less directional specificity.

There are a few limitations associated with this study. First, the stiffness matrix was derived from trapezium displacements of up to approximately 2 mm and therefore may not be applicable to displacements larger than 2 mm. Second, the carpal arch was assumed to have linear, elastic, and time invariant stiffness characteristics. Further studies can be designed to provide more advanced understanding of the nonlinear and viscoelastic stiffness characteristics of the carpal arch structure. Third, the structural stiffness of the carpal arch was determined from displacement perturbations applied to its lateral and distal end, i.e. the trapezium, while the other end of the distal arch was fixed. Therefore, the stiffness matrix from this study may not be applicable to studies investigating force transmission from the metacarpals, across the carpus, and to the forearm. Fourth, cadaveric hands were used to examine the stiffness characteristics of the carpal tunnel. Generalization of the results to the wrist structure of a living person is plausible considering that the mechanical properties under investigation is passive in nature and that the hand specimens were fresh frozen and then thawed in room temperature before experimentation. Lastly, only male specimens were used to determine the carpal arch's structural stiffness characteristics, and it remains to be investigated whether the stiffness behavior is gender dependent.

In conclusion, the three-dimensional stiffness characteristics of the wrist structure were determined using displacement perturbations to the carpal arch. The carpal arch structure exhibited an anisotropic stiffness behavior with principal stiffness components that are oblique to the conventional anatomical axes. The maximum principal stiffness occurred in the transverse plane and was pronated relative to the medial-lateral axis; it is attributed to the structural stability of the carpal tunnel and the strong transverse intercarpal ligaments. The less constraining articulation between the trapezium and scaphoid help explain the oblique orientation of the minimal stiffness axis. This study provides advanced characterization of the wrist's three-dimensional structural stiffness for improved insight into wrist biomechanics, stability, and function.