Abstract
Biologics exist in equilibrium between native, partially denatured, and denatured conformational states. The population of any of these states is dictated by their Gibbs energy and can be altered by changes in physical and solution conditions. Some conformations have a tendency to self-associate and aggregate, an undesirable phenomenon in protein therapeutics. Conformational equilibrium and self-association are linked thermodynamic functions. Given that any associative reaction is concentration dependent, conformational stability studies performed at different protein concentrations can provide early clues to future aggregation problems. This analysis can be applied to the selection of protein variants or the identification of better formulation solutions. In this review, we discuss three different aggregation situations and their manifestation in the observed conformational equilibrium of a protein.
Keywords: biologics, conformational equilibrium, protein aggregation, differential scanning calorimetry, isothermal chemical denaturation
Introduction
The expected growth of biologics over the next few years and their transformation from drugs administered mainly in hospital settings to drugs self-administered by patients, requires the fulfillment of strict safety and stability conditions. The long-term stability of biologics is a function of diverse physical and chemical factors that need to be addressed in an effective and rapid way. Among them, it is necessary to identify conditions that maximize the structural stability of the native state and prevent aggregation or other undesirable processes [1–4]. Maximizing structural stability and minimizing aggregation tendencies involve decisions in at least two different development stages: the selection of the protein variants with the top stability and/or aggregation profiles; and, the identification of the solution conditions (formulations) that maximize stability and minimize aggregation. These decisions will be facilitated by a better understanding of the existing linkage between conformational and self-association processes.
Conformational equilibrium in proteins
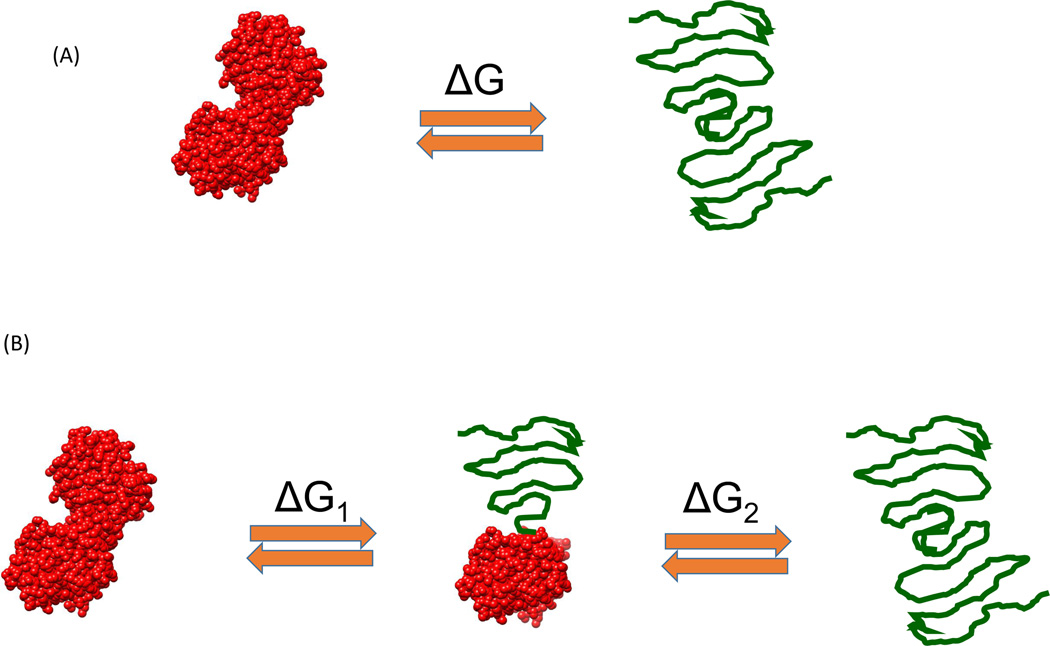
Proteins exist in equilibrium between the native, partially denatured, and fully denatured conformations. Even though there are an astronomical number of partially denatured (also referred to as partially folded) conformations, most never become populated. In fact, the native and/or denatured state equilibrium of most single-domain proteins can be accounted for by the two-state model, in which the population of partially denatured conformations is negligible [5]. Multidomain proteins can exhibit partially denatured conformations corresponding to states in which some domains are unfolded whereas the others remain folded [6]. Figure 1 illustrates two commonly observed situations. Figure 1A represents the two-state situation in which the native and fully denatured conformations are the only ones that become significantly populated. Figure 1B represents the situation in which a partially denatured conformation becomes populated in addition to the native and fully denatured states. The partially denatured state usually originates from the unfolding of the least-stable domain. In all cases, the stability of a protein or a structural domain is determined by the Gibbs energy of stability, ΔG, characteristic of each structure. The population or fraction of denatured protein or domain is given by Equation 1:
| [1] |
Figure 1.
Typical protein denaturation situations encountered in the laboratory. (A) The classical two-state situation in which protein denaturation occurs without the presence of partially denatured conformation. This situation is mostly observed for single-domain proteins or multidomain proteins with highly cooperative interdomain interactions. (B) The situation in which denaturation occurs with the presence of a significantly populated partially denatured state. This situation often occurs with multidomain proteins.
A large and positive ΔG minimizes the fraction of denatured protein or domain. Table 1 shows a look-up table with characteristic ΔG values and the corresponding populations of denatured protein. The percent of denatured protein is simply the fraction denatured multiplied by 100. Also, the actual concentration of denatured protein is simply the total protein concentration multiplied by the fraction denatured. For example, in a 100-mg/ml protein solution with a structural stability of 8 kcal/mol, the concentration of denatured protein is 0.1 Mg/ml. In protein engineering or formulation development, a common goal is to optimize the structural stability of the protein, which is equivalent to maximizing ΔG.
Table 1.
[LM2]a
| ΔG kcal/mol | % Denatured protein |
|---|---|
| 0 | 50 |
| 1.3 | 10 |
| 2.7 | 1 |
| 4.1 | 0.1 |
| 5.5 | 0.01 |
| 6.8 | 0.001 |
| 8.2 | 0.0001 |
| 9.6 | 0.00001 |
| 10.4 | 0.000001 |
Knowledge of ΔG enables us to calculate the population of denatured protein or domains. Given that denatured conformations are prone to aggregation, ΔG should have a crucial role in the selection of protein variants and formulation optimization.
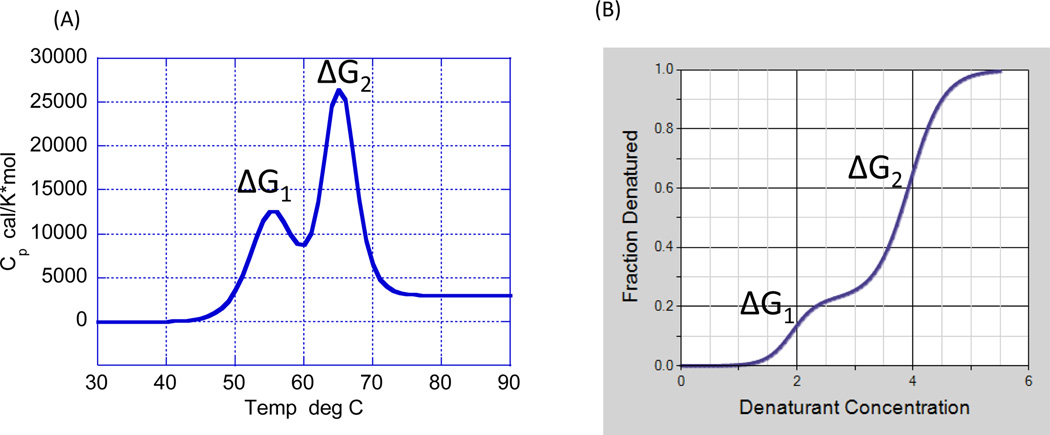
There are two techniques capable of measuring Gibbs energies and, therefore, able to provide a window into the conformational equilibrium of a protein: differential scanning calorimetry (DSC) and isothermal chemical denaturation (ICD). DSC induces protein denaturation by increasing the temperature of the solution [7–9], whereas ICD induces protein denaturation by the addition of a chemical denaturant, most commonly urea or guanidine hydrochloride [10–15]. Both techniques are able to determine ΔG not at high temperature or high denaturant concentration but at room temperature or zero denaturant concentration. In both cases, the necessary requirement for ΔG determination is that the experimental measurement is performed under reversible conditions. This condition is tested by scanning the same sample twice or by diluting the chemical denaturant concentration and recovering the original state. Figure 2 illustrates the type of data obtained by DSC and ICD for a protein characterized by the presence of two cooperative domains. In both cases, analysis of the data permits determination of ΔG1 and ΔG2, and their subsequent analysis [7–15].
Figure 2.
Differential scanning calorimetry (DSC) (A) and isothermal chemical denaturation (ICD) (B) allow measurement of the folding–unfolding reaction of a protein and determination of the Gibbs energy of stability (ΔG) for each step. Folding–unfolding thermodynamics can only be determined if the measurement is done under equilibrium conditions.
Thermodynamic linkage between conformational equilibrium and self-association
Different aggregation scenarios can be derived from the conformational equilibrium situations shown in Figure 1. Either the native, partially denatured, or denatured states might have a tendency to self-associate and form different types of aggregate. Some self-association processes are functionally and biologically important, such as those present in oligomeric proteins, and usually involve highly specific native state interactions. Other selfassociation processes are detrimental and undesirable, especially those occurring in protein engineering and during the development of therapeutic proteins, such as monoclonal antibodies [16]. These unwanted self-association processes are usually referred to as aggregation processes because they often lead to irreversible aggregates. In protein therapeutics, the presence of these aggregates not only reduces the activity of the protein, but can also trigger dangerous immune responses. From a physicochemical standpoint, the formation of these aggregates has been described in terms of different variants of the Lumry–Eyring model [16–21]. The basic idea is that the protein exists in equilibrium between different conformations and that some of those conformations have a tendency to selfassociate and form aggregates. The initial self-association is usually reversible or partially reversible and, depending on the protein and physical or chemical conditions, it can stay that way or eventually lead to irreversible aggregation. Reversible aggregation affects the conformational equilibrium in well-defined ways.
In this review, three different aggregation cases are considered to illustrate their impact in the conformational equilibrium of the protein. The first case is the one originating from native state self-association, the second is the one in which a partially denatured state self-associates, and the third is the one that originates from denatured state self-association. The resulting aggregates fall into classes 3, 5, and 6 aggregates according to the classification proposed by Joubert et al. [16].
Case 1: native state aggregation
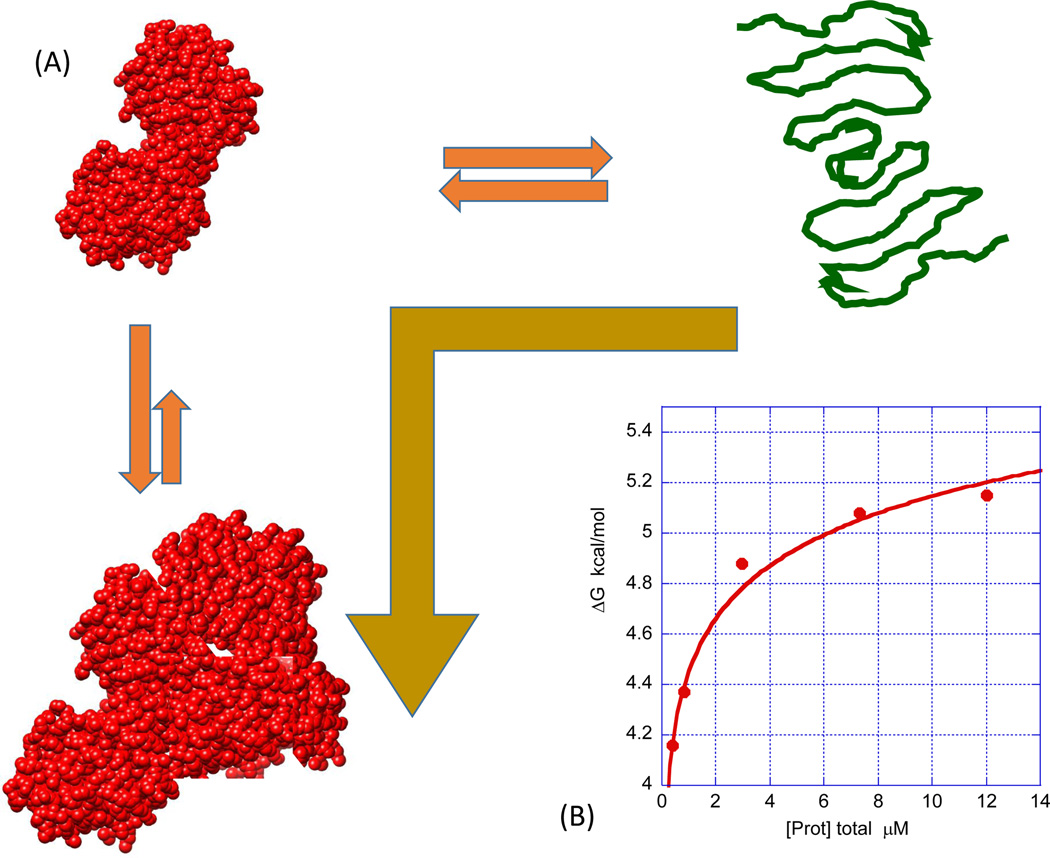
Figure 3 illustrates the situation in which aggregation originates from self-association of the native state. In this case, the equilibrium is shifted to the left, ΔG of the denatured and partially denatured states increases and, consequently, the stability of the native state increases. If this situation occurs, the measured ΔG, usually referred to as apparent ΔG, ΔGapp, is given by Equation 2 [22]:
| [2] |
where is equal to the value of the Gibbs energy extrapolated to zero protein concentration (in practice, a concentration low enough at which aggregation is not present), j is the average stoichiometry of the self-associated state, and KN,j the self-association constant. Equation 2 indicates that native state self-association will cause the measured Gibbs energy to increase as a function of protein concentration and that the magnitude of the increase is proportional to the self-association constant and the average size of the aggregates. These aggregates are small and fully or partially reversible (class 3 [16]). For the specific case in which the native state forms a dimer (j = 2), Equation 2 has an exact solution that can be expressed in terms of the total protein concentration as demonstrated before for the HIV-1 protease [23] (Figure 3B). In this case, it is possible to determine the dimerization constant that, under the conditions in Figure 3, is 1.6 × 10−8 M. For arbitrary degrees of oligomerization, there are no exact solutions for KN,j, but the fraction of aggregated protein can be calculated directly from the data even though j and KN,j cannot be determined (Equation 3):
| [3] |
where . In general, if experiments are performed at different protein concentrations, an increase in the measured ΔG with protein concentration is indicative of native state self-association. This effect is observed for both oligomeric proteins or proteins that exhibit unwanted aggregation (e.g., antibodies that exhibit native state aggregation).
Figure 3.
Self-association of the native state is characterized by an increase in ΔG upon increasing protein concentration (A). For this effect to occur, the association process and resulting aggregates must be fully or partially reversible, even though they might initiate the subsequent formation of irreversible aggregates. Self-association of the native state can be functionally relevant (oligomeric proteins) or detrimental (aggregation of monoclonal antibodies). (B) An example of the HIV-1 protease, which is a dimer in the native state and dissociates upon unfolding. Denaturation experiments were performed using a linear gradient of guanidine hydrochloride from 0 to 5.5 M (The Hunk Automated Protein Denaturation System, Unchained Labs, Norton, MA). The buffer was 10 mM sodium formate, pH 3.4. The final concentration of protease varied from 0.4 to 12 µM. The exact concentration was determined from the absorbance at 280 nm using an extinction coefficient of 25 530 M−1 cm−1 [23]. The gold arrow indicates that the equilibrium shifted towards the native conformations and that chemical or temperature denaturation occurs at higher values.
Case 2: partially denatured state aggregation
In some situations, partially denatured conformations have a higher tendency to self-associate than the native or denatured states. The situation is illustrated in Figure 4. In this case, the first transition, corresponding to the transition from monomeric native to self-associated partially denatured states, is shifted down upon increasing protein concentration, whereas the second transition, corresponding to the transition from the self-associated partially denatured to monomeric fully denatured state, is shifted up upon increasing protein concentration. Experimentally, this situation has been observed with recombinant human growth hormone (rHGH) at low pH [24]. rHGH is a monomeric protein that, upon denaturation at low pH, forms a partially denatured dimer that fully dissociates upon complete denaturation. It must be noted that, if the dimeric partially denatured state were the end point of the denaturation transition, it would result in only the destabilization of the native state. In the DSC experiments, as shown in Figure 5, the temperature of the first transition decreases with rHGH concentration, whereas that of the second transition increases with rHGH concentration. A similar behavior will be observed in chemical denaturation experiments. In this case, the first transition occurs at lower denaturant concentrations and the second transition at higher denaturant concentrations. Several monoclonal antibodies exhibit two chemical denaturation transitions. If this is the case, an assessment of native state aggregation requires that the two transitions exhibit higher ΔG values upon increasing protein concentration.
Figure 4.
Partially denatured conformations might have a higher tendency to aggregate than the native or fully denatured state, in which case aggregation occurs when the partially denatured state becomes populated. In this case, dissociation occurs upon full denaturation. This behavior is exhibited by recombinant human growth hormone at low pH [24]. Gold arrows indicate that the equilibrium is shifted towards the partially denatured conformations. The effect of this behavior is shown in Figure 5 (main text).
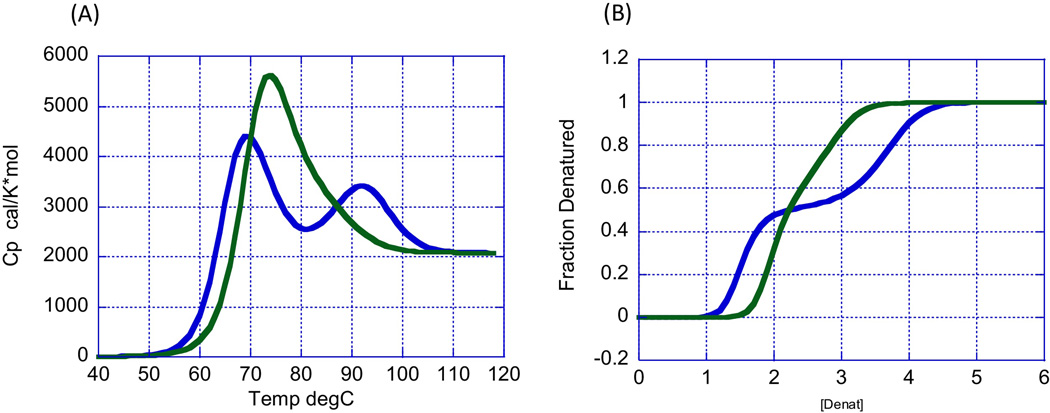
Figure 5.
[LM1](A) The heat capacity function of recombinant human growth hormone at pH 3 (10 mM glycine buffer) as reported by Kasimova et al. [24]. The blue curve corresponds to a concentration of 10 mg/ml and the green curve to a concentration of 2 mg/ml. Upon increasing concentration (blue curve), the first transition (native state to partially denatured state) occurs at a lower temperature and the second transition (partially denatured state to denatured state) occurs at a higher temperature. (B) Simulation of expected chemical denaturation of recombinant human growth hormone. Upon increasing protein concentration (blue curve), the first transition (native state to partially denatured state) is shifted to lower denaturant concentrations (lower ΔG) and the second transition (partially denatured state to denatured state) to higher denaturant concentrations (higher ΔG).
Case 3: denatured state aggregation
Figure 6 illustrates the situation in which aggregation originates from self-association of the denatured state. In its early stages, the process is fully or partially reversible (class 6 [16]). In this case, the equilibrium will be shifted to the right, ΔG will decrease and the stability of the native state will decrease. If this situation occurs, the measured ΔG is given by Equation 2 [22].
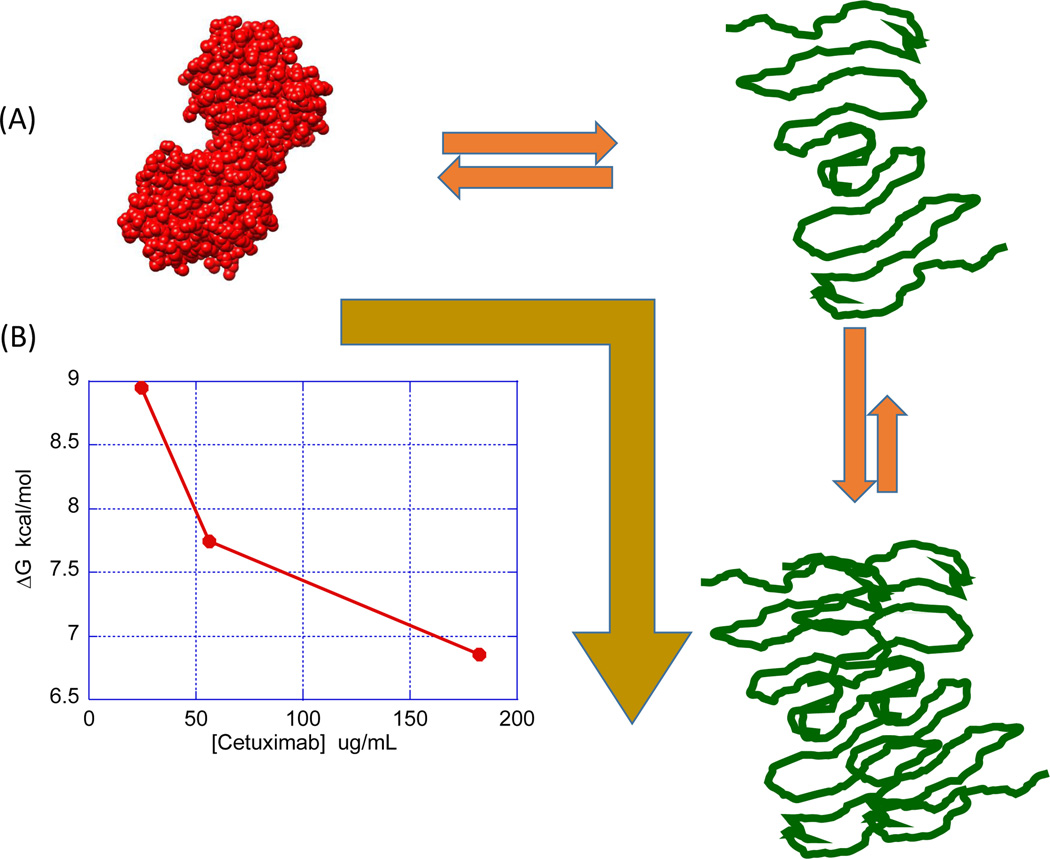
Figure 6.
Denatured state aggregation will pull the equilibrium to the right and decrease ΔG as the protein concentration increases (A). The gold arrow indicates that the equilibrium is shifted towards the denatured state. The decrease in ΔG indicates a lower stability of the native state. (B) Illustrates this situation by depicting the concentration dependence of ΔG for cetuximab in urea denaturation experiments. Chemical denaturation experiments were performed using a linear gradient of urea from 0 M to 9 M (The Hunk Automated Protein Denaturation System, Unchained Labs, Norton, MA). The buffer was 10 mM PBS, pH 7.5.
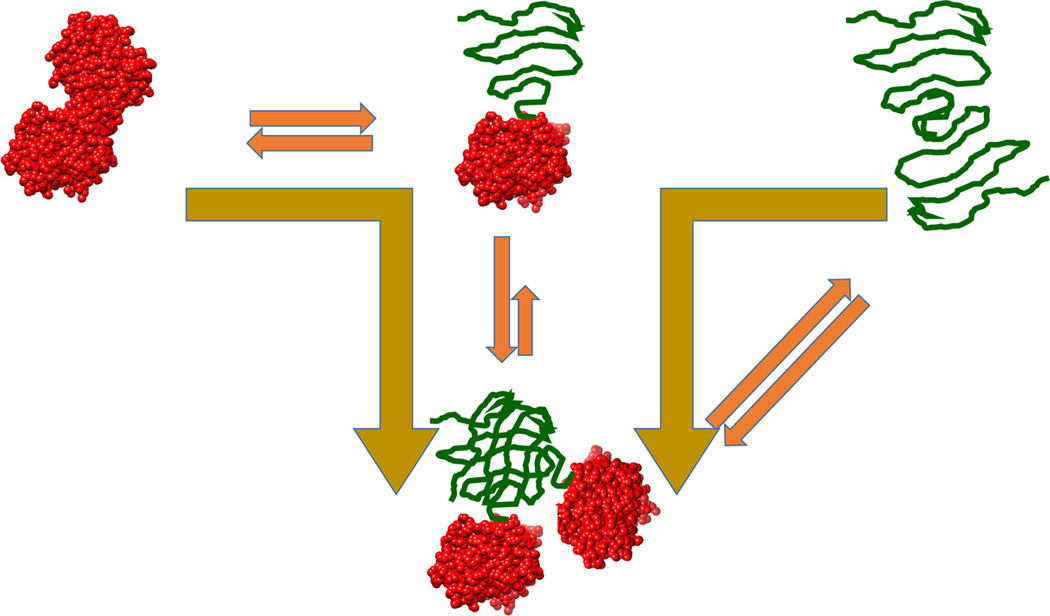
This behavior has been reported for cetuximab in urea denaturation experiments [22]. ΔG decreased from approximately 9 kcal/mol at 24 Mg/ml to 7 kcal/mol at 180 Mg/ml, consistent with denatured state aggregation. In those experiments, urea was able to resolve only one transition; however, subsequent experiments performed with guanidinium hydrochloride (GndnHCl), a more potent chemical denaturant, were able to resolve two transitions. However, only the first transition exhibited a consistent decrease in ΔG upon increasing antibody concentration, suggesting that the aggregating conformation is the partially denatured state emerging from the first transition. For several antibodies, CH2 domains have been identified as the low-stability domains, also responsible for the first transition observed in DSC experiments [25]. Also, partially denatured conformations in which the CH2 domains are unfolded can be prone to aggregate [26]. The second transition, involving the most stable domains, appeared to be independent of concentration, further emphasizing that, in this case, the least-stable domain is responsible for the observed aggregation. Figure 7 illustrates this situation. Even though the partially denatured state initiates the self-association process, full denaturation does not lead to dissociation of the aggregate. This situation is different than that observed with rHGH, in which full denaturation leads to dissociation of the oligomeric intermediates. For rHGH, this dissociation is reflected in a ΔG increase for the second transition upon increasing protein concentration. For cetuximab, the Gibbs energy of the second transition remains unchanged, strongly suggesting that the high-stability domain does not affect the selfassociation situation resulting from the denaturation of the low-stability domain. In this case, measures to prevent aggregation should be primarily aimed towards the least-stable domain.
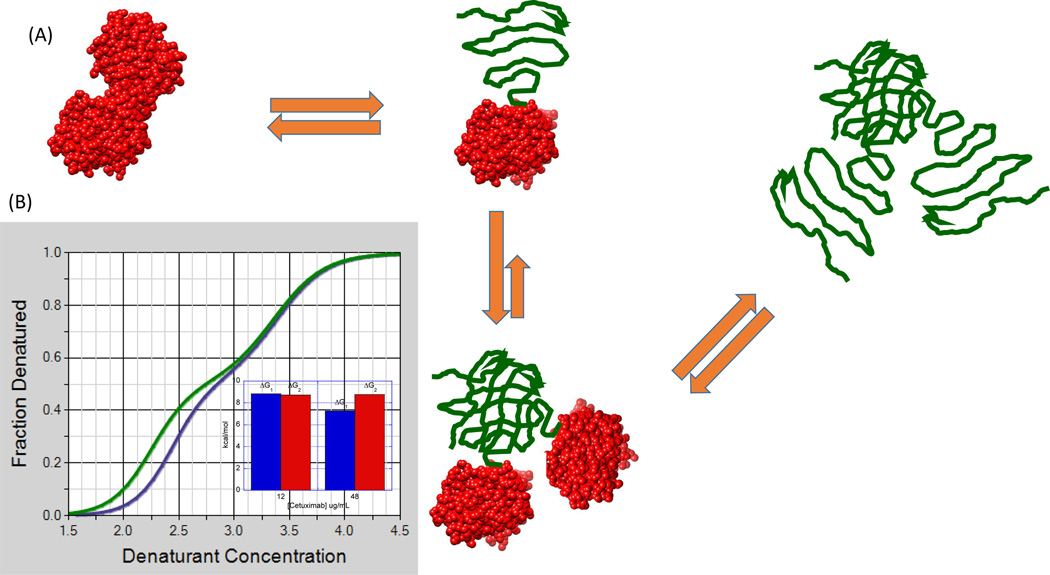
Figure 7.
Situation in which a partially denatured state exhibits a tendency to self-associate but full denaturation does not lead to dissociation as in Figure 4 (main text) (A). Even though the denatured high-stability domain might not exhibit an intrinsic tendency to self-associate, the entire protein remains aggregated through the denatured low-stability domain. In this situation, the ΔG of the first transition decreases with protein concentration, but the second one remains constant. This appears to be the case observed for the guanidinium hydrochloride denaturation of cetuximab obtained at 12 and 48 Mg/ml (B). Chemical denaturation experiments were performed using a linear gradient of guanidine hydrochloride from 0 M to 5.5 M with a buffer of 10 mM PBS, pH 7.5. (The Hunk Automated Protein Denaturation System, Unchained Labs, Norton, MA).
Concluding remarks
The analysis presented here indicates that different modes of partially or fully reversible self-association, which can eventually lead to irreversible aggregation, affect the concentration dependence of the conformational equilibrium of a protein in specific ways. Given that the conformational equilibrium and its concentration dependence can be measured by DSC or ICD, this analysis can provide valuable diagnosis and crucial information for the identification of better protein variants or better formulations. Preventing aggregation processes that are linked to the conformational equilibrium of a protein requires minimizing: (i) the concentration of aggregating species; and (ii) the self-association constant of the aggregating species. This task can be accelerated by quantitative knowledge of the conformation and/or self-association equilibrium.
Highlights.
Biologics exist in equilibrium between native, partially denatured, and denatured conformational states
The population of each state is dictated by their Gibbs energy, altered by changes in physical (e.g., temperature) and solution conditions (pH, salt, additives, etc.).
Some conformations have a tendency to self-associate and aggregate, an undesirable phenomenon in protein therapeutics
Aggregation tendencies can also be altered by changes in physical and solution conditions
Conformational equilibrium and self-association are linked thermodynamic functions
Any associative reaction, including aggregation, is concentration dependent
Conformational stability studies performed at different protein concentrations can provide early clues to future aggregation problems.
This analysis can be applied to protein variant selection or identification of better formulation solutions.
We discuss three different aggregation situations and their manifestation in the observed conformational equilibrium of a protein.
Acknowledgments
The authors are supported by grants from the National Science Foundation (MCB0641252) and the National Institutes of Health (GM56550).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Teaser: High structural stability and negligible aggregation are two sought-after properties of protein drugs. However, these properties are linked functions. Understanding their interdependence provides a rigorous way to select the best protein variants and design optimal formulations.
References
- 1.Ericsson UB, et al. Thermofuor-based high-throughput stability optimization of proteins for structural studies. Anal. Biochem. 2006;357:289–298. doi: 10.1016/j.ab.2006.07.027. [DOI] [PubMed] [Google Scholar]
- 2.Vedadi M, et al. Chemical screening methods to identify ligands that promote protein stability, protein crystallization and structure determination. Proc. Natl. Acad. Sci. U. S. A. 2006;103:15835–15840. doi: 10.1073/pnas.0605224103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Capelle MAH, et al. High throughput screening of protein formulation stability: practical considerations. Eur. J. Pharm. Biopharm. 2007;65:131–148. doi: 10.1016/j.ejpb.2006.09.009. [DOI] [PubMed] [Google Scholar]
- 4.Senisterra GA, Finerty PJ., Jr High throughput methods of assessing protein stability and aggregation. Mol. BioSyst. 2009;5:217–223. doi: 10.1039/b814377c. [DOI] [PubMed] [Google Scholar]
- 5.Privalov PL. Stability of proteins: small globular proteins. Adv. Protein Chem. 1979;33:167–239. doi: 10.1016/s0065-3233(08)60460-x. [DOI] [PubMed] [Google Scholar]
- 6.Privalov PL. Stability of proteins: proteins which do not present a single cooperative system. Adv. Protein Chem. 1982;35:1–104. [PubMed] [Google Scholar]
- 7.Brandts JF, et al. Thermodynamics of protein denaturation. Effect of pressure on the denaturation of ribonuclease A. Biochemistry. 1970;9:1038–1047. doi: 10.1021/bi00806a045. [DOI] [PubMed] [Google Scholar]
- 8.Privalov PL, Khechinashvili NN. A thermodynamic approach to the problem of stabilization of globular protein structure: a calorimetric study. J. Mol. Biol. 1974;86:665–684. doi: 10.1016/0022-2836(74)90188-0. [DOI] [PubMed] [Google Scholar]
- 9.Privalov G, et al. Precise scanning calorimeter for studying thermal properties of biological macromolecules in dilute solution. Anal. Biochem. 1995;232:79–85. doi: 10.1006/abio.1995.9957. [DOI] [PubMed] [Google Scholar]
- 10.Greene RF, Jr, Pace CN. Urea and guanidine hydrochloride denaturation of ribonuclease, lysozyme, alpha-chymotrypsin, and beta-lactoglobulin. J. Biol. Chem. 1974;249:5388–5393. [PubMed] [Google Scholar]
- 11.Pace CN, et al. Urea denaturation of barnase: pH dependence and characterization of the unfolded state. Biochemistry. 1992;31:2728–2734. doi: 10.1021/bi00125a013. [DOI] [PubMed] [Google Scholar]
- 12.Santoro MM, Bolen DW. Unfolding free energy changes determined by the linear extrapolation method. 1. Unfolding of phenylmethanesulfonyl.alpha.chymotrypsin using different denaturants. Biochemistry. 1988;27:8063–8068. doi: 10.1021/bi00421a014. [DOI] [PubMed] [Google Scholar]
- 13.Bolen DW, Santoro MM. Unfolding free energy changes determined by the linear extrapolation method. 2. Incorporation of dGn-u values in a thermodynamic cycle. Biochemistry. 1988;27:8069–8074. doi: 10.1021/bi00421a015. [DOI] [PubMed] [Google Scholar]
- 14.Myers JK, et al. Denaturant m values and heat capacity changes: relation to changes in accessible surface area of protein unfolding. Prot. Sci. 1995;4:2138–2148. doi: 10.1002/pro.5560041020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Freire E, et al. Chemical denaturation as a tool in the formulation optimization of biologics. Drug Discov. Today. 2013;18:1007–1013. doi: 10.1016/j.drudis.2013.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Joubert MK, et al. Classification and characterization of therapeutic antibody aggregates. J. Biol. Chem. 2011;286:25118–25133. doi: 10.1074/jbc.M110.160457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lumry R, Eyring H. Conformation changes in proteins. J. Phys. Chem. 1954;58:110–120. [Google Scholar]
- 18.Sanchez-Ruiz JM. Theoretical analysis of Lumry-Eyring models min differential scanning calorimetry. Biophys. J. 1992;61:921–935. doi: 10.1016/S0006-3495(92)81899-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Li Y, Roberts CJ. Protein aggregation pathways, kinetics, and thermodynamics. In: Roberts WWaCJ., editor. Aggregation of Therapeutic Proteins. John Wiley & Sons; 2010. pp. 63–102. [Google Scholar]
- 20.Arosio P, et al. Aggregation stability of a monoclonal antibody during downstream processing. Pharmaceutical Research. 2011;28:1884–1894. doi: 10.1007/s11095-011-0416-7. [DOI] [PubMed] [Google Scholar]
- 21.Brader ML, et al. Examination of thermal unfolding and aggregation profiles of a series of developable therapeutic monoclonal antibodies. Mol. Pharm. 2015;12:1005–1017. doi: 10.1021/mp400666b. [DOI] [PubMed] [Google Scholar]
- 22.Schon A, et al. Denatured state aggregation parameters derived from concentration dependence of protein stability. Anal. Biochem. 2015;488:45–50. doi: 10.1016/j.ab.2015.07.013. [DOI] [PubMed] [Google Scholar]
- 23.Todd MJ, et al. The structural stability of the HIV-1 protease. J. Mol. Biol. 1998;283:475–488. doi: 10.1006/jmbi.1998.2090. [DOI] [PubMed] [Google Scholar]
- 24.Kasimova MR, et al. The conformational equilibrium of human growth hormone. J. Mol. Biol. 1998;277:409–418. doi: 10.1006/jmbi.1997.1613. [DOI] [PubMed] [Google Scholar]
- 25.Ionescu RM, et al. Contribution of variable domains to the stability of humanized IgG1 monoclonal antibodies. J. Pharm. Sci. 2008;97:1414–1426. doi: 10.1002/jps.21104. [DOI] [PubMed] [Google Scholar]
- 26.Mehta SB, et al. Partial unfolding of a monoclonal antibody: role of a single domain in driving protein aggregation. Biochemistry. 2014;53:3367–3377. doi: 10.1021/bi5002163. [DOI] [PubMed] [Google Scholar]