Brain network characterization of high-risk preterm-born school-age children

Abstract

Higher risk for long-term cognitive and behavioral impairments is one of the hallmarks of extreme prematurity (EP) and pregnancy-associated fetal adverse conditions such as intrauterine growth restriction (IUGR). While neurodevelopmental delay and abnormal brain function occur in the absence of overt brain lesions, these conditions have been recently associated with changes in microstructural brain development. Recent imaging studies indicate changes in brain connectivity, in particular involving the white matter fibers belonging to the cortico-basal ganglia-thalamic loop. Furthermore, EP and IUGR have been related to altered brain network architecture in childhood, with reduced network global capacity, global efficiency and average nodal strength. In this study, we used a connectome analysis to characterize the structural brain networks of these children, with a special focus on their topological organization. On one hand, we confirm the reduced averaged network node degree and strength due to EP and IUGR. On the other, the decomposition of the brain networks in an optimal set of clusters remained substantially different among groups, talking in favor of a different network community structure. However, and despite the different community structure, the brain networks of these high-risk school-age children maintained the typical small-world, rich-club and modularity characteristics in all cases. Thus, our results suggest that brain reorganizes after EP and IUGR, prioritizing a tight modular structure, to maintain the small-world, rich-club and modularity characteristics. By themselves, both extreme prematurity and IUGR bear a similar risk for neurocognitive and behavioral impairment, and the here defined modular network alterations confirm similar structural changes both by IUGR and EP at school age compared to control. Interestingly, the combination of both conditions (IUGR + EP) does not result in a worse outcome. In such cases, the alteration in network topology appears mainly driven by the effect of extreme prematurity, suggesting that these brain network alterations present at school age have their origin in a common critical period, both for intrauterine and extrauterine adverse conditions.

Highlights

• •The structural brain network of high-risk children is characterized at school age.
• •The small-world and rich-club network design is maintained in high-risk preterm populations.
• •EP and IUGR similarly alter brain network integration and segregation patterns.
• •EP and IUGR differently affect the brain network topology.
• •The effect of EP prevails over the effect of IUGR when the two factors are combined.

1. Introduction

It is now commonly accepted that risk factors such as early exposure to extra-uterine environment or antenatal adverse conditions such as intrauterine growth restriction (IUGR) affect the brain structure. Extreme prematurity (EP) and IUGR have both been associated with regional changes in brain structures such as the cerebellum (Limperpoulos et al., 2005) and with reductions in gray matter (GM) and white matter (WM) volumes, specifically in the thalamus, hippocampus, orbitofrontal lobe, posterior cingulate cortex, and centrum semiovale (Ball et al., 2012, Padilla et al., 2011, Lodygensky et al., 2008). Other studies report further diminutions in cortical gray matter volume (Inder and Hüppi, 1999, Borradori-Tolsa et al., 2004), as well as in cortical surface gyrification (Dubois et al., 2008), proving the high susceptibility of the human brain to the consequences of altered fetal environment and/or premature birth. Yet, the structural reorganization of the brain following premature birth is striking and illustrates the functional and structural plasticity of the developing brain (Kostović et al., 2014).

These brain changes in the neonatal period have been linked to altered neurodevelopmental outcome later in life (Kwon et al., 2014, Jaekel et al., 2013, Ment et al., 2009). They have been associated with developmental disabilities such as cerebral palsy, mental retardation and a wide spectrum of learning disabilities and behavior disorders present in infancy and childhood (Ure et al., 2015, Ullman et al., 2015, Johnson and Marlow, 2011, Woodward et al., 2006). Detailed neuropsychological studies prove that in adolescence, children born very preterm show executive function impairments in tasks involving response inhibition, visual-perceptual tasks and mental flexibility (Johnson et al., 2011). In children born preterm, WM abnormalities particularly in the frontal lobe have been associated with impaired neurocognitive function (Duerden et al., 2013). Interestingly, moderately preterm infants with IUGR show the same incidence of about 40% of cognitive deficits as EP children (Guellec et al., 2011), leading to a large societal burden of neurocognitive under-achievement.

In this context, and since the development of functional connections is clearly dependent on the establishment of cerebral fiber pathways, their maturation and myelination (Supekar et al., 2012, Smyser et al., 2010;), we hypothesized that the extremely preterm born children (< 28 weeks gestation), and children born moderately preterm (28–37 weeks gestation) with IUGR will show different brain structural abnormalities depending on at what time in development the insult takes place, predisposing them to specific cognitive and behavioral deficits distinct from control preterm infants.

Diffusion MRI (dMRI) allows studying white matter tracts in-vivo and non-invasively by means of connectivity matrices (or connectomes) (Hagmann et al., 2012, Hagmann et al., 2008, Sporns and Zwi, 2004). A brain connectome can be seen as a network (equivalently, a graph), representing pairwise relations between interregional ensembles of neuronal elements (nodes), where the links represent anatomical connections formed by white-matter fiber paths (Meskadji et al., 2013, Sporns, 2012, Bullmore and Basset, 2011). This abstract representation of a complex system such as the brain makes graph theory a suitable framework for mathematical analysis. Indeed, this network model allows looking at the brain as an integrative complex system, and enables quantifying rates of brain structural variability in terms of measures of network integration, segregation and topology (some basic notions on network measures are resumed in Box 1, Box 2, Box 3).

Box 1. ∣Network integration.

Ability to rapidly combine specialized information from distributed brain regions.

Path length: number of steps required for moving from a given node to another. Generally, only the shortest path is considered, i.e. the average shortest distance between any two nodes.

Global efficiency: quantifies the exchange of information across the whole network where information is concurrently exchanged.

Node degree: represents the number of connections of a given node.

Node eccentricity: the greatest (geodesic) distance between this node at any other node in the network. It can be thought of as how far a node is from the node most distant from it in the graph.

Box 2. ∣Network segregation.

Ability for specialized processing to occur within densely interconnected groups of brain regions. Measures of segregation are related with clustering around individual nodes.

Local efficiency: quantifies a network's resistance to failure on a small scale. That is, the local efficiency of a node characterizes how well its neighbors exchange information when it is removed.

Clustering coefficient: Quantifies the number of connections that exist between the nearest neighbors of a node as a proportion of the maximum number of possible connections. It reflects presence of highly interconnected groups of nodes.

Betweenness centrality: is an indicator of a node's centrality in the network. It is equal to the number of shortest paths from all vertices to all other that pass through that node. A node with high betweenness centrality has a large influence on the transfer of items through the network.

Box 3. ∣Network topology.

Arrangement of the various elements of a network (links, nodes, etc). Human brains are characterized by ‘small-world’ network topology that combines high levels of local clustering among nodes and short paths linking nodes of a network.

Hubs: nodes with high degree. They are seen as central nodes that demonstrate a large proportion of shortest paths. This measure is closely related to the modularity of the network. Hubs can be described in terms of their roles in different network communities. Provincial hubs are connected mainly to nodes in their own modules, whereas connector hubs are connected to hub nodes in other modules.

Small-world network: characterized by the presence of abundant clustering of connections combined with short average distances between neuronal elements. In such networks, most nodes are not neighbors of one another, but can be reached from every other by a small number of hops or steps. These networks maximize information processing while minimizing wiring costs, support segregated and integrated information processing, and present resilience against pathology.

Modularity: measure of the structure of networks or graphs. Roughly, it quantifies the ease with which whole-brain network can be divided into distinct subnetworks or “modules” (also called groups, clusters or communities). Networks with high modularity have dense connections between nodes within modules but sparse connections between nodes in different modules.

Rich-club index: is a metric on networks designed to measure the extent to which well-connected nodes also connect to each others.

Connectomics has been mainly used in adult populations in the study of a broad spectrum of brain disorders such as epilepsy (Lemkaddem et al., 2014), schizophrenia (Griffa et al., 2015) and mild cognitive impairment (MCI), among others (see Griffa et al., 2013 for a review). In pediatric populations, connectomics has been used to study brain development beginning at its early stages and continuing through adolescence and adulthood (Pannek et al., 2014, Dennis and Thompson, 2014, Kim et al., 2014, Tymofiyeva et al., 2013, Hagmann et al., 2012, Fan et al., 2011). From this point of view, the human brain network can be considered to be a small-world network that is organized according to a hierarchical modular architecture, composed by communities of nodes highly interconnected between them, but sparsely connected with other modules (Bullmore and Sporns, 2009). This modular structure of brain networks is thought to be a crucial characteristic in terms of brain evolution and development (Meunier et al., 2009).

Prenatal (neuro)development is a highly dynamic process, with an initial phase of abundant formation of new connections, followed by a phase of selection and pruning of connections (Innocenti and Price, 2005). The major axonal projections are formed mainly between mid-gestation and term birth, leading to the establishment of all major macroscopic white matter tracts as early as birth. A recent global brain network study demonstrates that even early in development, human brain already exhibits an adult-like structural network organization, showing both small-world characteristics (Ratnarajah et al., 2013) and rich-club organization (Ball et al., 2012). Indeed, it has been shown that full-term newborns demonstrate already modular brain network architecture, even though this is subject to substantial changes across development. Yet, at birth, these tracts are in an immature state, supporting only limited, immature, functional interactions (Collin and Van den Heuvel, 2013).

Early postnatal development is characterized by a phase of exuberant axonal removal, which has been suggested to be roughly completed by the age of 2 years (Lamantia and Rakic, 1990). Following the first postnatal months, the surviving connections are strengthened by increases in axon diameter and myelination. From the connectome point of view, this phase translates to the connectome development being mainly driven by modulations in connection strength, involving specialization of the connectivity profile of regions. Indeed, Hagmann and colleagues demonstrated that node strength and efficiency is increased from 2 to 18 years, while the clustering coefficient decreases (Hagmann et al., 2010), showing an increasingly integrated connectome topology with development. In fact, across childhood, adolescence, and early adulthood, the connectome reorganizes into a more integrated topology, with increased segregation of anatomically clustered regions and increased integration between cortical regions that are spatially distributed, but functionally connected, into a subnetwork (Fair et al., 2009).

Both EP and IUGR conditions have been associated with alterations in the large-scale brain network structural topology and organization (Zubiaurre-Elorza et al., 2012, Esteban et al., 2010). These alterations have been further linked to abnormal scores in neurodevelopmental and socio-cognitive performance. Batallé and colleagues (Batalle et al., 2012) used diffusion-MRI based network analysis to describe quantitative differences in global brain connectivity in IUGR one-year-old children and associated these differences with impairments in neurodevelopmental outcome at two years of age. Long-term brain organization following EP and IUGR, and its relation with higher cognitive skills and social cognition at 6 years of age, has been further assessed by means of regional connectomics (Fischi-Gómez et al., 2014). At school age, longer gestational age has been associated with improved brain topological organization (Dae-Jin et al., 2014).

However, while EP and IUGR effects in brain connectivity have been studied independently, little is known about the effect of the combination of both factors. Moreover, network-based analyses in such populations mainly focus on the segregation and integration principles of their brain networks, neglecting, to some extent, the overall topological brain network organization. Yet, as assessed by Pessoa in (Pessoa, 2014): “while the number of connections is important in determining whether a region will operate as a hub, its structural topology is relevant, too”. In other words, while the connectivity strength of a certain brain region should be considered if we want to understand its impact on behavior, knowing the topology of this connectivity pattern is essential, too. Accordingly, a region that connects to just a few others will have much less of an impact than one that is more richly connected. That is, a region with local connectivity will contribute to local computations, whereas a region with more widespread connectivity will have a broader effect.

This study builds on our previous work, where the structural connectivity of preterm children and moderate preterm children with IUGR was compared and related to higher order cognitive and behavioral skills (Fischi-Gómez et al., 2014). However, rather than analyzing the regional structural connectivity by itself, here we used a connectome analysis to characterize the structural brain networks of these children, with a special focus on the topological organization. First, the modular topology of structural brain networks of these high-risk children is assessed and the similarity of their brain communities' structure compared using information theory derived metrics. Their brain network substrate is then analyzed by means of network organizational features and measures of network integration and segregation. The main goal is to globally study the brain network as an ensemble in order to find possible patterns of topological organization that may explain the similar incidence of neurocognitive and neurobehavioral impairment seen in these children at school age. Moreover, we explicitly explore the effect of the combination of extreme prematurity and IUGR on the overall brain network organization (i.e. topology), based on the hypothesis that the combination of these conditions would lead to a completely different brain network organization.

2. Material and methods

2.1. Subjects

51 premature born children at 6 years of age were recruited from the Child Developmental Units at the University Hospitals of Geneva and Lausanne. Perinatal data was prospectively recorded for all subjects, including birth weight (BW), gestational age at birth (GA) and gender. Children were classified as: (i) children born moderately preterm with normal growth (controls), (ii), children born at GA < 28 weeks (extremely preterm, EP), (ii) children born moderately preterm with additional IUGR (IUGR only, IUGR) and (iv) children born at GA < 28 weeks with additional IUGR (IUGR + EP) (see Table 1).

Table 1.

Sample characteristics of the study participants according to gestational age (GA) and presence of intrauterine growth restriction (IUGR). Cases with severe neurological impairment were not included in the study.

	Control (n = 8)	EP (n = 22)	IUGR (n = 11)	IUGR + EP (n = 10)
Gender (male/female)	3/5	9/13	5/6	7/3
GA [weeks]	32 (2.5)	26.7 (1)	32.5 (1.5)	26.7 (0.8)
BW [g]	1652.5 (402.4)	960.9 (193.5)	1181.8 (260.5)	657 (117.3)
BW z-score	− 0.3 (0.8)	0.3 (1)	− 2.1 (0.4)	− 1.5 (0.7)

Data is presented as mean (standard deviation) for continuous variables and count for categorical variables.

IUGR was defined as an estimated fetal weight below 10th percentile (confirmed at birth) and on criteria of placental insufficiency according to abnormal umbilical artery pulsatility index and/or cerebroplacental ratio and/or mean uterine artery pulsatility index as described in an earlier study (Borradori-Tolsa et al., 2004).

None of the children had any sign of prematurity-associated brain lesions on MRI at term equivalent age, as assessed by preterm brain injury scores (Woodward et al., 2006). At 6 years of age, their MRI scans were read as normal by experienced neuroradiologists. All of the recruited children were free from medication and from psychiatric or neurological diseases. Parental socio-economic status (SES) and maternal education was also recorded and assessed using the Largo scale (Largo et al., 1989).

2.2. Neurodevelopmental assessment

Infants' cognitive assessment was carried out using the French version of the Kaufman Assessment Battery for Children 1 (K-ABC 1) (Kaufman and Kaufman, 1983). More specifically, children were mainly tested for the overall cognitive outcome using the sequential and the simultaneous K-ABC scales and the mental processing composite score (MPC). The sequential processing scale primarily measures short-term memory and consists of subtests that measure problem-solving skills where the emphasis is on following a sequence or order. The simultaneous processing scale examines problem-solving skills that involve several processes at once. The sequential and simultaneous processing scales are combined to comprise the mental processing composite. The mental processing composite score is considered the global estimate of a child's level of intellectual functioning (Sattler, 1992).

2.3. MRI data acquisition

Children underwent MRI examinations on a 3T Siemens TrioTim system (Siemens Medical Solutions, Erlangen, Germany). For each subject, high-resolution T1-weighted (T1w) images were acquired using a 3D Magnetization Prepared Rapid Acquisition Gradient Echo (MPRAGE) protocol, with TE = 2.91 ms, TR = 2500 ms, TI = 1100 ms. Diffusion weighted images (DWI) were acquired using a diffusion sensitized single echo planar imaging (SE-EPI) sequence covering 30 diffusion directions (b = 1000 m/s²), and an additional image without diffusion-weighting (b0), with TR = 1020 ms and TE = 107 ms. The resolution of both scans was 1.8 × 1.8 × 2 mm³. All acquired images were visually inspected for apparent artifacts, and 2 subjects excluded accordingly. DWIs were corrected for eddy currents effects and simple head motions using FMRIB's diffusion toolbox (www.fmrib.ox.ac.uk).

2.4. Data processing

2.4.1. Structural connectome construction

The extraction of the whole brain structural connectivity matrices (connectomes) for each subject was performed using the Connectome Mapping Toolkit, a python-based open-source software that implements a full diffusion MRI processing pipeline, from raw diffusion/T1/T2 data to multi-resolution connection matrices (www.cmtk.org, (Daducci et al., 2012)). The high-resolution T1w volume is first registered to the diffusion space using the bbregister tool from Freesurfer software (http://surfer.nmr.mgh.harvard.edu/). From there, the whole processing pipeline can be sequentially divided in (i) WM-GM surface extraction and cortical and subcortical parcellation (again, using Freesurfer), (ii) streamline tractography (done by an in-house developed method implemented in the cmtk pipeline and (iii) connectome construction, by estimating the connection density between each pair of regions of interest (ROI). The connection density between two cortical or subcortical ROIs is calculated as the sum of all streamlines connecting these two ROIs divided by the length of the streamlines. This value is normalized by the size of the ROIs.

2.4.2. Brain network construction: defining nodes and edge weights

Brain network's nodes were defined as the cortical ROI centroids. Edge weights were characterized as the structural connectivity (SC) between each pair of cortical regions. Following (Fischi-Gómez et al., 2014), the SC was modeled as the product of 2 components. The first component is the group connection density (gCD), computed as the mean connection matrices in a given group. Since the mean is non-null if at least one of the elements is non-null, these group average connectivity matrices consist a support of the connectivity in each group and represent the maximum grid of connections for each group. The gCD matrices did not show any statistically significant differences between groups in terms of average strength and network density. This fact was expected due to the absence of gross brain pathology. The second component is the so-called connection efficacy, considered to be subject-dependent. It is computed as the mean fractional anisotropy (FA) value of the bundle connecting two cortical ROI. Thus, each individual participant contribution is considered to be the product of the group mean connection density and the individual connection efficacy.

2.4.3. Network features

Brain networks can help to understand the large-scale structural topology of brain connectivity (Bullmore and Sporns, 2009). They can be analyzed using graph theory measures, characterizing network structure (topology) and function, and measuring changes related to the refinement in specific metrics of networks topology (see Boxes 1, Box 2, Box 3 in the introduction section). Global description of the brain network includes measures of topological organization (modularity, small-world and rich-club indices), integration and segregation (Rubinov and Sporns, 2010).

2.4.3.1. Organizational measures

2.4.3.1.1. Small-world and rich-club attributes

The human brain connectome proved to be a small-world and rich-cub network (i.e. characterized by the presence of abundant clustering of connections combined with short average distances between neuronal elements (Sporns and Zwi, 2004)), favored by the presence of a rich-club set of tightly connected nodes (van den Heuvel and Sporns, 2011). It is organized according to a hierarchical modular architecture composed by communities of nodes highly interconnected between them but sparsely connected with other modules (Bullmore and Sporns, 2009). This modular structure of brain networks is thought to be a crucial characteristic of brain evolution and development (Meunier et al., 2009). In this study, we computed the normalized rich-club coefficients Φ_norm(k) for several degree values k as in Van den Heuvel and Sporns (2011). These coefficients describe the exceeding level of connectedness between high degree nodes compared to a randomized reference network. A value above 1 indicates a rich-club network architecture.

Small-world indices were computed with respect to the random equivalent network with same degree distribution of each subject (see (Bullmore and Sporns, 2012) for a comprehensive description of these measures).

2.4.3.1.2. Brain network modular architecture

In order to disentangle the existence of a network communities structure, for each brain network we computed its optimal modular decomposition, i.e. the complete subdivision of the network in non-overlapping modules. A large variety of conceptually different and competing methods for community detection in graphs have been proposed. However, in the context of brain network analysis, the modularity index Q is the preferred choice, as it is a popular and effective measure of network decomposability and quality of the partitions.

The modularity index Q, was originally introduced by (Newmann, 2006) and defined as the number of edges connecting nodes belonging to the same community, minus the expected value of interconnecting edges in absence of any community structure, i.e. in an equivalent random graph. Formally, Q can we expressed as (Newmann, 2006):

$$Q=\frac{1}{2}\left(A_{\mathit{ij}}-P_{\mathit{ij}}\right)\delta \left(C_i,C_j\right)$$

with A the binary or weighted adjacency matrix of network G (A_ij being an element of A), m the total number of edges in the graph, and the δ function expressing the co-occurrence of two nodes (i;j) in the same cluster, i.e. δ (C_i,C_j) = 1 iff Ci = Cj, with Ci community assignment of node i. P_ij expresses the expected number of edges between nodes i and j, in an equivalent random network. This probability of connection between two nodes is proportional to the product of their degree k:

$$P_{\mathit{ij}}=\frac{k_i{k}_j}{2m}.$$

2.4.3.1.3. Optimal modular decomposition of brain networks

In this work, the optimal modular decomposition was determined using the Brain Connectivity Toolbox (BCT) https://sites.google.com/site/bctnet/) by selecting the partition with the highest Q value from 100 runs of the Louvain algorithm (Blondel et al., 2008). Besides its computation efficiency, the choice of the Louvain algorithm was done based on the fact that it incorporates a notion of modular hierarchical structure that is well suited for brain analysis questions. The algorithm is composed of two steps iteratively repeated until convergence to a modularity maximum. First, each node is placed in a separate module, and all possible node moves between modules are evaluated in terms of modularity gain (step 1). When no individual move can further improve the Q value, nodes belonging to the same community are agglomerated (step 2) in order to form new ‘super-nodes'. Step one (moves evaluation) is repeated on the new ‘super-nodes' network. The two steps are repeated until convergence.

Following (Rubinov and Sporns, 2011), the partitions obtained with the Louvain algorithm were compared using the mutual information (MI) and variation of information (VI) indices described in Meila (2007). These two measures, based on the concept of entropy, quantify similarities and differences between graphs partitions. The mutual information (MI) quantifies how much information is shared by the two (different) partitions C_i and C_j of a given network G. Roughly speaking, MI tells how much we learn about C_i if we know C_j, and viceversa. Nevertheless the most commonly used measure of similarity in graph is the normalized mutual information (MIn), introduced by (Danon et al., 2005). This measure equals 1 if the two partitions are identical, whereas it has an expected value of 0 is the two partitions are independent.

The variation of information (VI) expresses the quantity of information intrinsic to the two partitions, corrected by the information shared by the two partitions. VI is up-bounded by the logarithm of the number of nodes (log n) and can be therefore normalized by this value, giving a rescaled value of VI to the range [0,1].

In short, one can assume that a partition effectively represents a group if the distance between subjects of the same group in terms of MIn and VIn is small (in other words, if MIn values are high and VIn values are small). These two measures were used to quantify the consistency of the brain modular architecture for the subjects belonging to the same group and to study the variability of the brain modular decomposition of EP, IUGR and IUGR + EP subjects when compared to the rest of the cohort.

2.4.3.1.4. Network community structure

In order to understand the organization of connectivity networks, it is important to determine the community structure underlying these complex networks. Indeed, considering that the study of brain networks is confounded by the fact that analysis consists of data collected from multiple subjects, it is important to identify communities representative of all subjects in a group. The consensus clustering provides a method to represent the consensus across multiple runs of a clustering algorithm, to determine the number of clusters in the data, and to assess the stability of the discovered clusters. In other words, this approach finds, the partition most representative of the actual community structure of a group.

In this study the representative brain network partition (or community structure) for each group was computed by means of the consensus clustering algorithm (CC) (Lancichinetti and Fortunato, 2012, Monti et al., 2003) (with a threshold value of the consensus matrix of tau = 0.3 and n = 100 iterations).

2.4.3.2. Brain network segregation and integration characteristics

The overall network connectivity and topology was examined by commonly used integration and segregation measures. From the structural connectome, we computed 3 global (average shortest path length, global efficiency and transitivity), and 6 average nodal (average node degree, efficiency, strength, clustering coefficient (clustering index), betweenness centrality and eccentricity) network measures. The final goal was to characterize network structure and function by measuring changes related to the refinement in specific metrics of networks topology (see (Rubinov and Sporns, 2010) for definitions and detailed information of the network measures).

2.5. Statistical analysis

Statistical case–control and case–case comparisons between groups were performed for (i) cognitive scores and (ii) measures of network integration and segregation using a Wilcoxon rank-sum test.

The optimal modular decomposition of each individual brain network was compared to the rest of the cohort in terms of MIn and VIn indices, using a Wilcoxon ranksum test. We tested three different settings: (i) intra-group comparison, where each subject's modular decomposition was compared to the rest of the subjects belonging to the same group, (ii) case–control comparison, where each of the EP, IUGR + EP and IUGR subjects were compared to the control subjects and (iii) case–case comparison, where EP, IUGR + EP and IUGR subjects were compared between them.

3. Results

In this study, connectome analysis was used to characterize the structural brain networks of children born extreme and moderately premature (with or without additional growth restriction, IUGR). Here, results are presented separately for the four groups with the moderately preterm children with normal intrauterine growth acting as control group.

3.1. Cognitive scores group differences

Table 2 shows the mean K-ABC scores for all groups, together with the standard deviation. In all K-ABC scales, higher scores are related to higher cognitive skills. Whilst the mental processing composite score, considered as the global estimate of a child's level of intellectual functioning, did not show any significant difference for any case group when compared to controls, all case groups (EP, IUGR and IUGR + EP) showed significantly reduced K-ABC simultaneous score compared to controls, with p = 0.0051 (EP), p = 0.03 (IUGR) and p = 0.0337 (IUGR + EP), respectively after FDR correction. No other statistical differences were found. No significant differences were found for the case–case comparisons (EP vs. IUGR, EP vs. IUGR + EP and IUGR vs. IUGR + EP).

Table 2.

Mean value and standard deviation (mean/std) for the neurocognitive scores for all groups under analysis.

Cognitive scores	CONTROL	EP	IUGR	IUGR + EP
K-ABC sequential	99.37/9.59	94.5/15.36	100.81/16.43	95.18/13.21
K-ABC simultaneous	109/7.25	96.90/9.99 (*)	101.45/8.86 (*)	95.54/15.87 (*)
K-ABC composite	105.12/8.90	95.04/11.75	101.18/13.11	93.54/16.86

For assessment of the cognitive outcome, we used the KABC sequential, simultaneous and composite scores. Higher K-ABC scores indicate higher cognitive performance. Significant differences (when compared to controls) are marked with (*). Statistical significance was declared at level 0.05 and the resulting p-values were FDR corrected.

3.2. Network features: group differences

3.2.1. Organizational measures

3.2.1.1. Small-world and rich-club attributes

For all groups, small-world characteristics of the networks were detected, with no significant differences (see Table 3). In the same line, for all subjects the presence of a rich-club of interconnected cortical and subcortical hubs was found. Again, the comparison of rich-club coefficients did not show conclusive differences among groups.

Table 3.

Mean small world indices for all groups and group-averaged number of clusters, modularity indices (mean ± standard deviation) for subject-wise brain network modular decomposition for the four groups.

	CTRL	EP	IUGR	IUGR + EP
Small-world index (swi)	2.9 ± 0.22	2.39 ± 0.42	3.03 ± 0.27	3.21 ± 0.51
Number of modules (n)	10.12 ± 0.64	9.35 ± 0.71	10.82 ± 0.75	9.7 ± 0.67
Modularity index (Q)	0.6868 ± 0.0102	0.7034 ± 0.0110	0.6990 ± 0.0225	0.6975 ± 0.0067

3.2.1.2. Brain network modular architecture

All subjects presented a modular architecture of their brain network, with overall comparable mean number of modules (or clusters) and mean modularity index (Q). Interestingly, and although the comparison showed no significant difference, EP children tended towards a smaller number of brain network modules (see Table 3), while IUGR children had a higher number.

Number of modules (n), modularity index (Q) and small world index (swi) for all case subjects (EP, IUGR and IUGR + EP) were compared to controls using a Wilcoxon ranksum test. No significant differences were found.

3.2.1.3. Optimal modular decomposition of brain networks

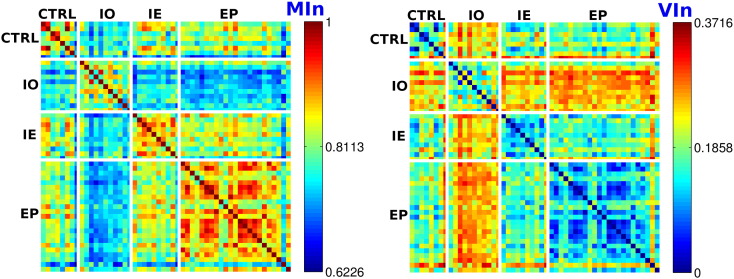
The optimal modular decomposition of each brain network was computed. The resulting network's decompositions were compared between subjects using the normalized mutual information (MIn) and variation of information (VIn) indices. Fig. 1 reports the MIn and VIn values between each pair of subjects' optimal modular decompositions. Each row of the matrix represents the MIn (resp. VIn) values of one subject network's decomposition with respect to the rest of the cohort. For visualization purposes, each matrix is divided in different blocks by white lines. The diagonal blocks represent the resulting MIn and VIn indices within the same groups of subjects (intra-group comparison), while the off-diagonal blocks characterize these values for the inter-group comparison. Higher MIn values together with lower VIn values in the diagonal blocks indicate similar modular topologies among subjects belonging to the same group. In this case, no statistical differences were found when comparing subjects belonging to the same group (repeated 2-sample Wilcoxon ranksum test). On the contrary, MIn and VIn distributions for subjects belonging to different groups (off-diagonal blocks) appeared significantly different in all cases (p < 0.05, FDR corrected), talking in favor of different, group-specific modular brain network structure.

Fig. 1.

Matrices representing respectively the normalized (a) MI (Min) and (b) VI (Vin) values between each pair of optimal modular decompositions. Each row of the matrix corresponds to a single subject. Each cell of the matrix depicts the Min and Vin values obtained when comparing each subject's optimal modular decomposition to the rest of the cohort (see color bars next to each matrix). White lines separate the subjects in the 4 different groups. Blocks in the diagonal of each matrix correspond to the intra-group comparison. Off-diagonal blocks correspond to the inter-groups comparison. CTRL: control subjects; IO: IUGR subjects; IE. IUGR + EP subjects; EP: EP subjects. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

It bears noting that EP and IUGR + EP subjects showed a relatively high inter-group similarity (maximum MIn average/minimum VIn average, see Fig. 1 and Table 5), which reflects a close modular structure.

Table 5.

Min and Vin average and standard deviation values for the case–control optimal modular decomposition comparison.

	MIn (mean ± std)	VIn (mean ± std)
CTRL–EP	0.79988 ± 0.056778 (*)	0.1955 ± 0.055527 (*)
CTRL–IUGR	0.76813 ± 0.04112 (*)	0.23726 ± 0.042292 (*)
CTRL–IUGR + EP	0.81224 ± 0.061895 (*)	0.1955 ± 0.055527 (*)

For each EP, IUGR and IUGR + EP subjects, resp. Its modular decomposition was compared to the control subjects by means of the normalized MI and VI indices. These indices were compared statistically using a Wilcoxon ranksum test. Significant differences are marked with (*). Min and Vin indices for all case subjects were significantly different when compared to controls. Statistical significance was declared at level 0.05 and the resulting p-values were FDR corrected.

Table 4, Table 5, Table 6 report the MIn and VIn mean and standard deviation values for both intra-group and inter-group comparisons. Statistically significant differences are marked with (*). When comparing subjects within the same group, the relatively high MIn values together with the lower VIn values prove the similar overall network structure of all subjects belonging to the same group, with no significant differences (see Table 4).

Table 4.

Min and Vin average and standard deviation values for the intra-group optimal modular decomposition comparison.

	MIn (mean ± std)	VIn (mean ± std)
CTRL–CTRL	0.81613 ± 0.081501	0.18418 ± 0.081337
EP–EP	0.86198 ± 0.056419	0.13186 ± 0.054544
IUGR–IUGR	0.82578 ± 0.050917	0.1818 ± 0.052754
IUGR + EP–IUGR + EP	0.85195 ± 0.049577	0.14386 ± 0.047798

For each subject, its modular decomposition was compared to the rest of the subjects in the same group by means of the normalized MI and VI indices. These indices were compared statistically using a Wilcoxon ranksum test. No differences were found in these indices among subjects of the same group.

Table 6.

Min and Vin average and standard deviation values for case–case optimal modular decomposition comparison.

	MIn (mean ± std)	VIn (mean ± std)
EP–IUGR	0.74954 ± 0.038688 (*)	0.2502 ± 0.038781 (*)
EP–IUGR + EP	0.81904 ± 0.048115 (*)	0.17442 ± 0.047043 (*)
IUGR–IUGR + EP	0.76368 ± 0.04176 (*)	0.23821 ± 0.040862 (*)

For each EP, IUGR + EP and IUGR subjects, resp., its modular decomposition was compared to the rest of the subjects by means of the normalized MI and VI indexes. These indexes were compared statistically using a Wilcoxon ranksum test. Significant differences are marked with (*). Min and Vin were significantly different in all cases. Statistical significance was declared at level 0.05 and the resulting p-values were FDR corrected.

As seen in Table 5, for EP, IUGR + EP and IUGR subjects, the modular structure of the brain networks when compared to controls appeared significantly different.

Table 6 shows that the EP and IUGR + EP subjects have a close brain network modular structure. Even if in all cases the resulting network decomposition was significantly different, the higher MIn values together with the lower VIn values talk in favor of a relatively similar modular structure.

3.2.1.4. Network community structure

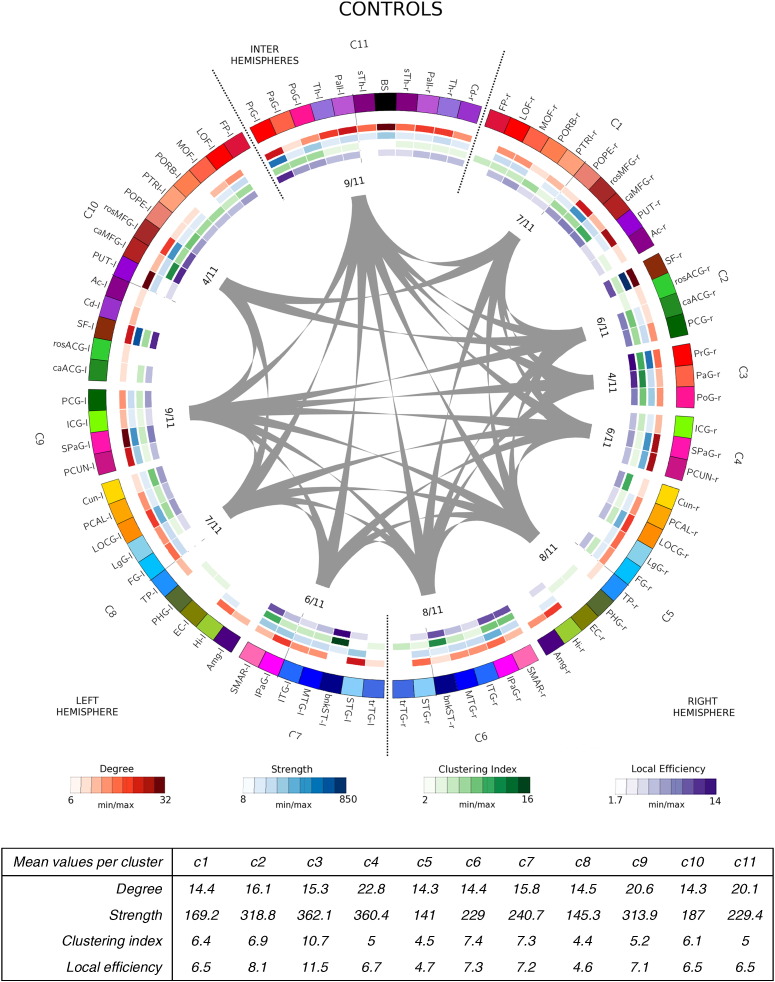
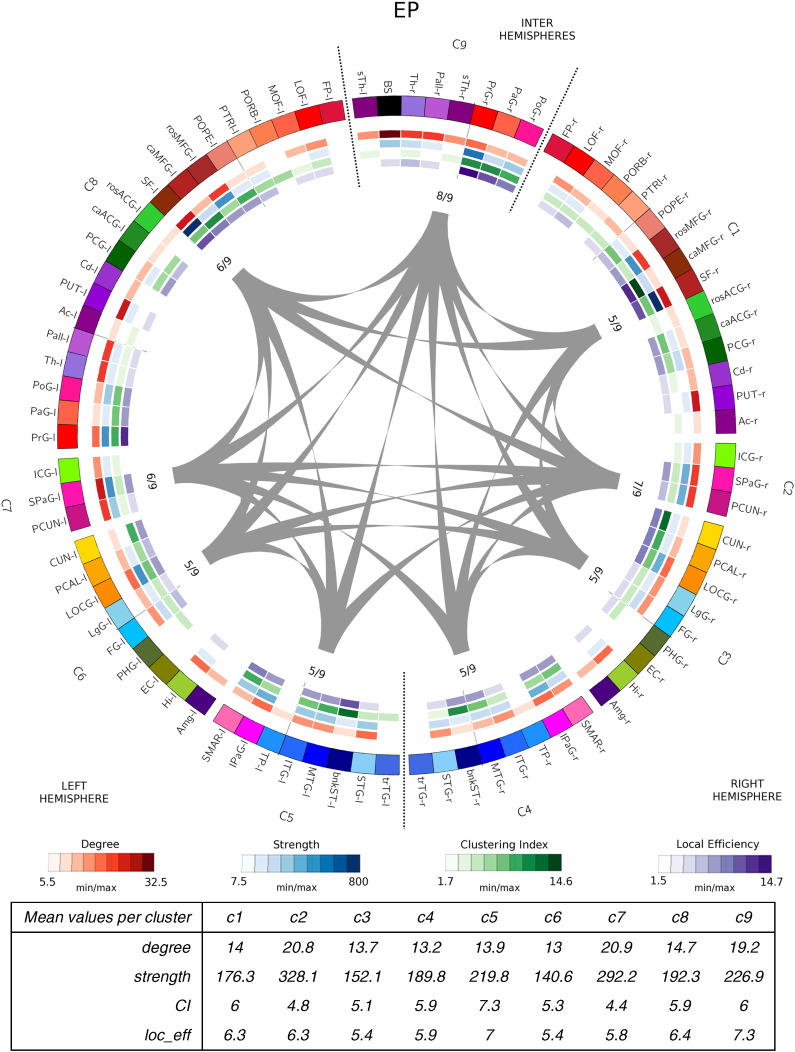
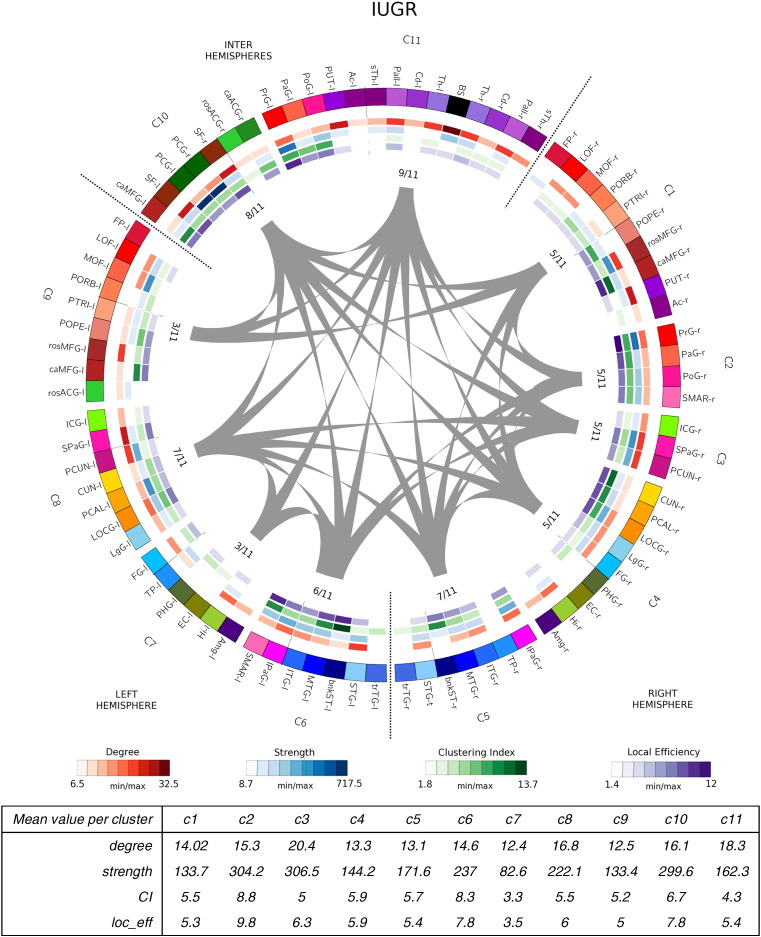
Network community structure for each group is shown in Fig. 2, Fig. 3, Fig. 4, Fig. 5. After running the consensus clustering algorithm, the four group-representative community structure partitions counted 11 clusters for control and IUGR subjects, 9 for EP and 10 clusters for IUGR + EP subjects. With the consensus clustering algorithm we obtained the partition the most representative of the actual community structure of each group, which do not necessarily match the averaged number of modules among subjects of the same group.

Fig. 2.

Network community structure for control subjects after running the consensus clustering algorithm. Controls' representative partition counts of 11 clusters (C1–C11). Cortical and subcortical regions are color-coded as follows: frontal regions: reds–maroons; limbic regions: greens; parietal regions: pinks; temporal regions: blues; occipital regions: yellows; subcortical regions: purples. Node list of abbreviations are found in Table 7 (r- and l- stand for right and left hemisphere, resp.). Right hemisphere clusters are composed by regions from the right hemisphere only. Left hemisphere's clusters contain regions from the left hemisphere only. Inter hemisphere cluster (C11) contains regions from both hemispheres. Gray lines indicated connections between different clusters. The inner values indicate the number of cluster to which each cluster connects to divided by the total number of clusters. Inner circles (heatmaps) show the network measures for each node: red: node degree; blue: node strength: green: node clustering index; purple: node local efficiency (see legend below for the respective values). The table below the image indicates for each cluster, the mean values of the network measures. For control subjects, temporal, occipital and parietal areas cluster almost symmetrically (C4, C5 and C6 clusters are equal to C7, C8 and C9, with the exception of the PCG-l in the left hemisphere, C9). Frontal areas also showed a symmetric pattern of clustering. The biggest differences between hemispheres are found in the limbic (in green) and central areas (PrG, PaG and PoG), which form two independent clusters in the right hemisphere (C2 and C3), but cluster with the frontal regions (C10) and subcortical regions (C11) respectively in the left hemisphere. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 3.

Network community structure for EP subjects after running the consensus clustering algorithm. EP subjects' representative partition counts of 9 clusters (C1-C9). Cortical and subcortical regions are color-coded as follows: frontal regions: reds–maroons; limbic regions: greens; parietal regions: pinks; temporal regions: blues; occipital regions: yellows; subcortical regions: purples. Node list of abbreviations are found in Table 7 (r- and l- stand for right and left hemisphere, resp.). Right hemisphere clusters are composed by regions from the right hemisphere only. Left hemisphere's clusters contain regions from the left hemisphere only. Inter hemisphere cluster (C9) contains regions from both hemispheres. Gray lines indicated connections between different clusters. The inner values indicate the number of cluster to which each cluster connects to divided by the total number of clusters. Inner circles (heatmaps) show the network measures for each node: red: node degree; blue: node strength: green: node clustering index; purple: nodal local efficiency (see legend below for the respective values). The table below the image indicates for each cluster, the mean values of the network measures. Here again, temporal (blue), occipital (yellow) and parietal (pink) areas cluster symmetrically among (C2, C3 and C4 clusters are equal to C5, C6 and C7), and the main differences are found in the frontal and limbic areas. In this case, limbic areas (green) cluster with the frontal areas (C1 and C8 clusters) in both hemispheres with central areas (PrG, PaG and PoG) clustering together also in the left hemisphere (C8), and with some subcortical areas from both right and left hemispheres (C9) in the right hemisphere. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 4.

Network community structure for IUGR subjects after running the consensus clustering algorithm. IUGR subject's representative partition counts of 11 clusters (C1–C11). Cortical and subcortical regions are color-coded as follows: Frontal regions: reds-maroons; Limbic regions: greens; Parietal regions: pinks; temporal regions: blues; occipital regions: yellows. Node list of abbreviations are found in Table 7 (r- and l- stand for right and left hemisphere, resp.). Right hemisphere clusters are composed by regions from the right hemisphere only. Left hemisphere's clusters contain regions from the left hemisphere only. Right–Left hemisphere clusters (C10 and C11) contain regions from both hemispheres. Gray lines indicated connections between different clusters. The inner values indicate the number of cluster to which each cluster connects to divided by the total number of clusters. Inner circles (heatmaps) show the network measures for each node: red: node degree; blue: node strength: green: node clustering index; purple: nodal local efficiency (see legend below for the respective values). The table below the image indicates for each cluster, the mean values of the network measures. On the right hemisphere, IUGR network community structure is practically equal to the control subjects, apart from the central regions that cluster with the SMAR also (C2). On the left hemisphere, C6 and C7 (temporal and some limbic regions — PHG, EC and Hi-) maintain the same pattern as EP and control subjects (clustering together and being almost symmetrical in both hemispheres). The only differences in this case are the occipital regions (CUN, PCAL, LOCG) and the LgG that cluster to the parietal regions in these subjects (C8). The main differences are found, again, in the limbic regions (cingular regions) that cluster interhemispherically (C10), and the central regions, that cluster with subcortical structures from both hemispheres (C11), such as in the control case (not the EP). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 5.

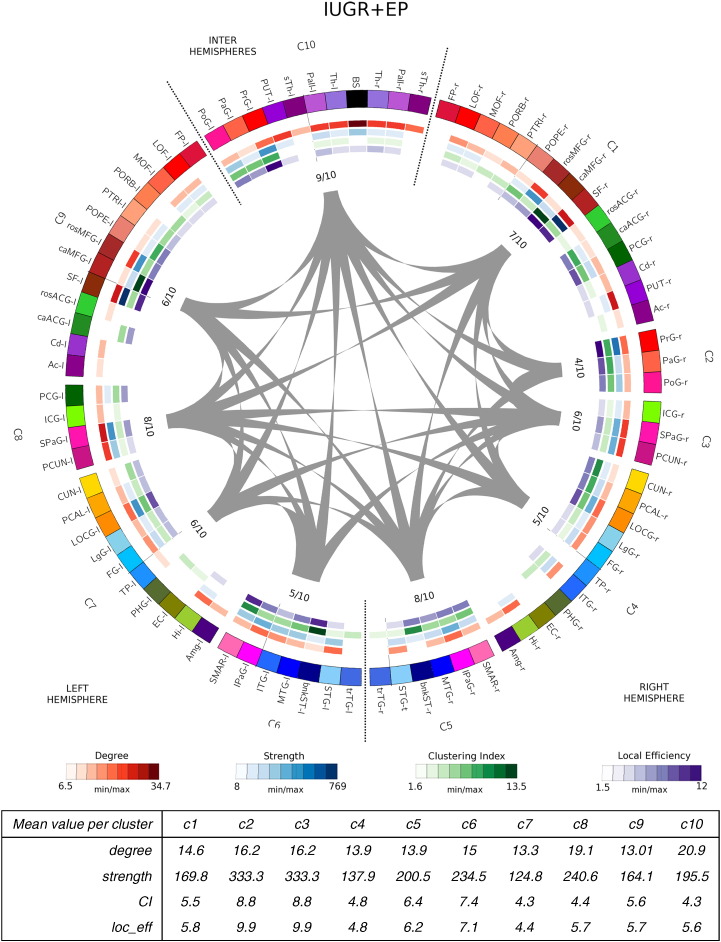
Network community structure for IUGR + EP subjects after running the consensus clustering algorithm. IUGR + EP subjects representative partition count of 10 clusters (C1–C10). Cortical and subcortical regions are color-coded as follows: frontal regions: reds–maroons; limbic regions: greens; parietal regions: pinks; temporal regions: blues; occipital regions: yellows. Node list of abbreviations are found in Table 7 (r- and l- stand for right and left hemisphere, resp.). Right hemisphere clusters are clusters composed by regions from the right hemisphere only. Left hemisphere's clusters, indicate clusters containing regions from the left hemisphere only. Right–Left hemisphere cluster (C10) contain regions from both hemispheres. Gray lines indicated connections between different clusters. The inner values indicate the number of cluster to which each cluster connects to divided by the total number of clusters. Inner circles (heatmaps) show the network measures for each node: red: node degree; blue: node strength: green: node clustering index; purple: nodal local efficiency (see legend below for the respective values). The table below the image indicates for each cluster, the mean values of the network measures. On the right hemisphere, IUGR + EP network community structure is equal to the EP subjects' structure (C1, C3, C4 and C5) except for the central regions (PrG, PaG and PoG) that form an independent cluster (C2) instead of clustering with some subcortical structures as in the EP case (see Fig. 3, cluster C9). For these subjects, as for controls and EP, temporal, occipital and parietal regions cluster symmetrically in both hemispheres (C3–C5 are equal to C6–C8, except for the PCG in C8). In the same line, C9 cluster of IUGR + EP subjects is similar to C9 cluster for EP subjects (see Fig. 3), except for the central regions of the left hemisphere (PrG, PaG, PoG) and the left pallidum and accumbens, that in the IUGR + EP case cluster with some subcortical structures interhemispherically (C10). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

The 4 connectograms were constructed using the Circos visualization tool, a visualization tool originally used for genomics data but adapted for brain analysis (see Irimia et al., 2012). In the connectograms shown in Fig. 2, Fig. 3, Fig. 4, Fig. 5, each cortical structure is assigned a unique RGB color, depending on the brain region they belong to (frontal: red-maroons; limbic: greens; parietal: pinks; temporal: blues; occipital: yellows and subcortical: purples). Clusters are named from C1 to C* (9, 10 or 11 depending on the group). Right hemisphere clusters are clusters composed by regions from the right hemisphere only. Left hemisphere's clusters, indicate clusters containing regions from the left hemisphere only. Inter hemisphere clusters contain regions from both hemispheres. Gray lines indicated connections between different clusters. The values close to each cluster connection indicate the number of clusters to which each cluster connects to, divided by the total number of clusters. The inner colored circles (known as heatmaps) represent, for each node of the network, different nodal measures; node degree in red, node strength in blue, node clustering index in green and node efficiency in purple (see legend below the connectograms). The scale of each measure is determined by the minimum and maximum values of these respective measures. The tables below the images indicate, for each cluster, the mean values of the network measures used in the analysis.

The visual inspection of the consensus clustering configurations corroborates the numerical results, and indicates that the main differences in modular structure among groups are found in the frontal and limbic regions. Indeed, while in the temporal, parietal and occipital regions nodes tend to cluster in a similar way in all cases, the frontal and limbic regions show higher dissimilarities between groups.

More specifically, for control subjects, temporal (blue), occipital (yellow) and parietal areas (pink) cluster almost symmetrically (C4, C5 and C6 clusters are equal to C7, C8 and C9, with the exception of the posterior cingulate giyrus (PCG-l) in the left hemisphere, C9). Frontal areas (red) also showed a symmetric pattern of clustering. The biggest differences between hemispheres are found in the limbic (in green) and central areas (precentral, paracentral and postcentral gyri, respectively PrG, PaG and PoG), which form two independent clusters in the right hemisphere (C2 and C3), but cluster with the frontal regions (C10) and subcortical regions (C11) respectively in the left hemisphere (see Fig. 2).

Concerning the EP subjects, temporal (blue), occipital (yellow) and parietal (pink) areas cluster symmetrically again (C2, C3 and C4 clusters are equal to C5, C6 and C7). Compared to controls, the main differences are found in the clusters composed by the frontal (red) and limbic areas (in green) (see Fig. 3). In this case, limbic areas cluster with the frontal areas (C1 and C8 clusters) in both hemispheres. Right hemisphere's central areas (PrG, PaG and PoG) cluster with some subcortical areas from both right and left hemispheres (C9), while left central areas cluster with left hemisphere's frontal and limbic areas (C8).

IUGR subjects' show the most different network community structure compared to the rest of subjects (see Fig. 4). On the right hemisphere, IUGR network community structure is practically equal to the control subjects, apart from the central regions that cluster with the supramarginal gyrus (SMAR) also (C2). On the left hemisphere the differences are more apparent. C6 and C7 (temporal and some limbic regions, namely the parahippocampal gyrus (PHG), the enthornial cortex (EC) and the hippocampus (Hi), maintain the same pattern as EP and control subjects (clustering together and being almost symmetrical in both hemispheres). However, for this group of subjects the cuneus (CUN), pericalcarine cortex (PCAL) and lateral occipital gyrus (LOCG) (occipital regions, in yellow) together with the lingual gyrus (LgG) (temporal, in blue) cluster this time with the parietal regions (in pink) and the isthmus cingulate gyrus (ICG), (see C8), instead of clustering with the fusiform gyurs (FG), the temporal pole (TP) and the PHG, EC and HI, as for the rest of the groups. Other striking differences are found, again, in the limbic regions (more precisely, the cingular regions) that cluster interhemispherically (C10), and the central regions, that cluster with subcortical structures from both hemispheres (C11), such as in the control case (not the EP).

IUGR + EP subjects displayed a network community structure close to the EP one. Indeed, on the right hemisphere, IUGR + EP network community structure is almost equal to the EP subjects' structure. As shown in Fig. 5, C1 and C3–C5 clusters in the IUGR + EP case are exactly the same as clusters C1–C4 in the EP case (see Fig. 3). The only difference on the right hemisphere clusters are found for the central regions (PrG, PaG and PoG) that form an independent cluster (C2) for the IUGR + EP case, instead of clustering with some subcortical structures as in the EP case (see Fig. 3, cluster C9). For these subjects, as for controls and EP, temporal (blue), occipital (yellow) and parietal regions (in pink) cluster symmetrically in both hemispheres (C3–C5 are equal to C6–C8, except for the PCG in C8). In the same line, C9 cluster of IUGR + EP subjects is similar to C9 cluster for EP subjects (see Fig. 3), except for the central regions of the left hemisphere (PrG, PaG, PoG) and the left pallidum (Pall) and accumbens (Ac), that in the IUGR + EP case cluster with some subcortical structures interhemispherically (C10).

These results allows us to hypothesize that IUGR + EP subjects are closer in modular brain structure to EP subjects, while IUGR subjects appear to have the most different structure with on average a higher number of modules.

Cluster-averaged network measures did not show clear differences among groups and clusters, albeit a slightly reduced degree, clustering index and local efficiency (on average) for all the case groups compared to controls (see tables below each connectogram, Fig. 2, Fig. 3, Fig. 4, Fig. 5). What remains clear, though, is that all case groups display an overall reduction in the node strength when the nodes are considered independently. Indeed, a closer look to the degree heatmap (in green), and specially to its respective legend, reflects that, while the minimum nodal strength for each groups range in between 7.5 and 8.7, the maximum values are clearly reduced in the case groups, being the IUGR subjects the ones that show the smallest maximum value. This finding is further supported by the statistical analysis, shown in the next section (Section 3.2.2, Integration and segregation measures).

3.2.2. Integration and segregation measures

In Table 8 we resume the mean and standard values for the network integration and segregation measures for all groups under analysis. As we can see from the table, for all cases, the averaged path length is increased while the global and local networks efficiencies are decreased, as well as the averaged nodal strength and the averaged clustering coefficient.

Table 8.

Mean and standard deviation (mean ± std) values for the network integration and segregation measures for all groups under analysis.

	CTRL	EP	IUGR	IUGR + EP
g_eff	6.9464 ± 0.2546	6.0749 ± 0.4717	5.9041 ± 0.4866	5.8670 ± 0.5428
trans	4.6149 ± 0.7814	4.6485 ± 0.7680	4.3738 ± 1.1838	4.1926 ± 0.9210
lambda	0.2024 ± 0.0077	0.2465 ± 0.0311	0.2510 ± 0.0432	0.2526 ± 0.0321
n_eff	6.4881 ± 1.3822	6.2962 ± 1.4447	5.9560 ± 1.4475	5.7657 ± 1.4045
n_str	213.0258 ± 14.7313	193.3104 ± 17.9609	182.1350 ± 23.0682	184.6044 ± 19.3097
CI	5.9477 ± 1.9507	5.9070 ± 2.0848	5.6234 ± 2.1106	5.3877 ± 2.0741

g_eff: global efficiency; trans: transitivity; lambda: average shortest path length; n_eff: averaged nodal efficiency; n_str: averaged nodal strength; CI: clustering index.

3.2.2.1. Case–control differences

As seen in Table 9, when compared to controls, EP children showed increased network averaged path length (p = 0.0025), and decreased global network efficiency (p = 0.00079) and averaged node strength (p = 0.0051). For IUGR subjects, significant decreased global network efficiency (p = 0.0089) and reduced averaged node strength (p = 0.017) was also found. IUGR + EP children showed, as EP children, increased network averaged path length (p = 0.034), and decreased global network efficiency (p = 0.0033) and averaged node strength (p = 0.015).

Table 9.

Network integration and segregation measures differences in the case–control comparisons for all subjects under study. Arrows indicate the sense of the difference (↓ indicates decreased values and ↑ increased). The p-value of the comparison is shown in parentheses. Statistical significance was declared at level 0.05 and the resulting p-values were FDR corrected. EP and IUGR subjects have similar network changes when compared to controls, except for the averaged path length that is increased for EP and IUGR + EP subjects. This is not the case for IUGR subjects.

	g_eff	trans	lambda	n_eff	n_str	CI
EP (vs CTRL)	↓ (0.00079)	n.s	↑ (0.0025)	n.s	↓ (0.0051)	n.s
IUGR (vs CTRL)	↓ (0.0089)	n.s	n.s	n.s	↓ (0.017)	n.s
IUGR + EP (vs CTRL)	↓ (0.0033)	n.s	↑ (0.034)	n.s	↓ (0.015)	n.s

g_eff: global efficiency; trans: transitivity; lambda: average shortest path length; n_eff: averaged nodal efficiency; n_str: averaged nodal strength; CI: clustering index. n.s: not significant.

3.2.2.2. Case–case differences

IUGR subjects showed smaller averaged node strength (p = 0.056) when compared to EP, while IUGR + EP children showed (compared to EP) a statistically significant decrease in global network efficiency (p = 0.032), global network transitivity (p = 0.007), and averaged node strength (p = 0.01), efficiency (p = 0.0043) and clustering index (p = 0.014). When comparing IUGR and IUGR + EP subjects, differences were found in global network efficiency, decreased for IUGR + EP subjects (p = 0.046) and in averaged node strength, increased in IUGR + EP children (p = 0.018). These results are summarized in Table 10.

Table 10.

Network integration and segregation measures differences in the case–case comparisons for all subjects under study. Arrows indicate the sense of the difference (↓ indicates decreased). The p-value of the comparison is shown in parentheses. Statistical significance was declared at level 0.05 and the resulting p-values were FDR corrected.

	g_eff	trans	lambda	n_eff	n_str	CI
IUGR (vs EP)	n.s	n.s	n.s	n.s	↓ (0.056)	n.s
IUGR + EP (vs EP)	↓ (0.032)	↓ (0.007)	n.s	↓ (0.0043)	↓ (0.01)	↓ (0.014)
IUGR + EP (vs IUGR)	↓ (0.046)	n.s	n.s	n.s	↓ (0.018)	n.s

g_eff: global efficiency; trans: transitivity; lambda: average shortest path length; n_eff: averaged nodal efficiency; n_str: averaged nodal strength; CI: clustering index. n.s: not significant.

4. Discussion

This study complements our previous study on preterm infants brain networks at school age (Fischi-Gómez et al., 2014). We have detected specific alterations in brain topology and structural organization after early exposure to extra-uterine environment (premature birth), following antenatal adverse conditions (such as IUGR).

Lancichinetti and Fortunato wrote: “network system typically display a modular organization, reflecting the existence of special affinities among nodes in the same module, which may be a consequence of their having similar features or the same roles in the network” (Lancichinetti and Fortunato, 2012). Relying on the work of Lancichinetti and Fortunato, we have decomposed each individual brain network in consistent modules and compared them within and between groups using several measures of clustering similarity. Both the MIn and VIn indices used in this study delivered an agreement on the degree of consistency between individuals' partitions in the same group. Thus, as the normalized mutual information (MIn) indices between partitions were high whereas the normalized variation of information (VIn) indices were relatively low, we can assume that one subject's partition is similar to another one in the same group. On the other hand, the significant differences found in both case–control and case–case comparisons (such as lower MIn indices and higher VIn indices) confirmed our hypothesis that modular brain network structure is group-specific (for EP, EP–IUGR, IUGR and controls). Although all four groups displayed very similar modularity index (see Table 4), the differences between partitions among groups were substantial (Table 5, Table 6, inter-group comparison), leading to the conclusion that each group of subjects possesses a specific global brain network organization in order to maintain the same level of modularity (Table 3). Indeed, our results suggest that the consensus clustering partition effectively represents the actual network community structure of each group.

The visual inspection of the group representative consensus clustering partitions (Fig. 2, Fig. 3, Fig. 4, Fig. 5) corroborates our analytical results. The most striking difference among groups is located in the frontal lobe and in the brain limbic areas (gyrus fornicates). In EP subject limbic regions (cingulate gyrus), left pallidum, and left thalamus are clustered with frontal regions, whereas in controls they form an independent cluster. This is in concordance with a recent study, which showed that alterations in frontal lobe pathways are found in young children born preterm (Duerden et al., 2013). These results also support our prior study (Fischi-Gómez et al., 2014), in which microstructural alterations in the prefrontal cortico-basal–thalamo-cortical loop (CBTCL) were present and correlated with socio-cognitive outcome in EP and IUGR children.

Ball et al. demonstrated that a rich-club network of densely connected cortical hubs is established before the time of normal birth (Ball et al., 2014). In our study, all subjects under analysis showed an evident rich-club organization of their brain networks with no significant differences between groups. Likewise, the actual modularity characteristics of all subjects were similar (all groups display roughly the same modularity index). Interestingly, the small-world network design was also maintained in our groups of high-risk preterm children, unlike in populations with neurological diseases such as Alzheimer's disease, ADHD, schizophrenia or epilepsy (Zhao et al., 2012, Liao et al., 2010, Yao et al., 2010). Taken all together, our results further prove that rich-club organization after premature birth is maintained even at school age and confirms the earlier findings of preserved rich-club organization in the newborn period (Ball et al., 2014). Therefore, we propose that altered maturation of prematurely born children is less likely to be explained by rich-club brain organization changes. A recent work from Karolis and colleagues, where the authors tested the brains rich club architecture in EP born adults, led to a similar conclusion (Karolis et al., 2016). Brain networks of extreme premature born adults during adulthood retained their rich-club organization.

In our analysis, network modular structure of EP, compared to controls and IUGR subjects, displayed the smallest number of clusters (9 clusters vs. 11 in controls). Yet, EP frontal clusters (i.e. the cluster containing the frontal regions (C1 and C8 in Fig. 3)), are bigger that in the rest of the subjects (C1 and C8 are formed by 14 and 20 regions, respectively). Thus, concordant with the work of Karolis et al. our results confirm their hypothesis that preterm brain disproportionately assigns larger share of white matter resources to its rich-club (Karolis et al., 2016).

Another striking difference in EP subjects' community structure is the different clustering pattern of the majority of the subcortical areas. In the EP, these areas cluster with the frontal and cingular regions and did not form a single inter hemispheric cluster, as seen in EP–IUGR, IUGR and controls. It is known that the role of the basal ganglia in supporting a global exchange of information is altered after premature birth (Fischi-Gómez et al., 2014). Our results are in concordance with this finding. Indeed, we provide evidence that structural connectivity and network topology appear altered after premature birth and/or IUGR, suggesting that altered fetal environment and nutrition and/or premature birth has an impact in the development of brain connectivity with an alteration in global network topology.

In our previous work, the structural connectivity alterations after EP and IUGR were already assessed. We have showed that the regional microstructural alteration is similar in both cases with reduced connectivity in the prefrontal cortico-basal ganglia-thalamo-cortical loop (Fischi-Gómez et al., 2014). One could therefore hypothesize that the combination of IUGR and EP would result in an additive alteration of their brain network's structural connectivity. Nevertheless, we did not found evidence to corroborate this hypothesis. On the contrary, our results allow us to hypothesize that IUGR + EP subjects are “closer” in brain modular structure to EP subjects and more “distant” to controls. While IUGR + EP subjects showed reduced network measures compared to EP subjects (see Table 10), their representative network partition was similar to the EP subjects (see Fig. 3, Fig. 5). Even if the nodal network measures for the IUGR + EP are closer to the IUGR (most likely due to the effect of prenatal growth restriction) the cortical and subcortical regions tend to cluster in the same way as they do in EP subjects. This suggests that, albeit the relative paucity of white matter resources, IUGR + EP subjects' brain reorganizes prioritizing a tight modular structure as much as EP subjects' brain does. In other words, these results may indicate that IUGR + EP structural connectivity appears to be mainly affected by extreme prematurity. This is in accordance with previous studies that conclude that the effect of extreme prematurity prevails over the effect of fetal growth restriction (Yanney and Marlow, 2004).

Preterm birth and adverse fetal conditions are associated not only with altered brain development but also with cognitive and behavioral deficits. Although the direct link between connectivity disruptions and neurocognitive impairment is far from clinical consensus, there is increasing evidence that regional connectivity abnormalities relate to specific neurocognitive deficits (Fischi-Gómez et al., 2014, Batalle et al., 2012). For instance, the fronto-parietal connectivity is known as being heavily implicated in effective network communication and function (Ball et al., 2014), and alterations in the frontal networks have been directly correlated with socio-cognitive impairments in these children (Fischi-Gómez et al., 2014). Indeed, even if the global brain organization remains intact after EP and IUGR, we show a significant reduction in brain network efficiency and in averaged node strength, suggesting that both EP and IUGR are, by themselves, risk factors for structural connectivity development, which lead to limited communication efficiency between brain network nodes.

Our previous work suggests that alterations in the structural brain substrate due to EP and IUGR are important factors that may affect neurobehavioral and cognitive performance (Fischi-Gómez et al., 2014). Although altered development of fiber bundles might play an important role in socio-cognitive outcome, network characteristics such as segregation and function integration might better characterize higher order cognitive impairments seen in these children. Brain segregation is referred to as specialized processing ability that occurs within densely interconnected groups of brain regions, while functional integration is considered as the ability of the brain to rapidly combine specialized information from distributed brain regions. Finally, higher values of global efficiency are thought to contribute to a better ability to transfer information between brain regions. When compared to controls EP, EP–IUGR and IUGR subjects showed significant reduction of global efficiency and nodal strength. This leads to conclusion that integrative pattern (i.e., the speed at which the information from different brain regions is combined once it has been processed in specialized regions) of their brain networks is disrupted. However, the direct link between altered integrative pattern and the cognitive task performance is still missing. Our results show that both groups show similar alliterations in network integration and segregation patterns. This may indicate that network integration might be particularly vulnerable to insults independently from intra-uterine (IUGR) or extra-uterine conditions (EP) and would confer with the similar risk in cognitive deficits in EP and moderately preterm IUGR infants, as previously shown (Guellec et al., 2011).

As a matter of fact, (Vertes and Bullmore, 2014) demonstrate that DTI networks gradually mature from local, proximity-based connectivity patterns designed to support primary functions to a more distributed, integrative topology thought to be favorable for supporting higher cognitive functioning. Particularly, during development brain communities' topology would move from local sub-networks partially overlapping with brain lobes, to more spatially distributed circuits (Collin and Van den Heuvel, 2013). Indeed, Ball et al. (2014) showed that during the third trimester of pregnancy, the number of connections between rich-club regions and the rest of the cortex increases significantly, speaking in favor of progression towards more efficient networks in order to support global and local exchange of information. In a normal population, the macro-structural network architecture required for normal brain function is already present at birth (Collin and Van den Heuvel, 2013). Thus, one might hypothesize that an abrupt interruption of previously mentioned process may lead to a structural reorganization of the available resources in order to adapt to the anatomical constraints. In simple terms, the reorganization of the brain connections would be directed towards the maintenance of global connectivity patterns. Our results are in agreement with this hypothesis, as EP, IUGR and IUGR + EP subjects all present a different network community structure but with similar network modularity. Indeed, the differences seen in the network community structure of our groups of subjects may reflect a different remodeling of the anatomical networks due to EP and IUGR or both.

The remodeling of anatomical networks over the course of postnatal development is thought to predominantly reflect the fact that myelination and maturation occur asynchronously across various axonal tracts (Vertes and Bullmore, 2014). From birth to pre-adolescence age the brain network's organization shows a decrease of the modularity index and an increase of the mean number of modules. These processes are suggested to be associated with pruning of short-range (intra-modular) connections, and strengthening of long-range associative tracts (inter-modular links) during development. Yet, despite having a relative shortage of white matter resources (Fischi-Gómez et al., 2014), EP and/or IUGRS maintain similar levels of modularity, rich-club architecture, and small-world design compared to controls. In summary, our results corroborate the hypothesis by Karolis and colleagues, that the modularity and rich-club organization is prioritized over peripheral connectivity after EP and/or IUGR.

5. Conclusion

In conclusion we provide evidence that, although brain networks of high-risk children maintain their modularity, small-world and rich-club attributes at school age, the underlying network community structure of these networks is differently affected by extreme prematurity and intrauterine growth restriction, indicating a particular vulnerability of processes underlying network integration.

Table 7.

List of abbreviations for the cortical and subcortical regions of interest (from Freesurfer parcellation). (source: http://neurolex.org/wiki/ and Atlas of the human brain, J.Mai.AP 3rd Edition).

Label	Anatomical region	Label	Anatomical region
LOF	Lateral orbito frontal gyrus	PCAL	Pericalcarine cortex
PORB	Pars orbitalis, orbital part of the inferior frontal gyrus	LOCG	Lateral occipital gyrus
FP	Frontal pole	LgG	Lingual gyrus
MOF	Medial orbito frontal gyrus	FG	Fusiform gyrus
PTRI	Pars triangularis, triangular part of the inferior frontal gyrus	PHG	Parahippocampal gyrus
POPE	Pars opercularis, inferior part of the inferior frontal gyrus	EC	Enthornial cortex
rosMFG	Middle frontal gyrus, rostral	TP	Temporal pole
SFG	Superior frontal gyrus	ITG	Inferior temporal gyrus
caMFG	Middle frontal gyrus, caudal	MTG	Middle temporal gyrus
PrG	Precental gyrus	bnkST	Superior temporal sulcus, banks region
PaG	Paracentral lobule	STG	Superior temporal gyrus
rosACG	Anterior cingulate gyrus, rostral	trTG	Transverse temporal gyrus
caACG	Anterior cingulate gyrus, caudal	Th	Thalamus
PCG	Posterior cingulate gyrus	Cd	Caudate
ICG	Isthmus cingulate gyrus	PUT	Putamen
PoG	Postcentral gyrus	Pall	Pallidum
SMAR	Supramarginal gyurs, inferior part of the parietal lobule	Ac	Accumbens
SPaG	Superior parietal gyrus	sTh	Sub-thalamus
IPaG	Inferior parietal gyrus	Hi	Hippocampus
PCUN	Precuneus	Amg	Amigdala
Cun	Cuneus	BS	Brain stem