Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Feb 22;6:21569. doi: 10.1038/srep21569

Mechanical characterization of the P56 mouse brain under large-deformation dynamic indentation

David B MacManus 1, Baptiste Pierrat 1, Jeremiah G Murphy 2, Michael D Gilchrist 1,a
PMCID: PMC4761928  PMID: 26898475

Abstract

The brain is a complex organ made up of many different functional and structural regions consisting of different types of cells such as neurons and glia, as well as complex anatomical geometries. It is hypothesized that the different regions of the brain exhibit significantly different mechanical properties, which may be attributed to the diversity of cells and anisotropy of neuronal fibers within individual brain regions. The regional dynamic mechanical properties of P56 mouse brain tissue in vitro and in situ at velocities of 0.71–4.28 mm/s, up to a deformation of 70 μm are presented and discussed in the context of traumatic brain injury. The experimental data obtained from micro-indentation measurements were fit to three hyperelastic material models using the inverse Finite Element method. The cerebral cortex elicited a stiffer response than the cerebellum, thalamus, and medulla oblongata regions for all velocities. The thalamus was found to be the least sensitive to changes in velocity, and the medulla oblongata was most compliant. The results show that different regions of the mouse brain possess significantly different mechanical properties, and a significant difference also exists between the in vitro and in situ brain.

Traumatic brain injury (TBI) is a major cause of death and disability worldwide, accounting for 1.7 million injuries, 275,000 hospitalizations, and 50,000 deaths in the United States each year1. In Europe, injuries are the leading cause of death between the ages of 15 and 44, with road accidents in Southern Europe and falls related to alcohol consumption in Northern Europe constituting the majority of these cases, and with head trauma accounting for the majority of trauma related deaths2. The high occurrence, physical and socioeconomic impact of TBIs3 has meant that it is an important focus area for research with many laboratories creating detailed 3D Finite Element models of the head and brain4,5,6,7. These models are used to investigate the effects that stresses and strains have on the brain and to identify which regions of the brain are subjected to maximum values of stress and strain. However, the brain is a complex organ made up of many different functional and structural regions consisting of different types of cells such as neurons and glia, as well as complex anatomical geometries8. It is hypothesized that the different regions of the brain exhibit significantly different mechanical properties, which may be attributed to the diversity of cells and anisotropy of neuronal fibers within individual brain regions. Current computer simulation models lack accurate constitutive data of the brain’s individual regions at dynamic strain rates that are comparable to those experienced during traumatic events. This data is required to correctly predict the stresses and strains produced in the brain during these scenarios, and to anticipate which regions are most susceptible to mechanical damage.

The current research presents tissue-level hyperelastic constitutive data for the mouse cortex, cerebellum, thalamus, and medulla, under large deformation dynamic indentation using a custom-built micro-indentation apparatus (Fig. 1). Indentation sites are highlighted in Fig. 2. Hyperelastic models are used to determine the nonlinear force-displacement response of mouse brain tissue at different velocities, using an inverse Finite Element (FE) approach (Fig. 3), hyperelastic data reported here can be used with existing viscoelastic data to model mouse brain tissue at these deformation rates. Indentation presents as an ideal loading modality for studying brain trauma. The stress fields which arise in the tissue due to these indentations are a combination of compressive, tensile and shearing forces, and are similar to those which occur during head impacts9,10,11,12,13 and to the forces applied to the brain by surgical equipment. However, there has been little published work on the micro-scale properties of brain tissue using the micro-indentation method to characterize the local hyperelastic response of different brain regions at dynamic rates.

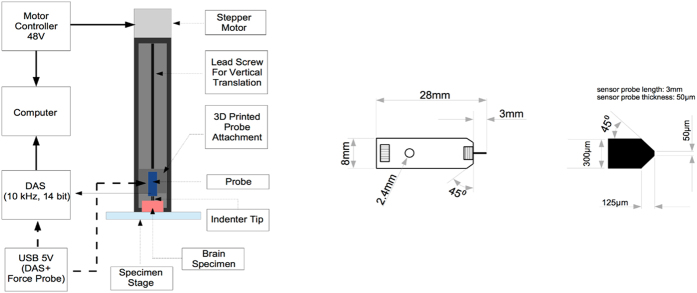
Figure 1.

Figure 1

Open in a new tab

(a) Schematic Diagram of Test Apparatus, (b) FemtoTools FTS-10000 Microforce Sensing Probe, detailed in MacManus (2015)39.

Figure 2. Sagittal section showing regions and Indentation Sites of the Mouse Brain.

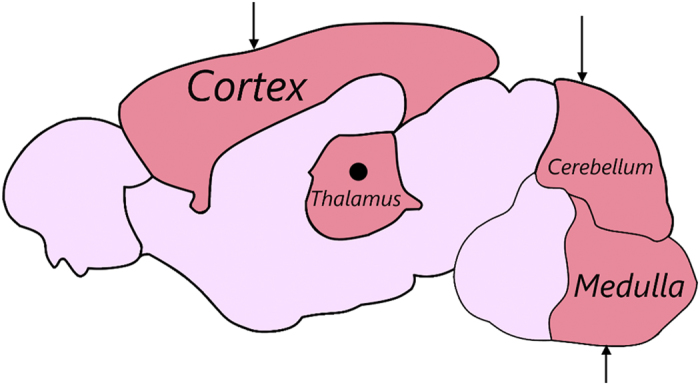
Figure 2

Open in a new tab

Indentations were performed to a depth of 70 μm at 0.71, 2.14, and 4.28 mm/s, on the surfaces of the cerebral cortex, cerebellum, and medulla oblongata. The mouse brain was then sectioned through the midline fissure to expose the thalamus tissue for indentation. The arrows indicate the direction that the indentation was performed for the cortex, cerebellum, and medulla oblongata. The thalamus was indented in the sagittal plane.

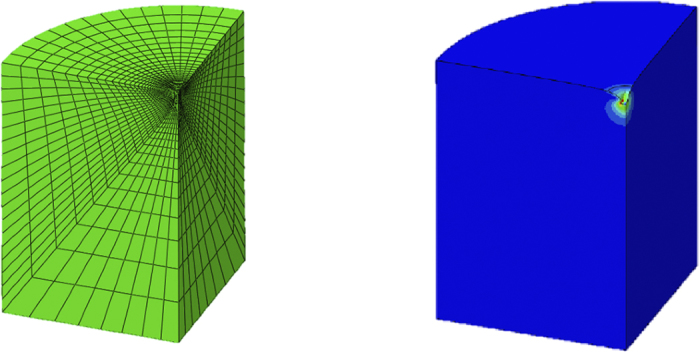
Figure 3. One-quarter Finite Element Model of Indentation Experiment on Mouse brain tissue in the reference (green) and deformed configurations which was used in the inverse Finite Element method to characterize the dynamic mechanical properties of mouse brain tissue.

Figure 3

Open in a new tab

Here, the first mechanical characterization study of the dynamic, hyperelastic response for different regions of the P56 mouse brain, under large-deformation indentation, in vitro and in situ, is presented. Indentations are performed at velocities ranging from 0.71–4.28 mm/s, comparable to those in both surgical and traumatic brain injury cases. The force-displacement data recorded from experiments is fit to three hyperelastic material models (Neo-Hookean, Mooney-Rivlin, and Ogden) using the inverse Finite Element method. These constitutive models were chosen based on their widespread use in the biomechanics community10,11,14,15,16,17,18, and ease of implementation in Finite Element programs. The models use a strain energy density function to relate stress and strain. The Neo-Hookean model uses the material parameter C10, where μ = 2C10, and the Mooney- Rivlin model uses parameters C10 and C01, where μ = 2(C10 + C01), and μ is the shear modulus. The shear modulus is used to interpret the rigidity of a specimen and can be used in material models to describe the deformation process of a material under applied forces. For an in-depth discussion of elasticity and hyperelastic models applied to soft tissue mechanics, readers are referred elsewhere10,11,14,19,20. The material parameters reported here, together with previously reported viscoelastic data10, can be implemented into computer models of the mouse head and brain to provide an approximation of the effect that trauma has on the individual regions of the organ.

Results

Force-displacement behavior of mouse brain tissue

A total of 180 mice were used in this study; ten mice were used for each velocity and region. Indentations were carried out at velocities of 0.71, 2.14, and 4.28 mm/s on the cerebral cortex, cerebellum, thalamus, and medulla oblongata of P56 mixed sex mice. These locations were chosen due to their vital physiological and psychological significance for quality of life, and to account for regional differences in brain tissues mechanical properties. Independent indentations were also performed on the cortex and cerebellum in situ to investigate if differences between in vitro and in situ tissue exist. Data from force-displacement curves were analysed up to a 70 μm displacement for each experiment (Fig. 4) to investigate the nonlinear loading response of brain tissue. The results show an increase in reaction force of the tissue with increasing velocity which highlights the rate dependent properties of the tissue. Each region demonstrates its own unique rate effect response, with the medulla being most sensitive to changes in velocity and the thalamus being least sensitive. The medulla was indented perpendicular to the fiber direction and was found to be the most compliant of the brain regions measured. The in situ cortex was less sensitive to changes in velocity and produced larger reaction forces at each velocity when compared with the in vitro cortex. Conversely, the in situ cerebellum exhibits a stronger rate effect compared with the in vitro cerebellum; however, the reaction forces are comparable at each velocity. It is evident from the force-displacement curves that each of the regions investigated have unique responses to the mechanical forces, and also to the rate of these applied forces, suggesting that some regions of the brain may be more susceptible to trauma than others.

Figure 4. Force-displacement curves of the in vitro cortex, cerebellum, thalamus, and medulla, at 0.71, 2.14, and 4.28 mm/s.

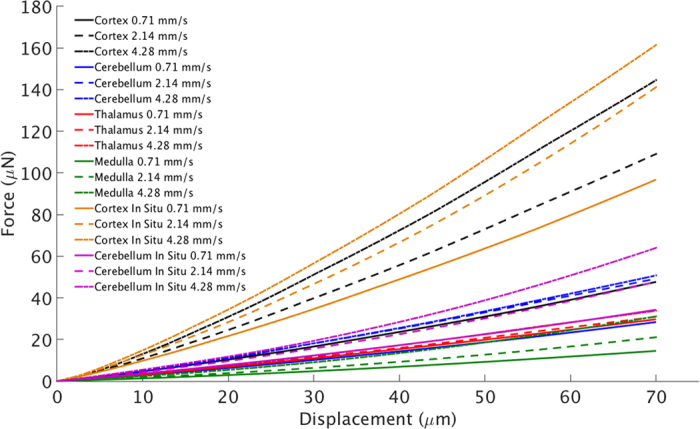
Figure 4

Open in a new tab

Also shown are the individual force-displacement curves for the in situ cortex and cerebellum for the same velocities. The different responses of the individual regions to mechanical loads are evident from this graph. What is most notable is the significantly larger forces recorded from the in vitro and in situ cerebral cortex at higher velocities compared with the other regions investigated.

Mechanical characterization of mouse tissue, in vitro

The force-displacement data from experiment were fit to three hyperelastic material models, Neo-Hookean, Mooney-Rivlin, Ogden, for each region and each velocity using the inverse Finite Element method. The tissue’s shear modulus for all regions increased with an increasing velocity, demonstrating a rate dependence property of the tissue. The cerebral cortex has shear moduli values of 2.22, 5.26, and 6.72 kPa at 0.71, 2.14, and 4.28 mm/s (Fig. 5a) respectively, corresponding to an overall increase of 67% between the lowest and highest velocities. The cerebellum, thalamus, and medulla experience total increases of 56%, 11%, and 71% in apparent shear moduli, respectively. Table 1 presents the material parameters for the three hyperelastic material models to which the data was fit; Neo-Hookean, Mooney-Rivlin, and Ogden. The data in Table 1 is in vitro data unless otherwise stated. Each of the models achieved an excellent fit with the data, R2 > 0.9 for all models. However, the Ogden model achieved a marginally better fit than the others. This is due to the nonlinear parameter, α, which accounts for the nonlinearity of the force-displacement curves. Most regions fit with the Ogden model achieved an R2 value of 0.999. The model with the lowest R2 value (0.976) was for the 4.28 mm/s cortex data when fit to the Mooney-Rivlin model. ANOVA with a post hoc test was carried out to compare the shear moduli values of each region to determine whether a statistically significant difference exists between the brain regions. A significant difference was found between the regions investigated and is reported in Fig. 5b. In vitro regions which were not significantly different comprised of the cerebellum and thalamus at all velocities, the medulla and thalamus at 2.14 and 4.28 mm/s, and the cerebellum and medulla at 4.28 mm/s. All other regions were significantly different for all velocities, in vitro, satisfying the hypothesis that brain regions possess their own unique mechanical properties.

Figure 5.

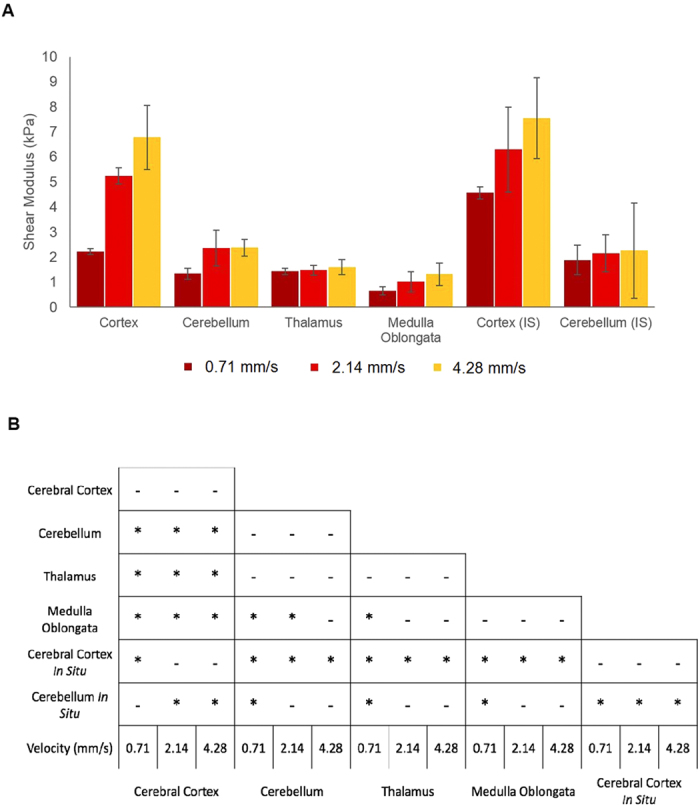
Figure 5

Open in a new tab

(A) Comparison of shear modulus for thalamus, medulla, and in vitro and in situ (IS) cortex and cerebellum. Each regions unique material properties are clearly presented here. Also evident is the difference of mechanical properties between the in vitro and in situ tissues under dynamic-rates. (B) *represents a statistically significant result from ANOVA post-hoc tests, - represents an insignificant difference. Each region is compared with the other regions for corresponding velocities. Significant differences between velocities in the same region are not presented.

Table 1. Presents regional brain tissue material parameters for the Neo-Hookean, Mooney-Rivlin and Ogden models, used to model brain tissue under mechanical loads, where C10, C01 are related to the shear modulus, μ is the shear modulus, and α is a nonlinear parameter.

Velocity (mm/s) Neo-Hookean Mooney-Rivlin
 Ogden
Cerebral Cortex C10 C10 C01 μ0 α
0.71 1.11 ± 0.06 0.90 ± 0.26 0.22 ± 0.12 2.09 ± 0.16 0.1 ± 0.83
R2 0.999 0.999 0.999
2.14 2.63 ± 0.16 2.19 ± 0.12 0.34 ± 0.05 5.11 ± 0.31 1.23 ± 0.49
R2 0.999 0.998 0.999
4.28 3.39 ± 0.64 1.62 ± 0.27 1.46 ± 0.41 6.44 ± 1.16 0.38 ± 0.63
R2 0.998 0.976 0.999
Cerebellum C10 C10 C01 μ0 α
0.71 0.67 ± 0.11 0.90 ± 0.26 0.22 ± 0.12 1.27 ± 0.20 0.26 ± 0.49
R2 0.999 0.999 0.999
2.14 1.18 ± 0.36 2.19 ± 0.12 0.34 ± 0.05 2.33 ± 0.70 1.54 ± 0.69
R2 0.999 0.998 0.999
4.28 1.19 ± 0.17 1.62 ± 0.27 1.46 ± 0.41 2.25 ± 0.32 0.10 ± 0.02
R2 0.999 0.999 0.999
Thalamus C10 C10 C01 μ0 α
0.71 0.72 ± 0.06 0.52 ± 0.06 0.16 ± 0.01 1.40 ± 0.11 1.19 ± 0.68
R2 0.998 0.997 0.998
2.14 0.74 ± 0.1 2.56 ± 0.11 0.15 ± 0.02 1.45 ± 0.17 0.89 ± 0.16
R2 0.998 0.998 0.999
4.28 0.81 ± 0.15 0.50 ± 0.12 0.20 ± 0.03 1.51 ± 0.27 0.13 ± 0.01
R2 0.999 0.998 0.999
Medulla Oblongata C10 C10 C01 μ0 α
0.71 0.33 ± 0.08 0.15 ± 0.04 0.16 ± 0.06 0.63 ± 0.01 0.29 ± 0.28
R2 0.997 0.999 0.998
2.14 0.51 ± 0.20 0.30 ± 0.09 0.13 ± 0.02 0.74 ± 0.18 −2.15 ± 0.08
R2 0.986 0.996 0.999
4.28 0.66 ± 0.23 0.53 ± 0.23 0.11 ± 0.004 1.17 ± 0.39 −1.07 ± 0.03
R2 0.989 0.991 0.994
Cerebral Cortex (In Situ) C10 C10 C01 μ0 α
0.71 2.29 ± 0.14 1.66 ± 0.13 0.52 ± 0.01 4.53 ± 0.26 1.73 ± 0.14
R2 0.999 0.998 0.999
2.14 3.30 ± 0.85 1.88 ± 0.81 0.97 ± 0.29 6.32 ± 1.55 1.11 ± 1.57
R2 0.995 0.996 0.997
4.28 3.76 ± 0.81 2.42 ± 0.82 1.10 ± 0.03 7.21 ± 1.48 0.59 ± 0.80
R2 0.999 0.999 0.999
Cerebellum (In Situ) C10 C10 C01 μ0 α
0.71 0.95 ± 0.29 0.64 ± 0.33 0.25 ± 0.09 1.74 ± 0.56 0.47 ± 2.14
R2 0.998 0.997 0.997
2.14 1.08 ± 0.37 0.94 ± 0.37 0.11 ± 0.04 2.09 ± 0.69 0.93 ± 0.37
R2 0.997 0.998 0.998
4.28 1.13 ± 0.95 0.99 ± 0.94 0.11 ± 0.01 2.02 ± 1.62 −0.29 ± 1.21
R2 0.990 0.991 0.993
Open in a new tab

Hyperelastic Material Parameters of P56 Murine Brain Regions.

Mechanical characterization of mouse tissue, in situ

The in situ force-displacement curves were fit to the same hyperelastic material models as the in vitro data. However, only the cortex and cerebellum regions could be investigated using this methodology. There is an apparent difference between the mechanical response of in situ and in vitro brain tissue, which is most notable and has previously been reported for the cortex21,22,23, but to the best of the authors knowledge there has been no reported data on in situ cerebellum tissue.

The cortex tissue experiences an increase in apparent shear modulus of 51%, 20%, and 10% between in vitro and in situ environments at 0.71, 2.14, and 4.28 mm/s, respectively. Conversely, the cerebellum initially exhibits a 70% increase in shear modulus between the in vitro and in situ cases for 0.71 mm/s. However, a reduction of 8% and 5% of the apparent shear moduli is experienced by the cerebellum at 2.14 and 4.28 mm/s, respectively.

Table 1 contains the mechanical properties of the in situ cortex and cerebellum for the Neo-Hookean, Mooney-Rivlin, and Ogden hyperelastic material models. Overall, each model achieved an excellent fit with the experimental data; the lowest R2 value was for the cerebellum with a value of 0.990 for the 4.28 mm/s Neo-Hookean data. The differences in apparent shear moduli for given velocities is presented graphically in Fig. 5a. Figure 5b presents the statistically significant differences between the regions investigated. For the in situ data, only the 0.71 mm/s in situ cortex was significantly different from the in vitro cortex data. The in situ cortex was significantly different from the in situ cerebellum and all other in vitro regions for each velocity. The in situ cerebellum was also significantly different compared with the in vitro cerebellum data for 0.71 mm/s. It is evident from these graphs (Fig. 5a,b) that the different regions of the brain possess significantly different mechanical properties.

Discussion

The current study presents the local mechanical properties of in vitro and in situ P56 mouse brain tissue at dynamic rates that have been hypothesized to cause injury, i.e. >10/s strain-rate and >10% strain10. Micro-indentation experiments were carried out on the cortex, cerebellum, thalamus, and medulla oblongata (Fig. 2). Velocities in the range 0.71–4.28 mm/s were applied locally to these regions to examine the regional differences in mechanical properties to the application of dynamic loading. The resulting shear moduli of the tissue increases with increasing velocity as shown in Fig. 5a which is consistent with previous studies10,11,14. For the in vitro study, it was found that each region had a unique response to the applied mechanical load with the cerebral cortex being the stiffest brain region investigated with values consistent of those reported previously for in vivo mouse cortex24. The thalamus was more compliant than the cortex and cerebellum but was stiffer than the medulla, which was the most compliant of the regions investigated, which is in agreement with previous results reported on the rat and porcine brains25,26. However, the cerebellum was found to be relatively stiffer in the mouse model presented here, compared to the porcine and rat models25,26, and less stiff relative to the cortex which is consistent with the viscoelastic properties of human cerebellum and cortex data reported previously27. The relative regional stiffness of the mouse brain is comparable to those of the rat brain reported by Finan et al.28, with the cortex being one of the stiffest regions, the thalamus was found to be less stiff than the cortex but stiffer than the medulla (brainstem), consistent with the results reported here. However, in the rat model, the cerebellum is reported as the most compliant region, whereas for the mouse model it is the medulla that was found to be the softest region. Also, previous studies have shown the thalamus to elicit a stiffer response compared with the cortex in the porcine and human brain29,30 which is inconsistent with mouse and rat data. The medulla was also found to be the most sensitive to changes in velocity with an overall increase in shear modulus of 71%, whereas the thalamus was found to be the least sensitive to changes in velocity with an overall increase in shear modulus of 11% between 0.71 and 4.28 mm/s. This might be a feature of slicing the brain tissue which is required to access this region, whereas all other regions were indented on their exterior surfaces. However, this currently suggests that the thalamus is weakly viscoelastic and should be investigated further in the context of its mechano-pathophysiology. The thalamus’ low rate-effect is especially significant in the context of repetitive concussion, as discussed by Smith et al.31. The data reported here, presented in Table 1, supports the hypothesis that different regions in the brain possess significantly different mechanical properties (Fig. 5) and elicit their own unique responses to the application of mechanical forces (Fig. 4).

The in situ cortex tissue (4.58 ± 0.28, 6.60 ± 0.17, 7.52 ± 0.16 kPa) was found to be stiffer than the in vitro tissue (2.22 ± 0.12, 5.26 ± 0.32, 6.78 ± 1.28 kPa) for all velocities, which agrees with Prevost et al.21, and Gefen et al.22. It is hypothesized that the higher values of cortex shear moduli in situ are caused by residual stresses in this region of the brain32 which are released upon the removal of the boundary condition applied by the skull. Conversely, for the cerebellum there was an insignificant difference between the in vitro and in situ cases suggesting that this region of the mouse brain has less residual strain. The mean moduli values of the in situ cerebellum (1.90 ± 0.58, 2.16 ± 0.74, 2.26 ± 1.90 kPa) were found to be less than those of the in vitro cerebellum (1.34 ± 0.22, 2.36 ± 0.72, 2.38 ± 0.34 kPa) for 2.14 and 4.28 mm/s, which is inconsistent with previous reports in the literature for cortex tissue21,22. However, these differences between in vitro and in situ cerebellum were found to be significant at the low velocity (0.71 mm/s) only (Fig. 5b).

The shear moduli and rate-effect results reported here could offer insight into how traumatic brain injury affects certain regions more than others in a mouse model of TBI such as those described previously33. It is evident from the data provided in Table 1 and Fig. 5 that the regions of the mouse brain exhibit regionally unique mechanical properties. A possible explanation for the differences in mechanical properties of brain tissue is the underlying cellular structure of these regions. Azevedo et al. have shown that the human cortex contains approximately 3.76 times more non-neuronal cells than neuronal cells, whereas the cerebellum contains 4.3 times more neuronal cells to non-neuronal cells, and the rest of the brain (RoB) contains 11.35 times more non-neuronal cells to neuronal cells34. Differences in the mechanical properties of these cells35,36 and how they interact with each other may offer a mechanical explanation for the regionally varying material properties of brain tissue. Further analysis of the distribution and density of cell types within specific brain regions is required for a more complete understanding of this as there is limited data on the number of cells and cell type in each region, such as neurons, astrocytes, GFAP-microglia, and oligodendrocytes.

While this research provides an advancement in the understanding of how different regions of the mouse brain respond to mechanical trauma, there are limitations to this work which may account for some of the discrepancies with others reported in the literature such as the use of a square cross-sectional indenter to indent the samples instead of a spherical or cylindrical punch. An axisymmetric probe would allow the use of an axisymmetric FE model which would decrease the computation time taken to perform the inverse FE procedure. Fresh human tissue is the ideal sample for determining the material properties of brain tissue under traumatic loading. However, the difficulties involved with obtaining fresh human tissue, due to increased post-mortem time, diseased, and elderly tissue samples, the obtained human tissue is usually not in an ideal state to quantify the true mechanical properties. The experimental temperature, 22 °C, used here may have an impact on the reported mechanical properties37, an experimental temperature of 37 °C may be more suitable but would need to be correlated with in vivo results to ensure that post-mortem effects don’t significantly alter the mechanical properties of in vitro tissue, even those measured at 37 °C. It has recently been suggested that the Neo-Hookean, and Mooney-Rivlin model employed here may not be adequate to accurately model brain tissue38 and that 6 or 8 term Ogden models may be more suitable for multi-modal deformation (compression-tension). However, the data presented here is uni-modal indentation, and the R2 values in Table 1 suggests that the current models used here are adequate to describe the behavior of mouse brain tissue under indentation up to 70 μm, and velocities between 0.71–4.28 mm/s, with overall R2 values of 0.996, 0.996, 0.998, for the Neo-Hookean, Mooney-Rivlin, and Ogden models, respectively.

The current research has, for the first time, characterized the dynamic mechanical properties of P56 mouse cortex, cerebellum, thalamus, and medulla, under large deformation. The mechanical properties of in situ cortex, and for the first time in situ cerebellum, have also been reported, and statistically significant differences between mouse brain regions have been established. We have used the inverse Finite Element method to fit the primary experimental data to three hyperelastic models, the Neo-Hookean, Mooney-Rivlin, and Ogden model, which have been shown to be capable of accurately describing the uni-modal deformation of brain tissue under large deformation indentation (mean R2 for all data = 0.997). The mechanical properties provided for these regions can be implemented immediately in current and next generation Finite Element models of the mouse brain with existing viscoelastic data of brain tissue10,11,14 to provide a qualitative approximation of how brain tissue may respond in traumatic impact injury events and neurosurgical scenarios. In order to fully describe the response of brain tissue in traumatic events both the loading and relaxation curves are required. The data presented here provides an in depth analysis of dynamic loading response of different regions of the mouse brain under large-deformation indentation. Future work will focus on coupling the hyperelastic loading and viscoelastic relaxation behavior of brain tissue to determine the time-dependent properties of the individual regions, and if a significant difference exists between them as has been shown here for the hyperelastic material parameters.

Methods

Experimental setup

A custom-built micro-indentation device was developed to investigate the local mechanical properties of brain tissue under dynamic loading conditions, (Fig. 1a)39. The device consists of three major components, the 3D-printed force-sensing probe stage, the linear stage (ZABER-LSQ), which moves the force-sensing probe stage in the vertical direction at speeds reaching 1 m/s, and a FemtoTools STS-10000 force sensing probe which is used to measure the reaction forces of the tissue with a 10 kHz sampling rate (Fig. 1b). The probe tip has a square cross sectional area of 50 × 50 μm.

Tissue preparation

Mouse specimens, previously euthanized by CO2 gas, were collected on the day of testing from University College Dublin’s Biomedical Facility for indentation experiments. The specimens consisted of post-natal 56-day old mixed male and female mice. Mixed sex mice were used as it has been previously reported that gender has no effect on the dynamic compressive response of brain tissue40. In order to perform the indentation experiments, the brains were removed from the animals by making a midline incision through the skin across the top of the head to gain access to the skull. A second midline incision, moving anteriorly from the occipital condyle, was made through the skull using a scalpel. Two lateral incisions were then made at an anterior and posterior point of the midline incision so that the bone could be removed and allow access to the brain. The brain was then separated from the spinal cord and removed from the skull. Proceeding removal from the skull, the brains were kept hydrated with Phosphate Buffer Saline while the cortical surfaces of the cortex, cerebellum, and medulla were indented. The brains were not fixed to the platen as the weight of the brain was sufficient to prevent the organ from moving during application of the low-force indentations. Following indentations of these regions, the brains were sectioned along the sagittal sulci to gain access to the thalamus. This procedure was adopted to ensure the brain is kept as intact as possible for measuring the mechanical properties. The in situ protocol involved making a midline incision through the top of the skull preceding two lateral incisions across the skull, above the region of interest, allowing the bone to be removed and the brain to remain encased in the remaining skull. Each brain is continuously hydrated throughout the experiment with Phosphate Buffer Solution. All tests were completed within 6 hours post-mortem in order to reduce the amount of proteolysis and necrosis that has been previously shown to reduce the stiffness of the tissue41,42.

Indentation protocol

Indentation tests were performed on in vitro (cortex, cerebellum, thalamus, and medulla, n = 120) and in situ (cortex and cerebellum, n = 60), mouse brains, up to 70 μm displacement, at velocities of 0.71, 2.14, and 4.28 mm/s, this encompasses a range of values which are both above and below the reported threshold for injury (10% strain, 10/s strain rate)10. To establish the contact point with the tissue, the indenter tip was brought into close proximity with the tissue. Once the indenter was sufficiently close to the tissue it was lowered in 2 μm increments until a force (<5 μN) was recorded from the indenter tip. If the force rose above 5 μN during this procedure, this region would not be measured and the indenter is moved to a new location for testing. No other preconditioning is performed on the sample as the sample is not preconditioned in vivo. The probe is then retracted 100 μm and the indentation is performed beyond 70 μm to ensure a constant velocity throughout indentation depth used for analysis. All tests were conducted at room temperature (~22 °C) and no tissue was reused after each indentation test due to the highly dissipative nature of brain tissue. The results were post-processed in MATLAB using a moving average filter over 10 data points. This procedure was performed to remove high frequency noise while keeping the indentation signal intact, this was ensured by monitoring the maximum indentation force at 70 μm before and after filtering so that the maximum force was not decreased.

The force-displacement curves were then imported into the inverse Finite Element model to determine the Neo-Hookean, Mooney-Rivlin, and Ogden material parameters. The Neo-Hookean model was chosen as it contains only one fitting parameter, C10, and many other hyperelastic models are extensions of the Neo-Hookean model, e.g. Mooney-Rivlin, and Yeoh. For the Neo-Hookean model the inverse Finite Element program is only required to fit one material parameter to the data allow the optimized value can be achieved with a greater confidence than those with more than one material parameter, giving an approximation for the value of the shear modulus. Once an approximation has been made for the shear modulus from the Neo-Hookean model, the force displacement data can then be applied to models containing more than one material parameter and their results be interpreted with greater confidence, as is in this case the Mooney-Rivlin, and Ogden hyperelastic material models. The Mooney-Rivlin model was chosen as it is an extension of the Neo-Hookean model to include the second strain invariant, I2, which describes the materials deviatoric deformation. Deviatoric deformation is required to fully describe a materials deformation. The Ogden model is used here due to its use in modelling the behavior of soft tissues by the biomechanics community10,11,14,18.

Statistical analysis

ANOVA with a post hoc analysis was performed with each region in vitro and in situ to determine if a statistically significant difference exists between the brain regions based on the shear modulus values determined from the Neo-Hookean material model for n = 10 samples of each region at each velocity.

Neo-Hookean hyperelastic model

The earliest hyperelastic material model based on the strain energy density function was put forward by Treloar in 1943 and is known as the Neo-Hookean material model20

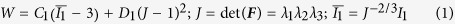graphic file with name srep21569-m1.jpg

where W is the strain energy density, C1 = 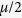Inline graphic, and μ is the shear modulus,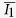Inline graphic is the first strain invariant of the isochoric part of the Cauchy strain tensor, I1 is the first strain invariant of the Cauchy strain tensor, λi is the stretch ratio in the principal directions, and D1  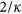= Inline graphic, where κ is the bulk modulus of the material is assumed to be 10,000 × μ. This value for bulk modulus assumes slight compressibility of the material.

Mooney-Rivlin hyperelastic model

The Mooney-Rivlin hyperelastic model was first proposed by Mooney (1940) as the most general form for a linear relationship between stress and strain in simple shear43. Rivlin used this model and the Neo-Hookean model in his earlier work on rubber elasticity. Suitable values of C10 and C01 can provide a better fit to experimental data than the Neo Hookean model

graphic file with name srep21569-m5.jpg

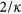where W is the strain energy density, μ = 2(C10+C01) and μ is the shear modulus, Inline graphic and Inline graphic are the first and second strain invariants of the isochoric part of the Cauchy strain tensor, respectively I2 is the second strain invariant of the Cauchy strain tensor, Jel is the elastic volume ratio, and D1  = Inline graphic, where κ is the bulk modulus of the material is assumed to be 10,000 × μ.

Ogden hyperelastic model

Soft biological tissue under compression, tension, and shear is often modelled well by the Ogden model11,14. In this study the Ogden model is extended to indentation using the inverse Finite Element method. The Ogden strain energy potential is expressed in terms of the principal stretches. The Abaqus formulation is of the form:

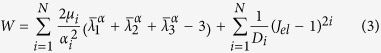graphic file with name srep21569-m9.jpg

where W is the strain energy density, μ is the shear modulus, 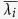Inline graphic are the principal stretches of the strain invariants of the isochoric part of the Cauchy strain tensor, λi are the stretch ratio in the principal directions, D1 = 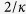Inline graphic, where κ is the bulk modulus of the material is assumed to be 10,000 × μ, and α is a material constant that is a real number, positive or negative44.

Inverse Finite Element analysis

Initial estimates for the material parameters are input to the inverse Finite Element analysis program (ABAQUS, Dassault Systemes, MATLAB, Mathworks) to determine the actual material parameters for the Neo-Hookean, Mooney-Rivlin, and Ogden hyperelastic models. Taking advantage of the model’s symmetry a one-quarter model was used. The model consisted of a rigid indenter tip geometry, modeled at one-quarter of the indenter geometry in Fig. 1b, consisting of 1006 linear quadrilateral R3D4 elements. The rigid indenter tip was initially in contact with a deformable cylinder, with a radius of 1000 μm and height of 1500 μm, consisting of 8160 linear hexahedral C3D8RH reduced integration, hybrid elements, which represents a sample of brain tissue. A fixed boundary condition was applied to the bottom face of the cylinder, and a displacement boundary condition of 70 μm was applied to the indenter tip. Once the initial estimate for material parameters has been input to the analysis, an ABAQUS finite element simulation of the experiment is performed. The force-displacement data from the indenter tip is extracted from the simulation result file and compared with the force-displacement curves from experiment. Once the data with the best fit has been determined, using the sum of absolute differences method, the analysis terminates and the material parameters providing the best fit between the experiment and simulation is found. This process is repeated for each region and velocity.

Additional Information

How to cite this article: MacManus, D. B. et al. Mechanical characterization of the P56 mouse brain under large-deformation dynamic indentation. Sci. Rep. 6, 21569; doi: 10.1038/srep21569 (2016).

Acknowledgments

This work was supported by Science Foundation Ireland (Grant No. 12/IP/1732).

Footnotes

Author Contributions D.B.M. performed the animal experiments and computational simulations and drafted the initial manuscript. B.P. developed the experimental apparatus to conduct the experiments and contributed to writing the manuscript. J.G.M. developed the continuum mechanics mathematical models and contributed to writing the manuscript. M.D.G. conceived of the original project plan and associated experiments and contributed to writing the manuscript. All authors contributed equally to reviewing the final manuscript.

References

  1. Faul M., Xu L., Wald M. M. & Coronado V. G. Traumatic brain injury in the United States: emergency department visits, hospitalizations, and deaths. Atlanta (GA): Centers for Disease Control and Prevention, National Center for Injury Prevention and Control (2010).
  2. Tagliaferri F., Compagone C., Korsic M., Servadei F. & Kraus J. A systematic review of brain injury epidemiology in Europe. Acta Neurochir. 148, 255–268 (2006). [DOI] [PubMed] [Google Scholar]
  3. Roozenbeek B., Maas A. I. R. & Menon D. K. Changing patterns in the epidemiology of traumatic brain injury. Nat. Rev. Neurol. 9, 231–236 (2013). [DOI] [PubMed] [Google Scholar]
  4. Kleiven S. & von Holst H. Consequences of head size following trauma to the human head. J. Biomech. 35, 153–160 (2002). [DOI] [PubMed] [Google Scholar]
  5. Mao H. et al. Development of a finite element human head model partially validated with thirty-five experimental cases. J. Biomech. Eng. 135, 111002–111002-15 (2013). [DOI] [PubMed] [Google Scholar]
  6. Horgan T. J. & Gilchrist M. D. The creation of three-dimensional finite element models for simulating head impact biomechanics. IJCrash 8 (4), 353–366 (2003). [Google Scholar]
  7. Willinger R., Kang H. S. & Diaw B. M. Development and validation of a human head mechanical model. C. R. Acad. Sci. Paris 327, II b, 125–131 (1999). [Google Scholar]
  8. England M. A. & Wakely J. in A Colour Atlas of the Brain & Spinal Cord, Structural features of the central nervous system. 10–17 (Mosby-Wolfe, 1996).
  9. El Sayed T., Mota A., Fraternali F. & Ortiz M. Biomechanics of traumatic brain injury. Comput. Methods Appl. Mech. Engrg. 197, 4692–4701 (2008). [Google Scholar]
  10. Rashid B., Destrade M. & Gilchrist M. D. Mechanical characterization of brain tissue in simple compression at dynamic strain rates. J. Mech. Behav. Biomed. Mat. 10, 23–38 (2012). [DOI] [PubMed] [Google Scholar]
  11. Rashid B., Destrade M. & Gilchrist M. D. Mechanical characterization of brain tissue in simple shear at dynamic strain rates. J. Mech. Behav. Biomed. Mat. 28, 71–85 (2013). [DOI] [PubMed] [Google Scholar]
  12. Giordano C., Cloots R. J. H., van Dommelen J. A. W. & Kleiven S. The influence of anisotropy on brain injury prediction. J. Biomech 47, 1052–1059 (2014). [DOI] [PubMed] [Google Scholar]
  13. Lin D. C., Shreiber D. I., Dimitriadis E. K. & Horkay F. Spherical indentation of soft matter beyond the Hertzian regime: numerical and experimental validation of hyperelastic models. Biomech. Model Mechanobiol. 8, 345–358 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Rashid B., Destrade M. & Gilchrist M. D. Mechanical characterization of brain tissue in tension at dynamic strain rates. J. Mech. Behav. Biomed. Mat. 33, 43–54 (2014). [DOI] [PubMed] [Google Scholar]
  15. Moerman K. M., Holt C. A., Evans S. L. & Simms C. K. Digital image correlation and finite element modelling as a method to determine mechanical properties of human soft tissue in vivo. J. Biomech 42, 1150–53 (2009). [DOI] [PubMed] [Google Scholar]
  16. Ho J. & Kleiven S. Dynamic response of the brain with vasculature: A three-dimensional computational study. J. Biomech 40, 3006–12 (2007). [DOI] [PubMed] [Google Scholar]
  17. Iivarinen J. T., Korhonen R. K. & Jurvelin J. S. Experimental and numerical analysis of soft tissue stiffness measurement using manual indentation device – significance of indentation geometry and soft tissue thickness. Skin Research and Technology 0, 1–8 (2013). [DOI] [PubMed] [Google Scholar]
  18. Elkin B. S., Ilankova A. & Morrison B. III Age-dependent regional mechanical properties of the rat hippocampus and cortex. J. Biomech. Eng. 132, 011010 (2009). [DOI] [PubMed] [Google Scholar]
  19. Ogden R. W. Large deformation isotropic elasticity – On the correlation of theory and experiment for incompressible rubberlike solids. Proc. R. Soc. Lond. A. 326, 565–584 (1972). [Google Scholar]
  20. Atkin R. J. & Fox N. in An Introduction to the Theory of Elasticity, Ch. 2, 79 (Dover, New York) (2005). [Google Scholar]
  21. Prevost T. P. et al. Dynamic mechanical response of brain tissue in indentation in vivo, in situ, and in vitro. Acta Biomaterialia 7, 4090–4101 (2011). [DOI] [PubMed] [Google Scholar]
  22. Gefen A. & Margulies S. S. Are in vivo and in situ brain tissue mechanically similar? J. Biomech. 37, 1339–52 (2004). [DOI] [PubMed] [Google Scholar]
  23. Gefen A., Gefen N., Zhu Q., Raghupathi R. & Margulies S. S. Age-dependent changes in material properties of the brain and braincase of the rat. J. Neurotrauma 20, 1163–1177 (2003). [DOI] [PubMed] [Google Scholar]
  24. Sharp A. A., Ortega A. M., Restrepo D., Curran-Everett D. & Gall K. In vivo penetration mechanical and mechanical properties of mouse brain tissue at micrometer scales. IEEE Trans. Biomed. Eng. 56, 45–53 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Elkin B. S., Ilankova A. & Morrison B. III Dynamic regional mechanical properties of the porcine brain: Indentation in the coronal plane. J. Biomech. Eng. 133, 071009-1-7 (2011). [DOI] [PubMed] [Google Scholar]
  26. Elkin B. S. & Morrison B. Viscoelastic properties of the P17 and adult rat brain from indentation in the coronal plane. J. Biomech. Eng. 135, 114507 (2013). [DOI] [PubMed] [Google Scholar]
  27. Zhang J., Green M. A., Sinkus R. & Bilston L. E. Viscoelastic properties of human cerebellum using magnetic resonance elastography. J. Biomech. 44, 1909–13 (2011). [DOI] [PubMed] [Google Scholar]
  28. Finan J. D., Elkin B. S., Pearson E. M., Kalbian I. L. & Morrison B. III Viscoelastic properties of the rat brain in the sagittal plane: Effects of anatomical structure and age. Ann. Biomed. Eng. 40, 70–78 (2012). [DOI] [PubMed] [Google Scholar]
  29. van Dommelen J. A. W., van der Sande T. P. J., Hrapko M. & Peters G. W. M. Mechanical properties of brain tissue by indentation: Interregional variation. J. Mech. Behav. Biomed. Mat. 3, 158–166 (2010). [DOI] [PubMed] [Google Scholar]
  30. Jin A., Zhu F., Mao H., Shen M. & Yang K. H. A comprehensive experimental study on material properties of human brain tissue. J. Biomech. 46, 2795–2801 (2013). [DOI] [PubMed] [Google Scholar]
  31. Smith D. H., Johnson V. E. & Stewart W. Chronic neuropathologies of single and repetitive TBI: substrates of dementia? Nat. Rev. Neurol. 9, 211–221 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Xu G., Bayly P. V. & Taber L. A. Residual stress in the adult mouse brain. Biomech. Model. Mechanobiol. 8, 253–62 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Weissenberger C. A. & Siren A. L. Experimental traumatic brain injury. Experimental & Translational Medicine 2 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Azevedo F. A. C. et al. Equal number of neuronal and non-neuronal cells make the human brain an isometrically scaled-up primate brain. J. Compar. Neurol. 513, 532–541 (2009). [DOI] [PubMed] [Google Scholar]
  35. Efremov Y. M. et al. Atomic Force Microscopy Study of the Arrangement and Mechanical Properties of Astrocytic Cytoskeleton in Growth Medium. Acta Naturae 3, 93–99 (2011). [PMC free article] [PubMed] [Google Scholar]
  36. Lu Y. B. et al. Viscoelastic properties of individual glial cells and neurons in the CNS. Proc. Nat. Accad. Sci. 103, 17759–64 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Hrapko M., van Dommelen J. A. W., Peters G. W. M. & Wismans J. S. H. M. The influence of test conditions on characterization of the mechanical properties of brain tissue. J. Biomech. Eng. 130, 031003-1-10 (2008). [DOI] [PubMed] [Google Scholar]
  38. Mihai L. A., Chin L., Janmey P. A. & Goriely A. A comparison of hyperelastic constitutive models applicable to brain and fat tissues. J. R. Soc. Interface 12, 20150486 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. MacManus D. B., Pierrat B., Murphy J. G. & Gilchrist M. D. Dynamic mechanical properties of mouse brain tissue using micro-indentation. J. Biomech. 48, 3213–3218 (2015). [DOI] [PubMed] [Google Scholar]
  40. Pervin F. & Chen W. W. Effect of inter-species, gender, and breeding on the mechanical behavior of brain tissue. NeuroImage 54, S98–S102 (2011). [DOI] [PubMed] [Google Scholar]
  41. Fountoulakis M., Hardmeier R., Hoger H. & Lubec G. Postmortem changes in the level of brain proteins. Exp. Neurol. 167, 86–94 (2001). [DOI] [PubMed] [Google Scholar]
  42. Ferrer I. et al. Brain protein preservation largely depends on the postmortem storage temperature: Implications for study of proteins in human neurologic diseases and management of brain banks: A BrainNet Europe study. J. Neuropathol. & Exp. Neurol. 66, 35–46 (2007). [DOI] [PubMed] [Google Scholar]
  43. Mooney M. A theory of large elastic deformation. J. App. Phys. 11, 582–592 (1940). [Google Scholar]
  44. Ogden R. W. Large deformation isotropic elasticity - On the correlation of theory and experiment for incompressible rubberlike solids. Proc. R. Soc. London. Series A, Mathematical and Physical Sciences 326, 565–584 (1972). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES