Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2016 Jan 28;7(4):622–626. doi: 10.1021/acs.jpclett.5b02792

Benzophenone Ultrafast Triplet Population: Revisiting the Kinetic Model by Surface-Hopping Dynamics

Marco Marazzi †,§,*, Sebastian Mai ‡, Daniel Roca-Sanjuán ∥, Mickaël G Delcey ⊥, Roland Lindh ⊥,#, Leticia González ‡, Antonio Monari †,§,*
PMCID: PMC4761974  PMID: 26821061

Abstract

graphic file with name jz-2015-02792j_0005.jpg

The photochemistry of benzophenone, a paradigmatic organic molecule for photosensitization, was investigated by means of surface-hopping ab initio molecular dynamics. Different mechanisms were found to be relevant within the first 600 fs after excitation; the long-debated direct (S1 → T1) and indirect (S1 → T2 → T1) mechanisms for population of the low-lying triplet state are both possible, with the latter being prevalent. Moreover, we established the existence of a kinetic equilibrium between the two triplet states, never observed before. This fact implies that a significant fraction of the overall population resides in T2, eventually allowing one to revisit the usual spectroscopic assignment proposed by transient absorption spectroscopy. This finding is of particular interest for photocatalysis as well as for DNA damages studies because both T1 and T2 channels are, in principle, available for benzophenone-mediated photoinduced energy transfer toward DNA.

Fast intersystem crossing (ISC) mechanisms occurring in organic molecules have been extensively studied in the last decades, especially by time-resolved experimental techniques.1−8 Nevertheless, it is only in the last years that reliable computational methods were developed in order to study the dynamical details of such processes.9−13 A comparison between experimental and theoretical results can be of particular interest in the case of aromatic ketones because different analyses of diverse experiments can lead to contradictory results. In this regard, a paradigmatic case is benzophenone (BP), a well-known building block in organic synthesis, recently becoming more and more interesting as a crucial agent in different applications. Indeed, thanks to its ability to efficiently absorb ultraviolet (UV) light, it may be used as a photoinitiator in phototherapeutic applications,14 as a UV-blocker to prevent photodegradation in polymers15 and soaps,16 as a photophysical probe to clarify peptide–peptide interactions,17 or as a photosensitizer to transfer energy to DNA.18,19 Given the wide applicability of BP in so many different fields (from materials science and technology to biology and pharmacology), a clear-cut insight into the mechanisms undergoing the initial photophysical and photochemical processes is necessary.

A number of questions are still open from previous experimental studies. After population of the lowest-lying singlet excited state S1—either by absorption in the UVA (S0 → S1) or after an ultrafast radiationless internal conversion from the optically brighter S2 state (S0 → S2 → S1)—two pathways have been postulated to populate the lowest-lying triplet state via a spin–orbit coupling (SOC) mechanism: direct (S1 → T1)1,3,4 or indirect (S1 → T2 → T1).2,6−8 This unresolved aspect leaves open questions concerning BP emission properties. Indeed, according to the previous mechanisms, only phosphorescence from the T1 minimum would be, in principle, expected. However, gas-phase experiments proposed a long-living emission following a biexponential decay, suggesting that dual phosphorescence could occur from both an unrelaxed and a vibrationally relaxed triplet state.5 Additionally, fluorescence was also observed as an E (eosin)-type delayed event20 (see Scheme 1).

Scheme 1. (a) Obtained Characteristic BP Coordinates at Franck–Condon (CASSCF(12,11)/ANO-S-VDZP level of theory) and (b) Possible Photochemical Mechanisms Involving BP, Including Photon Absorption (hνabs), Fluorescence (hνfluo), and Phosphorescence (hνph) from the Respective PES Minima (min).

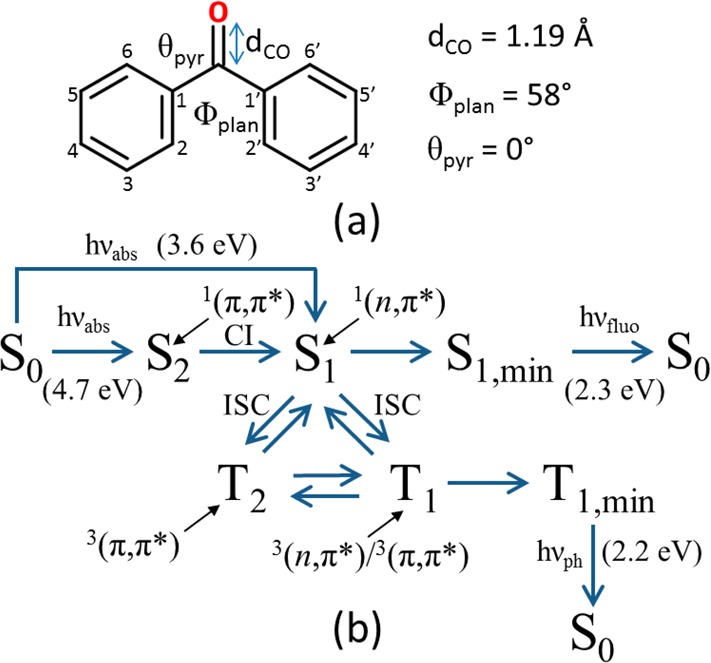
Scheme 1

Open in a new tab

The C=O distance (dCO) and improper dihedrals that measure the angle between phenyl planes (Φplan: C2–C1–C1′–C2′) and carbonyl carbon pyramidalization (θpyr: C=O–C1–C1′). Their evolution in time is shown in the Supporting Information.

The energy values are taken from the literature and correspond to the CASPT2(12,11)/ANO-L-VDZP//CASSCF(12,11)/ANO-L-VDZP level of theory.21 The electronic nature of the states is specified. CI: conical intersection; ISC: intersystem crossing.

At present, only one computational mechanistic study was reported on the photochemistry of BP, based on accurate (CASPT2//CASSCF) calculations of minimum energy paths (MEPs) and crossing points between potential energy surfaces (PESs).21 The results point toward an indirect population of the T1 state via the intermediate T2. Additionally, an S1 minimum was located, which could explain delayed fluorescence.

Here, we investigate BP photochemistry and photophysics from a different and complementary perspective, namely, directly taking into account the time evolution of the different excited states. To this aim, we used CASSCF-based nonadiabatic molecular dynamics including surface-hopping22 between electronic adiabatic states of same and different multiplicity, on the same footing. The CASSCF(12,11)/ANO-S-VDZP level of theory was selected for its qualitative agreement with more accurate CASPT2(12,11)/ANO-L-VDZP calculations while still being computationally efficient for dynamics.21 The selected active space includes two pairs of ππ* orbitals for each phenyl ring, a ππ* pair of orbitals centered on the carbonyl group and an n orbital of the oxygen atom. When including water as the solvent with the implicit polarizable continuum model,23 the same qualitative and semiquantitative optical properties were found for the most representative BP structures (see the Supporting Information). Hence, dynamics simulations were performed only in the gas phase.

Although, as previously stated, diverse unresolved questions need to be answered, there is agreement between theory and experiment concerning the electronic absorption of the Franck–Condon (FC) structure; because S1 and S2 states are, respectively, 1(n,π*) and 1(π,π*), the S0 → S2 electronic transition is more probable than the S0 → S1. Nevertheless, the first three low-lying triplet states are located below S1. Therefore, a direct (S0 → S1) or indirect (S0 → S2 → S1) population of the lowest-lying singlet excited state is a prerequisite for the subsequent intersystem crossing; at FC, S1 is almost degenerate in energy with T2 and T3 (0.07 eV at the CASPT2 level21), both 3(π,π*) states. According to the El-Sayed’s rules,24 an ISC process governed by a direct SOC interaction is efficient when a change in the molecular orbital type occurs, hence in principle favoring an S1 → T2,3 (that is, 1(n,π*) → 3(π,π*)) SOC mechanism. On the other hand, the larger energy separation between S1 and T1 (0.53 eV at the CASPT2 level21) and the fact that T1 is a mixed 3(n,π*)/3(π,π*) state21 due to the nonplanarity of the BP molecule (Scheme 1) suggest that a direct (S1 → T1) SOC mechanism should be disfavored but still possible. We note that we focus in this work on the ISC processes after excitation to the S1 state. While there might be relevant ISC pathways starting in S2, this state is located at much higher excitation energies, which we do not consider here. This can also be evidenced from a recent experimental study.25 Moreover, the S1 state is relevant in DNA photosensitization. Indeed, it appears at lower energies than the lowest-lying states of the nucleobases and can transfer its triplet energy to the triplet of thymine.19

The gas-phase nonadiabatic dynamics simulations were started on a set of 65 initial conditions. To this end, the ground-state PES was locally reproduced by a frequency calculation at the equilibrium geometry, that is, by a harmonic approximation, and phase space points were sampled from the Wigner distribution. Assuming a vertical S0 → S1 transition, all trajectories were run for a maximum of 600 fs, considering a stable triplet population as a criterion to stop the simulation (see the Supporting Information). All calculations and further analyses were performed with the SHARC (Surface Hopping including Arbitrary Couplings) software suite13 coupled to MOLCAS 8,26 including Cholesky decomposition for the calculation of the energy gradients.27,28

At 600 fs, 60% of the trajectories reached the triplet manifold, as evidenced from Figure 1. Besides singlet–triplet interconversion, the kinetic model reveals that the S1 exponential decay mainly results in the population of T1. Nevertheless, a population of 10% in T2 is also observed (within 600 fs), characterized by a distinctive characteristic formation time τ (ca. 4 times larger for T2, with respect to T1) and therefore cannot be neglected. T3 population, on the other hand, is a nonrelevant event (see the Supporting Information). The persistent T2 population is due to a kinetic equilibrium between T1 and T2 that governs the initial triplet manifold population, and it can play a role for BP ultrafast spectroscopic characterization, that is, before phosphorescence is observed. Experimentally, the time scale recorded for BP triplet formation is different depending on the environment. By picosecond time-resolved spectroscopy, a global τISC ≈ 25 ps was found for BP single crystals,8 which decreases in the liquid phase (τISC ≈ 6.5–16 ps, depending on the solvent7,29,30) and even more in the gas phase. Indeed, the latter was determined by photoelectron spectroscopy that assigned a lifetime of 5 ± 0.5 ps to the formation of T1 as the latter is considered as the stable final state.25 Our exponential kinetic models predict comparable values (3.38 and 4.47 ps) for T2, while the predicted τT1 (0.90 and 1.00 ps) was not experimentally detected.

Figure 1.

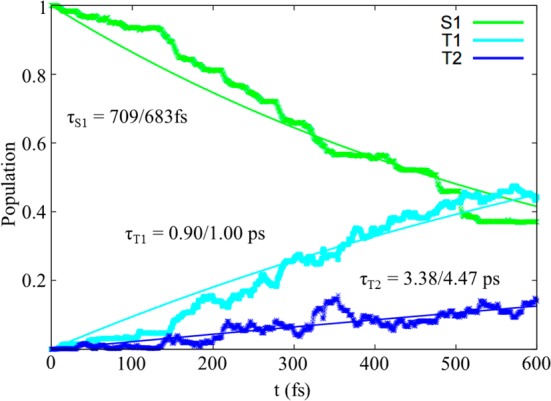
Figure 1

Open in a new tab

Kinetic models of the BP photoreactivity, based on global fitting to a single-exponential rate law. The S1 population decays over the time, giving rise to T1 and T2 formation. The lifetime values τ are shown; the first (second) number corresponds to a parallel (serial) kinetic model. The two curves are nearly identical between 0 and 600 fs. Equations and curves above 600 fs can be found in the Supporting Information.

In detail, two kinetic models were considered: (i) parallel formation of T1 and T2 from S1, congruent with our simulation results and (ii) serial formation of either T1 or T2 from S1, in agreement with the usual experimental fitting procedure.

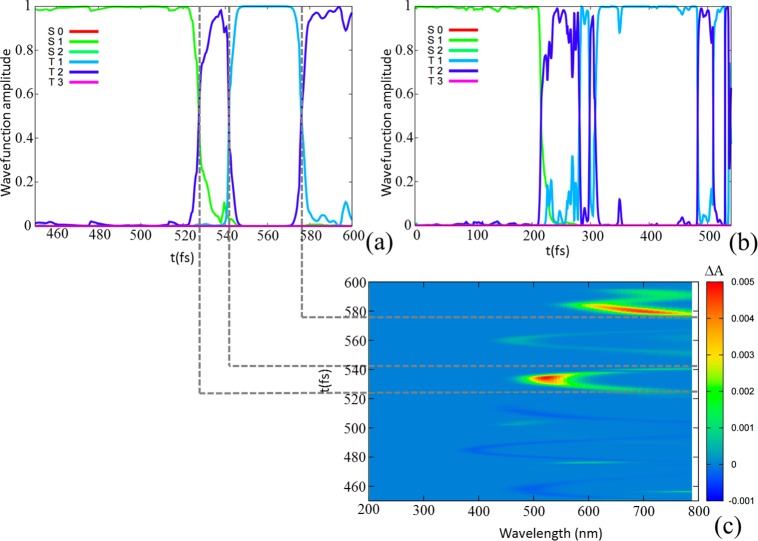
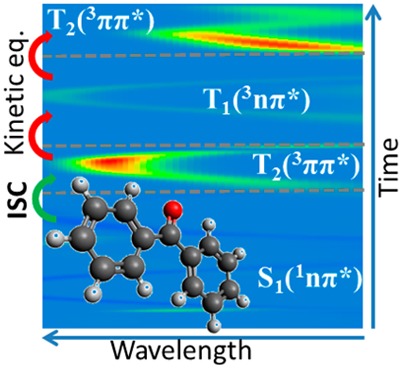
This apparent disagreement can be explained by the peculiarity of BP photophysics, as enlightened by our simulations. As can be seen in Figure 2a,b (and in the Supporting Information), after S0 → S1 vertical excitation, the system evolves toward a region where S1, T1, and T2 are almost degenerate in energy, while the T3 energy rises (in accordance with the CASPT2 MEP21). From the FC region to the ISC point, the dynamics is described exclusively by S1 (i.e., S2 is not populated), a 1(n,π*) state that shows mainly low-intensity stimulated S1 → S0 emission. Once the ISC point is reached, the triplet manifold is populated, and two signals (T1 → T3 and T2 → T3 excited-state absorptions) could, in principle, be detected by transient spectroscopy since, because of the quasi-degeneracy, T1 → T2 absorption would have a much too low excitation energy. Electronically, the T1 corresponds to a mixed 3(n,π*)/3(π,π*) state, while T2 and T3 are 3(π,π*) states; therefore, the T2 → T3 transition will have a significantly higher oscillator strength. Furthermore, because of T1 and T2 degeneracy, the two transitions will happen in the same spectral region, and hence, the brighter T2 → T3 transition will totally mask the low T1 → T3 intensity. This can be evidently evidenced from Figure 2c, where we reported the inhomogeneous31 time-dependent spectrum simulated for only one trajectory (see the Supporting Information); the excited-state absorption reaches its maximum intensity when T2 is populated, and then, it lowers its intensity by a factor 5 when populating T1, to reach again a maximum for the subsequent population of T2.

Figure 2.

Figure 2

Open in a new tab

Representative excited-state trajectories showing an S1 → T2 → T1 indirect mechanism and the subsequent equilibrium between T1 and T2 states (a,b). The transient absorption (ΔA) spectrum is simulated for one of the trajectories (c). Positive ΔA values correspond to excited-state absorption; negative ΔA values indicate stimulated emission.

This fact can also explain the reason for the experimental difficulties in assigning the eventual intermediate state of the proposed S1 → T2 → T1 indirect mechanism: (i) the fast dynamical equilibrium between T1 and T2 (in most of the trajectories, they exchange in just a few fs) challenges available state-of-the-art ultrafast spectroscopies, and (ii) it is not possible to distinguish the different triplet states in the experimental spectrum because their signals overlap when averaging on the ensemble trajectories. We therefore conclude that the experimentally determined gas-phase characteristic time (5.0 ± 0.5 ps) should most probably be referred to the population of T2, in qualitative agreement with our parallel (theoretically oriented) kinetic model (3.38 ps) and in quantitative agreement with our serial (experimentally oriented) kinetic model (4.5 ps). A direct comparison with the experimental kinetic model is nevertheless not a straightforward task because the fitting procedure is experimentally based on the signal strength but theoretically based on the population.

From a vibrational point of view, after 200 fs, when the overall triplet population is already 20%, T1 and T2 populations lose their vibrational coherence. This is also suggested by the time-dependent oscillations of dCO and Φplan, which end up being highly scattered after an initial coherent (i.e., in-phase vibration) period (Figures S4 and S5 in the Supporting Information).

On the other hand, the trajectories remaining in the initial S1 state indicate that S1 → S0 fluorescence is, in principle, possible, even though it results in a marginal process, as evidenced by the subpicosecond S1 lifetime (τS1 = 709 and 683 fs) obtained from our kinetic models (Figure 1). Indeed, a quasi-unitary ISC quantum yield32 coupled to low fluorescence quantum yield20 was experimentally found. Moreover, the detected delayed fluorescence20 can be explained in terms of recrossing events between singlet and triplet states (S1 → T1,2 → S1), as noticed in a small fraction (5%) of our trajectories and predicted by the high SOC values calculated along the MEP.21

Both indirect and direct mechanisms for triplet population were recognized in our photodynamics study, spanned all over the simulation time (see Figures 2 and 3 and the Supporting Information). The indirect process was found to be prominent, as previously suggested.21 Nevertheless, a relevant percentage (33% of the trajectories populating the triplet manifold) chose a direct process. Besides, even though the T1 state is ∼10 kcal/mol below T2 at the FC geometry, the SOC makes possible an S1 → T1 surface-hop already at the very first molecular vibration (Figure 3a), without requiring specific geometrical distortions. However, the direct process is also observed after several molecular vibrations (Figure 3b) because the energy gap is reduced during the dynamics, reaching a three-state (S1, T2, and T1) energy degeneracy, therefore generating a competition between S1 → T2(i.e., 1(n,π*) → 3(π,π*)) and S1 → T1 (i.e., 1(n,π*) → 3(n,π*)/3(π,π*)) potential surface-hops along the dynamics.

Figure 3.

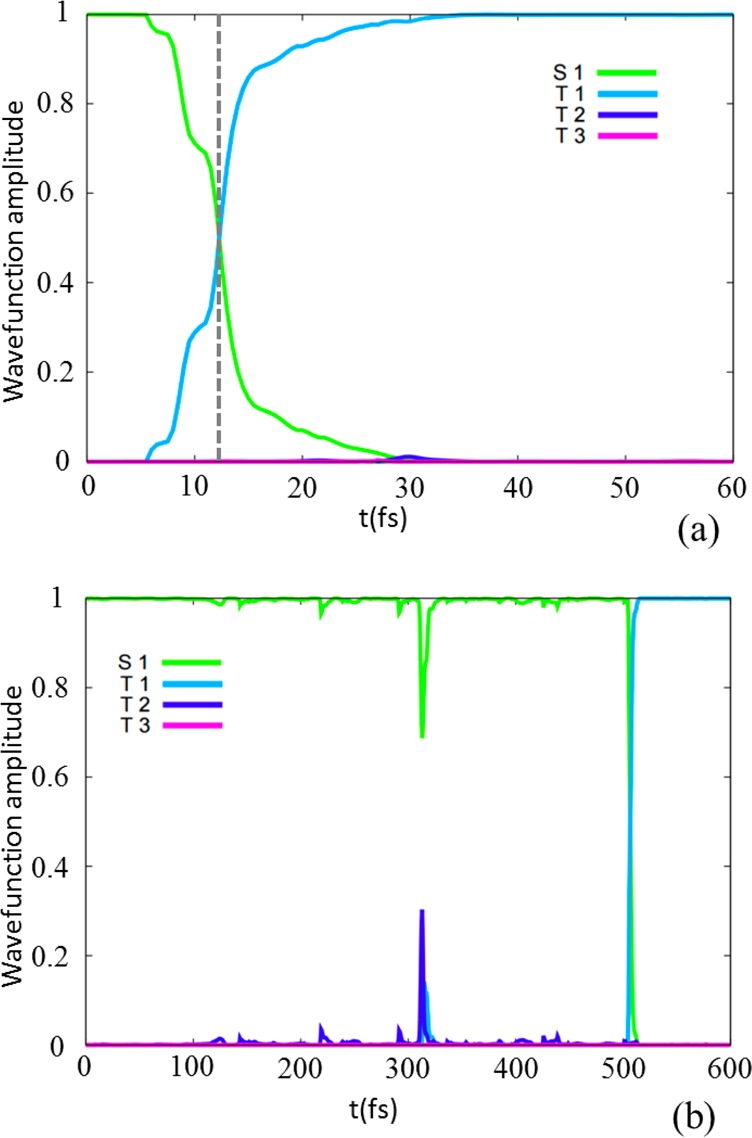
Figure 3

Open in a new tab

Representative excited-state trajectories showing an S1 → T1 direct mechanism at the first molecular vibration (a) or at a later stage (b).

In conclusion, we have shown by excited-state surface-hopping dynamics that BP can efficiently populate the triplet manifold by an ultrafast ISC process. The indirect mechanism S1 → T2 → T1 is favored with respect to the direct S1 → T1 one (ratio 2:1). Nevertheless, in both cases, a quite persistent equilibrium between T1 and T2 is observed at 600 fs (see Figure S2c in the Supporting Information), indicating an unrelaxed triplet manifold not detailed before and in agreement with previous gas-phase experiments.5 This finding makes it possible to revisit the common spectroscopic assignment and allow both triplet channels for DNA photosensitization and photocatalysis to open, enhancing the feasibility of the energy-transfer process. Note that in solution, energy transfer to the solvent can be an additional factor to be considered. More in general, these results are relevant not only for BP but also for the other members of the diaryl ketones family in which the lowest-energy singlet excited state has nπ* nature because no specific (i.e., system-dependent normal mode) molecular coordinate is explicitly involved in the process; this could be due to the extended (S1, T1, and T2) quasi-degeneracy and non-negligible SOCs between singlet and triplet PESs. Because of these findings, coupled to the mixed nπ*/ππ* nature of the lowest triplet state, we consider that nonadiabatic dynamics play an important role in correctly determining the photochemical behavior of such systems.

Acknowledgments

This work has been supported by Université de Lorraine and French CNRS. M.M. is grateful to the French National Research Agency (ANR) for a postdoctoral contract in the framework of the QMC=Chem project. D.R.-S. thanks the Spanish MINECO/FEDER (CTQ2014-58624-P project, JCI-2012-13431 Juan de la Cierva fellowship, and María de Maetzu program/MDM-2015-0538) and the Generalitat Valenciana (GV2015-057) for financial support. S.M. and L.G. acknowledge the Austrian Science Fund (FWF) for financial support through Project P25827 as well as the COST action CM1405 (MOLIM).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.5b02792.

  • Computational details, kinetic models parameters, single-point calculations of geometries along the potential energy surface, wavefunction amplitude graphs and geometrical analysis of the 39 trajectories populating the triplet manifold, Franck–Condon structure, and description of the transient absorption spectrum simulation (PDF)

The authors declare no competing financial interest.

Supplementary Material

jz5b02792_si_001.pdf (4.1MB, pdf)

References

  1. Ohmori N.; Suzuki T.; Ito M. Why Does Intersystem Crossing Occur in Isolated Molecules of Benzaldehyde, Acetophenone, and Benzophenone?. J. Phys. Chem. 1988, 92, 1086–1093. 10.1021/j100316a019. [DOI] [Google Scholar]
  2. Yabumoto S.; Sato S.; Hamaguchi H. Vibrational and Electronic Infrared Absorption Spectra of Benzophenone in the Lowest Excited Triplet State. Chem. Phys. Lett. 2005, 416, 100–103. 10.1016/j.cplett.2005.09.025. [DOI] [Google Scholar]
  3. El-Sayed M. A. Low Field Zeeman Effect and the Mechanism of the S1 → T1 Nonradiative Process. J. Chem. Phys. 1975, 62, 1579. 10.1063/1.430575. [DOI] [Google Scholar]
  4. Batley M.; Kearns D. R. The Second Triplet State of Benzophenone. Chem. Phys. Lett. 1968, 2, 423–425. 10.1016/0009-2614(68)80046-6. [DOI] [Google Scholar]
  5. Matsushita Y.; Kajii Y.; Obi K. Photochemical Reaction of Excited Benzophenone in the Gas Phase. J. Phys. Chem. 1992, 96, 4455–4458. 10.1021/j100190a061. [DOI] [Google Scholar]
  6. Miyasaka H.; Morita K.; Kamada K.; Mataga N. Femtosecond-Picosecond Laser Photolysis Studies on Photoreduction Process of Excited Benzophenone with N,N-Dimethylaniline in Acetonitrile Solution. Bull. Chem. Soc. Jpn. 1990, 63, 3385–3397. 10.1246/bcsj.63.3385. [DOI] [Google Scholar]
  7. Aloïse S.; Ruckebusch C.; Blanchet L.; Réhault J.; Buntinx G.; Huvenne J.-P. The Benzophenone S1(n,π*) → T1(n,π*) States Intersystem Crossing Reinvestigated by Ultrafast Absorption Spectroscopy and Multivariate Curve Resolution. J. Phys. Chem. A 2008, 112, 224–231. 10.1021/jp075829f. [DOI] [PubMed] [Google Scholar]
  8. Katoh R.; Kotani M.; Hirata Y.; Okada T. Triplet Exciton Formation in a Benzophenone Single Crystal Studied by Picosecond Time-Resolved Absorption Spectroscopy. Chem. Phys. Lett. 1997, 264, 631–635. 10.1016/S0009-2614(96)01389-9. [DOI] [Google Scholar]
  9. Mitrić R.; Petersen J.; Bonačić-Koutecký V. Laser-Field-Induced Surface-Hopping Method for the Simulation and Control of Ultrafast Photodynamics. Phys. Rev. A: At., Mol., Opt. Phys. 2009, 79, 053416. 10.1103/PhysRevA.79.053416. [DOI] [Google Scholar]
  10. Richter M.; Marquetand P.; González-Vázquez J.; Sola I.; González L. SHARC: Ab Initio Molecular Dynamics with Surface Hopping in the Adiabatic Representation Including Arbitrary Couplings. J. Chem. Theory Comput. 2011, 7, 1253–1258. 10.1021/ct1007394. [DOI] [PubMed] [Google Scholar]
  11. Granucci G.; Persico M.; Spighi G. Surface Hopping Trajectory Simulations with Spin-Orbit and Dynamical Couplings. J. Chem. Phys. 2012, 137, 22A501. 10.1063/1.4707737. [DOI] [PubMed] [Google Scholar]
  12. Cui G.; Thiel W. Generalized Trajectory Surface-Hopping Method for Internal Conversion and Intersystem Crossing. J. Chem. Phys. 2014, 141, 124101. 10.1063/1.4894849. [DOI] [PubMed] [Google Scholar]
  13. Mai S.; Richter M.; Ruckenbauer M.; Oppel M.; Marquetand P.; González L.. SHARC: Surface Hopping Including Arbitrary Couplings — Program Package for Non-Adiabatic Dynamics. http://sharc-md.org/ (2014).
  14. Carroll G. T.; Turro N. J.; Koberstein J. T. Patterning Dewetting in Thin Polymer Films by Spatially Directed Photocrosslinking. J. Colloid Interface Sci. 2010, 351, 556–560. 10.1016/j.jcis.2010.07.070. [DOI] [PubMed] [Google Scholar]
  15. Ibrahim N. A.; El-Zairy E. M. R.; Abdalla W. A.; Khalil H. M. Combined UV-Protecting and Reactive Printing of Cellulosic/wool Blends. Carbohydr. Polym. 2013, 92, 1386–1394. 10.1016/j.carbpol.2012.09.063. [DOI] [PubMed] [Google Scholar]
  16. Cuderman P.; Heath E. Determination of UV Filters and Antimicrobial Agents in Environmental Water Samples. Anal. Bioanal. Chem. 2007, 387, 1343–1350. 10.1007/s00216-006-0927-y. [DOI] [PubMed] [Google Scholar]
  17. Dorman G.; Prestwich G. D. Benzophenone Photophores in Biochemistry. Biochemistry 1994, 33, 5661–5673. 10.1021/bi00185a001. [DOI] [PubMed] [Google Scholar]
  18. Dumont E.; Monari A. Benzophenone and DNA: Evidence for a Double Insertion Mode and Its Spectral Signature. J. Phys. Chem. Lett. 2013, 4, 4119–4124. 10.1021/jz4021475. [DOI] [Google Scholar]
  19. Dumont E.; Wibowo M.; Roca-Sanjuán D.; Garavelli M.; Assfeld X.; Monari A. Resolving the Benzophenone DNA-Photosensitization Mechanism at QM/MM Level. J. Phys. Chem. Lett. 2015, 6, 576–580. 10.1021/jz502562d. [DOI] [PubMed] [Google Scholar]
  20. Brown R. E.; Singer L. A.; Parks J. H. Prompt and Delayed Fluorescence from Benzophenone. Chem. Phys. Lett. 1972, 14, 193–195. 10.1016/0009-2614(72)87176-8. [DOI] [Google Scholar]
  21. Sergentu D.-C.; Maurice R.; Havenith R. W. a.; Broer R.; Roca-Sanjuán D. Computational Determination of the Dominant Triplet Population Mechanism in Photoexcited Benzophenone. Phys. Chem. Chem. Phys. 2014, 16, 25393–25403. 10.1039/C4CP03277B. [DOI] [PubMed] [Google Scholar]
  22. Tully J. C. Molecular Dynamics with Electronic Transitions. J. Chem. Phys. 1990, 93, 1061–1071. 10.1063/1.459170. [DOI] [Google Scholar]
  23. Tomasi J.; Mennucci B.; Cammi R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3093. 10.1021/cr9904009. [DOI] [PubMed] [Google Scholar]
  24. El-Sayed M. A. Triplet State. Its Radiative and Nonradiative Properties. Acc. Chem. Res. 1968, 1, 8–16. 10.1021/ar50001a002. [DOI] [Google Scholar]
  25. Spighi G.; Gaveau M.-A.; Mestdagh J.-M.; Poisson L.; Soep B. Gas Phase Dynamics of Triplet Formation in Benzophenone. Phys. Chem. Chem. Phys. 2014, 16, 9610–9618. 10.1039/c4cp00423j. [DOI] [PubMed] [Google Scholar]
  26. Aquilante F.; Autschbach J.; Carlson R. K.; Chibotaru L. F.; Delcey M. G.; De Vico L.; Fdez Galván I.; Ferré N.; Frutos L. M.; Gagliardi L.; et al. Molcas 8: New Capabilities for Multiconfigurational Quantum Chemical Calculations across the Periodic Table. J. Comput. Chem. 2016, 37, 506. 10.1002/jcc.24221. [DOI] [PubMed] [Google Scholar]
  27. Boström J.; Delcey M. G.; Aquilante F.; Serrano-Andrés L.; Pedersen T. B.; Lindh R. Calibration of Cholesky Auxiliary Basis Sets for Multiconfigurational Perturbation Theory Calculations of Excitation Energies. J. Chem. Theory Comput. 2010, 6, 747–754. 10.1021/ct900612k. [DOI] [PubMed] [Google Scholar]
  28. Delcey M. G.; Freitag L.; Pedersen T. B.; Aquilante F.; Lindh R.; González L. Analytical Gradients of Complete Active Space Self-Consistent Field Energies Using Cholesky Decomposition: Geometry Optimization and Spin-State Energetics of a Ruthenium Nitrosyl Complex. J. Chem. Phys. 2014, 140, 174103. 10.1063/1.4873349. [DOI] [PubMed] [Google Scholar]
  29. Minns R. S.; Parker D. S. N.; Penfold T. J.; Worth G. A.; Fielding H. H. Competing Ultrafast Intersystem Crossing and Internal Conversion in the “Channel 3” Region of Benzene. Phys. Chem. Chem. Phys. 2010, 12, 15607–15615. 10.1039/c001671c. [DOI] [PubMed] [Google Scholar]
  30. Ramseier M.; Senn P.; Wirz J. Photohydration of Benzophenone in Aqueous Acid. J. Phys. Chem. A 2003, 107, 3305–3315. 10.1021/jp026663f. [DOI] [Google Scholar]
  31. Petit A.; Subotnik J. E. Calculating Time-Resolved Differential Absorbance Spectra for Ultrafast Pump-Probe Experiments with Surface Hopping Trajectories. J. Chem. Phys. 2014, 141, 154108. 10.1063/1.4897258. [DOI] [PubMed] [Google Scholar]
  32. Terazima M.; Hirota N. Measurement of the Quantum Yield of Triplet Formation and Short Triplet Lifetimes by the Transient Grating Technique. J. Chem. Phys. 1991, 95, 6490–6495. 10.1063/1.461824. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz5b02792_si_001.pdf (4.1MB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES