Morphogenetic implications of peristaltic fluid-tissue dynamics in the embryonic lung

Abstract

Peristalsis begins in the lung as soon as the smooth muscle forms, and persists until birth. Since the prenatal lung is liquid-filled, smooth muscle action can deform tissues and transport fluid far from the immediately adjacent tissues. Stretching of embryonic tissues and sensation of internal fluid flows have been shown to have potent morphogenetic effects. We hypothesize that these effects are at work in lung morphogenesis. To place that hypothesis in a quantitative framework, we analyze a model of the fluid-structure interactions between embryonic tissues and lumen fluid resulting from peristaltic waves that partially occlude the airway. We find that if the airway is closed, deformations are synchronized; by contrast, if the trachea is open, maximal occlusion precedes maximal pressure. We perform a parametric analysis of how occlusion, stretch, and flow depend on tissue stiffnesses, smooth muscle force, tissue shape and size, and fluid viscosity. We find that most of these relationships are governed by simple ratios.

Graphical Abstract

Introduction

Airway peristalsis (AP) produces spontaneous phasic airway contractions and transient, reversible airway occlusions throughout normal lung development (Jesudason et al., 2005; Pandya et al., 2006; Parvez et al., 2006; Schittny et al., 2000). AP begins as soon as the smooth muscle (SM) develops, concurrently with pseudoglandular branching (Fig 1A), and becomes more robust towards later stages of development. AP has been shown to influence lung development and blockage of AP interferes with lung development (reviewed in (Jesudason, 2009)), but the mechanisms remain unclear. We hypothesize (Jesudason, 2009) that AP critically modulates physical forces on airway cells, influencing the patterning of branching morphogenesis and, ultimately, the overall growth of the lung (Jesudason, 2006; Warburton and Olver, 1997). A more specific hypothesis would consider that AP involves fluid flow and multiple tissues; mechanosensing operates very differently in these different contexts. In further specificity, the physical inputs to the cells are not simply distinguished by on/off presence or absence, but by magnitude and timing, and also by orientation. With the aim of clarifying and refining our mechanobiological hypothesis, to more richly characterize these physical forces, we developed and analyzed a computational mechanical model of AP in the embryonic airway.

Figure 1.

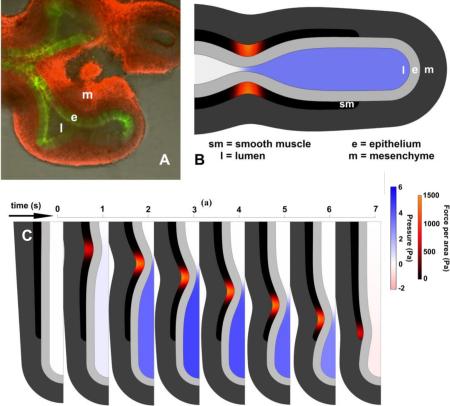
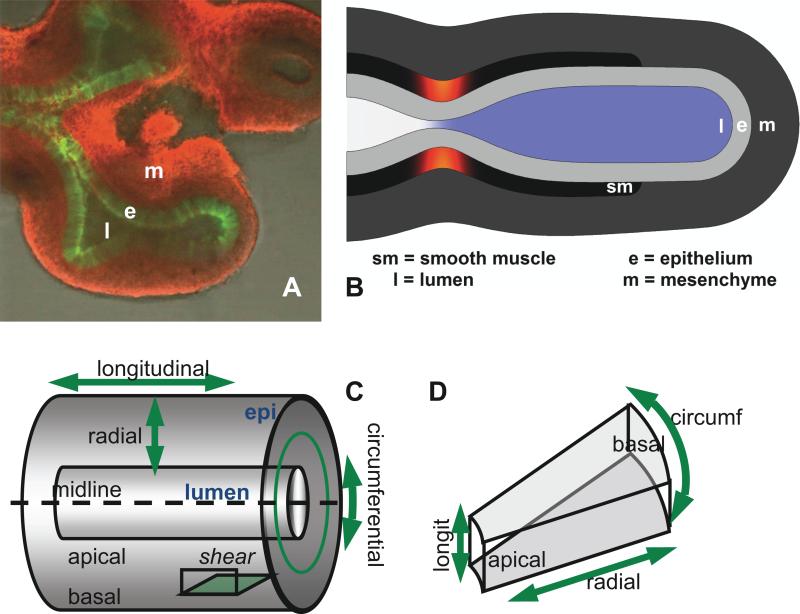
Geometry of embryonic lung and model. A. Explanted E11.5 mouse lung showing lumen (l), epithelium (e, green), and mesenchyme (m, red). Smooth muscle (sm) not visible. B. Embryonic lung idealized as unbranched tubule, with three uniform tissue layers plus lumen. Smooth muscle undergoes active circumferential contraction wave. Lumen color indicates pressure; smooth muscle color indicates contractile stress. C. Orientation in a tubule. Tissue can be stretched or compressed in radial, circumferential, and/or longitudinal directions, and can be sheared in radial-longitudinal interaction. D. Idealized epithelial cell from stalk region of a tubule. What deforms a tissue in a specific direction deforms its cells in the same direction.

Peristaltic pumping, for bulk transport, is widespread not just biologically, but also in industrial and medical applications. There are decades of research on the fluid-structure interactions of peristalsis. A comprehensive review of peristalsis modeling is outside the scope of this article, but we briefly outline here the geometric classifications and their significance. The physics and engineering of open-ended peristalsis are, by now, well understood. Peristalsis has been abundantly modeled as in an infinitely long tube (Burns and Parkes, 1967; Carew and Pedley, 1997; Fung and Yih, 1968; Grotberg and Jensen, 2004; Jaffrin and Shapiro, 1971; Pozrikidis, 1987; Shapiro et al., 1969; Yin and Fung, 1971) or in a finite-length tube open at both ends (Li and Brasseur, 1993), exhibiting richly varied behaviors including stalling and reflux. There are a few studies of blind-ended peristalsis in a channel of fixed length (Yaniv et al., 2012; Yaniv et al., 2009). However, to our knowledge, the mechanics of blind-ended peristalsis in a tube has until very recently (Aranda et al., 2015) not been studied.

In a concurrent paper (Bokka et al., in review), we examine the case of complete occlusion, estimating the deformations of individual cells in the epithelium with a purely geometric model, accounting for conservation of lumen and cell volume. In another concurrent paper (Bokka et al., in press), we analyze the effect of AP on transport of solutes, and discuss the morphogenetic implications of this modification of transport.

In this paper, we determine mechanical stresses on tissues and cells involved in AP, and some flow characteristics in the lumen. We quantitatively identify how the physical characteristics of lumen fluid, tissue stiffness, and SM contraction determine these outcomes. Because we hypothesize that mechanical stimulation alters branching morphogenesis, and want to clarify the mechanisms associated with that, we focus on the early development of the lung as the branches form, in the pseudoglandular period. Our mechanical model tracks the fluid-structure interactions of a tubule with three tissue layers and a liquid-filled lumen (Fig 1A). In the interest of parsimony, we omit other tissues such as blood vessels.

By the end of the pseudoglandular period, the lung is richly branched. In order to focus on the fundamental aspects of embryonic AP, we model the embryonic lung as an unbranched, radially symmetric tube, with a liquid-filled lumen (Fig 1BCD). This idealized shape corresponds to the beginning of the pseudoglandular period, before branching, but can also serve as a model of the immediate vicinity of a distal tip of a later branched embryonic stage. A wave of AP propagates from trachea to tip (Fig 1B).

Because AP is present in prenatal lungs of different species, at very different stages of development, and of very different sizes, we want to develop an understanding of the mechanics of AP in all these variations. Fortunately, what would be an enormous study in vivo becomes a relatively simple study in silico. We test the model on the full range of biologically plausible parameter values, and determine the importance and influence of tissue stiffness, lumen fluid viscosity, and smooth muscle force on measurable quantities such as deformations (strain, in several different orientations), fluid flow, pressure, and occlusion, as well as on less measurable quantities such as stress.

Results

Partial occlusion

Initially, AP is weak and uncoordinated, so occlusions are only partial (PO). In fetal pig and rabbit lungs in vitro, peristalsis results in partial occlusion only to about 50% (Schittny et al., 2000). This is mechanically a very different situation from complete occlusion (CO). In the later prenatal period, AP is robust and completely occludes (CO) the lumen, increasing pressure and resulting in substantial inflation of distal tips. We analyze the case of CO elsewhere (Bokka et al., in review). In this paper, which focuses on the pseudoglandular period when branching occurs, we focus on the developmentally appropriate partial occlusion (PO).

Short-range and long-range deformations

Tissue adjacent to the stenosis created by the contracting smooth muscle (SM) is stretched and compressed directly by the SM. But the SM contraction also creates a dynamic lumen pressure which stretches tissues far from the immediate vicinity of the SM. Away from the stenosis, pressure transients are uniform; the only significant pressure gradient is at the stenosis (Fig 2, Fig 3, Supp videos). Thus all stretches distal to the stenosis are synchronized. That is, the entire distal tubule is stretched simultaneously.

Fig 2.

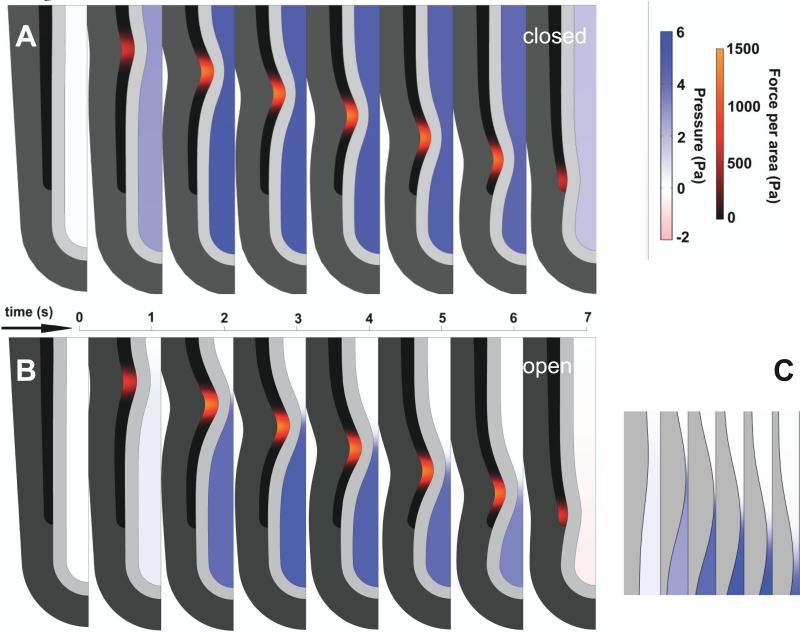
Sequence of frames from model simulations with open and closed end, with identical parameters (tissue stiffness, lumen viscosity, smooth muscle force input). Lumen color corresponds to pressure; smooth muscle color corresponds to contractile stress. A. Closed trachea. Lumen pressure is spatially uniform and increases as soon as AP begins. B. Open trachea. Lumen pressure negligible until occlusion is almost complete. Refilling in last frame corresponds to small negative pressure (pink). Pressure is uniform everywhere in the lumen except at the stenosis, where flow is fastest. Maximal occlusion shown ~ 90%. C. Detail of open ended AP at stenosis. Maximal occlusion occurs before maximal pressure. Pressure distal to pinch forces fluid leakage and reduces occlusion as wave moves distally.

Fig 3.

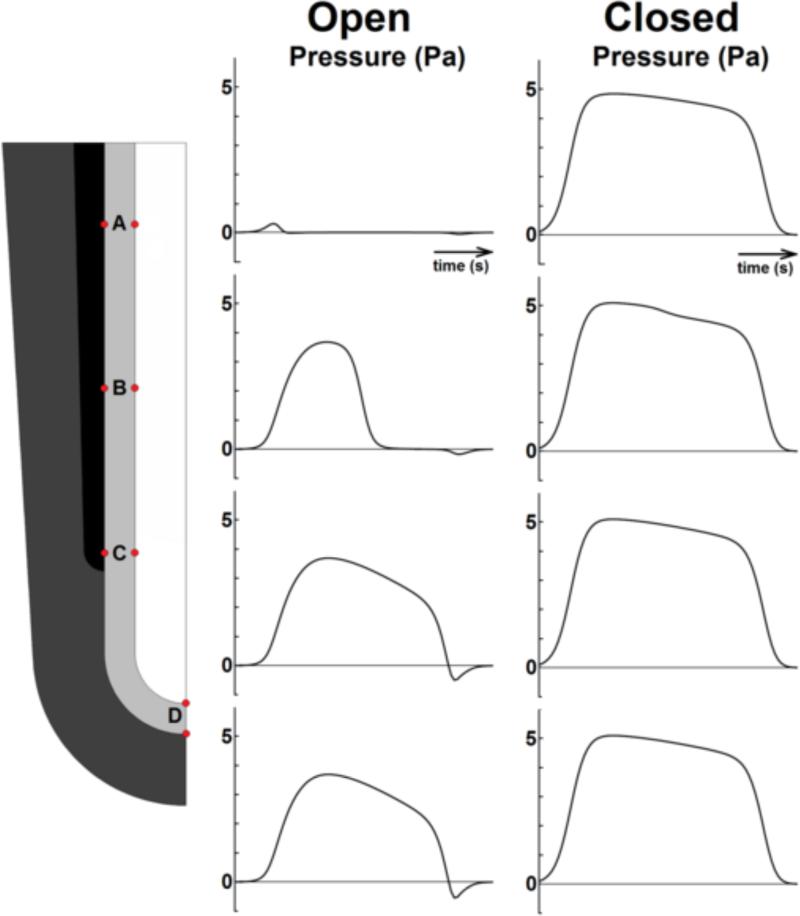
Time series of pressure from AP at 4 locations in lumen, with identical parameters, for trachea open or closed. For open trachea (left), areas closest to trachea (A) remain under low pressure; pressure drops as stenosis passes (B). Pressure is equalized everywhere distal to location of maximal occlusion, whether trachea is open or closed. If trachea is open (left), fluid leakage dissipates pressure. A blocked trachea (right) ensures equal pressure throughout lumen, which has the effect of synchronizing cell stretch.

The dynamics of partial occlusion are influenced by several factors, which we discuss in turn.

Open vs. closed tube

In the intact embryonic airway, the larynx is pinched closed, but will open under sufficient lumen pressure. In vitro, a trachea excised distal to the larynx will close up in a wound healing response, creating a sealed lumen. The trachea can be maintained in an open configuration by insertion of a stiff tube. Because the open and closed experimental situations are mechanically distinct, we consider both cases. We analyzed the mechanics of a simplified unbranched tube, partially occluded by AP, with open or closed larynx (Figs 2, 3).

With the lumen closed, pressure is uniform everywhere (Supp video 1, Figs 2A, 3); with the lumen open, pressure is uniform everywhere away from the stenosis (Supp video 2, Figs 2B, 3), but there is a large pressure gradient across the stenosis (Fig 2C). In a closed lumen, the pressure can get as high as the tissue and the closure will sustain. Given the same SM force, peak pressures are lower if the trachea is open, because pressure is relieved by leakage of lumen fluid (Fig 3).

In both cases, the tissue adjacent to the contraction is compressed circumferentially and stretched radially. This local tissue deformation is determined by the level of occlusion. For the same SM force, occlusion is 50% greater if the trachea is open, due to the pressure relief. Thus, for the same SM force, deformation of tissue at the stenosis is greater if the lumen is open (Figs 4ABC, 5AE).

Fig 4.

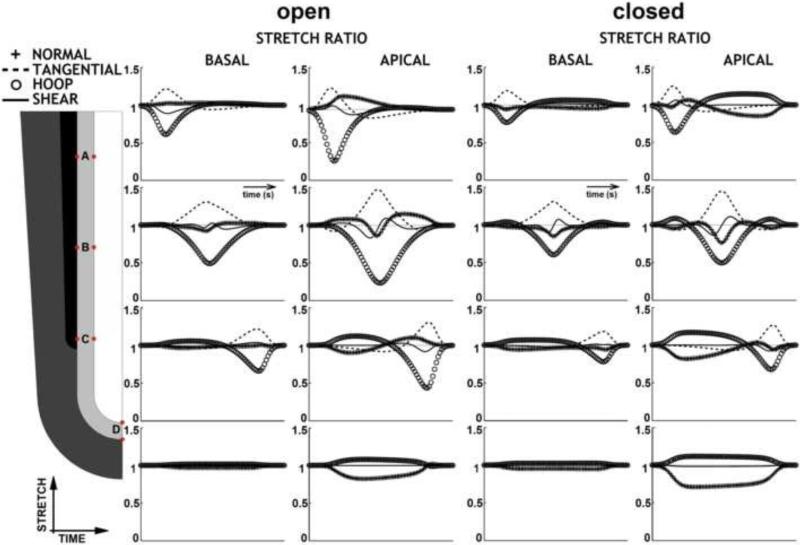
Stretch ratios in epithelium at 4 different locations, over time course of one AP wave, in 3 orthogonal directions plus shear, for open or closed trachea. Stretch ratio = 1 no deformation; <1 shortening/compression; >1 elongation/stretch. There are perceptible stretches and compressions in all directions at different times. Conservation of cell volume mandates that stretch in one direction is balanced by compression in another direction. Basal deformation is always less than apical deformation. Maximal stretch is of stalk cells at the stenosis; since occlusion is much greater for the same force in the open-trachea case, cell deformations at the stenosis are greater. At tip, stretch is greater when trachea is closed, because pressure is higher for the same SM force. Tip apico-basal compression is exactly half the tangential (surface) stretch. Shear is small in stalk, negligible at tip. Identical parameters. Maximal occlusion 90% (open trachea). Normal = apico-basal. Tangential = proximo-distal. Hoop = circumferential.

Fig 5.

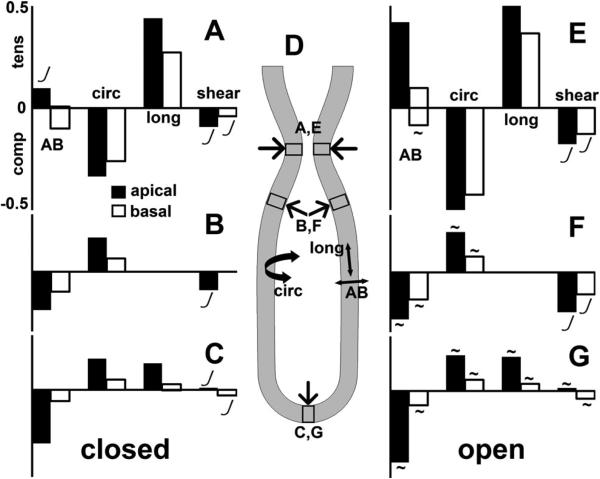
Stretch (strain) of tissue and cells in the different regions of lung tubule, for closed (A, B, C) and open (E, F, G) trachea, using same inputs. Strains reported in apicobasal (AB), circumferential (circ), and proximodistal/longitudinal (long) directions (D), plus shear. Maximum tensile (tens), compressive (comp), and shear strains reported separately for regions (D) of stenosis (A, E), shoulder (B, F), and tip (C, G). Strains are greater on cells’ apical ends (black bars) than basal ends (white bars). Tensile stretch in one direction is always balanced by compressive stretch in another direction. Strains in the stenotic region (A, E) mainly due to the peristaltic load from the smooth muscle; strains in shoulder (B, F) and tip (C, G) are due to the lumen pressure. Stenotic region (A, E) characterized by circumferential compression up to ~50% balanced by proximodistal extension. Shoulder (B, F) and tip (C, G) regions characterized by apicobasal compression up to ~50%, balanced by extension in the other directions. Larger strains are recorded for open trachea (E, F, G), than for closed trachea (A, B, C). Strains are proportional to force ratio (FT/E), except where marked non-linear (J). Strains are independent of lumen fluid viscosity, except as noted (~).

Tissue far from the contraction, e.g. at the tip, will only be stretched circumferentially where there is internal pressure. Thus, if the trachea is open, all tissue distal to the stenosis will be stretched simultaneously; if the trachea is closed, tissue both distal and proximal to the stenosis will be stretched simultaneously (Figs 2, 3, 4).

Time-dependence

For the developmentally normal case of an open trachea, the time of maximum occlusion precedes the time of maximal pressure (Fig 2C). Because pressure is uniform except at the stenosis (Fig 3), all tissue stretches distal to it are synchronized. If the trachea is closed, stretches are synchronized at all locations (Fig 4).

Airway SM has quick contraction and slow relaxation. For ease of analysis, however, we modeled the contraction using a symmetric waveform. We did test a symmetric waveform against a more realistic asymmetric waveform with a stronger leading edge and lighter trailing contraction. Qualitatively, all results were comparable. The asymmetric waveform gave greater maximum occlusion and pressure, because of more effective resistance to leakage.

Apical vs basal

As we noted in a concurrent paper (Bokka et al., in review), at every location, the apical side of the epithelium is subject to greater deformation than the basal side (Fig 4, Fig 5). Stretching of the basal epithelium is only significant at the stenosis (Fig 4ABC); it is negligible distal to SM activity (Fig 4D).

Directions of deformation

Stretches (and stresses) can be compressive or tensile in three directions: longitudinal (proximo-distal), circumferential, or apico-basal (radial) (Fig 1CD), or can be in any of three shear orientations combining two of the three directions. Because of the symmetry of our unbranched model, only one shear orientation is possible (longitudinal-radial).

In the distal tip region (Fig 4D, Fig 5CG), tissue shear is insignificant. Tissue shear is only observed at the shoulders and the stenosis, and it is small relative to the other strains (Fig 4ABC, Fig 5ABEF).

Because of volume conservation, the most significant tissue distortions are in opposite orientations in the tip region and the stenotic region (Fig 4, Fig 5). At the stenosis (Fig 4ABC, Fig 5AE), the primary distortion is circumferential compression, balanced by lengthening in the longitudinal and apico-basal (radial) directions. At the tip (Fig 4D, Fig 5CG), we see the opposite: the primary distortion is an increase in area balanced by apico-basal thinning.

Dependence on physical parameters

The dynamics of physical systems are often governed by nondimensional ratios of physically measurable dimensional parameters; different systems with the same nondimensional ratios have comparable behavior. This is the principle behind experimental testing of scale models. Flows in the embryonic lung are of very low Reynolds number (Re), which means that inertia plays no role in the flow. That does not, however, imply that fluid flow stops as soon as SM force stops; elastic energy stored in the tissue causes the lumen to refill, with a speed that depends in part on the fluid viscosity.

Most of the quantities measured in our model depend solely on the nondimensional force ratioFT/E, where F is SM force density, T is epithelial thickness, and E is tissue stiffness. In the interest of simplicity, and in the absence of direct evidence to the contrary, we assumed equal stiffness E of all three tissue layers.

Occlusion depends linearly on the force ratio FT/E, and is not dependent on lumen fluid viscosity. The same force ratio occludes an open-ended lumen more than a closed-end lumen due to fluid drainage and pressure relief: for tracheas with open end, O = 0.67 FT/E; closed O = 0.46 FT/E.

The magnitudes of compressive, tensile, and shear stretch are also governed by the force ratio FT/E. Maximal stretch in various regions of the tubule is generally linear in the force ratio, but shear has a nonlinear dependence on FT/E (Fig 5, J marks). For a tubule with a closed trachea, stretch depends only on FT/E, and does not depend on the viscosity of the lumen fluid (Fig 5ABC). However, in an open-ended tubule, maximal stretches depend on lumen fluid viscosity as well as FT/E (Fig 5EFG, ~ tilde marks).

Because embryonic lung tissue stiffnesses are unknown, for parsimony, we analyzed the model with equal stiffness in smooth muscle, epithelium, and mesenchyme. We also tested a version varying the relative stiffnesses of these tissues, with the assumption that SM was twice as stiff as mesenchyme, and epithelium of intermediate stiffness (200, 100, and 150 Pa respectively, yielding a composite stiffness of (Reuss) 116 Pa to (Voigt) 125 Pa). Resulting stresses, occlusion, etc. were qualitatively very similar, with minor quantitative differences from the equal-stiffness case. For example, maximal occlusion O in the open-end tubule was a linear function of FT/E, with O = 0.70 FT/E for uniform stiffness and O = 0.66 FT/E for Voigt composite stiffness, a 6% difference.

Lumen maximal pressure depends on physical parameters in a more complex way. For a closed trachea, lumen pressure due to AP does not depend on tissue stiffness or lumen fluid viscosity, only on SM force and tissue thickness: p = 0.087 FT. However, for an open trachea, maximal pressure is close to linear in lumen viscosity, and has a strongly nonlinear dependence on occlusion, or equivalently, on the force ratio FT/E.

Discussion

We know that AP stimulates growth and that the absence of AP retards growth, so we hypothesize that the mechanical stimulation from AP promotes growth (Jesudason, 2009). We also know that tracheal closure enhances branching so we hypothesize that the mechanical stimulation from lumen pressure promotes branching (Unbekandt et al., 2008). These hypotheses arise from experiments at the organ level, where it is hard to identify the specific mechanisms by which the mechanical inputs alter morphogenesis. At a minimum, mechanical stimulation can be expected to affect different tissues differently, and will affect different locations differently.

We also know that many in vitro systems show enhanced growth with mechanical stimulation. That growth enhancement by mechanical stimulation is shown in vitro generally at the cellular level. Some in vitro systems operate as tissues, so that we can more easily characterize forces on a tissue. However, many in vitro systems have an artificial geometry, often e.g. with adhesion to a rigid substrate, which is mechanically unrealistic as a model of in vivo mechanics. Our model uses a more natural 3D tubular geometry, and is thus able to make specific observations that are more relevant to the in vivo situation than in possible with many in vitro 2D systems; for example, our 3D model shows that in vivo, all stretches of the basal end of an epithelium will be smaller than stretches of the apical end.

Somewhere between the organ level and the cellular level is the local tissue level, where location matters, and the direction of deformation matters. We have, in this paper, clarified the different stresses and strains experienced locally in the stalk and the tip. AP deforms epithelial cells in the tip by compressing them apicobasally and stretching them laterally, whereas AP deforms epithelial cells in the stalk by compressing them laterally and stretching them apicobasally. If the mechanism of mechanical growth stimulation is indeed from stretch reception, we conclude that it must be from surface stretch in the tips or from apicobasal stretch in the stalks, not the reverse. Our model results open up other possibilities for hypothesized mechanisms. For example, AP compresses the epithelium in the stalk circumferentially as it is elongated apicobasally; this transient compression may play a role in organizing the cellular arrangement in the tissue, which could in turn affect, e.g. extension of the tubule.

Strain is a ratio of lengths, and stress is a force per unit area. Although they are related, they are not the same physically, and should not be considered equivalent biologically. Our model uses both quantities (Bokka, 2014), but because stress cannot be measured directly, we do not in this paper report stresses, only strains. We do report pressure, which is a stress and which is notoriously difficult to measure. Deformation (strain) is relatively easy to measure under the microscope, as is occlusion, but they are not complete surrogate measures for stresses. Strain has dramatic effects on cells, not just in terms of signaling; it has been shown to create a transient fluidization of the cytoskeleton, on a time scale (10⁰ - 10¹ s) comparable with that of AP (Trepat et al., 2007). Thus, a fuller understanding of the dynamics of AP and its effects on developing tissues would include dynamic modulation of the mechanics of tissues, such as the epithelium and SM, undergoing large transient strains.

This distinction between stress and strain suggests a new interpretation of previous studies on mechanical influences on lung branching morphogenesis. Tracheal occlusion enhances branching, presumably stimulating tissues through increased lumen pressure (Unbekandt et al., 2008). AP enhances lung growth, and it has been hypothesized that this too is primarily a pressure effect. However, an alternative hypothesis is that the cellular stimulus is not due literally to pressure, but due to stretch of a specific area. Our model compared the mechanics of AP with open and closed trachea. In most cases, when the trachea was closed, we saw higher maximal pressure but smaller deformations. The same SM force with a closed trachea generates higher transient pressure, but smaller deformations. Thus it would be important to clarify in an occlusion study the extent of AP, and it would be important in an AP study to clarify the resting internal pressure (Schittny et al., 2000).

We note that all AP stretches distal to the stenosis are synchronized (Fig 2, Fig 3, Fig 4). Stretch synchrony is also characteristic of the breathing lung. Synchrony and near-synchrony are important in learning and neural control. Stretch synchrony from AP substantially precedes stretch synchrony from fetal breathing movements, and could potentially be a mechanism of development of the autonomic control system of the lung.

Viscosity of the lumen fluid affects the mechanics of AP only if the trachea is open and fluid can drain and refill during AP. For an open trachea, as occurs in vivo, the more viscous the fluid, the greater the pressure from AP, and therefore the greater the stretch of the tip from AP. Thus there may be a complex interaction between AP, mechanical stimulation of growth and/or branching, and developmental disorders involving mucus production. In a concurrent paper (Bokka et al., in press), we report measurements of the viscosity of embryonic lung fluid, and discuss the nature of fluid flow in AP and its implications for morphogenesis.

Methods

For analysis of partial occlusion, we modeled the embryonic lung as a single unbranched, radially symmetric tube, with three tissue layers and a lumen (Fig 1). This idealized shape corresponds to the beginning of the pseudoglandular period, before branching, but can also serve as a model of the immediate vicinity of a distal tip of a later branched embryonic stage.

In the absence of specific evidence to the contrary, we opted for the most parsimonious assumptions in our model. Tissues were modeled as uniform, isotropic, Hookean, and undergoing finite strain. The lumen fluid was modeled as uniform, Newtonian, and creeping (Bokka et al., in press). The trachea was modeled as either open or closed. The peristaltic wave was modeled as a symmetric distributed contractile body force in the smooth muscle layer, with gradual onset and release, moving distally with constant velocity. Details of the equations and boundary conditions are in the Appendix.

The dynamic model was implemented in a finite element (FEM) package, COMSOL, with its Fluid-Structure module, bidirectional coupling, large-strain formulation, and ALE moving mesh. Although we considered the tissue to be incompressible, for convergence purposes, Poisson's ratio in the tissue was approximated by 0.45. The FEM model was verified against analytical results for a hollow sphere and an open tube.

For the parametric study, we varied input values linearly or logarithmically as appropriate to cover the whole range of estimated values for the embryonic lung (Table 1). Numerical convergence generally required occlusion to be < 95% and pressure < 15 Pa; simulations that failed to converge were not included in regressions. Statistical analysis was done in MATLAB and Excel. Relationships were considered nonlinear if R² < 0.98 for a linear or log-linear model.

Table 1.

Model parameters and variables

input parameter	symbol	units	range	references
tissue stiffness	E	Pa	20 - 400	(25, 26)1
lumen viscosity	μ	Pa-s	10−3 - 10−1	(27)2
contraction	F	pN/μm3	0.75 - 36	(28)3
lumen diameter		μm	15 - 50
epithelium thickness	T	μm	15
smooth muscle thickness		μm	15
wavespeed	vper	μm/s	67	(1)

output variable	symbol	units	range	references
occlusion	O	-	40-50%	(1)4
lumen pressure	p	Pa	100 - 400	(1, 29) 56(30)7

¹No studies report stiffness of embryonic lung tissue. Range is an estimate. Lower bound 20 Pa for amphibian embryos; upper bound 400 Pa for ASM cells in vitro.

²We assume that viscosity of airway lumen fluid in embryo is lower than that of neonatal airway mucus but higher than that of blood.

³Fetal pig airway SM 1-20 kPa, highest in trachea, lowest in bronchioles. We assume this as an upper bound, and that embryonic SM will likely be weaker by 1-2 orders of magnitude.

⁴Fetal pig, pseudoglandular stage

⁵Fetal mouse (lowest value).

⁶Fetal rabbit, static pressure.

⁷Fetal sheep, static pressure.

• Peristalsis in the prenatal airway critically modulates development.

• We developed a model of peristaltic fluid-tissue interactions in embryonic lung.

• Peristalsis flattens cells in the airway tip and elongates cells in the tubule stalk.

• Occlusion and most measures of stretch depend linearly on smooth muscle force.

Appendix: model equations

The equations governing the fluid-structure interactions are standard. Within the fluid (lumen), the Stokes equation μ∇²v – ∇p = 0 and continuity condition ∇·v = 0 apply. Within the solid (tissues), the force balance equation ∇·σ – F_bf = 0 holds, with body force force F_bf = 0 except in the smooth muscle, where circumferential contraction is modeled by a resulting net radial force density F_bf = –F_sme_r. We use the finite strain formulation; the deformation gradient tensor is F = I + ∇u and the Cauchy stress tensor is given by σ = J⁻¹FSF^T, where J = detF, and where S is the second Piola-Kirchhoff stress tensor.

The fluid and solid domains are coupled by boundary conditions at the apical surface of the epithelium, where the no-slip condition gives v = ∂u/∂t and the force balance gives σ·n = Γ·n i.e. the epithelium experiences a surface load Γ = μ(∇v + ∇v^T)– pI.

The geometry is taken to be axisymmetric, so the boundary conditions at r = 0 prescribe zero radial velocity. Except at the tracheal end, the distal tissue is free to move longitudinally; the tissue length is not constrained. At the tracheal end, the tissue is free to move radially, but set to zero longitudinal velocity. The fluid boundary condition at the trachea is either zero velocity (closed trachea) or zero normal stress (open trachea).

The force density of smooth muscle contraction (body force) is modeled spatiotemporally by the proximodistally symmetric waveform F_sm = F·exp(–ξ²/2w²)·f(t) where ξ = z – z₀ – v_per(t – t_on) with f(t) = ¼ (1 + tanh(τ_on))·(1 − tanh(τ_off)) where τ_on = (t – t_on)/δ and τ_off = (t – t_off)/δ, using t_off – t_on = 6s, δ = 0.5s and w = 10μm. We also tested an alternative asymmetric shape skewing the Gaussian with a faster onset and slower release, but for simplicity did not include results from those simulations in our parametric analysis.