On the Role of Internal Water on Protein Thermal Stability: the Case of Homologous G-domains

Abstract

In this work we address the question whether the enhanced stability of thermophilic proteins has a direct connection with internal hydration. Our model systems are two homologues G-domains of different stability: the mesophilic G domain of the Elongation-Factor thermal unstable protein from E. coli and the hyperthermophilic G domain of the EF-α protein from S. solfataricus. Using molecular dynamics simulation at the microsecond time-scale we show that both proteins host water molecules in internal cavities and that these molecules exchange with the external solution in the nanosecond time scale. The hydration free energy of these sites evaluated via extensive calculations is found to be favourable for both systems, with the hyperthermophilic protein offering a slightly more favourable environment to host water molecules. We estimate that under ambient conditions, the free energy gain due to internal hydration is about 1.3 kcal/mol in favor of the hyperthermophilic variant. However, we also find that at the high working temperature of the hyperthermophile, the cavities are rather dehydrated, meaning that at extreme conditions other molecular factors secure the stability of the protein. Interestingly, we detect a clear correlation between the hydration of internal cavities and the protein conformational landscape. The emerging picture is that internal hydration is an effective observable to probe the conformational landscape of proteins. In the specific context of our investigation, the analysis confirms that the hyperthermophilic G-domain is characterized by multiple states and it has a more flexible structure than its mesophilic homologue.

Introduction

Proteins from thermophilic or hyperthermophilic organisms are stable and functional at very high temperatures, up to the boiling point of water. Several molecular factors ensure this extreme stability and their combination results in different thermodynamic strategies for thermal adaptation^1-4. With respect to their mesophilic homologues, (hyper)thermophiles are generally enriched in charged amino-acids and cross-linked by a larger number of hydrogen bonds (HB) and salt-bridges that contribute to stabilize the protein fold^5-7. They have shorter loops that protect the fold from thermal excitation by reducing the extension of weak spots at the protein surface^2-4,8,9. Moreover, an optimized and extended hydrophobic packing in the protein core or at domain interfaces enhances the intramolecular cohesive forces¹⁰.

These factors depend, directly or indirectly, on the coupling between the protein and surrounding water. For example it has been demonstrated that the distribution of charged amino-acids at the protein surface and in contact with water can be effectively optimized to increase thermal stability^11,12. Moreover, the stabilizing contribution of salt-bridges partially buried in the protein matrix depends on the local polarity^5,13,14 while the presence of internal water molecules could alleviate the associated desolvation penalty^15,16. In this regard, it was proposed that (hyper)thermophiles could benefit from dense ion-pairing because of a higher internal dielectric constant¹⁷. Finally, the presence of water molecules inside internal cavities or superficial pockets also improves the molecular packing and extends the HB connectivity with potential effects on local kinetic stability¹⁸. In this regard it is worth noting that many thermophiles are also resistant to high pressure², in fact internal hydration could reduce the volume of internal voids which are thought to trigger pressure unfolding¹⁹ and at the same time make intramolecular HB patterns resistant to temperature and pressure stresses²⁰.

While protein hydration has been the object of intense and debated research^21-25 so far only sporadic investigations tried to link the interactions between protein and water to thermal stability, or to extreme adaptation in general^26-32. In a previous computational study of two homologous G-domains of different stability, it was observed that the thermal stability of the percolating water HB network enveloping the protein surface correlates to the different stabilities of the two molecules²⁷. Due to the different polarities and morphologies, a strong coupling between the protein surface and water was invoked for the hyperthermophilic domain^33,34.

The impact of the surface composition on the organization of the hydration layer was recently highlighted for two orthologous malate dehydrogenase (MDH) proteins, one being halophilic and the other thermophilic and non-halophilic, whose X-ray structures were resolved at high resolution³¹. At cryogenic temperature, the thermophilic MDH was found to be covered by extended networks of water clusters, mostly in pentagonal configurations, and showed a remarkably high level of hydration. These findings are in line with those reported for the hyperthermophilic b-glicosidase protein³⁵ and question the generality of the conclusion from a previous investigation according to which thermophilic proteins are less hydrated²⁶.

On the other hand, as shown in a more recent work on the homologous G-domains²⁹, the dynamics of individual water molecules in the hydration layer was found to be unaffected by the chemical composition of the proteins, since water relaxation mainly depends on an excluded volume effect³⁶. This result, later verified by other examples²⁵, agrees with the results from NMR experiments³² reporting a similar retardation factor for the hydration water of both an halophilic and a non-halophilic peptide of markedly different amino-acid composition.

Hydration dynamics provides only kinetic insights on the protein/water coupling, however an understanding of water’s contribution to protein stability in extreme conditions needs to be quantified from a thermodynamic point of view. For instance, an enhanced structuring of water at the surface of the protein fold could explain the systematic lower heat capacity of unfolding, ΔC_p, measured for (hyper)thermophiles with respect to mesophiles^26,37.

Another interesting question concerns the contribution from buried water to the overall stability gap between homologues. A seminal attempt to shed light on such issue was done by Yin, Hummer and Rasaiah³⁰ who used computational means to estimate the stability of water clusters in the nonpolar cavities of the tetrabrachion protein from the hyperthermophilic Staphylothermus marinus, whose optimal growth temperature is 365 K. This coiled coil assembly, made up of four helices, is characterized by a sequence of cavities located along the protein axis and, according to the crystallographic structure resolved at low temperature (T = 100 K), they are filled by water. Yin and coworkers found that at ambient temperature the largest cavity is preferentially hydrated with clusters comprising 4 to 9 molecules, being a necessary threshold to create a convenient environment for the water HB connectivity^22,38. By increasing temperature, the cavity dehydrates and the drying process marks the onset of denaturation. For a very similar system, the SNARE protein, the presence of internal water is instead destabilizing³⁹. In the very stable neutral variant (melting temperature T_m = 365 K) the four helices are tightly bound and no buried water is visible in the structure even if long residence molecules were detected by molecular dynamics simulations⁴⁰. On the contrary, in the less stable protein from S. cerevisiae (T_m = 328 K) three internal cavities are filled by water and when these cavities are removed by punctual mutations, the stability increases as monitored by a shift of T_m by about 6 K³⁹.

Estimating the increase in stability arising from internal water molecules, by performing single point mutations that promote/inhibit water filled cavities is, however, ambiguous. In fact, the different intramolecular interactions, like the HB propensity and the conformational reorganization, caused by the change of the amino-acid also contribute to the overall thermodynamical shift. In some cases, creating a host environment for water is stabilizing, as reported for BPTI⁴¹, subtilisin⁴², lysozyme⁴³ and lipases¹⁸, but for other proteins the reverse applies, as reported for iso-1-cytochrome⁴⁴, protease⁴⁵ and lysozyme T4 mutants⁴⁶.

Computer simulations, based on modern all-atom force fields, provide a unique tool to explore the specific role of water inside cavities and pockets^22,47-52. Free energy calculations and MD simulations successfully predict the hydration state of pockets of different chemical natures (polar vs nonpolar)^22,50,51,53, help to understand the relation between internal hydration and function as in the case of charge separation processes^54-57, ligand binding^58-60, allostery^61,62 and can be used to estimate the contribution to stability^50,63.

In this work we continue our investigation of the molecular mechanisms at the origin of extreme thermal stability by comparing the behavior of a representative pair of mesophilic/hyperthermophilic homologues: the G-domains of the Elongation Factor thermo unstable (EF-Tu) protein from the mesophilic Escherichia coli bacterium and EF-1α protein from the hyperthermophilic Sulfolobus solfataricus archaeon. The experimental melting temperatures of the two domains differ by about 40 K^64,65 and are qualitatively well reproduced in silico. By using extensive MD simulations at high temperature (T = 360 K) we previously probed the early steps of unfolding of the mesophilic domain. Conversely, in the same timescale and temperature range, the hyperthermophilic protein was found to remain stable⁹. Interestingly, for the folded states at ambient conditions, we noticed an extended hydration of internal cavities within the proteins. Buried water molecules were suggested to play a major role in regulating stability²⁹. Following this idea, we present here a precise study of both proteins’ internal hydration, and determine the contributions to their different stabilities arising from water molecules buried within the two domains.

Methods

System and MD simulations

The G-domain of the mesophilic EF-Tu (E. coli), PDB code 1EFC⁶⁶) and hyperthermophilic EF-1α (Sulfolobus solfataricus, PDB code 1SKQ⁶⁷) proteins were simulated in water solution and at ambient temperature for a time of 0.6 μs for each protein. The mesophilic domain ($\mathcal{M}$, 196 a.a.) was solvated with 7440 and the hyperthermophilic domain ($\mathcal{H}$, 226 a.a.) with 10673 water molecules. Counter-ions were added to neutralize the systems. In order to explore the behavior at high temperature, multiple simulations were carried out at T=360 K, see⁹. In particular, for the mesophilic protein, we collected 10 independent runs of length between 400 ns and 1.5 μs, each probing the early steps of the unfolding. For the hyperthermophilic domain, two independent simulations of 1 μs and 0.7 μs were used to probe its stability at high temperature.

To perform extensive simulations, we employed the NAMD parallel software⁶⁸. The two proteins were modeled using the chamm22⁶⁹ force field and water was represented by the charmm-TIP3P model. The system preparation and simulation protocol are detailed in our previous work^9,27,29.

Hydration dynamics

The exchange dynamics of water molecules between the protein hydration shell and the bulk solution was analyzed by computing the survival probability function N_w(t). To this aim we first defined the hydration shell by detecting water oxygen atoms within 4.5 Å of any heavy atom of the protein. The survival probability N_w(t)^70,71 counts how many water molecules, initially located within the hydration shell, remain in the shell for the subsequent time span t. This is formally defined as:

$$N_w\left(t\right)=\frac{1}{N_t}\sum _{n=1}^{N_t}\sum _j{P}_j(t_n,t).$$ (1)

where the indicator function P_j(t_n, t) takes the value 1 if the j-th water is found continously in the hydration shell between times t_n and t_n + t, or zero otherwise. N_t is the number of simulation time-frames of duration t. By computing N_w(t) we also measured the distribution of the continuous residence times τ_r of water in the hydration shell. Since we are interested in long time behavior, the analysis was performed on reduced trajectories with a time resolution of 20 ps.

Free energy calculations

Free energy differences were computed to estimate the water contribution to protein stability, measured on a limited number of molecules that hydrate the interior of the proteins. These water molecules were extracted from the ensemble of water molecules that were found within the hydration shell with a residence time τ_r > 5 ns. The frequency distributions of the contact of these molecules with individual amino acids of the proteins allowed to detect their most probable locations. Two particularly hydrated cavities were found in each protein. For a short stretch of the trajectory (100 ns), water molecules inside these pockets were ranked depending on their cumulative residence time, and among those having the larger total residence times, we selected a small subset for our calculations. For each selected molecule we extracted three representative configurations separated in time by at least 5 ns one from another. In order to characterize the localization and binding dynamics of the water molecules, Figure S1 of the Supplemental Information (SI) reports the time evolution of distances between water oxygens and a reference atom in each pocket.

For each site, a local hydration free energy, or equivalently, a local excess chemical potential for water was calculated. Starting from each representative configuration, an equilibration step was first conducted in the NPT ensemble. During the equilibration, all protein atoms and the water molecule of interest were restrained around their initial positions by a harmonic potential.

Free energy calculations were carried out following the framework used by Olano and Rick⁵⁰ to study hydration free energy of internal cavities in BPTI and barnase, which we briefly describe below. The excess free energy of hydration is obtained from a virtual thermodynamic cycle and therefore results from two independent components, the free energy required to remove a water molecule from the bulk solution (ΔG_wat) and the free energy required to add the water molecule to the protein cavity (ΔG_prot). Both were estimated via the free energy perturbation (FEP) method⁷².

At first a water molecule in the bulk liquid is decoupled from the rest of the system:

$$(N+1){\mathrm{H}}_2\mathrm{O}\stackrel{\Delta G_{\mathit{wat}}}{\to }N{\mathrm{H}}_2\mathrm{O}+{\mathrm{H}}_2{\mathrm{O}}_{\mathit{ni}}$$ (2)

In the second step, the non-interacting water (H₂O_ni), once localized inside the protein’s empty cavity (EC), is coupled to the rest of the system. This step is then further decomposed into a localization process and a coupling process:

$${\mathrm{H}}_2{\mathrm{O}}_{\mathit{ni}}+\text{protein}\left(\mathrm{EC}\right)\stackrel{\Delta G_{\mathit{loc}}}{\to }\text{protein}\left({\mathrm{H}}_2{\mathrm{O}}_{\mathit{ni}}^{\mathit{loc}}\right)$$ (3)

$$\text{protein}\left({\mathrm{H}}_2{\mathrm{O}}_{\mathit{ni}}^{\mathit{loc}}\right)\stackrel{\Delta G_{\mathit{inter}}}{\to }\text{protein}\left({\mathrm{H}}_2\mathrm{O}\right)$$ (4)

where ${\mathrm{H}}_2{\mathrm{O}}_{\mathit{ni}}^{\mathit{loc}}$ refers to a non-interacting water molecule which is restrained inside the protein cavity. Localization inside the cavity is enforced by a harmonic potential added to the Hamiltonian of the system. This potential confines the motion of the water molecule in its reference site inside the cavity of interest. Since we were interested in calculating the hydration free energy for many sites inside the cavities, we designed an ad hoc strategy to implement the restraint with respect to these positions.

For this purpose, for each internal water we identified the carbon atoms of the protein that, in the equilibrated configuration, lie within 5 Å of the oxygen atom of the water molecule. Among them, all possible combinations of five carbons were considered and the distance d₀ between their center of mass and the oxygen of the water molecule was measured. Finally the combination of the five carbons that produced the shortest distance (usually less than 0.1 Å) was selected. The center of mass of the carbons was then defined as the reference site and used to implement the harmonic restraint, $U_{\mathit{harm}}\left(t\right)=\frac{1}{2}{k}_{\mathit{harm}}{\left(d\right(t\left)\right)}^2$ with d(t) the time-dependent distance between the water oxygen and the carbons’ center of mass (k_harm = 10 kcal/(mol Ų)). The value of the constant was chosen such that it reproduces the fluctuations of the oxygen around the reference site in the unbiased trajectory. This procedure avoids the definition of a static reference point in space and thus the need of fitting the protein structure to a reference configuration during the dynamics⁵⁰.

For the non-interacting molecule the work of localizing due to U_harm is associated to a free energy contribution:

$$\Delta G_{\mathrm{loc}}=-k_{B}T\ln \left[\rho {(2\pi k_{B}T∕k_{\mathit{harm}})}^{3∕2}\right]$$ (5)

where k_B is the Boltzmann’s constant, T the temperature, and ρ the bulk density of water.

The local binding free energy of a water molecule in a given site was calculated by adding all the components:

$$\Delta G=\Delta G_{\mathit{wat}}+\Delta G_{\mathit{prot}}=\Delta G_{\mathit{wat}}+\Delta G_{\mathit{loc}}+\Delta G_{\mathit{inter}}$$ (6)

In our implementation, the free energy ΔG_inter is given by two terms. The first one measures the coupling between the water molecule and the environment in the presence of the harmonic restraint and is calculated using the FEP method as implemented in NAMD, while the second one removes the contribution from the harmonic restraint in the interacting system (see below). A coupling parameter λ taking values in the [0, 1] interval was used to gradually switch off first the electrostatic and then the VdW interactions of the water molecule in the cavity; by this annihilation process we accessed the quantity −ΔG_inter. The FEP procedure consisted of 11 windows along the coupling parameter λ. For each value of λ, the system was equilibrated for 500 ps, then statistics were accumulated for 2 ns. The simulations were performed in the NPT ensemble, and by using the same protocol as in our previous work⁹. In a similar way, we estimated ΔG_wat by simulating a system of pure water of 512 molecules. We obtained ΔG_wat = 6.2 ± 0.1 kcal/mol at T = 300 K, and ΔG_wat = 5.6 ± 0.1 kcal/mol at T = 360 K. While in ref.⁵⁰ the harmonic restraint is progressively removed along the coupling process so as to disappear completely for a fully interacting water molecule, in our implementation this term was removed only in a separate step and its contribution to ΔG_inter was estimated via an independent thermodynamic integration. In this procedure the harmonic constant k_harm was progressively scaled to zero (11 steps), and the free energy contribution of the restraint was evaluated by computing ∫ dk⟨∂U_harm/∂k_harm⟩_k along the path⁷². The ensemble average ⟨…⟩_k was estimated for a given value of the scaled constant k_harm = k.

We also point out that during the annihilation process, when all the interactions between the water molecule and the rest of the system are scaled down, other molecules may overlap with the annihilated one, thus occupying the reference site. In order to avoid artifacts arising from such overlaps, we added a harmonic repulsive wall between the tagged water molecule and those nearby. We verified that without this repulsive wall the overlaps occur rarely and only in the last windows of the FEP decoupling procedure; the effect on the estimated free energy is generally comparable to the statistical error. The harmonic restraint as well as the repulsive wall were implemented using the Collective Variables Module available in NAMD⁷³.

Clustering

In order to correlate the protein conformational fluctuations and the change of the internal hydration we have performed a cluster analysis of the trajectories sampled by the two systems at ambient temperature⁹. For the clustering procedure we used as a collective variable the fraction of native contacts Q defined below.

The number of native contacts $l_i^{\prime }$ for a given C_α site is the number of C_α atoms located within a cut-off distance of 8 Å in the crystallographic structure. Thus, the fraction of native contacts, referring to the whole molecule, is defined as

$$Q\left(t\right)=\frac{1}{N_{C_{\alpha }}}\sum _{i=1}^{N_{C_{\alpha }}}\frac{l_i\left(t\right)}{l_i^{\prime }}$$ (7)

where N_Cα is the number of C_α atoms, having $l_i^{\prime }$ native C_α contacts in the reference state and l_i(t) of them appearing also at time t $\left(l_i\right(t)\le l_i^{\prime })$.

The clustering was done using the well-established leader algorithm⁷⁴ with the following procedure. Each snapshot was represented by a vector of length equal to the number of C_α atoms (N_Cα), whose i–th component of the vector is the quantity $l_i\left(t\right)∕l_i^{\prime }$. Then, the distance between two snapshots was defined as

$$\begin{array}{cc}\hfill d(t,t^{\prime })=& \sqrt{\frac{1}{N_{C_{\alpha }}}\sum _{i=1}^{N_{C_{\alpha }}}{\left(L_i\right(t)-L_i(t^{\prime }\left)\right)}^2},\hfill \\ \hfill \text{with}{L}_i\left(t\right)=& \frac{l_i\left(t\right)}{l_i^{\prime }}\hfill \end{array}$$ (8)

The output of the clustering was mapped onto a network that was drawn with the use of a forced-based algorithm of the Gephi software⁷⁵.

Results

The exchange kinetics of internal water molecules

As a preliminary investigation we detected the water molecules that penetrate the internal cavities of the two proteins. In many crystallographic structures the positions of structural water molecules are resolved together with the protein. In the structure of the whole EF-Tu⁶⁶ and EF-1α⁶⁷ proteins, a few molecules are visible in the interior of each G-domain. However, these structures were resolved in the presence of substrates which possibly make inaccessible alternative sites. Moreover, according to several computational studies^49,51 when the protein is thermalized at ambient conditions locations alternative to the crystallographically determined sites are also sampled.

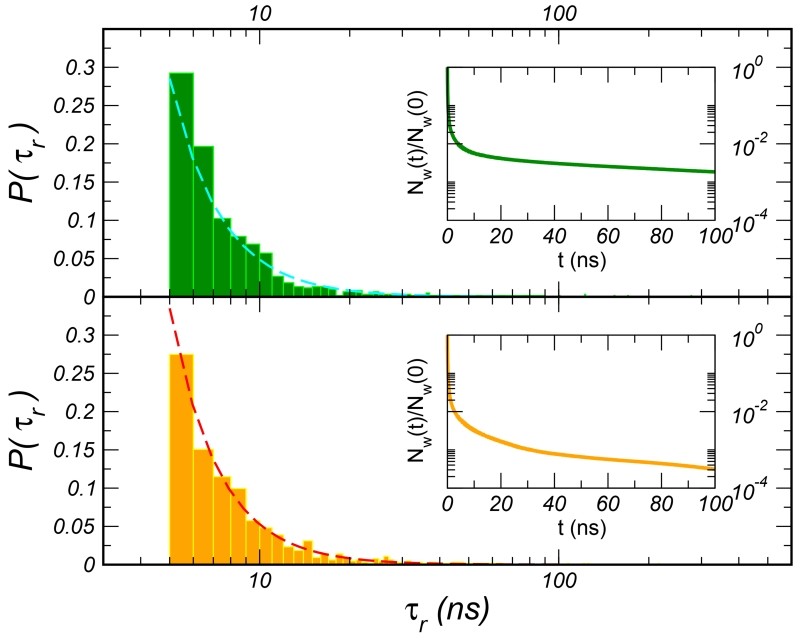
Exchange of these molecules with the external bulk solution occurs, as probed by both NMR^23,76 and simulations^49,77,78, on the nanosecond, or even longer timescale. In this work, we used this lower bound on the exchange time to fully map the solvent accessibility of the proteins’ interior. As already probed for other globular proteins^49,77,78, for these two G-domains, the probability that a water molecule persists in the hydration shell as a function of time, N_w(t), extends with a long tail in the nanoseconds range, as shown in the insets of 1. When performing an exponential fit of this long tail (t> 5 ns) we recover average characteristic times of ⟨τ_slow⟩ 41 ns and 16 ns for $\mathcal{M}$and $\mathcal{H}$, respectively. The dynamics concerns about 1% of the water molecules in the shell, the so-called structural water, mainly buried in internal cavities or superficial clefts. The distributions of the residence times τ_r for this ensemble of molecules is reported in the main plot of 1. The distributions, as commonly observed for other proteins⁷⁷, decay according to a power law, t^−α, with α ~ 2.6. This value is close to what is reported for cytochrome c (2.5)⁷⁷ and to the assumed distribution of reorientational times to interpret NMR experiments⁷⁹. In the simulation of the $\mathcal{M}$domain, one water molecule gets trapped in the protein matrix for about 80% of the simulation time, ~500 ns, causing the longest value of τ_slow for this system. In $\mathcal{H}$the longest residence time is somewhat shorter, ~250 ns.

Internal cavities sampled by water

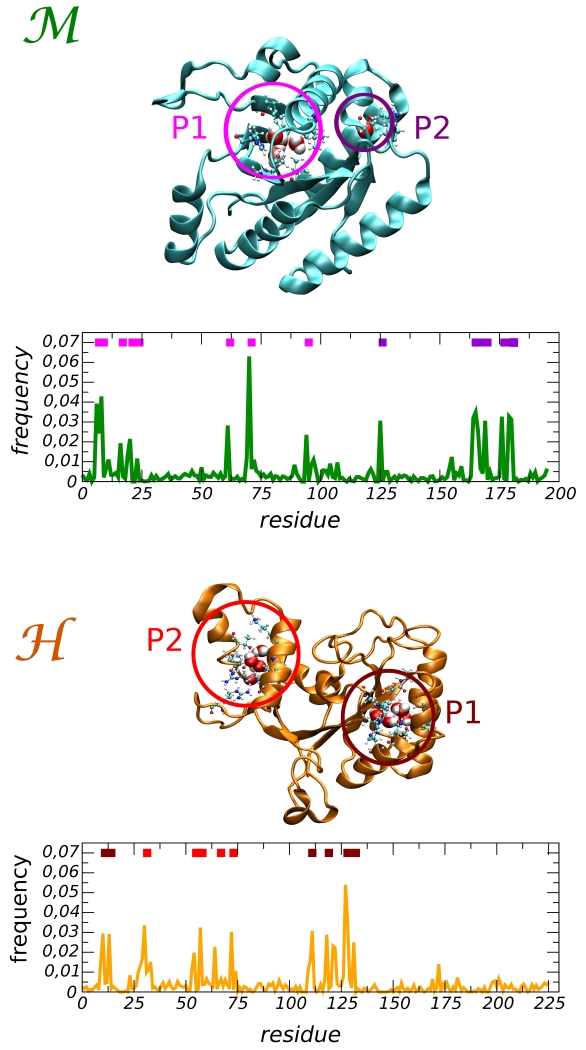
In order to map the internal cavities of the proteins we restricted our attention to those water molecules that have a residence time τ_r longer than 5 ns. The frequency distribution of their positions along the protein sequence is reported in 2. Two main pockets are found in each system, and their locations are indicated by the colored bars at the top of the x-axis. In the mesophilic domain the largest pocket, marked by the magenta bars, is located in the protein core. There a cluster of molecules is confined by a hydrophobic wall and a polar surface that offers several anchoring sites for hydrogen bonds. The pocket is accessible via a gateway near the P loop, a key region in the GTP binding site. Around this opening two buried water molecules are visible in the X-ray structure, see SI Table S1. The second pocket (violet bars) hosts a single isolated molecule. In our simulation, a single molecule penetrates into this pocket after about 100 ns, and gets trapped for the remainder of the simulation time. The water is caged by three hydrogen bonds formed with the residues S166 (backbone CO and NH groups) and W177 (backbone CO group). Interestingly, the observed binding matches the location of a structural water visible in the X-ray structure (SI Table S1).

In the hyperthermophilic protein, both pockets are filled with clusters of molecules. The first pocket (maroon bars) is found in proximity of the P loop. A portion of the pocket’s surface offers several HB pinning sites, mainly backbone groups, while the other part has a hydrophobic character. In the crystallographic structure three molecules are resolved in this pocket, see Supplemental Information Table S1. The second pocket (red bars) is created by a structural specific motif of the $\mathcal{H}$protein: the two small helices α¹ [E32-L45] and α² [E48-E63]. In our previous investigation we have shown that these structures confer stability to this region of the protein and prevent the local unfolding at high temperature that instead occurs in the $\mathcal{M}$domain⁹. The walls of this cavity are cross linked by ionic interactions, i.e. the highly stable ion-pairs R65-D31 and R58-E62, and these charged amino-acids create a highly polar environment. The fluctuations of these links are mediated by the presence of water that can form molecular bridges between the ionic groups (SI Table S3). We stress that in our simulations the ionic groups were all considered charged, however it is widely accepted that it is quite difficult to determine the protonation state of such buried charged groups, that in principle could also be influenced by the presence of water.

Local hydration free energies

We now discuss the contribution to protein stability stemming from these hydrated cavities. From the ensemble of long residence water molecules, we singled out a restricted set of molecules representative of the cavity hydration and with the longest residence times (τ_r > 15 ns). For practical reasons, this filtering was done considering a short stretch of the trajectory (100 ns). For each one of these molecules three different configurations, A, B, and C, separated from each other by at least 5 ns, were extracted from the trajectory and used to initiate the free energy calculations. This large ensemble allows to estimate the variability induced by the presence of multiple states of the pockets’ hydration, including i) changes in the internal location of the water molecule, ii) changes of the shape of the hosting cavity, and iii) long range effects due to the global fluctuations of the protein. The values of the hydration free energy, $\Delta G_i^k$, and of the associated statistical error, are reported in Supplementary Tables S4 and S5 for all the pockets and conformers of the $\mathcal{M}$and $\mathcal{H}$domains, respectively.

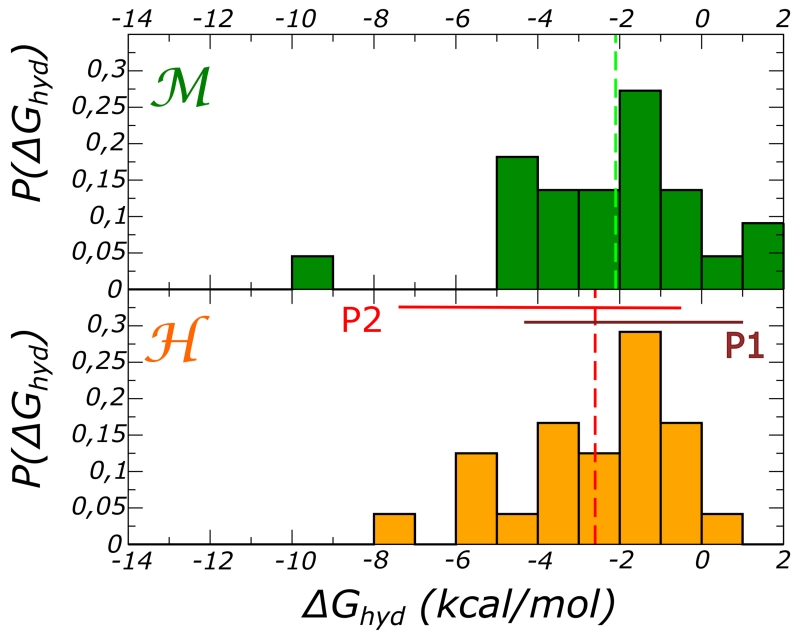
First we note that the hydration free energy is favorable for almost all the selected internal locations. However, we also remark the large variability of the $\Delta G_i^k$, with a single molecule experiencing different favorable interactions during its confinement in the pocket. This variability can be as high as 4 kcal/mol. In both proteins, some locations provide large contributions to protein stability, for instance −9.0 ± 0.3 ($\mathcal{M},{\mathrm{w}}_1^{P2}$) and −7.0 ± 0.3 kcal/mol ($\mathcal{H},{\mathrm{w}}_3^{P2}$). In both these cases, we observe high HB connectivity and strong packing (see data in SI Tables S2 and S3). When focusing on the average value associated to each pocket, we obtain ⟨ΔG_i⟩^P1 = −1.6 ± 0.3 and ⟨ΔG_i⟩^P2 = −5.5 ± 0.4 kcal/mol for the $\mathcal{M}$domain and ⟨ΔG_i⟩^P1 = −1.5 ± 0.3 and ⟨ΔG_i⟩^P2 = −3.6 ± 0.5 kcal/mol for the $\mathcal{H}$domain. The values are close to previous estimates of the insertion free energy for water into the cavities of other proteins as the bacteriorhodopsin⁴⁸, BPTI⁵⁰, and kinase A⁸⁰.

The distribution of the free energies are plotted in 3. The vertical lines indicate the averages, ⟨ΔG_i⟩ = −2.1 ± 0.3 kcal/mol and ⟨ΔG_i⟩ = −2.6 ± 0.4 kcal/mol for $\mathcal{M}$and $\mathcal{H}$, respectively. For the $\mathcal{M}$domain the distribution is shaped by the contributions from water hydrating the larger pocket (P2), on the contrary for the $\mathcal{H}$protein, the distribution reflects the different contribution from the two pockets.

The calculated $\Delta G_i^k$ is the free energy contribution to the protein’s stability from a single buried molecule localized in a specific site i and calculated for different states k of the local environment, including the presence of surrounding water molecules having different residence times. According to the analysis presented in^48,53, our values correspond to the insertion free energy of a molecule in the presence of n − 1 others. The ensemble of conformers Aⁱ, Bⁱ, Cⁱ helps us to sample several initial conditions of the hydrated cavities, i.e. different values of n − 1 (see SI Tables S2 and S3).

Global free energy of internal hydration

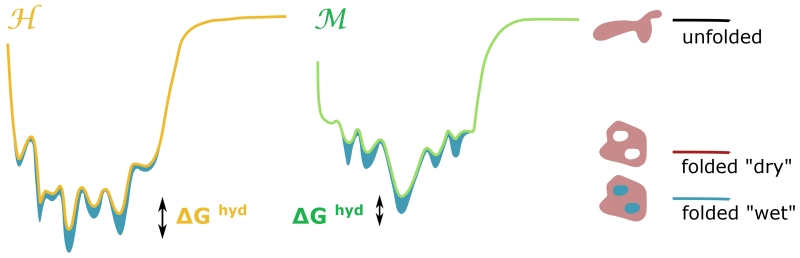
As discussed earlier, both proteins host several long residence water molecules at the same time. Therefore, in order to evaluate the total stabilization due to internal water molecules, we need to estimate their cumulative contribution, as represented schematically in 4. Hence, we determine a global free energy of internal hydration for both proteins based on our local estimates of water binding free energy.

For a given starting configuration k, the calculations described above provide local hydration free energies $\Delta G_i^k$ for each of 8 identified binding sites. Stability of an internal water molecule depends on many degrees of freedom, belonging to the protein as well as neighboring water. Direct calculation of well-converged free energy estimates could therefore be prohibitively long. We choose to obtain each binding free energy by combining data from three independent, local simulations (starting from different configurations). Each simulation is considered to sample one representative region of phase space, hence, their results are combined as if merging samples within the exponential average of FEP:

$$\exp (-\beta \Delta G_i)=\frac{1}{3}\sum _{k=1}^3\exp (-\beta \Delta G_i^k)$$ (9)

We assume additivity, meaning that the global free energy of internal hydration is estimated as the sum of local free energies weighted by the occupancy n_i of each site:

$$\Delta G_{\mathit{hyd}}=\sum _{i=1}^8-\frac{n_i}{\beta }\log \left(\frac{1}{3}\sum _{k=1}^3\exp (-\beta \Delta G_i^k)\right)$$ (10)

In turn, the mean occupancy of each site is obtained from the binding free energies as:

$$n_i=\frac{C}{1+\exp \left(\beta \Delta G_i\right)}$$ (11)

C is a factor common to all sites in one protein, and is fitted so that the total predicted occupancy matches the average number of bound water molecules measured in long simulations, in other words:

$$\sum _{i=1}^8{n}_i=\langle n_w\rangle$$ (12)

We find the optimal value of C to be 0.6 for both the mesophile and thermophile.

The term n_w can be calculated by scanning the trajectories and counting how many long-residence molecules are present at the same time in the interior of the proteins. Considering the molecules with residence time τ_r > 15 ns we obtain ⟨n_w⟩ = 4.7 for both proteins and for a less strict condition (τ_r > 5 ns) ⟨n_w⟩ = 9.8 and ⟨n_w⟩ = 10.4 for the $\mathcal{M}$and $\mathcal{H}$proteins, respectively.

Within this framework and counting ⟨n_w⟩ with the stricter condition (τ_r > 15 ns), we find ΔG_hyd = −15.7 ± 0.5 kcal/mol for the mesophile, and −17.0 ± 0.6 kcal/mol for the hyperthermophile, meaning that the relative stabilization of the $\mathcal{H}$protein with respect to $\mathcal{M}$by internal hydration is ΔΔG_hyd = 1.3 ± 0.5 kcal/mol. By releasing condition (12) on the total occupancy, the relative stabilisation of the $\mathcal{H}$protein with respect to $\mathcal{M}$is slightly larger, ΔΔG_hyd = 2.5 ± 0.9 kcal/mol. The same numerical results are obtained with an alternative formulation of the problem that we report in SI. The obtained value for the relative stability ΔΔG_hyd is a small but statistically meaningful number, and its possible effect on protein thermal stability is discussed below.

Unfortunately, for our EF-Tu and −1α G-domains, no thermodynamic values are available for the unfolding free energy ΔG^unf(T). The magnitude of the stability gap between homologues, i.e. ΔΔG^unf(T) at ambient conditions, can vary substantially depending on the pair. In some cases this gap can be as high as 20 kcal/mol but for many pairs its just on the order of a few kcal/mol^81,82. In order to quantify the possible effect of the stability gain due to the internal hydration (ΔΔG_hyd) we have considered two model systems. The first one is represented by a pair of homologues close to our proteins, namely the EF-1α from rabbit (mesophile) and from the thermophilic bacterium T. thermophilus⁸³. The second is a pair of mesophilic/hyperthermophilic proteins belonging to CheY family. For these pairs the available thermodynamic data^83,84 allow to estimate the unfolding free energy as a function of temperature and hence construct the stability curve, ΔG^unf(T). For each protein we upshifted the stability curve by ΔΔG_hyd = 1.3 kcal/mol (see above) and as expected the melting temperature of the proteins increases, ΔT_m is about 6 K. Depending on the value of the specific heat of unfolding $\Delta C_p^{\mathit{unf}}$, that controls the curvature of the stability curve, the shift of the melting temperature could be even larger. Thus, even a small contribution as that arising from internal hydration can result in an enhanced thermal stability. The details of this qualitative modelling are provided in SI, see Fig. S.3.

Alternative strategies to estimate the free energy contribution to stability stemming from the hydration of large cavities have been presented before and reporting for non-polar cavities and channels cooperative effects^22,48,53. For example in hydrophobic pockets of large volumes favorable hydration is found to take place only above a given threshold: about 4/5 water molecules should be hosted to compensate the loss of HBs due to the cavity nature²². Still, for cavities offering HB acceptor/donor sites, the size and cooperative effects are expected to be less important; for example in the case of a protein kinase, the progressive hydration of an internal cavity is associated to a stable free energy contribution of about −3 to −2 kcal/mol per added molecule⁸⁰. A detailed analysis of the problem is reserved for future work. Obviously, our conclusions also depend on the reconstructed distributions p(ΔG_i), here assumed to be representative of the cavities’ hydration, and on the residence time threshold used to determine the number of buried water molecules, ⟨n_w⟩.

While hereby we have considered only the contribution from internal hydration, we stress that a more complete view of the role of hydration on protein thermal stability would require to account for the changes in the solvatation of the external surface as well. This can be only approached using specific modelling techniques, as those explored recently by Harano⁸⁵ and Ham⁸⁶.

Hydration and global protein flexibility

The number of internal waters fluctuates over time and the penetration/escape dynamics correlates with the breathing soft-modes of the protein that visits different conformational states^78,87. For our proteins, the fluctuations are rather high (~ 40%) and have characteristic oscillation period ranging from tenths to one hundred nanoseconds. As a consequence the internal water contribution to protein stability varies substantially with the proteins’ conformational fluctuations.

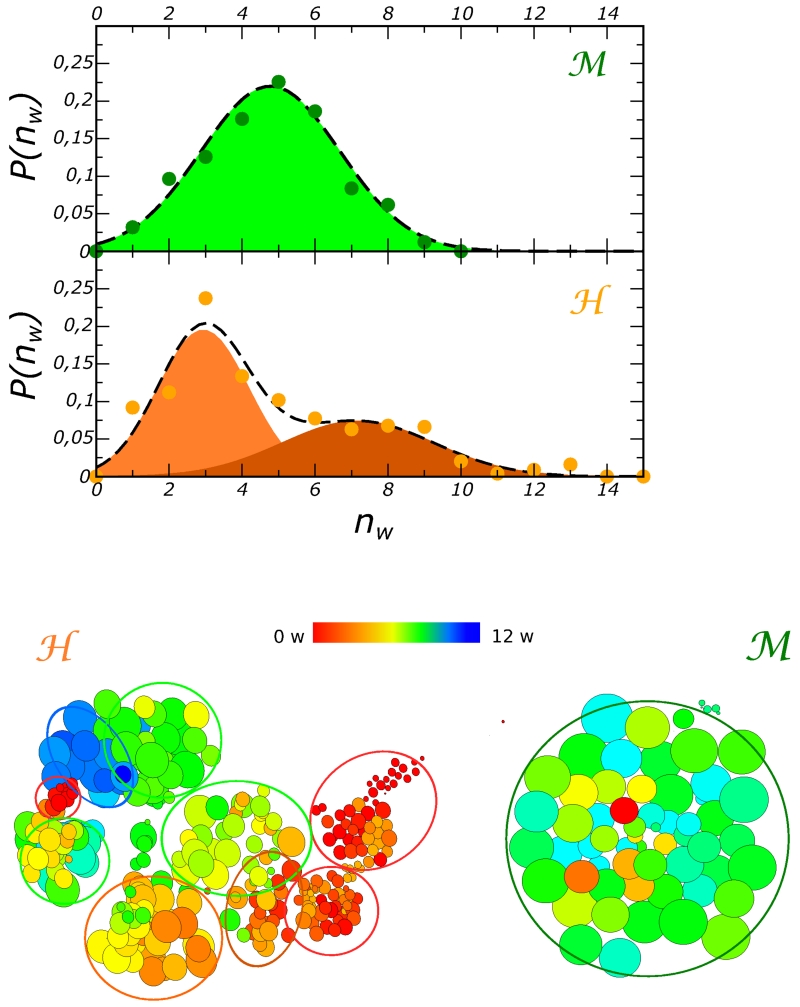
The distribution of the number of long residence water molecule p(n_w), is reported in 5 (top panel) for the residence time threshold τ_r > 15 ns. While for the $\mathcal{M}$domain the fluctuations of n_w produce an unimodal distribution, for $\mathcal{H}$the distribution is bi-modal. This two-state regime relates to the simultaneous hydration dynamics of the two cavities P1 and P2, while in $\mathcal{M}$only the hydration of pocket P2 varies substantially in time. Interestingly, we note that despite the qualitative differences, the hydrations dynamics of the internal cavities result in very similar overall compressibilities of the two proteins⁹, β_a ≃ 9 · 10⁻⁵ MPa⁻¹. Hence, internal hydration has similar effects on the global flexibility of the two proteins.

In the bottom panel of the figure we provide a more direct mapping of the internal hydration on the conformational landscape, represented as a network of states. In the specific case the network is obtained by clustering the trajectories and using the native contacts order parameter, Q⁹. The details of the calculation are provided in section Method. The size of each cluster is proportional to its occupation and the color scale reflects the average number of long residence water molecules computed for the configurations in each cluster.

For the $\mathcal{H}$domain, two zones of different color appear well separated kinetically; we do also note, however, that some basins that have similar Q values with rather different internal hydration are kinetically connected. For the mesophilic $\mathcal{M}$protein, the unimodal distribution of the internal hydration correlates with a compact conformational landscape. The correlation between the fluctuations of the internal hydration and the presence of multiple conformational states measured by conformational order parameters, such as the native contacts Q, supports the notion proposed some years ago⁷⁶, that the exchange dynamics of internal hydration could be used to probe roughness of the conformational landscape of proteins.

This gives quantitative support to the qualitative sketch of 4, where the free energy landscape of the protein is projected along a generic conformation reaction coordinate. The filled blue zones represent the internal water free energy contribution to stability as it varies along the conformational landscape of the folded state. The thermophile exhibits a broader variety of internal hydration states, some of which confer it additional stability. The tool we have used to investigate the correlation among the dynamics of internal hydration and the protein conformational landscape could result effective to explore the mechanism of unfolding caused by high temperature or pressure and to characterise the kinetic heterogeneity of these processes that have been related to a different transient hydration of internal cavities⁸⁸.

Stability at high temperature

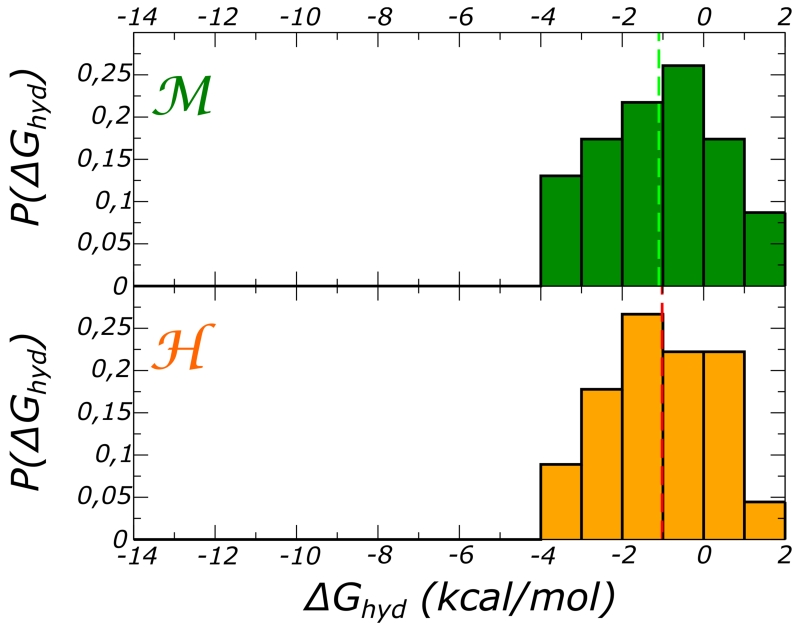
We address here the key issue of high temperature stability. For the same set of water molecules we evaluated the hydration free energy at T = 360 K. The calculations were performed starting from the same protein configurations used at T = 300 K, thus we assumed that the temperature excitation does not distort these representative conformations of the folded state. At high temperature, water binding free energy decreases substantially for most sites, in both proteins; water transfer into some of the protein sites is even unfavorable (6). As a result, there is no significant difference in overall free energy of internal hydration, yielding no clear contribution to the stability gap. The average ⟨ΔG_i⟩ is −1.8 and −1.6 kcal/mol, for $\mathcal{M}$and $\mathcal{H}$. A comparable decrease of the favorable hydration was reported also for nonpolar cavities, and in a less extended temperature window for the favorable hydration of BPTI cavity⁵⁰.

In the high temperature regime, it is difficult to estimate the overall contribution from internal water to the stability gap between the two proteins because the mesophilic homologue starts to unfold. The early step of unfolding was monitored in a set of independent simulations and occurred within a characteristic time of 100 to 300 ns⁹. We have estimated the number of long residence waters residing simultaneously in the protein matrix for each of these runs by restraining the calculation to the part of the trajectory before the unfolding event. For the hyperthermophilic domain two simulations of length 0.7 and 1 μs were used. Using a strict threshold (τ_r > 9.6 ns) we obtain ⟨n_w⟩ = 2.6 and ⟨n_w⟩ = 2 for $\mathcal{M}$and $\mathcal{H}$, respectively while for a less strict one (τ_r > 3.8 ns), the numbers are ⟨n_w⟩=3.6 vs ⟨n_w⟩ = 4.6 for $\mathcal{M}$and $\mathcal{H}$, respectively ¹. When estimating the ΔG_hyd via eq. 10 the contribution of internal hydration to the different stabilities (ΔΔG_hyd) can be negligible (0.7 kcal/mol) or even in favour of the mesophile (1.7 kcal/mol) depending on the values of ⟨n_w⟩. Therefore our results are not conclusive and not robust for this high temperature regime.

Alternatively, one could investigate the contribution of internal water hydrating the cavity P2 to the kinetic stability of the specific region α¹ [E32-L45] and α² [E48-E63] of the $\mathcal{H}$domain. Here, water could link these key secondary structures and indirectly favor the stability of the local ion-pairs. On the other hand, in the mesophilic homologue $\mathcal{M}$, the similar region represents the weakest point of the protein structure where unfolding early steps take place⁹. How transient internal hydration couples to the unfolding of this region and the associated kinetic barriers will be the object of a separate investigation.

Conclusion

In this work we investigated the internal hydration of two homologous proteins and estimated its contribution to the proteins’ different thermal stabilities. Namely, we compared the mesophilic EF-Tu and the hyperthermophilic EF-1α G-domains. Two internal cavities were found to be hydrated in both systems. The location of one of them is common for the two domains with an access near the P-loop at the catalytic site. The other ones are peripheral and domain specific.

In both systems, the per molecule hydration free energy was found to be favorable for all the sites and the protein configurations.

At ambient conditions, the free energy of internal hydration for the hyperthermophilic domain is more favorable than for the mesophilic one by 1.3 kcal/mol, and resulting in a sizeable contribution to the stability gap. At the high working temperature of the hyperthermophile (T = 365 K), the internal hydration free energy is systematically less favorable when compared to ambient condition, giving probably a negligible contribution to the stability gap between the two systems.

We also found a very clear correlation between the conformational fluctuations of the proteins, represented as a connected network of conformational states, and the fluctuations of the number of the long residence waters wetting the interior of the proteins. While the mesophilic protein is characterized by unimodal fluctuations around a single conformational or hydration state, the hyperthermophilic domain visits multiple states for both the protein conformation and the internal hydration. Again, this finding questions the general notion according to which thermophilic proteins are more rigid objects than their mesophilic counterparts.

Our investigation shows that thermal stabilization can be made possible by enhanced internal hydration. However, the thermodynamic gain results from different factors, such as the overall number of structural water and how the local internal polarity is configured. By in silico approaches one can envision a way to enhance thermal stability by using internal hydration and by targeting such factors selectively. One strategy is to tune the internal polarity of a cavity so as to increase the free energy gain. Alternatively, de novo new cavities can be created, possibly by creating pockets near the protein surface, to increase the number of structural waters that contribute to stability. Internal hydration can also be used to kinetically stabilize specific regions of the protein. However, it must be pointed out that the creation of cavities and their hydrated or dry states can result in a complex thermodynamic and kinetic response of the proteins, as pointed out in the context of pressure induced unfolding^19,88. Moreover, these changes however must be effective in a broad range of temperatures. A more systematic investigation on the internal and the total hydration of homologues of different protein families is reserved for future work and can benefit from recent methodological development for treating solvation contribution to protein stability^85,86.

Figure 1.

Frequency distribution of the long residence times τ_r for the $\mathcal{M}$(top) and $\mathcal{H}$(bottom) proteins along with the power-law fits (dashed lines). In the figure insets, the fraction of water molecules that continuously stay in the hydration shell as a function of time are plotted.

Figure 2.

Frequency distribution of long residence water molecules in the protein matrix for the $\mathcal{M}$(top) and the $\mathcal{H}$(bottom) domains. Two pockets are distinguished for each protein and indicated by the colored bars within the graphs. Their location in the 3D protein structure is shown at the top of each graph.

Figure 3.

Frequency distribution of the hydration free energy calculated from representative molecules hydrating the internal cavities of $\mathcal{M}$(top) and the $\mathcal{H}$(bottom) domains. The calculations were performed at T = 300 K. The vertical lines indicate the average value ⟨ΔG_i⟩.

Figure 4.

Schematic view of the contribution from internal water to protein stability (blue zone) as a function of a generic conformational coordinate. The free energy landscape associated with the most stable $\mathcal{H}$protein is represented in yellow, while that associated with the less stable $\mathcal{M}$protein is represented in green. We assume that the unfolding free energy is decomposed in two terms, one that measures the difference between the unfolded and “dry” folded state (with the internal cavities dehydrated), and another term (blue filled zone) that measures the gain from internal hydration of the cavities. The free energy gap between the two proteins then contains a contribution from the difference in internal hydration free energy, ΔΔG_hyd.

Figure 5.

Top panel. Frequency distribution of the number of long-residence water simultaneously located inside the protein matrix, n_w. For this plot the residence time threshold is τ_c > 15 ns. The colored zones represent the area underneath the Gaussian functions fitting the distributions.

Bottom panel. Network representation of the conformational landscapes sampled by the two proteins. The network is obtained by clustering the MD trajectories and using the native contacts order parameter Q. The color map represents the hydration states of internal sites, red indicates fully dehydration, while blue indicates maximal internal hydration.

Figure 6.

Frequency distribution of the hydration free energy at T=360 K calculated for the same set of water molecules used in 3. The top panel refers to $\mathcal{M}$; the bottom one, to the $\mathcal{H}$domain.