Frequency swept microwaves for hyperfine decoupling and time domain dynamic nuclear polarization

Abstract

Hyperfine decoupling and pulsed dynamic nuclear polarization (DNP) are promising techniques to improve high field DNP NMR. We explore experimental and theoretical considerations to implement them with magic angle spinning (MAS). Microwave field simulations using the high frequency structural simulator (HFSS) software suite are performed to characterize the inhomogeneous phase independent microwave field throughout a 198 GHz MAS DNP probe. Our calculations show that a microwave power input of 17 W is required to generate an average EPR nutation frequency of 0.84 MHz. We also present a detailed calculation of microwave heating from the HFSS parameters and find that 7.1% of the incident microwave power contributes to dielectric sample heating. Voltage tunable gyrotron oscillators are proposed as a class of frequency agile microwave sources to generate microwave frequency sweeps required for the frequency modulated cross effect, electron spin inversions, and hyperfine decoupling. Electron spin inversions of stable organic radicals are simulated with SPINEVOLUTION using the inhomogeneous microwave fields calculated by HFSS. We calculate an electron spin inversion efficiency of 56% at a spinning frequency of 5 kHz. Finally, we demonstrate gyrotron acceleration potentials required to generate swept microwave frequency profiles for the frequency modulated cross effect and electron spin inversions.

1. Introduction

Dynamic nuclear polarization (DNP) increases NMR sensitivity by transferring polarization from electron to nuclear spins [1]. In a series of seminal papers published in the early 1990's, Jacob Schaefer and his colleagues applied DNP to magic angle spinning (MAS) NMR experiments of polystyrene samples doped with stable organic radicals [2–4]. In the years since Schaefer's first experiments, MAS DNP has exploded in popularity [5–10]. Gains in NMR sensitivity from MAS DNP are approaching the theoretical limit of 660, which is determined by the gyromagnetic ratios of electron and proton spins [11–13]. Developments in high-power microwave sources and MAS DNP probe technology by Griffin and his colleagues at M.I.T. have played a critical role in the extension of DNP from field strengths of 1.4 T employed in Schaefer's original MAS DNP to experiments at 18.7 T [14–17]. Further advances in instrumentation are required to implement pulsed DNP and hyperfine decoupling schemes.

Pulsed techniques yield significant advantages over continuous wave irradiation to control and measure interactions in the solid state NMR Hamiltonian. As Schaefer demonstrated in his development of double resonance MAS NMR, short, powerful pulses permit the measurement of weak heteronuclear dipolar couplings (REDOR) [18], and also polarization transfer through weak dipolar couplings (TEDOR) [19]. Pulsed EPR techniques are also advantageous for DNP.

Performing high field DNP in the time domain can substantially improve electron to nuclear polarization transfer [20,21]. For example, modulation of the microwave frequency to increase the effective irradiation bandwidth improves DNP enhancements in cryogenic non-spinning experiments [22,23]. Time domain DNP also yields much higher enhancements for non-cryogenic NMR. The integrated solid effect (ISE) and nuclear orientation via electron spin locking (NOVEL) are pulsed DNP experiments that yield high signal enhancements at room temperature [24–29]. However, most time domain DNP experiments have only been demonstrated at lower frequencies (~9 GHz) where intense microwave fields are readily available. Extending pulsed DNP techniques to high frequency MAS NMR requires further microwave technology development.

Another analogy between Schaefer's pioneering experiments in MAS NMR and current developments in DNP is the decoupling of spins with a larger magnetic moment after the polarization transfer period. Proton decoupling after cross polarization (CP) is often critical to extending the relaxation time of the observed nuclei and providing high-resolution NMR spectra, as was demonstrated in Schaefer's original CPMAS experiments [30]. Paramagnetic relaxation effects (PREs) in MAS DNP experiments [31,32] could be similarly attenuated with electron decoupling after the DNP period, as proposed by Corzilius et al. [33].

Electron decoupling, also known as hyperfine decoupling and dynamic decoupling, was introduced by Jeschke and Schweiger in the context of pulsed EPR [34] and has been applied extensively to lengthen EPR relaxation times in nitrogen vacancy (NV) centers for experiments aimed at quantum computation [35,36]. In addition to improving spectral resolution and extending nuclear relaxation times, electron decoupling in MAS DNP could also improve the polarization enhancement of bulk spins by yielding control of the spin diffusion barrier. The spin diffusion barrier impedes the spread of enhanced proton polarization around the DNP polarizing agent [37,38]. Protons with strong hyperfine couplings could first be polarized through DNP, followed by an electron decoupling period during which the hyperfine couplings are attenuated and the polarized protons are brought into spin diffusion contact with bulk protons.

We discuss in the following sections how voltage tunable gyrotron oscillators could generate the microwave frequency profiles required for the inversion of electron spins and thus decoupling of hyperfine interactions. In particular, we show that EPR inversions are theoretically possible even with the inhomogeneous microwave field present within MAS rotors, and perform detailed electromagnetic simulations to characterize the microwave field intensity in a MAS DNP probe operating at 198 GHz. We also demonstrate modulations of the gyrotron acceleration potential suitable for the frequency modulated cross effect and electron spin inversions.

2. Microwave field calculations

We used Ansys HFSS (high frequency structural simulator) to calculate the 198 GHz electromagnetic field structure within our custom MAS DNP probe [39]. By solving for the phase independent field intensities, we are able to determine the dielectric sample heating and inhomogeneous _γSB_1S frequencies, where B_1S represents the microwave field orthogonal to the main magnetic field.

2.1. Microwave simulation geometry and parameters

We calculated the electromagnetic field structure for the sample geometry shown in Fig. 1a. Inside the stator is a 5-turn RF coil with a wire diameter of 0.686 mm. The rotor sheath is a sapphire cylinder with an outside diameter of 3.175 mm and has a wall thickness of 0.55 mm. Further details of the model geometry are given in the supplementary information. We assumed that all microwave power leaving the volume shown in Fig. 1a was lost to its surroundings. Our simulation models the sample as a frozen glycerol and water mixture. We simulate the effect of the sample on the 198 GHz field structure by setting the real part of the dielectric constant $\left({\epsilon }_r^{\prime }\right)$ to 3.5 and the loss tangent to 0.007, as previously determined by Nanni et al. [39]. The relative dielectric constant is defined as:

$${\epsilon }_r=\frac{{\epsilon }^{\prime }+i{\epsilon }^{\prime \prime }}{{\epsilon }_0}$$ (1)

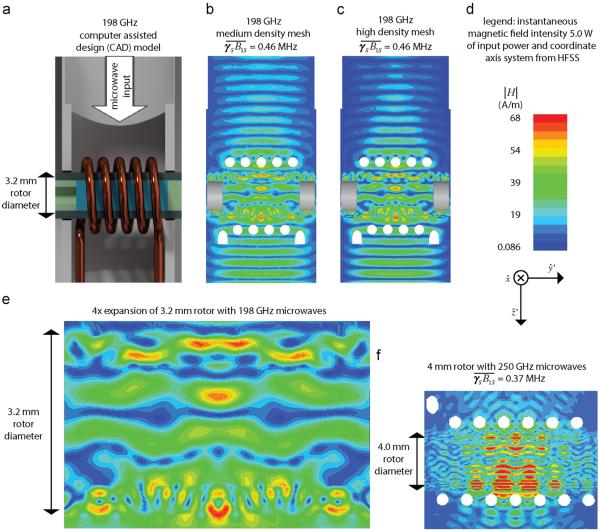
Fig. 1.

Simulations of the instantaneous magnetic field magnitude in the y′–z′ plane. These intensities are not representative of the _γSB_1S inhomogeneity as they are dependent on time. (a) A computer assisted design (CAD) representation of our MAS DNP probe. (b) A simulation with a Gaussian beam incident on the sample. The mesh in this simulation has 15,000 tetrahedra within the sample volume. (c) The same simulation as (b) but with a higher mesh of 48,000 tetrahedra in the sample. The microwave distribution is almost identical, suggesting the calculation has converged with respect to tetrahedral density within the mesh. (d) A scale with the magnetic field magnitude normalized to 5 W of input power. (e) An expansion of the simulation of (c) shows considerable fine structure within the sapphire. (f) Simulation of a 250 GHz microwave field structure on the model geometry given in Nanni et al. [39]. The qualitative structures are very similar to Nanni et al. The mesh in the simulation shown above has 94,000 tetrahedra in the sample volume.

Our simulations are normalized to microwave power levels we expect to achieve with our custom 198 GHz voltage tunable gyrotron, designed in collaboration with Bridge12 Technologies (Waltham, MA). We modeled the microwave input into the stator as a pure Gaussian beam with a waist of 3.175 mm and power of 5.0 W.

2.2. Calculation of _γSB_1S

HFSS solves the electromagnetic field structure with an initial excitation amplitude of |E₀|. Only the initial electric field magnitude, |E₀|, needs to be given because the magnetic component, |H₀|, is proportional and orthogonal to |E₀| for an electromagnetic wave traveling in free space. We calculated the initial electric field magnitude for our Gaussian beam propagating in free space and carrying 5 W of power (see Supplementary information):

$$\mid E_0\mid =\sqrt{\frac{4P_0}{\pi {\epsilon }_{0}c{w}_0^2}}=15,425\mathrm{V}∕\mathrm{m}$$ (2)

where ε₀ is the permittivity of free space, c is the speed of light, and w₀ = 3.175 mm is the beam waist of the Gaussian beam entering the stator.

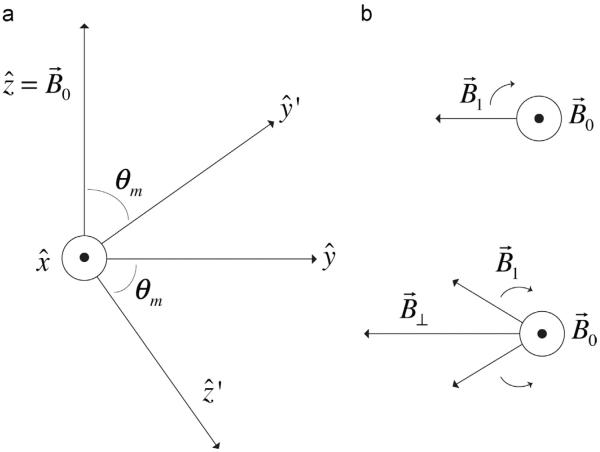
To determine the _γSB_1S within a specified volume, we first calculate the magnitude of the transverse components of the electromagnetic field. However, the HFSS calculation is not performed in the laboratory frame. We must account for this rotation of the HFSS coordinate axis from the laboratory frame to determine the magnitude of the magnetic field components orthogonal to the static field B₀ that contribute to the _γSB_1S. Referring to Fig. 2a we see that in the primed coordinate frame (HFSS simulation axis):

$$\widehat{y}=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill \sin \left({\theta }_m\right)\hfill \\ \hfill \cos \left({\theta }_m\right)\hfill \end{array}\right)$$ (3)

Fig. 2.

(a) Coordinate axis of simulation relative to the main magnetic field. $\widehat{z}$ is the incident axis of the Gaussian beam in the simulation, $\widehat{y}$. is the rotor axis and θ_m = 54.74°. (b) Decomposition of a linearly polarized magnetic vector into two oppositely rotating vectors with 1/2 the magnitude.

${\widehat{x}}^{\prime }=-\widehat{x}$, and θ_m is the magic angle. Note that ${\widehat{z}}^{\prime }$ is the incident axis of the Gaussian beam and ${\widehat{y}}^{\prime }$ is the long rotor axis of the sample (see Fig. 2a).

We define the physically significant quantity for EPR and DNP to be the volume average of the peak transverse magnetic field similar to the treatment in Macor et al. [40]:

$$\langle B_{\perp }\rangle =\frac{1}{V}{\int }_V\mid {\mathbf{B}}_{\perp }\mid dV=\frac{\mu }{V}{\int }_V\sqrt{{\mid \mathbf{H}\cdot \widehat{x}\mid }^2+{\mid \mathbf{H}\cdot \widehat{y}\mid }^2}dV$$ (4)

Note, this differs slightly from the procedure outlined in Nanni et al. in which the volume root mean square (RMS) is computed [39].

We also assume μ is constant throughout the entire sample and is approximated by the permeability of free space, μ₀ = 1.257 × 10⁻⁶ H/m. The permeability, μ, is a measure of the response of the material to an applied magnetic field in the similar way that the dielectric constant, ε, is the response of a material to an applied electric field. The detailed calculations including all numerical values and screen-shots from HFSS are given in the supplementary information.

When we integrate over the entire sample volume of 18.6 μL we find that 5.0 W of power gives an average γ_SB_1S of 0.46 MHz. 17 W of input power into the stator is required to generate the average γ_SB_1S of 0.84 MHz which is now commonly used in theoretical treatments of MAS DNP [41,42].

2.3. Consideration of linear vs. circularly polarized light

The microwave beam emitted from gyrotrons is linearly polarized, however electron spins only strongly interact with circularly polarized light. We can decompose the linearly oscillating field into two circularly polarized components that each have half the amplitude of the original beam as shown in Fig. 2b. The component rotating with the spins contributes to the nutation; the other can be neglected. This means that the average B_1S over the sample given is B_⊥/2. It should be noted that if B_⊥ is given as the RMS, B_⊥,RMS of a linearly oscillating field then, $B_{1S}=B_{\perp ,\mathit{RMS}}∕\sqrt{2}$. This is the treatment given in Nanni et al. [39] and Macor et al. [40].

2.4. Calculating dielectric sample heating

A concern often voiced about MAS DNP using high power microwaves is heating of the sample. This has already been calculated from similar electromagnetic field simulations [39,40]. For dielectric heating the generated power density per volume is:

$$W=\frac{1}{2}\omega {∊}_r^{\prime \prime }{∊}_0{\mid \mathbf{E}\mid }^2$$ (5)

where ω is the angular frequency of the incoming linearly polarized light. The power transferred to heat for a given volume of dielectric material is the integral:

$${\int }_{V}WdV=\frac{1}{2}\omega {∊}_r^{\prime \prime }{∊}_0{\int }_V{\mid \mathbf{E}\mid }^{2}dV$$ (6)

Using HFSS we solved this integral and found that 7.1% of the power goes into heating the sample for our 198 GHz system. As previously discussed, the ~1.0 W of power that contributes to dielectric heating is effectively dissipated in MAS DNP experiments by the sapphire rotor which is cooled by a high flow of cryogenic gas [13,39,43].

2.5. Comparison to microwave fields at 250 GHz

To determine the effect of geometry and frequency on the microwave field structure we applied our same analysis to the 4.0 mm DNP NMR probe modeled by Nanni et al. at 250 GHz as shown in Fig. 1f. The field structures are considerably different with the 3.2 mm rotor at 198 GHz, and the 4 mm rotor at 250 GHz. Calculating the microwave structure at the appropriate geometry and frequency are important aspects to understanding and optimizing MAS DNP performance.

The microwave intensities in the 4 mm rotor at 250 GHz are qualitatively similar to the structures seen previously, although we cannot directly compare the values because the stator geometries are not identical. The values in Nanni et al. include a silver coating applied to the inside of the stator that we have not modeled. The analysis given by Nanni et al. reports γ_SB_1S values of 0.84 MHz for a silver coated stator, and 0.70 MHz without the silver coating.

With 5 W of input power, we found an average value γ_sB_1S of 0.37 MHz within the sample at 250 GHz. However, if we take a volume RMS, as outlined by Nanni et al., we determine a RMS value of 0.46 MHz within the sample volume. This agrees well with the value of $0.49=0.70∕\sqrt{2}$ MHz, which accounts for the circularly polarized component at 250 GHz.

We calculated the standard deviation of the peak transverse magnetic field normalized to the mean transverse magnetic field within the sample as:

$$\widehat{\sigma }=\frac{\sqrt{\langle {B_{\perp }}^2\rangle -{\langle B_{\perp }\rangle }^2}}{\langle B_{\perp }\rangle }$$ (7)

The more homogenous γ_SB_1S distribution will have a standard deviation closer to 0. For our 198 GHz system we found $\widehat{\sigma }=0.28$. For the 250 GHz system outlined we found $\widehat{\sigma }=0.75$. This suggests that the transverse magnetic field is more homogenous within the sample for our 198 GHz system than the 250 GHz/4 mm probe absent of a silver coating applied to the inside of the stator.

2.6. Instantaneous microwave field compared to γ_SB_1S

The instantaneous microwave intensities shown in Fig. 1 do not accurately represent the γ_SB_1S distribution. This is because the microwave field intensity is time dependent and follows the 5 ps oscillation period of the 198 GHz microwaves. Fig. 3a clearly shows the microwave field intensity within the sample is strongly dependent on the phase of the microwaves as they propagate. We show a time dependent microwave field structure and the time independent γ_SB_1S distribution in Fig. 3b. The time (and phase) independent field structure is similar to the field structures shown in Nanni et al. [39]. Clearly the γ_SB_1S distribution is much more homogeneous than the instantaneous intensity of the microwaves. However, we note there is still a considerable inhomogeneity in the γ_SB_1S frequencies, which we account for in our simulations of EPR inversions in Section 4.

Fig. 3.

(a) Phase dependence of the microwave fields within the sample (b) comparison of a time dependent microwave field structure (top) and time independent _γSB_1S distribution (bottom).

3. Experimental considerations for MAS pulsed DNP

To give insight into the experimental requirements for performing MAS pulsed DNP, we calculated the amount of microwave power necessary to generate a π/2 pulse on the electron spin manifold. At 7 T, the inhomogeneously broadened nitroxide lineshape simulated with EasySpin [44] is approximately 750 MHz broad [45]. The γ_SB_1S frequency required to control this lineshape with a short (~1 ns) hard pulse is thus ~750 MHz and would require an |E₀| value of 4.5 × 10⁷ V/m, which corresponds to a microwave input power of 13 MW. Impressively, gyrotrons built for fusion research approach such power levels but do not generate more than 1.3 MW [46,47]. Using Eq. (6), we calculated the amount of dielectric heating in the sample, if it were possible to irradiate with 13 MW, to be 940 kW. Thus, increasing the microwave power to generate short hard pulses to excite the entire nitroxide lineshape at magnetic fields above 7 T is not experimentally feasible with current MAS DNP microwave coupling strategies.

One strategy for MAS pulsed DNP at high magnetic fields is to implement a microwave resonant structure with a high quality factor similar to high field non-spinning DNP probes [48,49]. For instance, an EPR cavity with a quality factor of 200 would still provide the frequency bandwidth sufficient to cover the entire nitroxide lineshape, but reduce the input power requirement from 13 MW to 67 kW. An additional advantage to such microwave resonance structures is the ability to separate the magnetic field component of the microwave field required to manipulate the electron spins from the electric component responsible for dielectric heating, as shown in Eqs. (4) and (6). However, a microwave resonator with a quality factor of 200 compared to the current quality factors in MAS DNP probes which are near unity, would be extremely hard to implement given the experimental requirements of MAS. For instance, the relatively large sample size, the RF coil, and the rotor lead to much lower microwave quality factors and worse coupling of the electromagnetic power into the sample than encountered in typical NMR and EPR experiments.

Stable organic radicals with more symmetric g-tensors, such as 1,3-bis(diphenylene)-2-phenylallyl (BDPA) and trityl [50], have major advantages as polarizing agents for pulsed DNP over nitroxides, including less inhomogeneous broadening of the EPR lineshapes and much longer electron spin relaxation times [43]. The long longitudinal relaxation (T_1S) [51] and narrow linewidth (~30 MHz at 140 GHz [52]) of BDPA made it an excellent DNP polarizing agent used by Schaefer, Griffin, and their colleagues to yield significant signal enhancements at room temperature in some of the first MAS DNP experiments [2,14]. More recently trityl and a sulfonated water-soluble analog of BDPA (SA-BDPA) have been well characterized as excellent DNP polarizing agents for the solid effect and Overhauser effect [52–56].

Again, we apply the results from our HFSS microwave field calculations and determine that 21 kW of microwave power are required to generate a 30 MHz γ_SB_1S field to effectively excite the BDPA lineshape with a hard microwave pulse of ~33 ns. Similar to the previous discussion, 110 W of power would be required if a microwave cavity with a quality factor of 200 was implemented. Our laboratory is engaged in designing such MAS microwave resonators. In the following sections, we propose strategies that can be implemented with the inhomogeneous γ_SB_1S frequencies currently available to perform time domain DNP and hyperfine decoupling with MAS.

4. Simulations of EPR inversions

The adiabatic full passage, or adiabatic inversion is a technique in which the magnetization of the sample is slowly swept 180 degrees from +S_z to −S_z [57,58]. Adiabatic pulses can yield broadband decoupling [59–62], even when the γB₁ frequency is much less than the spin resonance linewidth, as is currently the case for EPR in MAS DNP experiments. Adiabatic spin inversions can be accomplished by modulating the frequency of the RF (or microwave) field according to linear, tangential, and hyperbolic secant functions, among others. During the frequency sweep, the magnetization is largely locked along the direction of the effective field, provided the sweep rate is optimized, the γ_SB_1S is the appropriate frequency, and the relaxation times are long enough. One major advantage of adiabatic sweeps over pulsed magnetic resonance is that given a sufficiently strong microwave field, the inversion efficiency is essentially independent of B₁ inhomogeneities [57,58].

4.1. Conditions for an adiabatic inversion

When performing an adiabatic inversion, one comes up against two competing phenomena as described by Kupce and Freeman [57]. The effective field must be swept slowly enough that the magnetization of the sample is locked along it. However, if it is varied too slowly the extent of relaxation, particularly via spin– spin relaxation, becomes prohibitively large. The first condition is commonly described by a parameter known as the “adiabaticity factor” and is defined according to the following equation [57]:

$$Q\left(t\right)=\mid \frac{{\omega }_{\mathit{eff}}\left(t\right)}{\frac{d\theta \left(t\right)}{dt}}\mid$$ (8)

Here ω_eff (t) is the effective field in units of angular frequency, and dθ (t)/dt is the rate at which the angle of the effective field with the x–y plane is changing with time. A useful form of this equation can be realized by recognizing that ω_eff (t), the frequency offset, Δω(t, and the strength of the microwave field, ω₁(t), are related in the following manner:

$${\omega }_{\mathit{eff}}\left(t\right)={[\Delta \omega {\left(t\right)}^2+{\omega }_1{\left(t\right)}^2]}^{1∕2}$$ (9)

θ (t) can also be written in terms of the frequency offset and microwave strength:

$$\theta \left(t\right)={\tan }^{-1}\left(\frac{\Delta \omega \left(t\right)}{{\omega }_1\left(t\right)}\right)$$ (10)

Differentiating with respect to time yields:

$$\frac{d\theta \left(t\right)}{\mathit{dt}}=\frac{{\omega }_1\left(t\right)\frac{d\Delta \omega \left(t\right)}{\mathit{dt}}-\Delta \omega \left(t\right)\frac{d{\omega }_1\left(t\right)}{\mathit{dt}}}{{\omega }_1{\left(t\right)}^2+\Delta \omega {\left(t\right)}^2}$$ (11)

If we now rewrite Q (t) in terms of Δω(t) and ω₁(t), we obtain a general formula for the adiabaticity factor in terms of experimental variables:

$$Q\left(t\right)=\mid \frac{{[\Delta \omega {\left(t\right)}^2+{\omega }_1{\left(t\right)}^2]}^{\frac{3}{2}}}{{\omega }_1\left(t\right)\frac{d\Delta \omega \left(t\right)}{\mathit{dt}}-\Delta \omega \left(t\right)\frac{d{\omega }_1\left(t\right)}{\mathit{dt}}}\mid$$ (12)

In the special case of a linear sweep, which is the sweep function simulated in Section 4.3, the frequency offset is modulated as a function of time according to the following equation:

$$\Delta \omega \left(t\right)=\pm k\left(t-\frac{1}{2}\tau \right)$$ (13)

Here k is the sweep rate, τ is the total time of the sweep and t runs from 0 to τ. Additionally, the strength of the microwave field is held constant, so dω₁/dt = 0 and the time dependence of ω₁(t) can be dropped. Although there could be a substantial voltage and frequency dependence on the microwave power over a sweep range of 750 MHz that would be required to invert a nitroxide lineshape, the microwave power over a 40 MHz band, which is all that needed to invert a SA-BDPA resonance, is nearly constant during the frequency sweep. So for the inversion of SA-BDPA, the strength of the microwave field is assumed to be held constant. Putting these values into Eq. (12) renders the following for a linear sweep of the frequency offset:

$$Q\left(t\right)=\mid \frac{{\left[k^2(t-\tau ∕2){}^2+{\omega }_1^2\right]}^{\frac{3}{2}}}{\pm {\omega }_{1}k}\mid$$ (14)

The larger the adiabaticity factor, the better the inversion, so we need only concern ourselves with the minimum value of this function, which occurs when $t=\frac{1}{2}\tau$. Here the adiabaticity factor is equal to the expression given by Kupce and Freeman [57]:

$$Q_{\mathit{minimum}}=\frac{{\omega }_1^2}{k}$$ (15)

They suggest keeping the adiabaticity factor at a value of at least 1 for NMR. This is difficult in EPR, however, because the relaxation times for an electron are substantially shorter than for a nucleus, which we take into account in our simulations.

4.2. EPR simulations of SA-BDPA

The inversion of SA-BDPA EPR spectrum was calculated using the SPINEVOLUTION simulation package [64]. We used EPR parameters previously determined at 140 GHz of 40 mM SA-BDPA frozen in a d₈-glycerol/H₂O/D₂O (60/30/10)% glassy matrix at 80 K determined by Smith and his colleagues [48,56,65]. The inhomogeneous linewidth was 30 MHz, the spin lattice T_1S was 56 ms, and the phase memory time (homogeneous transverse relaxation) was 3.3 μs. The majority of the SA-BDPA linewidth arises from intramolecular hyperfine couplings.

Fig. 4a shows the 4 protons that were included in the simulations. There are 8 strongly coupled protons, each with a isotropic hyperfine interaction of ~5.1 MHz. We included the 4 protons shown in Fig. 4a in the spin simulations as a representative sample due to the computational demand of including more spins. An isotropic hyperfine interaction of 5.1 MHz was used in the simulations according to Haze et al. [56], and the dipolar hyperfine interaction was calculated explicitly.

Fig. 4.

Sulfonated BDPA (a) chemical structure and (b) energy minimized structure from GAMESS [63], indicating the 4 protons with strong hyperfine interactions included in the spin simulations (c) simulated EPR spectrum of sulfonated-BDPA from SPINEVOLUTION in red, SPINACH in blue, and a Lorentzian profile in dotted black that matches closely to experiment [56]. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

In order to calculate the hyperfine dipolar interactions, the computational package GAMESS was used to obtain the relative unpaired spin densities and the atomic coordinates for each of the spins [63]. The geometry of the energy minimized SA-BDPA structure is shown in Fig. 4b. Dipolar coupling between the hydrogen spins were neglected to shorten the calculation time.

The unpaired electron of SA-BDPA is highly delocalized over a large pi network. This delocalization was approximated by repeating the simulation for 33 different electron positions. Specifically, the atomic coordinates and relative unpaired spin densities at the nuclei of each of the 33 carbons were obtained from a density functional theory calculation of SA-BDPA. The calculation was performed using the GAMESS program, with a B3LYP functional, and a 6-31G** basis set [63]. Spin densities were obtained via Lowdin population analysis. Simulations were carried out for each electron position, weighted by the normalized spin density, and then summed.

Fig. 4c shows results from SPINEVOLUTION compared to those from SPINACH [66]. Both results approximate the Lorentzian profile of experimental results close enough for our theoretical treatment considering our goal is to demonstrate that broadband electron spin inversions at 198 GHz are possible with currently available microwave sources. Including more protons on the SA-BDPA molecule, along with those of the ice surrounding the molecule, would improve this agreement. Ultimately, the choice of simulation package comes to one of computation time. A five-spin system in SPINEVOLUTION is much faster with reasonable accuracy and thus allows for the exploration of more inversion parameters.

4.3. Simulations of electron spin inversions

To invert the electron spins of SA-BDPA, we simulated a linear frequency sweep from 20.5 MHz below the center of the EPR resonance to 20.5 MHz above the resonance, over a period of 13.75 μs. With a _γ1B_1S of 0.84 MHz, this yields an adiabaticity factor of 1.51 (from Eq. (15)). This adiabaticity factor can be improved with higher _γ1B_1S values. Also, more efficient sweep schemes exist than the linear sweep which yield better adiabaticity factors. These could also be implemented with frequency agile gyrotrons.

Using HFSS we computed the _γSB_1S in each of 75,295 voxels in the sample. The average _γSB_1S value over the entire sample was determined by averaging the values of all the voxels. This came out to a value of 0.84 MHz with 17 W of power input into the MAS stator and was used to optimize the sweep parameters.

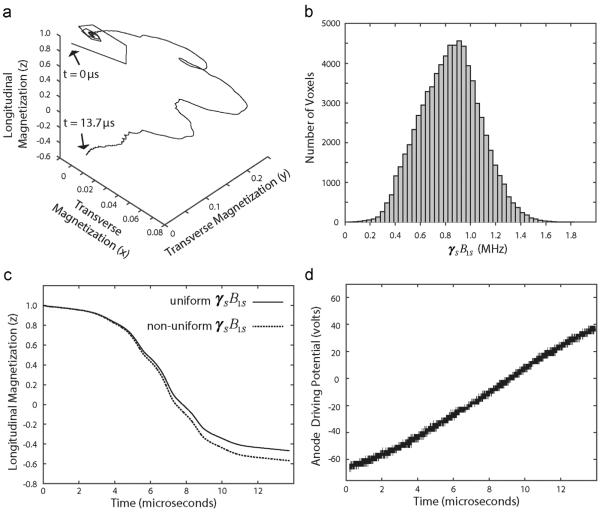
The tip of the magnetization vector's trajectory is shown in Fig. 5a. The inversion efficiency achieved with an entirely homogenous field of 0.84 MHz was 57%. In order to simulate the inhomogeneity of the microwave field, the microwave strengths generated in HFSS with an average _γ1B_1S of 0.84 MHz were binned into groups. Electron spin inversions were calculated on each bin, and the results were weighted according to the population distribution shown in Fig. 5b. This process was done using both 50 and 100 bins, both of which resulted in 46% spin inversion, indicating the binning of the microwave field inhomogeneity converges at less than 50 bins.

Fig. 5.

Adiabatic EPR inversions for MAS DNP. (a) Simulation of the EPR magnetization during an adiabatic inversion with a homogeneous _γSB_1S=0.84 MHz. (b) Histogram indicating the distribution of _γSB_1S frequencies in the 3.2 mm rotor at 200 GHz as determined by the HFSS model. (c) The longitudinal magnetization during adiabatic inversions with a homogeneous _γSB_1S (black line) and the inhomogeneous _γSB_1S calculated from the HFSS model (dotted line). (d) Voltage trace from an oscilloscope showing the estimated gyrotron potential required for the electron spin inversions.

Fig. 5c shows the time dependencies of the z components of the SA-BDPA magnetization under an adiabatic inversion in both the homogeneous, average field, and the real, inhomogeneous field. The similar magnetization profiles demonstrate that frequency swept microwave pulses are a robust strategy to invert electron spins in MAS experiments. To connect our theoretical analysis to experiments, we demonstrate in Fig. 5d the gyrotron acceleration profile required to produce the frequency sweep and electron spin inversion. All subsequent simulations discussed from here employ a homogeneous, average field of _γ1B_1S=0.84 MHz.

There are some factors that will attenuate the inversion percentages reported here. We first consider the dipolar interaction between electrons on nearby SA-BDPA molecules. In order to investigate this effect, inversion simulations on two SA-BDPA molecules as a function of inter-electron distance were performed. In the simulations, we also included the isotropic and dipolar hyperfine interactions of each electron with two protons within its own molecule. All proton-proton dipolar couplings were neglected. The effect of the inter-electron distance up to 150 Å on the electron spin inversion efficiency is shown in Fig. 6a. It can be seen that there is no inversion up to about 12 Å of separation, at which point the inversion efficiency achieves its maximum value rather quickly. Using a simple cubic lattice of electrons as a model, the average distance between an electron and its nearest neighbor at 40 mM is about 35 Å. As can be seen from the simulation, at this distance the inversion is essentially the same as the isolated case.

Fig. 6.

The effect of various parameters on electron spin inversion efficiencies. (a) Inter-electron spin separation (b) transverse homogenous electron relaxation time (c) spinning frequency.

Another parameter that can affect the inversion efficiency is the phase memory relaxation time. Fig. 6b shows the dependence of the inversion efficiency on T_2. A substantial amount of inversion is achieved at 3.3 μs.

Magic angle spinning can also affect the efficiency of the inversion. Simulations were conducted between 0 kHz and 30 kHz in steps of 2 kHz and are shown in Fig. 6c. We calculated an inversion efficiency of 56% at 5 kHz and 30 kHz. Slow to moderate spinning frequencies seem to have a negligible impact on the inversion efficiency.

5. Experimental gyrotron acceleration voltage profiles

Gyrotrons can provide continuous wave output powers of 10–100 W and are now commonly employed in high field MAS DNP experiments [67]. Here, we discuss how frequency agile gyrotron oscillators are excellent microwave sources for the implementation of the frequency modulated cross effect, adiabatic EPR inversions, and hyperfine decoupling in MAS DNP. Such fast-tuning gyrotron oscillators for high-field pulsed DNP have advantages over previously proposed gyrotron amplifiers in terms of duty cycle, cost, and the possibility to upgrade DNP NMR spectrometers currently in use.

5.1. Frequency agile gyrotron oscillators

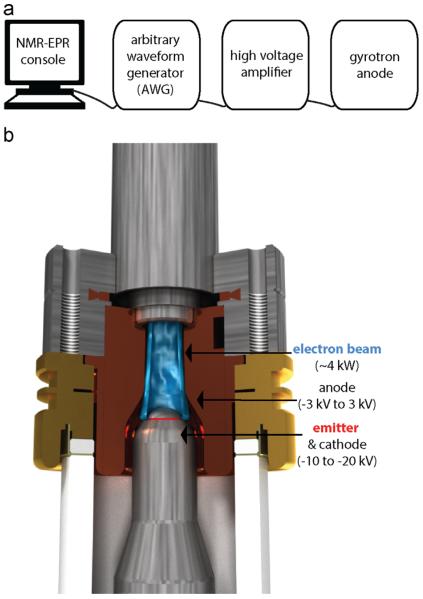
In gyrotron oscillators, an electron beam generated by an electron gun deposits microwave energy into an interaction cavity. A heated filament located beneath the surface of an annular barium emitter and a large (~10 to 20 kV) potential overcome the work function of electrons on the surface of the barium emitter. Electrons ejected from the emitter accelerate under the electric potential between the cathode and the anode (Fig. 7b) and approach relativistic speeds. In the field of the gyrotron's super-conducting magnet, the electrons follow a tight helical path about the magnetic field lines with a cyclotron resonant frequency of:

$${\Omega }_c=e{B}_0∕m$$ (16)

where Ω_C is the cyclotron resonant frequency, e is the charge of an electron, and m is the relativistic mass of an electron. The relativistic mass is:

$$m=\frac{m_e}{\sqrt{1-{\nu }^2∕c^2}}$$ (17)

where v is the velocity of the electron, c is the speed of light, and m_e is the rest mass of the electron.

Fig. 7.

High power microwave frequency agility scheme. (a) Flow chart showing setup connectivity from the software input to gyrotron connection for frequency modulation. (b) CAD solid model of the electron gun (purchased from Bridge12) indicating the electron beam, anode, cathode housing and the beam emitter.

As the electron beam passes through the cavity of the gyrotron, the high energy electrons deposit energy into the interaction cavity at the cyclotron resonant frequency. The velocity in Eq. (17) is a function of both the magnetic field and the electric field potential applied across the electron gun to accelerate the electron beam. Therefore, a modulation of the electric potential across the electron gun will lead to a change in the cyclotron resonant frequency and thus provide tuning of the microwave frequency, given the interaction cavity can support continuous frequency tuning [15].

5.2. Experimental anode potential modulations

Alberti et al. demonstrated fast frequency control and an instantaneous bandwidth of > 2 GHz from a voltage tunable gyrotron oscillator designed for DNP experiments at 263 GHz [68,69]. Idehara et al. recently demonstrated high power levels (> 100 W) during frequency modulations for DNP experiments at 460 GHz [70,71]. Following these demonstrations, we have integrated the control of the gyrotron anode potential into the NMR-EPR console (TecMag, TX) to allow for flexible control and synchronization of NMR pulse sequence elements and the rotor period with microwave pulses and EPR control. The NMR console has an arbitrary waveform generator (AWG) with a 10 ns step size that drives a high voltage amplifier. The high voltage amplifier (TREK, model 5/80) can generate ± 5 kV potential with ± 80 mA current and has a slew rate of 1 kV/μs. Fig. 7a shows how the anode potential is controlled from the NMR EPR console. This integrated EPR control gives us flexibility to implement the swept voltage profiles shown in Fig. 5d for adiabatic EPR spin inversion of the SA-BDPA line-shape and voltage modulations shown in Fig. 8a for the frequency modulated cross effect.

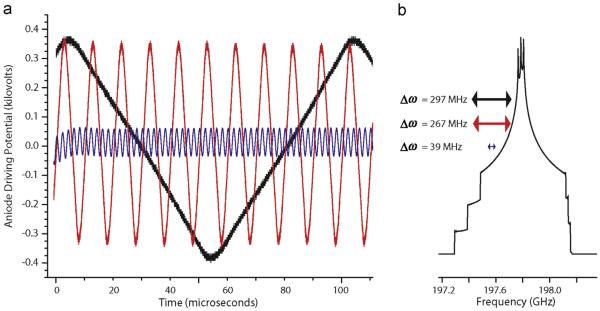
Fig. 8.

High power microwave frequency modulation scheme for the cross effect (CE) under MAS. (a) Anode driving potential modulations at selected frequencies of 10 kHz (black), 100 kHz (blue), and 500 kHz (red). (b) Predicted bandwidth of the microwave frequency output arising from modulating the anode potential overlaid on the nitroxide EPR lineshape at 7 T. The EPR spectrum is from EasySpin [44], and was simulated without homogeneous broadening in order to emphasize the ¹⁴N hyperfine couplings. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

We used a frequency dependence on the gyrotron acceleration voltage of 460 MHz/1.2 kV to determine the potentials shown in Figs. 5d and 8a [72]. Following Han and colleagues [73], we expect to correct for deviations from this linear response by altering the controlling voltage waveform. Fig. 8a shows the estimated voltage modulations required for the frequency modulated cross effect. Fig. 8b overlays predicted microwave frequency bandwidths of different modulation frequencies on the nitroxide lineshape at 7 T calculated with EasySpin [44]. The smaller voltage magnitude of the 500 KHz modulation compared to 10 kHz and 100 kHz reflects the limitation of the microwave frequency bandwidth at higher modulation frequencies due to the slew rate of the TREK HV amplifier.

6. Conclusions

We simulated the spatial intensity of microwave fields within a 198 GHz MAS DNP sample. Given these field strengths, we calculated that adiabatic EPR inversions should be possible with currently accessible DNP instrumentation, providing an immediate avenue for broadband hyperfine decoupling in rotating solids. We also show modulations of gyrotron acceleration potentials required to perform both hyperfine decoupling and the frequency modulated cross effect. All together, these results suggest a promising strategy for the implementation of time-domain DNP and hyperfine decoupling in rotating solids.