Abstract
Glycolysis, mitochondrial substrate oxidation, and the pentose phosphate pathway (PPP) are critical for neuronal bioenergetics and oxidation-reduction homeostasis, but quantitating their fluxes remains challenging, especially when processes such as hexose phosphate (i.e., glucose/fructose-6-phosphate) recycling in the PPP are considered. A hexose phosphate recycling model was developed which exploited the rates of glucose consumption, lactate production, and mitochondrial respiration to infer fluxes through the major glucose consuming pathways of adherent cerebellar granule neurons by replicating [13C]lactate labeling from metabolism of [1,2-13C2]glucose. Flux calculations were predicated on a steady-state system with reactions having known stoichiometries and carbon atom transitions. Non-oxidative PPP activity and consequent hexose phosphate recycling, as well as pyruvate production by cytoplasmic malic enzyme, were optimized by the model and found to account for 28±2 % and 7.7±0.2 % of hexose phosphate and pyruvate labeling, respectively. From the resulting fluxes, 52±6 % of glucose was metabolized by glycolysis, compared to 19±2 % by the combined oxidative/non-oxidative pentose cycle that allows for hexose phosphate recycling, and 29±8 % by the combined oxidative PPP/de novo nucleotide synthesis reactions. By extension, 62±6 % of glucose was converted to pyruvate, the metabolism of which resulted in 16±1 % of glucose oxidized by mitochondria and 46±6 % exported as lactate. The results indicate a surprisingly high proportion of glucose utilized by the pentose cycle and the reactions synthesizing nucleotides, and exported as lactate. While the in vitro conditions to which the neurons were exposed (high glucose, no lactate or other exogenous substrates) limit extrapolating these results to the in vivo state, the approach provides a means of assessing a number of metabolic fluxes within the context of hexose phosphate recycling in the PPP from a minimal set of measurements.
Keywords: mitochondria, pentose phosphate pathway, glycolysis, oxidative stress, bioenergetics, malic enzyme
Graphical Abstract
1. Introduction
The brain’s relatively high demand for glucose and oxygen is thought to reflect the importance of glycolysis and mitochondrial substrate oxidation for ATP synthesis, but the pentose phosphate pathway (PPP) is increasingly recognized as a potentially significant glucose consumer that is also critical for neuron viability (Fernandez-Fernandez et al., 2012). The PPP consists of oxidative and non-oxidative components that, respectively, function to produce reducing equivalents (NADPH) and nucleotide precursors (ribulose-5-phosphate), and to return excess pentose-phosphates to glycolysis during times of high NADPH demand (Stincone et al., 2014). There is mounting evidence that uninterrupted NADPH supply is essential for maintenance of antioxidant defenses and the protein thiol redox state (Ben-Yoseph et al., 1996; Dunn et al., 2014; Filosa et al., 2003; Herrero-Mendez et al., 2009; Levonen et al., 2014; Li et al., 2014). Glutathione and thioredoxin are critical electron donors for ROS scavenging and protection of protein thiols, but their redox potentials strongly depend on their respective reductases, whose activities in turn depend on NADPH supplied by the oxidative PPP. Indeed, depletion of glutathione in neurons can result in oxidative stress (Iguchi et al., 2012; Won et al., 2015), mitochondrial bioenergetic deficits (Vesce et al., 2005), and neurodegeneration (Chinta et al., 2007; Kirkland and Franklin, 2001; Sherer et al., 2003). Glucose consumption through the oxidative PPP is therefore essential for cellular redox homeostasis, in contrast to glycolytic consumption that contributes to maintenance of the cell’s bioenergetic state.
While the qualitative importance of the PPP and glycolysis to neuronal viability is recognized, their quantitative contributions to the glucose consumed remain uncertain. The interconnected nature of the oxidative and non-oxidative PPP with glycolysis, coupled with low levels of metabolites within the PPP, and the ‘recycling’ of hexose phosphates (HxP; glucose-6-phosphate and fructose-6-phosphate) through the PPP have made measurement of their absolute fluxes technically difficult and interpretation of metabolite isotope labeling experiments dependent on assumptions made about pathway behavior. The difference in rates of 14CO2 released from cells metabolizing [1-14C1] vs. [6-14C1]glucose underestimates absolute oxidative PPP flux because it does not account for recycling of unlabeled fructose-6-phosphate back into the oxidative PPP once converted to glucose-6-phosphate by HxP isomerase. In lieu of assessing absolute fluxes, oxidative and non-oxidative PPP activities are usually reported as a single pentose cycle (PC) activity, which reflects their net consumption of hexose phosphate relative to total glucose metabolism. Isotope enrichment of one or more metabolites downstream of the PC from carbon loss/exchange of isotopically labeled glucose within the PC is commonly used for relative measurements, but assumptions of negligible HxP recycling and nucleotide synthesis can, as recently pointed out, also lead to underestimation of activity (Rodriguez-Rodriguez et al., 2013). Furthermore, PPP flux is rarely determined simultaneously with glycolysis and mitochondrial activities, which is of interest especially because mitochondria are major producers of superoxide and other ROS for which NADPH is indirectly required for detoxification. Advances in simultaneous measurements of glycolytic, PPP, and mitochondrial activities are a prerequisite to further understand how these reactions regulate one another in healthy and stressed neurons.
The goal of this study was to quantitate fluxes through all major glucose consuming pathways by replicating the [13C]lactate pattern from metabolism of [1,2-13C2]glucose with a Microsoft Excel-based model that accounted for HxP recycling through the PPP. The model was developed to find solutions for the relative contributions of the non-oxidative PPP to isotopic labeling of the HxP pool and cytoplasmic malic enzyme to labeling of the pyruvate pool, within the constraints of the measured rates of glucose uptake, lactate production, and mitochondrial respiration. From the model, the results indicate extensive processing of glucose through both the oxidative and non-oxidative PPP, low pyruvate recycling through malic enzyme, and a surprisingly high rate of pyruvate conversion to lactate compared to oxidation by mitochondria.
2. Materials and Methods
Cerebellar granule neuron cultures
Cerebellar granule neurons were isolated from 5–7 day old Wistar rats (Harlan; Indianapolis, IN) as previously described (Jekabsons and Nicholls, 2006). Briefly, the rats were killed by decapitation and the cerebella removed, cleaned of non-neuronal tissue, and minced with a razor blade in phosphate buffered saline supplemented with 10 mM glucose, 1 mM EDTA, and 0.3% fatty acid-free bovine serum albumin. The tissue pieces were digested for 30 min with 0.5 mg/mL trypsin in the same buffer, centrifuged 5 min at 500xg, then triturated with flame-polished pipettes in phosphate buffered saline with 30 U/mL DNase and 50 μg/mL soybean trypsin inhibitor. The cells were pelleted at 500 xg for 5 min, resuspended in Minimal Essential Media with Earl’s salts supplemented with 20 mM KCl, 20 mM glucose, 2 mM glutamine, 10% fetal bovine serum, and 100 U/ml penicillin, 0.1 mg/ml streptomycin (cell culture media) and filtered through a 70 μm cell strainer. The cells were washed once, resuspended in cell culture media, and plated onto polyethyleneimine-coated 2-well Lab-Tek II chambered coverglass at 7×106 cells per well. The cells were cultured 6–9 days at 37°C and 5% CO2 95% air in cell culture media. One day after plating, the media was replaced with fresh media containing 10 μM cytosine β-D-arabinofuranoside to inhibit glia cell proliferation. All animal experiments were conducted in accordance with the National Institutes of Health guide for the care and use of laboratory animals. All effort was made to minimize animal stress and suffering and to reduce the number of animals used.
Flux measurements
Mitochondrial respiration rate of the adherent neurons was measured directly in the 2 well Lab-Tek chambers using a custom-made lid/electrode/stirrer as previously described, with minor modifications (Jekabsons, 2009). The cells were equilibrated for 60–75 min at 37°C in experimental buffer containing (in mM): 116 NaCl, 25 KCl, 20 TES pH 7.35, 10 glucose, 1.3 MgCl2, 1.3 CaCl2, 1.2 Na2SO4, 0.4 KH2PO4, 0.2 NaHCO3, 10% v/v dialyzed fetal bovine serum. The cells were washed in the same buffer and the chamber opening sealed with an acrylic lid fitted with a Clarke-type micro oxygen electrode (Microelectrodes, Inc., Bedford, NH) and a stir bar suspended to the inner surface with a mini-magnetic stirrer positioned above the lid. The final buffer volume was 2.1 mL. The entire assembly was placed at 37°C and chamber oxygen depletion (which did not exceed 50%) was measured over 30–45 min period using a chart recorder. Over this period, respiration rate remained constant, suggesting the cells had reached a pseudo metabolic steady-state, which can be maintained for at least 5 h based on continuous monitoring of respiration with a perfusion-mode oxygen electrode (Jekabsons and Nicholls, 2006). Preliminary experiments in which the neurons were treated with oligomycin and myxothiazol to inhibit mitochondrial respiration indicated that 5.9 ± 0.5 % of the measured respiration was non-mitochondrial, which was subtracted from all measured respiration rates to obtain the mitochondrial rates.
Immediately following measurement of respiration, the cells were washed in experimental buffer, then incubated for two sequential 60 min intervals at 37°C with 0.35 mL of the same buffer. Control Lab-Tek chambers without cells were incubated in parallel. The collected buffer was centrifuged for 2 min, 4°C, 21,000 xg, and the supernatant stored at −20°C for analysis of glucose and lactate. The samples (15 μL) were assayed in triplicate for glucose by the increase in absorbance at 340nm after 8 min incubation with 485 μL reaction buffer containing 100 mM triethanolamine, pH 7.6, 7 mM MgCl2, 2 mM ATP, 2 mM NADP, 1 U/ml hexokinase, and 1 U/ml glucose-6-phosphate dehydrogenase. Glucose standards between 9.0–10.0 mM were prepared in the experimental buffer and run in triplicate with each assay. The samples (20 μL) were assayed in triplicate for lactate by the increase in fluorescence (λex =340 nm, λem = 460 nm) after 70 min incubation with 480 μL reaction buffer containing 100 mM glycylglycine, pH 9.0, 100 mM glutamate, 1 mM NAD, 1 U/ml lactate dehydrogenase, and 1 U/ml glutamate-pyruvate transaminase. Lactate standards between 0–1.0 mM were prepared in experimental buffer and run in triplicate with each assay. In preliminary experiments, the rates of glucose consumption and lactate production did not differ significantly during 2 to 6 hours of incubation (data not shown), which further indicates maintenance of a pseudo metabolic steady-state over the time course of the current experiments.
[13C]lactate labeling from [1,2-13C2]glucose
Cerebellar granule neurons (7×106 cells per well plated in 2-well Lab-Tek chambers) were incubated for 1 h at 37°C with 0.6 mL experimental buffer containing 9.6 mM [1,2-13C2]glucose (Cambridge Isotope Laboratories, Andover, MA) rather than unlabeled glucose. The cells were further incubated 2 h 15 min at 37°C with 0.8 mL of fresh 1,2 13C glucose buffer (so 3 h 15 min total) to allow the glycolytic, pentose phosphate pathway, and TCA cycle metabolites to reach isotopic steady-state, as previously demonstrated for HepG2 cells (Hofmann et al., 2008; Maier et al., 2008) and fibroblasts (Munger et al., 2008). The cells were washed once, then incubated 60 min, 37°C with 0.35 mL of the same buffer. Parallel controls were run in each experiment and included wells without cells, and cells incubated with unlabeled glucose. The labeling pattern of metabolically produced lactate exported during the last hour (from 3 h 15 min to 4 h 15 min of exposure to [13C]glucose) was determined using the supernatants following centrifugation of the samples for 2 min, 21,000 xg, 4°C. The supernatants were stored at −20°C until processed for LC-MS/MS.
Lactate derivatization for LC-MS/MS
Samples and lactate standards (0–1.0 mM prepared in experimental buffer) were derivatized with 3-nitrophenylhydrazine as previously described (Uran et al., 2007), with minor modifications. The samples (50 μL) were extracted with 100 μL cold methanol for 30 min at −20°C, then centrifuged at 21,000 xg, −2°C for 10 min. Supernatants were supplemented with 75 μL 50 mM N-(3-dimethylaminopropyl)-N′-ethylcarbodiimide hydrochloride (prepared fresh in 98.5% ethanol, 1.5% pyridine) and 75 μL 140 mM 3-nitrophenylhydrazine hydrochloride (prepared fresh in 50% ethanol) and incubated for 2 h, 37°C. The derivatized samples were immediately stored at −20°C.
LC-MS/MS of derivatized lactate
The derivatized samples (10 μL) were separated on a Waters ACQUITY UHPLC system using a Synergi Hydro-RP C18 100Å column (100mm × 2.0 mm i.d., 2.5 μm; Phenomenex, Torrance, CA) maintained at 35°C. Samples were eluted over 5 min with a linear gradient of water (A)/acetonitrile (B) (both with 0.05% formic acid) from 80% A/20% B to 20% A/80% B using a flow rate of 0.30 ml/min. Each run was followed by a 2 min wash with 100% B, and a 3.5 min equilibration time in 80% A/20% B. A Waters ACQUITY™ XEVO QTOF Mass Spectrometer connected to the UHPLC system via an ESI interface (in negative ionization mode, capillary voltage 2.0 kV; cone voltage 25 V). The temperatures of the source and desolvation were 150°C and 450°C, respectively. Leucine-enkephalin was used as the lock mass, generating an [M-H]+ ion (m/z 554.2615 Da) and its fragment ions (m/z 236.1035 Da) at a concentration of 2 ng/mL and flow rate of 5 μl/min to ensure accuracy during the MS analysis. Tandem MS/MS was used with collision energies of 10, 20, 30 and 40 V. Fragment intensities corresponding to ions 224, 225 and 226 Da (the expected masses for M, M1, and M2 lactate derivatized with nitrophenylhydrazine, respectively) were confirmed, and peak areas of fragment ions 152 Da (3-nitrophenylhydrazine; 10 V collision energy) corresponding to these masses, were calculated. This analysis yielded linear standard curves with the unlabeled lactate standards. Corrections for background [13C] labeling were applied based on the results from the cells incubated with unlabeled glucose.
Monte Carlo simulations
Since the solutions for each experiment were based on the average [13C]lactate labeling pattern (i.e., 13C labeling was measured on different cell preparations than those used for measuring fluxes), the standard errors of the calculated fluxes (Table 5) were strictly based on variations in glucose uptake, lactate production, and mitochondrial respiration. To account for additional variability in the [13C]lactate measurements, 685 lactate labeling patterns were simulated from the mean and standard error of these experiments (Table 3). For this, two of the three labels were simulated (i.e., M/M1, M/M2, or M1/M2) and the third was calculated so that M+M1+M2 = 1. The simulated labeling patterns were randomly assigned to the six flux experiments, and the model used to solve for the flux ratios and unknown fluxes. Of the 685 simulations, 600 solutions were obtained (87.6 % success; 100 solutions for each flux experiment). One-hundred simulated means were obtained after randomly combining one simulation from each experiment. The highest and lowest fluxes from the simulations reflect additional uncertainty in the means beyond that reported by the SEMs (reported in parentheses in Table 5 and by ‘MCSim: X-Y’ in the text).
Table 5.
Solver optimized flux ratios and cerebellar granule neuron fluxes.
| Optimized Ratio | Model Result |
|---|---|
|
|
|
| J3a/(J0 + J3a) | 0.2800 ± 0.0221 (0.2603 – 0.2913) |
| J7/(2J2a + J3b + J7) | 0.0774 ± 0.0025 (0.0465 – 0.1278) |
| Reaction block | Flux |
|
|
|
| Glucose uptake/phosphorylation (J0) (pmol glucose/min × 106 cells) | 291 ± 23 |
| Oxidative PPP (J1) (pmol glucose-6-phosphate/min × 106 cells) | 254 ± 22 (245 – 261) |
| Glycolysis (upper; J2a) (pmol glucose-6-phosphate/min × 106 cells) | 150 ± 19 (143 – 156) |
| Glycolysis (lower; J2b) (pmol triose phosphate/min × 106 cells) | 357 ± 44 (338 – 368) |
| Non-oxidative PPP (J3) (pmol ribulose-5-phosphate/min × 106 cells) | 170 ± 20 (153 – 179) |
| Non-oxidative PPP (returned HxP; J3a) (pmol fructose-6-phosphate/min × 106 cells) | 113 ± 14 (102 – 119) |
| Non-oxidative PPP (HxP lost as CO2/TrP; J3b) (pmol triose phosphate/min × 106 cells) | 57 ± 7 (51 – 60) |
| Lactate production and export (J4) (pmol lactate/min × 106 cells) | 288 ± 46 |
| Mitochondrial pyruvate oxidation (J5) (pmol pyruvate/min × 106 cells) | 99 ± 5 (97 – 103) |
| Mitochondrial NADH oxidation (J6) (pmol NADH/min × 106 cells) | 69 ± 5 (50 – 80) |
| Cytoplasmic malic enzyme (J7) (pmol malate/min × 106 cells) | 30 ± 5 (17 – 53) |
| NADPH oxidation (J8) (pmol NADPH/min × 106 cells) | 538 ± 45 (514 – 566) |
| Nucleotide synthesis (J9) (pmol ribulose-5-phosphate/min × 106 cells) | 84 ± 26 (78 – 95) |
The model incorporated the rates of glucose consumption, lactate production, and mitochondrial respiration (Table 3) with the measured [13C]lactate pattern (Table 3) to optimize the flux ratios that determine the contribution of the non-oxidative pentose phosphate pathway (PPP) and malic enzyme to labeling of the hexose phosphate and pyruvate pools, respectively. This allowed the remaining fluxes to be calculated (Fig. 2). Data are mean ± SEM of six experiments. Numbers in parentheses reflect uncertainties predicted in the means beyond that reported by the SEMs, as determined from Monte Carlo simulations using the mean and SEM associated with measurements of 13C lactate labeling.
Table 3.
Flux measurements and [13C]lactate distribution with primary cerebellar granule neurons.
| Interval | Buffer [Glucose] (mM) | Buffer [Lactate] (mM) | |||
|---|---|---|---|---|---|
|
|
|
||||
| No cells | Cells | No Cells | Cells | ||
| 0–60 min | 10.06 ± 0.12 | 9.71 ± 0.11 | 0.007 ± 0.004 | 0.387 ± 0.052 | |
| 60–120 min | 10.08 ± 0.09 | 9.69 ± 0.11 | 0.008 ± 0.004 | 0.362 ± 0.060 | |
| J0 (pmol Glc/min × 106 cells) | J4 (pmol Lac/min × 106 cells) | JRR (pmol O/min × 106 cells) | |||
|
|
|
|
|||
| 291 ± 23 | 288 ± 46 | 564 ± 29 | |||
| Unlabeled lactate ( ) | Single labeled lactate ( ) | Double labeled lactate ( ) | |||
|
|
|
|
|||
| 0.5731 ± 0.0137 | 0.1855 ± 0.0097 | 0.2413 ± 0.0135 | |||
Seven million cerebellar granule neurons cultured in 2-well Lab-Tek chambers were equilibrated in experimental buffer for 60–70 min at 37°C. Mitochondrial respiration rate (JRR) was measured over 30–40 min in the chambers containing 2.1 mL buffer using a custom lid fitted with a micro-oxygen electrode. The cells were washed and incubated with 0.35 mL buffer over two 60 min intervals, with fresh buffer added after the first interval. Control chambers without cells were run in parallel. Consumption of glucose (J0) and production of lactate (J4) were averaged from the differences between the buffer with and without cells over the two intervals. In separate experiments, the [13C]lactate was assessed by liquid chromatography-tandem mass spectrometry after equilibrating cells with [1,2-13C2] glucose for five hours. Data are mean ± SEM of six (fluxes) or five ([13C]lactate) experiments.
3. Results and Discussion
3.1. System and Assumptions
With glucose as sole exogenous substrate, neuronal metabolism was simplified into nine reaction blocks that served as the template from which a model was developed to solve for all fluxes from four experimental measures- the rates of glucose consumption, lactate production, and mitochondrial respiration, which can readily be measured in the same preparation of adherent neurons (Jekabsons, 2009), and the pattern of [13C]lactate labeling from [1,2-13C2]glucose (Fig. 1). The strength of this approach is that these relatively straightforward measurements are used in a Microsoft Excel solver-based model to determine the absolute fluxes through all nine reaction blocks, including both the oxidative and non-oxidative PPP, while accounting for HxP recycling through the PPP, the use of ribose phosphates for nucleotide synthesis, and the combined contribution of glycolysis, the PPP, and the tricarboxylic acid (TCA) cycle (via cytoplasmic malic enzyme) to [13C]lactate labeling. A number of studies have used isotopically labeled glucose to assess glucose metabolism (Ben-Yoseph et al., 1994; Ben-Yoseph et al., 1995; Ben-Yoseph et al., 1996; Brekke et al., 2012; Herrero-Mendez et al., 2009; KATZ et al., 1966; KATZ and WOOD, 1960; KATZ and WOOD, 1963; Rodriguez-Rodriguez et al., 2013), but have been designed in such a way that they (a) are limited in scope by not considering mitochondrial activity as an integral component of glucose metabolism, (b) do not measure absolute fluxes (e.g., PPP activity expressed relative to glycolytic activity), (c) may underestimate PPP flux because of assumptions of no nucleotide synthesis/no HxP recycling, and/or (d) have not considered the possibility that pyruvate oxidation and the TCA cycle can affect the lactate labeling pattern via pyruvate recycling by malic enzyme. The present study describes one possible approach to addressing these difficulties without resorting to more difficult and time consuming 13C isotopomer analyses of multiple intracellular metabolites.
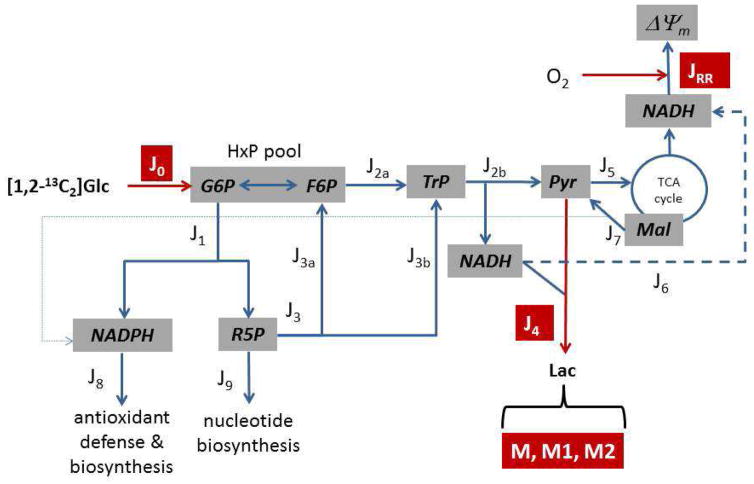
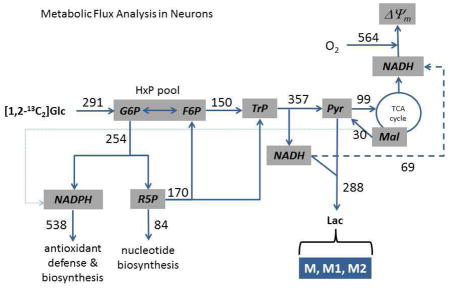
Figure 1. A simplified metabolic map of neuronal glucose catabolism for development of a model to determine reaction fluxes (Jx).
The reactions were grouped into blocks connected by the shared metabolites and included (J0) glucose transport and phosphorylation, (J1) oxidative pentose phosphate pathway (PPP), (J2a) the ‘upper’ reactions of glycolysis which consume hexose phosphates (HxP; G6P, glucose-6-phosphate; F6P, fructose-6-phosphate) and produce the triose phosphates (TrP; dihydroxyacetone phosphate and glyceraldehyde-3-phosphate), (J2b) the ‘lower’ reactions of glycolysis which consume TrP and produce pyruvate (Pyr), (J3) the non-oxidative PPP which returns pentose phosphates (R5P) to the HxP pool (J3a) and produces TrP (J3b), (J4) lactate production and export, (J5) mitochondrial pyruvate oxidation, (J6) mitochondrial oxidation of glycolytic NADH, (J7) export of mitochondrial malate (Mal) and oxidation by cytoplasmic malic enzyme, (J8) cytoplasmic NADPH oxidation, and (J9) consumption of ribose-5-phosphate by phosphoribosyl pyrophosphate synthase for nucleotide synthesis. The measured fluxes are denoted in red and include J0, J4, and mitochondrial respiration (JRR). In other experiments, neurons were given [1,2-13C2]glucose and the [13C] distribution in lactate was measured (where M, M1, and M2 denote unlabeled lactate, or [13C1], [13C2]lactate, respectively). These data were used in a model that allowed calculation of all remaining fluxes.
The model is valid during metabolic and isotopic steady-state conditions, and has the following assumptions: (a) the known stoichiometries among the reactions are constant, (b) glucose-6-phosphate and fructose-6-phosphate are in isotopic equilibrium, and thus form a single HxP pool (i.e., the reversible isomerization reaction proceeds at a substantially greater rate than glycolysis and the oxidative PPP), (c) unlabeled glyceraldehyde-3-phosphate produced by transketolase in the non-oxidative PPP is immediately used by transaldolase and therefore does not equilibrate with the glycolytic triose phosphates, (d) the non-oxidative PPP flux is unidirectional and proceeds towards fructose-6-phosphate/triose phosphate production, and (e) the anaplerotic reactions that replace TCA cycle carbon lost as a result of malate export and oxidation do not affect [13C] labeling of TCA cycle malate. While the first two assumptions are generally accepted in metabolic flux and tracer studies, it is worth commenting on the latter two. The non-oxidative PPP is reversible, but reverse flux and net pentose phosphate formation proceeds under conditions of high ribulose-5-phosphate demand for nucleotides relative to inadequate supply by the oxidative PPP when demand for NADPH is low. Such conditions are not likely to exist in post-mitotic neurons that have been shown to be sensitive to oxidative stress (Ben-Yoseph et al., 1996), compromised NADPH production (Herrero-Mendez et al., 2009), and glutathione depletion (Chinta et al., 2007). Thus, the PPP in this model is viewed as a pentose cycle rather than two independent pathways for pentose phosphate synthesis. While it is generally accepted that net flux through the non-oxidative PPP proceeds in the direction of pentose phosphate consumption in many cells, the error introduced by ignoring reverse ‘exchange’ flux is likely to be minimal as reverse flow was an order of magnitude smaller than forward flux in HepG2 cells (Maier et al., 2008), and the error introduced by assuming unidirectional flux was small from analysis of lactate labeling from [1-14C1] and [6-14C1]glucose (KATZ and Rognstad, 1967). Inclusion of malic enzyme in the model implies that there exist one or more anaplerotic reactions consuming endogenous pools of substrate to replace malate lost from the TCA cycle. The most important of these is likely glutamate dehydrogenase (Ahn and Antoniewicz, 2011). Without exogenous glutamine, the limited intracellular glutamate pool is extensively labeled from [13C]glucose (Waagepetersen et al., 2000b), and indeed enrichment of glutamate and α-ketoglutarate have been shown to be very similar (Brekke et al., 2012), indicating the exchange reaction may proceed sufficiently rapidly to allow equilibration of these two mitochondrial metabolites despite a net direction toward production of α-ketoglutarate (Amaral et al., 2011a). With these assumptions inherent to the metabolic system (Fig. 1), it was possible to develop a relatively simple model that exploited the solver function of Microsoft Excel to determine fluxes J1,J2a,J2b,J3,J5,J6,J7,J8, and J9 from measurements J0,J4, and JRR, and the fractional [13C]lactate labeling from [1,2 13C2]glucose.
3.2. Modeling [13C] labeling of the hexose phosphate pool by the pentose phosphate pathway
An important consequence of assuming isotopic equilibrium between glucose-6-phosphate and fructose-6-phosphate is the recycling of the latter from the non-oxidative PPP to the oxidative PPP, a process which results in extensive randomization of the first three carbons of the HxPs. From exogenous [1,2-13C2]glucose, HxP recycling generates eight labels, seven of which differ from the original label (Table 1). The labels are not equally represented since the extent of recycling that must occur to first generate each label differs, which in turn determines their respective contributions to the pool. As shown in Table 1, no recycling is necessary to produce [1-13C1] and [1,3-13C2]HxP as the exogenous [1,2-13C2] label passes through the oxidative and non-oxidative PPP, whereas one round of recycling is necessary to generate [2-13C1], [3-13C1], [2,3-13C2], and unlabeled (UL) HxP, while two rounds of recycling are necessary to generate [1,2,3-13C3] and [1,2-13C2]HxP. Using the notations of Fig. 1, the contribution of the non-oxidative PPP to labeling of the HxP pool is J3a/(J0 + J3a) and the contribution of exogenous glucose to the same pool is 1 − [J3a/(J0 + J3a)]. From Wood and Katz (WOOD and KATZ, 1958), the fraction of HxP which recycles (x-1) times is
Table 1.
Theoretical [13C]hexose phosphate distribution and abundance through multiple rounds of recycling through the oxidative and non-oxidative pentose phosphate pathways.
| Initial substrates | Substrates 1st recycle (33 − 1 combinations) | Substrates 2nd recycle (73 − 1 combinations | Substrates 3rd – 7th recycle (93 − 1 combinations) | ||||||||||||
|
|
|
|
|
||||||||||||
| G6P1 | G6P2 | G6P3 | G6P1 | G6P2 | G6P3 | G6P1 | G6P2 | G6P3 | G6P1 | G6P2 | G6P3 | ||||
|
|
|
|
|
||||||||||||
| 1,2* | 1,2* | 1,2* | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||
| 1,3 | 1,3 | 1,3 | 2 | 2 | 2 | 2 | 2 | 2 | |||||||
| 3 | 3 | 3 | 3 | 3 | 3 | ||||||||||
| 1,2* | 1,2* | 1,2* | 1,3 | 1,3 | 1,3 | 1,2 | 1,2 | 1,2 | |||||||
| 2,3 | 2,3 | 2,3 | 1,3 | 1,3 | 1,3 | ||||||||||
| UL | UL | UL | 2,3 | 2,3 | 2,3 | ||||||||||
| 1,2,3 | 1,2,3 | 1,2,3 | |||||||||||||
| 1,2* | 1,2* | 1,2* | UL | UL | UL | ||||||||||
| 1,2* | 1,2* | 1,2* | |||||||||||||
| Products | Products | Products | Products | ||||||||||||
|
|
|
|
|
||||||||||||
| F6P1 | F6P2 | TrP | F6P1 | F6P2 | TrP | F6P1 | F6P2 | TrP | F6P1 | F6P2 | TrP | ||||
|
|
|
|
|
||||||||||||
| 1,3 | 1 | UL | 1 | 1 | UL | 1 | 1 | UL | 1 | 1 | UL | ||||
| 2 | 2 | 2 | 2 | 2 | 2 | ||||||||||
| 3 | 3 | 3 | 3 | 3 | 3 | ||||||||||
| 1,3 | 1,3 | 1,2 | 1,2 | 1,2 | 1,2 | ||||||||||
| 2,3 | 2,3 | 1,3 | 1,3 | 1,3 | 1,3 | ||||||||||
| UL | UL | 2,3 | 2,3 | 2,3 | 2,3 | ||||||||||
| 1,2,3 | 1,2,3 | 1,2,3 | 1,2,3 | ||||||||||||
| UL | UL | UL | UL | ||||||||||||
| Contribution to pool | Contribution to pool | Contribution to pool | Contribution to pool | ||||||||||||
|
|
|
|
|
||||||||||||
| Label |
|
Label |
|
Label |
|
Label |
|
||||||||
|
|
|
|
|
||||||||||||
| All |
|
All |
|
All |
|
All |
|
||||||||
| 1 | W * 0.5 | 1 |
|
1 |
|
1 |
|
||||||||
| 1,3 | W * 0.5 | 2 |
|
2 |
|
2 |
|
||||||||
| 3 |
|
3 |
|
3 |
|
||||||||||
| 1,3 |
|
1,2 |
|
1,2 |
|
||||||||||
| 2,3 |
|
1,3 |
|
1,3 |
|
||||||||||
| UL |
|
2,3 |
|
2,3 |
|
||||||||||
| 1,2,3 |
|
1,2,3 |
|
||||||||||||
| UL |
|
UL |
|
||||||||||||
Numbers under ‘Label’, ‘G6P’, and ‘F6P’ denote the position of [13C] within glucose-6-phosphate/fructose-6-phosphate. J0 is the rate of HxP generated from [1,2-13C2]glucose. J3a is the rate of HxP generated by the non-oxidative PPP. is the relative amount of a specific label returning to the HxP pool (P) for the xth time (the subscript ‘L’ denotes the specific 13C label; e.g., L=1,3 refers to [1,3-13C2]HxP; UL = unlabeled HxP containing no enriched [13C], and m is the number of HxP combinations that yields label L). Each summation term (i.e., ) is the product of the fractional content of three hexose phosphates from the previous cycle reacting to generate label L. is the relative amount of all labeled HxP for the xth return (n reflects all possible combinations of three HxPs reacting. For the first, second, and third recycles n = 33−1, 73−1, and 93−1, respectively. For all subsequent cycles, n= 93−1). The * denotes the [1,2-13C2]HxP entering the pool from J0 to distinguish it from the same label derived from the non-oxidative PPP. In the steady-state where isotopic equilibrium has been reached, the combined fractional content of all labels from the non-oxidative PPP is J3a/(J0 + J3a) and the fractional content of each specific label is the sum of the contributions of the label from each respective round of recycling (i.e., the sum of the individual terms for each labeled species indicated for all cycles under “Contribution to pool”).
| (Eq. 1) |
where x is the number of times a HxP has returned to the pool via the non-oxidative PPP. It is important to note that ‘recycle’ and ‘return’ have different meanings- a HxP that returns to the pool does not recycle if it leaves the pool via glycolysis, whereas one that recycles must not only return, but also isomerize to glucose-6-phosphate and enter the oxidative PPP. It is apparent that the flux ratio J3a/(J0 + J3a) establishes the extent of recycling and thus the labeling pattern of the HxP pool. As such, this ratio served as a solver-optimized variable in the model.
To determine specific label abundance, all possible combinations of three substrates from J0 and recycled from J3a were delineated, and the known carbon atom transitions (Brekke et al., 2012; WOOD and KATZ, 1958) in the non-oxidative PPP were used to determine the labeling of all pairs of HxP products that return to the pool. For each combination, the relative yield of each label returning to the pool for the xth time depends on the fractional content of the reacting substrates:
| (Eq. 2) |
For this notation, x is the number of times returning to the pool (for x ≥ 2), L is the specific label of HxP product, and a, b, and c are the labels that, when processed through the oxidative and non-oxidative PPP, yield the label L. The sum of all such (m) combinations yielding label L ( ), relative to the sum of all possible combinations (n) of substrates ( ), reflects the fractional content of label L returning for the xth time through the non-oxidative PPP. The fractional content of label L from the xth return is then
| (Eq. 3) |
In this way, the flux ratio J3a/(J0 + J3a) optimized by the solver is linked to the fractional content of each label. The fraction of HxP that returns to the pool only once (x=1) is
| (Eq. 4) |
since equal amounts of [1-13C1] and [1,3-13C2]HxP are produced from three [1,2-13C2]glucose-6-phosphate entering the PPP. This process is repeated for eight HxP returns/seven recycles (which accounts for > 99.8% of the non-oxidative PPP produced HxP), such that the cumulative fractional content of all eight labels in the HxP pool from the non-oxidative PPP is the sum of the fractional content from each return ( ). For the experiments performed in this study, isotopic labeling of unlabeled (M), single-(M1), and double (M2)-labeled lactate was quantitated without resolving the different lactate isotopomers; thus, the theoretical lactate labeling pattern in the model combined the different isotopomers to calculate the fractional M, M1, and M2 content. Additionally, since the triple-labeled (M3) lactate signal measured in one experiment was less than 10 % of the M1 and M2 signals, and close to the background noise of the chromatogram (data not shown), M3 lactate was not routinely measured. The theoretical fractional labeling pattern was therefore based on M, M1, and M2 only and did not include the small predicted contribution of M3 (i.e., in the model, M+M1+M2 = 1).
3.3. Modeling 13C labeling of mitochondrial malate by the TCA cycle
From the model in Section 3.2, the solver function was unable to find a flux ratio J3a/(J0 + J3a) that replicated the measured M/M1/M2 lactate labeling within the constraints of J0, J4, and JRR (see Table 3). Thus, at least one other reaction must contribute to labeling of cytoplasmic pyruvate. Previous studies with neurons have shown that malic enzyme can, at least under some conditions, be a significant source of pyruvate (Amaral et al., 2011b; Bak et al., 2007; Cruz et al., 1998; Olstad et al., 2007) that could affect labeling of extracellular lactate. The contribution of malic enzyme to the pyruvate pool, J7/(2J2a + J3b + J7), was introduced into the model as a second solver-optimized flux ratio (Fig. 2). This required theoretical calculation of malate labeling as [13C] from pyruvate is incorporated into the TCA cycle metabolites. To optimize this ratio, an initial estimate of fractional malate labeling from pyruvate is required. Pyruvate labeling was estimated from metabolism of HxP (whose labeling is described in Section 3.2) and PC-derived triose phosphate (which is unlabeled; see Section 3.1) through glycolysis, assuming that 20 % of the HxP pool was from J3a (Table 2, ‘Pyruvate from HxP/TrP’). From this estimate, progressive 13C labeling of malate was determined over four rounds of the TCA cycle using the known carbon atom transitions that occur in the cycle (Table 2). The fractional amount of each malate label was calculated (top half of Table 2) from the probability of each pyruvate label (following decarboxylation of C1 via pyruvate dehydrogenase) reacting with an oxaloacetate label derived from the previous round, for all reactions producing each malate label (bottom half of Table 2). Loss of malate from the TCA cycle via export and subsequent oxidation by malic enzyme must be accompanied by an equivalent rate of carbon entry into the cycle. As discussed in Section 3.1, a primary anaplerotic reaction replacing lost malate is likely oxidation of endogenous glutamate to α-ketoglutarate by glutamate dehydrogenase. Fractional labeling of glutamate via the reversible nature of this reaction was not measured in this study (but glutamate labeling from [13C]glucose has been shown (Brekke et al., 2012; Waagepetersen et al., 2000b)), so it was assumed that isotopic equilibration between glutamate and α-ketoglutarate was achieved so that malate labeling was not affected by the introduction of carbon from glutamate into the cycle.
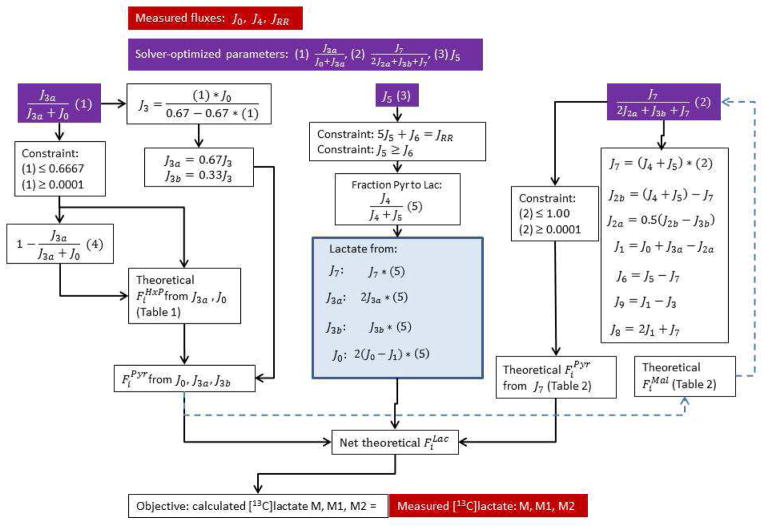
Figure 2. Flow diagram of the model used to calculate reaction fluxes.
The reaction flux notations are defined in Fig. 1. The non-linear solver function of Microsoft Excel was used, with the objective being that the calculated fractional content of unlabeled lactate equaled that measured experimentally, and the additional constraints that the calculated fractional content of M1 and M2 lactate equaled that measured experimentally. The calculated lactate labeling pattern was derived from the theoretical labeling pattern of the hexose phosphate pool (due to HxP producers J0 and J3a), the triose phosphate pool from J3b, and the TCA cycle malate pool as [13C]pyruvate enters the TCA cycle through J5 (Tables 1 and 2). Each of these pools in turn contributed to labeling of the pyruvate pool via J2a, J2b, and J7. The solver optimized the contribution of the non-oxidative PPP (NonPPP) to labeling of the HxP pool (J3a/(J0 + J3a)) and the contribution of malic enzyme to labeling of the pyruvate pool (J7/(2J2a + J3b + J7)) such that the objective was satisfied within the constraints imposed. Additional constraints were imposed upon the solver based on the structure of the system, the stoichiometries of the reactions, and the requirement that all fluxes were greater than or equal to zero. The dashed, blue arrows reflect the iterative process of the model, where the contribution of the NonPPP to the HxP pool was arbitrarily set to 0.2 so that an initial estimate of the malate labeling pattern could be made for an initial solver-derived solution. Based on first the solution, progressively refined HxP and malate pool labeling could be calculated from two additional iterations of the solver.
Table 2.
Theoretical [13C] distribution and abundance in malate through four rounds of the tricarboxylic acid cycle.
| Pyruvate from HxP/TrP | Initial Malate | Turn 1 TCA malate | Turn 2 TCA malate | Turn 3 TCA malate | ||||||||||
|
|
|
|
|
|||||||||||
| Label |
|
Label |
|
Label |
|
Label |
|
Label |
|
|||||
|
|
|
|
|
|||||||||||
| 1 |
|
UL | 1 | 1 |
|
1 |
|
1 |
|
|||||
| 2 |
|
2 |
|
2 |
|
2 |
|
|||||||
| 3 |
|
1,2 |
|
3 |
|
3 |
|
|||||||
| 1,2 |
|
UL |
|
1,2 |
|
4 |
|
|||||||
| 1,3 |
|
1,3 |
|
1,2 |
|
|||||||||
| 2,3 |
|
2,3 |
|
1,3 |
|
|||||||||
| 1,2,3 |
|
1,2,3 |
|
2,3 |
|
|||||||||
| UL |
|
UL |
|
1,4 |
|
|||||||||
| 2,4 |
|
|||||||||||||
| 3,4 |
|
|||||||||||||
| 1,2,3 |
|
|||||||||||||
| 1,2,4 |
|
|||||||||||||
| 1,3,4 |
|
|||||||||||||
| 2,3,4 |
|
|||||||||||||
| 1,2,3,4 |
|
|||||||||||||
| UL |
|
|||||||||||||
| Turn 1 TCA malate | Turn 2 TCA malate | Turn 3 TCA malate | Turn 4 TCA malate | |||||||||||
|
|
|
|
|
|||||||||||
| Label |
|
Label |
|
Label |
|
Label |
|
|||||||
|
|
|
|
|
|||||||||||
| 1 |
|
1 |
|
1 |
|
1 |
|
|||||||
| 2 |
|
2 |
|
2 |
|
2 |
|
|||||||
| 1,2 |
|
3 |
|
3 |
|
3 |
|
|||||||
| UL |
|
1,2 |
|
4 |
|
4 |
|
|||||||
| 1,3 |
|
1,2 |
|
1,2 |
|
|||||||||
| 2,3 |
|
1,3 |
|
1,3 |
|
|||||||||
| 1,2,3 |
|
2,3 |
|
2,3 |
|
|||||||||
| UL |
|
1,4 |
|
1,4 |
|
|||||||||
| 2,4 |
|
2,4 |
|
|||||||||||
| 3,4 |
|
3,4 |
|
|||||||||||
| 1,2,3 |
|
1,2,3 |
|
|||||||||||
| 1,2,4 |
|
1,2,4 |
|
|||||||||||
| 1,3,4 |
|
1,3,4 |
|
|||||||||||
| 2,3,4 |
|
2,3,4 |
|
|||||||||||
| 1,2,3,4 |
|
1,2,3,4 |
|
|||||||||||
| UL |
|
UL |
|
|||||||||||
Table 1 was used to estimate the initial distribution of [13C] in pyruvate from metabolism of [1,2-13C2]glucose through the non-oxidative PPP and glycolysis. The initial contribution of the non-oxidative PPP to labeling of the HxP pool (i.e., J3a/(J0 + J3a) in Table 1) was assumed as 0.2 and the initial contribution of malic enzyme to the pyruvate pool was assumed negligible. denotes the fractional [13C]HxP calculated from Table 1. The variable Y is the fraction of pyruvate produced by glycolytic processing of HxP (i.e., 2J2a/(2J2a + J3b) = 0.9049 in this example). The pyruvate labeling pattern from the HxP metabolized through glycolysis as well as the triose phosphate (TrP) derived from the PC and subsequently metabolized through glycolysis was calculated as indicated under “Pyruvate from HxP/TrP” and the results used to establish the initial fractional [13C]malate distribution through four successive rounds of the TCA cycle as indicated by the equations in the lower half of Table 2. All values were calculated using J0, J4, and JRR from Table 3. The upper half of Table 2 demonstrates increasingly diverse labeling of the malate pool as additional rounds of the TCA cycle occur through reaction with the invariant pyruvate pool (after oxidative decarboxylation to acetyl CoA by pyruvate dehydrogenase). Malate labeling following the fourth round of the TCA cycle (not shown) was identical to that following the third round, indicating that isotopic steady-state had been reached. From the 4th round labeling, the resulting [13C]pyruvate distribution from decarboxylation of C4 by malic enzyme was determined and used in conjunction with Table 1 to optimize the contribution of malic enzyme to the pyruvate pool using the solver function of Microsoft Excel. From the results of the initial solver solution, further optimization of the non-oxidative PPP and malic enzyme fluxes was conducted by running two additional iterations of the solver, based on refinement of the fractional HxP, malate, and pyruvate labeling patterns. The iterations were important in allowing the model to reach a solution that was independent of the initial assumptions about the contributions of the non-oxidative PPP and malic enzyme to production of HxP and pyruvate, respectively. xFMal and FPyr denote the fractional amounts of each labeled malate or pyruvate within their respective pools (and x = round of TCA cycle). For the equations, the F subscripts that are letters denote the following positional [13C]malate or pyruvate labeling: a- 1 or UL; b- 2 or 1,2; c- 3 or 1,3; d- 2,3 or 1,2,3; e- 1, 4, 1,4, or UL; f- 2, 2,4, 1,2, or 1,2,4; g- 3, 1,3, 3,4, 1,3,4; h- 2,3, 1,2,3, 2,3,4, or 1,2,3,4. The summation terms reflect the four (for rounds 2, 3) or eight (for round 4) different combinations of malate and pyruvate that yield the specified malate label for the current cycle.
The fractional M/M1/M2 pyruvate from decarboxylation of malate C4 by malic enzyme was incorporated into the labeling derived from the HxP pool via glycolysis, assuming that both reactions contribute to a single pool of cytoplasmic pyruvate. Theoretical M3 pyruvate, which was approximately 1.5% of the pyruvate derived from malic enzyme (Fig. 5), was excluded for the reasons discussed in Section 3.2. For the first iteration, the solver simultaneously adjusted J3a/(J0 + J3a) and J7/(2J2a + J3b + J7) using the calculations based on the initial ‘guess’ that 20 % of the HxP pool was from J3a to reproduce the measured M/M1/M2 lactate. Two additional iterations of the computations were added to refine the fractional labeling patterns of the HxP and malate pools based on results of the previous iteration. This typically resulted in progressively smaller modifications to the solver optimized ratios.
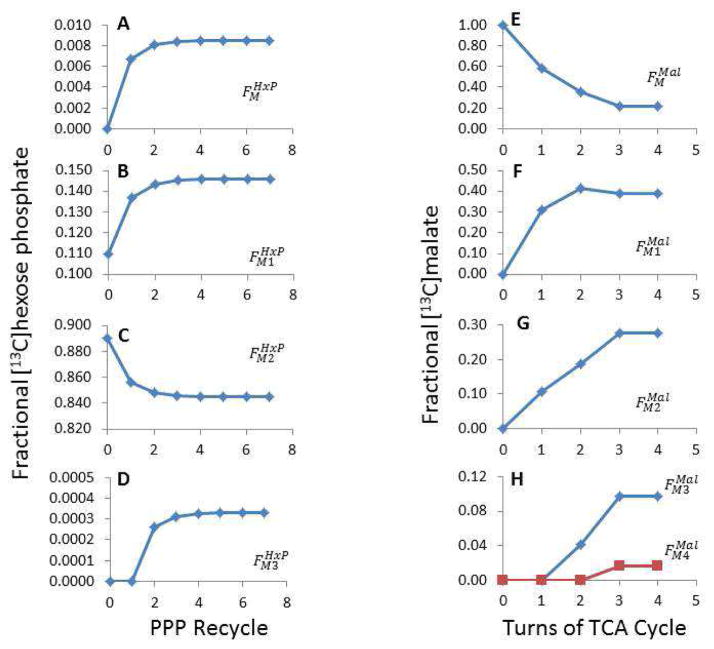
Figure 5.
Progressive changes to the theoretical fractional [13C] abundance in the hexose phosphate and malate pools as the isotope equilibrates.
The data from Table 3 were used in the model to optimize the flux ratios (see Table 5). The model considered seven rounds of hexose phosphate recycling from the non-oxidative PPP back through the HxP pool and the oxidative PPP, with the labeling pattern after the 7th recycle used for the final calculations (Table 1). A–D shows how the fractional [13C]HxP ( ) changes when additional rounds of recycling occur. The model also considered how [13C] in mitochondrial malate varied over 4 turns of the TCA cycle as [13C]oxaloacetate from the previous turn reacts with [13C]acetyl CoA derived from labeled pyruvate. E–H illustrates how the fractional malate labeling pattern ( ) varies over each turn of the TCA cycle.
The inclusion of malic enzyme as contributor to lactate required that the model be further modified, as the contribution of pyruvate oxidation (J5) and glycolytic NADH oxidation (J6) to JRR depended on J7 (i.e., J5/J6 ≠ 1). From the steady-state, the rate of pyruvate production by glycolysis is
| (Eq. 5) |
and the rate of NADH production and consumption are equal, so
| (Eq. 6) |
Substituting and solving for J6,
| (Eq. 7) |
Therefore, J5 was introduced as a third solver optimized component, constrained by measurement of JRR and the stoichiometry of oxygen consumed by J5 and J6 such that 5J5 + J6 = JRR. In turn, J7 is constrained to satisfy the measured [13C]lactate labeling pattern from metabolism of [1,2-13C2]glucose (Fig. 2).
3.4. Application of the model to cerebellar granule neurons
Neurons were equilibrated for 75 min at 37°C with glucose (10 mM) as the sole oxidizable substrate, after which time J0, J4, and JRR were measured over the next ≈3.5 h using a novel setup as previously described (Jekabsons, 2009). The advantage of this setup is that all three fluxes can be measured in the same population of undisturbed (adherent) neurons; moreover, if [13C]glucose is used, lactate labeling can also be measured in the same neurons, which reduces the uncertainty associated with measurements on different preparations. However, the logistics of the current study were such that [13C]lactate labeling was determined in separate experiments. The rates of glucose consumption and lactate production were nearly equivalent (Table 3), as found previously by others (Waagepetersen et al., 2000a) while mitochondrial respiration was similar to that measured using a perfusion-based system (Jekabsons and Nicholls, 2004; Jekabsons and Nicholls, 2006). Lactate present in the methanol-extracted buffer samples was derivatized with 3-nitrophenylhydrazine, thus predicting 224, 225, and 226 Da for M, M1, and M2 lactate; the 154 Da phenylhydrazine fragment from these masses was quantitated (Fig. 3). Unlabeled lactate standards ranging from 0–1.0 mM confirmed a linear increase in 224 Da abundance (not shown). The M/M1/M2 lactate from [1,2-13C2]glucose was corrected for the fractional background labeling of cells metabolizing unlabeled glucose (0.1625±0.0101 and 0.0189±0.0080 for M1 and M2, respectively).
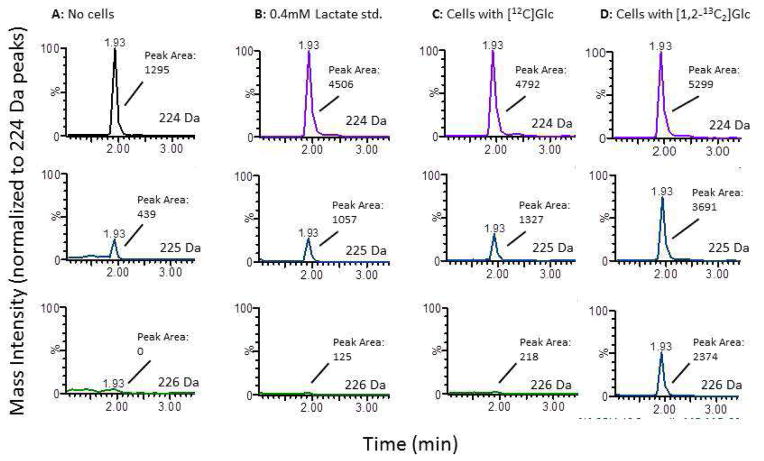
Figure 3. Representative liquid chromatography-tandem mass spectrometry chromatograms of lactate derivatized with 3-nitrophenylhydrazine.
Experimental buffer containing either 10 mM unlabeled glucose (C) or 10 mM [1,2-13C2]glucose (A, B, D) were incubated either without (A, B) or with (C, D) cerebellar granule neurons for up to 4.5 h. During the last hour, the cells were washed and incubated in new buffer, which was analyzed for M, M1, and M2 lactate. In B, the experimental buffer was spiked with 0.4 mM exogenous unlabeled lactate as standard. The samples were methanol-extracted, derivatized, and subjected to LC-MS/MS, and the 154 Da fragment quantitated from M (224 Da), M1 (225 Da), and M2 (226 Da) lactate. The LC retention times are shown. Each set of three chromatograms has been normalized to the peak area obtained from unlabeled lactate (i.e., 224 Da), but the absolute peak areas from the 154 Da fragment used to calculate the fractional labeling patterns are indicated.
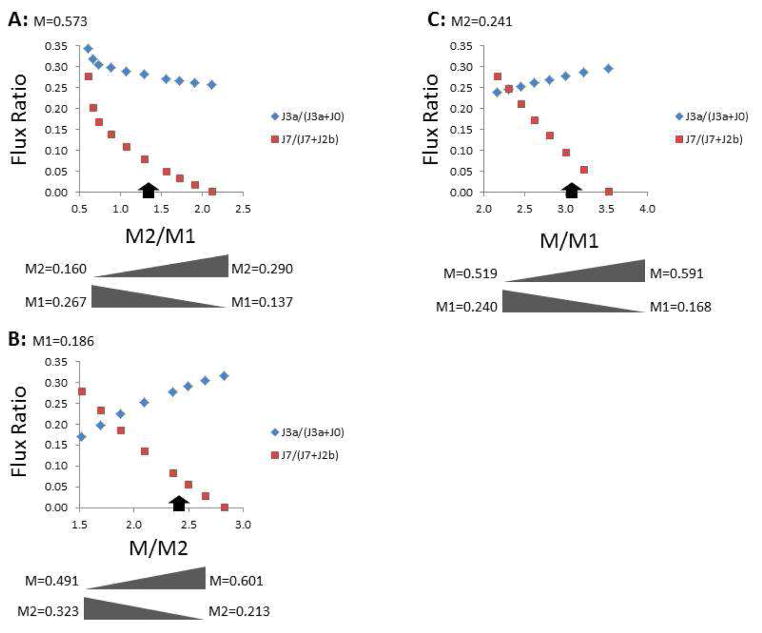
It was of interest to understand the behavior of the model by assessing the range of possible M/M1/M2 labeling for which solutions could be found. For this, J0, J4, JRR, and either M, M1, or M2 were held constant (using the means in Table 3) as the fractional content of the remaining two labels was varied (Fig. 4 and Table 4). For example, when the fraction of unlabeled lactate was 0.573 (Table 3), the model could find solutions when the M2/M1 ratio ranged from 0.60–2.12 (corresponding to M2 range from 0.160–0.290 and M1 from 0.137–0.267; Fig. 4A and Table 4). As the M2/M1 ratio increased, there was a pronounced decline in malic enzyme contribution to the cytoplasmic pyruvate pool (from 0.279 to 0.001) and a modest decline in PPP labeling of the HxP pool (from 0.345 to 0.257). The limitations to solutions were either in malic enzyme flux exceeding available NADH such that supply of M1 was inadequate for M2/M1 ≤ 0.60, or excess M1 resulting from the PPP flux required to maintain unlabeled lactate at 0.573 for M2/M1 ≥ 2.12. The measured labeling pattern fell about midway between these extremes (arrows in Fig. 4). Similar analyses were performed for constant M1 = 0.186 (Fig. 4B) or M2 = 0.241 (Fig. 4C). The tolerance of the model was also tested for hypothetical cells that are more oxidative (i.e., have higher respiration and lower lactate production) or glycolytic (i.e., have lower respiration and higher lactate production) than those measured in the current study (Table 4). The model found solutions for a broader range of lactate labeling for the oxidative cells, but was less tolerant if the cells were more glycolytic, which is not surprising given the expectation that the true M/M2 ratio would be closer to unity. Thus, the analysis was repeated for a hypothetical labeling of 0.54/0.10/0.36 (M/M1/M2), and indeed the range of solutions approximately doubled (Table 4). The model therefore yielded solutions for a range of M/M1/M2 lactate from [1,2-13C2]glucose, as well as for variations in the cells’ metabolic phenotype.
Figure 4. Range of possible solver-optimized flux ratios with variations in the fractional lactate labeling pattern.
The average rates of glucose consumption, lactate production, and mitochondrial respiration from Table 3 were used to test the limits of the fractional lactate labeling that yielded solutions based on all constraints within the model. In (A), the fraction of unlabeled lactate (M) was held constant at 0.573 (Table 3) while M1 and M2 lactate were varied as indicated below the graph. In (B), the fraction of M1 lactate was kept constant at 0.186, while the fractions of M and M2 lactate were varied. In (C), the fraction of M2 lactate was kept constant at 0.241 while the fractions of M and M1 lactate were varied. The range of possible flux ratios that yielded solutions, and the approximate solution to the experimentally measured M/M1/M2 lactate pattern (indicated by the black arrow) give an indication of the tolerance of the model for possible changes in the measured lactate labeling pattern, depending on the cells and conditions used.
Table 4.
Range of [13C]lactate that yield model solutions for cells differing in their metabolic profiles.
| Measured | More oxidative | More glycolytic | More glycolytic | |||||
|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|||||
| J0 | 291 | 291 | 291 | 291 | ||||
| J4 | 288 | 192 | 480 | 480 | ||||
| JRR | 564 | 845 | 282 | 282 | ||||
| Solution range for: |
|
|
|
|
||||
|
|
|
|
|
|||||
|
|
0.137 – 0.267 | 0.140 – 0.289 | 0.157 – 0.198 | 0.076 – 0.141 | ||||
|
|
0.160 – 0.290 | 0.138 – 0.287 | 0.229 – 0.270 | 0.319 – 0.384 | ||||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
|
|
0.491 – 0.601 | 0.400 – 0.600 | 0.566 – 0.582 | 0.519 – 0.553 | ||||
|
|
0.213 – 0.323 | 0.214 – 0.414 | 0.232 – 0.248 | 0.347 – 0.381 | ||||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
|
|
0.519 – 0.591 | 0.458 – 0.590 | 0.569 – 0.58 | 0.526 – 0.548 | ||||
|
|
0.168 – 0.240 | 0.169 – 0.301 | 0.179 – 0.190 | 0.092 – 0.114 |
If the measured fractional M/M1/M2 lactate was assumed 0.573, 0.186, and 0.241 ( respectively), then the model yielded solutions for the measured rates of glucose consumption (J0), lactate production (J4), and mitochondrial respiration rate (JRR), as well as for two arbitrary conditions where the cells can be considered more oxidative (i.e., dependent on mitochondrial ATP synthesis) or glycolytic. For each metabolic phenotype, the range of possible [13C]lactate patterns that yielded solutions was determined by varying two of the labels as the third was held constant. For the more glycolytic phenotype, lowering the unlabeled and single-labeled lactate and increasing the double-labeled lactate ( , and ) essentially doubled the range of labeling patterns that were possible, but remained more restrictive compared to cells having a more oxidative phenotype.
The fluxes measured from each preparation and the average lactate labeling pattern were used to solve for the remaining fluxes in all six experiments (Table 5). The optimized flux ratios indicate that the non-oxidative PPP produced 28.0±2.2 % (MCSim: 26.0 – 29.3 %) of hexose phosphates while malic enzyme produced 7.7±0.3 % (MCSim: 4.7 – 12.8 %) of cytoplasmic pyruvate. While the model replicated the average [13C]lactate labeling pattern when the fluxes from each of the six experiments were used, the success rate declined to 87.6% when variability was introduced in the [13C]lactate pattern by Monte Carlo simulation (see Materials and Methods). Thus, when simultaneous 13C/flux measurements are performed with primary neurons using the conditions described herein, it is expected that some results will fall outside this model’s solvable range despite its flexibility (Table 4, Fig. 4). From the results in Table 5, evolution of the labeling pattern of the HxP and malate pools upon seven recycles through the PPP and four turns of the TCA cycle to their respective steady-states was calculated (Fig. 5). Taking into account decarboxylation of malate C4, the pyruvate derived from malic enzyme was primarily M1 (0.266/0.507/0.227 for M/M1/M2, respectively; excluding M3, which was not measured in the exported lactate). Conversely, the pyruvate derived from the HxP pool was primarily unlabeled (0.504/0.073/0.423 for M/M1/M2, respectively), while the pyruvate derived from the non-oxidative PPP production of triose phosphate was entirely unlabeled. The relatively high flux through the non-oxidative PPP was thus partly a consequence of enriching the unlabeled pyruvate through the pentose cycle to satisfy the high fractional unlabeled lactate content, while the malic enzyme contribution was necessary to enrich M1 pyruvate to satisfy that which was measured.
Calculation of fluxes from the optimized ratios revealed new insights into neuronal glucose metabolism, albeit under conditions where other exogenous oxidizable substrates were absent. The glucose consumed by CGNs could be partitioned into that used by the PC (J3b/J0 = 19.5 ± 2.2 %; MCSim: 17.9 – 20.9 %), the reactions involved in nucleotide synthesis (J9/J0 = 28.9 ± 8.3 %; MCSim: 25.9 – 31.5 %), and glycolysis (J2a/J0 = 51.6 ± 6.1 %; MCSim: 50.3 – 54.3 %). The fate of glucose in the PC includes that lost as CO2 in the oxidative PPP (9.8 %) and as triose phosphate in the non-oxidative PPP (9.8 %). Similarly, glucose consumed by the reactions synthesizing nucleotides includes that lost as CO2 (4.8 %) in the oxidative PPP and that which ultimately is transformed to nucleotides (24.1 %). While it was not surprising that glycolysis was the major glucose consumer, nucleotide synthesis and the PC contributed to a greater extent than was expected. Previous studies have reported PC activity between 1–7 % in primary neurons (Ben-Yoseph et al., 1996; Brekke et al., 2012) or the brain (Dusick et al., 2007), 6–12 % in immortalized cells (Lee et al., 1998; Lin et al., 1993; Ross et al., 1994), and 16 % in intact adipose tissue (KATZ et al., 1966). The notably greater consumption by the PC in the present study may at least partly be attributed to HxP recycling that was not explicitly considered in the previous studies. Measurement of PC activity relies on fractional isotope enrichment of CO2 or metabolites downstream of the triose phosphates from isotopically labeled glucose as it passes through the oxidative PPP, non-oxidative PPP, glycolysis, and the TCA cycle (Asahina et al., 1995; Ben-Yoseph et al., 1994; Ben-Yoseph et al., 1995; Ben-Yoseph et al., 1996; Brekke et al., 2012; KATZ et al., 1966; Ross et al., 1994). However, isotope enrichment in CO2 or other metabolites is often viewed assuming negligible HxP recycling, as accounting for unlabeled CO2 from the oxidative PPP or the more complicated label randomization (Table 1) in other metabolites becomes more difficult. As highlighted by a recent study (Rodriguez-Rodriguez et al., 2013), lack of consideration for HxP recycling can underestimate glucose metabolism by the PC. While the extent of underestimation was not reported in (Rodriguez-Rodriguez et al., 2013), the current results suggest that the PC could be more active in neurons (≈ 4 % PC averaged from (Ben-Yoseph et al., 1996; Brekke et al., 2012; Dusick et al., 2007) vs 19 % in this study) than previously thought.
It is worth mentioning that absolute fluxes through the oxidative and non-oxidative PPP are not typically measured since isotope enrichments often yield only relative fluxes. By measuring JRR, J0, and J4 along with isotope enrichment in lactate, it was possible to calculate oxidative PPP flux (Fig. 2). Oxidative PPP flux was greater than that predicted from the PC alone, which indicated nucleotide synthesis was not negligible. In fact, 30.9±9.0 % (MCSim: 28.9 – 35.7 %) of HxP processed by the oxidative PPP was diverted into nucleotides, while 46.1±6.0 % (MCSim: 42.9 – 47.4 %) was returned to the HxP pool and 23.0±3.0 % (MCSim: 21.4 – 23.7 %) was metabolized by the PC. Remarkably, J1 was 87.0±1.8 % (MCSim: 84.2 – 89.7 %) of the rate of glucose uptake and 1.71±0.24-fold (MCSim: 1.63 – 1.80) greater than glycolytic flux (Table 5). In total, 14.5 % of glucose was lost as CO2 in the oxidative PPP. This substantial flux may reflect the critical requirement of NADPH to neuronal viability, and the quantitative importance of the oxidative PPP in supplying this reducing equivalent, as 94 % was produced by this pathway compared to 6 % by malic enzyme. While it is surprising that 29 % of glucose was used for nucleotide synthesis, this result does not violate our initial assumption of ‘low’ nucleotide synthesis, as the oxidative PPP demand for G6P (254 pmol/min) was 3-fold higher than the consumption of R5P (84 pmol/min). Ribulose-5-phosphate production was therefore well in excess of that needed for nucleotide synthesis, and so while the absolute flux to nucleotides was more than negligible, it was relatively low compared to the rate at which it was supplied by the oxidative PPP.
Glycolytic processing of HxP was responsible for generating 77.6.0±0.1 % (MCSim: 73.5 – 80.6 %) of pyruvate (and thus lactate), while 14.7±0.1 % (MCSim: 13.2 – 15.6 %) was produced via glycolytic processing of PC-derived triose phosphate and the remaining 7.7±0.2 % (MCSim: 4.6 – 12.8 %) was from malic enzyme. Neurons consume more oxygen and produce less lactate than many cells, and so the majority of pyruvate is often assumed to be oxidized by mitochondria rather than reduced to lactate. However, under the current conditions where no exogenous lactate was present, and accounting for glucose shunted for nucleotide synthesis, it was found that 73.0±2.6 % (MCSim: 72.4 – 73.4 %) of pyruvate was reduced to lactate while only 27.0±2.6 % (MCSim: 26.6 – 27.6 %) was oxidized by mitochondria. The neurons thus exhibited more substantial ‘aerobic glycolysis’ than suggested by the measurements of J0 and J4. The relatively high non-oxidative PPP supply of glycolytic metabolites as well as the exogenous concentrations of glucose (10 mM) and lactate (0 mM) may be contributing factors to this phenomenon. Despite the high proportion of pyruvate shunted to lactate, the proportion of ATP derived from glycolysis vs. mitochondrial oxidative phosphorylation cannot be confidently determined from these data, as the proportion of oxygen used for ATP synthesis vs. proton leak was not determined.
The main goal of this study was to infer fluxes through the major glucose-consuming pathways from minimal experimental data by developing a model which accounted for 13C randomization in lactate as [1,2-13C2]glucose undergoes HxP recycling in the PPP and pyruvate recycling in the TCA cycle via cytoplasmic malic enzyme. While the model has provided broader insight into the metabolic state of partially depolarized neurons (with 25 mM KCl), there are limitations to extrapolating these data to the in vivo state, particularly with respect to the relatively high proportion of pyruvate converted to lactate, and the non-negligible carbon flux to nucleotides. First, the neurons were supplied with approximately 3–8 fold higher extracellular glucose concentrations compared to that present in the brain, which may promote glycolysis and lactate formation at the expense of mitochondrial pyruvate oxidation, as has been shown for cultured, immortalized cells (Cruz et al., 1999) and the intact brain (Harada et al., 1993). The extent to which this Crabtree effect may have occurred in our neurons remains to be determined, but it could partly explain the high (73 %) proportion of pyruvate shunted to lactate. Second, the use of lactate-free buffer may have also contributed to higher lactate efflux via the monocarboxylate transporter because of more favorable thermodynamics compared to in vivo where extracellular lactate levels are estimated to be 0.5 – 1.5 mM (Barros and Deitmer, 2010; Dienel, 2012; Harada et al., 1993). Third, the relatively large flux of ribose-5-phosphate to nucleotides may partly reflect an artifact of ribose efflux since extracellular ribose, present at 10–100 μM in the brain (see (Wei et al., 2009)), was not included in the experimental buffer. Such conditions could favor facilitative efflux of ribose formed from non-enzymatic decomposition of ribose-5-phosphate or its isomerized product ribose-1-phosphate. While no ribose-specific facilitative transporter has been identified in mammalian cells, one or more GLUT transporters may catalyze efflux. The protozoan GLUT LmGT2 has been shown to transport ribose, albeit at a rate about 8-fold less than glucose under ideal conditions where both sugars are not simultaneously present (Naula et al., 2010). Assuming the neuronal GLUT transporters have a similar preference for glucose over ribose, the rate of efflux of the latter could, in principle, account for 43% ([291/8]/84) of the apparent nucleotide synthesis rate. The efflux rate would likely be much less than this given the low level of intracellular ribose compared to glucose and the competition of glucose and ribose for binding to the GLUT transporters, as has been shown for ribose uptake into COS cells (Lager et al., 2003). The buffer composition in this study may therefore favor glucose conversion to lactate over its oxidation by mitochondria, as well as apparent glucose shunting to nucleotides by ribose efflux.
4. Summary and Conclusions
A model has been developed to determine fluxes through the major glucose consuming reactions in neurons from measurements of glucose uptake, lactate production, respiration, and [13C]lactate labeling from [1,2-13C2]glucose. The solver function of Microsoft Excel was used to optimize the contribution of the non-oxidative PPP to labeling of the HxP pool while accounting for HxP recycling, the contribution of malic enzyme to labeling of the pyruvate pool, and the contribution of pyruvate oxidation to mitochondrial respiration. The model found solutions over a range of possible M/M1/M2 lactate measurements and metabolic phenotypes with glucose as the sole exogenous substrate available. In primary cerebellar granule neurons, glycolysis was the primary glucose consumer (52 %), but metabolism via the pentose cycle (19 %) was greater than previous studies that have not taken HxP recycling into account. Nucleotide synthesis is often assumed negligible in neurons, but it was found to account for 29 % of glucose consumed. Malic enzyme accounted for 8 % of pyruvate produced, compared to 77 % for glycolytic processing of hexose phosphates and 15 % for glycolytic processing of triose phosphates derived from the pentose cycle. Although neurons primarily rely on mitochondrial oxidative phosphorylation for ATP production, 73 % of the pyruvate was exported as lactate. While further tests of the validity of this model are required by direct measurements of intracellular 13C labeling of HxP, malate, and pyruvate pools, the relatively straightforward approach described here to quantifying fluxes through all major glucose consuming reactions from minimal experimental data is an important step toward developing a systems-level understanding of energy metabolism and redox regulation in adherent neurons.
Highlights.
A model was developed to quantitate neuronal metabolism from 13C2 glucose.
13C randomization in lactate due to hexose phosphate recycling was determined.
Glycolysis and the pentose cycle accounted for 52 and 19 %, resp. of glucose used.
Only 16% of glucose was used by mitochondria vs. 46% by lactate dehydrogenase.
This approach yielded extensive flux information from minimal experiments.
Acknowledgments
We thank Penni Bolton for care of the animals and Dr. Mahmoud ElSohly for financial support.
Funding Information
This work was supported by Grant No. R15NS060107 from the National Institute of Neurological Disorders and Stroke (to MBJ). Dr. ElSohly and the NIH had no role in the design, execution, interpretation, and reporting of the experiments described herein.
Abbreviations list
- PPP
pentose phosphate pathway
- PC
pentose cycle
- HxP
hexose phosphate (referring to both glucose-6-phosphate and fructose-6-phosphate)
- TCA
tricarboxylic acid
- M
a metabolite having no 13C atoms derived from [1,2-13C2]glucose
- M1
a metabolite having one 13C atom derived from [1,2-13C2]glucose
- M2
a metabolite having two 13C atoms derived from [1,2-13C2]glucose
- M3
a metabolite having three 13C atoms derived from [1,2-13C2]glucose
- Jx
flux through reaction x
Footnotes
Declarations of Interest
The authors declare no conflicts of interest.
Author contribution statement
HMG, BA, YHW, and IAK contributed to experimental design and performed experiments; MBJ developed the model and experimental approach, performed experiments, and wrote the paper.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Hoda M. Gebril, Email: hmgebril@go.olemiss.edu.
Bharathi Avula, Email: bavula@olemiss.edu.
Yan-Hong Wang, Email: wangyh@olemiss.edu.
Ikhlas A. Khan, Email: ikhan@olemiss.edu.
References
- 1.Ahn WS, Antoniewicz MR. Metabolic flux analysis of CHO cells at growth and non-growth phases using isotopic tracers and mass spectrometry. Metab Eng. 2011:598–609. doi: 10.1016/j.ymben.2011.07.002. [DOI] [PubMed] [Google Scholar]
- 2.Amaral AI, Teixeira AP, Hakonsen BI, Sonnewald U, Alves PM. A comprehensive metabolic profile of cultured astrocytes using isotopic transient metabolic flux analysis and C-labeled glucose. Front Neuroenergetics. 2011a:5. doi: 10.3389/fnene.2011.00005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Amaral AI, Teixeira AP, Sonnewald U, Alves PM. Estimation of intracellular fluxes in cerebellar neurons after hypoglycemia: importance of the pyruvate recycling pathway and glutamine oxidation. J Neurosci Res. 2011b:700–710. doi: 10.1002/jnr.22571. [DOI] [PubMed] [Google Scholar]
- 4.Asahina T, Kashiwagi A, Nishio Y, Ikebuchi M, Harada N, Tanaka Y, Takagi Y, Saeki Y, Kikkawa R, Shigeta Y. Impaired activation of glucose oxidation and NADPH supply in human endothelial cells exposed to H2O2 in high-glucose medium. Diabetes. 1995:520–526. doi: 10.2337/diab.44.5.520. [DOI] [PubMed] [Google Scholar]
- 5.Bak LK, Waagepetersen HS, Melo TM, Schousboe A, Sonnewald U. Complex glutamate labeling from [U-13C]glucose or [U-13C]lactate in co-cultures of cerebellar neurons and astrocytes. Neurochem Res. 2007:671–680. doi: 10.1007/s11064-006-9161-4. [DOI] [PubMed] [Google Scholar]
- 6.Barros LF, Deitmer JW. Glucose and lactate supply to the synapse. Brain Res Rev. 2010:149–159. doi: 10.1016/j.brainresrev.2009.10.002. [DOI] [PubMed] [Google Scholar]
- 7.Ben-Yoseph O, Boxer PA, Ross BD. Oxidative stress in the central nervous system: monitoring the metabolic response using the pentose phosphate pathway. Dev Neurosci. 1994:328–336. doi: 10.1159/000112127. [DOI] [PubMed] [Google Scholar]
- 8.Ben-Yoseph O, Boxer PA, Ross BD. Assessment of the role of the glutathione and pentose phosphate pathways in the protection of primary cerebrocortical cultures from oxidative stress. J Neurochem. 1996:2329–2337. doi: 10.1046/j.1471-4159.1996.66062329.x. [DOI] [PubMed] [Google Scholar]
- 9.Ben-Yoseph O, Camp DM, Robinson TE, Ross BD. Dynamic measurements of cerebral pentose phosphate pathway activity in vivo using [1,6-13C2,6,6-2H2]glucose and microdialysis. J Neurochem. 1995:1336–1342. doi: 10.1046/j.1471-4159.1995.64031336.x. [DOI] [PubMed] [Google Scholar]
- 10.Brekke EM, Walls AB, Schousboe A, Waagepetersen HS, Sonnewald U. Quantitative importance of the pentose phosphate pathway determined by incorporation of 13C from [2-13C]- and [3-13C]glucose into TCA cycle intermediates and neurotransmitter amino acids in functionally intact neurons. J Cereb Blood Flow Metab. 2012:1788–1799. doi: 10.1038/jcbfm.2012.85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chinta SJ, Kumar MJ, Hsu M, Rajagopalan S, Kaur D, Rane A, Nicholls DG, Choi J, Andersen JK. Inducible alterations of glutathione levels in adult dopaminergic midbrain neurons result in nigrostriatal degeneration. J Neurosci. 2007:13997–14006. doi: 10.1523/JNEUROSCI.3885-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Cruz F, Scott SR, Barroso I, Santisteban P, Cerdan S. Ontogeny and cellular localization of the pyruvate recycling system in rat brain. J Neurochem. 1998:2613–2619. doi: 10.1046/j.1471-4159.1998.70062613.x. [DOI] [PubMed] [Google Scholar]
- 13.Cruz HJ, Moreira JL, Carrondo MJ. Metabolic shifts by nutrient manipulation in continuous cultures of BHK cells. Biotechnol Bioeng. 1999:104–113. doi: 10.1002/(sici)1097-0290(1999)66:2<104::aid-bit3>3.0.co;2-#. [DOI] [PubMed] [Google Scholar]
- 14.Dienel GA. Brain lactate metabolism: the discoveries and the controversies. J Cereb Blood Flow Metab. 2012:1107–1138. doi: 10.1038/jcbfm.2011.175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Dunn L, Allen GF, Mamais A, Ling H, Li A, Duberley KE, Hargreaves IP, Pope S, Holton JL, Lees A, Heales SJ, Bandopadhyay R. Dysregulation of glucose metabolism is an early event in sporadic Parkinson’s disease. Neurobiol Aging. 2014:1111–1115. doi: 10.1016/j.neurobiolaging.2013.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Dusick JR, Glenn TC, Lee WN, Vespa PM, Kelly DF, Lee SM, Hovda DA, Martin NA. Increased pentose phosphate pathway flux after clinical traumatic brain injury: a [1,2-13C2]glucose labeling study in humans. J Cereb Blood Flow Metab. 2007:1593–1602. doi: 10.1038/sj.jcbfm.9600458. [DOI] [PubMed] [Google Scholar]
- 17.Fernandez-Fernandez S, Almeida A, Bolanos JP. Antioxidant and bioenergetic coupling between neurons and astrocytes. Biochem J. 2012:3–11. doi: 10.1042/BJ20111943. [DOI] [PubMed] [Google Scholar]
- 18.Filosa S, Fico A, Paglialunga F, Balestrieri M, Crooke A, Verde P, Abrescia P, Bautista JM, Martini G. Failure to increase glucose consumption through the pentose-phosphate pathway results in the death of glucose-6-phosphate dehydrogenase gene-deleted mouse embryonic stem cells subjected to oxidative stress. Biochem J. 2003:935–943. doi: 10.1042/BJ20021614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Harada M, Sawa T, Okuda C, Matsuda T, Tanaka Y. Effects of glucose load on brain extracellular lactate concentration in conscious rats using a microdialysis technique. Horm Metab Res. 1993:560–563. doi: 10.1055/s-2007-1002177. [DOI] [PubMed] [Google Scholar]
- 20.Herrero-Mendez A, Almeida A, Fernandez E, Maestre C, Moncada S, Bolanos JP. The bioenergetic and antioxidant status of neurons is controlled by continuous degradation of a key glycolytic enzyme by APC/C-Cdh1. Nat Cell Biol. 2009:747–752. doi: 10.1038/ncb1881. [DOI] [PubMed] [Google Scholar]
- 21.Hofmann U, Maier K, Niebel A, Vacun G, Reuss M, Mauch K. Identification of metabolic fluxes in hepatic cells from transient 13C-labeling experiments: Part I. Experimental observations. Biotechnol Bioeng. 2008:344–354. doi: 10.1002/bit.21747. [DOI] [PubMed] [Google Scholar]
- 22.Iguchi Y, Katsuno M, Takagi S, Ishigaki S, Niwa J, Hasegawa M, Tanaka F, Sobue G. Oxidative stress induced by glutathione depletion reproduces pathological modifications of TDP-43 linked to TDP-43 proteinopathies. Neurobiol Dis. 2012:862–870. doi: 10.1016/j.nbd.2011.12.002. [DOI] [PubMed] [Google Scholar]
- 23.Jekabsons MB. A systems biology approach to investigating apoptotic stimuli as effectors of cell metabolism: practical application of top-down control analysis to attached neurons. Int J Mol Sci. 2009:702–722. doi: 10.3390/ijms10020702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Jekabsons MB, Nicholls DG. In situ respiration and bioenergetic status of mitochondria in primary cerebellar granule neuronal cultures exposed continuously to glutamate. J Biol Chem. 2004:32989–33000. doi: 10.1074/jbc.M401540200. [DOI] [PubMed] [Google Scholar]
- 25.Jekabsons MB, Nicholls DG. Bioenergetic analysis of cerebellar granule neurons undergoing apoptosis by potassium/serum deprivation. Cell Death Differ. 2006:1595–1610. doi: 10.1038/sj.cdd.4401851. [DOI] [PubMed] [Google Scholar]
- 26.KATZ J, LANDAU BR, BARTSCH GE. The pentose cycle, triose phosphate isomerization, and lipogenesis in rat adipose tissue. J Biol Chem. 1966:727–740. [PubMed] [Google Scholar]
- 27.KATZ J, Rognstad R. The labeling of pentose phosphate from glucose-14C and estimation of the rates of transaldolase, transketolase, the contribution of the pentose cycle, and ribose phosphate synthesis. Biochemistry. 1967:2227–2247. doi: 10.1021/bi00859a046. [DOI] [PubMed] [Google Scholar]
- 28.KATZ J, WOOD HG. The use of glucose-C14 for the evaluation of the pathways of glucose metabolism. J Biol Chem. 1960:2165–2177. [PubMed] [Google Scholar]
- 29.KATZ J, WOOD HG. The use of C14O2 yields from glucose-1- and -6-C14 for the evaluation of the pathways of glucose metabolism. J Biol Chem. 1963:517–523. [PubMed] [Google Scholar]
- 30.Kirkland RA, Franklin JL. Evidence for redox regulation of cytochrome C release during programmed neuronal death: antioxidant effects of protein synthesis and caspase inhibition. J Neurosci. 2001:1949–1963. doi: 10.1523/JNEUROSCI.21-06-01949.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lager I, Fehr M, Frommer WB, Lalonde S. Development of a fluorescent nanosensor for ribose. FEBS Lett. 2003:85–89. doi: 10.1016/s0014-5793(03)00976-1. [DOI] [PubMed] [Google Scholar]
- 32.Lee WN, Boros LG, Puigjaner J, Bassilian S, Lim S, Cascante M. Mass isotopomer study of the nonoxidative pathways of the pentose cycle with [1,2-13C2]glucose. Am J Physiol. 1998:E843–E851. doi: 10.1152/ajpendo.1998.274.5.E843. [DOI] [PubMed] [Google Scholar]
- 33.Levonen AL, Hill BG, Kansanen E, Zhang J, Darley-Usmar VM. Redox regulation of antioxidants, autophagy, and the response to stress: implications for electrophile therapeutics. Free Radic Biol Med. 2014:196–207. doi: 10.1016/j.freeradbiomed.2014.03.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Li M, Sun M, Cao L, Gu JH, Ge J, Chen J, Han R, Qin YY, Zhou ZP, Ding Y, Qin ZH. A TIGAR-regulated metabolic pathway is critical for protection of brain ischemia. J Neurosci. 2014:7458–7471. doi: 10.1523/JNEUROSCI.4655-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lin YY, Cheng WB, Wright CE. Glucose metabolism in mammalian cells as determined by mass isotopomer analysis. Anal Biochem. 1993:267–273. doi: 10.1006/abio.1993.1118. [DOI] [PubMed] [Google Scholar]
- 36.Maier K, Hofmann U, Reuss M, Mauch K. Identification of metabolic fluxes in hepatic cells from transient 13C-labeling experiments: Part II. Flux estimation. Biotechnol Bioeng. 2008:355–370. doi: 10.1002/bit.21746. [DOI] [PubMed] [Google Scholar]
- 37.Munger J, Bennett BD, Parikh A, Feng XJ, McArdle J, Rabitz HA, Shenk T, Rabinowitz JD. Systems-level metabolic flux profiling identifies fatty acid synthesis as a target for antiviral therapy. Nat Biotechnol. 2008:1179–1186. doi: 10.1038/nbt.1500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Naula CM, Logan FJ, Wong PE, Barrett MP, Burchmore RJ. A glucose transporter can mediate ribose uptake: definition of residues that confer substrate specificity in a sugar transporter. J Biol Chem. 2010:29721–29728. doi: 10.1074/jbc.M110.106815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Olstad E, Olsen GM, Qu H, Sonnewald U. Pyruvate recycling in cultured neurons from cerebellum. J Neurosci Res. 2007:3318–3325. doi: 10.1002/jnr.21208. [DOI] [PubMed] [Google Scholar]
- 40.Rodriguez-Rodriguez P, Fernandez E, Bolanos JP. Underestimation of the pentose-phosphate pathway in intact primary neurons as revealed by metabolic flux analysis. J Cereb Blood Flow Metab. 2013:1843–1845. doi: 10.1038/jcbfm.2013.168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ross BD, Kingsley PB, Ben-Yoseph O. Measurement of pentose phosphate-pathway activity in a single incubation with [1,6-13C2,6,6-2H2]glucose. Biochem J. 1994:31–38. doi: 10.1042/bj3020031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Sherer TB, Betarbet R, Testa CM, Seo BB, Richardson JR, Kim JH, Miller GW, Yagi T, Matsuno-Yagi A, Greenamyre JT. Mechanism of toxicity in rotenone models of Parkinson’s disease. J Neurosci. 2003:10756–10764. doi: 10.1523/JNEUROSCI.23-34-10756.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Stincone A, Prigione A, Cramer T, Wamelink MM, Campbell K, Cheung E, Olin-Sandoval V, Gruning N, Kruger A, Tauqeer AM, Keller MA, Breitenbach M, Brindle KM, Rabinowitz JD, Ralser M. The return of metabolism: biochemistry and physiology of the pentose phosphate pathway. Biol Rev Camb Philos Soc. 2014 doi: 10.1111/brv.12140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Uran S, Landmark KE, Hjellum G, Skotland T. Quantification of 13C pyruvate and 13C lactate in dog blood by reversed-phase liquid chromatography-electrospray ionization mass spectrometry after derivatization with 3-nitrophenylhydrazine. J Pharm Biomed Anal. 2007:947–954. doi: 10.1016/j.jpba.2007.04.001. [DOI] [PubMed] [Google Scholar]
- 45.Vesce S, Jekabsons MB, Johnson-Cadwell LI, Nicholls DG. Acute glutathione depletion restricts mitochondrial ATP export in cerebellar granule neurons. J Biol Chem. 2005:38720–38728. doi: 10.1074/jbc.M506575200. [DOI] [PubMed] [Google Scholar]
- 46.Waagepetersen HS, Sonnewald U, Larsson OM, Schousboe A. A possible role of alanine for ammonia transfer between astrocytes and glutamatergic neurons. J Neurochem. 2000a:471–479. doi: 10.1046/j.1471-4159.2000.0750471.x. [DOI] [PubMed] [Google Scholar]
- 47.Waagepetersen HS, Sonnewald U, Larsson OM, Schousboe A. Compartmentation of TCA cycle metabolism in cultured neocortical neurons revealed by 13C MR spectroscopy. Neurochem Int. 2000b:349–358. doi: 10.1016/s0197-0186(99)00143-6. [DOI] [PubMed] [Google Scholar]
- 48.Wei Y, Chen L, Chen J, Ge L, He RQ. Rapid glycation with D-ribose induces globular amyloid16 like aggregations of BSA with high cytotoxicity to SH-SY5Y cells. BMC Cell Biol. 2009:10. doi: 10.1186/1471-2121-10-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Won SJ, Kim JE, Cittolin-Santos GF, Swanson RA. Assessment at the single-cell level identifies neuronal glutathione depletion as both a cause and effect of ischemia-reperfusion oxidative stress. J Neurosci. 2015:7143–7152. doi: 10.1523/JNEUROSCI.4826-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.WOOD HG, KATZ J. The distribution of C14 in the hexose phosphates and the effect of recycling in the pentose cycle. J Biol Chem. 1958:1279–1282. [PubMed] [Google Scholar]