Directional patterns of cross frequency phase and amplitude coupling within the resting state mimic patterns of fMRI functional connectivity

Abstract

Functional imaging investigations into the brain's resting state interactions have yielded a wealth of insight into the intrinsic and dynamic neural architecture supporting cognition and behavior. Electrophysiological studies however have highlighted the fact that synchrony across large-scale cortical systems is composed of spontaneous interactions occurring at timescales beyond the traditional resolution of fMRI, a feature that limits the capacity of fMRI to draw inference on the true directional relationship between network nodes. To approach the question of directionality in resting state signals, we recorded resting state functional MRI (rsfMRI) and electrocorticography (ECoG) from four human subjects undergoing invasive epilepsy monitoring. Using a seed-point based approach, we employed phase-amplitude coupling (PAC) and biPhase Locking Values (bPLV), two measures of cross-frequency coupling (CFC) to explore both outgoing and incoming connections between the seed and all non-seed, site electrodes. We observed robust PAC between a wide range of low-frequency phase and high frequency amplitude estimates. However, significant bPLV, a CFC measure of phase-phase synchrony, was only observed at specific narrow low and high frequency bandwidths. Furthermore, the spatial patterns of outgoing PAC connectivity were most closely associated with the rsfMRI connectivity maps. Our results support the hypothesis that PAC is relatively ubiquitous phenomenon serving as a mechanism for coordinating high-frequency amplitudes across distant neuronal assemblies even in absence of overt task structure. Additionally, we demonstrate that the spatial distribution of a seed-point rsfMRI sensorimotor network is strikingly similar to specific patterns of directional PAC. Specifically, the high frequency activities of distal patches of cortex owning membership in a rsfMRI sensorimotor network were most likely to be entrained to the phase of a low frequency rhythm engendered from the neural populations at the seed-point, suggestive of greater directional coupling from the seed out to the site electrodes.

Introduction

Since the initial proposal of meaningful neural activities within the resting state period in fMRI (Biswal et al., 1995), there has been a growing momentum within systems neuroscience to explore and contextualize the role that spontaneous, synchronous neural responses play in brain physiology and cognition. Empirical recordings of resting state BOLD fMRI oscillations have yielded tremendous insight into the brain's intrinsic and dynamic architecture. It is now well-established that the presence of statistical dependencies within resting state fMRI (rsfMRI) signals reflects a core, intrinsic organization (Greicius et al., 2009; Keller et al., 2014; O'Reilly et al., 2013) that tends to mimic patterns of evoked, task-based behavioral activity (Cole et al., 2014; Smith et al., 2009). rsfMRI is now widely applied within the research arena to illuminate, quantify and characterize dynamic patterns of functional connectivity across distributed, long-distance cortical networks as well as within local cortical neighborhoods (Biswal et al., 2010; Hutchison et al., 2013). Yet despite the extensive success of resting state fMRI in repositioning functional connectivity within the broader scope of functional neuroanatomy, studies interrogating the neurophysiological dynamics of functional connectivity have lagged substantially behind imaging-based investigations.

Initial electrophysiological efforts correlated simultaneously acquired electroencephalography (EEG) with the time-varying infra-slow-frequency fluctuations in the BOLD signal (<0.1 Hz) that define the resting state functional connectivity (Jann et al., 2010; Mantini et al., 2007). Statistical relationships were noted between various intrinsic networks and a full range of the canonical neurophysiological frequency bands as well as DC-coupled infraslow oscillations (e.g. the slow cortical potential; Hiltunen et al., 2014). More recent EEG as well as magnetoencephalography (MEG) studies have explored various regression approaches as well as linear coupling metrics of both phase (Hillebrand et al., 2012) and amplitude components (Brookes et al., 2011; de Pasquale et al., 2010) of resting state signals in an effort to better characterize the spatiotemporal signatures of functional connectivity at approximate millisecond timescales.

Taken together, the majority of imaging and electrophysiological resting state studies of functional connectivity have led to an overall spatiotemporal complexity that reflects a basic level of linear realized synchrony across and between neocortical networks (see Schölvinck et al., 2013 for a review). However, it has been proposed that resting state dynamical network behavior is not solely a function of linear interactions on an infra-slow time scale; rather network synchrony is a product of the interplay between the underlying long-distance structural connectivity and local processing dynamics (Cabral et al., 2011). Relying on imaging-based modeling inferences, these authors hypothesized that only a characterization of the underlying networks' phase oscillators would lead to a richer understanding of the contributions that resting state neural interactions provide to overall computation and brain-state dynamics. An underlying assumption to this framework is that resting state interactions must be defined by a degree of nonlinear, cross-frequency coupling (CFC) that would serve to entrain or coordinate higher-frequency activity in multiple, spatially-distant yet anatomically connected local neural populations (Singer, 2013).

In line with this hypothesis, two resting state MEG reports have revealed the presence of significant, within-network phase-amplitude coupling (PAC) between low-frequency phase estimates and higher-frequency gamma amplitude values (Florin and Baillet, 2015; Osipova et al., 2008). These studies extend to the resting state the principled mechanistic hypothesis of PAC, namely that band-limited, low-frequency oscillations serve to entrain local high-frequency activities between distally-housed network nodes with minimal lag time. Based on task driven synchrony, PAC thus provides a mechanism for the coordination of the long-distance communication necessary to orchestrate cognition and behavior (Canolty and Knight, 2010). Therefore, this observation within the resting state is reflective of a much deeper level of cortical interaction (Buzsáki and Draguhn, 2004) unfolding in a behaviorally independent context.

Here we use human electrocorticographic (ECoG) recordings to support and expand on these initial resting-state, cross-frequency interactions. Relative to scalp-based methods, ECoG records high frequency (i.e. high gamma [HG] band ~70–200 Hz) activity at much higher fidelity and spatial specificity (Crone et al., 2006). Critically, HG best reflects increases in broadband firing rates subserving local cortical processing (Manning et al., 2009; Miller et al., 2014) and has been shown to reflect patterns of rsfMRI functional connectivity (Keller et al., 2013; Ko et al., 2013), and is thus integral to forming a complete picture of resting state interactions.

Resting state fMRI and sub-dural ECoG recordings were separately acquired from 4 individuals with electrode coverage spanning lateral parietal-temporal cortices. We employed a seed-point strategy whereby a pre-selected motor electrode identified the sensorimotor network and served as the reference point for computing patterns of synchrony. ECoG electrodes were identified as owning membership to a cortical sensorimotor network based on individual seed-point rsfMRI functional connectivity. We then computed biPhase Locking Value (bPLV), a nonlinear measure of cross-frequency phase-phase interactions (Darvas et al., 2009a,b) as well as PAC, and contrasted coupling metrics from electrodes within- and out-of- the sensorimotor network. Our overall goal was to test whether within a well-established intrinsic network (i.e. the sensorimotor network), synchrony within the resting state is organized by cross-frequency phase entrainment. Our guiding hypotheses are built on previous task-based modulations of long-range CFC during motor execution (Darvas et al., 2009b; Yanagisawa et al., 2012). Specifically, because both PAC and bPLV have been theorized as computational mechanisms supporting the coordination of active motor behaviors, our goal was to determine whether these same mechanisms supervise or coordinate spontaneous activities within the resting sensorimotor system. Further, based on recent evidence demonstrating CFC causal directionality through a behaviorally driven asymmetry of bPLV (Darvas et al., 2009b) and PAC (Fontolan et al., 2014), we hypothesized that that phase and amplitude CFC may yield insight into the directionality across an rsfMRI-defined neural network during the resting state. The identification and characterization of non-linear coupling through electrophysiology is critical for fostering insight into the endogenous, dynamic processes that give rise to the resting state functional connectivity phenomenon.

Materials & methods

Subjects

Three epilepsy subjects (1 female; age range 19–38) were recruited from the Seattle Regional Epilepsy Center at Harborview Medical Center (HMC) and one subject (1 female; age 13) was recruited from the Epilepsy Unit at Seattle Children's Hospital (SCH). All patients were undergoing long-term ECoG monitoring for surgical treatment of intractable epilepsy. Resting-state recordings were acquired 1) pre-operatively using fMRI and 2) post-operatively from sub-durally placed platinum ECoG electrode arrays (Ad-Tech, Racine, WI). Placement and positioning of ECoG electrode arrays were determined exclusively on clinical requirements for each individual patient. All measurements reported here come from macro-grid electrodes with a 2.3 mm exposed surface diameter per electrode and a 1 cm inter-electrode distance. All patients provided informed consent in accordance with the University of Washington Institutional Review Boards or informed assent according to the Seattle Children's Hospital IRB policies.

Acquisition

MR imaging acquisition

Images were acquired pre-operatively on a Philips 3 T Achieva for HMC patients and on a Seimens 3 T Magnetom scanner for the SCH patient. All images were acquired using an 8-channel SENSE head coil. For anatomical volume registration and surface reconstructions, a magnetization prepared rapid gradient echo (MPRAGE) high-resolution T1 sequence (repetition time (TR)/echo time (TE)/flip angle: 6.5 milliseconds (ms)/3 ms/8°; matrix size of 256 × 256 and with 170 sagittally collected slices with a slice thickness of 1 mm) was acquired.

Resting state fMRI

At both sites, a standard resting state fMRI (rsfMRI) Echo Planar sequence was utilized to establish functional connectivity maps for each participant. This sequence consisted of an 8-minute rsfMRI sequence (TR/TE/FA: 2000/21/90) with 38 axially oriented slices, 3.5 mm in-plane resolution with a matrix size of 64 × 64. For all subjects, five ‘dummy’ volumes were included but not acquired to stabilize T1 equilibration effects. Subjects were asked to lie still with eyes open while staring at a centrally placed cross-hair.

Electrocorticography acquisition

Resting state and behavioral ECoG recordings were conducted at the patient's bedside. For the resting state recordings, the patient was asked to remain awake and silent with eyes open and generate as little movement as possible during an 8 min free-running recording session. A Guger g.USBamps (GugerTec, Graz, Austria) amplifier system was used for all electrophysiological recordings. Data from 64 channels for each patient were sampled at 1200 Hz with respect to a standard scalp reference electrode (HMC patients) or a subgaleal reference electrode (SCH patient). All recordings were DC-coupled, hardware (low-pass at 500 Hz and high-pass at 0.1 Hz) and notch filtered at 60 Hz. The BCI2000 software suite (Schalk et al., 2004) was utilized for stimulus presentation during the motor screen behavioral task (see below).

Functional screening

To identify a seed-point electrode for ECoG and rsfMRI functional connectivity analyses, we first conducted a simple, visually-cued motor screening task requiring each subject to perform overt movement of their tongue and hand in response to a visual cue. In this task, the subject was presented a visual cue prompting them to move either their tongue or the hand contralateral to the ECoG grid placement. The cue was presented for 3 s and followed by a 3 second inter trial interval. The purpose of this session was to identify electrodes that demonstrated task-driven modulation of HG activity during overt motor movement relative to rest. Significant (p < 0.05; Student's t-test) contrasts were employed to identify cortical areas showing an increase in HG power (70–200 Hz) power during active task execution relative to rest. The electrode that showed the largest resulting t-value was selected from the full montage and labeled as the seed-point for all subsequent functional connectivity approaches.

Analysis

Imaging

Resting state fMRI analysis

Standard rsfMRI pre-processing steps were implemented in FEAT (FMRI Expert Analysis Tool) Version 6.0, part of FSL (FMRIB's Software Library, www.fmrib.ox.ac.uk/fsl) to remove non-neuronal sources of variance. These included skull stripping using BET, motion correction (realignment to the center volume) with FSL MCFLIRT, spatial smoothing using a 6 mm full-width half-maximum (FWHM) Gaussian kernel, grand-mean intensity normalization and a high-pass linear drift removal. To limit the effect of physiological noise on functional connectivity, the overall time series was then temporally low-pass filtered removing frequencies above 0.2 Hz. Additionally, ventricular CSF signal, white matter (WM) and whole brain, global signal were extracted. Each 4D data set was entered into a multiple regression analysis, treating the movement parameters, CSF, WM and global signal as nuisance variables.

A seed point analysis strategy was employed to estimate motor functional connectivity maps for each individual patient. An 8 mm spherical seed-point was centered on the cortical tissue directly beneath the selected electrode as determined from the motor screening results. Seed-point functional connectivity maps were then generated by a voxelwise regression of the mean time-course of all voxels within the seed-point using FSL FILM. Each map was converted into Z-scores using a general linear model approach (FSL FEAT). The Z (Gaussianised T/F) statistic images were thresholded using GRF-theory-based maximum height thresholding with a (corrected) significance threshold of p < 0.05. Whole brain maps were generated for each individual and overlaid onto the native cortical surface rendering (see below).

Electrocorticography

Pre-processing

All ECoG data pre-processing and analyses were conducted in the MATLAB computing environment (The MathWorks, Natick, MA). Preprocessing (functional screening and resting state recordings) included manual inspection for channels or time periods contaminated with obvious non-physiologic artifact or substantial inter-ictal activity. For each subject, the data were then re-referenced to the common average across all good channels. Signals were then notch-filtered to remove line noise at 60, 120 & 180 Hz using 4^th-order Butterworth filters. For the purposes of the functional screening (motor) data only, power spectra were derived for the HG band using the absolute square of the analytic amplitude estimate from the Hilbert transform. Data were then log transformed to approximate a normal distribution. For individual resting state runs, we then computed the biPhase locking values and phase amplitude coupling. For CFC computation, we estimated the instantaneous analytic amplitude and phases for each clean data set using a complex wavelet transform with the Morlet wavelet.

biPhase locking value (bPLV)

The biPhase locking value bPLV is a non-linear measure of CFC. Its application to task related data within the motor domain and its properties are described in detail in (Darvas et al., 2009a). Here we give a brief overview of the methods. The bPLV tests for the presence of modulation of one frequency f₁ by a second frequency f₂, e.g. by a multiplicative non-linearity. This approach yields two sidebands: a signal that arises at the sum (i.e. f₃ = f₁ + f₂) and subtraction (i.e. f₃ = f₁ – f₂) of the two frequencies. It is important to note that f₁ and f₂ are assumed to be completely independent and can arise from very different neural mechanisms. The bPLV tests whether the phase of f₃ is locked to the sum of the phases of f₁ and f₂. Here we test for signals X at f₁, Y at f₂ and Z at f₃ for all paired interactions across a ECoG montage that is specific to 1) a seed electrode to all other electrodes and 2) vice versa. When (f₁ + f₂) and f₃ are locked at different electrodes, the presence of a bPLV can be interpreted as a coupled interaction. For example, when X and Y are measured in a single electrode and Z elsewhere, the bPLV can be seen as a directional measure, since two independent processes (X, Y) at one site influence a distant site (Z), but not necessarily vice versa. In its earlier applications, bPLV has been mostly used in an event-related fashion, where the presence of non-linear coupling was examined with respect to a specific, external event. In our present study, such events do not exist and we are interested in measuring the spontaneous, endogenous bPLV across a neural system. The event related definition of the bBLV, as e.g. given in (Darvas et al., 2009a), can be readily rewritten to measure ongoing bPLV over time. Let θ_X(t_i,f₁),θ_Y(t_i,f₂) and θ_Z(t_i,f₁+f₂) be the instantaneous phase estimates of signal X, Y and Z for the ith sample, then the bPLV estimate of T samples is given by:

$${\mathrm{bPLV}}_{XYZ}({\mathrm{f}}_1,{\mathrm{f}}_2)=\mid \frac{1}{\mathrm{T}}\sum _{\mathrm{i}=1}^{\mathrm{T}}{e}^{\mathrm{i}({\theta }_{\mathrm{X}}({\mathrm{t}}_i,{\mathrm{f}}_1)+{\theta }_Y({\mathrm{t}}_i,{\mathrm{f}}_2)-{\theta }_Z({\mathrm{t}}_i,{\mathrm{f}}_1+{\mathrm{f}}_2))}\mid .$$ (1)

In the case of perfect phase coupling, the bPLV is equal to one, and in the case of complete asynchrony, it is zero. However, this is only true for the limiting case of □ → ∞. Here, we average over 8 s of data at a sampling rate of 1200 Hz, i.e. T = 576,000. Also note, that since we average the continuous zero lag phase over full time, the number of independent estimates of phase is dependent on frequency, e.g. alpha frequencies at 10 Hz are averaged over 10 times fewer effectively uncorrelated samples than f = 100 Hz. Thus, the resulting map bPLV_XYZ(f₁,f₂) over the two coupling frequencies f₁ and f₂, even under the null hypothesis of no coupling, has a frequency dependent bias. In order to accommodate this bias, we carried out a normalization step for each frequency pair (f₁, f₂), which is described in detail in the following section on statistical testing. Our efforts were guided by previous studies on CFC revealing significant low-to-high frequency coupling (Canolty and Knight, 2010; Darvas et al., 2009b; Florin and Baillet, 2015). We focused here on coupling of low frequency (1–40 Hz, in 1 Hz steps) to high frequencies (70–200 Hz, in 1 Hz steps). Because of the asymmetric nature of this coupling, we consider two distinct situations, outgoing bPLV, where X and Y are taken from the motor-defined, seed electrode and Z is elsewhere on the ECoG array (i.e. site electrode) and incoming bPLV, where X and Y are elsewhere and Z is the recorded at the seed electrode. Finally, to examine the specificity of bPLV coupling, we computed and compared the conjugated sideband component (f₂ – f₁) for each computed multiplicative interaction (as described in Darvas et al., 2009a) spanning identical frequency ranges.

Phase amplitude coupling (PAC)

PAC is a well-established method to test for CFC and has been extensively discussed in the literature see e.g., (Canolty and Knight, 2010) for a discussion of the functional role of PAC, for e.g. (Onslow et al., 2011; Penny et al., 2008; Tort et al., 2010) technical aspects of this method. We used an amplitude normalized version of PAC, as described in (Florin and Baillet, 2015), to measure the free running coupling with this modality across our full resting state recording. For preferred-phase calculations, where typically HG amplitude is binned over a low frequency phase, e.g. theta or alpha, in a range from – pi to pi, we computed a pseudo Z-score to highlight the phase dependent amplitude changes vs. average amplitude over time. We normalized instantaneous amplitude in each phase bin with its mean and standard deviation over time. The rationale for amplitude normalization is to provide a measure of PAC independent of absolute amplitude for any given electrode. Here, this procedure allowed for the collapsing of frequency, f₁ (phase) by frequency, f₂ (amplitude) maps across a group of subjects and electrodes with different electrode coverage but with similar differences in distance. As for the asymmetric nature of bPLV, we considered two cases of directionality, outgoing i.e. the low frequency phase at the seed electrode coupling to high frequency amplitude at any non-seed, site electrode on the ECoG grid or vice versa for incoming connections.

Surface rendering and co-registration

Surface reconstructions of cortical anatomy were performed using previously published methods (Blakely et al., 2009; Hermes et al., 2010). Briefly, preoperative magnetic resonance images (MRI) are co-registered with postoperative Computed Tomography (CT) scans using the Statistical Parametric Mapping software package. Three-dimensional reconstructions of the pial surface were generated using Freesurfer (http://surfer.nmr.mgh.harvard.edu/) and custom code implemented in MATLAB. Electrode positions estimated from postoperative CT were projected to the reconstructed pial surface using the method outlined by Hermes and colleagues (Hermes et al., 2010).

Electrode labeling

Multiple rsfMRI motor functional connectivity maps were generated across an array of weighted, statistically significant thresholds. For each patient, Z-scores were scaled from a minimum threshold of Z > 2 through the maximum individual Z-score value for a given patient. Each rsfMRI seed-point functional connectivity map was finally projected onto the brain surface using custom MATLAB scripts. Functional maps were warped into native T1 space using affine transformation and a tri-linear interpolation to bring the functional data into native 1³ mm space. Data were then rendered onto surface space using the MATLAB isosurface 3D projection algorithm and scaled to T1 surface by linear superposition of voxels meeting threshold and weighted by spherical Gaussian kernels using a standard deviation of 3 mm centered at the location of each active voxel coordinate.

Finally, for each scaled rsfMRI functional connectivity map, ECoG electrodes were selected and identified as belonging to the ‘within-network’ or ‘out-of-network’ based on any overlap with the rsfMRI functional connectivity estimates. Magnitude effects of functional connectivity differ tremendously at the individual level. We defined network membership across all values of rsfMRI functional connectivity estimates which allowed for a contrast of our coupling metrics across different number of channels owning within-network membership relative to those defined as out-of-network. This data driven approach was specifically utilized to avoid a bias in the selection of network membership.

Identification and selection of coupled frequencies

For both coupling procedures, i.e. bPLV and PAC, we computed a mean (across subjects) interaction map from the low frequency range (1–40 Hz) to the high frequency range (70–200 Hz) for incoming and outgoing interactions from each seed to all site ECoG electrodes. Note that the seed electrode can interact with itself, as both bPLV and PAC are asymmetrical interaction measures. This resulted in 64 maps from each subject and 256 in total for 4 subjects, where each pixel represents an interaction frequency pair, corresponding either to the two independent phases (bPLV) or phase and amplitude (PAC). We were interested in common properties across maps in order to isolate and select significantly coupled frequencies. Because each subject 1) had varying spatial coverage, 2) the ECoG was recorded during the resting state and 3) different seed electrodes (based on different functional localizer characteristics) were identified for each subject, it would be difficult to interpret specific measures of interaction. Instead we focused on common features in the interactions maps that were based on the commonality as identified through the functional label derived from the rsfMRI motor functional connectivity maps, which is the membership label of a particular electrode in our two-way interaction measure (within-network or out-of-network). Therefore, we divided all 256 coupling maps for each PAC and bPLV incoming & outgoing algorithm, into interactions from the seed (or with the seed) to another ‘within-network’ site electrode or ‘out-of network’ site electrode. With this distinction in place, we computed a two-sided t-test, with unequal sample sizes, for each frequency pair (f₁, f₂) or pixel in that 2D map, revealing significant differences between within-network interactions and out-of-network interactions. Sample sizes will not be equal, as there are typically more of the latter. Since the test is pixel-wise, the frequency dependent bias in our estimation of e.g. the bPLV, as noted in the previous section, was converted into a normalized t-statistic. Both the bPLV and the PAC values come from unknown distributions. Therefore, we resorted to a non-parametric permutation test, to determine significant t-values. We applied a cluster based maximum statistic (Bullmore et al., 1999) to account for multiple comparison correction across the whole map. Under the null hypothesis, i.e. no functional difference between within-network and out-of-network electrodes, we randomly exchanged labels for the interactions maps and would not expect a significant difference. For each permutation, we randomly shuffled the labels of our total set of 256 maps, and draw a number of within-network and out-of-network maps without replacement, equal to our original t-test. For these permuted sets, we then computed a new t-statistic and applied a threshold to the resulting t-statistic map, based on the 99 (p < 0.01) percentile for a t-statistic with 254 degrees of freedom. We identified clusters in the map above this threshold and recorded (for each label-shuffle permutation) the maximum cluster size across the whole map. A sufficiently dense histogram of maximum cluster sizes was established based on 10,000 permutation steps under the null-hypothesis. Finally, this histogram was used to identify significant clusters in the original t-statistic map, by applying the same threshold and accepting only clusters in the 95 percentile of our maximum cluster size distribution, i.e. which have p<0.05 of occurring randomly under the null hypothesis (see Fig. S1 for visual description of procedure).

Time series shuffling and permutation statistical testing

Our permutation cluster test guided selection of peak frequency patterns to investigate the spatial distribution of CFC at the individual subject level. We selected the peak range of coupled low frequency phase estimates and high frequency amplitude or phase profiles. This resulted in a pooled phase estimate for φX(f₁) at a 11–15 Hz range peak value and for φX(f₂), φY(f₁ + f₂) spanning a 85–95 Hz window for bPLV incoming calculations and φX(f₁) within 16–20 Hz range peak value and for φX(f₂,t), φY(f₁ + f₂,t) spanning a 133–143 Hz window for outgoing bPLV patterns. PAC estimates for each individual were computed over the peak frequency regions for the low frequency phase estimated across the 6–10 Hz bin and amplitude estimates binned across 74–84 Hz range.

To test for statistical significance across individual paired-channel interactions, we applied standard permutation tests to shuffled time series data. This approach serves to generate a null distribution of no significant CFC for both interaction metrics. For each shuffle, phase data were binned again into 8 sec time windows across the full duration of a recording. Time segment order was then randomly shuffled and bPLV and PAC were re-estimated as noted between the seed and all site electrodes and vice versa. The maximum value at a 95% confidence interval threshold across all couplings per shuffle was estimated and entered into the distribution. 1000 shuffles were conducted for each individual to generate surrogate CFC distributions. This approach is by nature more conservative than traditional total random phase shuffle. Specifically, it does not completely decimate all phase continuity as in the case for a completely random full time series phase shuffle (which would eliminate all synchrony — Hurtado et al., 2004; see Foster and Parvizi, 2012 for a similar approach as applied to the resting state). More specifically, our shuffling and permutation technique preserves the general local phase evolution within a time segment while disrupting the global temporal structure across the full time series. Finally, we computed the mean 95^th percentile confidence intervals of each bPLV and PAC null distribution. Any between real seed and site electrode pair showing greater bPLV or PAC estimates relative to the null distribution at an alpha level of 0.05 was considered statistically significant.

Linear regression analysis

We used a linear regression model to examine the relationship between the seed-site or site-seed CFC magnitude and resting state functional connectivity metrics at the level of individual electrodes. We began by Z-normalizing CFC metrics across both CFC domains and subjects to facilitate a cross metric comparison. Then electrode center coordinates were warped into raw echo-planar space using a tri-linear transform. Mean, un-scaled Z-score values were calculated from a 4 mm (full diameter) spherical sample placed directly below the center coordinate of all electrodes within a montage. Across all channels within each subject montage, Pearson's r correlations were calculated between average functional connectivity (Z-scores) and normalized CFC estimates and applying an ordinary least squares model fit. Finally, all regressions were normalized using a Fisher's r-to-z transform.

Results

Seed electrode selection

Electrode coverage varied slightly from subject to subject, but generally spanned the lateral temporal and parietal areas including precentral zones for all four subjects. We first established seed-based rsfMRI maps of functional connectivity for each individual using a data-driven approach to select a seed-point across all electrodes within each individual subject montage. A functional localizer task was utilized to identify seed-points. All subjects performed an overt-motor screen task during ECoG recording to identify functional electrodes responding during cued movement of the contralateral (from the placement of the grid) hand as well as tongue (Fig. 1A). The resulting electrode with the highest T score (i.e. HG power with respect to rest) across these two functional conditions was then selected as the seed electrode. Note the range of electrode coverage across all subjects was greatest across the lateral extent of temporoparietal zone. In order to select seed electrodes from homologous cortical regions across subjects, we excluded any electrode outside of classic motor regions (e.g. occipital responding channels in subject 2). Subjects 1 & 2 each showed minimal HG responses during cued tongue movement but extensive responses on hand trials. Conversely, subjects 3 & 4 showed little to no HG power modulation during the cued hand execution but had more widespread pattern of activity during the tongue movements. This response pattern across subjects was likely related to the specific placement and coverage of the ECoG grid. Therefore, the highest responding hand electrode for subjects 1 & 2 and the tongue electrode for subjects 3 & 4 was selected as the seed point for all subsequent connectivity analyses.

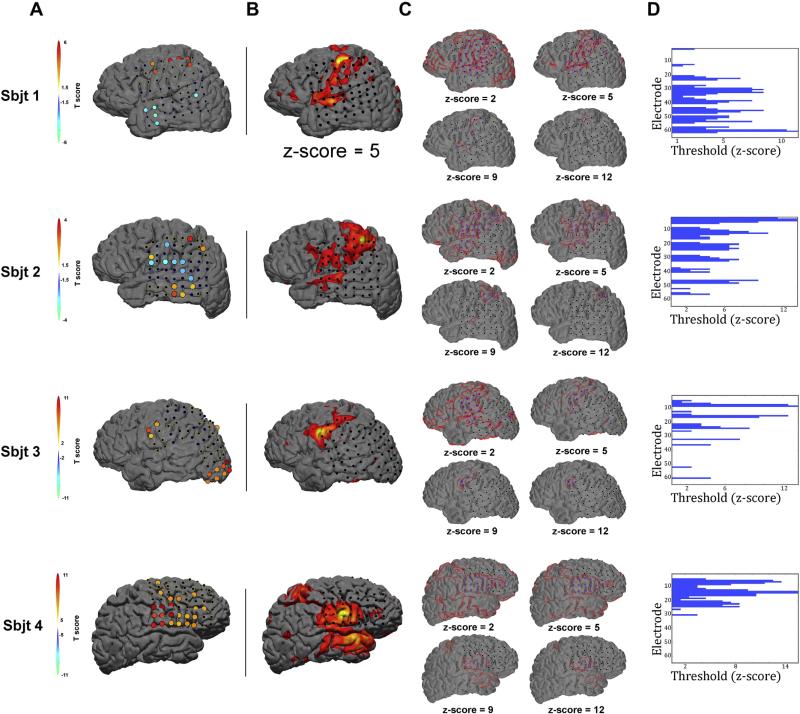
Fig. 1.

Seed selection, rsfMRI map development and network classification. To objectively identify an electrode to serve as a seed point throughout our analyses, we employed a simple cued hand/tongue (with trials randomly interleaved) motor task during ECoG recording. A) Shows the results from a two-tailed student's T-test contrasting log HG power during cued movement relative to rest. For each subject (aligned in rows), the highest positive responding electrode (i.e. warm colored T-value) was selected as the seed electrode and thus served as the seed location for all functional connectivity analyses (green dot in B). Note, the 64-channel montages for subjects 3 & 4 (i.e. rows 3 & 4) were changed between motor screening and resting state recordings. In this case, only active electrodes during resting state were considered as candidates for the seed electrode. Seed-point rsfMRI functional connectivity maps were generated according to standard methodology applying well-established statistical thresholding procedures. B) Shows a typical map at an approximate mid-range threshold value (Z-score = 5) for each subject. However, at the single subject level, threshold values can vary prior to group normalization procedures (c.f. (Zhang et al., 2009)). Therefore, to avoid a bias in the electrode selection process based on threshold differences, we generated twelve Z-score defined ‘rsfMRI threshold maps’ for each subject. C) Shows 4 representative threshold maps for each subject. Electrodes overlapping with each resulting rsfMRI seed-point functional connectivity map (outlined in red) were considered ‘within-network’ electrodes (blue electrodes) while all others were labeled as out-of-network (black electrodes). This process was repeated for all thresholds and subjects. D) Shows a histogram of the network membership label (blue color) for all electrodes within a montage by rsfMRI threshold (x-axis).

Identification of within-network and out-of-network site electrodes

We then generated hand (subjects 1 & 2) and tongue (subjects 3 & 4) rsfMRI functional connectivity maps. For each subject the center coordinates of the selected seed were used to identify and select the underlying cortical tissue to serve as the seed point for a voxel-wise regression of rsfMRI functional connectivity (green dot in Fig. 1B). As typical for single subject approaches, the resulting seed-point functional connectivity maps showed a range of statistically significant Z-score thresholds across all subjects (Fig. 1C; c.f. Zhang et al., 2009). All subjects showed at least a maximum threshold value of Z = 13. Electrodes were labeled as either overlapping with the seed-point rsfMRI map (within-network) or lying outside of it (out-of-network — see Fig. 1 C, D for visual description). This approach resulted in a range of within-network and out-of-network site electrodes, as defined by rsfMRI functional connectivity thresholds. For example, at a threshold of Z = 13, 2 subjects showed only the seed electrode as a within-network member and 2 subjects showed the seed electrode and only one nearest neighbor site as within-network members. Further, a Z-score threshold of 5 resulted in a total of 75 electrode pairings across the 4 subjects. The total number of coupled pairs for each rsfMRI threshold is shown in Fig. 2A. The group-mean maximum distance (estimated as center to center distance between channel pairs on the grid, in cm) between the seed electrode and within-network site electrodes decreased as a function of rsfMRI threshold (Fig. 2B).

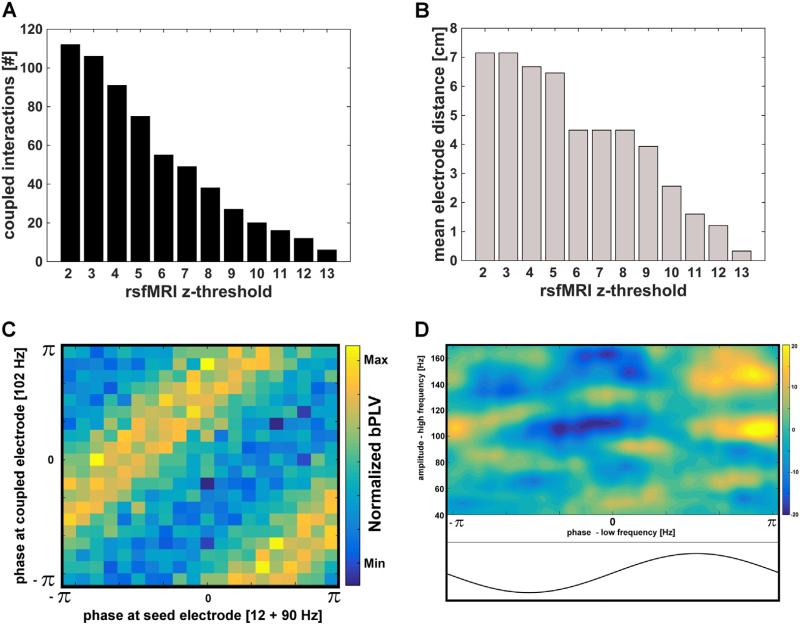
Fig. 2.

Metrics and demonstration of non-linear coupling within resting state ECoG signals. A) The total number of coupled (including source locking i.e. a seed to itself) of within-network interactions across all subjects for each rsfMRI threshold. B) Group mean distance metrics between the seed electrode and all within-network site electrodes as a function of rsfMRI threshold. To estimate mean distance, the maximum distance between a seed and a within-network site electrode for each imaging based threshold was determined and averaged across 4 subjects. C) Example phase-phase (in radians) spectrogram illustrating the existence of biPhase outgoing coupling (i.e. bPLV) between the signal at the seed (x-axis) and a site electrode (y-axis) from a single subject (subject 1). For the seed electrode, the sum of phase f₁ (in this case 12 Hz) and f₂ (90 Hz) is locked to the phase of f₃, which is calculated as the sum of these two frequencies (in this case 102 Hz) at a site, within-network electrode (y-axis). The magnitude of bPLV is related to the consistency or degree of this cross-frequency locking. Here, for the case of zero or random locking, one would expect a uniform distribution across all angles, whereas in this case stripes were evident in the spectrogram indicating a preferred (i.e. coupled) phase locking. D) A phase-amplitude coupling (PAC) outgoing representative example from subject 1. The normalized amplitude (heat map reflects Z-scores) across all high frequencies (y-axis) from a site, within-network electrode shows a relative, preferred phase from a low-frequency signal (in this example, 8 Hz) at the seed electrode (x-axis).

Resting state ECoG, non-linear coupling measures

We then calculated bPLV and PAC across all seed to site electrode pairs (see Fig. 2C & D). Fig. 2C demonstrates the existence of bPLV between a seed electrode and a within-network site electrode from subject 1. As evidenced by higher biPhase locking values (heat map), the mean phase of f₃ shows preferential coupling to the mean sum of phase of f₁ and f₂. Because this interaction is unidirectional, the presence of f₁ and f₂ at the seed electrode (as in this example) locking to the phase of f₃ at the distal, site electrode is suggestive of an outgoing (i.e. from the seed out) pattern of coupling. Similarly, Fig. 2D shows an example of PAC between a seed electrode and a within-network, site electrode. It is important to note that these plots are merely representative examples demonstrating the presence of CFC within ECoG signals in the absence of externally-directed behavioral events. Our main objective here is to characterize the global spatiotemporal patterns of CFC within resting state signals. Therefore to identify mean frequencies showing significant CFC, we binned (across subjects) all within-network and out-of-network electrodes for each rsfMRI threshold value and computed group level statistics contrasting the CFC characteristics across these two functional distinctions.

Group-level cross-frequency coupling characteristics

We utilized a conservative statistical approach to identify frequency specific CFC patterns at the group level. Based on numerous previous studies (Canolty and Knight, 2010; Darvas et al., 2009b; Florin and Baillet, 2015) and computational efficiency, we limited our analysis to a specific low frequency to high frequency CFC. Figs. 3 and 4 show frequency-by-frequency interaction maps plotting bPLV or PAC contrasts between within-network and out-of-network sites. At the group level, we contrasted mean bPLV and PAC between within-network and out-of-network electrode pairs using t-tests with unequal sample sizes (Fig. S1) and minimizing the effects of multiple contrasts by applying a pixel cluster correction. This identified peak frequency clusters (maximum cluster size effect — see Fig. S1B & C) at a p < 0.05 level to eliminate spurious effects from the original label contrasts. This combined statistical analysis resulted in 12 corrected bPLV & PAC maps (e.g. at each rsfMRI threshold) per incoming (Fig. 3) and outgoing (Fig. 4) CFC metric.

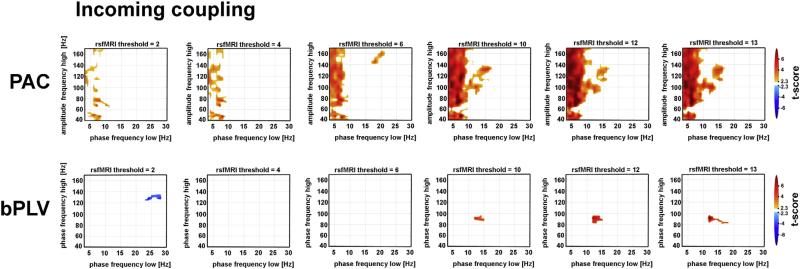
Fig. 3.

Frequency–frequency CFC maps contrasting within-network to out-of-network coupling from incoming patterns of connectivity. Spectrograms reflect mean PAC and bPLV contrasts for incoming couplings across the full resting state period, binned into different rsfMRI threshold maps (columns). For all plots, warm colored pixels denote greater mean CFC (t-values) for within-network seed-site pairs relative to out-of-network seed-site pairs. The top row shows the PAC results where the x-axis represents the low frequency spectrum at the site electrode at which phase information is significantly coupled to the higher frequency amplitudes at the seed electrode. bPLV results are shown in the bottom row and represent frequencies (x-axis: φX(f₁) & y-axis: φY(f₂)) whose phase sum together at the site electrode and lock to the phase of φY(f₁ + f₂) at the seed electrode. Importantly, f₁, f₂ and f₃ can be completely independent from one another.

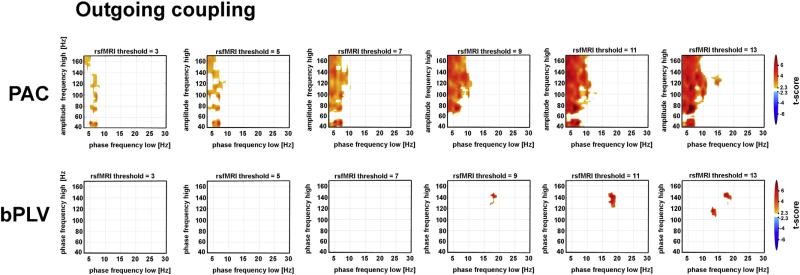
Fig. 4.

Frequency–frequency CFC maps contrasting within-network to out-of-network coupling from outgoing patterns of connectivity. Spectrograms reflect mean PAC and bPLV for outgoing couplings across the full resting state period, binned into different rsfMRI threshold maps (columns). The results are presented identically as in Fig. 4, with the exception that the PAC, as a reflection of outgoing couplings, show the low-frequency phase estimates at the seed electrodes (x-axis) coupled to the amplitudes estimates of frequencies at the site electrode (y-axis). Similarly, bPLV results are shown in the bottom row and represent frequencies (x-axis: φX(f₁) & y-axis: φY(f₂)) whose phase sum together at the seed electrode and lock to the phase of φY(f₁ + f₂) at the site electrode.

Our approach revealed the presence of significant CFC specific to seed-site channel pairs located within the resting state network, as labeled by fMRI. Across both incoming and outgoing maps, significant PAC was much more prominent and widespread relative to bPLV. Similar to resting state PAC estimates extracted from single electrodes (Foster and Parvizi, 2012), prominent PAC was noted across a broad range of high frequency amplitudes (40–160 Hz) and prominent low frequency phase spectrum (i.e. 1–10 Hz) with peaks in both occurring both in the delta, theta and low alpha ranges. The magnitude of this effect was greatest at higher rsfMRI thresholds (rsfMRI Z-scores > 9, Figs. 3 & 4), though we also observed significant PAC across all lower rsfMRI threshold values.

It is important to note that the use of the t-statistic ensures robustness vs. outliers, as these would increase the overall sample variance and thus lower the t-statistic. This carries over into the permutation test as well, since the joint variance, which scales the differences of the means in the t-statistics stays the same under the label swapping procedure. Critically, this means that findings of CFC for a given rsfMRI Z-score threshold are due to contributions from all electrodes identified to be in-network.

Significant bPLV in contrast was not as robust. Only small, specific clusters were observed and generally only at high rsfMRI thresholds (Z-score > 10 for incoming couplings and Z-score > 9 for outgoing couplings — see Fig. S2 for all bPLV maps). The exception to this observation was a significant cluster appearing in rsfMRI Z-score map = 5 (Fig. S2). Notably, the range of frequencies revealing significant bPLV coupling within the resting state were nearly identical to bPLV estimates during motor execution tasks (Darvas et al., 2009a,b). These included low frequency phase coupling that was nearly exclusively within the beta range, with f₁ peaking between 13 and 20 Hz. Finally, under the two-tailed t-test classification, we also observed one negative responding cluster at a rsfMRI threshold of Z-score = 2. This effect indicates greater bPLV between seed and out-of-network electrodes pairs at this threshold relative to seed and within-network pairs (Fig. 3).

Incoming vs. outgoing coupling as a measure of directionality

For both CFC approaches, incoming and outgoing coupling can be loosely interpreted as a causal interaction in the Granger sense. Unlike traditional phase locking measures, such as the phase-locking value (PLV, Lachaux et al., 1999) or phase coherence where the interaction between two signals X and Y is symmetric with respect to the order of the signals, this is generally not the case for the bPLV (F. Darvas et al., 2009b) or PAC (Fontolan et al., 2014). This asymmetry enables the use of the bPLV as a directional measure, if it is (for instance) calculated between two disparate signals, X and Y. In this case, B_XYZ(f₁,f₂,t) reduces to B_XXY(f₁,f₂,t) and its value quantifies the strength of interaction from X to Y, if the phases in X at f₁ and f₂ are independent. Specifically, as the case X is directional to Y in the Granger model (Granger, 2001), because knowledge of φX(f₁,t) and φX(f₂,t) can be used to predict φY(f₁ + f₂,t), but not vice versa. Further, this argument does readily generalize to PAC, which is also an asymmetric measure of interaction. Here, the existence of a coupling between e.g. a low-frequency phase of X entrains or predicts the amplitude gain of Y at a distant site. This framework has been shown as a general measure of directionality during top-down auditory cognition (Fontolan et al., 2014).

Here, directional CFC was computed as 1) the phase of the low-frequency rhythm originating at the seed electrode coupling to high frequency responses at other non-seed site electrodes as a measure of outgoing connectivity and 2) the high-frequency activities originating at the seed electrode being entrained to the phase of low frequency oscillations from all site electrodes as a measure of incoming connectivity.

While the distinction of relative directionality of peak coupling frequency ranges did not result in any remarkable PAC differences, notable frequency coupling effects were evident in the bPLV analyses. Specifically, a pattern of statistically significant incoming bPLV emerged beginning at rsfMRI threshold Z = 10 whereby a common phase-phase interaction occurred at frequencies centered at approximately (f₁: ~13 Hz, f₂: ~90 Hz). This specific frequency–frequency phase synchrony is well aligned with previously published event-related bPLV ECoG results during a motor execution task (Darvas et al., 2009b). In contrast, common phase-phase outgoing interactions were seen at frequencies centered at approximately (f₁: ~18 Hz, f₂: ~138 Hz). There is no spurious coupling (in this instance to the 120 Hz harmonic of the line noise) as the bPLV measure as we implemented and used it, only tests for up-coupling of frequencies, i.e. 18 Hz phase and 138 Hz phase in this case couple to the phase of 156 Hz. Finally, these characteristic frequency parameters were specific to the multiplicative summation (f₁ + f₂) sideband of bPLV coupling (Fig. S3).

Spatial characteristics of significant resting state CFC

Using the selected peak frequency coupling parameters from the group level analyses, we computed PAC and bPLV from seed to all site electrodes at the individual level. We then generated a null distribution of both PAC and bPLV estimates using standard non-parametric permutation tests from time segment shuffled data and tested significant CFC by deriving 95% CI from this distribution. Electrodes displaying signifi-cant CFC are shown on individual subject surface renderings in Fig. 5. Across all subjects, a cumulative sum of 65 electrodes showed signifi-cant CFC when binned across all bPLV and PAC incoming and outgoing values. Similar to the group level analyses, resting state PAC was more prominent with respect to bPLV estimates with more than double the number of electrodes showing significant PAC (Fig. 6B).

Fig. 5.

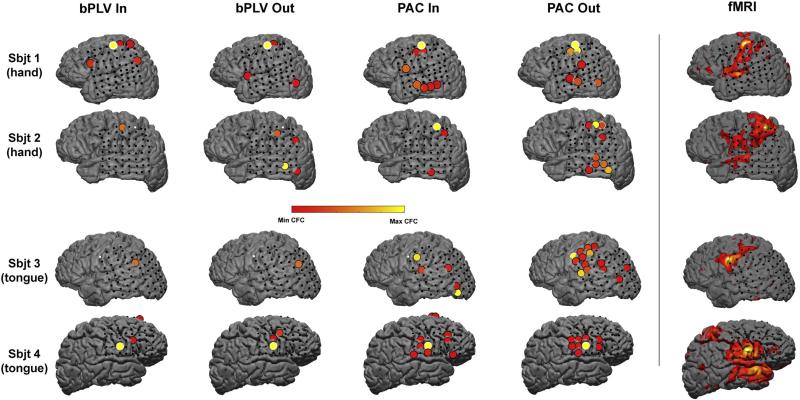
Spatial patterns of significant directional CFC in the resting state. The spatial distribution of directional bPLV and PAC estimates were mapped back onto the original electrode montage for each individual participant (shown in rows). The heat map reveals the magnitude of coupling with respect to our permutation statistical test. For each contrast map, seed electrodes are either bordered in white (if significantly coupled onto itself) or plotted as a white dot (if no significant coupling occurred). The seed electrode was chosen for each participant through use of a functional localizer task. The electrode showing the strongest statistically significant response during an overt hand (subjects 1 & 2) or tongue (subjects 3 & 4) task was selected as the seed point for all connectivity analyses. Significantly coupled site electrodes with the seed are ballooned to more clearly reveal the spatial location of that electrode. The original rsfMRI map is plotted in the left most column as a visual reference. Note the qualitative similarities between significant PAC outgoing coupling and the rsfMRI maps. This also reveals that electrode coverage in all subjects does not span the full spatial extent of the rsfMRI functional connectivity maps.

Fig. 6.

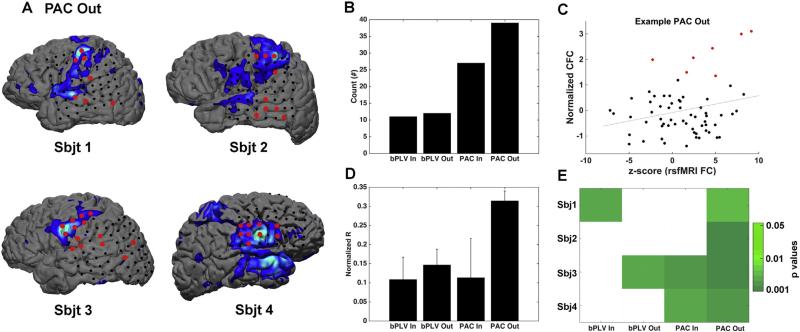
Spatial characterization of incoming and outgoing cross-frequency coupling (CFC) metrics. A. For each subject, PAC outgoing connectivity and rsfMRI maps were overlaid in order to illustrate the remarkable similarities in spatial patterns across the two maps. Note, the color scheme for the fMRI was adjusted (relative to Figs. 1 & 5) to a cool scheme and significantly coupled electrodes were inflated in size to better reveal the contrast between single electrode and the underlying fMRI data. For these purposes, significantly coupled electrodes were colored red independent of coupling magnitude. B. Reveals the cumulative sum of significant (at an alpha level of 0.05 with respect to the shuffling permutation test) coupled interactions. C. Example of a significant linear regression from a representative subject, plotting rsfMRI Z-scores relative to the normalized PAC outgoing values across all electrodes within that montage. Red points denote electrodes with statistically significant CFC. D. Normalized correlation coefficients (r-to-z-transformed correlation) binned across subjects for each cross-frequency coupling metric. Bars reflect standard error of the mean. E. A matrix revealing statistically significant (in green) regressions between CFC and rsfMRI maps for each subject.

The most prominent spatial distribution feature across significant CFC estimates occurred for the PAC outgoing connections (Figs. 5 & 6A). For both bPLV directional estimates (incoming and outgoing) and PAC incoming estimates, there was qualitatively little predictable spatial distribution pattern spanning the cortical surface. However, PAC outgoing connections resembled the rsfMRI functional connectivity seed points to a much greater degree. To quantify the spatial similarities between maps, we applied simple linear regression and ordinary least squares fitting to the rsfMRI Z-score estimates extracted from the cortical tissue directly beneath all electrodes within a montage and normalized CFC metrics (Fig. 6C–E). The mean normalized r coefficient between PAC outgoing and rsfMRI seed point motor connectivity maps was higher relative to the other estimates of CFC. However, across all 4 subjects, this effect failed to reach statistical significance (CS = 6.57, p = 0.0868, Kruskal–Wallis one-way analysis of variance by ranks). Although this particular analysis is clearly underpowered, the only consistent finding across all 4 subjects was a significant correlation between PAC outgoing connections and rsfMRI connectivity maps (Fig. 5E). Subject 3 did show similar patterns of correlation across 3 of the 4 measures of CFC and 2 out of 4 subject showed significant relationships between patterns of PAC incoming CFC and fMRI connectivity. Thus, while the spatial patterns of significant outgoing PAC connectivity most closely mimic (both qualitatively and quantitatively) patterns of rsfMRI functional connectivity, additional patterns of CFC are clearly present within the resting state and likely serve to drive intrinsic computational synchrony.

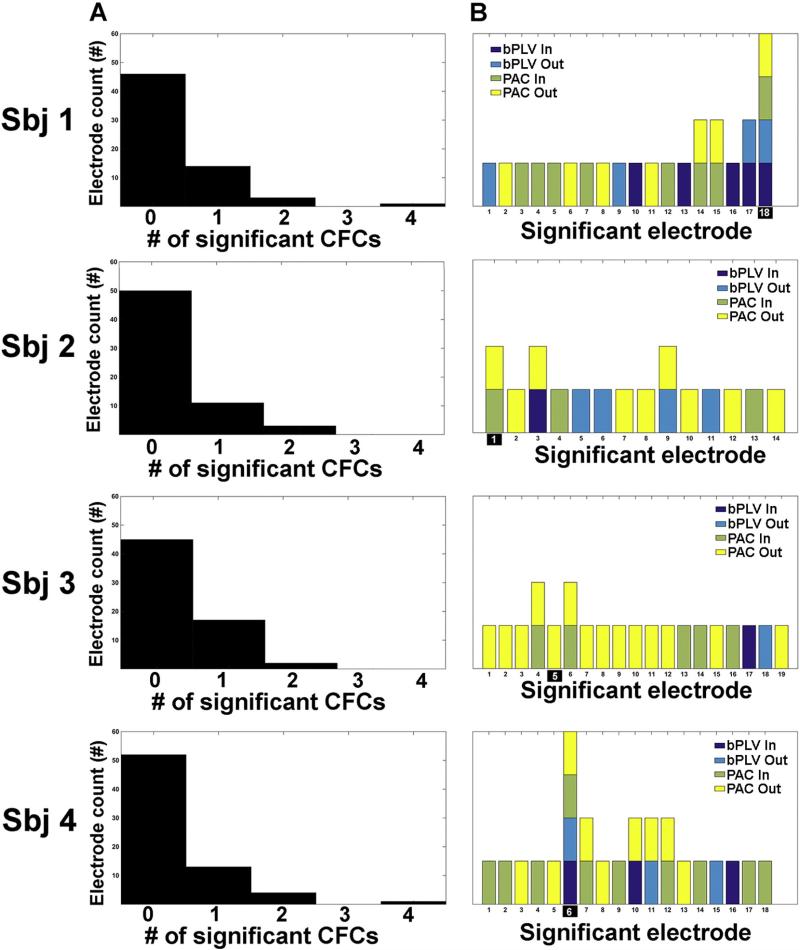
Despite the presence of significant resting state phase-amplitude and phase-phase coupling in all subjects, there was very little overlap that occurred between different CFC measures. Of the 65 significantly coupled electrodes (either incoming or outgoing), only 11 (or approximately 17%) non-seed, site electrodes showed greater than 1 form of significant CFC (see Fig. 7B). Outside of the seed electrodes, no other electrode showed more than 2 significant forms of resting state CFC. Of the 11 electrodes showing greater than one form of significant CFC, 6 showed overlap between PAC incoming and outgoing synchrony and 1 showed overlap between bPLV incoming and outgoing couplings.

Fig. 7.

Pattern characteristics of significant CFC within the resting state. A. Shows a histogram of the number of electrodes showing significant couplings. Notice that the majority of electrodes across a montage for each individual subject were not significantly coupled in either direction with the seed electrodes (e.g. on average 47 out of 64 electrodes were not significantly coupled with the seed electrode). For electrodes where significant coupling occurred, the vast majority of these electrodes showed only one significant form of mean coupling when binned across the full time series of the 8 minute resting state. B. This effect was broken down further into the specific electrodes CFC estimates. As can be seen, the large majority of significantly coupled electrodes were only coupled in one direction and under one CFC metric.

Discussion

We reveal the presence of both cross-frequency phase-amplitude and phase-phase coupling in the resting state between neocortical populations across a sensorimotor network that were specifically identified by native rsfMRI functional connectivity. Using data-driven methodology and conservative statistical permutation approaches, we observed phase-amplitude coupling across a broad range of gamma frequencies and a limited range of lower frequency phase estimates, generally within the high theta to low alpha range. The contributing frequencies driving this coupling are in good agreement with previous resting state MEG reports (Florin and Baillet, 2015; Foster and Parvizi, 2012; Osipova et al., 2008) as well as PAC during task execution over homologous cortical loci (Yanagisawa et al., 2012). Further, we noted the presence of significant cross frequency phase-phase coupling but at generally more specific high and low band-limited frequency ranges.

Additionally, we reveal for the first time a good degree of spatial correspondence between the varying spatial patterns of a rsfMRI seed point connectivity map and the directionally selective CFC. Importantly, both imaging and electrophysiological connectivity metrics originated from identical cortical loci. This relationship was greatest for PAC outgoing connections relative to other metrics of directional CFC. That is, we observed that the best spatial match to the patterns of rsfMRI seed point motor maps occurred when the phase of low frequency oscillations at the seed electrode significantly entrained the high frequency amplitude estimates at site electrodes. This observation is suggestive that, in the absence of overt task structure, low frequency oscillatory behavior from neural assemblies at the seed region drives the gain control of local processing dynamics at distal site electrodes. Globally, these results suggest that voxelwise correlations of resting state BOLD signals associated with a seed-point are, in part, associated with the entrainment of a low frequency rhythm originating at that seed locale. We did however observe significant relationships between rsfMRI maps as well as other CFC spatial patterns, suggestive of additional and highly dynamic interactions across the neocortical surface.

Importantly, all electrophysiological recordings of macro-scale oscillating signals were acquired via indwelling, sub-dural electrode arrays. As a consequence, the signals were sampled with a high degree of spatial specificity. Furthermore, because field potentials are recorded directly from the cortical surface and thus completely bypass dural and scalp influences, they are minimally impacted by zero-lag volume conduction. Despite this possibility, we note the presence of significant of cross-frequency phase-amplitude and phase-phase couplings across long distances (e.g. >4 cm) as well as matching spatial patterns of fMRI connectivity, signals based on hemodynamics. The current results are thus robust with respect to the low-amplitudes of high frequency signals and are highly spatially and temporally specific. Collectively, these results support the hypothesis that CFC is not only able to entrain high frequency state dynamics during task execution (Canolty and Knight, 2010), but exists in endogenous, spontaneous signals, engendered directionally across discrete, spatially-organized neural populations in the absence of overt, goal-directed behavior.

We were specifically interested in characterizing the degree to which dynamical patterns of phase coupling spanning multiple time scales drive connectivity across a well established intrinsic network (i.e. the sensorimotor network). We choose to specifically contrast bPLV and PAC estimates at the group level to identify global frequency parameters of CFC associated with resting state networks as labeled by fMRI. We selected this approach not only because both methods have been shown to support and coordinate active information processing across sensorimotor regions during overt motor task (Darvas et al., 2009b; Yanagisawa et al., 2012) but also because of discrepancies in rsfMRI functional connectivity maps, e.g. use of hand functional connectivity maps from two subjects and tongue functional connectivity maps from the other 2 subjects. Furthermore, there were also differences in electrode coverage across patients. However, our hypothesis was that the regions spanning the sensorimotor system would exhibit similar electrophysiological resting state functional connectivity characteristics irrespective of specific anatomy (hand vs. tongue connectivity). By binning all within-network electrodes together across subjects and specifically contrasting CFC with out-of-network channels, we tested this hypothesis and the accumulative results likely reflect global properties of sensorimotor functional connectivity maps. Our strict statistical criteria likely prevented spurious CFC at this group level. Such shared characteristics may also reflect electrophysiological properties of other large-scale cortical networks such as the default mode network (DMN) (Foster and Parvizi, 2012) or dorsal attention network (Florin and Baillet, 2015). For example, Foster and Parvizi, 2012, revealed that the low-frequency PAC entrainment rhythm within the resting state varied as a function of functional cortical boundary with oscillators in the DMN cycling in the theta range and an oscillators within the inferior visual cortex in the alpha range. Clearly future ECoG studies will need to investigate CFC across additional spatially defined cortical network hubs to support such a hypothesis. However, Foster and Parvizi's (2012) contribution raises the suggestion that the low-frequency entrainment dynamics in the resting state may in part be defined by the characteristic idling rhythm inherent to different functional systems of the cortex (c.f. Groppe et al., 2013) as been for example seen with theta-gamma PAC within the hippocampus (Lisman and Jenson, 2013). Sensorimotor systems are classically defined as owning both ‘idling’ rhythms at both the Beta range (12–30 Hz) as well as the alpha ‘Mu’ range (8–12 Hz) (Mackay, 1997). Thus, it is curious to note that the peak low frequency rhythms reflected in both PAC (6–10 Hz) and bPLV (~13 Hz for incoming and ~18 Hz for outgoing) connectivity. Taken together, it is conceivable PAC estimates entrained by the Mu rhythm provides a more prominent role in coordinating wide-spread local activities across the sensorimotor system within the resting state while Beta reflects more specific functional features of resting state synchrony.

Neurophysiological mechanisms of CFC

Numerous studies have now converged on the hypothesis that PAC presents as a candidate mechanism facilitating the synchronization of local activities across spatially disparate neural populations (i.e. local-to-global coupling; see Canolty et al., 2006; Canolty and Knight, 2010; Voytek et al., 2010). The rationale for this candidate signal propagation model posits that event-related high frequency bursts (i.e. within the HG band) reflect local computational activity. When the need arises to coordinate multiple, spatially distinct neural populations for the successful execution of behavior, the phases of local low-frequency oscillations serve as a synchronization or gating mechanism to time-lock the excitability or gain of high frequency activities with minimal time lag (Canolty and Knight, 2010; Florin and Baillet, 2015). Within the resting state, this phenomenon has been observed across the cortex using MEG roughly within the same band-limited low (predominately within the 1–10 Hz range) and high frequency ranges noted here. Florin & Baillet (Florin and Baillet, 2015) observed widespread PAC across the cortical surface during the resting state. They revealed that different spectral PAC profiles emerged that roughly conformed to the spatial patterns of established large-scale rsfMRI cortical networks, suggesting PAC between low-frequency phase estimates and high frequency amplitude signals serves as underlying mechanism for long distance resting state interactions. Unfortunately these authors did not have native rsfMRI data to directly relate the two measures. Here we selected ECoG electrodes based on a defined functional connectivity criteria (overlap with resting state fMRI functional connectivity maps from each individual participant). Consequently, we were able to directly contrast CFC with rsfMRI functional connectivity from identical neural populations from each subject. Because of the inherent high degree of spatial speci-ficity of ECoG (i.e. avoids spatial uncertainty due to source modeling and noise covariance), our results extend this hypothesis and suggest that presence of low frequency phase coupling to high frequency amplitudes is a specific feature of rsfMRI sensorimotor functional connectivity.

Non-linear phase-phase interactions have received considerably less investigation. This is the first report to demonstrate the presence of significant bPLV within the resting state. bPLV is a complex measure probing dynamic cortical interactions across multiple yet independent phase estimates (Darvas et al., 2009a,b). The result is a measure of asymmetric phase-phase coupling across discrete neural populations. Cortical phase synchrony has been studied extensively at multiple temporal and spatial scales (Boonstra et al., 2006; Hutt et al., 2003; Kreuz et al., 2007; Lachaux et al., 1999) and relates directly to a temporal onset synchrony of the underlying neuronal firing patterns (Murthy and Fetz, 1996). One prevalent hypothesis regarding cortical-cortical cross-frequency phase uniformity is that it supports communication between two regions (Schnitzler and Gross, 2005). However, when such coupling is expressly linear (i.e., classic PLV), it comes at the expense of independent computation occurring specifically in those two regions at those frequencies, an approach which may be problematic for cortical areas with heterogeneous functional characteristics requiring integration across multiple time scales. bPLV, on the other hand, is a proposed mechanism for assembly coordination between regions that preserves functional independence between neural populations at multiple time scales (Darvas et al., 2009a,b). Thus, the existence of significant bPLV between seed and site electrodes suggest the presence of complex, dynamic phase integration across multiple time-scales within the resting state.

Global phase entrainment properties within the resting state

Qualitative contrasts between CFC measures, both at the group and individual levels, establish the hypothesis that phase-amplitude coupling relative to cross frequency phase-phase coupling is a much more prominent and wide-spread form of neocortical, non-linear resting state synchrony. Unlike phase-amplitude coupling, where typically a low-bandwidth gamma amplitude couples to a relatively slow (<10 Hz) phase, biPhase coupling requires tight, specific timing to occur in order to drive phase occurrences across multiple frequencies. It is conceivable that the presence of an overarching coordinating event (e.g. behaviorally mediated phase resetting) is necessary to drive complex cross-frequency phase-phase couplings between disparate neuronal populations within a large-scale cortical system. For example, relative to a resting baseline, our previous work has shown the presence of consistent and significant bPLV across a well-established anatomical pathway (premotor connections to primary cortex) during a cued movement task (Darvas et al., 2009b). Importantly, the noted frequency ranges driving bPLV in this scenario were identical to the frequency patterns of bPLV that were observed in the current context, one that provided no specific phase resetting or external coordinating event. Although we did find evidence of significant similarity between bPLV and rsfMRI results when contrasted across all electrodes in 2 of the contrasts (Fig. 6D), the qualitative comparison of significantly coupled channel pairs was dramatically dissimilar to the rsfMRI maps. Thus, based on the current evidence, we argue that top-down influences or goal-directed behavioral events may be a necessary contingency to foster significant patterns of biPhase coupling within the resting state.

Directional measures of synchrony

We found evidence of consistent, significant relationships between rsfMRI motor maps and PAC outgoing estimates, two measures of connectivity driven by endogenous signals recorded from the same neocortical seed point. This finding is noteworthy because it is the first to reveal that neural populations that showed correlated resting state BOLD fluctuations to the time course established by a seed region are also likely to show high frequency entrainment to the phase of low frequency rhythm from that same seed population. More specifically, these data suggest that the resting state sensorimotor network is, in part, shaped neural populations whose high frequency activities are entrained to the low frequency phase of the neural assemblies located within the seed region. This is a preliminary hypothesis as both measures of connectivity were not acquired simultaneously and clearly additional forms of CFC serve to drive resting state computation. Nonetheless, these data lay the foundation for an intriguing global hypothesis that generic membership (i.e. functional connectivity) within ubiquitous, large-scale networks such as the DMN maybe specifically shaped by the directional entrainment from neural assemblies at a seed point. Such a measure of directionality may begin, for instance, to reveal the presence of global directionality across a network within the resting state, an observation that may serve as a more accurate biomarker for tracking patterns of degeneration in Alzheimer's Disease as neuropathology spreads to or away from highly connected hubs.

Limitations

An additional characteristic of the spatial pattern of directional CFC that was noted was the fact that an overwhelming majority of identified seed-to-site channel pairs (~83%) showed only one form of significant resting state CFC (Fig. 7B). This indicates that (as a general principle) the large-scale populations that drive ECoG surface potentials only show one form of significant coupling when binned across an 8 minute resting state period. However, this observation is based on mean CFC, averaged across an 8-minute period of task-free rest. Contemporary rsfMRI studies have illuminated the fact that functional connectivity is not a static process but rather more generally defined as a dynamic, ongoing process (Hutchison et al., 2013). Thus our computational approach (i.e. integrating across the full time series) is likely discarding a much more dynamic and underlying process within the resting state. Our initial hypotheses centered on revealing and subsequently characterizing the presence or absence of cross-frequency phase-amplitude and phase-phase coupling as a function of rsfMRI network label. Future studies will clearly need to explore the degree to which CFC exists as a dynamic process in the resting state and whether significant patterns of CFC can simultaneously subsist across two distance neural populations.

An overall, inherent limitation to use of ECoG as an investigative tool for human neurophysiology is the sampling population from which recordings can be made. In the current context, all imaging and electro-physiological recordings were taken from individuals with partial, intractable epilepsy and thus should be taken with some degree of caution. This fact also clearly points out another major limitation to use of ECoG as tool of inquiry; namely limited spatial sampling resolution. Despite the high spatial specificity, ECoG spatial coverage is solely dependent upon the clinical needs and requirements for clinical monitoring. It is entirely conceivable that distinct patterns of CFC, defined by band-limited differences of low-frequency phase entrainment, exist across functional or cytoarchitectural boundaries. For instance, Foster & Parvizi, (Foster and Parvizi, 2012) noted that at single electrodes housed within the medial parietal zone of the DMN or within the visual cortex along the inferior occipital stream showed high frequency amplitude coupling differences to delta and alpha range oscillations, respectively. We took a completely data-driven and unbiased approach to select frequency-coupling parameters for both bPLV and PAC measures. We made an assumption of similar connectivity properties across the sensorimotor network constructed by different functional localizers. Future efforts will have to examine whether coupling across frequency profiles results in variable spatial maps.

One additional consideration here is the influence of contralateral connectivity within and across the sensorimotor system. Unfortunately, due to the limitations inherent to ECoG, typical clinical needs prohibit sampling across the cortical hemispheres. Nonetheless, it is well established that motor systems receive contralateral connections from the homologous cortical regions, a fact that fueled the initial resting state functional connectivity hypotheses (Biswal et al., 1995). rsfMRI studies have shown that motor regions positively correlate with the time course of a seed point placed in the contralateral motor region as well as cluster together using ICA decomposition metrics (Biswal et al., 2010). Therefore, it is clear that spontaneous interactions that define cortical connectivity across the sensorimotor system are influenced by contralateral interactions and likely serve to shape the topography of a network including the distribution of CFC. It is conceivable that contralateral influences in the current results maybe one influence guiding the observed spatial variability across participants.

Conclusions

We reveal the existence of significant phase-amplitude and phase-phase coupling within the resting state recorded directly from the human cortical surface and that patterns of outgoing PAC connectivity best reflect patterns of native rsfMRI functional connectivity estimates. These non-linear CFC functional connectivity metrics within the resting state reveals a dynamical system of directed interaction and integration, one that is driven by the low frequency phase coupling. At a systems level, these results contribute to an ongoing narrative suggesting that the existence of highly complex and dynamic events define the resting state (Schölvinck et al., 2013). Electrophysiological studies of the resting state have lagged substantially behind functional MR imaging based approaches, despite the fact that electrophysiological methods will be critical for characterizing the structure, nature and flow of spontaneous activity over the entire range of spatial, temporal, and spectral scales. It is the characterization of resting state interactions at the time scale of neural coding that will be necessary for understanding the computational operations that such spontaneous but associated neural activities support.