Best (but oft-forgotten) practices: expressing and interpreting associations and effect sizes in clinical outcome assessments

Abstract

This article reviews methods used to facilitate the interpretation and evaluation of group-level differences in clinical outcome assessments. These methods complement and supplement tests of statistical significance. Examples, including studies in nutrition, are used to illustrate the application of the interpretation methods for group-level comparisons from experimental or observational studies. In addition, specific pitfalls of evaluating change in meta-analysis studies are described. A set of recommendations is provided. This review is intended as an introduction for the novice and as a refresher for the experienced researcher.

BACKGROUND

Clinical outcome assessments

Clinical outcome assessment (COA)⁵ is an umbrella term referring to patient-reported outcomes (PROs), clinician-reported outcomes, observer-reported outcomes, and performance-based outcomes measures. COAs “measure a patient’s symptoms, overall mental state, or the effects of a disease or condition on how the patient functions and can be used to determine whether or not a drug has been demonstrated to provide treatment benefit” (1). Nutritional clinical trials may assess the safety and effectiveness of weight-loss therapies or therapies intended to protect or promote nutritional health. Although many of the COAs used in nutritional studies include familiar measures, such as weight and glycated hemoglobin, many measures are unfamiliar and present challenges in relation to the interpretation of scores.

PROs

PROs are a subset of a larger group of patient-reported measures that includes self-reports about individual characteristics (e.g., weight, height), behavior (e.g., diet, exercise), experiences with care (e.g., communication with doctors), and social support (2). PRO measures range from single items to multidimensional instruments with multiple subscales. The Food and Drug Administration (FDA) (3) defines a PRO as “any report of the status of a patient’s health condition that comes directly from the patient, without interpretation of the patient’s response by a clinician or anyone else.”

Thus, a host of outcomes such as physical functioning; symptoms such as nausea and vomiting, pain, fatigue, depression; and treatment satisfaction are PROs (4).

PROs are often relevant in studying a variety of symptoms and conditions (e.g., gastrointestinal illness, pain) that cannot be assessed adequately without a patient’s evaluation and when the patient’s input is needed to determine the impact of a disease or a treatment (5). To be useful to patients and other decision makers (e.g., clinicians, researchers, regulatory agencies, reimbursement authorities) who are stakeholders in health care, a PRO assessment needs to measure what it is intended to measure reliably and validly (3, 4, 6–8).

FDA perspective

The FDA developed a guidance related specifically to the design and use of PRO measures (Guidance for Industry Patient-Reported Outcome Measures: Use in Medical Product Development to Support Labeling Claims) to support drug approvals and label claims (3, 9). The FDA publicly announced that the recommendations outlined in the PRO guidance should be followed in the development of COAs (10, 11).

Within the draft and final PRO guidance documents (3, 9), the FDA outlined the evidence necessary to document adequate psychometric properties and included a section specifically addressing the need for information and evidence related to the interpretation of PRO results. The focus of the interpretation section changed from the evaluation of group differences in the draft guidance (9) to the evaluation of individual differences in the final guidance (3). The interpretation methods presented in this article primarily focus on the group-level context. Other published articles focus on interpreting individual change (12–14).

COA interpretation

This article highlights aspects of the research stakeholders must consider when evaluating the meaningfulness of COA results, including the design and focus of the study, the quality of the data collection procedures (as much as possible based on the available information), the appropriateness of any preplanned hypotheses, the relevance of the COA measure used, and the meaningfulness of the results for the intended objectives (Figure 1). The target audience for these aspects is the novice, but information is also included to provide a refresher for the experienced researcher.

FIGURE 1.

Aspects to consider before interpreting clinical outcome assessment results.

Aspects to consider before interpreting COA results

Group compared with individual comparisons

Typically, COA study results, as with other study results, are presented at the group level, including the statistical significance of between-group mean differences and possibly the magnitude of these differences. In addition, evaluating the statistical significance of individual changes can provide a comprehensive picture of the study findings, because one learns, for example, whether there is an overall difference between groups, as well as how many individuals benefit (get significantly better), stay the same, or get worse (significantly decline) in the groups being compared (12, 15).

Sample size, study design, and statistical significance of group differences

The sample size for studies that incorporate COAs may be selected for other endpoints and may be larger than required for the COA comparisons. Hence, small differences can still be statistically significant. In addition to considerations regarding statistical power, Lang and colleagues (16) and Jacobson and Truax (17) remind us that a P value is not synonymous with meaningfulness. This is especially true in meta-analyses, where sample sizes can become large due to the accumulation across all studies.

Context

The context of the study provides one filter for interpretation. Issues such as financial burden, health resources needed, and general risks and benefits of an intervention should be considered when reviewing and comparing COA results. Small benefits may be very worthy of pursuit if the trade-offs necessary to obtain the benefits are trivial (18).

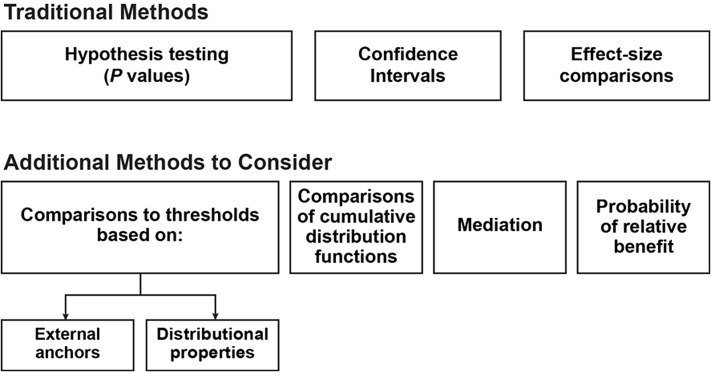
Traditional methods to consider for interpreting COA results

Hypothesis testing P values

The first step in interpreting differences in COA scores is statistical group-level comparisons (Figure 2), including the selection of an appropriate statistical test and α level (perhaps adjusted for multiple comparisons). The resulting probability value (P value) can be interpreted as the probability of observing results as extreme or more extreme given the null hypothesis of no group difference. However, a small observed P value does not prove that the null is false, nor does a large P value prove that the null is true. Rather, the P value provides statistical evidence to inform conclusions as to whether there is sufficient evidence (beyond chance) to make the assumed null hypothesis untenable.

FIGURE 2.

Traditional methods and additional methods to consider when interpreting clinical outcome assessment results.

Statistical significance is influenced by sample size. A small group-level difference can be determined as significant when based on a very large sample size, and a large group-level difference may not be statistically significant when based on a very small sample size (19). As an example, suppose data from a study were used to compare mean weight loss for a group of patients taking an experimental treatment with a group of patients taking a placebo treatment. If differences between the mean weight decreases are evaluated and a small P value (<0.001) is observed, this signifies that, assuming no true difference between the treatment and placebo, the probability that this mean weight-loss difference (or one more extreme) between the 2 groups is due to chance alone is small and unlikely, calling into question the assumption of no true treatment difference on which the statistical test is based. The therapy is celebrated as a success until further reflection highlights that it costs $10,000 per patient per week, and the “significant” weight loss was only 115 g, on average.

In contrast, Rosnow and Rosenthal (20) describe the effect of aspirin treatment on the incidence of fatal and nonfatal myocardial infarction (MI). Less than 1% of participants taking aspirin compared with 2% of participants in the placebo group had an MI in the timeframe evaluated. Although the product-moment correlation between treatment group and MI status was only 0.034, with a small decreased risk of MI, the real cost of aspirin was judged as trivial in this study compared with the potential benefit (20).

In summary, statistical significance testing is important when interpreting COA results, but it should not be confused with the magnitude or meaningfulness of the difference.

CIs

Although P values provide one indication of potentially noteworthy findings, CIs provide an indication about the direction and strength of an effect (21). For example, in the weight-loss example described in the previous section, suppose that the 95% CI ranged from 10 to 220 g for the difference in a 115-g mean weight loss. This would mean that some would show a difference as low as 10 g and others as large as 220 g for samples drawn from the same population. Sample size affects CIs in much the same way they influence P values; for a given level of confidence (e.g., 95%), the width of the CI will narrow as the sample size increases.

Effect size comparisons

An effect size offers information for evaluating the group-level change or difference between groups beyond a P value or a CI (22–24). In Cohen’s highly cited publication (25), he stated that statistically significant differences do not mean plain English “different” and recommended the use of effect size measures to facilitate interpretation of group-level differences. More recently, Cumming (26) recommended including effect sizes, CIs, and meta-analysis when conducting research in response to the heightened concern that published literature may be “incomplete or untrustworthy” and to avoid flaws associated with reliance solely on the practice of null-hypothesis significance testing. As an example, an effect size value can be used as a guide to the size of a treatment group difference relative to a control group. Just as there are many types of hypotheses, however, there are many variants for expressing effect sizes. A list of commonly used effect size formulas is provided in Table 1.

TABLE 1.

Common effect size formulas¹

Formula	Method	Example
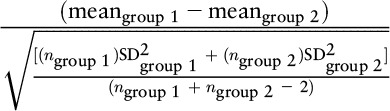	Cohen’s d	(5 − 4) /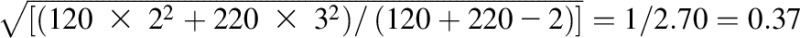
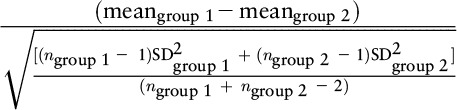	Hedges’s g	(5 − 4) /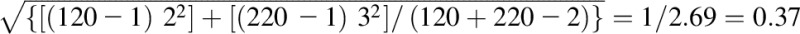
(meangroup 1 – meangroup 2) / SDgroup 2	Glass’s Δ	(5 − 4) / 3 = 0.33
(meanfollow-up – meanbaseline) / SDbaseline	Effect size estimate of change	(10 − 5) / 5 = 1
(meanfollow-up – meanbaseline) / SDchange	Standardized response mean	(10 − 5) / 2 = 2.5
(meanfollow-up – meanbaseline) / SDchange in stable group	Guyatt’s responsiveness statistic	(10 − 5) / 3 = 1.667

¹In the example, there are 2 groups: group 1 and group 2. Group 1 is the treatment group, and group 2 is considered the control group. Mean_{group 1} = 5, mean_{group 2} = 4, n_{group 1} = 120, n_{group 2} = 220, SD_{group 1} = 2, SD_{group 2} = 3, mean_follow-up = 10, mean_baseline = 5, SD_baseline = 5, SD_change = 2, SD_{change in stable group} = 3.

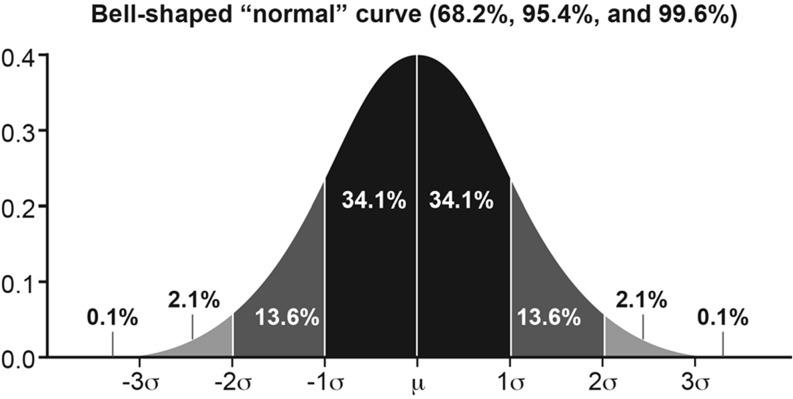
One common effect size formula is the standardized mean difference (SMD) between 2 groups, which is computed as the difference in the mean values divided by a relevant SD such as the SD of the group designated as the control group, the pooled SD of the groups at baseline, or the pooled SD at follow-up (27, 28). Assuming a normal distribution, the value of an effect size using the SMD formula can be interpreted directly as a z score from a standard normal distribution (shown in Figure 3). For example, if the SMD is 1 and the pooled SD at follow-up is used in the denominator, then the results can be interpreted as the “average patient” in the experimental treated group is one SD above the “average patient” in the control group. An alternative and complementary interpretation is that the score of the “average patient” in the treated group exceeded (i.e., was more favorable when positive change is favorable) that of 84% of patients in the control group (84 = 0.1 + 2.1 + 13.6 + 34.1 + 34.1) (29).

FIGURE 3.

Normal distribution. The value of an effect size by using the standard mean difference formula can be interpreted directly as a z score from a standard normal distribution.

Durant and colleagues (30) provide a real-world effect size application based on review of a meta-analysis study focused on school-based interventions designed to decrease childhood obesity. A key result from the meta-analysis was a pooled effect size of –0.29 (SMD in BMI) in favor of the intervention combining nutrition and physical activity compared with no intervention (control group). To provide meaning for this value, the researchers converted the SMD into the probability that a student randomly selected from the intervention group would have a lower BMI than a student randomly selected from the control group. (The SMD was defined by using a pooled SD, presumably at follow-up, but no statement was explicitly made whether it was at baseline or follow-up.) Although an effect size of 0 would result in a probability of 50%, –0.29 translates into 58%, a difference of 8% above a null finding.

An alternative effect size formula is the standardized response mean—the change in score divided by the SD of change (28, 31, 32). For clarity, Olejink and Algina (33) recommend reporting SDs for both groups, details for computing different denominators, and the formula for the effect size measure used. This information facilitates interpretation and transparency, allowing stakeholders to calculate effect size differently, if desired. Furthermore, Cohen’s rule of thumb for effect size magnitudes is based on the pooled SD, so caution should be exercised when classifying differences without consideration of the effect size formula. If the effect size is based on the SD of change, for example, the correlation between the values at the 2 time points may lead to differences in the estimated effect size (34).

In the simple case, data are available for the separate pieces of an effect size, including the means and SDs needed to facilitate the computation of the selected effect size. In other situations, such as in meta-analysis literature, components may be obtained through additional formulas to convert the provided statistics into an effect size format. For example, Cohen’s d can be computed based on reported t statistics. As an example, suppose the objective is to obtain Cohen’s d based on the pooled SD and the supplied statistic is the t test.

In addition to the general effect size unit, the magnitude of effects may be reported as a correlation or an OR. It is often useful, especially for meta-analysis, to convert from one effect size statistic to another. Various formulas are available to facilitate these conversions, as well as to help stakeholders judge the magnitude of an effect size value. For example, one may want to compare effect size measures based on correlations (r) with those based on SDs [Cohen’s d: (mean of group 1 − mean of group 2) / (pooled SD of both groups)]. A small effect size is typically r = 0.100 or 0.200 SD units, a medium effect size is r = 0.243 or 0.500 SD units, and a large effect size is r = 0.371 or 0.800 SD units: r = d / [(d² + 4)^0.5] = 0.8 / [(0.8² + 4)^0.5] = 0.8 / [(0.64 + 4)^0.5] = 0.8 / [(4.64)^0.5] = 0.8 / 2.154 = 0.371 (35, 36). Within the field of epidemiology, RR reduction has been posed as a metric to standardize effect sizes when comparing public heath interventions (37).

Meta-analysis depends on the accuracy and availability of information reported for each study. When combining studies, it is important to consider the appropriateness of the study designs and outcomes reported, as well as to correctly use the available formulas. In meta-analysis, interpretation of results and the way studies are conducted extend beyond a single study to a collection of studies. Mistakes related (at least in part) to errors in the calculation of effect sizes are not uncommon in meta-analyses.

For example, Kirsch and colleagues (38) meta-analyzed 6 weight-loss studies comparing the efficacy of cognitive-behavior therapy (CBT) alone with CBT plus hypnotherapy and concluded that “the addition of hypnosis substantially enhanced treatment outcome.” The authors reported a mean effect size (expressed as Cohen’s d) of 1.96. After correcting several transcription and computational inaccuracies in the original meta-analysis, Allison and Faith (39) found that these 6 studies yielded a much smaller mean effect size (0.26). Moreover, if one questionable study is removed from the analysis, the effect sizes for the remaining 5 studies become more homogeneous, and the mean (0.21) is no longer statistically significant. As such, the addition of hypnosis to CBT for weight loss was believed to enhance the treatment outcome to a small extent at most.

Through review of published meta-analysis studies, Gøtzsche and colleagues (40) found that a high proportion of meta-analyses based on SMD showed errors and that, although the statistical process is ostensibly simple, data extraction is particularly liable to errors that can negate or even reverse the findings of the study. Common problems included erroneous numbers of patients, means, SDs, and signs of the effect size estimates. These errors have implications for researchers and suggest that consumers, including journal reviewers and policy makers, should approach meta-analytic results with caution. When performing a meta-analysis, the quality review process should include independent checks to verify that the appropriate articles are included (or excluded), the data elements provided are logged correctly, the appropriate formulas are used, and the computations are accurate. Including 2 researchers for each task, with one researcher performing the primary tasks and the other researcher independently performing the tasks and comparing results with those of the primary researcher, will increase the accuracy of the data and ultimately the accuracy of the conclusions based on the computations.

In addition to pitfalls related to the accuracy of data or use of appropriate effect size formulas, it is important to consider the type of group comparison. Readers should view effect size results based on extreme groups with great caution unless the selection of these groups is sufficiently justified. In a review of reported epidemiologic risks, Kavvoura and colleagues (41) observed, “Paradoxically, the smallest presented relative risks were based on the contrasts of extreme quintiles; on average, the relative risk magnitude was 1.41-, 1.42-, and 1.36-fold larger in contrasts of extreme quartiles, extreme tertiles, and above-versus-below median values, respectively (P < 0.001).” One possibility is that the more extreme groupings were chosen for comparisons when the less extreme groupings would not provide the desired positive conclusion (42). Moreover, it should be noted that this finding was based primarily on comparisons between studies on different topics, not within a study on the same topic (if it occurred here, it would suggest a risk relation that is J- or U-shaped). The use of the extreme groupings inflated the effect size, and due to the missing information, the results may lead to incorrect conclusions and interpretations.

Use of effect size measures within the American Journal of Clinical Nutrition

Effect size methods and measures are not new. However, despite their usefulness, they are not widely presented in the literature. As a targeted review of their current use, we randomly selected 42 articles in the current volume of the American Journal of Clinical Nutrition (∼15% of the articles published January–November 2015) and categorized the results by using the abstract as the primary source. The most common methods provided for interpreting results were P values (95%; 40/42) and CIs (45%; 19/42). ORs, HRs, and RR values with CIs were the most common type of effect size in the sample (35.7%; 15/42). None of the articles reported a Cohen’s d value or SMD.

Methods from the COA field for interpreting results

Comparisons to thresholds based on external anchors

A common practice outlined in the draft PRO guidance (9) and described in many applications (43–47) is to evaluate whether differences observed exceed a threshold based on a minimally important difference (MID): the smallest difference that can be interpreted as important to patients. The draft PRO guidance endorsed using this type of threshold as a logical comparison to rule out differences less than or equal to the threshold but acknowledged that in practice, this was rarely implemented. Furthermore, in the MID literature, various terms and definitions have been used for the thresholds, with distinctions made for definitions based on MIDs compared with minimally clinically important differences or clinically meaningful differences (4, 47).

A team of researchers at McMaster University (Hamilton, Ontario, Canada) pioneered the use of self-reported retrospective measures of change as external anchors (48). Specifically, in this approach, mean changes in the COA scores over time are compared with responses to a global rating of overall change. Typically, the global rating is a single retrospective question that addresses the reporter’s overall perception of change in the construct underlying the COA and uses a balanced ordinal response scale. For example, responses to a global question about change in a patient’s disease status could be used to anchor a COA addressing the severity of various disease-related symptoms.

As another example, suppose there is a study in asthma that includes an anchor question with 7 categories for positive change or improvement, 1 category for no change, and 7 categories for negative change or deterioration in health status. Patients are classified based on their response to this anchor question, and then the mean changes in subscale scores on the target COA are calculated for each anchor classification.

For each subscale, the mean change is evaluated for each category of the anchor to ensure that the pattern of changes is monotonic, with the largest positive mean change for (anchor) category indicating the most improvement on the anchor question, the next largest positive mean change for the category indicating the next largest improvement on the anchor, and so forth. This evaluation provides evidence to support the appropriateness of the anchor (see below for additional information about anchor selection). For example, the group of patients reporting “a little improvement” on the anchor question may be used to estimate the MID by using their mean change on the subscale (e.g., mean change for “a little improvement” = 5). This estimates the MID for within-group change (49). If one is interested in the between-group MID, then mean change in the “no-change group” can be subtracted from the mean change in the “a little improvement group” (e.g., mean change for the no-change group = 0.5; threshold = 5 − 0.5 = 4.5 points) (4). If the mean change in the no-change group = 0, then these methods provide identical results; however, if the mean change in the no-change group is nonzero, the resulting MID estimate will be different. Therefore, it is important to understand the approach used by the authors before using a published MID.

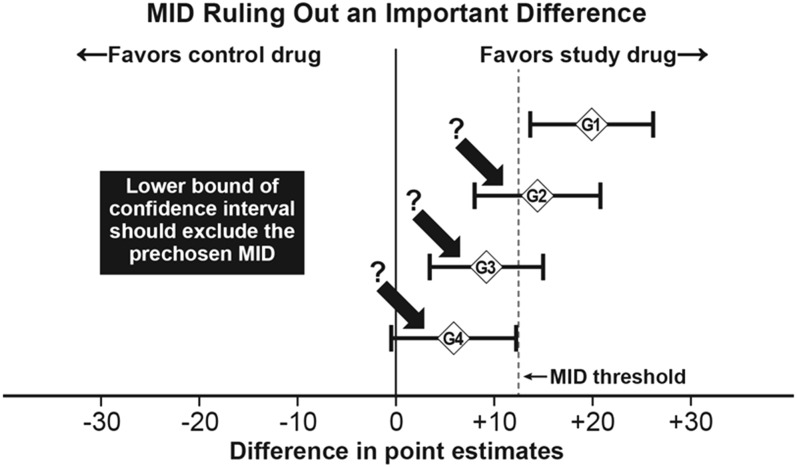
A threshold derived in this manner can provide a useful supplement to statistically significant group mean improvements in evaluating the meaningfulness of an observed improvement or deterioration. McNeil and Patrick’s illustration of how to apply the group-level threshold to interpret the meaningfulness of group mean differences [R McNeil (FDA) and D Patrick (University of Washington), personal communication, 1997] is shown in Figure 4. Four group comparisons (G1–G4) are provided, including CIs for mean differences. In addition, the MID threshold is shown as a vertical line for evaluating differences favoring the study drug. The first group comparison (G1) is the only one that meets both statistical significance (the CI does not include zero) and threshold (the CI exceeds the chosen threshold). The G2 and G3 comparisons are statistically significant but are not meaningful based on the threshold, and the G4 comparison does not meet the planned statistical significance.

FIGURE 4.

Application of statistical and MID-based classifications for group mean differences. Example of how to apply a group-level threshold to interpret the meaningfulness of group mean differences. Four group comparisons (G1–G4) are provided, including CIs for mean differences. The reference line provides the threshold for determining differences favoring the study drug. The first group comparison (G1) is the only comparison that meets both statistical significance (the CI does not include zero) and threshold (the CI exceeds the chosen threshold). The G2 and G3 comparisons are statistically significant but are not meaningful based on the threshold, and the G4 comparison does not meet the planned statistical significance. MID, minimally important difference. Adapted from R McNeil (FDA) and D Patrick (University of Washington), personal communication, 1997, with permission.

Selection of the anchor

When using a threshold based on an external anchor, the choice of anchor is critical. Evidence should be provided to justify the appropriateness of the anchor. The anchor measure should be interpretable and bear an appreciable correlation (see below for guidance) with the targeted COA of interest. An anchor may pertain, for instance, to general or overall health status (e.g., mild, moderate, severe) at the time asked or within a relatively short recall period. Hays and colleagues (49) suggested a correlation of at least 0.371, based on this being large according to Cohen’s rules of thumb.

Selected anchors may be cross-sectional (classification based on a relevant external measure at one time point) or longitudinal (classification based on change assessed through a relevant external measure) in nature. Cross-sectional anchors may be based on disease-related severity classes, such as a classification of severe malnutrition; external non–disease-related criteria, such as the loss of a job; or health states judged through hypothetical scenario frameworks (50).

Longitudinal anchors are most commonly used and include retrospective ratings of change from patients, clinicians, or other stakeholders, as well as changes in disease-related outcomes. Hudgens and colleagues (51) report differences in thresholds based on whether the anchors were collected prospectively or retrospectively. Specifically, although the results for identifying MIDs were similar across anchors for the 6 target scales, not all scale-level change scores increased monotonically for the retrospective anchors. Fayers and Hays (52) and others warn that retrospective global ratings can be biased due to response shift because of, for example, adaptation to illness, recall bias between visits, and implicit theories of change (15, 31, 53, 54).

Furthermore, studies have suggested that baseline impairment level may bias threshold estimates based on retrospective ratings. For example, Engel and colleagues (55) evaluated the impact of weight loss and weight regain on scores for an obesity-specific health-related quality-of-life (HRQOL) measure. Their results indicated that patients reporting more severe impairments at the start of the study reported greater improvements in HRQOL for the same weight loss than those with less severe impairments at the beginning. Weight regain impact on HRQOL was greater for those with more severe impairments at the start. Although these results suggest a bias related to baseline characteristics, we caution that these results may be due, at least in part, to regression to the mean (56).

Hays and colleagues (49) suggest reporting the correlation between the anchor responses, baseline scores, and postintervention scores, in addition to the correlation with the change scores. Ideally, the anchor responses should correlate with approximately equal magnitude at the baseline and postintervention time points (57). Retrospective anchors may be acceptable, depending on the situation. However, retrospective questions may, in at least some instances, correlate more strongly with the postintervention scores than they do with the baseline, because current status unduly influences the retrospective perception of change and may bias the results based on the anchor. When available, researchers may want to consider using criterion-referenced anchors based on difference in PRO means between impaired and normal samples or between different levels of severity (4, 49, 58, 59).

One way to potentially avoid recall bias is to incorporate status anchor measures into the clinical trial or observational study (in addition to or instead of the retrospective anchor items) to define the threshold. Instead of the retrospective change questions (e.g., relative to baseline, how has your overall health status changed?), these status anchors (e.g., what is your overall health status now?) can be assessed serially, one point at a time, to focus on the patient’s present state at multiple time points, thus avoiding potential recall bias but not losing the patient-reported perspective. Mulhall and colleagues (60) provide an example related to erectile dysfunction, where the relation between various outcomes was evaluated by using a repeated-measures, longitudinal, mixed-effects model incorporating status anchors. Similar longitudinal analyses have been replicated with various COA measures and anchors and in numerous therapeutic areas (61, 62).

Comparisons to thresholds based on distributional properties

Another common practice involves noting the COA score that equates to effect sizes deemed to be MIDs in previous studies. Often, this is used as a supportive method to the anchor-based method, because it does not estimate the MID from the study data. A common distribution-based threshold that is based on the effect size statistic is defined as 0.5 SDs (where the SD is the COA measure’s baseline SD); others have advocated for 0.2 SDs. These suggestions are based on Cohen’s rules of thumb: 0.2 as a small effect size and 0.5 as a medium effect size (46, 63).Therefore, this method relies solely on the statistical distribution of values through a mean and an SD to help interpret differences.

Comparisons of cumulative distribution functions

Another evaluation tool for quantitative outcomes is the comparison of cumulative distribution functions (CDFs). A CDF is a basic plot of the cumulative proportion of a sample at each possible outcome change score; a typical representation plots the change from baseline scores on the x axis and the proportion of the sample experiencing that level of change (the proportion at that score plus the proportion at all scores less than that particular score) on the y axis. Visual inspection of CDFs (either empirical or smooth plots) provides for the inspection of group-level differences, with complete separation (no overlapping areas) of the CDFs by group membership representing superiority/inferiority across the continuum of outcome scores.

A more informative method for comparison of the CDFs is to compute CIs based on survival methods (CDFs implemented as survival density functions) and to test the difference between the curves at the maximum point or comparisons based on AUC methods by using either parametric (e.g., maximum likelihood smoothing) or nonparametric (e.g., adding trapezoids) methods (4, 13, 64). Cappelleri and Bushmakin (4) suggest assigning individuals who drop out of the study to the worst possible score or change score when dropout status is considered informative. [This practice may be more reasonable for studies involving physical health outcomes than mental health outcomes (65).] Furthermore, if a measure has multiple scoring algorithms, it is necessary to consider the type of score (original score compared with transformed scores) when comparing groups or the interpretation may be biased. For example, percent change from baseline may be more extreme for transformed than for original scores (66).

Mediation

A relatively new recommendation is to use statistical mediation analysis to further support the interpretation of COA scores and changes in these scores, provided that the total effect of the independent variable on the dependent variable is of sufficient magnitude (4). Mediation analysis involves the assessment of interrelations among a set of variables simultaneously based on a postulated substantive (subject matter) framework. In the most basic mediation model, the dependent outcome (e.g., physical functioning) is predicted indirectly by one independent variable (e.g., treatment group) and directly by the mediator variable (e.g., weight reduction). In this example, the model estimates provide information about the relation between the treatment group assignment and increases in physical functioning through reduction in weight, the mediator. Understanding these relations can provide clarity about the mechanism of action for a treatment or other type of intervention so that further development or examinations can focus on the aspects that provide the most improvement (59).

Cook and colleagues (67) provide an additional example related to eating disorders and exercise. The mediation model in this study included eating disorder symptom severity as the dependent outcome, which was predicted indirectly by exercise behavior and directly by exercise dependence. Results indicated that exercise dependence is a significant mediator for the relation between exercise and eating disorder symptom severity, providing evidence to support a target psychological component (exercise dependence) for future interventions, with the goal of decreasing eating disorder severity.

Using a group-level threshold for an individual or an individual-level threshold for a group

Group-level thresholds have erroneously been applied for individual-level interpretations. However, the amount of change necessary to be meaningful will be larger for an individual than for a group of individuals. Group change and individual change have different SEs, and thus it has been noted that group-level estimates cannot be used to define responders (12, 52).

For individual comparisons, a minimum criterion is that the individual has improved an amount that is statistically significant (i.e., the observed individual change is greater than the measurement error associated with the COA). Computing a CI for the individual by using the measure’s SE of measurement or computing the reliable change index is an appropriate method to classify individuals as responders or nonresponders (12).

Probability of relative benefit

Differences between treatment groups at a specific follow-up time or change from baseline can be evaluated nonparametrically with Wilcoxon’s rank-sum test by using ridit analysis (59, 68, 69). This type of analysis is well suited for ordinal responses and is related to the receiver operating characteristic curve for the binary case. The Mann-Whitney U statistic from Wilcoxon’s rank-sum test gets converted, by using ridit analysis, to a probability that represents the chance that a randomly selected patient from the treatment group has a more favorable response than a randomly selected patient from the control group. For instance, the method may be used to address the following question: what is the likelihood that a randomly selected patient in the treatment group would have a greater reduction in physical functioning relative to a randomly selected patient in the control group? Related interpretation tools are the probability-probability plot and the probability-probability index, which provide an alternative way to evaluate the mean difference in percentile rank for responses or outcomes for different treatments (70).

DISCUSSION

The use of COAs in clinical trials, observational studies, and clinical practice provides patient-focused information to help guide decisions, including decisions in nutrition science. However, because of the wide variety of instruments, varied scoring rules, and the competitive COA development environment (e.g., potential lack of details due to ownership and strict licensure of a COA), interpretation of COA results within and across studies can be difficult. Furthermore, because studies are rarely powered for the COA comparisons, researchers must be proactive in planning, implementing, and making conclusions based on COA results.

Using examples, this article offers a review of potential methods that can be used to facilitate interpretation of group-level evaluations based on COAs to equip researchers with a basic understanding of these measures. It includes aspects to consider before reviewing statistical results and recommendations for how to be an educated stakeholder when drawing conclusions and implications from COA-based information. Before considering COA results, it is important that the measure be well developed and properly evaluated to support its use in the context of the study under review. In addition, the quality of the study design, sample size, and data collection methods should be appropriate for the intended objective of the evaluation.

Given favorable review of the COA and the study, the first step in evaluating COA results should consist of the main statistical analysis and inference based on established statistical methods (e.g., repeated measures or random coefficient models when the data are longitudinal) and the main objectives, including computation of CIs and measures of effect size, if available. Recent guidance from the FDA addresses the need for CIs and effect size values to support P values when developing an integrated summary of effectiveness section for inclusion in either new drug applications or biologics license applications for efficacy endpoints based on COAs and non-COAs. The guidance states, “A presentation of p-values alone would not be adequate” (71). An ideal next step, based on the recommendations within this article, should incorporate judgment by using an appropriate unit of comparison, such as a prespecified threshold, and review of the complete distribution of change by using tools such as the CDF.

As part of the overall plan, further investigation on applying existing techniques to COA, such as mediation or ridit analysis, should be considered to gain insights into potential next steps or to begin to explain the reason for the changes. Collectively, consideration of these methods before interpreting COA results should facilitate a careful evaluation in nutritional science—with the ultimate goal of enhanced decision making based on relevant information from a patient's perspective.