Unpacking the origins of in-cell crowding

The living cell, the fundamental unit of biological organization, was discovered in its apparent simplicity by van Leeuwenhoek in the 17th century. Scientists since then have continued to unpack nested levels of amazingly complex cellular structure and organization, right down to the atomic level. However, one of the cell’s simplest properties is not yet understood, perhaps even misunderstood. The interior of the cell contains a high concentration of dissolved solutes, principally ions, metabolites, proteins, and RNA. In a word, it is crowded in there. Estimates range from 30% to 40% by volume occupied by protein and RNA solutes, depending on the cell type and compartment (1). Biochemists and biophysicists have long been concerned that these high concentrations impart significantly nonideal solution behavior. The vast majority of measurements of equilibria and rates have been made in vitro. Although the ionic strength, osmolality, pH, and redox potential environment inside the cell can be matched with suitable buffers, the concern is that the effects of the macromolecular solutes, principally protein and RNA, are not accounted for. The crucial and currently unanswered questions are, How relevant is the plethora of in vitro experiments to in vivo conditions? Are measured equilibrium constants, rates, and other thermodynamic data significantly different? If so, by how much and in what direction? In principle one can address this directly by in vivo measurements, but the experiments are difficult, and the answers have been slow in coming. In PNAS Smith et al. (2), by measuring a protein folding equilibrium in vivo, now provide some answers—and they are surprising.

To appreciate the surprise, it is helpful to briefly touch on the more than three-decade history of the macromolecular crowding field. The notable feature of macromolecules as cosolvents that is missing from simple buffers is their size. All molecules in solution effectively exclude each other; they cannot overlap, due to what is termed the hard-core or van der Waals repulsion. An early pioneer in this field, Minton (3), explicitly emphasized “excluded volume as a determinant of macromolecular structure and reactivity,” whereas Ellis (4) stressed the “obvious” aspect of this, meaning that a large excluded volume is a property of all macromolecules. An extensive review covers much of the subsequent literature (5). Of course, solutes can cause nonideal behavior through a second mechanism, strong intermolecular interactions such as electrostatic and hydrophobic effects. Although crowding is now often used as a synonym for any effects of concentrated solutes, for the purpose of this commentary I will take crowding to refer to the excluded volume effects, as originally defined (3, 4), because disentangling size effects and interaction effects is precisely where the advances of Smith et al. (2) lie. I also discuss effects on equilibria only. Given our recently revised understanding of equilibrium effects, it seems premature to discuss the more complex effects of crowding on rates, involving changes in thermodynamics, kinetics, and viscosity.

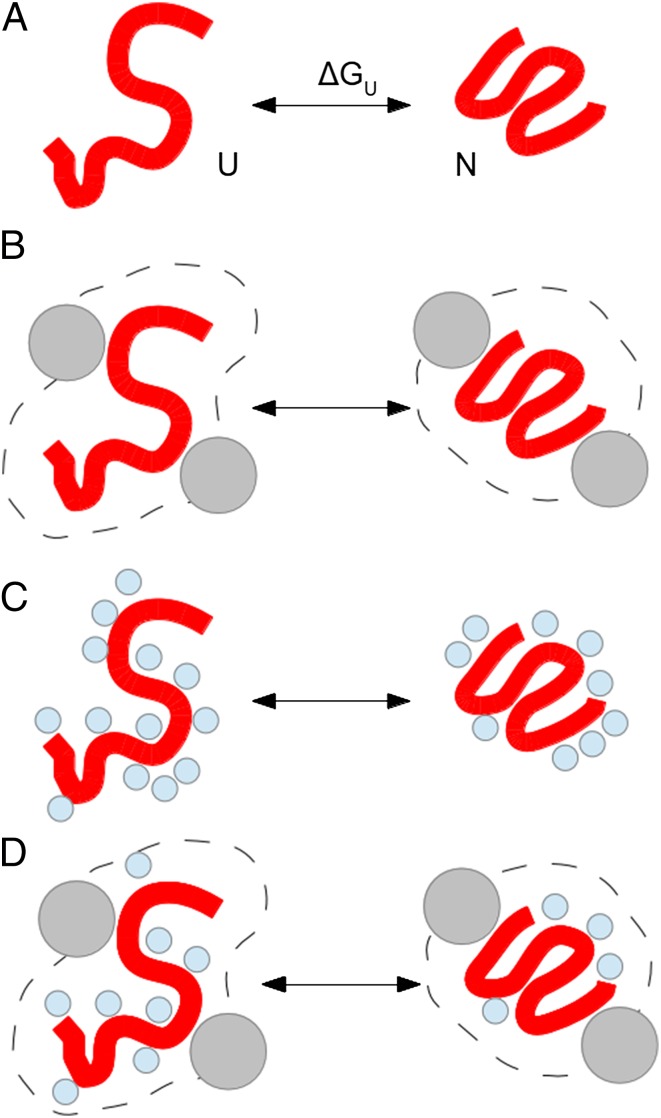
In brief, the classic model of crowding through excluded volume effects is depicted in Fig. 1. In the “reference state solution,” buffer or water (Fig. 1A), a protein is in equilibrium between the unfolded state and native folded state. The addition of large crowding molecules (Fig. 1B) raises the protein’s activity because its excluded volume (delineated by the dotted line) is inaccessible to the centers of the crowding molecules. The activity change produced by the crowding molecules favors the folded state of the protein because this has a smaller excluded volume. Concomitantly, in this model the effective concentration of the protein is increased by crowding molecules because it is excluded from the volume occupied by the latter and so is confined to a smaller effective volume than the actual solution volume. This effect favors oligomerization of proteins and higher association constants (lower dissociation constants) for ligand binding. As stated, these seem to be obvious and inescapable effects of the large excluded volume of a macromolecule. Moreover, the effect should increase as the excluded volume of the crowding molecule increases.

Fig. 1.

(A) Protein equilibrium between unfolded state (U) and folded native state (N), characterized by an unfolding free energy ΔG_U. (B) Hard-core repulsion prevents crowding macromolecules (gray spheres) from entering the protein’s excluded volume, indicated by the dashed line. (C) The solvent is in fact always packed with water, ions, and small metabolites (cyan spheres) that also exclude the protein. (D) Effect of macromolecular crowding agents must account for the fact that each of them displaces many smaller solvent molecules.

However, this is not what Smith et al. (2) found. Using state-of-the-art in vivo NMR experiments they studied the folding equilibrium of the small protein SH3 in Escherichia coli cells. First, the raw data show that the protein is less stable inside the cells (figure 1 in ref. 2). After suitable corrections for metabolite effects, the protein stability was found to be indistinguishable from that in buffer. Second, they studied the effects of concentrated protein cosolvents in vitro (figure 1 in ref. 2) and found that they destabilize SH3. Either excluded volume effects are being counteracted by interaction effects or our expectation about excluded volume effects is wrong. Even before the work of Smith et al. (2), there were several indications of the latter. First, the model of Fig. 1 A and B predicts a generic “baseline” stabilization of all folded protein states, all higher oligomer states, and all ligand-protein bound states, whereas the evidence suggests very variable degrees of effect. Second, size effects should be purely entropic, whereas enthalpic contributions are often seen (6, 7). Third, crucially, in an earlier study Pielak and coworkers (6) did not find the dependence on crowding molecule size predicted by the conventional model of Fig. 1 A and B. Here they examine the size dependence in more detail by comparing the effect on SH3 stability of the neutral polymers dextran, Ficoll, and PEG vs. their corresponding monomers glucose, sucrose, and ethylene glycol, respectively: chemically identical pairs of molecules of vastly different size. For each of these widely used crowding agents, the larger form is less effective at stabilizing the protein, exactly opposite of the prediction of the conventional crowding model depicted in Fig. 1 A and B. However, the observed behavior is predicted (8) by more rigorous but less widely known statistical mechanical treatments of excluded volume [hard sphere fluid mixture theories (9)]. The physical explanation for the counterintuitive weaker crowding power of larger molecules (at the same volume concentration) is indicated in Fig. 1 C and D. These statistical mechanical theories tell us that the cosolvent-induced change in the protein activity not only depends on the size of the cosolvent molecules, but also on the number of them excluded by the protein. In the absence of the crowding macromolecules the solvent volume is of course occupied by other small molecules, principally water and ions, which also cannot overlap each other or the protein. A single large crowding macromolecule will displace many smaller solvent molecules, reducing the exclusion effect on protein activity (Fig. 1D).

The other relevant fact that comes from these theories is that the effect of excluded volume is strongly dependent on the packing fraction of the solvent—how much of the total volume is filled by the hard-core volume of all of the molecules. If this is increased, excluded volume effects grow larger (8, 10). This provides one explanation for the quite different effects Smith et al. (2) see for the crowding agents dextran, Ficoll, and PEG vs. proteins. If the former, neutral molecules increase the net packing efficiency of the solvent (polymer plus water plus ions), whereas charged proteins and RNA in the cell do not, then the neutral polymers may indeed stabilize proteins and promote bound and oligomeric states. However, they would be quite unrealistic models for the solvent milieu of a cell. In addition, proteins and RNA have many charged groups to potentially make intermolecular interactions. That this is a factor is indicated by the pH/charge dependence of SH3 stability (figure 1 in ref. 2). Our understanding of intermolecular interactions in concentrated solutions is not as advanced as that of size-exclusion effects, however, and more in vivo thermodynamics studies of the kind pioneered by Smith et al. (2) will be essential for progress.