Abstract
The purpose of this study was to explore the reliability of estimating three-dimensional (3D) angular kinematics and kinetics of a swimmer derived from digitized video. Two high-level front crawl swimmers and one high level backstroke swimmer were recorded by four underwater and two above water video cameras. One of the front crawl swimmers was digitized at 50 fields per second with a window for smoothing by a 4th order Butterworth digital filter extending 10 fields beyond the start and finish of the stroke cycle (FC1), while the other front crawl (FC2) and backstroke (BS) swimmer were digitized at 25 frames per second with the window extending five frames beyond the start and finish of the stroke cycle. Each camera view of one stroke cycle was digitized five times yielding five independent 3D data sets from which whole body centre of mass (CM) yaw, pitch, roll, and torques were derived together with wrist and ankle moment arms with respect to an inertial reference system with origin at the CM. Coefficients of repeatability ranging from r = 0.93 to r = 0.99 indicated that both digitising sampling rates and extrapolation methods are sufficiently reliable to identify real differences in net torque production. This will enable the sources of rotations about the three axes to be explained in future research. Errors in angular kinematics and displacements of the wrist and ankles relative to range of motion were small for all but the ankles in the X (swimming) direction for FC2 who had a very vigorous kick. To avoid large errors when digitising the ankles of swimmers with vigorous kicks it is recommended that a marker on the shank could be used to calculate the ankle position based on the known displacements between knee, shank, and ankle markers.
Key points.
Using the methods described, an inverse dynamics approach based on 3D position data digitized manually from multiple camera views above and below the water surface is sufficiently reliable to yield insights regarding torque production in swimming additional to those of other approaches.
The ability to link the torque profiles to swimming actions and technique is enhanced by having additional data such as wrist and ankle displacements that can be obtained readily from the digitized data.
An additional marker on the shank should be used to improve accuracy and reliability of calculating the ankle motion for swimmers with a vigorous kick.
Key words: Inverse dynamics, reliability, swimming, angular kinetics, asymmetry
Introduction
One of the fundamental principles of swimming is to minimise resistance by maintaining good alignment between the longitudinal axis of the body and the intended line of progression (Counsilman, 1973; Maglischo, 2003). Most studies of body alignment in swimming have focused on the effect of body roll on performance in front crawl, for example, Lui et al. (1993); Payton et al. (1997); Cappaert et al. (1998); Castro et al. (2003); Yanai (2004); Seifert et al. (2005); Sanders and Psycharakis (2009). However, with the exception of Yanai (2004) who applied the model of Dapena (1978) to determine the role of the buoyancy force in generating body roll in front crawl swimming, there is a dearth of research in which the rotational torques that produce body rotations have been quantified. Although Sanders et al., (2015b) have quantified torques to explain the pattern of yaw (rotation about the antero-posterior axis) in a single breaststroke swimmer, torques do not appear to have been determined to explain yaw and pitch (rotation about the transverse axis) in front crawl swimming and in backstroke.
Because yaw and pitch inevitably affect resistance, such analyses can lead to interventions to improve performance (Czabañski and Koszcyc, 1979; Sanders, 2013) and to minimise stresses within the body that lead to injury. For example, an asymmetrical kick to realign the body following an asymmetrical pull in breaststroke may create injurious valgus stresses in knee (Rodeo, 1999).
Linear and angular kinematics and kinetics can be obtained using the inverse dynamics approach defined by Whittlesey and Robertson (2004) as ‘the process by which forces and moments of force are indirectly determined from the kinematics and inertial properties of moving bodies’. The position of the centre of mass (CM) can be obtained by modelling the body as a series of rigid links. An inertial reference system can be defined from the three-dimensional (3D) coordinates transformed from the digitized two-dimensional (2D) camera images. In the case of human swimming the reference system comprises orthogonal axes aligned with the external inertial reference system of the calibrated space with origin at the swimmer’s CM. Angular motion about the horizontal axis aligned with the swimming direction corresponds to ‘roll’; motion about the vertical axis corresponds to ‘yaw’; and rotation about the horizontal axis perpendicular to the swimming direction corresponds to ‘pitch’. Linear and angular velocities can be derived from linear and angular displacements with respect to the reference axes obtained from the digitized coordinates. Angular momenta of body segments with respect to each axis are then determined and net torques about each axis obtained as derivatives of the whole body angular momentum about each axis. Thus, the inverse dynamics approach can be very useful in swimming research to provide detailed information about linear and angular motion.
Given that torques are the product of the forces and their moment arms with respect to the axis of rotation, quantifying both the torque and its moment arm enables interpretation of the effect of swimming technique on body alignment. Consequently, the effect of technique and technique asymmetries on performance can be assessed (Sanders et al, 2012). Sanders et al. (2015c) have shown that the inverse dynamics approach with appropriate smoothing and extrapolation techniques can be used to obtain reliable net force profiles despite the need to digitize manually due to the constraints of the aquatic environment. Like net forces, calculation of net torque is influenced by some sources of variability related to the digitizing process including the variability of the CM position. However, the mathematical process is different. Whereas net forces are calculated by obtaining the second derivative of CM position, net torques are derived from angular momentum. In turn angular momentum is the sum of local and remote angular momenta of the body segments. The segment remote angular momentum terms are affected by variability in digitizing segment endpoints to determine the segment center of mass position, its derivative, and its displacement from the CM. Given these additional sources of variability it cannot be assumed that variability in the calculation of net torques due to variability in digitizing is similar in magnitude to the variability in the calculation of net forces. Therefore, the reliability of calculating net torques to enable the rotational motion of the body to be explained must be conducted as a separate analysis. Currently there is a paucity of data regarding the reliability of net torques obtained from manual digitization of swimmers. Thus, the purpose of this study was to establish the reliability of determining net torques acting on a swimmer and the moment arms associated with the upper limb and lower limb actions.
Methods
The methods in terms of participants and collection of data are identical to those described by Sanders, Gonjo, and McCabe (2105) and, indeed, the raw 3D data set is identical. Briefly, the data were from a front crawl specialist (S1: age: 18yrs; height: 180.5cm; weight: 72.6kg; 50m front crawl long course PB 25.00s) and a front crawl and backstroke swimmer (S2: 18yrs; height: 186.0 cm; weight: 76.0 kg; back crawl: 50m short course PB 25.26s; 100m 59.32s; 200m 2:08.2; front crawl short course PB 50m 23.32s; 100m 51.80s; 200m 1:51.81). The 3D data representing the 13 segment body model were input to a MATLAB (Mathworks, Inc.) analysis program enabling calculation of whole body centre of mass (CM), perpendicular distances of the right and left wrist and right and left ankle with respect to each axis of the internal reference system, segmental and whole body angular momentum, and torques about the internal reference axes (Sanders et al., 2015c). Right and left wrists and right and left ankles were used to represent hand and foot motion respectively due to the large errors associated with estimating distal landmarks of the feet and hands obscured by turbulent water. The data from the study of Sanders et al. (2015c) comprised 4 x 25m front crawl maximal sprints by S1 4 x 50m front and back crawl sprints by S2 without breathing while swimming through the calibrated space. The fastest front crawl sprint of S1 (FC1) and S2 (FC2) and the fastest back crawl sprint of S2 (BS) were selected for further analysis.
In the study of linear kinematics and kinetics in the Sanders et al. (2015c) study, it was found that, although the reliability was better when sampling at 50 Hz than at 25 Hz, sampling at 25 Hz also achieved acceptable reliability. This is important given the labour intensive nature of manually digitising full body models. The calibration frames used for S1 and S2 differed slightly in dimension (for S1: 4.5 in length (X); 1.5m in height (Y); and 1.0 m in width (Z); for S2: 6.0m length (X); 2.5m in height (Y); and 2.0m width) and so the fields of view of the cameras were larger for FC2 and BS than for FC1 as described by Sanders, Gonjo, and McCabe (2015). Given that the effect of sampling rate and calibration frame size might be different for angular kinematics and angular kinetics compared to the results for linear kinematic and kinetics found in the previous study this issue was of some interest in this study also.
It should be noted that although there are errors due to digitising the landmarks of the calibration frame as reported by Psycharakis et al. (2005), the predominant source of errors is associated with the digitising of the landmarks of the swimmer. From that perspective, the size of the field of view of the cameras, which depends on the space required to be enclosed and usually encompasses the whole calibration frame, is the important consideration rather than the dimensions of the calibration frame per se. Given that the fields of camera view were similar, being determined by the need to allow for two stroke cycles (to be sure of capturing one complete cycle), the pixel density of the markers on the calibration frames was equivalent at each venue.
Data processing
The data processing procedure has been described previously (Sanders et al., 2015c). Briefly, one front crawl stroke cycle (SC), defined as the period between the frame corresponding to the entry of the 3rd metacarpal tip of one hand to the instant of entry of the same hand, was manually digitized using the Ariel Performance Analysis System (APAS) system. In terms of the protocol, all that differed between the trial of S1 (FC1) and the trials of S2 (FC2 and BS) was the number of extrapolation points (10 vs 5) and the digitising sampling frequency (50 Hz for FC1 – i.e. fields digitised vs 25 Hz for FC2 and BS i.e. frames digitised without separating into fields). Extrapolation reduces distortion of the endpoints which occurs in the digital filtering process due to the filter needing a span of points. While digitising more points would also provide insurance against this distortion it demands increased time devoted to digitising and also a larger field of view of the cameras. The first limits the number of participants, conditions, and trials, and the second limits the accuracy and reliability of the digitising and the variables calculated subsequently.
The digitising process was repeated five times by the same experienced operator with digitizing conducted on separate days and no repeats of the same camera view on the same day. Each of the five repeat digitizations was input to a customised MATLAB (Mathworks, Inc.) analysis program to calculate all variables. A 4th order Butterworth filter with a 4Hz cut-off frequency was applied after extrapolating the data by reflection to an additional 20 points beyond the start and finish of the SC (30 points of additional data at each end for FC1 and 25 points of additional data at each end for FC2 and BS) as added insurance against distortion of the endpoints of the data set. After trimming the data to the period of the SC the data were then converted to 101 points, again by Fourier transform and inverse transform, representing percentiles of the SC. The use of the Fourier series transform is regarded as highly appropriate when analysing periodic data, such as in swimming (Bartlett, 1977).
Calculation of variables
Variables were calculated in the manner described by Sanders et al., 2015b). Body segment parameter data comprising segment masses and proportional segment centre of mass locations, and segment moments of inertia were obtained from the e-Zone program (Deffeyes and Sanders, 2005; Sanders et al, 2015a).
The head and neck were combined as a single segment for calculation of linear and angular kinematics and kinetics. Similarly the thorax and abdomen were combined as a single segment (referred to as the ‘trunk’) for calculation of linear and angular kinematics and kinetics. However, because the hips and shoulders rotate somewhat independently about the long axes of the thorax and abdomen respectively angular kinematics and kinetics of the thorax and abdomen about their longitudinal axes were calculated separately.
The CM was determined by taking moments about the X, Y, Z reference axes of the segment centres of mass in conjunction with the body segment parameter data output by the e-Zone program. Paths of the hands, represented by the wrists, and paths of the feet, represented by the ankles, were expressed relative to the CM. Linear and angular segmental kinematics were determined from the digitised segment endpoint coordinates using standard inverse dynamics approaches.
The angle of yaw of the trunk was determined as the angle between the projection onto the XZ plane of the position vector (v) of the midpoint of the shoulders with respect to the midpoint of the hips and the X axis. Computationally this was:
| (Eq 1) |
Where vi(z) and vi(x) are the Z and X components of v respectively at the ith time percentile.
The angular momentum vector (H) of each segment (s) was calculated as the sum of local (HL) and transfer (HT) terms calculated using the methods of Dapena (1978). The components of the angular momentum vector represent rotations about the external horizontal X axis (roll), the vertical Y axis (Yaw) and the horizontal Z axis (pitch). To calculate the local angular momentum contribution (HL) the angular momentum of the segment about an instantaneous axis of rotation perpendicular to the long axis of the segment was determined as:
| (Eq 2) |
Where HLtrsi is the local angular momentum of segment s about its own transverse axis at the ith time percentile expressed in the external reference system; Itrs is the moment of inertia of segment s about its transverse axis obtained from the e-Zone program (Deffeyes and Sanders, 2005) and ɷsi is the angular velocity vector of segment s at the ith time percentile.
To obtain the segment angular velocity vector an orientation vector was defined as the unit vector (R) in the direction of the long axis of the segment. The magnitude of the angular velocity of the segment was:
| (Eq 3) |
Where ti is the time at the ith percentile. The angular velocity vector was then
| (Eq 4) |
This yields an angular velocity vector perpendicular to the plane determined by Ri+1 and Ri-1. Angular momentum of the limb segments about their longitudinal axes was regarded as negligible relative to the magnitude of the angular momentum about their transverse axis and therefore ignored in accordance with Dapena (1978).
Given that the upper and lower torso are large segments that rotate about their longitudinal axis in swimming angular momenta of those segments about their long axes were calculated. The same process described above was applied except that the orientation vectors were the line between the shoulders for the upper torso and between the hips for the lower torso. It was deemed necessary to treat the trunk as two segments comprising upper torso (including the head and neck) and lower torso when assessing angular momentum about the long axis due to the relative independence of hip and shoulder rotation in swimming (Cappaert, 1998; Payton et. al., 1999; Psycharakis and Sanders, 2008). The anatomical division of the upper and lower torso was the plane perpendicular to the long axis of the body passing through the xiphoid process. Moments of inertia of these segments about their long axes were obtained from the output of the e-Zone program. The angular momentum of the whole trunk (including the head and neck) was then the vector sum of local and transfer terms of the combined trunk segment about its instantaneous transverse axis, and the local and transfer terms of the upper and lower torso about their long axes.
The contributions of the transfer components to angular momentum about each of the orthogonal axes of the external reference frame were computed using:
| (Eq 5) |
Where HTsi is the transfer term of the angular momentum of segment s at the ith time percentile and vsi is the vector obtained by subtracting the location of the segment centre of mass from the CM.
Torque at the ith time percentile acting on each segment s was determined as:
| (Eq 6) |
Statistical analysis
The standard deviation of the five digitizing trials was obtained for each percentile of the time profile for each variable. The error measure was obtained as the mean of the 101 standard deviations expressed as a percentage of the range of the data from minimum to maximum. Expressing average error as a percentage of the range rather than the mean is appropriate in this case for two reasons a) some variables were not referenced to a baseline of zero and b) the range of oscillation of the data about a mean value is more important that the mean value given that in a cyclical activity the mean is actually the baseline about which the motion is occurring rather than being the indicator of magnitude of the motion.
Repeatability (R2)of the time-profile of each variable expressed as a time-normalised time-series was obtained using the method of Kadaba et al. (1989). Kadaba et al’s which was designed specifically for comparing the repeatability of time-normalised time series data. A correlation coefficient R was also obtained as the square root of R2.
Results
Table 1 (FC1), Table 2 (FC2) and Table 3 (BS) display the average error, range, average error expressed as a percentage of the range (average error%), R2 and R for the variables of interest. These include yaw, pitch, roll (degrees), torque (N.m) about each of the X (roll), Y (yaw), and Z (pitch) axes, and moment arms (m) of right and left wrists and right and left ankles in terms of X displacement (from the Y and Z axes), Y displacement (from the X and Z axes) and Z displacement (from the X and Y axes).
Table 1.
Average error, range, average error%, R2 and R for the angular kinematic and kinetic variables and moment arms for FC1 (sampled at 50 fields per second with 10 fields beyond each end of the stroke cycle).
| Variable | Average Error | Range | Average Error% | R2 | R |
|---|---|---|---|---|---|
| Shoulder Roll | 1.627 | 76.85 | 2.12 | .996 | .998 |
| Hip Roll | .946 | 40.74 | 2.32 | .996 | .998 |
| Knee Roll | 2.06 | 70.20 | 2.94 | .989 | .994 |
| Ankle Roll | 3.45 | 138.3 | 2.49 | .992 | .996 |
| Pitch | .244 | 3.87 | 6.32 | .958 | .979 |
| Yaw | .942 | 12.33 | 7.65 | .933 | .966 |
| Torque X | 10.42 | 239.6 | 4.35 | .974 | .987 |
| Torque Y | 34.56 | 404.2 | 8.55 | .909 | .954 |
| Torque Z | 13.78 | 446.6 | 3.08 | .983 | .991 |
| Wrist Disp X L | .0177 | 1.225 | 1.44 | .998 | .999 |
| Wrist Disp X R | .0165 | 1.228 | 1.35 | .998 | .999 |
| Wrist Disp Y L | .0077 | .653 | 1.10 | .999 | .999 |
| Wrist Disp Y R | .0055 | .575 | .954 | .999 | .999 |
| Wrist Disp Z L | .0100 | .304 | 3.29 | .987 | .993 |
| Wrist Disp Z R | .0169 | .273 | 6.19 | .924 | .961 |
| Ankle Disp X L | .0037 | .079 | 4.66 | .991 | .995 |
| Ankle Disp X R | .0046 | .161 | 2.85 | .975 | .988 |
| Ankle Disp Y L | .0097 | .390 | 2.477 | .993 | .997 |
| Ankle Disp Y R | .0093 | .353 | 2.64 | .993 | .996 |
| Ankle Disp Z L | .0098 | .163 | 6.04 | .950 | .975 |
| Ankle Disp Z R | .0072 | .198 | 3.65 | .976 | .988 |
Table 2.
Average error, range, average error%, R2 and R for the angular kinematic and kinetic variables and moment arms for FC2 (sampled at 25 frames per second with 5 fields beyond each end of the stroke cycle).
| Variable | Average Error | Range | Average Error% | R2 | R |
|---|---|---|---|---|---|
| Shoulder Roll | 2.67 | 114.9 | 2.32 | .996 | .998 |
| Hip Roll | 1.60 | 93.41 | 1.71 | .997 | .998 |
| Knee Roll | 3.28 | 77.7 | 4.22 | .976 | .988 |
| Ankle Roll | 5.86 | 174.7 | 3.36 | .982 | .991 |
| Pitch | .466 | 12.53 | 3.72 | .975 | .987 |
| Yaw | .752 | 11.39 | 6.61 | .957 | .978 |
| Torque X | 7.14 | 107.11 | 3.80 | .971 | .986 |
| Torque Y | 35.61 | 481.96 | 7.39 | .923 | .960 |
| Torque Z | 25.59 | 546.37 | 4.68 | .971 | .985 |
| Wrist Disp X L | .026 | 1.44 | 1.83 | .997 | .999 |
| Wrist Disp X R | .021 | 1.44 | 1.60 | .998 | .999 |
| Wrist Disp Y L | .013 | .837 | 1.50 | .998 | .999 |
| Wrist Disp Y R | .012 | .920 | 1.39 | .998 | .999 |
| Wrist Disp Z L | .012 | .405 | 3.05 | .988 | .994 |
| Wrist Disp Z R | .016 | .405 | 3.81 | .974 | .987 |
| Ankle Disp X L | .018 | .098 | 18.30 | .707 | .841 |
| Ankle Disp X R | .015 | .125 | 12.26 | .833 | .913 |
| Ankle Disp Y L | .017 | .425 | 3.98 | .984 | .992 |
| Ankle Disp Y R | .016 | .491 | 3.21 | .986 | .993 |
| Ankle Disp Z L | .009 | .188 | 4.83 | .969 | .984 |
| Ankle Disp Z R | .008 | .223 | 3.57 | .977 | .988 |
Table 3.
Average error, range, average error%, R2 and R for the angular kinematic and kinetic variables and moment arms for BS (sampled at 25 frames per second with 5 fields beyond each end of the stroke cycle).
| Variable | Average Error | Range | Average Error% | R2 | R |
|---|---|---|---|---|---|
| Shoulder Roll | 2.02 | 109.8 | 1.84 | .997 | .999 |
| Hip Roll | 1.38 | 85.35 | 1.62 | .998 | .999 |
| Knee Roll | 1.79 | 174.6 | 1.02 | .998 | .999 |
| Ankle Roll | 2.19 | 212.24 | 2.19 | .998 | .999 |
| Pitch | .56 | 6.16 | 9.07 | .901 | .949 |
| Yaw | .63 | 12.80 | 4.90 | .959 | .980 |
| Torque X | 7.14 | 107.1 | 6.67 | .930 | .975 |
| Torque Y | 15.46 | 137.0 | 11.29 | .858 | .926 |
| Torque Z | 20.80 | 385.2 | 5.40 | .954 | .977 |
| Wrist Disp X L | .0079 | 1.361 | .57 | .999 | .999 |
| Wrist Disp X R | .0051 | 1.296 | .40 | .999 | .999 |
| Wrist Disp Y L | .0048 | 1.003 | .48 | .999 | .999 |
| Wrist Disp Y R | .0042 | 1.162 | .36 | .999 | .999 |
| Wrist Disp Z L | .0088 | .501 | 1.77 | .993 | .997 |
| Wrist Disp Z R | .0068 | .534 | 1.26 | .998 | .999 |
| Ankle Disp X L | .0116 | .207 | 5.59 | .932 | .965 |
| Ankle Disp X R | .0047 | .181 | 2.56 | .991 | .995 |
| Ankle Disp Y L | .0066 | .439 | 1.51 | .996 | .998 |
| Ankle Disp Y R | .0033 | .378 | 0.89 | .999 | .999 |
| Ankle Disp Z L | .0097 | .327 | 2.96 | .987 | .993 |
| Ankle Disp Z R | .0060 | .341 | 1.75 | .997 | .998 |
Mean average error% for FC1, FC2, and BS were 3.64%, 4.63% and 3.05% respectively. However, the errors for the ankle of FC2, particularly in the X direction, were large (18.3% for the left ankle and 12.3% for the right ankle). This was due to difficulty in seeing the ankle markers due to turbulence and to the small range of motion affecting the. Mean average error%. When the ankle measures were removed from the comparison, the average errors were very similar across FC1, FC2, and BS (3.61%, 3.40%, and 3.26% respectively), The R2 and R values show that the time series patterns were very consistent except for the X displacement of the ankles of FC2.
As an example, Figure 1 displays the shoulder roll patterns of FC1, FC2, and BS. The net torques about the X (roll) axis that affect shoulder roll are shown in Figure 2. Figures 3 and 4 show the Z displacement for the wrists and ankles respectively to illustrate the moment arms of vertically directed forces of the hands and feet respectively about the X axis.
Figure 1.
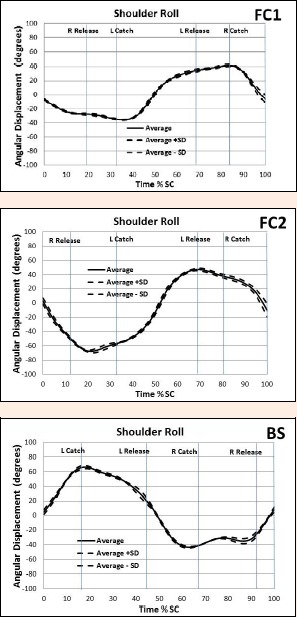
Shoulder roll for FC1, FC2, and BS.
Figure 2.
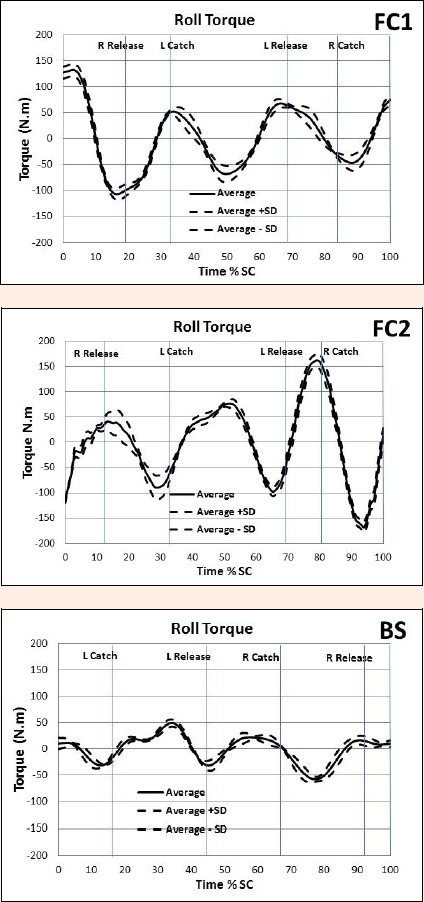
Net torque about the X axis for FC1, FC2, and BS.
Figure 3.
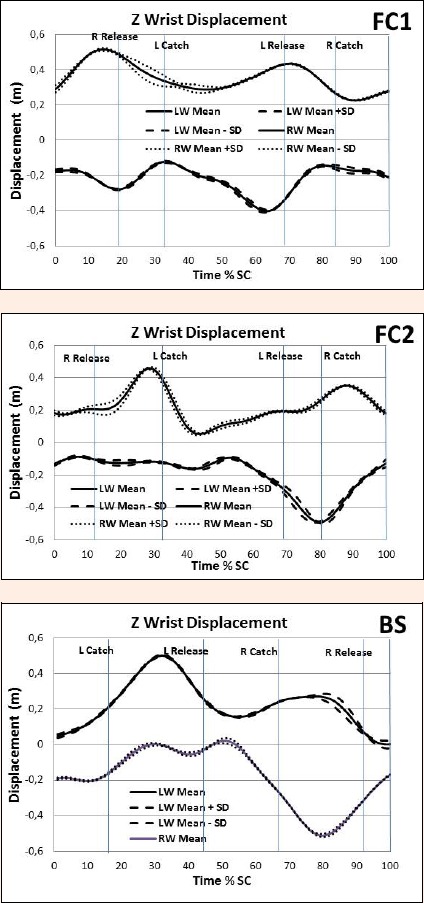
Left (L) and right (R) wrist Z displacement for FC1, FC2 and BS.
Figure 4.
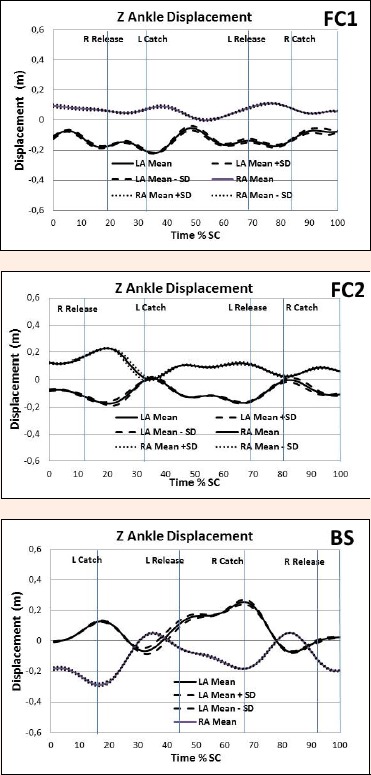
Left (L) and right (R) ankle Z displacement for FC1, FC2 and BS.
Discussion
The purpose of this study was to explore the reliability of estimating 3D angular kinematics and kinetics of a swimmer derived from digitized video. This supplements the work of Sanders et al. (2105c) establishing the reliability of linear kinematics and kinetics. The major concern is whether torques can be derived with sufficient reliability to enable valid comparisons between swimmers, strokes, swimming speeds and other conditions such as breathing and non-breathing stroke cycles in front crawl. The variability of the torques determined in this study was less than 10% with the exception of torques about the Y axis (pitch) in BS. Thus, although there are additional sources of variability when calculating net torques about the CM, as described in the introduction, reliability is generally of a similar magnitude to that of linear accelerations (directly related to net forces) of the CM reported by Sanders et al. (2015c) and was not greatly affected by the differences in sampling rate or calibration frames.
The errors in angular kinematics, and linear displacements of the wrist and ankles were generally small except for the X component of the ankles in FC2. This was due to the vigorous kick of that particular swimmer creating turbulence that greatly reduced the visibility of the ankle marker. Based on this result, it is recommended that an additional marker be placed on the shank at known distance from the ankle and knee markers and in a direct line between them. When visibility affects digitising for particular swimmers the ankle joint position can then be calculated by digitising the shank marker.
High reliability of angular kinematic and angular kinetic patterns facilitates interpretation regarding the effects of swimming actions on rotations about the three axes of the external reference frame with its origin through the swimmer’s CM. For example, Figure 1 shows that the patterns of shoulder roll of FC1 and FC2 differ with regard to the amount of negative roll (clockwise when looking at the swimmer from the front) and that FC2 rolls al in his body roll pattern than FC1. Inter-individual differences in technique and coordination such as these are in accordance with observations of other researchers, for example Figueiredo et al. (2102). The patterns of roll torque of both FC1 and FC2 reflect the effect of the six beat kick pattern used by the swimmers in this study and therefore have three periods of positive torque and three periods of negative torque during the stroke cycle. Although these torques affect the roll motion of the body as a whole rather than just the shoulders, their influence is apparent in the patterns of shoulder roll. As a consequence the shoulder roll pattern does not entirely resemble a single sinusoid but reflects the influence of the kicking action as well as the action of the upper limbs. The influence of the kick on the roll patterns of the shoulders has been observed in other studies (Sanders and Psycharakis, 2009). With regard to the action of the upper limbs, the greater clockwise roll than anticlockwise roll of FC2 is likely to be linked to the difference in hand path of the right and left hands during their underwater phases. Differences in hand path are known to be linked to asymmetries in shoulder roll (Psycharakis and McCabe, 2011; Sanders et al., 2011). Figure 3 indicates that the right hand of FC2 is wider at the time of its catch than the left hand was at the time of its catch. Given that the hand is below the CM, it would be expected that the inward sweep of the right hand following the catch of the right hand would assist the clockwise roll and this may partially account for the greater clockwise roll than anticlockwise roll.
In backstroke much of the torque to reverse the roll rotation is produced during the period when the hand sweeps inward and downward from its wide position attained during the pull (Figure 3). Although the explanation isn’t obvious, an interesting difference between the kicking pattern of FC2 and BS is that the Z displacement of the ankles is smallest near the time of the catch in FC2 and it largest near the time of the catch in BS. As a consequence, the differences in pattern of the moment arm magnitudes would produce differences between FC2 and BS in the patterns of torque production about the X axis and thereby the timing of the body roll. Scrutiny of the torque patterns of FC2 and BS in conjunction with the wrist Z and ankle Z indicates that the moment arms of the wrists coincide closely with the peak torques whereas the moment arms of the ankles tend to be small at those times. This provides some evidence that roll is produced primarily by the actions of the upper limbs rather than the lower limbs for these swimmers. In the case of front crawl, the rolling torque could be due to a combination of the difference in alignment of the buoyancy and weight forces as suggested by Yanai (2004) and the effect of the pulling upper limbs. Of course, the moment arms due to the displacement along the Y axis and the effect of inward and outward motions needs to be taken into account also. Nevertheless, the potential to interpret the effect of the kinematic characteristics of technique such as moment arms and motions of the upper and lower limbs in combination with the net torques about the axes of rotation is apparent.
Although the reliability of obtaining angular kinematics, moment arms, and net torques using manual digitising of standard video has been established in this study it must be recognised that this reliability has been based on only two camera systems, venues, and calibration spaces and sampling rates (50 Hz and 25 Hz). Also, due to the labour intensiveness of conducting such a study it has been done for only two front crawl swimmers and a backstroke swimmer. As noted with regard to the ankle data of FC2, differences in reliability can occur across swimmers and paces due to differences in the turbulence produced. Future research could also establish the reliability of additional variables including the reliability of estimating duration of phases within the stroke and index of coordination (Chollet et al., 2000; 2008; Seifert et al., 2005).
Conclusion
In this study it has been found that angular kinematics and kinetics of swimmers can be derived with sufficient reliability to enable rotations about the three principal axes aligned with the external reference system to be explained in terms of torque production and its links to the actions of swimmers. This will enable further studies to be conducted to explain the techniques of swimmers and the differences between them observed by swimming researchers. These include differences between swimming strokes, the causes of asymmetries in swimming including breathing (Castro et al., 2006; Payton et al, 1999; Psycharakis and McCabe, 2011; Seifert et al., 2005; 2008), disability (Osborough et al., 2010; Satkunskiene et al, 2005) and changes within swimmers across a race (Alberty et al, 2008; Figueiredo et al, 2012; McCabe et al., 2011; Suito et al, 2008).
Acknowledgements
The authors declare that there is no conflict of interest with regard to this paper for any author.
Biographies

Ross H. SANDERS
Employment
Professor and Head of Exercise and Sport Science at The University of Sydney in the Faculty of Health Sciences.
Degree
PhD
Research interests
Biomechanics and motor control and learning with specific emphasis on movement asymmetries and rhythms.
E-mail: ross.sanders@sydney.edu.au

Tomohiro GONJO
Employment
PhD student at Centre for Aquatics Research and Education (CARE), The University of Edinburgh.
Degree
MSc
Research interests
Biophysical research of front crawl and back crawl in swimming.
E-mail: T.Gonjo@sms.ed.ac.uk

Carla B. MCCABE
Employment
Biomechanist at the School of Sport, University of Ulster.
Degree
PhD
Research interests
Biomechanical analysis of swimming and aquatic exercise.
E-mail: c.mccabe@ulster.ac.uk
References
- Alberty M., Sidney M., Pelayo P., Toussaint H. (2008) Stroking characteristics during time to exhaustion tests. Medicine and Science in Sports and Exercise 41(3), 637-644. [DOI] [PubMed] [Google Scholar]
- Bartlett R. (1977) Introduction to Sports Biomechanics. London: E & FN Spon; 196. [Google Scholar]
- Cappaert J.M. (1998) Biomechanics of swimming analysed by three-dimensional techniques. Biomechanics and Medicine in Swimming VIII, Proceedings of the VIII International Symposium on Biomechanics and Medicine in Swimming. Eds: Keskinen K., Komi P., Hollander A.P. Jyväskylä (Finland): University of Jyväskylä Press; 141-145. [Google Scholar]
- Castro F., Minghelli F., Floss J., Guimaraes A. (2003) Body roll angles in front crawl swimming at different velocities. Biomechanics and Medicine in Swimming IX. Ed: Chatard J.C. St Etienne: University of St Etienne Publications; 111-114. [Google Scholar]
- Castro F.A.S., Vilas-Boas J.P., Guimaraes A.C.S. (2006) Effect of swimming intensity and breathing in front crawl body roll angles for swimmers and triathletes. Brazilian Journal of Biomechanics 7, 85-90. [Google Scholar]
- Chollet D., Chalies S., Chatard J.C. (2000) A new index of coordination for the crawl: description and usefulness. International Journal of Sport Medicine 21, 54-59. [DOI] [PubMed] [Google Scholar]
- Chollet D., Seifert L., Carter M. (2008) Arm coordination in elite backstroke swimmers. Journal of Sports Sciences 26, 675-682. [DOI] [PubMed] [Google Scholar]
- Counsilman J.E. (1973) The Science of Swimming. Englewood Cliffs, N.J. Prentice-Hall. [Google Scholar]
- Czabañski B., Koszcyc T. (1979) Relationship of stroke asymmetry and speed of breastroke swimming. Swimming III. Eds: Terauds J., Bedingfield E.W. Baltimore: University Park Press; 148-152. [Google Scholar]
- Dapena J. (1978) A method to determine the angular momentum of a human body about three orthogonal axes passing through its center of gravity. Journal of Biomechanics 11, 251-256. [DOI] [PubMed] [Google Scholar]
- Deffeyes J., Sanders R.H. (2005) Elliptical zone body segment modelling software: digitizing, modelling and body segment parameter calculation. Proceedings of XXIII International Symposium on Biomechanics in Sports. Ed: Wang Q. The China Institute of Sports Science, Beijing: 749-752. [Google Scholar]
- Figueiredo P., Seifert L., Vilas-Boas J.P., Fernandes R.J. (2012) Individual profiles of spatio-temporal coordination in high intensity swimming. Human Movement Science 31, 1200-1212. [DOI] [PubMed] [Google Scholar]
- Giakis G., Baltzopoulos V., Bartlett R.M. (1998) Improved extrapolation techniques in recursive digital filtering: A comparison of least squares and prediction. Journal of Biomechanics 31, 87-91. [DOI] [PubMed] [Google Scholar]
- Kadaba M.P., Ramakrishnan M.E., Wootten J., Gainey G., Gorton G., Cochran G.V.B. (1989) Repeatability of kinematic, kinetic, and electromyographic data in normal adult gait. Journal of Orthopaedic Research 7, 849-860. [DOI] [PubMed] [Google Scholar]
- Lui Q, Hay J.G., Andrews J.G. (1993) Body roll and handpath in freestyle swimming: an experimental study. Journal of Applied Biomechanics 9, 238-253. [Google Scholar]
- McCabe C.B., Psycharakis S., Sanders R. (2011) Kinematic differences between front crawl sprint and distance swimmers at sprint pace. Journal of Sports Sciences 29(2), 115-123. [DOI] [PubMed] [Google Scholar]
- Maglischo E.W. (2003) Swimming Fastest. Champaign, Il., Human Kinetics Publishers. [Google Scholar]
- Osborough C.D., Payton C.J., Daly D. (2010) Influence of swimming speed on inter-arm coordination in competitive unilateral arm amputee front crawl swimmers. Human Movement Science 29, 921-931. [DOI] [PubMed] [Google Scholar]
- Payton C.J., Bartlett R.M., Baltzopoulos V., Coombs R. (1999) Upper extremity kinematics and body roll during preferred-side breathing and breath-holding front crawl swimming. Journal of Sports Sciences 17(9), 689-696. [DOI] [PubMed] [Google Scholar]
- Payton C.J., Hay J.G., Mullineaux D.R. (1997) The effect of body roll on hand speed and hand path in front crawl swimming-A simulation study. Journal of Applied Biomechanics 13, 300-315. [Google Scholar]
- Psycharakis S.G., Sanders R.H. (2008) Shoulder and hip roll changes during 200m front crawl swimming. Medicine and Science in Sports and Exercise 40(12), 2129-2136. [DOI] [PubMed] [Google Scholar]
- Psycharakis S.G., Sanders R., Mill F. (2005) A Calibration Frame for 3D Swimming Analysis. Proceeding of XXIIIth International Symposium on Biomechanics in Sports. Ed: Wang Q. The China Institute of Sports Science, Beijing: 901-904. [Google Scholar]
- Psycharakis S.G., McCabe C. (2011) Shoulder and hip roll differences between breathing and non-breathing conditions in front crawl swimming. Journal of Biomechanics 44(9), 1752-1756. [DOI] [PubMed] [Google Scholar]
- Psycharakis S.G., Sanders R.H. (2010) Body roll in swimming: A review. Journal of Sports Sciences 28(3), 229-236. [DOI] [PubMed] [Google Scholar]
- Rodeo S.A. (1999) Knee pain in competitive swimming. Clinics in Sports Medicine 8(3), 159-163. [DOI] [PubMed] [Google Scholar]
- Sanders R.H., Psycharakis S.G. (2009) Rolling rhythms in front crawl swimming with six-beat kick. Journal of Biomechanics 42, 273-279. [DOI] [PubMed] [Google Scholar]
- Sanders R.H. (2013) How do asymmetries affect swimming performance? Journal of Swimming Science 21(1), Summer. Available form URL: http://swimmingcoach.org/journal/manuscript-sanders-vol21.pdf [Google Scholar]
- Sanders R.H., Thow J., Alcock A., Fairweather M., Riach I., Mather F. (2012) How can asymmetries in swimming be measured? Journal of Swimming Science 19(1), Spring. Available form URL: http://swimmingcoach.org/journal/manuscript-sanders-vol19.pdf [Google Scholar]
- Sanders R.H., Thow J., Fairweather M. (2011) Asymmetries in swimming: Where do they come from? Journal of Swimming Science 18, Fall Available form URL: http://swimmingcoach.org/journal/manuscript-sanders-vol18.pdf [Google Scholar]
- Sanders R.H., Chiu C.Y., Gonjo T., Thow J., Oliveira N., Psycharakis S.G., Payton C.J., McCabe C.B. (2015a) Reliability of the elliptical zone method of estimating body segment parameters of swimmers. Journal of Sports Science and Medicine 14, 215-244. [PMC free article] [PubMed] [Google Scholar]
- Sanders R.H., Fairweather M.M., Alcock A., McCabe C.B. (2015b) An approach to identifying the effect of technique asymmetries on body alignment in swimming exemplified by a case study of a breaststroke swimmer. Journal of Sport Science and Medicine, 14, 304-314. [PMC free article] [PubMed] [Google Scholar]
- Sanders R.H., Gonjo T., McCabe C.B. (2015c) Reliability of three-dimensional linear kinematics and kinetics of swimming derived from digitized video at 25 and 50 Hz with 10 and 5 frame extensions to the 4th order Butterworth smoothing window. Journal of Sports Science and Medicine 14, 441-451. [PMC free article] [PubMed] [Google Scholar]
- Satkunskiene D., Schega L., Kunze K., Birzinyte K., Daly D. (2005) Coordination in arm movements during crawl stroke in elite swimmers with a loco-motor disability. Human Movement Science 24, 54-65. [DOI] [PubMed] [Google Scholar]
- Seifert L., Chollet D., Allard P. (2005) Arm coordination symmetry and breathing effect in front crawl. Human Movement Science 24(2), 234-256. [DOI] [PubMed] [Google Scholar]
- Seifert L, Chehensse A., Tourney-Chollet C, Lemaitre F., Chollet D. (2008) Effect of breathing pattern on arm coordination symmetry in front crawl. Journal of Strength and Conditioning Research 22(5), 1670-1676. [DOI] [PubMed] [Google Scholar]
- Suito H., Ilegami Y., Nunome H., Sano S., Shinkai H., Tsujimoto N. (2008) The effect of fatigue on the underwater arm stroke motion in the 100-m front-crawl. Journal of Applied Biomechanics 24(4), 316-324. [DOI] [PubMed] [Google Scholar]
- Vint P.F., Hinrichs R.N. (1996) Endpoint error in smoothing and differentiation raw kinematic data: An evaluation of four popular methods. Journal of Biomechanics 29(12), 1637-1642. [PubMed] [Google Scholar]
- Whittlesey S.N., Robertson D.G. (2004) Two dimensional inverse dynamics. Research Methods in Biomechanics. Eds: Robertson D.G.E., et al. Chapter 5. Champaign, IL: Human Kinetics; 103. [Google Scholar]
- Yanai T. (2004) Buoyancy is the primary source of generating body roll in front crawl swimming. Journal of Biomechanics 37, 605-612. [DOI] [PubMed] [Google Scholar]


