Abstract
Objective
Most frequency data on violence are non-normally distributed, which can lead to faulty conclusions when not modeled appropriately. And, we can't prevent what we can't accurately predict. We therefore review a series of methods specifically suited to analyze frequency data, with specific reference to the psychological study of sexual aggression. In the process, we demonstrate a model comparison exercise using sample data on college men's sexual aggression.
Method
We used a subset (n=645) of a larger longitudinal dataset to demonstrate fitting and comparison of six analytic methods: OLS regression, OLS regression with a square-root-transformed outcome, Poisson regression, negative binomial regression, zero-inflated Poisson regression, and zero-inflated negative binomial regression. Risk and protective factors measured at Time 1 predicted frequency of SA at Time 2 (8 months later) within each model. Models were compared on overall fit, parsimony, and interpretability based upon previous findings and substantive theory.
Results
As we predicted, OLS regression assumptions were untenable. Of the count-based regression models, the negative binomial model fit the data best; it fit the data better than the Poisson and zero-inflated Poisson models, and it was more parsimonious than the zero-inflated negative binomial model without a significant degradation in model fit.
Conclusion
In addition to more accurately modeling violence frequency data, count-based models have clear interpretations that can be disseminated to a broad audience. We recommend analytic steps investigators can use when analyzing count outcomes as well as further avenues researchers can explore in working with non-normal data on violence.
Keywords: violence, measurement, frequency data, non-normal data, count data, Poisson, negative binomial, zero-inflated models, sexual aggression
Although interpersonal violence is a major social problem with significant public health impact, it is often statistically infrequent in general samples. Researchers who study violence often must predict frequencies of relatively low base-rate phenomena, such as total number of aggressive behaviors or victimization experiences that occur within a given timeframe. Because fractions of violent acts or a negative number of acts often do not make sense, these represent count variables containing only positive integers. Contrast this with related attitudinal or dispositional variables, such as acceptance of violence or general hostility, which are often normally distributed. Analytic model selection affects accurately researchers can estimate associations between predictors and outcomes. Within an overall literature, poor model fit and ambiguity concerning statistically significant associations can lead to mixed findings across studies and make translating findings to interventions challenging or possibly even misguided. The goals of this paper are to (1) briefly review analytic methods for predicting count outcomes; (2) demonstrate the performance of these methods when applied to data on risk and protective factors associated with sexual aggression (SA) frequency; and (3) recommend analytic steps researchers can take when predicting count outcomes.
In the past researchers have chosen to normalize count data on violence by applying square-root or logarithmic transformations (e.g., Malamuth, Sockloskie, Koss, & Tanaka, 1991). These transformed variables are then assumed to be normally distributed and analyzed using ordinary least squares (OLS) regression (Cohen, Cohen, West, & Aiken, 2003). This strategy has been used because these non-linear transformations can reduce skewness in frequency data, and OLS regression has been found to be robust to slight non-normality that might remain. However, transformations are not likely to solve this problem with violence frequencies because there are often large proportions of respondents who report no violence. Another option has been to recode count variables as dichotomous or ordinal, then analyze them using logistic or probit regression. In dichotomized data the distinction often lies between those who have experienced or perpetrated violence and those who have not, which eliminates all differentiation between low (i.e., one) and elevated frequencies (i.e., any value greater than one). When constructing three or more ordered categories, it is challenging to find meaningful cut-points among those who have experienced or perpetrated violence.
Alternatively, there is a group of models based on the Poisson distribution that are well-positioned to handle count data (Long, 1997; McCullagh & Nelder, 1989). These analytic options are generally underutilized in many of the social and behavioral sciences (Cohen, et al., 2003). Exceptions include economics, sociology, and criminology—the latter two disciplines commonly use these models to predict rates of violent behavior (e.g., Watts & McNulty, 2013), incarcerations (e.g., van Schellen, Apel, & Nieuwbeerta, 2012), and violent crime recidivism (e.g., Burraston, Cherrington, & Bahr, 2012). This tradition in sociology and criminology dates back at least to the National Research Council panel Criminal Careers and “Career Criminals” (Blumstein, Cohen, Roth, & Visher, 1986) and was propelled a decade later by Land, McCall, and Nagin's (1996) primer and empirical demonstrations. Although these methods of analyzing count data have been discussed in the psychology literature (see Gardner, Mulvey, & Shaw, 1995), they are not often used. This includes psychological research on violence, which is vexing given their rate of application in related disciplines. Our hope is that this overview and demonstration, grounded within the psychological study of violence, will aid in breaking down this apparent disciplinary silo.
In the sections that follow, we describe and demonstrate different approaches to modeling count data by applying them to sample data set collected with the aim of predicting SA perpetration frequency. SA frequency is commonly measured as the number of sexually aggressive acts a respondent discloses having perpetrated within a specified timeframe. Although the definition of SA varies across studies, even the most liberal and comprehensive definitions produce positively skewed frequencies. Approximately 25% of college-age men report perpetrating SA, defined as attempted or completed nonconsensual sexual acts ranging from unwanted contact to rape, since age 14. These rates have been quite consistent dating back to the earliest surveys (Koss, Gidycz, & Wisniewski, 1987). Like many variables representing the frequency of violence or victimization, the average frequency of SA is low. However, a small proportion of individuals report frequent perpetration, which creates wide variation within the sample. Poor model fit and ambiguities concerning statistically significant associations increase inconsistency across studies and ultimately create obstacles to accumulating a consistent knowledge base on risk and protective factors to guide prevention and intervention efforts.
Count-Specific Analytic Methods
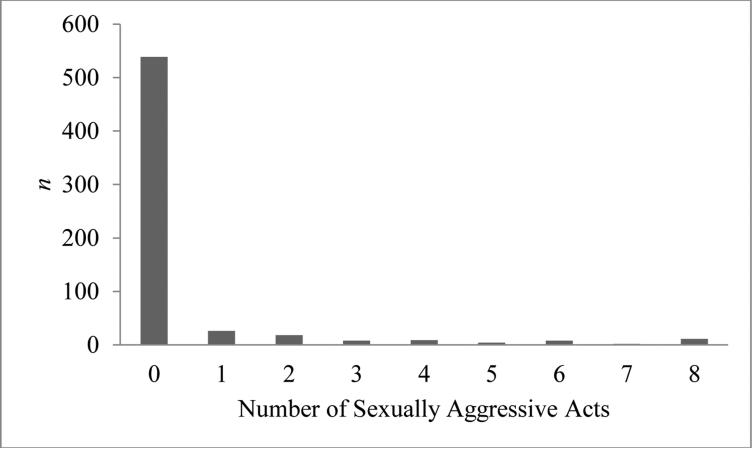
There are a variety of count-specific analytic methods based upon the Poisson distribution. Standard Poisson regression uses maximum likelihood estimation with raw coefficients that represent natural logs of predictor influence on average rate of change in an outcome. This is similar to more commonly-used logistic regression, where raw coefficients reflect the natural log of predictor influence on the average odds of a specified event (see Long, 1997, for an overview). To facilitate interpretation, Poisson regression coefficients can be transformed to incidence rate ratios similar to how logistic regression coefficients can be clearly expressed as odds ratios. An assumption of Poisson regression is, once conditioned upon covariates, predicted events are assumed to be independent. For example, perpetrating one sexual assault should have no impact on the probability of predicting future assaults once predictors are modeled. A second assumption is equidispersion, meaning the Poisson distribution contains a single parameter, where the conditional mean equals the conditional variance. In Poisson regression, therefore, as SA is conditioned upon risk and protective factors, the conditional variance of SA is constrained to equal the conditional mean. Although Poisson regression would more accurately model count data compared with OLS regression, the equidispersion assumption may be too restrictive for many forms of violence, including most measures of SA, where the conditional variance would exceed the conditional mean. This characteristic is known as overdispersion (Long, 1997) and could result from inherent heterogeneity among individuals (Nagin & Land, 1993) or from unmeasured risk or protective factors needed to explain variation in violence or victimization frequency across individuals. Overdispersion is common in the case of SA because most individuals do not offend, which leads to low average frequencies; however, a few chronically offend, which stretches the variance well beyond the mean of the distribution (see Figure 1 in the Method for an approximate illustration).
Figure 1.
Distribution of observed sexual aggression frequency at Wave 2.
Failure to account for overdispersion leads to deflated standard error estimates associated with regression coefficients, artificially inflating coefficient significance levels (Land, McCall, & Nagin, 1996). It is very important, therefore, to test for overdispersion—often denoted as alpha (α) in statistical tests—and account for it when it is significant. One way to account for overdispersion is by estimating a negative binomial regression model. In our example, the negative binomial distribution assumes that individual-level instances of SA are Poisson-distributed but allows individuals to vary in their average rates of SA (Greenwood & Yule, 1920; Land, McCall, & Nagin, 1996). In allowing individuals’ rates to vary, a parameter and standard error are estimated to test overdispersion. In this sense, a Poisson regression model is nested within a negative binomial regression model, where the additional parameter is a random effect representing variability among individuals’ rates (Gardner, Mulvey, & Shaw, 1995). The results of Poisson and negative binomial models can therefore be interpreted similarly, and the fit of the two models can easily be compared. Although negative binomial regression is less parsimonious due to the additional estimated dispersion parameter, it is more flexible than Poisson regression and more accurate in modeling frequency data containing a higher proportion of zeroes (Land, McCall, & Nagin, 1996).
When a frequency distribution contains a very high proportion of zeros, such as occurs when most respondents do not report perpetrating SA, the dispersion parameter estimated within negative binomial regression may not fully account for variability among individuals. Another extension of the Poisson distribution, the zero-inflated model, assumes frequencies come from two distinct populations. In the case of SA, the two populations could be those who might perpetrate and those who will not. Typically, zero-inflated models involve a combination of count and binary logistic regression. The logistic model is estimated to discriminate participants who might perpetrate SA based on their scores on both the outcome and predictors from participants who would not perpetrate SA. The latter group is known as the “true-zero” group. Simultaneously, a count model, using either Poisson or negative binomial regression, is estimated with only data from participants not classified in the true-zero group, which signifies that they might perpetrate SA as judged by the logistic portion of the model (Atkins & Gallop, 2007). It is not necessary to specify the same predictors in the logistic and count models, adding flexibility in approaching two separate yet related research questions: First, what factors influence the odds of classification in the group of individuals who will not perpetrate SA versus those who might? Second, what factors influence the SA rate among individuals classified in the group that might perpetrate? The results from both the logistic and count models include intercepts/thresholds, coefficients, and associated standard errors. The trade-off for potentially improved fit and specificity, however, is that zero-inflated models generally estimate many more parameters than standard Poisson or negative binomial regressions and thereby sacrifice parsimony—defined here as number of estimated parameters in a model. In addition, it is important to note zero-inflated models are often considered finite mixture models because they mix different distributions within the same overall model in order to simultaneously analyze data from two distinct subpopulations. Before fitting a zero-inflated model—or any model, for that matter—researchers should consider substantive theory and previous findings in their area of violence research to infer how their outcomes may be distributed and decide if the notion of unobserved heterogeneity within the data makes sense. In our example, it is reasonable to assume the sample may contain a large subgroup of individuals that would not engage in SA and another small subgroup that might (author citation).
Empirical Demonstration: Predicting SA
We can assume based on previous findings that SA frequency will be non-normal in our sample data, thus violating assumptions of OLS regression. Normalizing the data will not likely be effective due to the large proportion of the sample that reports no sexually aggressive acts (see Figure 1). From this expectation, we can infer that a Poisson-based regression approach might be most appropriate. However, the standard Poisson regression assumption of equidispersion is often untenable (Long, 1997), which suggests that a negative binomial or zero-inflated model may be better options. In fact, recent findings within the SA literature suggest unobserved heterogeneity among individuals in terms of their SA across time (author citation; author citation), with one group of men who do not perpetrate and other groups of men who commit more than one act but demonstrate different patterns of offending over time. Fitting a zero-inflated model to data on SA frequency is supported under these circumstances. These previous findings, however, also demonstrate how attitudes toward women and general sexual behavior both significantly account for the patterns of group membership. Because these variables are included as predictors in the present regression models, it becomes less clear whether the SA outcome would contain multiple subgroups once conditioned upon the risk and protective factors. Thus, existing knowledge and common sense suggests we compare fit for negative binomial, zero-inflated Poisson, and zero-inflated negative binomial regression models. For a more complete demonstration, we tested six analytic approaches in prospective analyses to predict SA frequency. The analytic approaches included OLS regression of both raw and transformed SA frequency, Poisson regression, negative binomial regression, zero-inflated Poisson regression, and zero-inflated negative binomial regression.
Method
Sample
Data for this example were taken from a larger longitudinal dataset of college men's attitudes, behaviors, and experiences related to SA. The methods used to collect the data have been described elsewhere (author citation) and will be briefly summarized here. Sample recruitment began when the men were in their first year of college in 2008. All first-year, full-time male students at the university (n = 1,472) were sent an electronic mail message inviting them to come to the student health center to complete a confidential, 20 to 30-minute self-report survey on men's attitudes and behaviors regarding relationships with women. In addition to using email recruitment, an announcement was posted in the student newspaper and flyers distributed around campus. Wave 1 data collection occurred over a 1-week period in March-April 2008 and ended once the target sample size of 800 was achieved. Five individuals were excluded from the study because they were not 18 years of age at the time of Wave 1 data collection.
All men who completed Wave 1 surveys were contacted via email to participate in follow-up surveys at the end of their second (82% follow-up rate), third (75% follow-up rate), and fourth (72% follow-up rate) years of college. Study procedures were similar across data collection waves. At Waves 2, 3, and 4, participants were provided with a survey that had a confidential, unique code that linked their surveys. Prior to completing surveys at each Wave, men provided written informed consent. Local institutional review board approval from the university and a Certificate of Confidentiality from the National Institutes of Health were obtained prior to data collection. No personal identifiers were included on the surveys. After completing the surveys, participants deposited their surveys (without consent forms attached) into a locked box. Then they received payment for their participation and were provided a referral sheet of counseling resources. Respondents were paid $20.00 for their participation at Waves 1 and 2, and $25.00 at Waves 3 and 4.
Although four waves of data were available, the current demonstration required only two. Three combinations of the available data were fit and compared including: Wave 1 → Wave 2, Wave 1→ Wave 3, and Wave 1 →Wave 4. Each comparison involved risk and protective factors assessed at the first wave predicting SA frequency at the later wave. The outcomes were similar across the three combinations. Therefore, we present only the analyses involving Waves 1 and 2 (n = 650). This combination offered the most complete data while maintaining a prospective example. Participants were on average 18.56 years at Wave 1 (SD = 0.51) and 89% were white. The sample was representative of the population of 1st-year male students in terms of age and race based on data provided from the Office of Institutional Research. Attrition was unrelated to the respondent's race (χ2=1.91, p=.59), age (F=.77, p=.38), or SA at Wave 1 (F=.09, p=.76). The distribution of observed SA frequency is depicted in Figure 1, illustrating the positive skew and preponderance of zeros. Visual inspection of scatterplots confirmed that each individual predictor is associated with SA in the hypothesized directions within these data.
Measures
Each model included nine empirically-established predictors of SA derived from the Theory of Planned Behavior and supported by prior studies (Tharp, DeGue, Valle, Brookmeyer, Massetti, & Matjasko, 2013; author citation). The Theory of Planned Behavior includes three key constructs—attitudes, norms, and control—that are hypothesized to predict intended or actual behavior (Fishbein, 1967). The results of several studies have supported hypotheses that rape supportive beliefs, hostility towards women, and superficial charm respectively increase the likelihood of sexually aggressive behaviors (Abbey, McAuslan, & Ross, 1998; Knight & Knight, 2003; 2005; Koss et al., 1985; Malamuth, Linz, Heavey, Barnes, & Acker, 1995; White & Humphrey, 1997; author citation). Research also supports the importance of norms in furthering our understanding of the epidemiology and prevention of SA (Burt, 1980; Check & Malamuth, 1983; Hall & Barongan, 1997; Montano, Kasprzyk, & Taplin, 1997; author citation). This includes not only peer norms, such as peer approval of forced sex (Abbey & McAuslan, 2004; Abbey, Wenger, Pierce, & Jacques-Tiura, 2012, author citation), but also perceptions of sanctions against SA (Foshee, Linder, MacDougall, & Bangdiwala, 2001; Riggs & O'Leary, 1989), and norms conveyed through pornography (Malamuth, Hald, & Koss, 2012). Further, research supports the role of control in predicting SA. Sexual compulsivity (Knight & Knight, 2005; author citation), impulsivity (Knight & Knight, 2003), and alcohol misuse reduce control over SA behaviors and have been found to be related to an increased likelihood of engaging in SA (Abbey, 2002; Abbey, Jacques-Tiura, & LeBreton, 2011; Giancola, 2002).
Predictors
In the demonstration data set, three measures assessed attitudes: Rape supportive beliefs, hostility towards women, and superficial charm. Rape supportive beliefs were assessed with 19 items from the Rape Supportive Beliefs Scale (Lonsway & Fitzgerald, 1995). Items were answered using a 5-point scale, with higher mean scores indicating higher levels of rape supportive attitudes (α = .90; e.g., “When women talk and act sexy, they are inviting rape”). Hostility towards women was assessed with an 8-item scale adapted by Koss and Gaines (1993) from the Hostility Toward Women Scale (Check, Malamuth, Elias, & Burton, 1985). Items were answered using a 5-point scale, with higher scores reflecting higher levels of hostility (α = .90; e.g., “Many times a woman appears to care, but really just wants to use me”). Superficial charm was assessed with a 6-item scale that assessed attitudes that people can be easily conned (Knight, 2007). The items were answered on a 5-point scale, with higher scores indicative of higher levels of superficial charm (α = .90; e.g., “I can easily charm someone into doing almost anything for me”).
Three variables assessed for norms: peer approval of forced sex, perceived negative sanctions against SA, and pornography exposure. Peer approval of forced sex was assessed with 6 items (Abbey & McAuslan, 2004) answered with a 4-point scale, with higher mean scores indicating greater perceptions that peers would approve of various strategies to obtain sex with a woman (α = .78; e.g., “Do your friends approve of getting a woman drunk or high to have sex?”). Perceived negative sanctions against SA was assessed with 3 items (Foshee et al., 2001) answered on a 4-point scale, with higher scores indicating greater perceptions that SA would not be sanctioned; e.g. “Bad things will happen to people who are sexually aggressive to girls.” Pornography exposure assessed how many hours a week a respondent looked at sexually explicit material in magazines or on the internet. Responses ranged from none (27%), less than one hour (45%) 1-2 hours (18%), 3-4 hours (7%), and more than 4 hours (3%).
Perceived control was assessed with three measures: Sexual compulsivity, impulsivity, and high-risk drinking. Sexual compulsivity was assessed with the 10-item Sexual Compulsivity Scale (Kalichman & Rompa, 2001). Items were answered with a 4–point scale, and higher scores indicated higher levels of sexually compulsive behaviors (α =.83; e.g., “I have to struggle to control my sexual thoughts and behaviors”). Impulsivity was assessed with the Impulsiveness Questionnaire (Eysenck, Pearson, Easting, & Allsopp, 1985) and included 19 items answered with a yes/no format. Higher scores indicated greater levels of impulsivity (α =.79; e.g., “Do you often get involved in things you later wish you could get out of?”). High risk drinking was assessed with one item that measured how often the respondent had gotten drunk within the past 30 days (Wechsler, Davenport, Dowdall, Moeykens, & Castillo, 1994).
Sexual aggression frequency
The revised Sexual Experiences Survey (SES; Koss et al., 2007) was used to assess SA. The SES is the most widely used measure of SA among college students and has demonstrated good reliability and validity (Koss et al., 1987; Koss & Gidycz, 1985). The scale uses behaviorally-specific questions to assess if, and how many times (0 to 3+), a respondent perpetrated behaviors that constitute completed rape, attempted rape, sexual coercion, or unwanted sexual contact. SA frequency was calculated by totaling the number of perpetrations for each man during his second year of college (Wave 2).
Analytic Strategy
We first assessed the assumptions of OLS regression using both raw and square root transformed SA frequency, including normality of raw and transformed SA frequency scores, normality of residuals (individual estimates from the analysis contrasted with observed scores), and homoscedasticity (consistency of residual variance across values of the predictor). Then we estimated a series of regression models: (1) OLS using untransformed SA frequency scores; (2) OLS using square root transformed SA scores, (3) Poisson regression; (4) negative binomial regression; (5) zero-inflated Poisson (ZIP) regression; and (6) zero-inflated negative binomial (ZINB) regression. Finally, we compared the models on the criteria detailed below.
We conducted all analyses in SAS v. 9.2 using the REG procedure for models 1 and 2 and the COUNTREG procedure for models 3 through 6. Although we used SAS to estimate and compare distributions, many of these models can be estimated using SPSS, Stata, Mplus, and the free, open-source R package (see http://www.ats.ucla.edu/stat/ for resources including annotated sample syntax and outputs). All predictors of SA were standardized to z-scores (M =0, SD=1) and were the same in each model, including both parts of the zero-inflated models. SA frequency was the outcome of model 1 and 3 through 6. Square root-transformed SA frequency was the outcome in Model 2. Data were complete for 8 of the 10 predictors used in these analyses; the pornography and often drunk variables were over 99.5% complete (Little's MCAR test: χ2 = 17.80, df = 16, p = .336). In total, only 5 cases had missing data and they were excluded leaving a sample size of 645 cases that were consistently included across all analyses.
Model comparisons involved three general criteria: overall model fit, parsimony, and interpretability. Overall model fit was compared using the Akaike Information Criterion (AIC) and adjusted Vuong likelihood ratio tests (Vuong, 1989). The AIC is a comparative fit index—calculated as (−2*) + 2*p, where indicates the model loglikelihood value and p indicates the number of model estimated parameters—with lower scores indicating better model fit. The Vuong test is used for pair-wise model comparisons under the null hypothesis that both models fit the data equally well. A significant Vuong test statistic, therefore, indicates one model fits the data significantly better than the other. Parsimony is generally indicated by the number of parameters estimated in each model and is taken into account by both AIC values and the Akaike- and Schwartz-adjusted Vuong statistics used in this study. When two models fit the data similarly, as evidenced by close AIC values or non-significant Vuong test statistics, the more parsimonious model is traditionally favored as long as it can be clearly interpreted. We visually inspected the extent to which each count-based model over- and under-predicted the observed SA frequency to supplement our comparison of fit statistics. A model over-predicts SA frequency when model-predicted probabilities are higher than the observed probabilities; under-prediction is signified when model-predicted probabilities are lower that observed probabilities.
Results
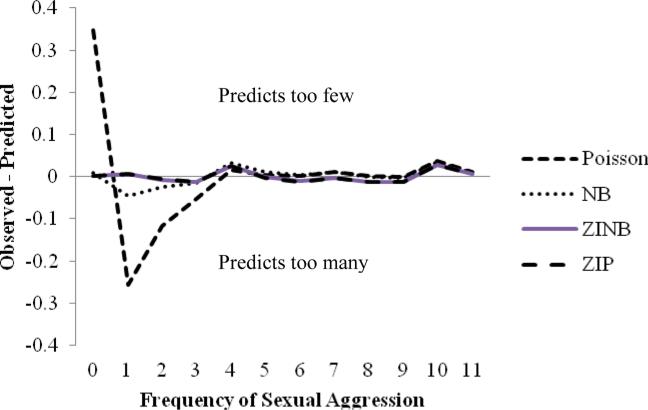
Descriptive statistics for the untransformed and square-root transformed SA frequency scores as well as the predictors used in each model are presented in Table 1. Figure 2 depicts plots of differences between the observed and model-predicted probabilities of models 3 through 6 across the frequency of sexual aggression, illustrating how close the predictions of each model were to the observed SA frequency distribution.
Table 1.
Descriptive statistics for unstandardized variables
| Mean | SD | Min, Max | |
|---|---|---|---|
| Untransformed SA | 1.29 | 5.94 | 0, 104 |
| Square root transformed SA | 0.39 | 1.06 | 0, 10.20 |
| Hostility toward Women | 1.60 | .82 | 1, 5.00 |
| Rape Myth Acceptance | 1.24 | .62 | 0, 3.30 |
| Charm | 2.13 | .92 | 0, 4.00 |
| Peer | .28 | .40 | 0, 3.00 |
| Sanctions | 2.18 | .65 | 0, 3.00 |
| Pornography | 1.14 | .98 | 0, 4.00 |
| Compulsion | .43 | .40 | 0, 2.50 |
| Impulsivity | 6.50 | 4.01 | 0, 19.00 |
| Often drunk | 3.78 | 6.54 | 0, 41.00 |
Note: SA = Sexual Aggression.
Figure 2.
Differences between the observed and model-predicted probabilities across sexual aggression frequency.
Models 1 & 2: OLS Regression
In a preliminary step, we evaluated the assumptions of the two OLS regression models by testing normality of the outcome variables, normality of residuals, and homoscedasticity. Supporting our interpretation of Figure 1, SA is significantly skewed and kurtotic (skewness = 10.71, SE = .10, t = 107.10, p < .001; kurtosis = 3.80, SE = .10, t = 38.0, p < .001); square root transformation did little to correct these issues (skewness = 154.62, SE = .19, t = 813.79, p < .001; kurtosis = 19.54, SE = .19, t = 102.84, p < .001). Residuals from both OLS models were also significantly skewed (untransformed SA: 2.35, S.E. = .10, p < .05); square root transformed SA: 1.84, S.E. = .10, p < .05) and kurtotic (untransformed: 5.55, S.E. = .19, p < .05; transformed: 2.86, S.E. = .19, p < .05). Finally, residuals were plotted against predicted values and visually inspected, indicating heteroscedasticity. Although OLS assumptions were violated, we present results of these models in Table 2 as comparison points. Four of the nine predictors of SA frequency reached statistical significance in both models 1 and 2. AIC cannot be considered for model 2 because the square-root transformed SA outcome variable differs from the other models.
Table 2.
Regression model estimates
| OLS | Square root | Poisson | Negative binomial | ZI Poisson | ZI Negative binomial | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B | SE | B | SE | B | SE | B | SE | B | SE | B | SE | |
|
Predicting increasing frequency of SA
| ||||||||||||
| Intercept | 1.16*** | .16 | .38*** | .04 | −.38*** | .05 | −.68*** | .14 | 1.54*** | .06 | .78* | .31 |
| HTW | .01 | .21 | .05 | .05 | .10* | .05 | .13 | .19 | −.19** | .06 | −.07 | .21 |
| RMA | .30 | .21 | .09 | .05 | .15** | .05 | .45* | .20 | .15* | .05 | .21 | .22 |
| Charm | .05 | .21 | .05 | .04 | .21*** | .05 | .23 | .17 | −.08** | .05 | .04 | .20 |
| Peer | .35 | .18 | .07 | .04 | −.05 | .03 | .25 | .20 | .14*** | .04 | .04 | .19 |
| Sanctions | −.39* | .17 | −.09* | .04 | −.28*** | .04 | −.20 | .15 | −.19** | .04 | −.24 | .15 |
| Pornography | .06 | .18 | .01 | .04 | .06 | .04 | .14 | .16 | .01 | .04 | .05 | .14 |
| Compulsion | .43* | .18 | .11** | .04 | .28*** | .03 | .16 | .16 | .06 | .04 | −.01 | .16 |
| Impulsivity | .44* | .18 | .08* | .04 | .33*** | .04 | .37* | .16 | .31*** | .05 | .56** | .20 |
| Often drunk | .75*** | .18 | .18*** | .04 | .28*** | .03 | .48** | .18 | .05** | .03 | .07 | .11 |
| α a | 9.40*** | 1.25 | 2.52** | .93 | ||||||||
|
Predicting membership in the true-zero SA group | ||||||||||||
| Intercept | 1.85*** | .13 | .99* | .40 | ||||||||
| HTW | −.31* | .15 | −.31 | .24 | ||||||||
| RMA | −.25 | .15 | −.33 | .24 | ||||||||
| Charm | −.23 | .14 | −.26 | .22 | ||||||||
| Peer | −.06 | .12 | −.30 | .29 | ||||||||
| Sanctions | .19 | .12 | .15 | .17 | ||||||||
| Pornography | −.08 | .12 | −.09 | .18 | ||||||||
| Compulsion | −.16 | .11 | −.29 | .25 | ||||||||
| Impulsivity | −.08 | .12 | .29 | .25 | ||||||||
| Often drunk | −.39** | .11 | −.81** | .29 | ||||||||
| AIC | 1830 | --- | 2824 | 1129 | 1484 | 1108 | ||||||
Note: OLS = Ordinary least squares; ZI = Zero-inflated; HTW = Hostility toward Women; RMA = Rape Myth Acceptance; SA = Sexual Aggression; AIC = Akaike Information Criterion.
p<.05
p<.01
p<.001 (all two-tailed).
Overdispersion parameter estimate.
Models 3-4: Poisson & Negative Binomial Regression
The Poisson regression model estimated 10 parameters and suggests seven of the nine covariates significantly predict SA frequency (see Table 2); however, Figure 2 illustrates the Poisson regression model failed to accurately reflect the observed data across the low range of SA frequency, underpredicting the observed proportion of zeros and overpredicting the proportion of ones and twos. A negative binomial regression model was then tested, which estimated 11 parameters including the dispersion parameter. Although the negative binomial model suggests fewer significant predictors compared with the Poisson model (Table 2), there is significant overdispersion (α = 9.40, p < .001). This suggests the significance levels in the Poisson regression are artificially inflated. Figure 2 illustrates that the negative binomial model reflected the observed proportion of SA across the frequency range reasonably well. This pattern of results suggests the Poisson regression model did not adequately account for overdispersion in the observed data, likely leading to artificially low p-values.
Models 5-6: Zero-Inflated Models
Another method of accounting for overdispersion is to fit zero-inflated models, which assume two distinct populations: in this case, men who ostensibly could perpetrate SA and those who could not. We first estimated a ZIP model with 20 parameters. The logistic portion of the model revealed two variables significantly predicted membership in the true-zero group (see Table 2). For example, those who drank more heavily were less likely to be classified in the true-zero group, meaning they were more likely to be classified in the group of men who might perpetrate SA. The Poisson portion of the model suggested seven of the nine variables significantly predicted SA frequencies among the men who might perpetrate. Figure 2 illustrates that the ZIP model accurately estimated the observed proportions across the entire range of SA frequency.
We then estimated a ZINB model with 21 parameters. Although the ZIP model accounts for variability among individual rates by modeling latent heterogeneity, the negative binomial portion of this model suggested significant overdispersion persisted within the count portion of the model (α = 2.52, p < .01). Accordingly, the ZINB model suggested far fewer significant predictors compared with the ZIP model. The logistic portion of the ZINB model, similar to the ZIP model, suggested two variables negatively predicted membership in the true-zero group. The negative binomial portion of the model suggested only one variable predicted frequency of SA (see Table 2). Figure 2 illustrates that the negative binomial regression model reflected the observed counts well across the SA frequency range.
Model Comparison
As previously noted, basic yet important assumptions of the OLS regression models were violated. Therefore, the Poisson-based models were compared on overall model fit, parsimony, and interpretability. First, the Poisson regression model was compared with the negative binomial regression model. The negative binomial model outperformed the Poisson model based on several criteria. Specifically, the significant dispersion parameter estimated as part of the negative binomial model suggested the equidispersion assumption of Poisson regression was violated; this calls into question the model fit and trustworthiness of the standard errors and p values. A likelihood ratio test (asymptotically distributed χ2) also suggested the negative binomial model fit the data significantly better than the Poisson model (LRT = 1696, df = 1, p < .001). These results were corroborated by the AIC values (see Table 2) and significant Akaike- and Schwartz-adjusted Vuong tests (p's < .01), indicating the negative binomial model fit the data significantly better than the Poisson model. The negative binomial model was slightly less parsimonious than the Poisson model because the former contained one additional estimated parameter.
Second, the negative binomial model was compared with the ZINB model. The ZINB model had a lower AIC value than the negative binomial model (see Table 2) and looks to fit the data more closely (Figure 2); but the fit was not significantly better, as indicated by the adjusted Vuong tests (Akaike-adjusted: z = 1.90, p = .06; Schwartz-adjusted: z = −1.23, p = .22), failing to justify the several additional parameters estimated in the ZINB model. The negative binomial and ZINB models were judged to fit the data equally well; therefore, the negative binomial model favored because it is more parsimonious. For completeness, the negative binomial model was also compared with the ZIP model. Although Figure 2 shows the ZIP model more accurately estimated the observed data compared with the negative binomial model, the negative binomial model fit the data reasonably well and was much more parsimonious as judged by using the AIC values and Vuong test statistics (Akaike-adjusted: z = 3.38, p < .001; Schwartz-adjusted: z = 3.67, p < .001). Although the zero-inflated models most accurately estimated the observed frequency distribution (Figure 2), they did so by estimating almost twice as many parameters as the standard negative binomial model. With regard to interpretation, SA is known to have a low-base-rate; therefore, the negative binomial distribution makes intuitive sense, especially given this outcome is conditioned on mostly positive predictors.
Discussion
The SA frequency variable used in our demonstrations was positively skewed with a preponderance of zeros, as are most frequencies of violence. In a preliminary step, we showed these data violated basic assumptions of OLS regression, even when SA frequency was transformed by taking the square-root of each score. Of the Poisson-based regression models, the negative binomial model was ultimately selected. Several factors were considered in the model comparison and selection process, including model fit, parsimony, previous findings, and substantive theory in the field. With only one additional parameter, the negative binomial model fit the data significantly better than the Poisson regression model. Although the zero-inflated models most accurately estimated the observed frequency of SA, the standard negative binomial model was almost as accurate with approximately half the estimated parameters.
Research Implications
The steps we followed in our demonstration of the model-fitting process have implications for researchers who collect frequency data on relatively low base-rate behaviors or experiences, such as violent behavior or victimization. These steps include: (1) consider theory and previous findings in the research area; (2) visually examine the outcome frequency distribution, plots of relationships between the outcome and each predictor, and plots of residuals; (3) test assumptions of plausible models; (4) estimate and compare plausible models that meet analytic assumptions; and (5) consider fit, parsimony, and interpretability in selecting the final model. The fifth step connects with the initial step by utilizing theory and previous findings to aid model interpretation. We recommend other violence researchers be mindful of the pitfalls inherent in predicting low base rate behaviors and use a similar model-testing and comparison approach to find the most accurate, plausible, and interpretable findings.
Although coefficients were similar across the regular Poisson and negative binomial models, the Poisson model identified seven of the nine SA predictors as significant (p<.05) whereas the negative binomial model identified only three significant predictors. This may seem odd as each SA predictor included in the models has been established across multiple studies. In fact, nine follow-up negative binomial models indicated each risk and protective factor was a significant predictor of SA frequency in the hypothesized direction (all p's < .01) when modeled as the only predictor. This suggests a degree of overlap in these predictors of SA—several predictors did not significantly affect the average SA rate above and beyond the effects of other predictors in the negative binomial model. Overdispersion was not accounted for in the Poisson models, leading to artificially deflated standard errors and inflated significance levels (Land, McCall, & Nagin, 1996). In this example, therefore, negative binomial regression identified the strongest predictors of SA whereas inflated standard errors in the Poisson and zero-inflated Poisson models led to less accurate results.
Clinical and Policy Implications
It is important to accurately estimate the effects of risk and protective factors on frequencies of violence and victimization because practitioners and policy-makers use this empirical evidence to develop and assess the outcomes of prevention and intervention programs. The overarching goal, therefore, is to generalize findings to a broader population and context. The process detailed in this article can be used to avoid both misfitting models as well as overfitting models to the point they may no longer be generalizable or predictive in a broader context (Long, 1997; Silver, 2012). Furthermore, although Poisson-based regression analyses may seem more complex than more commonly-used methods, paradoxically, the results can be expressed in very understandable terms appropriate for broad audiences. For example, in standard negative binomial regression, the coefficient for often drunk is .48, which can be transformed by exponentiation to a more interpretable incidence rate ratio of 1.63. The interpretation is, therefore, for every one-unit (1 SD) increase in the often drunk predictor, the SA frequency rate increases by a factor of 1.62 or 62%, holding the other predictors constant.
Limitations
Our coverage of modeling options for count data is not complete; further options are available, including hurdle models (Atkins & Gallop, 2007), Poisson regression with scaled dispersion parameters (McCullagh & Nelder, 1989), and analysis of average rates across units (e.g., schools or communities; Hutchinson & Holtman, 2005). Researchers may also be interested in moving beyond zero-inflated models to explore a greater degree of unobserved heterogeneity within their data on violence (e.g., Greene & Davis, 2011; see author citation for a brief overview). Finally, in our sample data it is possible that men could have endorsed multiple survey items related to behaviors they enacted within a single SA incident. If this is the case, it would invalidate the assumption of independence of our SA outcome. This cannot be discerned from our demonstration data and raises a larger measurement-related issue that will take revision of several widely-used measures to adequately address.
Conclusions
We present overviews of several methods for analyzing count data on violence, including four regression models based on the Poisson distribution. We then demonstrated these methods in a model-comparison process, regressing SA frequency on predictors selected based upon psychological theory and past findings. In doing so we outline an intuitive sequence researchers may use toward arriving at accurate and interpretable findings when faced with similar data-analytic issues. The negative binomial model fit the data best in our demonstration, due to the fact that this model accurately estimated the observed SA frequency distribution while maintaining a high degree of parsimony. We do not suggest results of previous studies predicting SA frequency are invalid or that negative binomial regression is appropriate for all count data on violence. Rather, our intention is to encourage researchers who study violence from a psychological perspective to utilize these count-specific models and a systematic model comparison process to analyze their frequency data.
Acknowledgments
This research was supported by two grants to Martie P. Thompson from the Eunice Kennedy Shriver National Institute of Child Health and Human Development at the National Institutes of Health (award numbers R03HD053444 and R15HD065568). The content is solely the responsibility of the authors and does not necessarily represent the official views of the Eunice Kennedy Shriver National Institute of Child Health and Human Development or the National Institutes of Health.
Contributor Information
Kevin M. Swartout, Department of Psychology, Georgia State University
Martie P. Thompson, Department of Public Health Sciences, Clemson University
Mary P. Koss, Health Promotion Sciences Division, Mel and Enid Zuckerman College of Public Health, University of Arizona
Nan Su, Department of Mathematical Sciences, Clemson University..
References
- Abbey A. Alcohol-related sexual assaults: A common problem among college students. Journal of Studies on Alcohol. 2002;(14):118–128. doi: 10.15288/jsas.2002.s14.118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abbey A, Jacques-Tiura AJ, LeBreton JM. Risk factors for sexual aggression in young men: An expansion of the confluence model. Aggressive Behavior. 2011;37:450–464. doi: 10.1002/ab.20399. doi.org/10.1002/ab.20399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abbey A, McAuslan P. A longitudinal examination of male college students' perpetration of sexual assault. Journal of Consulting and Clinical Psychology. 2004;72(5):747–756. doi: 10.1037/0022-006X.72.5.747. doi: 10.1037/0022-006x.72.5.747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abbey A, McAuslan P, Ross LT. Sexual assault perpetration by college men: The role of alcohol, misperception of sexual intent, and sexual beliefs and experiences. Journal of Social and Clinical Psychology. 1998;17:167–195. doi.org/10.1521/jscp.1998.17.2.167. [Google Scholar]
- Abbey A, McAuslan P, Zawacki T, Clinton AM, Buck PO. Attitudinal, experiential, and situational predictors of sexual assault perpetration. Journal of Interpersonal Violence. 2001;16:784–807. doi: 10.1177/088626001016008004. doi.org/10.1177/088626001016008004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abbey A, Wegner R, Pierce J, Jacques-Tiura AJ. Patterns of sexual aggression in a community sample of young men: Risk factors associated with persistence, desistance, and initiation over a one year interval. Psychology of Violence. 2012;2:1–15. doi: 10.1037/a0026346. doi:10.1037/a0026346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atkins DC, Gallop RJ. Re-thinking how family researchers model infrequent outcomes: A tutorial on count regression and zero-inflated models. Journal of Family Psychology. 2007;21:726–735. doi: 10.1037/0893-3200.21.4.726. doi.org/10.1037/0893-3200.21.4.726. [DOI] [PubMed] [Google Scholar]
- Blumstein A, Cohen J, Roth JA, Visher CA. Criminal Careers and “Career Criminals”: Volume 1. National Academies Press; Washington, DC: 1986. [Google Scholar]
- Burraston BO, Cherrington DJ, Bahr SJ. Reducing juvenile recidivism with cognitive training and a cell phone follow-up: An evaluation of the realvictory program. International Journal of Offender Therapy and Comparative Criminology. 2012;56(1):61–80. doi: 10.1177/0306624X10388635. doi:10.1177/0306624X10388635. [DOI] [PubMed] [Google Scholar]
- Burt MR. Cultural myths and supports for rape. Journal of Personality and Social Psychology. 1980;38:217–230. doi: 10.1037//0022-3514.38.2.217. doi.org/10.1037/0022-3514.38.2.217. [DOI] [PubMed] [Google Scholar]
- Check JV, Malamuth NM. Sex role stereotyping and reactions to depictions of stranger versus acquaintance rape. Journal of Personality and Social Psychology. 1983;45:344–356. doi.org/10.1037/0022-3514.45.2.344. [Google Scholar]
- Check JVP, Malamuth NM, Elias B, Burton SA. On hostile ground. Psychology Today. 1985;19:56–61. [Google Scholar]
- Cohen J, Cohen P, West SG, Aiken LS. Applied multiple regression/correlation analysis for the behavioral sciences. 3rd ed. Lawrence Erlbaum Associates Publishers; Mahwah, NJ US: 2003. [Google Scholar]
- Eysenck SBG, Pearson PR, Easting G, Allsopp JF. Age norms for impulsiveness, venturesomeness, and empathy in adults. Personality and Individual Differences. 1985;6:613–619. doi.org/10.1016/0191-8869(85)90011-X. [Google Scholar]
- Fishbein M. Readings in attitude theory and management. Wiley; New York, NY: 1967. [Google Scholar]
- Foshee VA, Linder F, MacDougall JE, Bangdiwala S. Gender differences in the longitudinal predictors of adolescent dating violence. Preventive Medicine. 2001;32(2):128–141. doi: 10.1006/pmed.2000.0793. doi: 10.1006/pmed.2000.0793. [DOI] [PubMed] [Google Scholar]
- Gardner W, Mulvey EP, Shaw EC. Regression analyses of counts and rates: Poisson, overdispersed Poisson, and negative binomial models. Psychological Bulletin. 1995;118(3):392–404. doi: 10.1037/0033-2909.118.3.392. doi:10.1037/0033-2909.118.3.392. [DOI] [PubMed] [Google Scholar]
- Giancola PR. Alcohol-related aggression during the college years: Theories, risk factors, and policy implications. Journal of Studies on Alcohol. 2002;14:129–139. doi: 10.15288/jsas.2002.s14.129. [DOI] [PubMed] [Google Scholar]
- Glass GV, Hopkins KD. Statistical methods in education and psychology. 3rd ed. Allyn & Bacon; Needham Heights, MA: 1996. [Google Scholar]
- Greene PL, Davis KC. Latent profiles of risk among a community sample of men: Implications for sexual aggression. Journal of Interpersonal Violence. 2011;26:1463–1477. doi: 10.1177/0886260510369138. doi.org/10.1177/0886260510369138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenwood M, Yule GU. An inquiry into the nature of frequency distributions representative of multiple happenings with particular reference to the occurrence of multiple attacks of disease or of repeated accidents. Journal of the Royal Statistical Society. 1920;83:255–279. [Google Scholar]
- Hall GN, Barongan C. Prevention of sexual aggression: Sociocultural risk and protective factors. American Psychologist. 1997;52:5–14. doi: 10.1037//0003-066x.52.1.5. doi.org/10.1037/0003-066X.52.1.5. [DOI] [PubMed] [Google Scholar]
- Hutchinson MK, Holtman MC. Analysis of count data using Poisson regression. Research in Nursing & Health. 2005;28:408–418. doi: 10.1002/nur.20093. doi:10.1002/nur.20093. [DOI] [PubMed] [Google Scholar]
- Kalichman SC, Rompa D. The sexual compulsivity scale: Further development and use with HIV-positive persons. Journal of Personality Assessment. 2001;76:379–395. doi: 10.1207/S15327752JPA7603_02. doi.org/10.1207/S15327752JPA7603_02. [DOI] [PubMed] [Google Scholar]
- Knight RA, Sims-Knight JE. The developmental antecedents of sexual coercion against women: Testing alternative hypotheses with structural equation modeling. Annals of the New York Academy of Sciences. 2003;989:72–85. doi: 10.1111/j.1749-6632.2003.tb07294.x. doi.org/10.1111/j.1749-6632.2003.tb07294.x. [DOI] [PubMed] [Google Scholar]
- Knight RA, Sims-Knight JE. Testing an etiological model for male juvenile sexual offending against females. Journal of Child Sexual Abuse. 2005;13:33–55. doi: 10.1300/j070v13n03_03. doi.org/10.1300/J070v13n03_03. [DOI] [PubMed] [Google Scholar]
- Knight R. MIDSI Clinical Manual. Auger Enterprises. 2007 [Google Scholar]
- Koss MP, Abbey A, Campbell R, Cook S, Norris J, Testa M, White J. Revising the SES: A collaborative process to improve assessment of sexual aggression and victimization. Psychology of Women Quarterly. 2007;31:357–370. doi.org/10.1111/j.1471-6402.2007.00385.x. [Google Scholar]
- Koss MP, Gidycz CA. Sexual Experiences Survey: Reliability and validity. Journal of Consulting and Clinical Psychology. 1985;53:422–423. doi: 10.1037//0022-006x.53.3.422. doi.org/10.1037/0022-006X.53.3.422. [DOI] [PubMed] [Google Scholar]
- Koss M, Gidycz C, Wisniewski N. The scope of rape: Incidence and prevalence of sexual aggression and victimization in a national sample of higher education students. Journal of Consulting and Clinical Psychology. 1987;58:162–170. doi: 10.1037//0022-006x.55.2.162. doi.org/10.1037/0022-006X.55.2.162. [DOI] [PubMed] [Google Scholar]
- Land KC, McCall PL, Nagin DS. A comparison of Poisson, negative binomial, and semiparametnc mixed Poisson regression models with empirical applications to criminal careers data. Sociological Methods & Research. 1996;24(4):387–440. [Google Scholar]
- Long JS. Regression models for categorical and limited dependent variables. Sage; Thousand Oaks, CA: 1997. [Google Scholar]
- Lonsway KA, Fitzgerald LF. Attitudinal antecedents of rape myth acceptance: A theoretical and empirical reexamination. Journal of Personality and Social Psychology. 1995;68(4):704–711. doi: 10.1037/0022-3514.68.4.704. [Google Scholar]
- Malamuth NM, Hald G, Koss M. Pornography, individual differences in risk and men's acceptance of violence against women in a representative sample. Sex Roles. 2012;66(7-8):427–439. doi:10.1007/s11199-011-0082-6. [Google Scholar]
- Malamuth NM, Heavy CL, Linz D. Predicting men's antisocial behavior against women: The interaction model of sexual aggression. In: Hall GN, Hirschman R, Graham J, Zaragoza M, editors. Sexual aggression: Issues in etiology, assessment, and treatment. Hemisphere; Washington DC: 1993. pp. 63–97. [Google Scholar]
- Malamuth NM, Linz D, Heavey CL, Barnes G, Acker M. Using the confluence model of sexual aggression to predict men's conflict with women: A 10-year follow-up study. Journal of Personality and Social Psychology. 1995;69:353–369. doi: 10.1037//0022-3514.69.2.353. doi.org/10.1037/0022-3514.69.2.353. [DOI] [PubMed] [Google Scholar]
- Malamuth NM, Sockloskie RJ, Koss MP, Tanaka JS. Characteristics of aggressors against women: testing a model using a national sample of college students. Journal of Consulting and Clinical Psychology. 1991;59:670–681. doi: 10.1037//0022-006x.59.5.670. doi.org/10.1037/0022-006X.59.5.670. [DOI] [PubMed] [Google Scholar]
- McCullagh P, Nelder JA. Generalized linear models. 2nd ed. Chapman and Hall; London: 1989. [Google Scholar]
- Montano DE, Kasprzyk D, Taplin SH. The theory of reasoned action and the theory of planned behavior. In: Glanz K, Lewis ML, Rimer BK, editors. Health behavior and health research: Theory, research, and practice. Vol. 2. Jossey-Bass; San Francisco, CA: 1997. pp. 85–112. [Google Scholar]
- Nagin DS, Land K. Age, Criminal Careers, and Population Heterogeneity: Specification and Estimation of a Nonparametric Mixed Poisson Model. Criminology. 1993;31:327–362. [Google Scholar]
- Riggs DS, O'Leary KD. A theoretical model of courtship aggression Violence in dating relationships: Emerging social issues. Praeger Publishers; New York, NY, England: 1989. pp. 53–71. [Google Scholar]
- Silver N. The signal and the noise: Why most predictions fail but some don’t. Penguin Press; London: 2012. [Google Scholar]
- Tharp A, DeGue S, Valle L, Brookmeyer KA, Massetti GM, Matjasko JL. A systematic qualitative review of risk and protective factors for sexual violence perpetration. Trauma, Violence and Abuse. 2013;14(2):133–167. doi: 10.1177/1524838012470031. doi:10.1177/1524838012470031. [DOI] [PubMed] [Google Scholar]
- van Schellen M, Apel R, Nieuwbeerta P. ‘Because you're mine, I walk the line’? Marriage, spousal criminality, and criminal offending over the life course. Journal of Quantitative Criminology. 2012;28(4):701–723. doi:10.1007/s10940-012-9174-x. [Google Scholar]
- Vuong QH. Likelihood ratio tests for model selection and non-nested hypotheses. Econometrica. 1989;57:307–333. doi.org/10.2307/1912557. [Google Scholar]
- Watts SJ, McNulty TL. Childhood abuse and criminal behavior: Testing a general strain theory model. Journal of Interpersonal Violence. 2013;28(15):3023–3040. doi: 10.1177/0886260513488696. doi:10.1177/088626051348869. [DOI] [PubMed] [Google Scholar]
- Wechsler H, Davenport A, Dowdall G, Moeykens B, Castillo S. Health and behavioral consequences of binge drinking in college. Journal of the American Medical Association. 1994;272:1672–1677. doi.org/10.1001/jama.1994.03520210056032. [PubMed] [Google Scholar]
- White JW, Humphrey JA. A longitudinal approach to the study of sexual assault. In: Schwartz M, editor. Researching sexual violence against women. Sage; Thousand Oaks, CA: 1997. pp. 22–42. [Google Scholar]