structSSI: Simultaneous and Selective Inference for Grouped or Hierarchically Structured Data

Abstract

The 𝖱 package structSSI provides an accessible implementation of two recently developed simultaneous and selective inference techniques: the group Benjamini-Hochberg and hierarchical false discovery rate procedures. Unlike many multiple testing schemes, these methods specifically incorporate existing information about the grouped or hierarchical dependence between hypotheses under consideration while controlling the false discovery rate. Doing so increases statistical power and interpretability. Furthermore, these procedures provide novel approaches to the central problem of encoding complex dependency between hypotheses.

We briefly describe the group Benjamini-Hochberg and hierarchical false discovery rate procedures and then illustrate them using two examples, one a measure of ecological microbial abundances and the other a global temperature time series. For both procedures, we detail the steps associated with the analysis of these particular data sets, including establishing the dependence structures, performing the test, and interpreting the results. These steps are encapsulated by 𝖱 functions, and we explain their applicability to general data sets.

1. Introduction

When testing potentially dependent multiple hypotheses according to standard multiple testing schemes, the following dilemma emerges: powerful testing methods, including the Benjamini-Hochberg (BH) procedure (Benjamini and Hochberg 1995), require the independence of test statistics associated with hypotheses to ensure control of the false discovery rate (FDR) while those methods that control for error under general dependence structures, such as the Benjamini-Yekutieli (BY) procedure (Benjamini and Yekutieli 2001), tend to be unnecessarily conservative in identifying true alternatives. Unless more information about the source of dependence between the multiple hypotheses is known, not much can be done to simultaneously increase the power of a testing procedure and maintain control of the FDR.

Here, however, lies insight that can be used to guide the design of more sophisticated multiple testing procedures: by examining data on a case by case basis and incorporating the specific structure of dependence between the p values associated with multiple hypotheses, a testing scheme can be constructed that performs optimally for the set of hypotheses of interest in the data under investigation. Often, it is known that multiple hypotheses share a natural underlying group, hierarchical, nested, or network structure of dependence, and this information should be explicitly utilized in performing multiple comparisons.

Not only does this improve the power of the testing procedure while controlling FDR, it contributes to the narrative and interpretability of results; for example, more than supplying a list of individually significant hypotheses controlled at a particular level α, these procedures output the clusters within which the experimental signal is most prevalent. Guided by these principles, several multiple testing methods have been derived that explicitly account for known, experiment-specific patterns of dependence between hypotheses.

Notably, for the intermediate situation, in which assuming independence between test satistics is invalid, but controlling for arbitrary dependence structures is over-conservative, the BH and BY procedures have natural extensions, the group Benjamini-Hochberg (GBH) procedure of Hu, Zhao, and Zhou (2010), and the hierarchical false discovery rate (HFDR) controlling procedure of Benjamini and Yekutieli (2001, 2003), and both techniques are made accessible to 𝖱 (𝖱 Core Team 2014) users through the package structSSI (Sankaran 2014). The GBH procedure is applicable whenever a group dependence structure between hypotheses is visible before any testing is performed. For example, in a genetics differential expression experiment, we may group hypotheses according to what overall function they perform or pathway they belong to. The HFDR procedure is applicable whenever hypotheses can be hierarchically arranged. For example, in a quantitative trait loci (QTL) analysis, the hypothesis that a particular chromosomal region is associated with a particular brain response is a parent hypothesis to the subhypotheses that any of the subregions on the chromosome are associated with this brain response.

Grouped and hierachically dependent hypotheses arise in diverse research contexts:

1. Genes in microarray experiments can be grouped according to the Gene Ontology.

2. Hypotheses associated with microbiota in metagenomic experiments exhibit dependence associated with their phylogenetic taxonomy.

3. Questions in QTL analysis and time series often involve testing hypotheses at multiple resolutions in the data.

4. Studies of clinical trials have a natural grouping according to primary and secondary endpoints.

Several papers have demonstrated the promise of these methods in diverse disciplines; however, despite the increasing attention paid to multiple testing and the variety of packages implementing multiple testing techniques, there are still no other packages on the Comprehensive 𝖱 Archive Network (CRAN) available except package structSSI that render either the GBH or HFDR procedures directly usable (Hothorn, Bretz, and Westfall 2008; Pollard, Dudoit, and Laan 2004; Blanchard, Dickhaus, Hack, Konietschke, Rohmeyer, Rosenblatt, Scheer, and Werft 2010; Dabney and Storey 2014; Strimmer 2008).

The outline of this paper is as follows. In Section 2, we motivate the necessity for procedures to perform simultaneous and selective inference, and we briefly summarize traditional methodology. Then, we introduce the two recent techniques implemented in this package: the GBH and HFDR procedures. The purpose of these sections is to sketch the theoretical and conceptual properties of these methods, which we refer to in our data analysis examples. These data analysis examples are the focus of Section 3. We apply both the GBH and HFDR procedures to two data sets. In each instance, we explain the data, the functions used in testing, and the interpretation of results. We further identify the data analysis decisions that may be encountered in practice and outline principles that can be used to inform those decisions.

2. Selective and simultaneous inference background

In this section, we survey the fundamental concepts and techniques associated with testing multiple hypotheses that will be referenced throughout the remainder of this paper.

2.1. Traditional motivation and methodology

Recall that the selective and simultaneous inference problem involves controlling for false positives while identifying true signals when the number of hypotheses under consideration is large (Farcomeni 2009; Dudoit, Shaffer, and Boldrick 2003; Reiner, Yekutieli, and Benjamini 2003; Benjamini 2010b).

If each individual hypothesis is controlled at level α, then a proportion α of all null hypotheses in the multiple testing situation will be false positives. When the number of discoveries becomes large, as is often the case when testing a large number of hypotheses, this can become a serious problem, leading researchers to have confidence in a larger number of discoveries than is acceptable.

To overcome this problem, a natural response is to define a new type of error rate that takes into account the multiple hypothesis tests being performed and that, unlike the α probability that a single hypothesis is a false positive, can be interpreted from a multiple hypothesis testing perspective. A widely-utilized definition historically is the family-wise error rate (FWER), defined as the probability of at least one false positive among all the outcomes of a multiple testing procedure (Benjamini and Hochberg 1995). Many procedures are designed to control the FWER at some prespecified level. However, when the number of hypotheses increases, this definition of error can become unjustifiably stringent, restricting the ability to identify true discoveries (Dudoit, Keleç, and Van Der Laan 2008; Benjamini 2010a).

The false discovery rate

The FDR, defined in Benjamini and Hochberg (1995), is a formulation of error-rate in the multiple-testing context designed in response to the over-conservative performance of the FWER. The fundamental idea behind the FDR is that the proportion of false positives among all discoveries is a more meaningful value to control than the absolute number of false positives. Thus, while procedures controlling the FWER attempt to prevent any false positives from arising during multiple testing, the FDR allows a prespecified proportion of false-positives among the large number of hypotheses being tested in order to facilitate improvements in power.

We now define the FDR more formally. Suppose we are testing hypotheses H₁, …, H_N. Let R be the number of hypotheses rejected by some testing scheme, and let V be the number of false positives, that is, hypotheses that were rejected but which are in truth null. Then, the FDR is defined as $\mathrm{F}\mathrm{D}\mathrm{R}=𝖤(\frac{V}{R})$ when R > 0 and 0 when R = 0. This is exactly the expected proportion of false positives among all rejected hypotheses.

Benjamini-Hochberg procedure review

In addition to defining the FDR, Benjamini and Hochberg (1995) provided a step-up procedure, now known as the BH procedure, for controlling the FDR at level α. As the methods implemented in structSSI are extensions of BH to more general settings, we here provide a formal statement of the procedure.

Let H₁, H₂, …, H_N be the multiple hypotheses under consideration, and let p₁, p₂, …, p_N be the corresponding p values resulting from tests of each of the individual hypotheses. Suppose that we want to control the FDR at level α.

First, order the p values so that p₍₁₎ ≤ p₍₂₎ ≤ ⋯ ≤ p_(N). Now, let $k=\text{max}\{i:p_{(i)}\le \frac{i\alpha }{N}\}$. Reject those hypotheses H_(i) associated with p values satisfying p_(i) ≤ p_(k). If no such k exists, then do not reject any hypotheses. If these p values are independent, then this procedure was proven to control the FDR at level π₀α, where π₀ is the proportion of true null hypotheses among all those being tested. Since π₀ is generally unknown and typically close to 1, this method is most often used to control the FDR at level α. Notice that, not only does this procedure not integrate any information about dependence structure into inference, it does not generally control the FDR in settings where such dependence is present (Benjamini and Hochberg 1995, 2000).

2.2. New techniques

Several studies have proposed multiple testing procedures that specifically incorporate known dependence information between hypotheses (Zhong, Tian, Li, Storch, and Wong 2004; Farcomeni 2009; Dudoit et al. 2008; Benjamini and Yekutieli 2003; Hu et al. 2010). In this section, we overview the two that are implemented in structSSI: the GBH procedure of Hu et al. (2010) and the HFDR procedure of Benjamini and Yekutieli (2003) and Yekutieli (2008). Though the particular steps employed between the two procedures are very different, both rely on the insight that known relationships between the multiple hypotheses in question can be employed to focus on subsets of hypotheses that are more likely to contain true discoveries. More specifically, in the GBH procedure, hypotheses are grouped based on known dependence information; the proportion of alternative hypotheses in each group is estimated, and the original p values are reweighted to emphasize the groups with higher estimated proportions of true discoveries. The HFDR procedure, on the other hand, arranges hypotheses on a tree according to their dependence information and restricts attention to those families of hypotheses whose parents on the tree have been rejected.

Group Benjamini-Hochberg procedure

Before defining the GBH procedure, we describe the statistical context and introduce notation. We suppose that N hypotheses H₁, H₂, …, H_N have been tested, and individual unadjusted p values have been found for each. We further suppose that we can bin these N hypotheses into K distinct groups, where each group contains n_g hypotheses, g = 1, …, K. We define n_g,0 to be the number of true null hypotheses and n_g,1 = n_g − n_g,0 to be the number of true alternative hypotheses within group g. Hence, ${\pi }_{g,0}=\frac{n_{g,0}}{n_g}$ is the proportion of true null hypotheses in group g and ${\pi }_{g,1}=\frac{n_{g,1}}{n_g}=1-{\pi }_{g,0}$ is the proportion of true alternative hypotheses in group g. We can then let ${\pi }_0=\frac{1}{N}{\sum }_{g=1}^K{n}_g{\pi }_{g,0}$ be the proportion of true null hypotheses in the overall set of N hypotheses. Our goal is to employ estimates of these values to design a multiple testing procedure. We first define the GBH procedure assuming that π_g,0 is known for each group g. This is known as the oracle case.

Definition 1

Oracle group Benjamini-Hochberg procedure

1. For each hypothesis i contained in group g, reweight its associated p value P_g,i to create the weighted p values, denoted $P_{g,i}^w=\frac{{\pi }_{g,0}}{{\pi }_{g,1}}{P}_{g,i}$. In the case that π_g,1 = 0, set $P_{g,i}^w=\infty$. If π_g,1 = 0 for every g ∈ {1, …, K}, then do not reject any hypotheses and terminate the procedure. Otherwise, continue to Step 2.

2. Pool all the weighted hypotheses together and sort them, so that $P_{(1)}^w\le P_{(2)}^w\le \cdots \le P_{(N)}^w$.

3. Let $k=\text{max}\{i:P_{(i)}^w\le \frac{i{\alpha }^w}{N}\}$, where ${\alpha }^w=\frac{\alpha }{1-{\pi }_0}$. If such a k exists, reject the k hypotheses associated with $P_{(1)}^w,\dots ,P_{(k)}^w$; otherwise, do not reject any hypotheses.

Hence, if the proportion of true null hypotheses is smaller than the proportion of true alternatives within a given group, then each hypothesis within that group is more likely to be a true alternative and the reweighted p values will be smaller than the corresponding unweighted ones, making their rejection more likely. Conversely, if there is a higher proportion of true null hypotheses than true alternatives within a group, then the reweighted p values will be inflated, making their rejection less likely.

The last step is the BH procedure applied to these adjusted p values, where α is adjusted to take advantage of the fact that the BH procedure controls the FDR at level π₀α. Indeed, this procedure can be interpreted as the BH procedure with focus of rejections redirected towards more promising intradependent groups, that is, the groups that have a higher estimated proportion of true discoveries.

Next, we remove the assumption that the proportion of true null hypotheses in each group is known. This modified procedure is known as the adaptive GBH procedure (Hu et al. 2010).

Definition 2

Adaptive group Benjamini-Hochberg procedure

1. For each group g, estimate π_g,0 by π̂_g0.

2. Apply the oracle GBH procedure, with π_g,0 replaced by π̂_g,0.

Various methods of estimating π_g,0 have been developed, and each has unique properties (Hu et al. 2010; Storey, Taylor, and Siegmund 2004; Benjamini, Krieger, and Yekutieli 2006; Benjamini and Hochberg 2000). Part of the appeal of the adaptive GBH procedure is that it does not rely upon a specific type of estimator: Hu, Zhou, and Zhao Hu et al. (2010) have shown that the adaptive GBH procedure asymptotically controls the FDR as long as the estimator π̂_g,0 is either unbiased or asymptotically conservative.

As this estimation is essential for use of the GBH procedure in practice, we supply three estimation procedures in package structSSI: the tail proportion of p values estimator of Storey et al. (2004), the least-slope method of Benjamini and Hochberg (2000), and the two-stage method of Benjamini et al. (2006). Examples of their use are highlighted in the adaptive GBH example in Section 3.

Hierarchical false discovery rate controlling procedure

Like the GBH procedure, the HFDR procedure leverages specific information on the dependence structure between hypotheses to focus attention on subsets of hypotheses that are more likely candidates for discoveries. However, rather than reweighting p values, the procedure achieves this focus by arranging families of related hypotheses along a tree and restricting attention to particular subtrees that are more likely to contain alternative hypotheses; specifically, children hypotheses are considered for rejection if and only if their parents are rejected. The essential idea is that hierarchical application of an FDR controlling procedure among families of related hypotheses implies global, tree-wide FDR control.

As in the above discussion of GBH, suppose that there are N hypotheses to be tested, H₁, H₂, …, H_N, and suppose that they can be arranged on a tree with L levels. Associate each hypothesis, besides the root, with a parent hypothesis on the level directly above it. That is, hypotheses H_i on level L(i) ∈ {2, …, L} is associated with a parent hypothesis on level L(i) − 1, which we will denote by Par (i). Reindex the hypotheses so that H₁, …, H_T are the parent hypotheses. Then, we can group the hypotheses into T +1 families, where one of the families is the root hypothesis and each of the other families of hypotheses is defined as a set of hypotheses sharing the same parent. We denote these families by 𝒯₀, 𝒯₁, …, 𝒯_T, where 𝒯₀ = {H_i : L(i) = 1} and 𝒯_t = {H_i : Par (i) = t}. Test statistics associated with hypotheses within the same family 𝒯_t are assumed independent.

Definition 3

Hierarchical false discovery rate controlling procedure

1. Test 𝒯₀, the root hypothesis. If it is significant, proceed.

2. Test the hypotheses in family 𝒯₁ simultaneously, using the BH procedure to control the FDR at level α.

3. For each rejected node i in 𝒯₁, simultaneously test its family of children hypotheses.

4. While children nodes continue to be rejected, repeat Step 3, with 𝒯₁ replaced by the family of children associated with the immediately previous rejected hypothesis.

Essentially, this algorithm requires that:

1. Hypotheses contained in the same family are tested simultaneously, and FDR is controlled within families.

2. A family of hypotheses on a given level is tested if and only if its parent hypothesis is rejected.

Care is required in the characterization of FDR control for this algorithm. In particular, the α FDR control rate used in the BH procedure applied to each family 𝒯_t is not preserved at the tree-wide level. To understand the notion of FDR control for the HFDR procedure, consider several variations of the usual FDR, each of interest in the hierarchical testing setting:

1. FDR_tree: The proportion of discoveries over the entire tree that are false discoveries.

2. FDR_L: The proportion of discoveries within an a priori specificied level L of the tree that are false discoveries.

3. FDR_tips: The proportion of discoveries on the tips of the tree that are false discoveries.

Given the outcome of the HFDR procedure, Benjamini and Yekutieli (2003) and Yekutieli (2008) prove universal upper bounds for two of these FDR variations,

$$\mathrm{F}\mathrm{D}{\mathrm{R}}_{\mathit{\text{tree}}}\le 2{\delta }^{*}\alpha ,$$

$$\mathrm{F}\mathrm{D}{\mathrm{R}}_{\mathit{\text{tips}}}\le 2{\delta }^{*}L\alpha ,$$

where α is the FDR control level for each application of the BH procedure, L is the total number of levels in the testing tree, and δ^* is an inflation factor analytically bounded above by 1.44 and found through simulation study to be near one in most testing situations (Benjamini and Yekutieli 2003; Yekutieli 2008). Further, in their study, they advocate the following estimator, applicable to all three characterizations of the tree FDR,

$$\widehat{\mathrm{F}\mathrm{D}\mathrm{R}}≔\left[\frac{\#\text{discoveries}+\#\text{families tested}}{\#\text{discoveries}+1}\right]\alpha ,$$

where a discovery is defined as an adjusted p value below α within the entire tree, at prespecified level L, or at the tips, for FDR_tree, FDR_L and FDR_tips, respectively. structSSI supplies these estimates for the full tree and tip FDR, via the function EstimatedHFDRControl.

We can now point out several consequences of this procedure that are relevant from a researcher’s perspective. First, notice that, unlike testing within groups, which only explicitly utilizes stratified information, when using a tree, we can specifically model the nested, hierarchical relationships between hypotheses. Typically the specific arrangement is motivated by the design of the experiment or the structure of the data analysis problem. For example, in a microarray study, the hypothesis that a functional pathway in the gene ontology is significantly associated with an experimental variable may depend on the status of a broader category within the ontology.

Notice that the HFDR procedure only takes into account the topology of the tree; in particular, it disregards branch lengths. Therefore, while these branch lengths may be important in determining groups when applying the GBH procedure to hierarchical data, they have no effect on the outcome of the HFDR method.

Another consequence is that, when rejecting hypotheses along the tree, we can gain insight at several levels of resolution, from more general to more specific hypotheses. For example, during a single iteration of the testing procedure applied to a microarray study, we might be able to simultaneously associate very specific functional pathways and very general categories with an experimental variable of interest.

These characteristics of the HFDR procedure – the ability to explicitly take into account known information related to the hierarchical structure present in data and associated hypotheses as well as the potential to conduct a multiresolution search for significant discoveries – supply reasons for the procedure’s usefulness apart from its control of the FDR and increased power over classical procedures.

3. Data analysis examples

In this section, we demonstrate the application of both the GBH and the HFDR controlling procedures to real data. The first example is from the field of microbial ecology. In such data, we are given the evolutionary relationships between individual microbes and their abundances in different ecological environments; we test multiple hypotheses to uncover associations between the individual microbes and their prevalence in these different environments. The second example is a time series of global surface temperature from the Goddard Institute for Space Studies (Shumway and Stoffer 2000). We test multiple hypotheses, each corresponding to whether there is a significant increasing trend in global temperature at a variety of time resolutions: has there been an increase in temperature in the last century? in any quarter-century window? in any decade in particular?

Despite emerging from disparate contexts and being motivated by different questions, these two data analyses are conceptually unified by a need to test multiple hypotheses with a known dependence structure. For the microbes, the dependence structure is encoded in the evolutionary tree between microbes. For the time series, the strength of dependence between time windows is given by how many years apart they are – the closer together, the more correlated. We now proceed to describe the application of structSSI procedures to these two data sets, with the goal that the following sections can serve as a guide for analysis in a variety of contexts in which structurally dependent hypotheses arise.

3.1. Microbial abundance data

The microbial abundance data set included in package structSSI, called chlamydiae, describes the microbial community structures of 26 samples in seven environments via a table of abundances of 21 types of microbes across these samples. It is a small subset of the GlobalPatterns data set specific to the Chlamydiae bacteria taxon. The GlobalPatterns data was the subject of Caporaso et al. (2011), and is available through the Bioconductor package phyloseq (McMurdie and Holmes 2011). The goal of Caporaso et al. (2011) was to understand the composition and variation of microbial communities between environments. For example, with this data, we can begin to ask whether particular microbes, labeled by their operational taxonomic unit (OTU) number, are more or less abundant between any of the environments.

Before going further, we load and survey the data.

R> library("structSSI")
R> library("phyloseq")
R> data("chlamydiae", package = "structSSI")
R> chlamydiae

phyloseq-class experiment-level object
otu_table()   OTU Table:         [ 21 taxa and 26 samples ]
sample_data() Sample Data:       [ 26 samples by 7 sample variables ]
tax_table()   Taxonomy Table:    [ 21 taxa by 7 taxonomic ranks ]
phy_tree()    Phylogenetic Tree: [ 21 tips and 20 internal nodes ]

The abundance data, auxiliary sample data, taxonomic assignments, and phylogenetic tree are all stored in a specialized phyloseq data class. This data set is amenable to the methods in package structSSI due to its large scale and hierarchical structure. This is highlighted by the potential to investigate questions about microbial community structure at varying resolutions. For example, individual species, taxonomic families, and higher ranks, such as phyla, may exhibit different patterns of community structure and variation across environmental samples. For each microbe and collection of microbes within this phylum, we seek to analyze the association between prevalence and environment; i.e., does the microbe or collection of microbes have a preferred environment? More precisely, we will determine whether individual microbes or taxonomic groups of microbes are more or less abundant between the seven sample environment types.

Adaptive group Benjamini-Hochberg procedure

One approach to this problem involves the adaptive GBH procedure. To test for individual microbe associations between abundance and sample type, we can perform multiple F tests. The current standard practice would be to then apply the BH multiple testing correction to the resulting p values. This, however, is not conceptually valid: recall from Section 2.1 that the BH correction requires independence of hypotheses, and it is known that microbes that are closely related at tips of the phylogenetic tree are more likely to share abundance patterns between sample types. Further, since we can integrate this dependence structure into our analysis using the taxonomic table, the adaptive GBH procedure is readily applicable. We will consider groups defined by the family phyla levels of the microbial taxonomy.

First, we perform individual hypothesis tests to see whether or not there is an association between environment type and abundance.

R> taxaPValues <- numeric(length = ntaxa(chlamydiae))
R> names(taxaPValues) <- taxa_names(chlamydiae)
R> environments <- sample_data(chlamydiae)$SampleType
R> abundances <- otu_table(chlamydiae)
R> for (taxaIndex in 1:ntaxa(chlamydiae)) {
+    abundModel <- summary(lm(as.vector(abundances[taxaIndex, ]) ~
+      environments))
+    taxaPValues[taxaIndex] <- with(abundModel, pf(fstatistic[1],
+      fstatistic[2], fstatistic[3], lower.tail = FALSE))
+  }

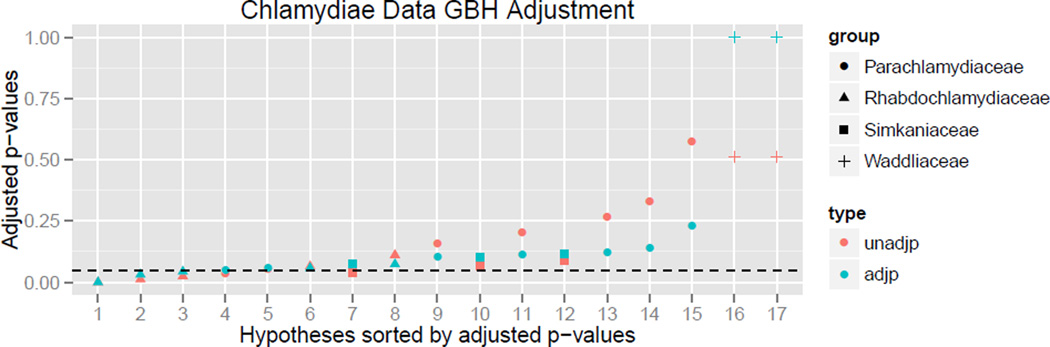
Before adjustment for multiple testing, six microbes are found to be significantly differentially abundant between environments, refer to Figure 1.

Figure 1.

Results of the adaptive GBH procedure on the chlamydiae data set.

Next, we perform the GBH correction. First, we group hypotheses according to the taxonomic family that the corresponding microbes belong to. If a hypothesis does not have a family label, we discard it from our analysis.

The arguments to the Adaptive.GBH function are a vector of the unadjusted p values, a vector with coordinate i containing the group label of the hypothesis in coordinate i of the unadjusted p values vector, the α FDR control level, and the method for estimating the proportion of null hypotheses within each group. We use "lsl", the lowest-slope method for estimating the proportion of true null hypotheses within each group (Benjamini and Hochberg 2000).

R> chlamydiae.families <- na.omit(tax_table(chlamydiae)[, "Family"])
R> taxaPValues <- taxaPValues[taxa_names(chlamydiae.families)]
R> family.AGBH <- Adaptive.GBH(unadj.p = taxaPValues,
+    group.index = matrix(chlamydiae.families), method = "lsl")
R> summary(family.AGBH)

GBH adjusted p values:
          unadjp      adjp               group adj.significance
253897 1.813e-05 9.671e-05 Rhabdochlamydiaceae              ***
249365 1.189e-02 3.172e-02 Rhabdochlamydiaceae                *
152689 2.461e-02 4.375e-02 Rhabdochlamydiaceae                *
544430 3.446e-02 5.169e-02   Parachlamydiaceae                .
547579 5.550e-02 5.770e-02   Parachlamydiaceae                .
25769  6.491e-02 5.770e-02 Rhabdochlamydiaceae                .
217851 3.692e-02 7.397e-02        Simkaniaceae                .
239522 1.110e-01 7.397e-02 Rhabdochlamydiaceae                .
2920   1.568e-01 1.038e-01   Parachlamydiaceae                -
89521  6.488e-02 1.038e-01        Simkaniaceae                -
[only 10 most significant hypotheses shown] 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 '-' 1

 Estimated proportion of hypotheses that are null, within each group:
        Waddliaceae   Parachlamydiaceae        Simkaniaceae
             1.0000              0.4286              0.6667
Rhabdochlamydiaceae
             0.4000
 Significance across groups:
                     adj.significance
group                 - . * ***
  Parachlamydiaceae   5 2 0 0
  Rhabdochlamydiaceae 0 2 2 1
  Simkaniaceae        2 1 0 0
  Waddliaceae         2 0 0 0

We now reject three hypotheses. Notice that, in addition to specifying which microbes are significantly differentially abundant between environments, we are supplied with estimates of the proportion of microbes within each family likely to be differentially abundant between environments. For example, in this particular application, the adaptive GBH procedure identifies microbes from the family Rhabdochlamydiaceae as more likely to be differentially abundant between environments, and it is not surprising that all significant microbes belong to that family. Further, observe in Figure 1 that the original family p values are scaled by a factor proportional to the estimated signal strength in that group.

Hierarchical false discovery rate controlling procedure

To explicitly account for the hierarchical dependence between microbes, we can apply the HFDR procedure. Rather than analyzing only whether different microbes are differentially abundant between environments, we will test whether broader taxonomic groups are associated with environments. To apply the HFDR procedure, we must identify the tree representative of the hierarchical dependence, and in this case the evolutionary tree is a natural choice. Specifically, we will provide the edgelist of the phylogenetic tree as input into structSSI as a proxy for the dependence between types of microbes. We must also supply unadjusted p values associated with each node in the tree; in this case, a hypothesis at a node in the phylogenetic tree will test whether the collection of descendant microbes are significantly differentially abundant between environment types. We use the structSSI function treePValues to aggregate abundances of individual microbes to higher levels in the tree and test whether those aggregated abundances are significantly different between environments.

R> library("igraph")
R> library("ape")
R> chl.tree <- get.edgelist(as.igraph(phy_tree(chlamydiae)))
R> chl.pval <- treePValues(chl.tree, abundances, environments)

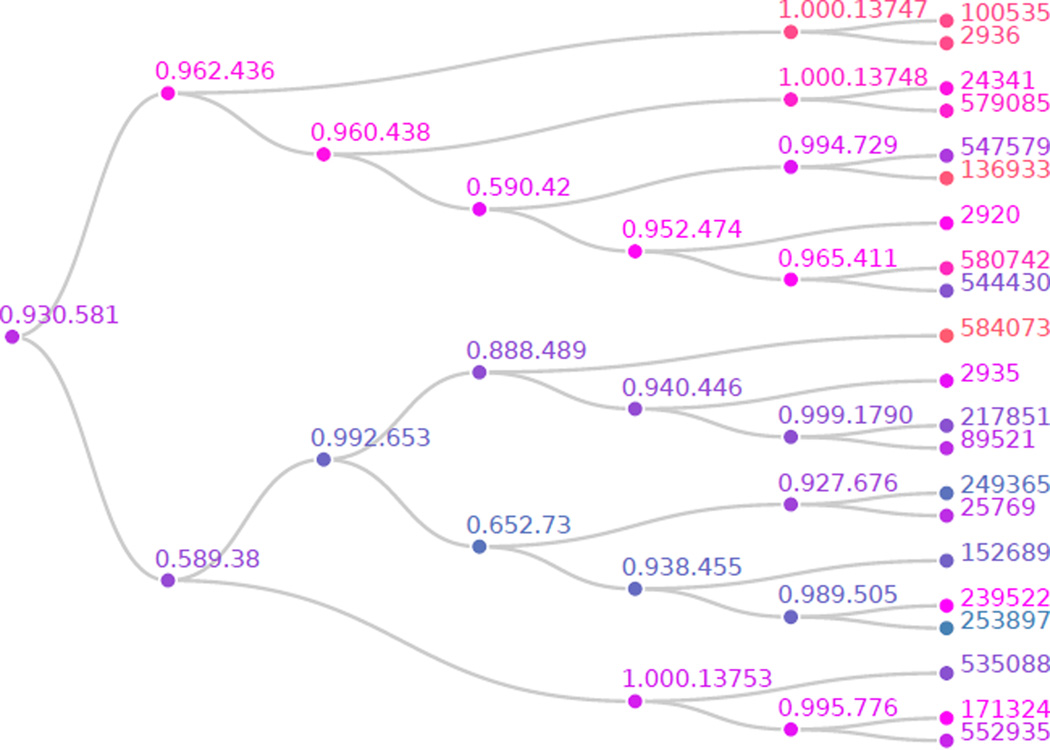
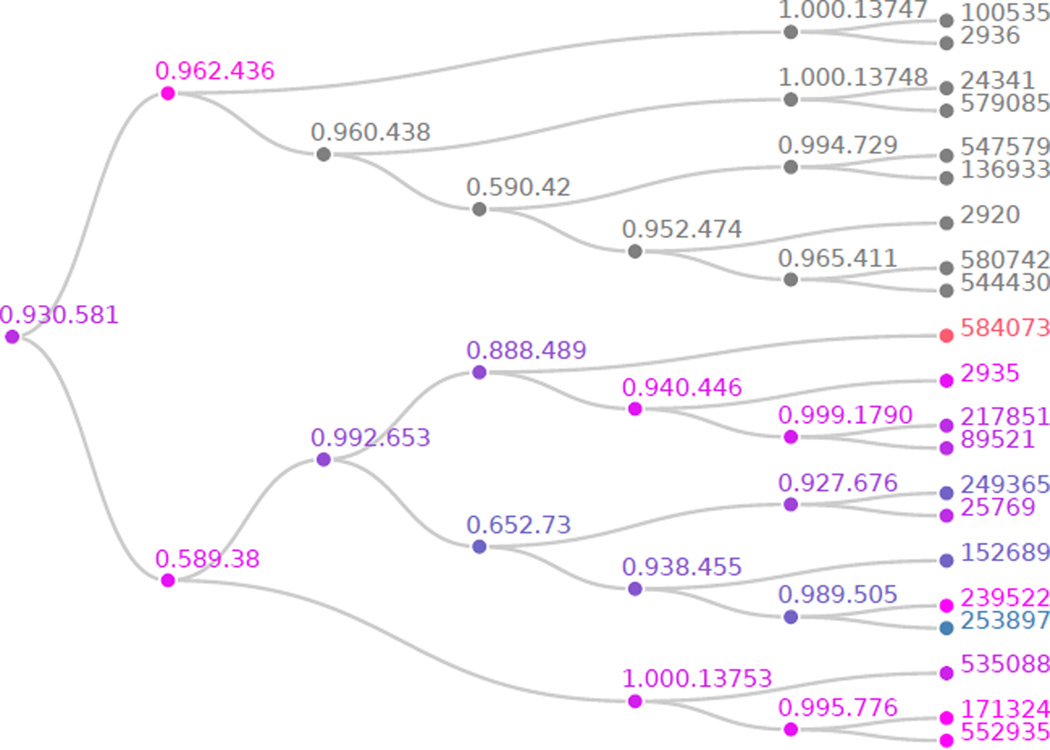
The results of these unadjusted hypothesis tests are depicted in Figure 2. A total of 25 are found significant at the α = 0.10 significance level. Those hypotheses that are blue are rejected at the α level before any multiple testing adjustment; we fail to reject those that are orange. More precisely, a p value of exactly 0, α, or 1 would correspond to a node color of pure blue, magenta, or orange, respectively, with all other p value colors interpolated between these. Notice that, even before performing the HFDR procedure, half of the tree contains many significant hypotheses while the other does not. If we were performing a standard multiple testing correction, this structure would not be evident. This is exactly the type of situation where the HFDR procedure is most relevant. We will see soon that the HFDR procedure fails to reject hypothesis 0.962.436 of the tree and does not expend any testing power correcting for p values on that side of the tree. Instead, it focuses the adjustment, and hence testing power, on those hypotheses on the bottom of the tree, which we can already see are more likely to be significant. We now perform the HFDR procedure and visualize the result in Figure 3. This is done by supplying the unadjusted p values and the edgelist between unadjusted hypotheses names describing the tree to the function hFDR.adjust.

R> chl.hfdr <- hFDR.adjust(chl.pval, chl.tree, alpha = 0.1)
R> summary(chl.hfdr)

Number of hypotheses: 41
Number of tree discoveries: 20
Estimated tree FDR: 0.1524
Number of tip discoveries: 8
Estimated tips FDR: 0.2222

 hFDR adjusted p-values:
             unadjp      adjp adj.significance
253897    1.813e-05 3.627e-05              ***
0.652.73  1.059e-02 2.119e-02                *
249365    1.189e-02 2.379e-02                *
152689    2.461e-02 2.461e-02                *
0.989.505 2.067e-02 2.461e-02                *
0.938.455 1.749e-02 3.497e-02                *
0.888.489 4.001e-02 4.001e-02                *
0.992.653 2.104e-02 4.208e-02                *
0.927.676 4.860e-02 4.860e-02                *
0.930.581 6.356e-02 6.356e-02                *
[only 10 most significant hypotheses shown]
---
Signif. codes:  0 '***' 0.002 '**' 0.02 '*' 0.1 '.' 0.2 '-' 1

Figure 2.

Differential microbial abundance hypotheses tree p values before HFDR adjustment. The tip labels are OTU IDs, the internal node labels are common ancestors in the associated phylogenetic tree. The shade of any particular node corresponds to the outcome of the associated hypothesis test when considered independently of all other tests.

Figure 3.

Differential microbial abundance hypotheses tree p values after HFDR adjustment. The tip labels are OTU IDs, the internal node labels are common ancestors in the associated phylogenetic tree. The shade of any particular node corresponds to the outcome of the associated hypothesis test when considered independently of all other tests. Those hypotheses that are blue, magenta, or orange, have p values below, at or above α = 0.10, the threshold for each BH application to sibling pairs.

After adjustment, we reject 20 hypotheses at the α = 0.10 level. We find that most collections of microbes on the bottom of the tree are differentially abundant. Indeed, this pattern is visible down to the species level – it is not always the case that hypotheses are found to be significant at all resolutions in the tree, as is the case with the temperature data in Section 3.2. Further, observe that the adjustment follows a simple pattern, since every parent has only two children, the BH adjustment keeps the smaller p value the same and the doubles the larger one.

Further, the full tree FDR is about 0.15, a modest increase over the FDR control rate of α = 0.10 used in testing families recursively over the hierarchy, and the tip FDR is about 2α.

More than providing information about the individual microbe abundance hypotheses, the HFDR procedure allows us to see levels in the phylogenetic tree that are more or less differentially abundant between environments. Indeed, the choice of testing individual species of microbes is somewhat arbitrary; one could test whether families, genera, or classes of microbes are significantly differentially abundant between environments. The HFDR procedure allows us to analyze the question of differential microbial abundance at every taxonomic resolution while still controlling the FDR.

Further, note that the reallocation of power for the HFDR procedure is consistent with the estimates of π̂₀ in the adaptive GBH procedure. For example, the family Rhabdochlamydiaceae are the tips descending from nodel 0.652.73 in the plots of the chlamydiae hypotheses tree, which are found by both methods to be enriched for differential abundance.

3.2. Global temperature data

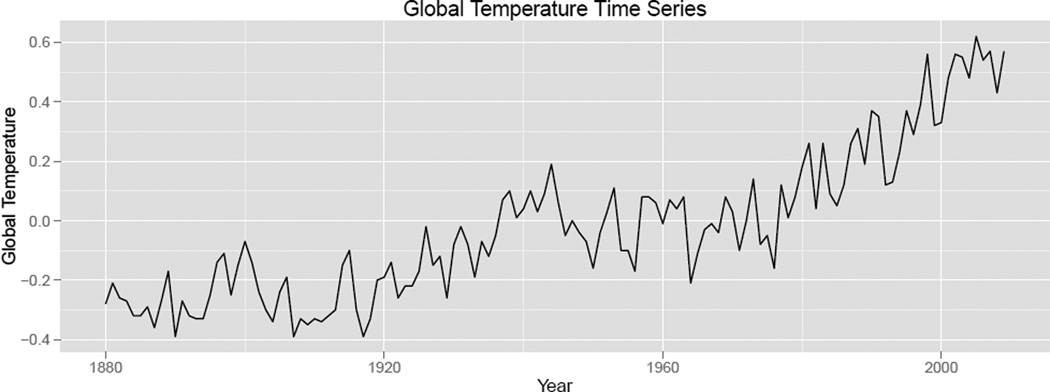
In this data set we analyze changes in global surface temperature between 1880 and 2009. The essential question of interest is whether there have been significant trends in global temperature since 1880. However, as in the microbial abundance example, there are many resolutions with which we can frame this question. In this case, the different resolutions are different time scales. For example, we may want to detect whether there is a significant trend in global temperature each decade, each quarter century, or over the entire time span of the data set. Using the GBH technique, we test hypotheses at a particular time scale resolution while leveraging information about how closely together the different windows are. We presume the dependence between these different hypotheses is structured by the number of years between the time windows being tested.

Using the HFDR procedure, we are able to test hypotheses at multiple time resolutions, proceeding to finer resolutions only if a significant trend was detected at the coarser resolution. Hence, the HFDR procedure allows us to test at multiple resolutions, avoiding any arbitrary choice for which time scale to test, while still controlling the FDR.

First, we perform individual hypothesis tests at multiple time resolutions, without accounting for simultaneous inference. In particular, we divide the 130 years over which the temperatures are measured into two resolutions. The first, more broad resolution, which we refer to as depth one, divides the 130 year period into five windows of size 26 years. The second, finer resolution, which we refer to as depth two, divides the same period into 10 windows of size 13 years. We test whether there is a significant increasing trend in temperature over each of these windows.

R> AllTimePval <- coef(summary(lm(temp ~ year, data = gtemp)))["year",
+    "Pr(>|t|)"]
R> names(AllTimePval) <- "D0"
R> nYears <- nrow(gtemp)
R> chunk <- function(x, n) split(x, sort(rank(x) %% n))

R> pValsFromChunks <- function(chunk, depth.label) {
+    pvalDepth <- vector(length = length(chunk))
+    names(pvalDepth) <- paste(depth.label, 1:length(chunk), sep = "")
+    for (subset in 1:length(chunk)) {
+       curTimes <- chunk[[subset]]
+       pvalDepth[subset] <- coef(summary(lm(temp ~ year,
+         data = gtemp[curTimes,])))["year", "Pr(>|t|)"]
+     }
+     return(pvalDepth)
+ }

R> depth1 <- chunk(1:nYears, 5)
R> depth2 <- chunk(1:nYears, 10)
R> pValsDepth1 <- pValsFromChunks(depth1, "D1-")
R> pValsDepth2 <- pValsFromChunks(depth2, "D2-")
R> unadjp <- c(AllTimePval, pValsDepth1, pValsDepth2)
R> unadjp

       D0      D1-1      D1-2      D1-3      D1-4      D1-5      D2-1
1.797e-40 1.217e-01 2.037e-04 9.969e-01 8.350e-02 6.424e-08 3.949e-01
     D2-2      D2-3      D2-4      D2-5      D2-6      D2-7      D2-8
9.333e-01 7.400e-01 7.579e-02 2.528e-04 6.858e-01 4.679e-01 1.725e-02
     D2-9     D2-10
8.111e-02 8.435e-02

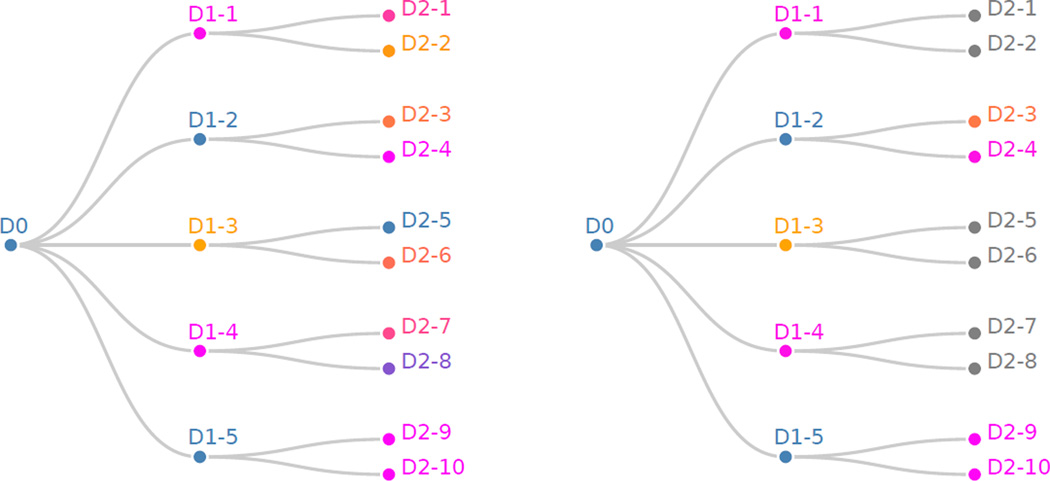
In the vector of unadjusted p values above, D0 denotes the hypothesis that there is an increasing trend in global temperature over the entire 130 year data set. The hypothesis D1-i denotes the hypothesis that there is an increasing trend in global temperature in the ith window of size 26 years. For example, the hypothesis D1-2 tests whether there was a significant increasing trend in global temperature between 1906 and 1931. We can visualize the unadjusted p values in Figure 6 (left). As in the above visualizations, hypotheses are shaded blue and orange depending on whether they are rejected or not. Note that 5 hypotheses are rejected, 3 at the depth two resolution, and those that are rejected seem to be frequently linked with each other, justifying our modeling of dependence structure using this tree.

Figure 6.

Left: Hypotheses tree p values for the global temperature data before HFDR adjustment is performed. Nodes closer to the root represent the test for a trend at a larger time scale, while nodes closer to the base test for trends within time subsets. Right: HFDR adjustment applied to global temperature time series.

We now consider how to use this dependence structure to adjust the p values for multiple testing error using both the GBH and HFDR procedures.

Group Benjamini-Hochberg procedure

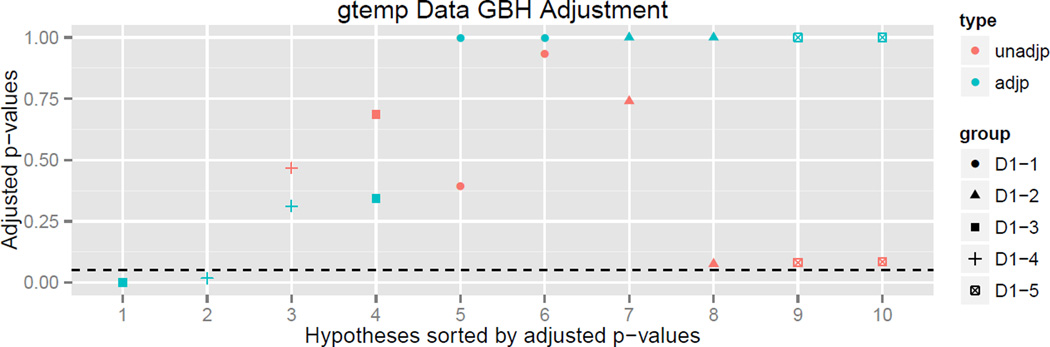
To apply the GBH procedure to the question of whether there is an increasing trend in temperature over multiple time windows over the 130 year span of the data, we choose to test each of the 13 depth two windows and perform a GBH adjustment using the depth one window membership to create a grouping.

For example, the hypothesis associated with the window between 1919 and 1931 belongs to depth two and has an unadjusted p value of 0.0758. Since the window 1919–1931 is a subset of the depth one window 1909–1931, we will group it along with the window 1909–1918 when performing the GBH adjustment.

R> depth.2.unadjp <- unadjp[-c(1:6)]
R> depth.1.groups <- rep(paste("D1", 1:5, sep = "-"), each = 2)
R> gtemp.AGBH <- Adaptive.GBH(depth.2.unadjp, depth.1.groups,
+    method = "tst")
R> gtemp.AGBH

GBH adjusted p values:
         unadjp      adjp group adj.significance
D2-5  0.0002528 0.0005056  D1-3              ***
D2-8  0.0172526 0.0172526  D1-4                *
D2-7  0.4678910 0.3119274  D1-4                -
D2-6  0.6858234 0.3429117  D1-3                -
D2-1  0.3949242 1.0000000  D1-1                -
D2-2  0.9333085 1.0000000  D1-1                -
D2-3  0.7400278 1.0000000  D1-2                -
D2-4  0.0757946 1.0000000  D1-2                -
D2-9  0.0811059 1.0000000  D1-5                -
D2-10 0.0843518 1.0000000  D1-5                -
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 '-' 1
 Estimated proportion of hypotheses that are null, within each group:
D1-1 D1-2 D1-3 D1-4 D1-5
 1.0  1.0  0.5  0.5  1.0

The π₀ estimates for the proportion of null hypotheses within each of the depth one groupings suggests an increasing proportion of significance in windows D1-3 and D1-4. Of course, these estimates are only approximate and further investigation is required. The two-step test procedure requires a large number of hypotheses within each group to accurately estimate π₀ for each group. Nonetheless, the finding is suggestive and warrants further analysis.

Hierarchical false discovery rate controlling procedure

We now apply the HFDR procedure to the same global temperature data set. This is accomplished by supplying an edgelist describing the tree, called gtemp.el below, and the vector of unadjusted p values to the function hFDR.adjust. The result is visualized in Figure 6 (right).

R> gtemp.el <- matrix(nrow = 15, ncol = 2)
R> gtemp.el[, 1] <- c(rep("D0", 5), rep(paste("D1", 1:5, sep = "-"),
+    each = 2))
R> gtemp.el[, 2] <- c(paste("D1", 1:5, sep = "-"),
+    paste("D2", 1:10, sep = "-"))
R> gtemp.hfdr <- hFDR.adjust(unadjp, gtemp.el)
R> gtemp.hfdr

hFDR adjusted p-values:
         unadjp      adjp adj.significance
D0    1.797e-40 1.797e-40              ***
D1-1  1.217e-01 1.522e-01                -
D1-2  2.037e-04 5.094e-04              ***
D1-3  9.969e-01 9.969e-01                -
D1-4  8.350e-02 1.392e-01                -
D1-5  6.424e-08 3.212e-07              ***
D2-1  3.949e-01        NA              <NA>
D2-2  9.333e-01        NA              <NA>
D2-3  7.400e-01 7.400e-01                 -
D2-4  7.579e-02 1.516e-01                 -
D2-5  2.528e-04        NA              <NA>
D2-6  6.858e-01        NA              <NA>
D2-7  4.679e-01        NA              <NA>
D2-8  1.725e-02        NA              <NA>
D2-9  8.111e-02 8.435e-02                 .
D2-10 8.435e-02 8.435e-02                 .
---
Signif. codes:  0 '***' 0.001 '**' 0.01  '*' 0.05 '.' 0.1 '-' 1

Notice that the results in the hypotheses testing tree in Figure 6 (right) correspond naturally with the time series plot of global temperature over time. In particular, the time series seems relatively stable between 1880 and 1920, increasing between 1910 and 1940, stable up to 1980, and increasing again until 2009. This appearance of windows of increasing trend is formally justified by the significance of the depth one windows D1-2 (1906–1931), D1-5 (1984–2009), D2-9 (1984–1996), and D2-10 (1996–2009). However, the most significant adjusted depth two p values according to the HFDR procedure are above the α significance threshold. This is in fact a benefit of testing hypotheses hierarchically. We can find significance at some coarse levels but not at finer ones in a principled way without arbitrarily selecting a threshold window size to define groups, or worse, fishing for significance at a number of window sizes, and only reporting the most significant one.

We can estimate the FDR variations for this hierarchical testing realization, and we again find the tree and tip FDR to be modest increases over the original α = 0.05.

Further, note the differences between the results of the Adpative GBH and HFDR procedures applied to the gtemp data. In particular, the hypotheses within D1-3 and D1-4 windows are only declared significant in the adaptive GBH procedure, while the D1-2 and D1-5 hypotheses are only declared significant in the HFDR procedure. The source of this contrast is most likely the small sample sizes used to estimate π̂₀ in the adaptive GBH procedure, and as mentioned before, these results cannot be taken as conclusive.

Finally, this ability to evaluate hypotheses at multiple resolutions can sometimes lead to more complex narratives, as evidenced by the fact that, in Figure 6 (left), the hypothesis D2-5 has a significant p value while its parent, D1-3, does not. This is an example of a more general pattern, in which aggregating data can either wash out inconsistent signals or amplify coherent ones. Though the resulting interpretations are potentially more complex, this richer structure is nonetheless more informative than the output of traditional testing methods which ignore such structure.

4. Conclusion

As techniques associated with the collection of large-scale data become more sophisticated, and as more information regarding the underlying structure of relations within data becomes available, the promise of testing procedures that capitalize on known hierarchical associations becomes increasingly apparent. The package structSSI is designed to facilitate application of recent developments to these structurally rich data.

Figure 4.

Global temperature data, as measured by the Goddard Institute for Space Studies (Shumway and Stoffer 2000). We are interested in the detection of trends at multiple levels of resolution while maintaining control of the FDR.

Figure 5.

Results of the adaptive GBH procedure applied to the gtemp data set.

Table 1.

A summary of the differences between the adaptive GBH and HFDR procedures.

	Adaptive GBH	HFDR
Hypotheses structure	Group.	Hierarchical.
Independence assumption	The test-statistics associated with hypotheses in different groups are mutually independent.	The test-statistics associated with hypotheses that are immediate children of a parent hypothesis are mutually independent.
Estimates π0.	Yes.	No.
FDR control	FDR ≤ α.	$\mathrm{F}\mathrm{D}\mathrm{R}\approx \left[\frac{\#\text{discoveries}+\#\text{families tested}}{\#\text{discoveries}+1}\right]\alpha$