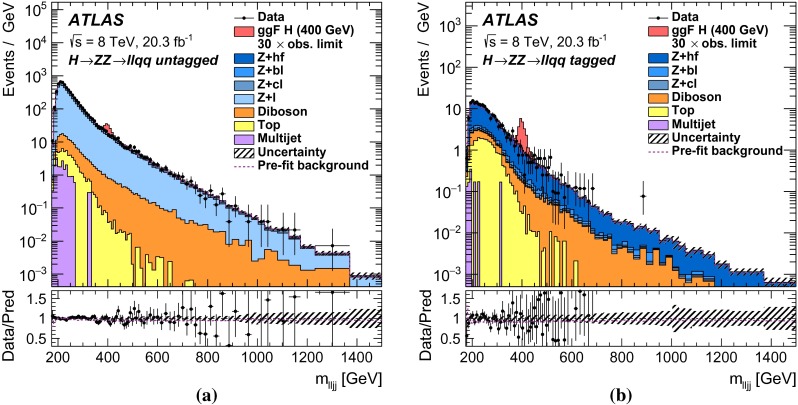
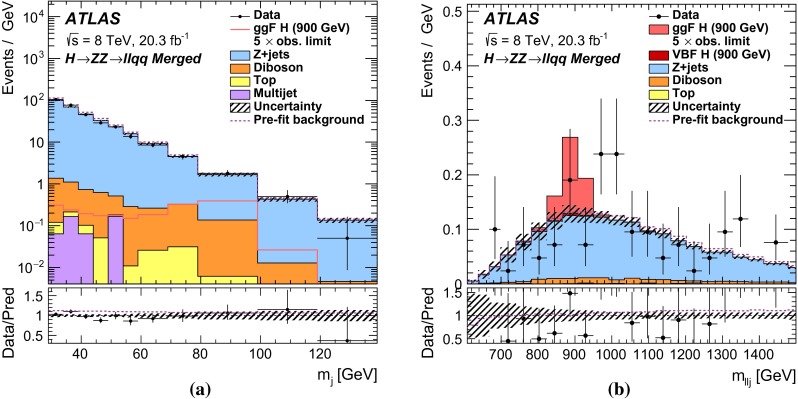
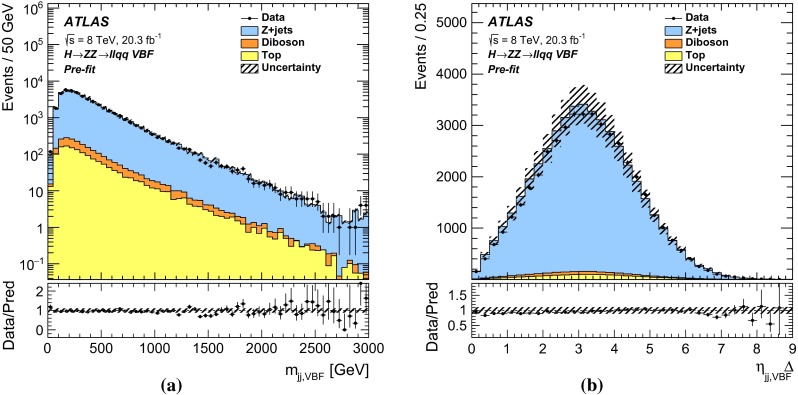
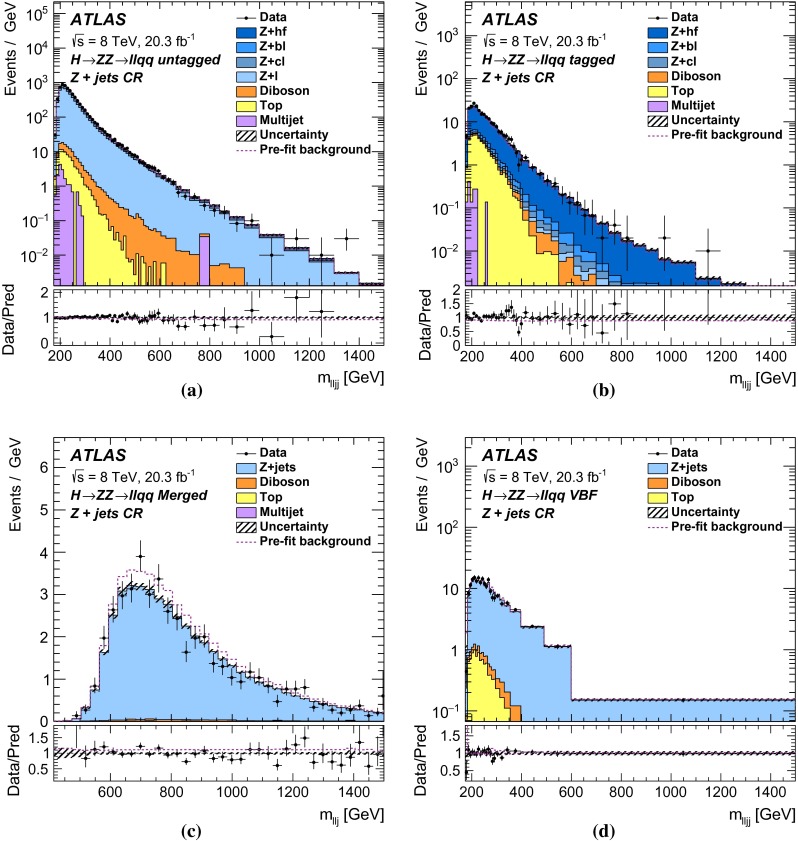
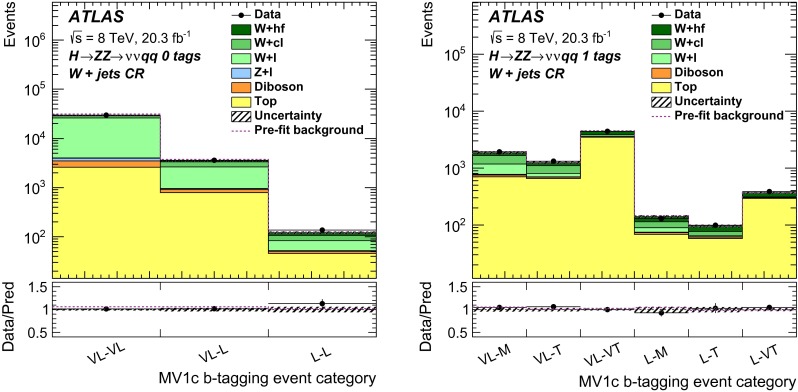
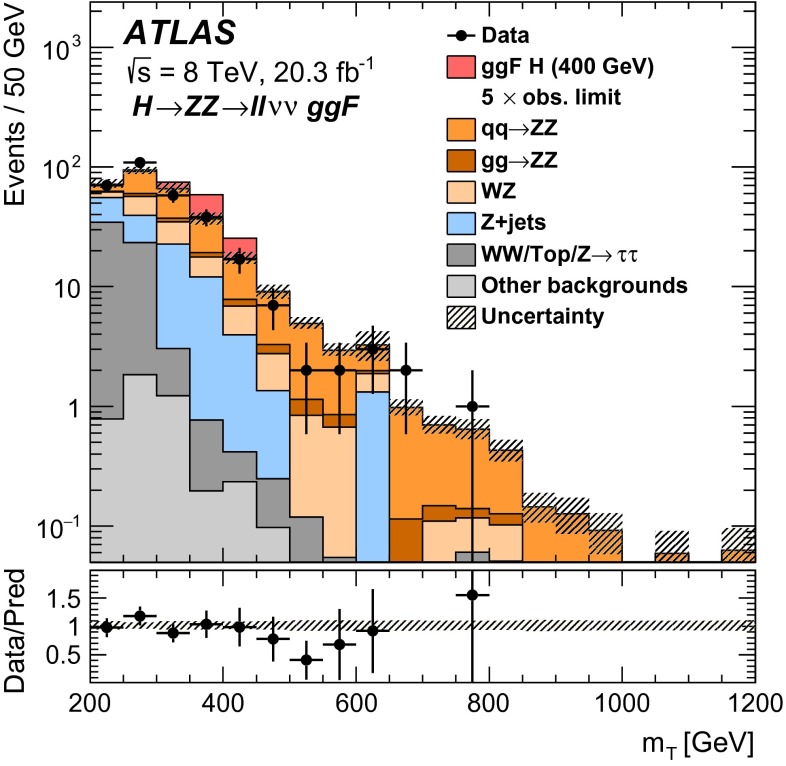
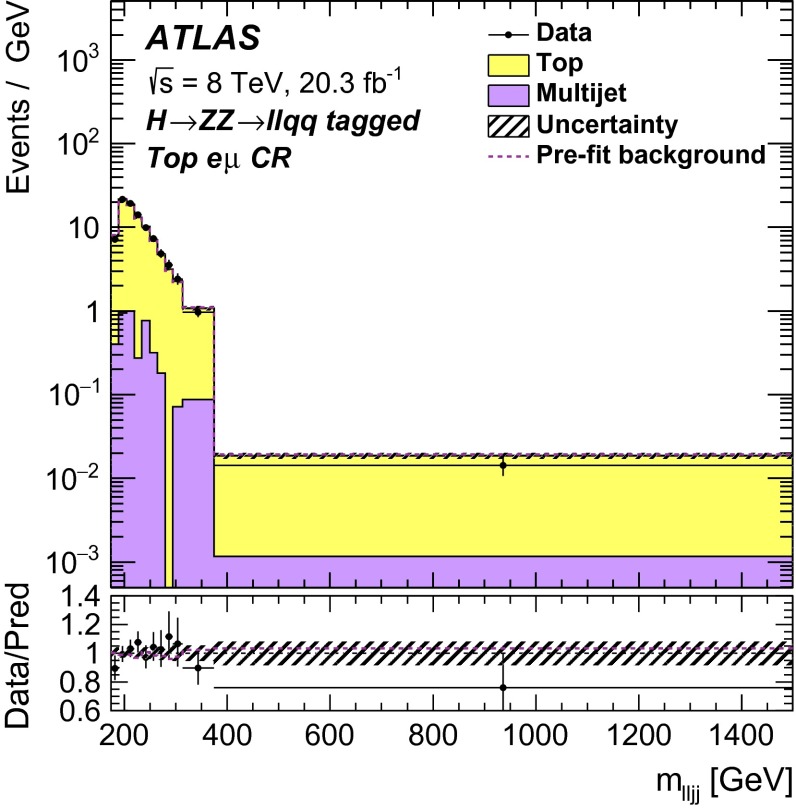
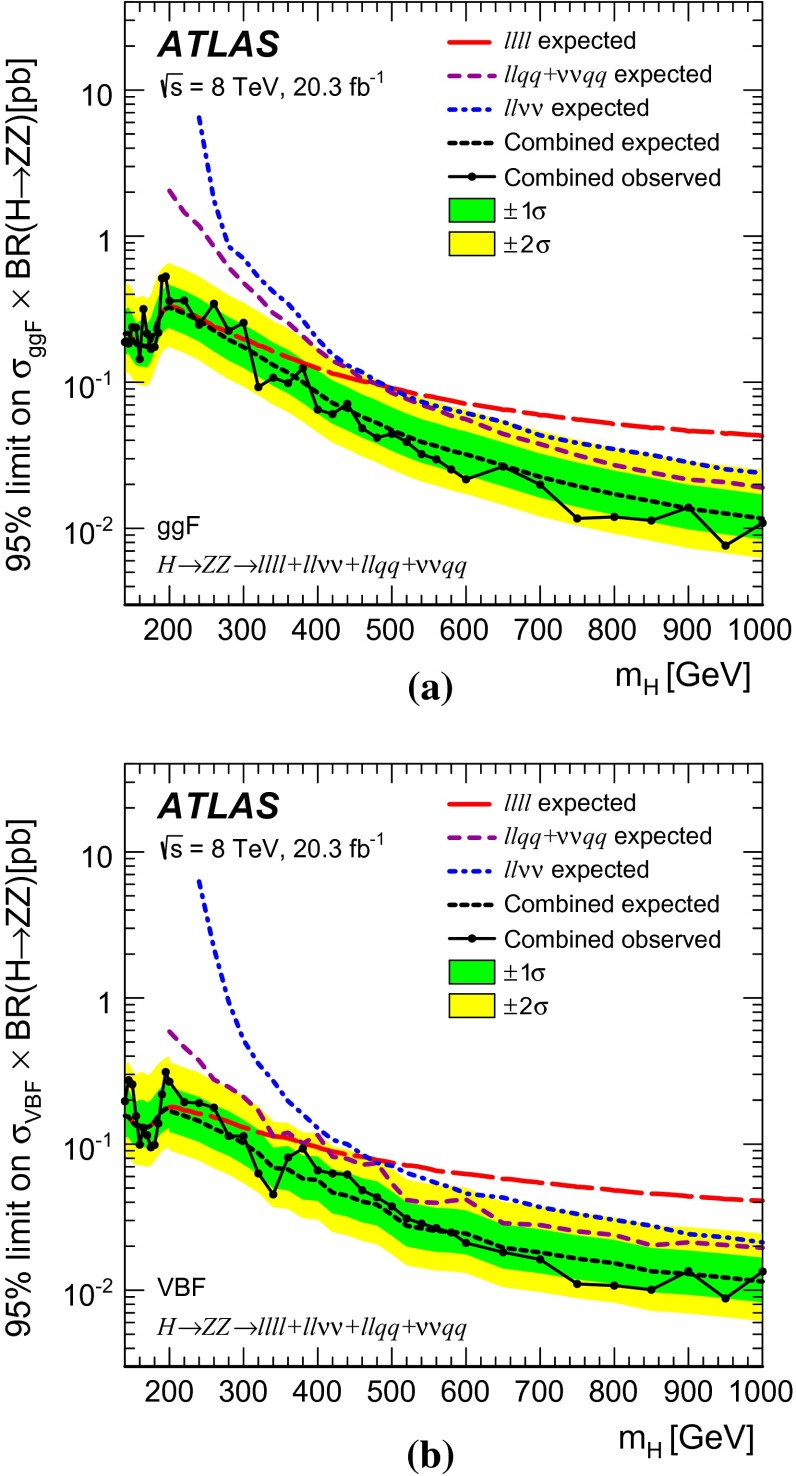
Atlas Collaboration229,
G Aad
G Aad
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
B Abbott
B Abbott
113Department of Physics, McGill University, Montreal, QC Canada
113,
J Abdallah
J Abdallah
151Department of Physics, University of Pennsylvania, Philadelphia, PA USA
151,
O Abdinov
O Abdinov
11Physics Department, University of Athens, Athens, Greece
11,
R Aben
R Aben
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
M Abolins
M Abolins
90Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
90,
O S AbouZeid
O S AbouZeid
158Department of Physics, University of Coimbra, Coimbra, Portugal
158,
H Abramowicz
H Abramowicz
153INFN Sezione di Pisa, Pisa, Italy
153,
H Abreu
H Abreu
152National Research Centre ‘Kurchatov Institute’ B.P.Konstantinov Petersburg Nuclear Physics Institute, St. Petersburg, Russia
152,
R Abreu
R Abreu
116Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
116,
Y Abulaiti
Y Abulaiti
146Graduate School of Science, Osaka University, Osaka, Japan
146,
B S Acharya
B S Acharya
164Czech Technical University in Praha, Praha, Czech Republic
164,
L Adamczyk
L Adamczyk
38Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
38,
D L Adams
D L Adams
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
J Adelman
J Adelman
108Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
108,
S Adomeit
S Adomeit
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
T Adye
T Adye
131INFN Sezione di Napoli, Naples, Italy
131,
A A Affolder
A A Affolder
74SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
74,
T Agatonovic-Jovin
T Agatonovic-Jovin
13Institute of Physics, Azerbaijan Academy of Sciences, Baku, Azerbaijan
13,
J Agricola
J Agricola
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
J A Aguilar-Saavedra
J A Aguilar-Saavedra
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
S P Ahlen
S P Ahlen
22Department of Physics Engineering, Gaziantep University, Gaziantep, Turkey
22,
F Ahmadov
F Ahmadov
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
G Aielli
G Aielli
133Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM USA
133,
H Akerstedt
H Akerstedt
146Graduate School of Science, Osaka University, Osaka, Japan
146,
T P A Åkesson
T P A Åkesson
81ZITI Institut für technische Informatik, Ruprecht-Karls-Universität Heidelberg, Mannheim, Germany
81,
A V Akimov
A V Akimov
96Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
96,
G L Alberghi
G L Alberghi
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
J Albert
J Albert
169Dipartimento di Fisica, Sapienza Università di Roma, Roma, Italy
169,
S Albrand
S Albrand
55Dipartimento di Fisica, Università della Calabria, Rende, Italy
55,
M J Alconada Verzini
M J Alconada Verzini
71E. Andronikashvili Institute of Physics, Iv. Javakhishvili Tbilisi State University, Tbilisi, Georgia
71,
M Aleksa
M Aleksa
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
I N Aleksandrov
I N Aleksandrov
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
C Alexa
C Alexa
26Physikalisches Institut, University of Bonn, Bonn, Germany
26,
G Alexander
G Alexander
153INFN Sezione di Pisa, Pisa, Italy
153,
T Alexopoulos
T Alexopoulos
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
M Alhroob
M Alhroob
113Department of Physics, McGill University, Montreal, QC Canada
113,
G Alimonti
G Alimonti
91KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
91,
L Alio
L Alio
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
J Alison
J Alison
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
S P Alkire
S P Alkire
35Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj Napoca, Romania
35,
B M M Allbrooke
B M M Allbrooke
149INFN Sezione di Pavia, Pavia, Italy
149,
P P Allport
P P Allport
74SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
74,
A Aloisio
A Aloisio
104Department of Physics and Astronomy, University College London, London, UK
104,
A Alonso
A Alonso
36University Politehnica Bucharest, Bucharest, Romania
36,
F Alonso
F Alonso
71E. Andronikashvili Institute of Physics, Iv. Javakhishvili Tbilisi State University, Tbilisi, Georgia
71,
C Alpigiani
C Alpigiani
76Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
76,
A Altheimer
A Altheimer
35Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj Napoca, Romania
35,
B Alvarez Gonzalez
B Alvarez Gonzalez
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
D Álvarez Piqueras
D Álvarez Piqueras
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
M G Alviggi
M G Alviggi
104Department of Physics and Astronomy, University College London, London, UK
104,
B T Amadio
B T Amadio
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
K Amako
K Amako
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
Y Amaral Coutinho
Y Amaral Coutinho
24INFN Sezione di Bologna, Bologna, Italy
24,
C Amelung
C Amelung
23Department of Physics, Dogus University, Istanbul, Turkey
23,
D Amidei
D Amidei
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
S P Amor Dos Santos
S P Amor Dos Santos
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
A Amorim
A Amorim
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
S Amoroso
S Amoroso
48School of Physics, Shandong University, Shandong, China
48,
N Amram
N Amram
153INFN Sezione di Pisa, Pisa, Italy
153,
G Amundsen
G Amundsen
23Department of Physics, Dogus University, Istanbul, Turkey
23,
C Anastopoulos
C Anastopoulos
139Ohio State University, Columbus, OH USA
139,
L S Ancu
L S Ancu
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
N Andari
N Andari
108Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
108,
T Andeen
T Andeen
35Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj Napoca, Romania
35,
C F Anders
C F Anders
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
G Anders
G Anders
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
J K Anders
J K Anders
74SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
74,
K J Anderson
K J Anderson
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
A Andreazza
A Andreazza
91KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
91,
V Andrei
V Andrei
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
S Angelidakis
S Angelidakis
9Department of Physics, University of Arizona, Tucson, AZ USA
9,
I Angelozzi
I Angelozzi
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
P Anger
P Anger
44Departamento de Física, Universidad Técnica Federico Santa María, Valparaiso, Chile
44,
A Angerami
A Angerami
35Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj Napoca, Romania
35,
F Anghinolfi
F Anghinolfi
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
A V Anisenkov
A V Anisenkov
109Institut für Physik, Universität Mainz, Mainz, Germany
109,
N Anjos
N Anjos
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
A Annovi
A Annovi
124Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
124,
M Antonelli
M Antonelli
47Department of Physics, Nanjing University, Jiangsu, China
47,
A Antonov
A Antonov
98INFN Sezione di Lecce, Lecce, Italy
98,
J Antos
J Antos
144Center for High Energy Physics, University of Oregon, Eugene, OR USA
144,
F Anulli
F Anulli
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
M Aoki
M Aoki
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
L Aperio Bella
L Aperio Bella
18Department of Physics, Humboldt University, Berlin, Germany
18,
G Arabidze
G Arabidze
90Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
90,
Y Arai
Y Arai
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
J P Araque
J P Araque
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
A T H Arce
A T H Arce
45Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
45,
F A Arduh
F A Arduh
71E. Andronikashvili Institute of Physics, Iv. Javakhishvili Tbilisi State University, Tbilisi, Georgia
71,
J-F Arguin
J-F Arguin
95Department of Physics, Kyushu University, Fukuoka, Japan
95,
S Argyropoulos
S Argyropoulos
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
M Arik
M Arik
19Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
19,
A J Armbruster
A J Armbruster
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
O Arnaez
O Arnaez
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
V Arnal
V Arnal
82Faculty of Applied Information Science, Hiroshima Institute of Technology, Hiroshima, Japan
82,
H Arnold
H Arnold
48School of Physics, Shandong University, Shandong, China
48,
M Arratia
M Arratia
28Department of Physics, Brandeis University, Waltham, MA USA
28,
O Arslan
O Arslan
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
A Artamonov
A Artamonov
97Physics Department, Lancaster University, Lancaster, UK
97,
G Artoni
G Artoni
23Department of Physics, Dogus University, Istanbul, Turkey
23,
S Asai
S Asai
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
N Asbah
N Asbah
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
A Ashkenazi
A Ashkenazi
153INFN Sezione di Pisa, Pisa, Italy
153,
B Åsman
B Åsman
146Graduate School of Science, Osaka University, Osaka, Japan
146,
L Asquith
L Asquith
149INFN Sezione di Pavia, Pavia, Italy
149,
K Assamagan
K Assamagan
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
R Astalos
R Astalos
144Center for High Energy Physics, University of Oregon, Eugene, OR USA
144,
M Atkinson
M Atkinson
165Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
165,
N B Atlay
N B Atlay
141Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK USA
141,
K Augsten
K Augsten
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
M Aurousseau
M Aurousseau
145LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
145,
G Avolio
G Avolio
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
B Axen
B Axen
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
M K Ayoub
M K Ayoub
117INFN Sezione di Milano, Milano, Italy
117,
G Azuelos
G Azuelos
95Department of Physics, Kyushu University, Fukuoka, Japan
95,
M A Baak
M A Baak
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
A E Baas
A E Baas
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
M J Baca
M J Baca
18Department of Physics, Humboldt University, Berlin, Germany
18,
C Bacci
C Bacci
134Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
134,
H Bachacou
H Bachacou
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
K Bachas
K Bachas
154Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
154,
M Backes
M Backes
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
M Backhaus
M Backhaus
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
P Bagiacchi
P Bagiacchi
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
P Bagnaia
P Bagnaia
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
Y Bai
Y Bai
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
T Bain
T Bain
35Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj Napoca, Romania
35,
J T Baines
J T Baines
131INFN Sezione di Napoli, Naples, Italy
131,
O K Baker
O K Baker
176Faculté des Sciences Semlalia, Université Cadi Ayyad, LPHEA-Marrakech, Marrakech, Morocco
176,
E M Baldin
E M Baldin
109Institut für Physik, Universität Mainz, Mainz, Germany
109,
P Balek
P Balek
129Nagasaki Institute of Applied Science, Nagasaki, Japan
129,
T Balestri
T Balestri
148Department of Physics, Oxford University, Oxford, UK
148,
F Balli
F Balli
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
E Banas
E Banas
39Cavendish Laboratory, University of Cambridge, Cambridge, UK
39,
Sw Banerjee
Sw Banerjee
173Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
173,
A A E Bannoura
A A E Bannoura
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
H S Bansil
H S Bansil
18Department of Physics, Humboldt University, Berlin, Germany
18,
L Barak
L Barak
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
E L Barberio
E L Barberio
88University of Iowa, Iowa City, IA USA
88,
D Barberis
D Barberis
50Physics Department, Tsinghua University, Beijing, 100084 China
50,
M Barbero
M Barbero
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
T Barillari
T Barillari
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
M Barisonzi
M Barisonzi
164Czech Technical University in Praha, Praha, Czech Republic
164,
T Barklow
T Barklow
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
N Barlow
N Barlow
28Department of Physics, Brandeis University, Waltham, MA USA
28,
S L Barnes
S L Barnes
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
B M Barnett
B M Barnett
131INFN Sezione di Napoli, Naples, Italy
131,
R M Barnett
R M Barnett
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
Z Barnovska
Z Barnovska
5Istanbul Aydin University, Istanbul, Turkey
5,
A Baroncelli
A Baroncelli
134Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
134,
G Barone
G Barone
23Department of Physics, Dogus University, Istanbul, Turkey
23,
A J Barr
A J Barr
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
F Barreiro
F Barreiro
82Faculty of Applied Information Science, Hiroshima Institute of Technology, Hiroshima, Japan
82,
J Barreiro Guimarães da Costa
J Barreiro Guimarães da Costa
57Marian Smoluchowski Institute of Physics, Jagiellonian University, Kraków, Poland
57,
R Bartoldus
R Bartoldus
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
A E Barton
A E Barton
72High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
72,
P Bartos
P Bartos
144Center for High Energy Physics, University of Oregon, Eugene, OR USA
144,
A Basalaev
A Basalaev
123P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
123,
A Bassalat
A Bassalat
117INFN Sezione di Milano, Milano, Italy
117,
A Basye
A Basye
165Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
165,
R L Bates
R L Bates
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
S J Batista
S J Batista
158Department of Physics, University of Coimbra, Coimbra, Portugal
158,
J R Batley
J R Batley
28Department of Physics, Brandeis University, Waltham, MA USA
28,
M Battaglia
M Battaglia
137Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
137,
M Bauce
M Bauce
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
F Bauer
F Bauer
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
H S Bawa
H S Bawa
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
J B Beacham
J B Beacham
111CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
111,
M D Beattie
M D Beattie
72High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
72,
T Beau
T Beau
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
P H Beauchemin
P H Beauchemin
161Departamento de Fisica Teorica y del Cosmos and CAFPE, Universidad de Granada, Granada, Spain
161,
R Beccherle
R Beccherle
124Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
124,
P Bechtle
P Bechtle
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
H P Beck
H P Beck
17Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA USA
17,
K Becker
K Becker
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
M Becker
M Becker
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
S Becker
S Becker
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
M Beckingham
M Beckingham
170INFN Sezione di Roma Tor Vergata, Roma, Italy
170,
C Becot
C Becot
117INFN Sezione di Milano, Milano, Italy
117,
A J Beddall
A J Beddall
19Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
19,
A Beddall
A Beddall
19Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
19,
V A Bednyakov
V A Bednyakov
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
C P Bee
C P Bee
148Department of Physics, Oxford University, Oxford, UK
148,
L J Beemster
L J Beemster
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
T A Beermann
T A Beermann
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
M Begel
M Begel
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
J K Behr
J K Behr
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
C Belanger-Champagne
C Belanger-Champagne
87Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
87,
W H Bell
W H Bell
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
G Bella
G Bella
153INFN Sezione di Pisa, Pisa, Italy
153,
L Bellagamba
L Bellagamba
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
A Bellerive
A Bellerive
29Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
29,
M Bellomo
M Bellomo
86Department of Physics, Indiana University, Bloomington, IN USA
86,
K Belotskiy
K Belotskiy
98INFN Sezione di Lecce, Lecce, Italy
98,
O Beltramello
O Beltramello
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
O Benary
O Benary
153INFN Sezione di Pisa, Pisa, Italy
153,
D Benchekroun
D Benchekroun
135Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
135,
M Bender
M Bender
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
K Bendtz
K Bendtz
146Graduate School of Science, Osaka University, Osaka, Japan
146,
N Benekos
N Benekos
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
Y Benhammou
Y Benhammou
153INFN Sezione di Pisa, Pisa, Italy
153,
E Benhar Noccioli
E Benhar Noccioli
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
J A Benitez Garcia
J A Benitez Garcia
159Centro de Física Nuclear da Universidade de Lisboa, Lisboa, Portugal
159,
D P Benjamin
D P Benjamin
45Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
45,
J R Bensinger
J R Bensinger
23Department of Physics, Dogus University, Istanbul, Turkey
23,
S Bentvelsen
S Bentvelsen
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
L Beresford
L Beresford
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
M Beretta
M Beretta
47Department of Physics, Nanjing University, Jiangsu, China
47,
D Berge
D Berge
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
E Bergeaas Kuutmann
E Bergeaas Kuutmann
166State Research Center Institute for High Energy Physics, Protvino, Russia
166,
N Berger
N Berger
5Istanbul Aydin University, Istanbul, Turkey
5,
F Berghaus
F Berghaus
169Dipartimento di Fisica, Sapienza Università di Roma, Roma, Italy
169,
J Beringer
J Beringer
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
C Bernard
C Bernard
22Department of Physics Engineering, Gaziantep University, Gaziantep, Turkey
22,
N R Bernard
N R Bernard
86Department of Physics, Indiana University, Bloomington, IN USA
86,
C Bernius
C Bernius
110School of Physics and Astronomy, University of Manchester, Manchester, UK
110,
F U Bernlochner
F U Bernlochner
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
T Berry
T Berry
77Department of Physics, Hampton University, Hampton, VA USA
77,
P Berta
P Berta
129Nagasaki Institute of Applied Science, Nagasaki, Japan
129,
C Bertella
C Bertella
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
G Bertoli
G Bertoli
146Graduate School of Science, Osaka University, Osaka, Japan
146,
F Bertolucci
F Bertolucci
124Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
124,
C Bertsche
C Bertsche
113Department of Physics, McGill University, Montreal, QC Canada
113,
D Bertsche
D Bertsche
113Department of Physics, McGill University, Montreal, QC Canada
113,
M I Besana
M I Besana
91KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
91,
G J Besjes
G J Besjes
36University Politehnica Bucharest, Bucharest, Romania
36,
O Bessidskaia Bylund
O Bessidskaia Bylund
146Graduate School of Science, Osaka University, Osaka, Japan
146,
M Bessner
M Bessner
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
N Besson
N Besson
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
C Betancourt
C Betancourt
48School of Physics, Shandong University, Shandong, China
48,
S Bethke
S Bethke
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
A J Bevan
A J Bevan
76Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
76,
W Bhimji
W Bhimji
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
R M Bianchi
R M Bianchi
125National Research Nuclear University MEPhI, Moscow, Russia
125,
L Bianchini
L Bianchini
23Department of Physics, Dogus University, Istanbul, Turkey
23,
M Bianco
M Bianco
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
O Biebel
O Biebel
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
D Biedermann
D Biedermann
16Department for Physics and Technology, University of Bergen, Bergen, Norway
16,
S P Bieniek
S P Bieniek
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
M Biglietti
M Biglietti
134Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
134,
J Bilbao De Mendizabal
J Bilbao De Mendizabal
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
H Bilokon
H Bilokon
47Department of Physics, Nanjing University, Jiangsu, China
47,
M Bindi
M Bindi
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
S Binet
S Binet
117INFN Sezione di Milano, Milano, Italy
117,
A Bingul
A Bingul
19Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
19,
C Bini
C Bini
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
S Biondi
S Biondi
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
C W Black
C W Black
150Dipartimento di Fisica, Università di Pavia, Pavia, Italy
150,
J E Black
J E Black
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
K M Black
K M Black
22Department of Physics Engineering, Gaziantep University, Gaziantep, Turkey
22,
D Blackburn
D Blackburn
138Department of Physics, New York University, New York, NY USA
138,
R E Blair
R E Blair
6Division of Physics, TOBB University of Economics and Technology, Ankara, Turkey
6,
J-B Blanchard
J-B Blanchard
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
J E Blanco
J E Blanco
77Department of Physics, Hampton University, Hampton, VA USA
77,
T Blazek
T Blazek
144Center for High Energy Physics, University of Oregon, Eugene, OR USA
144,
I Bloch
I Bloch
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
C Blocker
C Blocker
23Department of Physics, Dogus University, Istanbul, Turkey
23,
W Blum
W Blum
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
U Blumenschein
U Blumenschein
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
G J Bobbink
G J Bobbink
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
V S Bobrovnikov
V S Bobrovnikov
109Institut für Physik, Universität Mainz, Mainz, Germany
109,
S S Bocchetta
S S Bocchetta
81ZITI Institut für technische Informatik, Ruprecht-Karls-Universität Heidelberg, Mannheim, Germany
81,
A Bocci
A Bocci
45Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
45,
C Bock
C Bock
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
M Boehler
M Boehler
48School of Physics, Shandong University, Shandong, China
48,
J A Bogaerts
J A Bogaerts
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
D Bogavac
D Bogavac
13Institute of Physics, Azerbaijan Academy of Sciences, Baku, Azerbaijan
13,
A G Bogdanchikov
A G Bogdanchikov
109Institut für Physik, Universität Mainz, Mainz, Germany
109,
C Bohm
C Bohm
146Graduate School of Science, Osaka University, Osaka, Japan
146,
V Boisvert
V Boisvert
77Department of Physics, Hampton University, Hampton, VA USA
77,
T Bold
T Bold
38Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
38,
V Boldea
V Boldea
26Physikalisches Institut, University of Bonn, Bonn, Germany
26,
A S Boldyrev
A S Boldyrev
99Dipartimento di Matematica e Fisica, Università del Salento, Lecce, Italy
99,
M Bomben
M Bomben
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
M Bona
M Bona
76Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
76,
M Boonekamp
M Boonekamp
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
A Borisov
A Borisov
130Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
130,
G Borissov
G Borissov
72High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
72,
S Borroni
S Borroni
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
J Bortfeldt
J Bortfeldt
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
V Bortolotto
V Bortolotto
60Physics Department, University of Texas at Dallas, Richardson, TX USA
60,
K Bos
K Bos
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
D Boscherini
D Boscherini
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
M Bosman
M Bosman
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
J Boudreau
J Boudreau
125National Research Nuclear University MEPhI, Moscow, Russia
125,
J Bouffard
J Bouffard
2Physics Department, SUNY Albany, Albany, NY USA
2,
E V Bouhova-Thacker
E V Bouhova-Thacker
72High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
72,
D Boumediene
D Boumediene
34National Institute of Physics and Nuclear Engineering, Bucharest, Romania
34,
C Bourdarios
C Bourdarios
117INFN Sezione di Milano, Milano, Italy
117,
N Bousson
N Bousson
114School of Physics, University of Melbourne, Melbourne, VIC Australia
114,
A Boveia
A Boveia
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
J Boyd
J Boyd
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
I R Boyko
I R Boyko
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
I Bozic
I Bozic
13Institute of Physics, Azerbaijan Academy of Sciences, Baku, Azerbaijan
13,
J Bracinik
J Bracinik
18Department of Physics, Humboldt University, Berlin, Germany
18,
A Brandt
A Brandt
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
G Brandt
G Brandt
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
O Brandt
O Brandt
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
U Bratzler
U Bratzler
156Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisboa, Portugal
156,
B Brau
B Brau
86Department of Physics, Indiana University, Bloomington, IN USA
86,
J E Brau
J E Brau
116Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
116,
H M Braun
H M Braun
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
S F Brazzale
S F Brazzale
164Czech Technical University in Praha, Praha, Czech Republic
164,
W D Breaden Madden
W D Breaden Madden
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
K Brendlinger
K Brendlinger
122Group of Particle Physics, University of Montreal, Montreal, QC Canada
122,
A J Brennan
A J Brennan
88University of Iowa, Iowa City, IA USA
88,
L Brenner
L Brenner
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
R Brenner
R Brenner
166State Research Center Institute for High Energy Physics, Protvino, Russia
166,
S Bressler
S Bressler
172INFN Sezione di Roma Tre, Roma, Italy
172,
K Bristow
K Bristow
145LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
145,
T M Bristow
T M Bristow
46Department of Modern Physics, University of Science and Technology of China, Anhui, China
46,
D Britton
D Britton
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
D Britzger
D Britzger
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
F M Brochu
F M Brochu
28Department of Physics, Brandeis University, Waltham, MA USA
28,
I Brock
I Brock
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
R Brock
R Brock
90Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
90,
J Bronner
J Bronner
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
G Brooijmans
G Brooijmans
35Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj Napoca, Romania
35,
T Brooks
T Brooks
77Department of Physics, Hampton University, Hampton, VA USA
77,
W K Brooks
W K Brooks
32Instituto de Fisica, Universidade de Sao Paulo, São Paulo, Brazil
32,
J Brosamer
J Brosamer
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
E Brost
E Brost
116Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
116,
J Brown
J Brown
55Dipartimento di Fisica, Università della Calabria, Rende, Italy
55,
P A Bruckman de Renstrom
P A Bruckman de Renstrom
39Cavendish Laboratory, University of Cambridge, Cambridge, UK
39,
D Bruncko
D Bruncko
144Center for High Energy Physics, University of Oregon, Eugene, OR USA
144,
R Bruneliere
R Bruneliere
48School of Physics, Shandong University, Shandong, China
48,
A Bruni
A Bruni
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
G Bruni
G Bruni
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
M Bruschi
M Bruschi
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
N Bruscino
N Bruscino
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
L Bryngemark
L Bryngemark
81ZITI Institut für technische Informatik, Ruprecht-Karls-Universität Heidelberg, Mannheim, Germany
81,
T Buanes
T Buanes
14Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
14,
Q Buat
Q Buat
142Department of Physics, Oklahoma State University, Stillwater, OK USA
142,
P Buchholz
P Buchholz
141Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK USA
141,
A G Buckley
A G Buckley
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
S I Buda
S I Buda
26Physikalisches Institut, University of Bonn, Bonn, Germany
26,
I A Budagov
I A Budagov
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
F Buehrer
F Buehrer
48School of Physics, Shandong University, Shandong, China
48,
L Bugge
L Bugge
119B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
119,
M K Bugge
M K Bugge
119B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
119,
O Bulekov
O Bulekov
98INFN Sezione di Lecce, Lecce, Italy
98,
D Bullock
D Bullock
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
H Burckhart
H Burckhart
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
S Burdin
S Burdin
74SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
74,
C D Burgard
C D Burgard
48School of Physics, Shandong University, Shandong, China
48,
B Burghgrave
B Burghgrave
108Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
108,
S Burke
S Burke
131INFN Sezione di Napoli, Naples, Italy
131,
I Burmeister
I Burmeister
43Departamento de Física, Pontificia Universidad Católica de Chile, Santiago, Chile
43,
E Busato
E Busato
34National Institute of Physics and Nuclear Engineering, Bucharest, Romania
34,
D Büscher
D Büscher
48School of Physics, Shandong University, Shandong, China
48,
V Büscher
V Büscher
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
P Bussey
P Bussey
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
J M Butler
J M Butler
22Department of Physics Engineering, Gaziantep University, Gaziantep, Turkey
22,
A I Butt
A I Butt
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
C M Buttar
C M Buttar
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
J M Butterworth
J M Butterworth
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
P Butti
P Butti
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
W Buttinger
W Buttinger
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
A Buzatu
A Buzatu
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
A R Buzykaev
A R Buzykaev
109Institut für Physik, Universität Mainz, Mainz, Germany
109,
S Cabrera Urbán
S Cabrera Urbán
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
D Caforio
D Caforio
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
V M Cairo
V M Cairo
37West University in Timisoara, Timisoara, Romania
37,
O Cakir
O Cakir
4Department of Physics, Ankara University, Ankara, Turkey
4,
N Calace
N Calace
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
P Calafiura
P Calafiura
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
A Calandri
A Calandri
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
G Calderini
G Calderini
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
P Calfayan
P Calfayan
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
L P Caloba
L P Caloba
24INFN Sezione di Bologna, Bologna, Italy
24,
D Calvet
D Calvet
34National Institute of Physics and Nuclear Engineering, Bucharest, Romania
34,
S Calvet
S Calvet
34National Institute of Physics and Nuclear Engineering, Bucharest, Romania
34,
R Camacho Toro
R Camacho Toro
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
S Camarda
S Camarda
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
P Camarri
P Camarri
133Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM USA
133,
D Cameron
D Cameron
119B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
119,
R Caminal Armadans
R Caminal Armadans
165Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
165,
S Campana
S Campana
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
M Campanelli
M Campanelli
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
A Campoverde
A Campoverde
148Department of Physics, Oxford University, Oxford, UK
148,
V Canale
V Canale
104Department of Physics and Astronomy, University College London, London, UK
104,
A Canepa
A Canepa
159Centro de Física Nuclear da Universidade de Lisboa, Lisboa, Portugal
159,
M Cano Bret
M Cano Bret
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
J Cantero
J Cantero
82Faculty of Applied Information Science, Hiroshima Institute of Technology, Hiroshima, Japan
82,
R Cantrill
R Cantrill
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
T Cao
T Cao
40Department of Physics, Carleton University, Ottawa, ON Canada
40,
M D M Capeans Garrido
M D M Capeans Garrido
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
I Caprini
I Caprini
26Physikalisches Institut, University of Bonn, Bonn, Germany
26,
M Caprini
M Caprini
26Physikalisches Institut, University of Bonn, Bonn, Germany
26,
M Capua
M Capua
37West University in Timisoara, Timisoara, Romania
37,
R Caputo
R Caputo
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
R Cardarelli
R Cardarelli
133Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM USA
133,
F Cardillo
F Cardillo
48School of Physics, Shandong University, Shandong, China
48,
T Carli
T Carli
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
G Carlino
G Carlino
104Department of Physics and Astronomy, University College London, London, UK
104,
L Carminati
L Carminati
91KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
91,
S Caron
S Caron
106Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
106,
E Carquin
E Carquin
32Instituto de Fisica, Universidade de Sao Paulo, São Paulo, Brazil
32,
G D Carrillo-Montoya
G D Carrillo-Montoya
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
J R Carter
J R Carter
28Department of Physics, Brandeis University, Waltham, MA USA
28,
J Carvalho
J Carvalho
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
D Casadei
D Casadei
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
M P Casado
M P Casado
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
M Casolino
M Casolino
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
E Castaneda-Miranda
E Castaneda-Miranda
145LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
145,
A Castelli
A Castelli
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
V Castillo Gimenez
V Castillo Gimenez
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
N F Castro
N F Castro
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
P Catastini
P Catastini
57Marian Smoluchowski Institute of Physics, Jagiellonian University, Kraków, Poland
57,
A Catinaccio
A Catinaccio
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
J R Catmore
J R Catmore
119B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
119,
A Cattai
A Cattai
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
J Caudron
J Caudron
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
V Cavaliere
V Cavaliere
165Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
165,
D Cavalli
D Cavalli
91KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
91,
M Cavalli-Sforza
M Cavalli-Sforza
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
V Cavasinni
V Cavasinni
124Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
124,
F Ceradini
F Ceradini
134Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
134,
B C Cerio
B C Cerio
45Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
45,
K Cerny
K Cerny
129Nagasaki Institute of Applied Science, Nagasaki, Japan
129,
A S Cerqueira
A S Cerqueira
24INFN Sezione di Bologna, Bologna, Italy
24,
A Cerri
A Cerri
149INFN Sezione di Pavia, Pavia, Italy
149,
L Cerrito
L Cerrito
76Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
76,
F Cerutti
F Cerutti
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
M Cerv
M Cerv
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
A Cervelli
A Cervelli
17Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA USA
17,
S A Cetin
S A Cetin
19Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
19,
A Chafaq
A Chafaq
135Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
135,
D Chakraborty
D Chakraborty
108Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
108,
I Chalupkova
I Chalupkova
129Nagasaki Institute of Applied Science, Nagasaki, Japan
129,
P Chang
P Chang
165Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
165,
J D Chapman
J D Chapman
28Department of Physics, Brandeis University, Waltham, MA USA
28,
D G Charlton
D G Charlton
18Department of Physics, Humboldt University, Berlin, Germany
18,
C C Chau
C C Chau
158Department of Physics, University of Coimbra, Coimbra, Portugal
158,
C A Chavez Barajas
C A Chavez Barajas
149INFN Sezione di Pavia, Pavia, Italy
149,
S Cheatham
S Cheatham
152National Research Centre ‘Kurchatov Institute’ B.P.Konstantinov Petersburg Nuclear Physics Institute, St. Petersburg, Russia
152,
A Chegwidden
A Chegwidden
90Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
90,
S Chekanov
S Chekanov
6Division of Physics, TOBB University of Economics and Technology, Ankara, Turkey
6,
S V Chekulaev
S V Chekulaev
159Centro de Física Nuclear da Universidade de Lisboa, Lisboa, Portugal
159,
G A Chelkov
G A Chelkov
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
M A Chelstowska
M A Chelstowska
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
C Chen
C Chen
64Department of Physics, Duke University, Durham, NC USA
64,
H Chen
H Chen
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
K Chen
K Chen
148Department of Physics, Oxford University, Oxford, UK
148,
L Chen
L Chen
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
S Chen
S Chen
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
X Chen
X Chen
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
Y Chen
Y Chen
67Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
67,
H C Cheng
H C Cheng
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
Y Cheng
Y Cheng
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
A Cheplakov
A Cheplakov
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
E Cheremushkina
E Cheremushkina
130Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
130,
R Cherkaoui El Moursli
R Cherkaoui El Moursli
135Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
135,
V Chernyatin
V Chernyatin
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
E Cheu
E Cheu
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
L Chevalier
L Chevalier
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
V Chiarella
V Chiarella
47Department of Physics, Nanjing University, Jiangsu, China
47,
G Chiarelli
G Chiarelli
124Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
124,
G Chiodini
G Chiodini
73II Physikalisches Institut, Justus-Liebig-Universität Giessen, Giessen, Germany
73,
A S Chisholm
A S Chisholm
18Department of Physics, Humboldt University, Berlin, Germany
18,
R T Chislett
R T Chislett
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
A Chitan
A Chitan
26Physikalisches Institut, University of Bonn, Bonn, Germany
26,
M V Chizhov
M V Chizhov
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
K Choi
K Choi
61DESY, Hamburg and Zeuthen, Germany
61,
S Chouridou
S Chouridou
9Department of Physics, University of Arizona, Tucson, AZ USA
9,
B K B Chow
B K B Chow
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
V Christodoulou
V Christodoulou
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
D Chromek-Burckhart
D Chromek-Burckhart
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
J Chudoba
J Chudoba
127Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
127,
A J Chuinard
A J Chuinard
87Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
87,
J J Chwastowski
J J Chwastowski
39Cavendish Laboratory, University of Cambridge, Cambridge, UK
39,
L Chytka
L Chytka
115Department of Physics, The University of Michigan, Ann Arbor, MI USA
115,
G Ciapetti
G Ciapetti
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
A K Ciftci
A K Ciftci
4Department of Physics, Ankara University, Ankara, Turkey
4,
D Cinca
D Cinca
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
V Cindro
V Cindro
75II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
75,
I A Cioara
I A Cioara
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
A Ciocio
A Ciocio
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
F Cirotto
F Cirotto
104Department of Physics and Astronomy, University College London, London, UK
104,
Z H Citron
Z H Citron
172INFN Sezione di Roma Tre, Roma, Italy
172,
M Ciubancan
M Ciubancan
26Physikalisches Institut, University of Bonn, Bonn, Germany
26,
A Clark
A Clark
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
B L Clark
B L Clark
57Marian Smoluchowski Institute of Physics, Jagiellonian University, Kraków, Poland
57,
P J Clark
P J Clark
46Department of Modern Physics, University of Science and Technology of China, Anhui, China
46,
R N Clarke
R N Clarke
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
W Cleland
W Cleland
125National Research Nuclear University MEPhI, Moscow, Russia
125,
C Clement
C Clement
146Graduate School of Science, Osaka University, Osaka, Japan
146,
Y Coadou
Y Coadou
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
M Cobal
M Cobal
164Czech Technical University in Praha, Praha, Czech Republic
164,
A Coccaro
A Coccaro
138Department of Physics, New York University, New York, NY USA
138,
J Cochran
J Cochran
64Department of Physics, Duke University, Durham, NC USA
64,
L Coffey
L Coffey
23Department of Physics, Dogus University, Istanbul, Turkey
23,
J G Cogan
J G Cogan
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
L Colasurdo
L Colasurdo
106Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
106,
B Cole
B Cole
35Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj Napoca, Romania
35,
S Cole
S Cole
108Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
108,
A P Colijn
A P Colijn
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
J Collot
J Collot
55Dipartimento di Fisica, Università della Calabria, Rende, Italy
55,
T Colombo
T Colombo
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
G Compostella
G Compostella
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
P Conde Muiño
P Conde Muiño
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
E Coniavitis
E Coniavitis
48School of Physics, Shandong University, Shandong, China
48,
S H Connell
S H Connell
145LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
145,
I A Connelly
I A Connelly
77Department of Physics, Hampton University, Hampton, VA USA
77,
V Consorti
V Consorti
48School of Physics, Shandong University, Shandong, China
48,
S Constantinescu
S Constantinescu
26Physikalisches Institut, University of Bonn, Bonn, Germany
26,
C Conta
C Conta
121Department of Physics, Massachusetts Institute of Technology, Cambridge, MA USA
121,
G Conti
G Conti
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
F Conventi
F Conventi
104Department of Physics and Astronomy, University College London, London, UK
104,
M Cooke
M Cooke
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
B D Cooper
B D Cooper
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
A M Cooper-Sarkar
A M Cooper-Sarkar
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
T Cornelissen
T Cornelissen
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
M Corradi
M Corradi
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
F Corriveau
F Corriveau
87Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
87,
A Corso-Radu
A Corso-Radu
163Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
163,
A Cortes-Gonzalez
A Cortes-Gonzalez
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
G Cortiana
G Cortiana
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
G Costa
G Costa
91KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
91,
M J Costa
M J Costa
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
D Costanzo
D Costanzo
139Ohio State University, Columbus, OH USA
139,
D Côté
D Côté
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
G Cottin
G Cottin
28Department of Physics, Brandeis University, Waltham, MA USA
28,
G Cowan
G Cowan
77Department of Physics, Hampton University, Hampton, VA USA
77,
B E Cox
B E Cox
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
K Cranmer
K Cranmer
110School of Physics and Astronomy, University of Manchester, Manchester, UK
110,
G Cree
G Cree
29Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
29,
S Crépé-Renaudin
S Crépé-Renaudin
55Dipartimento di Fisica, Università della Calabria, Rende, Italy
55,
F Crescioli
F Crescioli
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
W A Cribbs
W A Cribbs
146Graduate School of Science, Osaka University, Osaka, Japan
146,
M Crispin Ortuzar
M Crispin Ortuzar
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
M Cristinziani
M Cristinziani
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
V Croft
V Croft
106Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
106,
G Crosetti
G Crosetti
37West University in Timisoara, Timisoara, Romania
37,
T Cuhadar Donszelmann
T Cuhadar Donszelmann
139Ohio State University, Columbus, OH USA
139,
J Cummings
J Cummings
176Faculté des Sciences Semlalia, Université Cadi Ayyad, LPHEA-Marrakech, Marrakech, Morocco
176,
M Curatolo
M Curatolo
47Department of Physics, Nanjing University, Jiangsu, China
47,
C Cuthbert
C Cuthbert
150Dipartimento di Fisica, Università di Pavia, Pavia, Italy
150,
H Czirr
H Czirr
141Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK USA
141,
P Czodrowski
P Czodrowski
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
S D’Auria
S D’Auria
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
M D’Onofrio
M D’Onofrio
74SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
74,
M J Da Cunha Sargedas De Sousa
M J Da Cunha Sargedas De Sousa
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
C Da Via
C Da Via
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
W Dabrowski
W Dabrowski
38Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
38,
A Dafinca
A Dafinca
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
T Dai
T Dai
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
O Dale
O Dale
14Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
14,
F Dallaire
F Dallaire
95Department of Physics, Kyushu University, Fukuoka, Japan
95,
C Dallapiccola
C Dallapiccola
86Department of Physics, Indiana University, Bloomington, IN USA
86,
M Dam
M Dam
36University Politehnica Bucharest, Bucharest, Romania
36,
J R Dandoy
J R Dandoy
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
N P Dang
N P Dang
48School of Physics, Shandong University, Shandong, China
48,
A C Daniells
A C Daniells
18Department of Physics, Humboldt University, Berlin, Germany
18,
M Danninger
M Danninger
168INFN Sezione di Roma, Roma, Italy
168,
M Dano Hoffmann
M Dano Hoffmann
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
V Dao
V Dao
48School of Physics, Shandong University, Shandong, China
48,
G Darbo
G Darbo
50Physics Department, Tsinghua University, Beijing, 100084 China
50,
S Darmora
S Darmora
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
J Dassoulas
J Dassoulas
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
A Dattagupta
A Dattagupta
61DESY, Hamburg and Zeuthen, Germany
61,
W Davey
W Davey
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
C David
C David
169Dipartimento di Fisica, Sapienza Università di Roma, Roma, Italy
169,
T Davidek
T Davidek
129Nagasaki Institute of Applied Science, Nagasaki, Japan
129,
E Davies
E Davies
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
M Davies
M Davies
153INFN Sezione di Pisa, Pisa, Italy
153,
P Davison
P Davison
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
Y Davygora
Y Davygora
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
E Dawe
E Dawe
88University of Iowa, Iowa City, IA USA
88,
I Dawson
I Dawson
139Ohio State University, Columbus, OH USA
139,
R K Daya-Ishmukhametova
R K Daya-Ishmukhametova
86Department of Physics, Indiana University, Bloomington, IN USA
86,
K De
K De
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
R de Asmundis
R de Asmundis
104Department of Physics and Astronomy, University College London, London, UK
104,
A De Benedetti
A De Benedetti
113Department of Physics, McGill University, Montreal, QC Canada
113,
S De Castro
S De Castro
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
S De Cecco
S De Cecco
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
N De Groot
N De Groot
106Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
106,
P de Jong
P de Jong
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
H De la Torre
H De la Torre
82Faculty of Applied Information Science, Hiroshima Institute of Technology, Hiroshima, Japan
82,
F De Lorenzi
F De Lorenzi
64Department of Physics, Duke University, Durham, NC USA
64,
D De Pedis
D De Pedis
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
A De Salvo
A De Salvo
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
U De Sanctis
U De Sanctis
149INFN Sezione di Pavia, Pavia, Italy
149,
A De Santo
A De Santo
149INFN Sezione di Pavia, Pavia, Italy
149,
J B De Vivie De Regie
J B De Vivie De Regie
117INFN Sezione di Milano, Milano, Italy
117,
W J Dearnaley
W J Dearnaley
72High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
72,
R Debbe
R Debbe
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
C Debenedetti
C Debenedetti
137Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
137,
D V Dedovich
D V Dedovich
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
I Deigaard
I Deigaard
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
J Del Peso
J Del Peso
82Faculty of Applied Information Science, Hiroshima Institute of Technology, Hiroshima, Japan
82,
T Del Prete
T Del Prete
124Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
124,
D Delgove
D Delgove
117INFN Sezione di Milano, Milano, Italy
117,
F Deliot
F Deliot
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
C M Delitzsch
C M Delitzsch
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
M Deliyergiyev
M Deliyergiyev
75II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
75,
A Dell’Acqua
A Dell’Acqua
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
L Dell’Asta
L Dell’Asta
22Department of Physics Engineering, Gaziantep University, Gaziantep, Turkey
22,
M Dell’Orso
M Dell’Orso
124Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
124,
M Della Pietra
M Della Pietra
104Department of Physics and Astronomy, University College London, London, UK
104,
D della Volpe
D della Volpe
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
M Delmastro
M Delmastro
5Istanbul Aydin University, Istanbul, Turkey
5,
P A Delsart
P A Delsart
55Dipartimento di Fisica, Università della Calabria, Rende, Italy
55,
C Deluca
C Deluca
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
D A DeMarco
D A DeMarco
158Department of Physics, University of Coimbra, Coimbra, Portugal
158,
S Demers
S Demers
176Faculté des Sciences Semlalia, Université Cadi Ayyad, LPHEA-Marrakech, Marrakech, Morocco
176,
M Demichev
M Demichev
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
A Demilly
A Demilly
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
S P Denisov
S P Denisov
130Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
130,
D Derendarz
D Derendarz
39Cavendish Laboratory, University of Cambridge, Cambridge, UK
39,
J E Derkaoui
J E Derkaoui
135Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
135,
F Derue
F Derue
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
P Dervan
P Dervan
74SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
74,
K Desch
K Desch
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
C Deterre
C Deterre
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
P O Deviveiros
P O Deviveiros
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
A Dewhurst
A Dewhurst
131INFN Sezione di Napoli, Naples, Italy
131,
S Dhaliwal
S Dhaliwal
23Department of Physics, Dogus University, Istanbul, Turkey
23,
A Di Ciaccio
A Di Ciaccio
133Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM USA
133,
L Di Ciaccio
L Di Ciaccio
5Istanbul Aydin University, Istanbul, Turkey
5,
A Di Domenico
A Di Domenico
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
C Di Donato
C Di Donato
104Department of Physics and Astronomy, University College London, London, UK
104,
A Di Girolamo
A Di Girolamo
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
B Di Girolamo
B Di Girolamo
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
A Di Mattia
A Di Mattia
152National Research Centre ‘Kurchatov Institute’ B.P.Konstantinov Petersburg Nuclear Physics Institute, St. Petersburg, Russia
152,
B Di Micco
B Di Micco
134Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
134,
R Di Nardo
R Di Nardo
47Department of Physics, Nanjing University, Jiangsu, China
47,
A Di Simone
A Di Simone
48School of Physics, Shandong University, Shandong, China
48,
R Di Sipio
R Di Sipio
158Department of Physics, University of Coimbra, Coimbra, Portugal
158,
D Di Valentino
D Di Valentino
29Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
29,
C Diaconu
C Diaconu
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
M Diamond
M Diamond
158Department of Physics, University of Coimbra, Coimbra, Portugal
158,
F A Dias
F A Dias
46Department of Modern Physics, University of Science and Technology of China, Anhui, China
46,
M A Diaz
M A Diaz
32Instituto de Fisica, Universidade de Sao Paulo, São Paulo, Brazil
32,
E B Diehl
E B Diehl
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
J Dietrich
J Dietrich
16Department for Physics and Technology, University of Bergen, Bergen, Norway
16,
S Diglio
S Diglio
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
A Dimitrievska
A Dimitrievska
13Institute of Physics, Azerbaijan Academy of Sciences, Baku, Azerbaijan
13,
J Dingfelder
J Dingfelder
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
P Dita
P Dita
26Physikalisches Institut, University of Bonn, Bonn, Germany
26,
S Dita
S Dita
26Physikalisches Institut, University of Bonn, Bonn, Germany
26,
F Dittus
F Dittus
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
F Djama
F Djama
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
T Djobava
T Djobava
51Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
51,
J I Djuvsland
J I Djuvsland
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
M A B do Vale
M A B do Vale
24INFN Sezione di Bologna, Bologna, Italy
24,
D Dobos
D Dobos
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
M Dobre
M Dobre
26Physikalisches Institut, University of Bonn, Bonn, Germany
26,
C Doglioni
C Doglioni
81ZITI Institut für technische Informatik, Ruprecht-Karls-Universität Heidelberg, Mannheim, Germany
81,
T Dohmae
T Dohmae
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
J Dolejsi
J Dolejsi
129Nagasaki Institute of Applied Science, Nagasaki, Japan
129,
Z Dolezal
Z Dolezal
129Nagasaki Institute of Applied Science, Nagasaki, Japan
129,
B A Dolgoshein
B A Dolgoshein
98INFN Sezione di Lecce, Lecce, Italy
98,
M Donadelli
M Donadelli
24INFN Sezione di Bologna, Bologna, Italy
24,
S Donati
S Donati
124Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
124,
P Dondero
P Dondero
121Department of Physics, Massachusetts Institute of Technology, Cambridge, MA USA
121,
J Donini
J Donini
34National Institute of Physics and Nuclear Engineering, Bucharest, Romania
34,
J Dopke
J Dopke
131INFN Sezione di Napoli, Naples, Italy
131,
A Doria
A Doria
104Department of Physics and Astronomy, University College London, London, UK
104,
M T Dova
M T Dova
71E. Andronikashvili Institute of Physics, Iv. Javakhishvili Tbilisi State University, Tbilisi, Georgia
71,
A T Doyle
A T Doyle
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
E Drechsler
E Drechsler
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
M Dris
M Dris
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
E Dubreuil
E Dubreuil
34National Institute of Physics and Nuclear Engineering, Bucharest, Romania
34,
E Duchovni
E Duchovni
172INFN Sezione di Roma Tre, Roma, Italy
172,
G Duckeck
G Duckeck
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
O A Ducu
O A Ducu
26Physikalisches Institut, University of Bonn, Bonn, Germany
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
26,85,
D Duda
D Duda
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
A Dudarev
A Dudarev
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
L Duflot
L Duflot
117INFN Sezione di Milano, Milano, Italy
117,
L Duguid
L Duguid
77Department of Physics, Hampton University, Hampton, VA USA
77,
M Dührssen
M Dührssen
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
M Dunford
M Dunford
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
H Duran Yildiz
H Duran Yildiz
4Department of Physics, Ankara University, Ankara, Turkey
4,
M Düren
M Düren
52Nevis Laboratory, Columbia University, Irvington, NY USA
52,
A Durglishvili
A Durglishvili
51Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
51,
D Duschinger
D Duschinger
44Departamento de Física, Universidad Técnica Federico Santa María, Valparaiso, Chile
44,
M Dyndal
M Dyndal
38Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
38,
C Eckardt
C Eckardt
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
K M Ecker
K M Ecker
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
R C Edgar
R C Edgar
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
W Edson
W Edson
2Physics Department, SUNY Albany, Albany, NY USA
2,
N C Edwards
N C Edwards
46Department of Modern Physics, University of Science and Technology of China, Anhui, China
46,
W Ehrenfeld
W Ehrenfeld
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
T Eifert
T Eifert
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
G Eigen
G Eigen
14Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
14,
K Einsweiler
K Einsweiler
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
T Ekelof
T Ekelof
166State Research Center Institute for High Energy Physics, Protvino, Russia
166,
M El Kacimi
M El Kacimi
135Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
135,
M Ellert
M Ellert
166State Research Center Institute for High Energy Physics, Protvino, Russia
166,
S Elles
S Elles
5Istanbul Aydin University, Istanbul, Turkey
5,
F Ellinghaus
F Ellinghaus
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
A A Elliot
A A Elliot
169Dipartimento di Fisica, Sapienza Università di Roma, Roma, Italy
169,
N Ellis
N Ellis
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
J Elmsheuser
J Elmsheuser
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
M Elsing
M Elsing
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
D Emeliyanov
D Emeliyanov
131INFN Sezione di Napoli, Naples, Italy
131,
Y Enari
Y Enari
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
O C Endner
O C Endner
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
M Endo
M Endo
118Dipartimento di Fisica, Università di Milano, Milano, Italy
118,
J Erdmann
J Erdmann
43Departamento de Física, Pontificia Universidad Católica de Chile, Santiago, Chile
43,
A Ereditato
A Ereditato
17Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA USA
17,
G Ernis
G Ernis
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
J Ernst
J Ernst
2Physics Department, SUNY Albany, Albany, NY USA
2,
M Ernst
M Ernst
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
S Errede
S Errede
165Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
165,
E Ertel
E Ertel
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
M Escalier
M Escalier
117INFN Sezione di Milano, Milano, Italy
117,
H Esch
H Esch
43Departamento de Física, Pontificia Universidad Católica de Chile, Santiago, Chile
43,
C Escobar
C Escobar
125National Research Nuclear University MEPhI, Moscow, Russia
125,
B Esposito
B Esposito
47Department of Physics, Nanjing University, Jiangsu, China
47,
A I Etienvre
A I Etienvre
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
E Etzion
E Etzion
153INFN Sezione di Pisa, Pisa, Italy
153,
H Evans
H Evans
61DESY, Hamburg and Zeuthen, Germany
61,
A Ezhilov
A Ezhilov
123P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
123,
L Fabbri
L Fabbri
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
G Facini
G Facini
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
R M Fakhrutdinov
R M Fakhrutdinov
130Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
130,
S Falciano
S Falciano
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
R J Falla
R J Falla
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
J Faltova
J Faltova
129Nagasaki Institute of Applied Science, Nagasaki, Japan
129,
Y Fang
Y Fang
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
M Fanti
M Fanti
91KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
91,
A Farbin
A Farbin
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
A Farilla
A Farilla
134Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
134,
T Farooque
T Farooque
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
S Farrell
S Farrell
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
S M Farrington
S M Farrington
170INFN Sezione di Roma Tor Vergata, Roma, Italy
170,
P Farthouat
P Farthouat
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
F Fassi
F Fassi
135Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
135,
P Fassnacht
P Fassnacht
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
D Fassouliotis
D Fassouliotis
9Department of Physics, University of Arizona, Tucson, AZ USA
9,
M Faucci Giannelli
M Faucci Giannelli
77Department of Physics, Hampton University, Hampton, VA USA
77,
A Favareto
A Favareto
50Physics Department, Tsinghua University, Beijing, 100084 China
50,
L Fayard
L Fayard
117INFN Sezione di Milano, Milano, Italy
117,
P Federic
P Federic
144Center for High Energy Physics, University of Oregon, Eugene, OR USA
144,
O L Fedin
O L Fedin
123P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
123,
W Fedorko
W Fedorko
168INFN Sezione di Roma, Roma, Italy
168,
S Feigl
S Feigl
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
L Feligioni
L Feligioni
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
C Feng
C Feng
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
E J Feng
E J Feng
6Division of Physics, TOBB University of Economics and Technology, Ankara, Turkey
6,
H Feng
H Feng
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
A B Fenyuk
A B Fenyuk
130Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
130,
L Feremenga
L Feremenga
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
P Fernandez Martinez
P Fernandez Martinez
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
S Fernandez Perez
S Fernandez Perez
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
J Ferrando
J Ferrando
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
A Ferrari
A Ferrari
166State Research Center Institute for High Energy Physics, Protvino, Russia
166,
P Ferrari
P Ferrari
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
R Ferrari
R Ferrari
121Department of Physics, Massachusetts Institute of Technology, Cambridge, MA USA
121,
D E Ferreira de Lima
D E Ferreira de Lima
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
A Ferrer
A Ferrer
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
D Ferrere
D Ferrere
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
C Ferretti
C Ferretti
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
A Ferretto Parodi
A Ferretto Parodi
50Physics Department, Tsinghua University, Beijing, 100084 China
50,
M Fiascaris
M Fiascaris
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
F Fiedler
F Fiedler
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
A Filipčič
A Filipčič
75II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
75,
M Filipuzzi
M Filipuzzi
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
F Filthaut
F Filthaut
106Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
106,
M Fincke-Keeler
M Fincke-Keeler
169Dipartimento di Fisica, Sapienza Università di Roma, Roma, Italy
169,
K D Finelli
K D Finelli
150Dipartimento di Fisica, Università di Pavia, Pavia, Italy
150,
M C N Fiolhais
M C N Fiolhais
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
L Fiorini
L Fiorini
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
A Firan
A Firan
40Department of Physics, Carleton University, Ottawa, ON Canada
40,
A Fischer
A Fischer
2Physics Department, SUNY Albany, Albany, NY USA
2,
C Fischer
C Fischer
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
J Fischer
J Fischer
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
W C Fisher
W C Fisher
90Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
90,
E A Fitzgerald
E A Fitzgerald
23Department of Physics, Dogus University, Istanbul, Turkey
23,
N Flaschel
N Flaschel
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
I Fleck
I Fleck
141Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK USA
141,
P Fleischmann
P Fleischmann
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
S Fleischmann
S Fleischmann
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
G T Fletcher
G T Fletcher
139Ohio State University, Columbus, OH USA
139,
G Fletcher
G Fletcher
76Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
76,
R R M Fletcher
R R M Fletcher
122Group of Particle Physics, University of Montreal, Montreal, QC Canada
122,
T Flick
T Flick
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
A Floderus
A Floderus
81ZITI Institut für technische Informatik, Ruprecht-Karls-Universität Heidelberg, Mannheim, Germany
81,
L R Flores Castillo
L R Flores Castillo
60Physics Department, University of Texas at Dallas, Richardson, TX USA
60,
M J Flowerdew
M J Flowerdew
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
A Formica
A Formica
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
A Forti
A Forti
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
D Fournier
D Fournier
117INFN Sezione di Milano, Milano, Italy
117,
H Fox
H Fox
72High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
72,
S Fracchia
S Fracchia
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
P Francavilla
P Francavilla
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
M Franchini
M Franchini
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
D Francis
D Francis
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
L Franconi
L Franconi
119B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
119,
M Franklin
M Franklin
57Marian Smoluchowski Institute of Physics, Jagiellonian University, Kraków, Poland
57,
M Frate
M Frate
163Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
163,
M Fraternali
M Fraternali
121Department of Physics, Massachusetts Institute of Technology, Cambridge, MA USA
121,
D Freeborn
D Freeborn
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
S T French
S T French
28Department of Physics, Brandeis University, Waltham, MA USA
28,
F Friedrich
F Friedrich
44Departamento de Física, Universidad Técnica Federico Santa María, Valparaiso, Chile
44,
D Froidevaux
D Froidevaux
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
J A Frost
J A Frost
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
C Fukunaga
C Fukunaga
156Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisboa, Portugal
156,
E Fullana Torregrosa
E Fullana Torregrosa
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
B G Fulsom
B G Fulsom
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
T Fusayasu
T Fusayasu
102School of Physics and Astronomy, Queen Mary University of London, London, UK
102,
J Fuster
J Fuster
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
C Gabaldon
C Gabaldon
55Dipartimento di Fisica, Università della Calabria, Rende, Italy
55,
O Gabizon
O Gabizon
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
A Gabrielli
A Gabrielli
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
A Gabrielli
A Gabrielli
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
G P Gach
G P Gach
38Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
38,
S Gadatsch
S Gadatsch
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
S Gadomski
S Gadomski
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
G Gagliardi
G Gagliardi
50Physics Department, Tsinghua University, Beijing, 100084 China
50,
P Gagnon
P Gagnon
61DESY, Hamburg and Zeuthen, Germany
61,
C Galea
C Galea
106Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
106,
B Galhardo
B Galhardo
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
E J Gallas
E J Gallas
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
B J Gallop
B J Gallop
131INFN Sezione di Napoli, Naples, Italy
131,
P Gallus
P Gallus
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
G Galster
G Galster
36University Politehnica Bucharest, Bucharest, Romania
36,
K K Gan
K K Gan
111CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
111,
J Gao
J Gao
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
33,85,
Y Gao
Y Gao
46Department of Modern Physics, University of Science and Technology of China, Anhui, China
46,
Y S Gao
Y S Gao
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
F M Garay Walls
F M Garay Walls
46Department of Modern Physics, University of Science and Technology of China, Anhui, China
46,
F Garberson
F Garberson
176Faculté des Sciences Semlalia, Université Cadi Ayyad, LPHEA-Marrakech, Marrakech, Morocco
176,
C García
C García
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
J E García Navarro
J E García Navarro
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
M Garcia-Sciveres
M Garcia-Sciveres
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
R W Gardner
R W Gardner
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
N Garelli
N Garelli
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
V Garonne
V Garonne
119B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
119,
C Gatti
C Gatti
47Department of Physics, Nanjing University, Jiangsu, China
47,
A Gaudiello
A Gaudiello
50Physics Department, Tsinghua University, Beijing, 100084 China
50,
G Gaudio
G Gaudio
121Department of Physics, Massachusetts Institute of Technology, Cambridge, MA USA
121,
B Gaur
B Gaur
141Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK USA
141,
L Gauthier
L Gauthier
95Department of Physics, Kyushu University, Fukuoka, Japan
95,
P Gauzzi
P Gauzzi
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
I L Gavrilenko
I L Gavrilenko
96Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
96,
C Gay
C Gay
168INFN Sezione di Roma, Roma, Italy
168,
G Gaycken
G Gaycken
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
E N Gazis
E N Gazis
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
P Ge
P Ge
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
Z Gecse
Z Gecse
168INFN Sezione di Roma, Roma, Italy
168,
C N P Gee
C N P Gee
131INFN Sezione di Napoli, Naples, Italy
131,
Ch Geich-Gimbel
Ch Geich-Gimbel
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
M P Geisler
M P Geisler
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
C Gemme
C Gemme
50Physics Department, Tsinghua University, Beijing, 100084 China
50,
M H Genest
M H Genest
55Dipartimento di Fisica, Università della Calabria, Rende, Italy
55,
S Gentile
S Gentile
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
M George
M George
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
S George
S George
77Department of Physics, Hampton University, Hampton, VA USA
77,
D Gerbaudo
D Gerbaudo
163Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
163,
A Gershon
A Gershon
153INFN Sezione di Pisa, Pisa, Italy
153,
S Ghasemi
S Ghasemi
141Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK USA
141,
H Ghazlane
H Ghazlane
135Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
135,
B Giacobbe
B Giacobbe
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
S Giagu
S Giagu
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
V Giangiobbe
V Giangiobbe
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
P Giannetti
P Giannetti
124Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
124,
B Gibbard
B Gibbard
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
S M Gibson
S M Gibson
77Department of Physics, Hampton University, Hampton, VA USA
77,
M Gilchriese
M Gilchriese
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
T P S Gillam
T P S Gillam
28Department of Physics, Brandeis University, Waltham, MA USA
28,
D Gillberg
D Gillberg
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
G Gilles
G Gilles
34National Institute of Physics and Nuclear Engineering, Bucharest, Romania
34,
D M Gingrich
D M Gingrich
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
N Giokaris
N Giokaris
9Department of Physics, University of Arizona, Tucson, AZ USA
9,
M P Giordani
M P Giordani
164Czech Technical University in Praha, Praha, Czech Republic
164,
F M Giorgi
F M Giorgi
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
F M Giorgi
F M Giorgi
16Department for Physics and Technology, University of Bergen, Bergen, Norway
16,
P F Giraud
P F Giraud
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
P Giromini
P Giromini
47Department of Physics, Nanjing University, Jiangsu, China
47,
D Giugni
D Giugni
91KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
91,
C Giuliani
C Giuliani
48School of Physics, Shandong University, Shandong, China
48,
M Giulini
M Giulini
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
B K Gjelsten
B K Gjelsten
119B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
119,
S Gkaitatzis
S Gkaitatzis
154Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
154,
I Gkialas
I Gkialas
154Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
154,
E L Gkougkousis
E L Gkougkousis
117INFN Sezione di Milano, Milano, Italy
117,
L K Gladilin
L K Gladilin
99Dipartimento di Matematica e Fisica, Università del Salento, Lecce, Italy
99,
C Glasman
C Glasman
82Faculty of Applied Information Science, Hiroshima Institute of Technology, Hiroshima, Japan
82,
J Glatzer
J Glatzer
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
P C F Glaysher
P C F Glaysher
46Department of Modern Physics, University of Science and Technology of China, Anhui, China
46,
A Glazov
A Glazov
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
M Goblirsch-Kolb
M Goblirsch-Kolb
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
J R Goddard
J R Goddard
76Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
76,
J Godlewski
J Godlewski
39Cavendish Laboratory, University of Cambridge, Cambridge, UK
39,
S Goldfarb
S Goldfarb
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
T Golling
T Golling
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
D Golubkov
D Golubkov
130Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
130,
A Gomes
A Gomes
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
R Gonçalo
R Gonçalo
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
J Goncalves Pinto Firmino Da Costa
J Goncalves Pinto Firmino Da Costa
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
L Gonella
L Gonella
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
S González de la Hoz
S González de la Hoz
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
G Gonzalez Parra
G Gonzalez Parra
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
S Gonzalez-Sevilla
S Gonzalez-Sevilla
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
L Goossens
L Goossens
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
P A Gorbounov
P A Gorbounov
97Physics Department, Lancaster University, Lancaster, UK
97,
H A Gordon
H A Gordon
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
I Gorelov
I Gorelov
105Louisiana Tech University, Ruston, LA USA
105,
B Gorini
B Gorini
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
E Gorini
E Gorini
73II Physikalisches Institut, Justus-Liebig-Universität Giessen, Giessen, Germany
73,
A Gorišek
A Gorišek
75II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
75,
E Gornicki
E Gornicki
39Cavendish Laboratory, University of Cambridge, Cambridge, UK
39,
A T Goshaw
A T Goshaw
45Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
45,
C Gössling
C Gössling
43Departamento de Física, Pontificia Universidad Católica de Chile, Santiago, Chile
43,
M I Gostkin
M I Gostkin
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
D Goujdami
D Goujdami
135Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
135,
A G Goussiou
A G Goussiou
138Department of Physics, New York University, New York, NY USA
138,
N Govender
N Govender
145LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
145,
E Gozani
E Gozani
152National Research Centre ‘Kurchatov Institute’ B.P.Konstantinov Petersburg Nuclear Physics Institute, St. Petersburg, Russia
152,
H M X Grabas
H M X Grabas
137Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
137,
L Graber
L Graber
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
I Grabowska-Bold
I Grabowska-Bold
38Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
38,
P O J Gradin
P O J Gradin
166State Research Center Institute for High Energy Physics, Protvino, Russia
166,
P Grafström
P Grafström
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
K-J Grahn
K-J Grahn
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
J Gramling
J Gramling
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
E Gramstad
E Gramstad
119B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
119,
S Grancagnolo
S Grancagnolo
16Department for Physics and Technology, University of Bergen, Bergen, Norway
16,
V Gratchev
V Gratchev
123P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
123,
H M Gray
H M Gray
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
E Graziani
E Graziani
134Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
134,
Z D Greenwood
Z D Greenwood
79Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
79,
K Gregersen
K Gregersen
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
I M Gregor
I M Gregor
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
P Grenier
P Grenier
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
J Griffiths
J Griffiths
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
A A Grillo
A A Grillo
137Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
137,
K Grimm
K Grimm
72High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
72,
S Grinstein
S Grinstein
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
Ph Gris
Ph Gris
34National Institute of Physics and Nuclear Engineering, Bucharest, Romania
34,
J-F Grivaz
J-F Grivaz
117INFN Sezione di Milano, Milano, Italy
117,
J P Grohs
J P Grohs
44Departamento de Física, Universidad Técnica Federico Santa María, Valparaiso, Chile
44,
A Grohsjean
A Grohsjean
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
E Gross
E Gross
172INFN Sezione di Roma Tre, Roma, Italy
172,
J Grosse-Knetter
J Grosse-Knetter
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
G C Grossi
G C Grossi
79Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
79,
Z J Grout
Z J Grout
149INFN Sezione di Pavia, Pavia, Italy
149,
L Guan
L Guan
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
J Guenther
J Guenther
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
F Guescini
F Guescini
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
D Guest
D Guest
176Faculté des Sciences Semlalia, Université Cadi Ayyad, LPHEA-Marrakech, Marrakech, Morocco
176,
O Gueta
O Gueta
153INFN Sezione di Pisa, Pisa, Italy
153,
E Guido
E Guido
50Physics Department, Tsinghua University, Beijing, 100084 China
50,
T Guillemin
T Guillemin
117INFN Sezione di Milano, Milano, Italy
117,
S Guindon
S Guindon
2Physics Department, SUNY Albany, Albany, NY USA
2,
U Gul
U Gul
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
C Gumpert
C Gumpert
44Departamento de Física, Universidad Técnica Federico Santa María, Valparaiso, Chile
44,
J Guo
J Guo
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
Y Guo
Y Guo
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
S Gupta
S Gupta
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
G Gustavino
G Gustavino
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
P Gutierrez
P Gutierrez
113Department of Physics, McGill University, Montreal, QC Canada
113,
N G Gutierrez Ortiz
N G Gutierrez Ortiz
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
C Gutschow
C Gutschow
44Departamento de Física, Universidad Técnica Federico Santa María, Valparaiso, Chile
44,
C Guyot
C Guyot
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
C Gwenlan
C Gwenlan
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
C B Gwilliam
C B Gwilliam
74SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
74,
A Haas
A Haas
110School of Physics and Astronomy, University of Manchester, Manchester, UK
110,
C Haber
C Haber
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
H K Hadavand
H K Hadavand
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
N Haddad
N Haddad
135Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
135,
P Haefner
P Haefner
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
S Hageböck
S Hageböck
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
Z Hajduk
Z Hajduk
39Cavendish Laboratory, University of Cambridge, Cambridge, UK
39,
H Hakobyan
H Hakobyan
177Faculté des Sciences, Université Mohamed Premier and LPTPM, Oujda, Morocco
177,
M Haleem
M Haleem
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
J Haley
J Haley
114School of Physics, University of Melbourne, Melbourne, VIC Australia
114,
D Hall
D Hall
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
G Halladjian
G Halladjian
90Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
90,
G D Hallewell
G D Hallewell
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
K Hamacher
K Hamacher
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
P Hamal
P Hamal
115Department of Physics, The University of Michigan, Ann Arbor, MI USA
115,
K Hamano
K Hamano
169Dipartimento di Fisica, Sapienza Università di Roma, Roma, Italy
169,
A Hamilton
A Hamilton
145LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
145,
G N Hamity
G N Hamity
139Ohio State University, Columbus, OH USA
139,
P G Hamnett
P G Hamnett
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
L Han
L Han
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
K Hanagaki
K Hanagaki
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
K Hanawa
K Hanawa
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
M Hance
M Hance
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
P Hanke
P Hanke
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
R Hanna
R Hanna
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
J B Hansen
J B Hansen
36University Politehnica Bucharest, Bucharest, Romania
36,
J D Hansen
J D Hansen
36University Politehnica Bucharest, Bucharest, Romania
36,
M C Hansen
M C Hansen
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
P H Hansen
P H Hansen
36University Politehnica Bucharest, Bucharest, Romania
36,
K Hara
K Hara
160Departamento de Fisica, Universidade do Minho, Braga, Portugal
160,
A S Hard
A S Hard
173Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
173,
T Harenberg
T Harenberg
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
F Hariri
F Hariri
117INFN Sezione di Milano, Milano, Italy
117,
S Harkusha
S Harkusha
92Graduate School of Science, Kobe University, Kobe, Japan
92,
R D Harrington
R D Harrington
46Department of Modern Physics, University of Science and Technology of China, Anhui, China
46,
P F Harrison
P F Harrison
170INFN Sezione di Roma Tor Vergata, Roma, Italy
170,
F Hartjes
F Hartjes
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
M Hasegawa
M Hasegawa
67Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
67,
Y Hasegawa
Y Hasegawa
140Faculty of Science, Okayama University, Okayama, Japan
140,
A Hasib
A Hasib
113Department of Physics, McGill University, Montreal, QC Canada
113,
S Hassani
S Hassani
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
S Haug
S Haug
17Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA USA
17,
R Hauser
R Hauser
90Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
90,
L Hauswald
L Hauswald
44Departamento de Física, Universidad Técnica Federico Santa María, Valparaiso, Chile
44,
M Havranek
M Havranek
127Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
127,
C M Hawkes
C M Hawkes
18Department of Physics, Humboldt University, Berlin, Germany
18,
R J Hawkings
R J Hawkings
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
A D Hawkins
A D Hawkins
81ZITI Institut für technische Informatik, Ruprecht-Karls-Universität Heidelberg, Mannheim, Germany
81,
T Hayashi
T Hayashi
160Departamento de Fisica, Universidade do Minho, Braga, Portugal
160,
D Hayden
D Hayden
90Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
90,
C P Hays
C P Hays
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
J M Hays
J M Hays
76Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
76,
H S Hayward
H S Hayward
74SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
74,
S J Haywood
S J Haywood
131INFN Sezione di Napoli, Naples, Italy
131,
S J Head
S J Head
18Department of Physics, Humboldt University, Berlin, Germany
18,
T Heck
T Heck
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
V Hedberg
V Hedberg
81ZITI Institut für technische Informatik, Ruprecht-Karls-Universität Heidelberg, Mannheim, Germany
81,
L Heelan
L Heelan
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
S Heim
S Heim
122Group of Particle Physics, University of Montreal, Montreal, QC Canada
122,
T Heim
T Heim
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
B Heinemann
B Heinemann
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
L Heinrich
L Heinrich
110School of Physics and Astronomy, University of Manchester, Manchester, UK
110,
J Hejbal
J Hejbal
127Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
127,
L Helary
L Helary
22Department of Physics Engineering, Gaziantep University, Gaziantep, Turkey
22,
S Hellman
S Hellman
146Graduate School of Science, Osaka University, Osaka, Japan
146,
D Hellmich
D Hellmich
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
C Helsens
C Helsens
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
J Henderson
J Henderson
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
R C W Henderson
R C W Henderson
72High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
72,
Y Heng
Y Heng
173Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
173,
C Hengler
C Hengler
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
A Henrichs
A Henrichs
176Faculté des Sciences Semlalia, Université Cadi Ayyad, LPHEA-Marrakech, Marrakech, Morocco
176,
A M Henriques Correia
A M Henriques Correia
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
S Henrot-Versille
S Henrot-Versille
117INFN Sezione di Milano, Milano, Italy
117,
G H Herbert
G H Herbert
16Department for Physics and Technology, University of Bergen, Bergen, Norway
16,
Y Hernández Jiménez
Y Hernández Jiménez
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
R Herrberg-Schubert
R Herrberg-Schubert
16Department for Physics and Technology, University of Bergen, Bergen, Norway
16,
G Herten
G Herten
48School of Physics, Shandong University, Shandong, China
48,
R Hertenberger
R Hertenberger
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
L Hervas
L Hervas
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
G G Hesketh
G G Hesketh
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
N P Hessey
N P Hessey
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
J W Hetherly
J W Hetherly
40Department of Physics, Carleton University, Ottawa, ON Canada
40,
R Hickling
R Hickling
76Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
76,
E Higón-Rodriguez
E Higón-Rodriguez
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
E Hill
E Hill
169Dipartimento di Fisica, Sapienza Università di Roma, Roma, Italy
169,
J C Hill
J C Hill
28Department of Physics, Brandeis University, Waltham, MA USA
28,
K H Hiller
K H Hiller
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
S J Hillier
S J Hillier
18Department of Physics, Humboldt University, Berlin, Germany
18,
I Hinchliffe
I Hinchliffe
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
E Hines
E Hines
122Group of Particle Physics, University of Montreal, Montreal, QC Canada
122,
R R Hinman
R R Hinman
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
M Hirose
M Hirose
157Faculdade de Ciências, Universidade de Lisboa, Lisboa, Portugal
157,
D Hirschbuehl
D Hirschbuehl
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
J Hobbs
J Hobbs
148Department of Physics, Oxford University, Oxford, UK
148,
N Hod
N Hod
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
M C Hodgkinson
M C Hodgkinson
139Ohio State University, Columbus, OH USA
139,
P Hodgson
P Hodgson
139Ohio State University, Columbus, OH USA
139,
A Hoecker
A Hoecker
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
M R Hoeferkamp
M R Hoeferkamp
105Louisiana Tech University, Ruston, LA USA
105,
F Hoenig
F Hoenig
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
M Hohlfeld
M Hohlfeld
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
D Hohn
D Hohn
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
T R Holmes
T R Holmes
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
M Homann
M Homann
43Departamento de Física, Pontificia Universidad Católica de Chile, Santiago, Chile
43,
T M Hong
T M Hong
125National Research Nuclear University MEPhI, Moscow, Russia
125,
L Hooft van Huysduynen
L Hooft van Huysduynen
110School of Physics and Astronomy, University of Manchester, Manchester, UK
110,
W H Hopkins
W H Hopkins
116Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
116,
Y Horii
Y Horii
103Department of Physics, Royal Holloway University of London, Surrey, UK
103,
A J Horton
A J Horton
142Department of Physics, Oklahoma State University, Stillwater, OK USA
142,
J-Y Hostachy
J-Y Hostachy
55Dipartimento di Fisica, Università della Calabria, Rende, Italy
55,
S Hou
S Hou
151Department of Physics, University of Pennsylvania, Philadelphia, PA USA
151,
A Hoummada
A Hoummada
135Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
135,
J Howard
J Howard
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
J Howarth
J Howarth
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
M Hrabovsky
M Hrabovsky
115Department of Physics, The University of Michigan, Ann Arbor, MI USA
115,
I Hristova
I Hristova
16Department for Physics and Technology, University of Bergen, Bergen, Norway
16,
J Hrivnac
J Hrivnac
117INFN Sezione di Milano, Milano, Italy
117,
T Hryn’ova
T Hryn’ova
5Istanbul Aydin University, Istanbul, Turkey
5,
A Hrynevich
A Hrynevich
93Faculty of Science, Kyoto University, Kyoto, Japan
93,
C Hsu
C Hsu
145LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
145,
P J Hsu
P J Hsu
151Department of Physics, University of Pennsylvania, Philadelphia, PA USA
151,
S-C Hsu
S-C Hsu
138Department of Physics, New York University, New York, NY USA
138,
D Hu
D Hu
35Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj Napoca, Romania
35,
Q Hu
Q Hu
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
X Hu
X Hu
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
Y Huang
Y Huang
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
Z Hubacek
Z Hubacek
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
F Hubaut
F Hubaut
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
F Huegging
F Huegging
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
T B Huffman
T B Huffman
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
E W Hughes
E W Hughes
35Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj Napoca, Romania
35,
G Hughes
G Hughes
72High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
72,
M Huhtinen
M Huhtinen
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
T A Hülsing
T A Hülsing
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
N Huseynov
N Huseynov
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
J Huston
J Huston
90Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
90,
J Huth
J Huth
57Marian Smoluchowski Institute of Physics, Jagiellonian University, Kraków, Poland
57,
G Iacobucci
G Iacobucci
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
G Iakovidis
G Iakovidis
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
I Ibragimov
I Ibragimov
141Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK USA
141,
L Iconomidou-Fayard
L Iconomidou-Fayard
117INFN Sezione di Milano, Milano, Italy
117,
E Ideal
E Ideal
176Faculté des Sciences Semlalia, Université Cadi Ayyad, LPHEA-Marrakech, Marrakech, Morocco
176,
Z Idrissi
Z Idrissi
135Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
135,
P Iengo
P Iengo
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
O Igonkina
O Igonkina
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
T Iizawa
T Iizawa
171Dipartimento di Fisica, Università di Roma Tor Vergata, Roma, Italy
171,
Y Ikegami
Y Ikegami
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
K Ikematsu
K Ikematsu
141Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK USA
141,
M Ikeno
M Ikeno
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
Y Ilchenko
Y Ilchenko
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
D Iliadis
D Iliadis
154Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
154,
N Ilic
N Ilic
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
T Ince
T Ince
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
G Introzzi
G Introzzi
121Department of Physics, Massachusetts Institute of Technology, Cambridge, MA USA
121,
P Ioannou
P Ioannou
9Department of Physics, University of Arizona, Tucson, AZ USA
9,
M Iodice
M Iodice
134Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
134,
K Iordanidou
K Iordanidou
35Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj Napoca, Romania
35,
V Ippolito
V Ippolito
57Marian Smoluchowski Institute of Physics, Jagiellonian University, Kraków, Poland
57,
A Irles Quiles
A Irles Quiles
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
C Isaksson
C Isaksson
166State Research Center Institute for High Energy Physics, Protvino, Russia
166,
M Ishino
M Ishino
68Section de Physique, Université de Genève, Geneva, Switzerland
68,
M Ishitsuka
M Ishitsuka
157Faculdade de Ciências, Universidade de Lisboa, Lisboa, Portugal
157,
R Ishmukhametov
R Ishmukhametov
111CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
111,
C Issever
C Issever
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
S Istin
S Istin
19Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
19,
J M Iturbe Ponce
J M Iturbe Ponce
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
R Iuppa
R Iuppa
133Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM USA
133,
J Ivarsson
J Ivarsson
81ZITI Institut für technische Informatik, Ruprecht-Karls-Universität Heidelberg, Mannheim, Germany
81,
W Iwanski
W Iwanski
39Cavendish Laboratory, University of Cambridge, Cambridge, UK
39,
H Iwasaki
H Iwasaki
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
J M Izen
J M Izen
41CERN, Geneva, Switzerland
41,
V Izzo
V Izzo
104Department of Physics and Astronomy, University College London, London, UK
104,
S Jabbar
S Jabbar
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
B Jackson
B Jackson
122Group of Particle Physics, University of Montreal, Montreal, QC Canada
122,
M Jackson
M Jackson
74SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
74,
P Jackson
P Jackson
1Department of Physics, University of Adelaide, Adelaide, Australia
1,
M R Jaekel
M R Jaekel
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
V Jain
V Jain
2Physics Department, SUNY Albany, Albany, NY USA
2,
K Jakobs
K Jakobs
48School of Physics, Shandong University, Shandong, China
48,
S Jakobsen
S Jakobsen
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
T Jakoubek
T Jakoubek
127Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
127,
J Jakubek
J Jakubek
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
D O Jamin
D O Jamin
114School of Physics, University of Melbourne, Melbourne, VIC Australia
114,
D K Jana
D K Jana
79Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
79,
E Jansen
E Jansen
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
R Jansky
R Jansky
62Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
62,
J Janssen
J Janssen
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
M Janus
M Janus
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
G Jarlskog
G Jarlskog
81ZITI Institut für technische Informatik, Ruprecht-Karls-Universität Heidelberg, Mannheim, Germany
81,
N Javadov
N Javadov
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
T Javůrek
T Javůrek
48School of Physics, Shandong University, Shandong, China
48,
L Jeanty
L Jeanty
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
J Jejelava
J Jejelava
51Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
51,
G-Y Jeng
G-Y Jeng
150Dipartimento di Fisica, Università di Pavia, Pavia, Italy
150,
D Jennens
D Jennens
88University of Iowa, Iowa City, IA USA
88,
P Jenni
P Jenni
48School of Physics, Shandong University, Shandong, China
48,
J Jentzsch
J Jentzsch
43Departamento de Física, Pontificia Universidad Católica de Chile, Santiago, Chile
43,
C Jeske
C Jeske
170INFN Sezione di Roma Tor Vergata, Roma, Italy
170,
S Jézéquel
S Jézéquel
5Istanbul Aydin University, Istanbul, Turkey
5,
H Ji
H Ji
173Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
173,
J Jia
J Jia
148Department of Physics, Oxford University, Oxford, UK
148,
Y Jiang
Y Jiang
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
S Jiggins
S Jiggins
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
J Jimenez Pena
J Jimenez Pena
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
S Jin
S Jin
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
A Jinaru
A Jinaru
26Physikalisches Institut, University of Bonn, Bonn, Germany
26,
O Jinnouchi
O Jinnouchi
157Faculdade de Ciências, Universidade de Lisboa, Lisboa, Portugal
157,
M D Joergensen
M D Joergensen
36University Politehnica Bucharest, Bucharest, Romania
36,
P Johansson
P Johansson
139Ohio State University, Columbus, OH USA
139,
K A Johns
K A Johns
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
K Jon-And
K Jon-And
146Graduate School of Science, Osaka University, Osaka, Japan
146,
G Jones
G Jones
170INFN Sezione di Roma Tor Vergata, Roma, Italy
170,
R W L Jones
R W L Jones
72High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
72,
T J Jones
T J Jones
74SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
74,
J Jongmanns
J Jongmanns
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
P M Jorge
P M Jorge
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
K D Joshi
K D Joshi
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
J Jovicevic
J Jovicevic
159Centro de Física Nuclear da Universidade de Lisboa, Lisboa, Portugal
159,
X Ju
X Ju
173Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
173,
C A Jung
C A Jung
43Departamento de Física, Pontificia Universidad Católica de Chile, Santiago, Chile
43,
P Jussel
P Jussel
62Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
62,
A Juste Rozas
A Juste Rozas
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
M Kaci
M Kaci
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
A Kaczmarska
A Kaczmarska
39Cavendish Laboratory, University of Cambridge, Cambridge, UK
39,
M Kado
M Kado
117INFN Sezione di Milano, Milano, Italy
117,
H Kagan
H Kagan
111CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
111,
M Kagan
M Kagan
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
S J Kahn
S J Kahn
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
E Kajomovitz
E Kajomovitz
45Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
45,
C W Kalderon
C W Kalderon
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
S Kama
S Kama
40Department of Physics, Carleton University, Ottawa, ON Canada
40,
A Kamenshchikov
A Kamenshchikov
130Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
130,
N Kanaya
N Kanaya
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
S Kaneti
S Kaneti
28Department of Physics, Brandeis University, Waltham, MA USA
28,
V A Kantserov
V A Kantserov
98INFN Sezione di Lecce, Lecce, Italy
98,
J Kanzaki
J Kanzaki
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
B Kaplan
B Kaplan
110School of Physics and Astronomy, University of Manchester, Manchester, UK
110,
L S Kaplan
L S Kaplan
173Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
173,
A Kapliy
A Kapliy
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
D Kar
D Kar
145LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
145,
K Karakostas
K Karakostas
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
A Karamaoun
A Karamaoun
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
N Karastathis
N Karastathis
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
M J Kareem
M J Kareem
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
E Karentzos
E Karentzos
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
M Karnevskiy
M Karnevskiy
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
S N Karpov
S N Karpov
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
Z M Karpova
Z M Karpova
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
K Karthik
K Karthik
110School of Physics and Astronomy, University of Manchester, Manchester, UK
110,
V Kartvelishvili
V Kartvelishvili
72High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
72,
A N Karyukhin
A N Karyukhin
130Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
130,
L Kashif
L Kashif
173Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
173,
R D Kass
R D Kass
111CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
111,
A Kastanas
A Kastanas
14Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
14,
Y Kataoka
Y Kataoka
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
C Kato
C Kato
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
A Katre
A Katre
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
J Katzy
J Katzy
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
K Kawagoe
K Kawagoe
70Dipartimento di Fisica, Università di Genova, Genova, Italy
70,
T Kawamoto
T Kawamoto
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
G Kawamura
G Kawamura
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
S Kazama
S Kazama
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
V F Kazanin
V F Kazanin
109Institut für Physik, Universität Mainz, Mainz, Germany
109,
R Keeler
R Keeler
169Dipartimento di Fisica, Sapienza Università di Roma, Roma, Italy
169,
R Kehoe
R Kehoe
40Department of Physics, Carleton University, Ottawa, ON Canada
40,
J S Keller
J S Keller
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
J J Kempster
J J Kempster
77Department of Physics, Hampton University, Hampton, VA USA
77,
H Keoshkerian
H Keoshkerian
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
O Kepka
O Kepka
127Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
127,
B P Kerševan
B P Kerševan
75II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
75,
S Kersten
S Kersten
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
R A Keyes
R A Keyes
87Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
87,
F Khalil-zada
F Khalil-zada
11Physics Department, University of Athens, Athens, Greece
11,
H Khandanyan
H Khandanyan
146Graduate School of Science, Osaka University, Osaka, Japan
146,
A Khanov
A Khanov
114School of Physics, University of Melbourne, Melbourne, VIC Australia
114,
A G Kharlamov
A G Kharlamov
109Institut für Physik, Universität Mainz, Mainz, Germany
109,
T J Khoo
T J Khoo
28Department of Physics, Brandeis University, Waltham, MA USA
28,
V Khovanskiy
V Khovanskiy
97Physics Department, Lancaster University, Lancaster, UK
97,
E Khramov
E Khramov
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
J Khubua
J Khubua
51Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
51,
S Kido
S Kido
67Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
67,
H Y Kim
H Y Kim
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
S H Kim
S H Kim
160Departamento de Fisica, Universidade do Minho, Braga, Portugal
160,
Y K Kim
Y K Kim
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
N Kimura
N Kimura
154Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
154,
O M Kind
O M Kind
16Department for Physics and Technology, University of Bergen, Bergen, Norway
16,
B T King
B T King
74SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
74,
M King
M King
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
S B King
S B King
168INFN Sezione di Roma, Roma, Italy
168,
J Kirk
J Kirk
131INFN Sezione di Napoli, Naples, Italy
131,
A E Kiryunin
A E Kiryunin
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
T Kishimoto
T Kishimoto
67Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
67,
D Kisielewska
D Kisielewska
38Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
38,
F Kiss
F Kiss
48School of Physics, Shandong University, Shandong, China
48,
K Kiuchi
K Kiuchi
160Departamento de Fisica, Universidade do Minho, Braga, Portugal
160,
O Kivernyk
O Kivernyk
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
E Kladiva
E Kladiva
144Center for High Energy Physics, University of Oregon, Eugene, OR USA
144,
M H Klein
M H Klein
35Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj Napoca, Romania
35,
M Klein
M Klein
74SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
74,
U Klein
U Klein
74SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
74,
K Kleinknecht
K Kleinknecht
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
P Klimek
P Klimek
146Graduate School of Science, Osaka University, Osaka, Japan
146,
A Klimentov
A Klimentov
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
R Klingenberg
R Klingenberg
43Departamento de Física, Pontificia Universidad Católica de Chile, Santiago, Chile
43,
J A Klinger
J A Klinger
139Ohio State University, Columbus, OH USA
139,
T Klioutchnikova
T Klioutchnikova
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
E-E Kluge
E-E Kluge
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
P Kluit
P Kluit
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
S Kluth
S Kluth
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
J Knapik
J Knapik
39Cavendish Laboratory, University of Cambridge, Cambridge, UK
39,
E Kneringer
E Kneringer
62Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
62,
E B F G Knoops
E B F G Knoops
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
A Knue
A Knue
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
A Kobayashi
A Kobayashi
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
D Kobayashi
D Kobayashi
157Faculdade de Ciências, Universidade de Lisboa, Lisboa, Portugal
157,
T Kobayashi
T Kobayashi
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
M Kobel
M Kobel
44Departamento de Física, Universidad Técnica Federico Santa María, Valparaiso, Chile
44,
M Kocian
M Kocian
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
P Kodys
P Kodys
129Nagasaki Institute of Applied Science, Nagasaki, Japan
129,
T Koffas
T Koffas
29Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
29,
E Koffeman
E Koffeman
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
L A Kogan
L A Kogan
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
S Kohlmann
S Kohlmann
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
Z Kohout
Z Kohout
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
T Kohriki
T Kohriki
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
T Koi
T Koi
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
H Kolanoski
H Kolanoski
16Department for Physics and Technology, University of Bergen, Bergen, Norway
16,
I Koletsou
I Koletsou
5Istanbul Aydin University, Istanbul, Turkey
5,
A A Komar
A A Komar
96Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
96,
Y Komori
Y Komori
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
T Kondo
T Kondo
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
N Kondrashova
N Kondrashova
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
K Köneke
K Köneke
48School of Physics, Shandong University, Shandong, China
48,
A C König
A C König
106Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
106,
T Kono
T Kono
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
R Konoplich
R Konoplich
110School of Physics and Astronomy, University of Manchester, Manchester, UK
110,
N Konstantinidis
N Konstantinidis
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
R Kopeliansky
R Kopeliansky
152National Research Centre ‘Kurchatov Institute’ B.P.Konstantinov Petersburg Nuclear Physics Institute, St. Petersburg, Russia
152,
S Koperny
S Koperny
38Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
38,
L Köpke
L Köpke
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
A K Kopp
A K Kopp
48School of Physics, Shandong University, Shandong, China
48,
K Korcyl
K Korcyl
39Cavendish Laboratory, University of Cambridge, Cambridge, UK
39,
K Kordas
K Kordas
154Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
154,
A Korn
A Korn
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
A A Korol
A A Korol
109Institut für Physik, Universität Mainz, Mainz, Germany
109,
I Korolkov
I Korolkov
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
E V Korolkova
E V Korolkova
139Ohio State University, Columbus, OH USA
139,
O Kortner
O Kortner
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
S Kortner
S Kortner
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
T Kosek
T Kosek
129Nagasaki Institute of Applied Science, Nagasaki, Japan
129,
V V Kostyukhin
V V Kostyukhin
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
V M Kotov
V M Kotov
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
A Kotwal
A Kotwal
45Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
45,
A Kourkoumeli-Charalampidi
A Kourkoumeli-Charalampidi
154Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
154,
C Kourkoumelis
C Kourkoumelis
9Department of Physics, University of Arizona, Tucson, AZ USA
9,
V Kouskoura
V Kouskoura
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
A Koutsman
A Koutsman
159Centro de Física Nuclear da Universidade de Lisboa, Lisboa, Portugal
159,
R Kowalewski
R Kowalewski
169Dipartimento di Fisica, Sapienza Università di Roma, Roma, Italy
169,
T Z Kowalski
T Z Kowalski
38Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
38,
W Kozanecki
W Kozanecki
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
A S Kozhin
A S Kozhin
130Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
130,
V A Kramarenko
V A Kramarenko
99Dipartimento di Matematica e Fisica, Università del Salento, Lecce, Italy
99,
G Kramberger
G Kramberger
75II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
75,
D Krasnopevtsev
D Krasnopevtsev
98INFN Sezione di Lecce, Lecce, Italy
98,
M W Krasny
M W Krasny
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
A Krasznahorkay
A Krasznahorkay
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
J K Kraus
J K Kraus
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
A Kravchenko
A Kravchenko
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
S Kreiss
S Kreiss
110School of Physics and Astronomy, University of Manchester, Manchester, UK
110,
M Kretz
M Kretz
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
J Kretzschmar
J Kretzschmar
74SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
74,
K Kreutzfeldt
K Kreutzfeldt
52Nevis Laboratory, Columbia University, Irvington, NY USA
52,
P Krieger
P Krieger
158Department of Physics, University of Coimbra, Coimbra, Portugal
158,
K Krizka
K Krizka
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
K Kroeninger
K Kroeninger
43Departamento de Física, Pontificia Universidad Católica de Chile, Santiago, Chile
43,
H Kroha
H Kroha
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
J Kroll
J Kroll
122Group of Particle Physics, University of Montreal, Montreal, QC Canada
122,
J Kroseberg
J Kroseberg
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
J Krstic
J Krstic
13Institute of Physics, Azerbaijan Academy of Sciences, Baku, Azerbaijan
13,
U Kruchonak
U Kruchonak
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
H Krüger
H Krüger
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
N Krumnack
N Krumnack
64Department of Physics, Duke University, Durham, NC USA
64,
A Kruse
A Kruse
173Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
173,
M C Kruse
M C Kruse
45Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
45,
M Kruskal
M Kruskal
22Department of Physics Engineering, Gaziantep University, Gaziantep, Turkey
22,
T Kubota
T Kubota
88University of Iowa, Iowa City, IA USA
88,
H Kucuk
H Kucuk
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
S Kuday
S Kuday
4Department of Physics, Ankara University, Ankara, Turkey
4,
S Kuehn
S Kuehn
48School of Physics, Shandong University, Shandong, China
48,
A Kugel
A Kugel
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
F Kuger
F Kuger
174Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies-Université Hassan II, Casablanca, Morocco
174,
A Kuhl
A Kuhl
137Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
137,
T Kuhl
T Kuhl
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
V Kukhtin
V Kukhtin
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
Y Kulchitsky
Y Kulchitsky
92Graduate School of Science, Kobe University, Kobe, Japan
92,
S Kuleshov
S Kuleshov
32Instituto de Fisica, Universidade de Sao Paulo, São Paulo, Brazil
32,
M Kuna
M Kuna
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
T Kunigo
T Kunigo
68Section de Physique, Université de Genève, Geneva, Switzerland
68,
A Kupco
A Kupco
127Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
127,
H Kurashige
H Kurashige
67Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
67,
Y A Kurochkin
Y A Kurochkin
92Graduate School of Science, Kobe University, Kobe, Japan
92,
V Kus
V Kus
127Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
127,
E S Kuwertz
E S Kuwertz
169Dipartimento di Fisica, Sapienza Università di Roma, Roma, Italy
169,
M Kuze
M Kuze
157Faculdade de Ciências, Universidade de Lisboa, Lisboa, Portugal
157,
J Kvita
J Kvita
115Department of Physics, The University of Michigan, Ann Arbor, MI USA
115,
T Kwan
T Kwan
169Dipartimento di Fisica, Sapienza Università di Roma, Roma, Italy
169,
D Kyriazopoulos
D Kyriazopoulos
139Ohio State University, Columbus, OH USA
139,
A La Rosa
A La Rosa
137Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
137,
J L La Rosa Navarro
J L La Rosa Navarro
24INFN Sezione di Bologna, Bologna, Italy
24,
L La Rotonda
L La Rotonda
37West University in Timisoara, Timisoara, Romania
37,
C Lacasta
C Lacasta
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
F Lacava
F Lacava
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
J Lacey
J Lacey
29Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
29,
H Lacker
H Lacker
16Department for Physics and Technology, University of Bergen, Bergen, Norway
16,
D Lacour
D Lacour
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
V R Lacuesta
V R Lacuesta
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
E Ladygin
E Ladygin
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
R Lafaye
R Lafaye
5Istanbul Aydin University, Istanbul, Turkey
5,
B Laforge
B Laforge
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
T Lagouri
T Lagouri
176Faculté des Sciences Semlalia, Université Cadi Ayyad, LPHEA-Marrakech, Marrakech, Morocco
176,
S Lai
S Lai
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
L Lambourne
L Lambourne
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
S Lammers
S Lammers
61DESY, Hamburg and Zeuthen, Germany
61,
C L Lampen
C L Lampen
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
W Lampl
W Lampl
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
E Lançon
E Lançon
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
U Landgraf
U Landgraf
48School of Physics, Shandong University, Shandong, China
48,
M P J Landon
M P J Landon
76Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
76,
V S Lang
V S Lang
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
J C Lange
J C Lange
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
A J Lankford
A J Lankford
163Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
163,
F Lanni
F Lanni
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
K Lantzsch
K Lantzsch
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
A Lanza
A Lanza
121Department of Physics, Massachusetts Institute of Technology, Cambridge, MA USA
121,
S Laplace
S Laplace
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
C Lapoire
C Lapoire
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
J F Laporte
J F Laporte
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
T Lari
T Lari
91KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
91,
F Lasagni Manghi
F Lasagni Manghi
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
M Lassnig
M Lassnig
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
P Laurelli
P Laurelli
47Department of Physics, Nanjing University, Jiangsu, China
47,
W Lavrijsen
W Lavrijsen
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
A T Law
A T Law
137Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
137,
P Laycock
P Laycock
74SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
74,
T Lazovich
T Lazovich
57Marian Smoluchowski Institute of Physics, Jagiellonian University, Kraków, Poland
57,
O Le Dortz
O Le Dortz
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
E Le Guirriec
E Le Guirriec
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
E Le Menedeu
E Le Menedeu
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
M LeBlanc
M LeBlanc
169Dipartimento di Fisica, Sapienza Università di Roma, Roma, Italy
169,
T LeCompte
T LeCompte
6Division of Physics, TOBB University of Economics and Technology, Ankara, Turkey
6,
F Ledroit-Guillon
F Ledroit-Guillon
55Dipartimento di Fisica, Università della Calabria, Rende, Italy
55,
C A Lee
C A Lee
145LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
145,
S C Lee
S C Lee
151Department of Physics, University of Pennsylvania, Philadelphia, PA USA
151,
L Lee
L Lee
1Department of Physics, University of Adelaide, Adelaide, Australia
1,
G Lefebvre
G Lefebvre
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
M Lefebvre
M Lefebvre
169Dipartimento di Fisica, Sapienza Università di Roma, Roma, Italy
169,
F Legger
F Legger
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
C Leggett
C Leggett
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
A Lehan
A Lehan
74SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
74,
G Lehmann Miotto
G Lehmann Miotto
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
X Lei
X Lei
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
W A Leight
W A Leight
29Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
29,
A Leisos
A Leisos
154Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
154,
A G Leister
A G Leister
176Faculté des Sciences Semlalia, Université Cadi Ayyad, LPHEA-Marrakech, Marrakech, Morocco
176,
M A L Leite
M A L Leite
24INFN Sezione di Bologna, Bologna, Italy
24,
R Leitner
R Leitner
129Nagasaki Institute of Applied Science, Nagasaki, Japan
129,
D Lellouch
D Lellouch
172INFN Sezione di Roma Tre, Roma, Italy
172,
B Lemmer
B Lemmer
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
K J C Leney
K J C Leney
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
T Lenz
T Lenz
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
B Lenzi
B Lenzi
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
R Leone
R Leone
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
S Leone
S Leone
124Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
124,
C Leonidopoulos
C Leonidopoulos
46Department of Modern Physics, University of Science and Technology of China, Anhui, China
46,
S Leontsinis
S Leontsinis
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
C Leroy
C Leroy
95Department of Physics, Kyushu University, Fukuoka, Japan
95,
C G Lester
C G Lester
28Department of Physics, Brandeis University, Waltham, MA USA
28,
M Levchenko
M Levchenko
123P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
123,
J Levêque
J Levêque
5Istanbul Aydin University, Istanbul, Turkey
5,
D Levin
D Levin
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
L J Levinson
L J Levinson
172INFN Sezione di Roma Tre, Roma, Italy
172,
M Levy
M Levy
18Department of Physics, Humboldt University, Berlin, Germany
18,
A Lewis
A Lewis
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
A M Leyko
A M Leyko
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
M Leyton
M Leyton
41CERN, Geneva, Switzerland
41,
B Li
B Li
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
H Li
H Li
148Department of Physics, Oxford University, Oxford, UK
148,
H L Li
H L Li
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
L Li
L Li
45Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
45,
L Li
L Li
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
S Li
S Li
45Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
45,
X Li
X Li
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
Y Li
Y Li
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
Z Liang
Z Liang
137Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
137,
H Liao
H Liao
34National Institute of Physics and Nuclear Engineering, Bucharest, Romania
34,
B Liberti
B Liberti
133Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM USA
133,
A Liblong
A Liblong
158Department of Physics, University of Coimbra, Coimbra, Portugal
158,
P Lichard
P Lichard
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
K Lie
K Lie
165Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
165,
J Liebal
J Liebal
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
W Liebig
W Liebig
14Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
14,
C Limbach
C Limbach
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
A Limosani
A Limosani
150Dipartimento di Fisica, Università di Pavia, Pavia, Italy
150,
S C Lin
S C Lin
151Department of Physics, University of Pennsylvania, Philadelphia, PA USA
151,
T H Lin
T H Lin
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
F Linde
F Linde
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
B E Lindquist
B E Lindquist
148Department of Physics, Oxford University, Oxford, UK
148,
J T Linnemann
J T Linnemann
90Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
90,
E Lipeles
E Lipeles
122Group of Particle Physics, University of Montreal, Montreal, QC Canada
122,
A Lipniacka
A Lipniacka
14Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
14,
M Lisovyi
M Lisovyi
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
T M Liss
T M Liss
165Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
165,
D Lissauer
D Lissauer
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
A Lister
A Lister
168INFN Sezione di Roma, Roma, Italy
168,
A M Litke
A M Litke
137Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
137,
B Liu
B Liu
151Department of Physics, University of Pennsylvania, Philadelphia, PA USA
151,
D Liu
D Liu
151Department of Physics, University of Pennsylvania, Philadelphia, PA USA
151,
H Liu
H Liu
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
J Liu
J Liu
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
J B Liu
J B Liu
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
K Liu
K Liu
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
L Liu
L Liu
165Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
165,
M Liu
M Liu
45Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
45,
M Liu
M Liu
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
Y Liu
Y Liu
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
M Livan
M Livan
121Department of Physics, Massachusetts Institute of Technology, Cambridge, MA USA
121,
A Lleres
A Lleres
55Dipartimento di Fisica, Università della Calabria, Rende, Italy
55,
J Llorente Merino
J Llorente Merino
82Faculty of Applied Information Science, Hiroshima Institute of Technology, Hiroshima, Japan
82,
S L Lloyd
S L Lloyd
76Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
76,
F Lo Sterzo
F Lo Sterzo
151Department of Physics, University of Pennsylvania, Philadelphia, PA USA
151,
E Lobodzinska
E Lobodzinska
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
P Loch
P Loch
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
W S Lockman
W S Lockman
137Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
137,
F K Loebinger
F K Loebinger
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
A E Loevschall-Jensen
A E Loevschall-Jensen
36University Politehnica Bucharest, Bucharest, Romania
36,
A Loginov
A Loginov
176Faculté des Sciences Semlalia, Université Cadi Ayyad, LPHEA-Marrakech, Marrakech, Morocco
176,
T Lohse
T Lohse
16Department for Physics and Technology, University of Bergen, Bergen, Norway
16,
K Lohwasser
K Lohwasser
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
M Lokajicek
M Lokajicek
127Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
127,
B A Long
B A Long
22Department of Physics Engineering, Gaziantep University, Gaziantep, Turkey
22,
J D Long
J D Long
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
R E Long
R E Long
72High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
72,
K A Looper
K A Looper
111CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
111,
L Lopes
L Lopes
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
D Lopez Mateos
D Lopez Mateos
57Marian Smoluchowski Institute of Physics, Jagiellonian University, Kraków, Poland
57,
B Lopez Paredes
B Lopez Paredes
139Ohio State University, Columbus, OH USA
139,
I Lopez Paz
I Lopez Paz
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
J Lorenz
J Lorenz
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
N Lorenzo Martinez
N Lorenzo Martinez
61DESY, Hamburg and Zeuthen, Germany
61,
M Losada
M Losada
162Dep Fisica and CEFITEC of Faculdade de Ciencias e Tecnologia, Universidade Nova de Lisboa, Caparica, Portugal
162,
P Loscutoff
P Loscutoff
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
P J Lösel
P J Lösel
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
X Lou
X Lou
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
A Lounis
A Lounis
117INFN Sezione di Milano, Milano, Italy
117,
J Love
J Love
6Division of Physics, TOBB University of Economics and Technology, Ankara, Turkey
6,
P A Love
P A Love
72High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
72,
N Lu
N Lu
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
H J Lubatti
H J Lubatti
138Department of Physics, New York University, New York, NY USA
138,
C Luci
C Luci
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
A Lucotte
A Lucotte
55Dipartimento di Fisica, Università della Calabria, Rende, Italy
55,
F Luehring
F Luehring
61DESY, Hamburg and Zeuthen, Germany
61,
W Lukas
W Lukas
62Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
62,
L Luminari
L Luminari
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
O Lundberg
O Lundberg
146Graduate School of Science, Osaka University, Osaka, Japan
146,
B Lund-Jensen
B Lund-Jensen
147Department of Physics, University of Oslo, Oslo, Norway
147,
D Lynn
D Lynn
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
R Lysak
R Lysak
127Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
127,
E Lytken
E Lytken
81ZITI Institut für technische Informatik, Ruprecht-Karls-Universität Heidelberg, Mannheim, Germany
81,
H Ma
H Ma
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
L L Ma
L L Ma
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
G Maccarrone
G Maccarrone
47Department of Physics, Nanjing University, Jiangsu, China
47,
A Macchiolo
A Macchiolo
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
C M Macdonald
C M Macdonald
139Ohio State University, Columbus, OH USA
139,
B Maček
B Maček
75II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
75,
J Machado Miguens
J Machado Miguens
122Group of Particle Physics, University of Montreal, Montreal, QC Canada
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
122,126,
D Macina
D Macina
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
D Madaffari
D Madaffari
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
R Madar
R Madar
34National Institute of Physics and Nuclear Engineering, Bucharest, Romania
34,
H J Maddocks
H J Maddocks
72High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
72,
W F Mader
W F Mader
44Departamento de Física, Universidad Técnica Federico Santa María, Valparaiso, Chile
44,
A Madsen
A Madsen
166State Research Center Institute for High Energy Physics, Protvino, Russia
166,
J Maeda
J Maeda
67Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
67,
S Maeland
S Maeland
14Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
14,
T Maeno
T Maeno
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
A Maevskiy
A Maevskiy
99Dipartimento di Matematica e Fisica, Università del Salento, Lecce, Italy
99,
E Magradze
E Magradze
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
K Mahboubi
K Mahboubi
48School of Physics, Shandong University, Shandong, China
48,
J Mahlstedt
J Mahlstedt
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
C Maiani
C Maiani
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
C Maidantchik
C Maidantchik
24INFN Sezione di Bologna, Bologna, Italy
24,
A A Maier
A A Maier
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
T Maier
T Maier
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
A Maio
A Maio
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
S Majewski
S Majewski
116Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
116,
Y Makida
Y Makida
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
N Makovec
N Makovec
117INFN Sezione di Milano, Milano, Italy
117,
B Malaescu
B Malaescu
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
Pa Malecki
Pa Malecki
39Cavendish Laboratory, University of Cambridge, Cambridge, UK
39,
V P Maleev
V P Maleev
123P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
123,
F Malek
F Malek
55Dipartimento di Fisica, Università della Calabria, Rende, Italy
55,
U Mallik
U Mallik
63Institut für Kern- und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
63,
D Malon
D Malon
6Division of Physics, TOBB University of Economics and Technology, Ankara, Turkey
6,
C Malone
C Malone
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
S Maltezos
S Maltezos
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
V M Malyshev
V M Malyshev
109Institut für Physik, Universität Mainz, Mainz, Germany
109,
S Malyukov
S Malyukov
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
J Mamuzic
J Mamuzic
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
G Mancini
G Mancini
47Department of Physics, Nanjing University, Jiangsu, China
47,
B Mandelli
B Mandelli
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
L Mandelli
L Mandelli
91KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
91,
I Mandić
I Mandić
75II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
75,
R Mandrysch
R Mandrysch
63Institut für Kern- und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
63,
J Maneira
J Maneira
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
A Manfredini
A Manfredini
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
L Manhaes de Andrade Filho
L Manhaes de Andrade Filho
24INFN Sezione di Bologna, Bologna, Italy
24,
J Manjarres Ramos
J Manjarres Ramos
159Centro de Física Nuclear da Universidade de Lisboa, Lisboa, Portugal
159,
A Mann
A Mann
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
A Manousakis-Katsikakis
A Manousakis-Katsikakis
9Department of Physics, University of Arizona, Tucson, AZ USA
9,
B Mansoulie
B Mansoulie
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
R Mantifel
R Mantifel
87Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
87,
M Mantoani
M Mantoani
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
L Mapelli
L Mapelli
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
L March
L March
145LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
145,
G Marchiori
G Marchiori
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
M Marcisovsky
M Marcisovsky
127Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
127,
C P Marino
C P Marino
169Dipartimento di Fisica, Sapienza Università di Roma, Roma, Italy
169,
M Marjanovic
M Marjanovic
13Institute of Physics, Azerbaijan Academy of Sciences, Baku, Azerbaijan
13,
D E Marley
D E Marley
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
F Marroquim
F Marroquim
24INFN Sezione di Bologna, Bologna, Italy
24,
S P Marsden
S P Marsden
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
Z Marshall
Z Marshall
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
L F Marti
L F Marti
17Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA USA
17,
S Marti-Garcia
S Marti-Garcia
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
B Martin
B Martin
90Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
90,
T A Martin
T A Martin
170INFN Sezione di Roma Tor Vergata, Roma, Italy
170,
V J Martin
V J Martin
46Department of Modern Physics, University of Science and Technology of China, Anhui, China
46,
B Martin dit Latour
B Martin dit Latour
14Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
14,
M Martinez
M Martinez
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
S Martin-Haugh
S Martin-Haugh
131INFN Sezione di Napoli, Naples, Italy
131,
V S Martoiu
V S Martoiu
26Physikalisches Institut, University of Bonn, Bonn, Germany
26,
A C Martyniuk
A C Martyniuk
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
M Marx
M Marx
138Department of Physics, New York University, New York, NY USA
138,
F Marzano
F Marzano
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
A Marzin
A Marzin
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
L Masetti
L Masetti
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
T Mashimo
T Mashimo
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
R Mashinistov
R Mashinistov
96Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
96,
J Masik
J Masik
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
A L Maslennikov
A L Maslennikov
109Institut für Physik, Universität Mainz, Mainz, Germany
109,
I Massa
I Massa
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
L Massa
L Massa
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
N Massol
N Massol
5Istanbul Aydin University, Istanbul, Turkey
5,
P Mastrandrea
P Mastrandrea
148Department of Physics, Oxford University, Oxford, UK
148,
A Mastroberardino
A Mastroberardino
37West University in Timisoara, Timisoara, Romania
37,
T Masubuchi
T Masubuchi
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
P Mättig
P Mättig
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
J Mattmann
J Mattmann
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
J Maurer
J Maurer
26Physikalisches Institut, University of Bonn, Bonn, Germany
26,
S J Maxfield
S J Maxfield
74SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
74,
D A Maximov
D A Maximov
109Institut für Physik, Universität Mainz, Mainz, Germany
109,
R Mazini
R Mazini
151Department of Physics, University of Pennsylvania, Philadelphia, PA USA
151,
S M Mazza
S M Mazza
91KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
91,
L Mazzaferro
L Mazzaferro
133Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM USA
133,
G Mc Goldrick
G Mc Goldrick
158Department of Physics, University of Coimbra, Coimbra, Portugal
158,
S P Mc Kee
S P Mc Kee
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
A McCarn
A McCarn
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
R L McCarthy
R L McCarthy
148Department of Physics, Oxford University, Oxford, UK
148,
T G McCarthy
T G McCarthy
29Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
29,
N A McCubbin
N A McCubbin
131INFN Sezione di Napoli, Naples, Italy
131,
K W McFarlane
K W McFarlane
56AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Kraków, Poland
56,
J A Mcfayden
J A Mcfayden
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
G Mchedlidze
G Mchedlidze
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
S J McMahon
S J McMahon
131INFN Sezione di Napoli, Naples, Italy
131,
R A McPherson
R A McPherson
169Dipartimento di Fisica, Sapienza Università di Roma, Roma, Italy
169,
M Medinnis
M Medinnis
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
S Meehan
S Meehan
145LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
145,
S Mehlhase
S Mehlhase
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
A Mehta
A Mehta
74SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
74,
K Meier
K Meier
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
C Meineck
C Meineck
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
B Meirose
B Meirose
41CERN, Geneva, Switzerland
41,
B R Mellado Garcia
B R Mellado Garcia
145LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
145,
F Meloni
F Meloni
17Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA USA
17,
A Mengarelli
A Mengarelli
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
S Menke
S Menke
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
E Meoni
E Meoni
161Departamento de Fisica Teorica y del Cosmos and CAFPE, Universidad de Granada, Granada, Spain
161,
K M Mercurio
K M Mercurio
57Marian Smoluchowski Institute of Physics, Jagiellonian University, Kraków, Poland
57,
S Mergelmeyer
S Mergelmeyer
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
P Mermod
P Mermod
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
L Merola
L Merola
104Department of Physics and Astronomy, University College London, London, UK
104,
C Meroni
C Meroni
91KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
91,
F S Merritt
F S Merritt
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
A Messina
A Messina
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
J Metcalfe
J Metcalfe
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
A S Mete
A S Mete
163Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
163,
C Meyer
C Meyer
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
C Meyer
C Meyer
122Group of Particle Physics, University of Montreal, Montreal, QC Canada
122,
J-P Meyer
J-P Meyer
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
J Meyer
J Meyer
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
H Meyer Zu Theenhausen
H Meyer Zu Theenhausen
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
R P Middleton
R P Middleton
131INFN Sezione di Napoli, Naples, Italy
131,
S Miglioranzi
S Miglioranzi
164Czech Technical University in Praha, Praha, Czech Republic
164,
L Mijović
L Mijović
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
G Mikenberg
G Mikenberg
172INFN Sezione di Roma Tre, Roma, Italy
172,
M Mikestikova
M Mikestikova
127Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
127,
M Mikuž
M Mikuž
75II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
75,
M Milesi
M Milesi
88University of Iowa, Iowa City, IA USA
88,
A Milic
A Milic
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
D W Miller
D W Miller
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
C Mills
C Mills
46Department of Modern Physics, University of Science and Technology of China, Anhui, China
46,
A Milov
A Milov
172INFN Sezione di Roma Tre, Roma, Italy
172,
D A Milstead
D A Milstead
146Graduate School of Science, Osaka University, Osaka, Japan
146,
A A Minaenko
A A Minaenko
130Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
130,
Y Minami
Y Minami
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
I A Minashvili
I A Minashvili
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
A I Mincer
A I Mincer
110School of Physics and Astronomy, University of Manchester, Manchester, UK
110,
B Mindur
B Mindur
38Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
38,
M Mineev
M Mineev
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
Y Ming
Y Ming
173Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
173,
L M Mir
L M Mir
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
T Mitani
T Mitani
171Dipartimento di Fisica, Università di Roma Tor Vergata, Roma, Italy
171,
J Mitrevski
J Mitrevski
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
V A Mitsou
V A Mitsou
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
A Miucci
A Miucci
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
P S Miyagawa
P S Miyagawa
139Ohio State University, Columbus, OH USA
139,
J U Mjörnmark
J U Mjörnmark
81ZITI Institut für technische Informatik, Ruprecht-Karls-Universität Heidelberg, Mannheim, Germany
81,
T Moa
T Moa
146Graduate School of Science, Osaka University, Osaka, Japan
146,
K Mochizuki
K Mochizuki
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
S Mohapatra
S Mohapatra
35Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj Napoca, Romania
35,
W Mohr
W Mohr
48School of Physics, Shandong University, Shandong, China
48,
S Molander
S Molander
146Graduate School of Science, Osaka University, Osaka, Japan
146,
R Moles-Valls
R Moles-Valls
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
K Mönig
K Mönig
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
C Monini
C Monini
55Dipartimento di Fisica, Università della Calabria, Rende, Italy
55,
J Monk
J Monk
36University Politehnica Bucharest, Bucharest, Romania
36,
E Monnier
E Monnier
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
J Montejo Berlingen
J Montejo Berlingen
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
F Monticelli
F Monticelli
71E. Andronikashvili Institute of Physics, Iv. Javakhishvili Tbilisi State University, Tbilisi, Georgia
71,
S Monzani
S Monzani
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
R W Moore
R W Moore
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
N Morange
N Morange
117INFN Sezione di Milano, Milano, Italy
117,
D Moreno
D Moreno
162Dep Fisica and CEFITEC of Faculdade de Ciencias e Tecnologia, Universidade Nova de Lisboa, Caparica, Portugal
162,
M Moreno Llácer
M Moreno Llácer
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
P Morettini
P Morettini
50Physics Department, Tsinghua University, Beijing, 100084 China
50,
D Mori
D Mori
142Department of Physics, Oklahoma State University, Stillwater, OK USA
142,
M Morii
M Morii
57Marian Smoluchowski Institute of Physics, Jagiellonian University, Kraków, Poland
57,
M Morinaga
M Morinaga
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
V Morisbak
V Morisbak
119B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
119,
S Moritz
S Moritz
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
A K Morley
A K Morley
150Dipartimento di Fisica, Università di Pavia, Pavia, Italy
150,
G Mornacchi
G Mornacchi
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
J D Morris
J D Morris
76Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
76,
S S Mortensen
S S Mortensen
36University Politehnica Bucharest, Bucharest, Romania
36,
A Morton
A Morton
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
L Morvaj
L Morvaj
103Department of Physics, Royal Holloway University of London, Surrey, UK
103,
M Mosidze
M Mosidze
51Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
51,
J Moss
J Moss
111CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
111,
K Motohashi
K Motohashi
157Faculdade de Ciências, Universidade de Lisboa, Lisboa, Portugal
157,
R Mount
R Mount
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
E Mountricha
E Mountricha
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
S V Mouraviev
S V Mouraviev
96Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
96,
E J W Moyse
E J W Moyse
86Department of Physics, Indiana University, Bloomington, IN USA
86,
S Muanza
S Muanza
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
R D Mudd
R D Mudd
18Department of Physics, Humboldt University, Berlin, Germany
18,
F Mueller
F Mueller
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
J Mueller
J Mueller
125National Research Nuclear University MEPhI, Moscow, Russia
125,
R S P Mueller
R S P Mueller
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
T Mueller
T Mueller
28Department of Physics, Brandeis University, Waltham, MA USA
28,
D Muenstermann
D Muenstermann
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
P Mullen
P Mullen
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
G A Mullier
G A Mullier
17Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA USA
17,
J A Murillo Quijada
J A Murillo Quijada
18Department of Physics, Humboldt University, Berlin, Germany
18,
W J Murray
W J Murray
131INFN Sezione di Napoli, Naples, Italy
170INFN Sezione di Roma Tor Vergata, Roma, Italy
131,170,
H Musheghyan
H Musheghyan
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
E Musto
E Musto
152National Research Centre ‘Kurchatov Institute’ B.P.Konstantinov Petersburg Nuclear Physics Institute, St. Petersburg, Russia
152,
A G Myagkov
A G Myagkov
130Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
130,
M Myska
M Myska
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
B P Nachman
B P Nachman
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
O Nackenhorst
O Nackenhorst
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
J Nadal
J Nadal
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
K Nagai
K Nagai
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
R Nagai
R Nagai
157Faculdade de Ciências, Universidade de Lisboa, Lisboa, Portugal
157,
Y Nagai
Y Nagai
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
K Nagano
K Nagano
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
A Nagarkar
A Nagarkar
111CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
111,
Y Nagasaka
Y Nagasaka
59Physics Department, Southern Methodist University, Dallas, TX USA
59,
K Nagata
K Nagata
160Departamento de Fisica, Universidade do Minho, Braga, Portugal
160,
M Nagel
M Nagel
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
E Nagy
E Nagy
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
A M Nairz
A M Nairz
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
Y Nakahama
Y Nakahama
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
K Nakamura
K Nakamura
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
T Nakamura
T Nakamura
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
I Nakano
I Nakano
112Department of Physics, University of Massachusetts, Amherst, MA USA
112,
H Namasivayam
H Namasivayam
41CERN, Geneva, Switzerland
41,
R F Naranjo Garcia
R F Naranjo Garcia
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
R Narayan
R Narayan
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
D I Narrias Villar
D I Narrias Villar
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
T Naumann
T Naumann
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
G Navarro
G Navarro
162Dep Fisica and CEFITEC of Faculdade de Ciencias e Tecnologia, Universidade Nova de Lisboa, Caparica, Portugal
162,
R Nayyar
R Nayyar
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
H A Neal
H A Neal
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
P Yu Nechaeva
P Yu Nechaeva
96Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
96,
T J Neep
T J Neep
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
P D Nef
P D Nef
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
A Negri
A Negri
121Department of Physics, Massachusetts Institute of Technology, Cambridge, MA USA
121,
M Negrini
M Negrini
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
S Nektarijevic
S Nektarijevic
106Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
106,
C Nellist
C Nellist
117INFN Sezione di Milano, Milano, Italy
117,
A Nelson
A Nelson
163Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
163,
S Nemecek
S Nemecek
127Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
127,
P Nemethy
P Nemethy
110School of Physics and Astronomy, University of Manchester, Manchester, UK
110,
A A Nepomuceno
A A Nepomuceno
24INFN Sezione di Bologna, Bologna, Italy
24,
M Nessi
M Nessi
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
M S Neubauer
M S Neubauer
165Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
165,
M Neumann
M Neumann
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
R M Neves
R M Neves
110School of Physics and Astronomy, University of Manchester, Manchester, UK
110,
P Nevski
P Nevski
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
P R Newman
P R Newman
18Department of Physics, Humboldt University, Berlin, Germany
18,
D H Nguyen
D H Nguyen
6Division of Physics, TOBB University of Economics and Technology, Ankara, Turkey
6,
R B Nickerson
R B Nickerson
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
R Nicolaidou
R Nicolaidou
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
B Nicquevert
B Nicquevert
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
J Nielsen
J Nielsen
137Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
137,
N Nikiforou
N Nikiforou
35Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj Napoca, Romania
35,
A Nikiforov
A Nikiforov
16Department for Physics and Technology, University of Bergen, Bergen, Norway
16,
V Nikolaenko
V Nikolaenko
130Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
130,
I Nikolic-Audit
I Nikolic-Audit
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
K Nikolopoulos
K Nikolopoulos
18Department of Physics, Humboldt University, Berlin, Germany
18,
J K Nilsen
J K Nilsen
119B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
119,
P Nilsson
P Nilsson
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
Y Ninomiya
Y Ninomiya
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
A Nisati
A Nisati
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
R Nisius
R Nisius
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
T Nobe
T Nobe
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
M Nomachi
M Nomachi
118Dipartimento di Fisica, Università di Milano, Milano, Italy
118,
I Nomidis
I Nomidis
29Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
29,
T Nooney
T Nooney
76Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
76,
S Norberg
S Norberg
113Department of Physics, McGill University, Montreal, QC Canada
113,
M Nordberg
M Nordberg
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
O Novgorodova
O Novgorodova
44Departamento de Física, Universidad Técnica Federico Santa María, Valparaiso, Chile
44,
S Nowak
S Nowak
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
M Nozaki
M Nozaki
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
L Nozka
L Nozka
115Department of Physics, The University of Michigan, Ann Arbor, MI USA
115,
K Ntekas
K Ntekas
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
G Nunes Hanninger
G Nunes Hanninger
88University of Iowa, Iowa City, IA USA
88,
T Nunnemann
T Nunnemann
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
E Nurse
E Nurse
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
F Nuti
F Nuti
88University of Iowa, Iowa City, IA USA
88,
B J O’Brien
B J O’Brien
46Department of Modern Physics, University of Science and Technology of China, Anhui, China
46,
F O’grady
F O’grady
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
D C O’Neil
D C O’Neil
142Department of Physics, Oklahoma State University, Stillwater, OK USA
142,
V O’Shea
V O’Shea
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
F G Oakham
F G Oakham
29Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
29,
H Oberlack
H Oberlack
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
T Obermann
T Obermann
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
J Ocariz
J Ocariz
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
A Ochi
A Ochi
67Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
67,
I Ochoa
I Ochoa
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
J P Ochoa-Ricoux
J P Ochoa-Ricoux
32Instituto de Fisica, Universidade de Sao Paulo, São Paulo, Brazil
32,
S Oda
S Oda
70Dipartimento di Fisica, Università di Genova, Genova, Italy
70,
S Odaka
S Odaka
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
H Ogren
H Ogren
61DESY, Hamburg and Zeuthen, Germany
61,
A Oh
A Oh
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
S H Oh
S H Oh
45Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
45,
C C Ohm
C C Ohm
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
H Ohman
H Ohman
166State Research Center Institute for High Energy Physics, Protvino, Russia
166,
H Oide
H Oide
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
W Okamura
W Okamura
118Dipartimento di Fisica, Università di Milano, Milano, Italy
118,
H Okawa
H Okawa
160Departamento de Fisica, Universidade do Minho, Braga, Portugal
160,
Y Okumura
Y Okumura
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
T Okuyama
T Okuyama
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
A Olariu
A Olariu
26Physikalisches Institut, University of Bonn, Bonn, Germany
26,
S A Olivares Pino
S A Olivares Pino
46Department of Modern Physics, University of Science and Technology of China, Anhui, China
46,
D Oliveira Damazio
D Oliveira Damazio
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
E Oliver Garcia
E Oliver Garcia
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
A Olszewski
A Olszewski
39Cavendish Laboratory, University of Cambridge, Cambridge, UK
39,
J Olszowska
J Olszowska
39Cavendish Laboratory, University of Cambridge, Cambridge, UK
39,
A Onofre
A Onofre
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
P U E Onyisi
P U E Onyisi
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
C J Oram
C J Oram
159Centro de Física Nuclear da Universidade de Lisboa, Lisboa, Portugal
159,
M J Oreglia
M J Oreglia
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
Y Oren
Y Oren
153INFN Sezione di Pisa, Pisa, Italy
153,
D Orestano
D Orestano
134Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
134,
N Orlando
N Orlando
154Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
154,
C Oropeza Barrera
C Oropeza Barrera
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
R S Orr
R S Orr
158Department of Physics, University of Coimbra, Coimbra, Portugal
158,
B Osculati
B Osculati
50Physics Department, Tsinghua University, Beijing, 100084 China
50,
R Ospanov
R Ospanov
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
G Otero y Garzon
G Otero y Garzon
27Department of Physics, Boston University, Boston, MA USA
27,
H Otono
H Otono
70Dipartimento di Fisica, Università di Genova, Genova, Italy
70,
M Ouchrif
M Ouchrif
135Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
135,
F Ould-Saada
F Ould-Saada
119B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
119,
A Ouraou
A Ouraou
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
K P Oussoren
K P Oussoren
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
Q Ouyang
Q Ouyang
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
A Ovcharova
A Ovcharova
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
M Owen
M Owen
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
R E Owen
R E Owen
18Department of Physics, Humboldt University, Berlin, Germany
18,
V E Ozcan
V E Ozcan
19Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
19,
N Ozturk
N Ozturk
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
K Pachal
K Pachal
142Department of Physics, Oklahoma State University, Stillwater, OK USA
142,
A Pacheco Pages
A Pacheco Pages
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
C Padilla Aranda
C Padilla Aranda
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
M Pagáčová
M Pagáčová
48School of Physics, Shandong University, Shandong, China
48,
S Pagan Griso
S Pagan Griso
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
E Paganis
E Paganis
139Ohio State University, Columbus, OH USA
139,
F Paige
F Paige
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
P Pais
P Pais
86Department of Physics, Indiana University, Bloomington, IN USA
86,
K Pajchel
K Pajchel
119B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
119,
G Palacino
G Palacino
159Centro de Física Nuclear da Universidade de Lisboa, Lisboa, Portugal
159,
S Palestini
S Palestini
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
M Palka
M Palka
38Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
38,
D Pallin
D Pallin
34National Institute of Physics and Nuclear Engineering, Bucharest, Romania
34,
A Palma
A Palma
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
Y B Pan
Y B Pan
173Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
173,
E Panagiotopoulou
E Panagiotopoulou
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
C E Pandini
C E Pandini
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
J G Panduro Vazquez
J G Panduro Vazquez
77Department of Physics, Hampton University, Hampton, VA USA
77,
P Pani
P Pani
146Graduate School of Science, Osaka University, Osaka, Japan
146,
S Panitkin
S Panitkin
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
D Pantea
D Pantea
26Physikalisches Institut, University of Bonn, Bonn, Germany
26,
L Paolozzi
L Paolozzi
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
Th D Papadopoulou
Th D Papadopoulou
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
K Papageorgiou
K Papageorgiou
154Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
154,
A Paramonov
A Paramonov
6Division of Physics, TOBB University of Economics and Technology, Ankara, Turkey
6,
D Paredes Hernandez
D Paredes Hernandez
154Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
154,
M A Parker
M A Parker
28Department of Physics, Brandeis University, Waltham, MA USA
28,
K A Parker
K A Parker
139Ohio State University, Columbus, OH USA
139,
F Parodi
F Parodi
50Physics Department, Tsinghua University, Beijing, 100084 China
50,
J A Parsons
J A Parsons
35Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj Napoca, Romania
35,
U Parzefall
U Parzefall
48School of Physics, Shandong University, Shandong, China
48,
E Pasqualucci
E Pasqualucci
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
S Passaggio
S Passaggio
50Physics Department, Tsinghua University, Beijing, 100084 China
50,
F Pastore
F Pastore
134Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
134,
Fr Pastore
Fr Pastore
77Department of Physics, Hampton University, Hampton, VA USA
77,
G Pásztor
G Pásztor
29Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
29,
S Pataraia
S Pataraia
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
N D Patel
N D Patel
150Dipartimento di Fisica, Università di Pavia, Pavia, Italy
150,
J R Pater
J R Pater
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
T Pauly
T Pauly
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
J Pearce
J Pearce
169Dipartimento di Fisica, Sapienza Università di Roma, Roma, Italy
169,
B Pearson
B Pearson
113Department of Physics, McGill University, Montreal, QC Canada
113,
L E Pedersen
L E Pedersen
36University Politehnica Bucharest, Bucharest, Romania
36,
M Pedersen
M Pedersen
119B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
119,
S Pedraza Lopez
S Pedraza Lopez
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
R Pedro
R Pedro
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
S V Peleganchuk
S V Peleganchuk
109Institut für Physik, Universität Mainz, Mainz, Germany
109,
D Pelikan
D Pelikan
166State Research Center Institute for High Energy Physics, Protvino, Russia
166,
O Penc
O Penc
127Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
127,
C Peng
C Peng
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
H Peng
H Peng
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
B Penning
B Penning
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
J Penwell
J Penwell
61DESY, Hamburg and Zeuthen, Germany
61,
D V Perepelitsa
D V Perepelitsa
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
E Perez Codina
E Perez Codina
159Centro de Física Nuclear da Universidade de Lisboa, Lisboa, Portugal
159,
M T Pérez García-Estañ
M T Pérez García-Estañ
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
L Perini
L Perini
91KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
91,
H Pernegger
H Pernegger
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
S Perrella
S Perrella
104Department of Physics and Astronomy, University College London, London, UK
104,
R Peschke
R Peschke
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
V D Peshekhonov
V D Peshekhonov
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
K Peters
K Peters
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
R F Y Peters
R F Y Peters
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
B A Petersen
B A Petersen
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
T C Petersen
T C Petersen
36University Politehnica Bucharest, Bucharest, Romania
36,
E Petit
E Petit
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
A Petridis
A Petridis
1Department of Physics, University of Adelaide, Adelaide, Australia
1,
C Petridou
C Petridou
154Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
154,
P Petroff
P Petroff
117INFN Sezione di Milano, Milano, Italy
117,
E Petrolo
E Petrolo
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
F Petrucci
F Petrucci
134Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
134,
N E Pettersson
N E Pettersson
157Faculdade de Ciências, Universidade de Lisboa, Lisboa, Portugal
157,
R Pezoa
R Pezoa
32Instituto de Fisica, Universidade de Sao Paulo, São Paulo, Brazil
32,
P W Phillips
P W Phillips
131INFN Sezione di Napoli, Naples, Italy
131,
G Piacquadio
G Piacquadio
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
E Pianori
E Pianori
170INFN Sezione di Roma Tor Vergata, Roma, Italy
170,
A Picazio
A Picazio
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
E Piccaro
E Piccaro
76Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
76,
M Piccinini
M Piccinini
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
M A Pickering
M A Pickering
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
R Piegaia
R Piegaia
27Department of Physics, Boston University, Boston, MA USA
27,
D T Pignotti
D T Pignotti
111CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
111,
J E Pilcher
J E Pilcher
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
A D Pilkington
A D Pilkington
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
J Pina
J Pina
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
M Pinamonti
M Pinamonti
164Czech Technical University in Praha, Praha, Czech Republic
164,
J L Pinfold
J L Pinfold
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
A Pingel
A Pingel
36University Politehnica Bucharest, Bucharest, Romania
36,
S Pires
S Pires
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
H Pirumov
H Pirumov
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
M Pitt
M Pitt
172INFN Sezione di Roma Tre, Roma, Italy
172,
C Pizio
C Pizio
91KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
91,
L Plazak
L Plazak
144Center for High Energy Physics, University of Oregon, Eugene, OR USA
144,
M-A Pleier
M-A Pleier
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
V Pleskot
V Pleskot
129Nagasaki Institute of Applied Science, Nagasaki, Japan
129,
E Plotnikova
E Plotnikova
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
P Plucinski
P Plucinski
146Graduate School of Science, Osaka University, Osaka, Japan
146,
D Pluth
D Pluth
64Department of Physics, Duke University, Durham, NC USA
64,
R Poettgen
R Poettgen
146Graduate School of Science, Osaka University, Osaka, Japan
146,
L Poggioli
L Poggioli
117INFN Sezione di Milano, Milano, Italy
117,
D Pohl
D Pohl
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
G Polesello
G Polesello
121Department of Physics, Massachusetts Institute of Technology, Cambridge, MA USA
121,
A Poley
A Poley
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
A Policicchio
A Policicchio
37West University in Timisoara, Timisoara, Romania
37,
R Polifka
R Polifka
158Department of Physics, University of Coimbra, Coimbra, Portugal
158,
A Polini
A Polini
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
C S Pollard
C S Pollard
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
V Polychronakos
V Polychronakos
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
K Pommès
K Pommès
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
L Pontecorvo
L Pontecorvo
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
B G Pope
B G Pope
90Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
90,
G A Popeneciu
G A Popeneciu
26Physikalisches Institut, University of Bonn, Bonn, Germany
26,
D S Popovic
D S Popovic
13Institute of Physics, Azerbaijan Academy of Sciences, Baku, Azerbaijan
13,
A Poppleton
A Poppleton
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
S Pospisil
S Pospisil
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
K Potamianos
K Potamianos
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
I N Potrap
I N Potrap
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
C J Potter
C J Potter
149INFN Sezione di Pavia, Pavia, Italy
149,
C T Potter
C T Potter
116Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
116,
G Poulard
G Poulard
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
J Poveda
J Poveda
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
V Pozdnyakov
V Pozdnyakov
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
P Pralavorio
P Pralavorio
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
A Pranko
A Pranko
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
S Prasad
S Prasad
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
S Prell
S Prell
64Department of Physics, Duke University, Durham, NC USA
64,
D Price
D Price
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
L E Price
L E Price
6Division of Physics, TOBB University of Economics and Technology, Ankara, Turkey
6,
M Primavera
M Primavera
73II Physikalisches Institut, Justus-Liebig-Universität Giessen, Giessen, Germany
73,
S Prince
S Prince
87Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
87,
M Proissl
M Proissl
46Department of Modern Physics, University of Science and Technology of China, Anhui, China
46,
K Prokofiev
K Prokofiev
60Physics Department, University of Texas at Dallas, Richardson, TX USA
60,
F Prokoshin
F Prokoshin
32Instituto de Fisica, Universidade de Sao Paulo, São Paulo, Brazil
32,
E Protopapadaki
E Protopapadaki
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
S Protopopescu
S Protopopescu
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
J Proudfoot
J Proudfoot
6Division of Physics, TOBB University of Economics and Technology, Ankara, Turkey
6,
M Przybycien
M Przybycien
38Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
38,
E Ptacek
E Ptacek
116Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
116,
D Puddu
D Puddu
134Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
134,
E Pueschel
E Pueschel
86Department of Physics, Indiana University, Bloomington, IN USA
86,
D Puldon
D Puldon
148Department of Physics, Oxford University, Oxford, UK
148,
M Purohit
M Purohit
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
P Puzo
P Puzo
117INFN Sezione di Milano, Milano, Italy
117,
J Qian
J Qian
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
G Qin
G Qin
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
Y Qin
Y Qin
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
A Quadt
A Quadt
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
D R Quarrie
D R Quarrie
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
W B Quayle
W B Quayle
164Czech Technical University in Praha, Praha, Czech Republic
164,
M Queitsch-Maitland
M Queitsch-Maitland
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
D Quilty
D Quilty
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
S Raddum
S Raddum
119B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
119,
V Radeka
V Radeka
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
V Radescu
V Radescu
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
S K Radhakrishnan
S K Radhakrishnan
148Department of Physics, Oxford University, Oxford, UK
148,
P Radloff
P Radloff
116Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
116,
P Rados
P Rados
88University of Iowa, Iowa City, IA USA
88,
F Ragusa
F Ragusa
91KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
91,
G Rahal
G Rahal
178Faculté des Sciences, Université Mohammed V-Agdal, Rabat, Morocco
178,
S Rajagopalan
S Rajagopalan
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
M Rammensee
M Rammensee
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
C Rangel-Smith
C Rangel-Smith
166State Research Center Institute for High Energy Physics, Protvino, Russia
166,
F Rauscher
F Rauscher
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
S Rave
S Rave
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
T Ravenscroft
T Ravenscroft
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
M Raymond
M Raymond
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
A L Read
A L Read
119B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
119,
N P Readioff
N P Readioff
74SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
74,
D M Rebuzzi
D M Rebuzzi
121Department of Physics, Massachusetts Institute of Technology, Cambridge, MA USA
121,
A Redelbach
A Redelbach
174Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies-Université Hassan II, Casablanca, Morocco
174,
G Redlinger
G Redlinger
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
R Reece
R Reece
137Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
137,
K Reeves
K Reeves
41CERN, Geneva, Switzerland
41,
L Rehnisch
L Rehnisch
16Department for Physics and Technology, University of Bergen, Bergen, Norway
16,
J Reichert
J Reichert
122Group of Particle Physics, University of Montreal, Montreal, QC Canada
122,
H Reisin
H Reisin
27Department of Physics, Boston University, Boston, MA USA
27,
M Relich
M Relich
163Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
163,
C Rembser
C Rembser
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
H Ren
H Ren
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
A Renaud
A Renaud
117INFN Sezione di Milano, Milano, Italy
117,
M Rescigno
M Rescigno
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
S Resconi
S Resconi
91KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
91,
O L Rezanova
O L Rezanova
109Institut für Physik, Universität Mainz, Mainz, Germany
109,
P Reznicek
P Reznicek
129Nagasaki Institute of Applied Science, Nagasaki, Japan
129,
R Rezvani
R Rezvani
95Department of Physics, Kyushu University, Fukuoka, Japan
95,
R Richter
R Richter
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
S Richter
S Richter
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
E Richter-Was
E Richter-Was
38Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
38,
O Ricken
O Ricken
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
M Ridel
M Ridel
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
P Rieck
P Rieck
16Department for Physics and Technology, University of Bergen, Bergen, Norway
16,
C J Riegel
C J Riegel
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
J Rieger
J Rieger
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
M Rijssenbeek
M Rijssenbeek
148Department of Physics, Oxford University, Oxford, UK
148,
A Rimoldi
A Rimoldi
121Department of Physics, Massachusetts Institute of Technology, Cambridge, MA USA
121,
L Rinaldi
L Rinaldi
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
B Ristić
B Ristić
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
E Ritsch
E Ritsch
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
I Riu
I Riu
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
F Rizatdinova
F Rizatdinova
114School of Physics, University of Melbourne, Melbourne, VIC Australia
114,
E Rizvi
E Rizvi
76Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
76,
S H Robertson
S H Robertson
87Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
87,
A Robichaud-Veronneau
A Robichaud-Veronneau
87Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
87,
D Robinson
D Robinson
28Department of Physics, Brandeis University, Waltham, MA USA
28,
J E M Robinson
J E M Robinson
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
A Robson
A Robson
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
C Roda
C Roda
124Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
124,
S Roe
S Roe
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
O Røhne
O Røhne
119B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
119,
S Rolli
S Rolli
161Departamento de Fisica Teorica y del Cosmos and CAFPE, Universidad de Granada, Granada, Spain
161,
A Romaniouk
A Romaniouk
98INFN Sezione di Lecce, Lecce, Italy
98,
M Romano
M Romano
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
S M Romano Saez
S M Romano Saez
34National Institute of Physics and Nuclear Engineering, Bucharest, Romania
34,
E Romero Adam
E Romero Adam
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
N Rompotis
N Rompotis
138Department of Physics, New York University, New York, NY USA
138,
M Ronzani
M Ronzani
48School of Physics, Shandong University, Shandong, China
48,
L Roos
L Roos
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
E Ros
E Ros
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
S Rosati
S Rosati
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
K Rosbach
K Rosbach
48School of Physics, Shandong University, Shandong, China
48,
P Rose
P Rose
137Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
137,
P L Rosendahl
P L Rosendahl
14Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
14,
O Rosenthal
O Rosenthal
141Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK USA
141,
V Rossetti
V Rossetti
146Graduate School of Science, Osaka University, Osaka, Japan
146,
E Rossi
E Rossi
104Department of Physics and Astronomy, University College London, London, UK
104,
L P Rossi
L P Rossi
50Physics Department, Tsinghua University, Beijing, 100084 China
50,
J H N Rosten
J H N Rosten
28Department of Physics, Brandeis University, Waltham, MA USA
28,
R Rosten
R Rosten
138Department of Physics, New York University, New York, NY USA
138,
M Rotaru
M Rotaru
26Physikalisches Institut, University of Bonn, Bonn, Germany
26,
I Roth
I Roth
172INFN Sezione di Roma Tre, Roma, Italy
172,
J Rothberg
J Rothberg
138Department of Physics, New York University, New York, NY USA
138,
D Rousseau
D Rousseau
117INFN Sezione di Milano, Milano, Italy
117,
C R Royon
C R Royon
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
A Rozanov
A Rozanov
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
Y Rozen
Y Rozen
152National Research Centre ‘Kurchatov Institute’ B.P.Konstantinov Petersburg Nuclear Physics Institute, St. Petersburg, Russia
152,
X Ruan
X Ruan
145LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
145,
F Rubbo
F Rubbo
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
I Rubinskiy
I Rubinskiy
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
V I Rud
V I Rud
99Dipartimento di Matematica e Fisica, Università del Salento, Lecce, Italy
99,
C Rudolph
C Rudolph
44Departamento de Física, Universidad Técnica Federico Santa María, Valparaiso, Chile
44,
M S Rudolph
M S Rudolph
158Department of Physics, University of Coimbra, Coimbra, Portugal
158,
F Rühr
F Rühr
48School of Physics, Shandong University, Shandong, China
48,
A Ruiz-Martinez
A Ruiz-Martinez
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
Z Rurikova
Z Rurikova
48School of Physics, Shandong University, Shandong, China
48,
N A Rusakovich
N A Rusakovich
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
A Ruschke
A Ruschke
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
H L Russell
H L Russell
138Department of Physics, New York University, New York, NY USA
138,
J P Rutherfoord
J P Rutherfoord
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
N Ruthmann
N Ruthmann
48School of Physics, Shandong University, Shandong, China
48,
Y F Ryabov
Y F Ryabov
123P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
123,
M Rybar
M Rybar
165Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
165,
G Rybkin
G Rybkin
117INFN Sezione di Milano, Milano, Italy
117,
N C Ryder
N C Ryder
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
A F Saavedra
A F Saavedra
150Dipartimento di Fisica, Università di Pavia, Pavia, Italy
150,
G Sabato
G Sabato
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
S Sacerdoti
S Sacerdoti
27Department of Physics, Boston University, Boston, MA USA
27,
A Saddique
A Saddique
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
H F-W Sadrozinski
H F-W Sadrozinski
137Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
137,
R Sadykov
R Sadykov
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
F Safai Tehrani
F Safai Tehrani
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
M Sahinsoy
M Sahinsoy
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
M Saimpert
M Saimpert
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
T Saito
T Saito
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
H Sakamoto
H Sakamoto
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
Y Sakurai
Y Sakurai
171Dipartimento di Fisica, Università di Roma Tor Vergata, Roma, Italy
171,
G Salamanna
G Salamanna
134Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
134,
A Salamon
A Salamon
133Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM USA
133,
J E Salazar Loyola
J E Salazar Loyola
32Instituto de Fisica, Universidade de Sao Paulo, São Paulo, Brazil
32,
M Saleem
M Saleem
113Department of Physics, McGill University, Montreal, QC Canada
113,
D Salek
D Salek
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
P H Sales De Bruin
P H Sales De Bruin
138Department of Physics, New York University, New York, NY USA
138,
D Salihagic
D Salihagic
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
A Salnikov
A Salnikov
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
J Salt
J Salt
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
D Salvatore
D Salvatore
37West University in Timisoara, Timisoara, Romania
37,
F Salvatore
F Salvatore
149INFN Sezione di Pavia, Pavia, Italy
149,
A Salvucci
A Salvucci
60Physics Department, University of Texas at Dallas, Richardson, TX USA
60,
A Salzburger
A Salzburger
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
D Sammel
D Sammel
48School of Physics, Shandong University, Shandong, China
48,
D Sampsonidis
D Sampsonidis
154Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
154,
A Sanchez
A Sanchez
104Department of Physics and Astronomy, University College London, London, UK
104,
J Sánchez
J Sánchez
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
V Sanchez Martinez
V Sanchez Martinez
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
H Sandaker
H Sandaker
119B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
119,
R L Sandbach
R L Sandbach
76Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
76,
H G Sander
H G Sander
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
M P Sanders
M P Sanders
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
M Sandhoff
M Sandhoff
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
C Sandoval
C Sandoval
162Dep Fisica and CEFITEC of Faculdade de Ciencias e Tecnologia, Universidade Nova de Lisboa, Caparica, Portugal
162,
R Sandstroem
R Sandstroem
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
D P C Sankey
D P C Sankey
131INFN Sezione di Napoli, Naples, Italy
131,
M Sannino
M Sannino
50Physics Department, Tsinghua University, Beijing, 100084 China
50,
A Sansoni
A Sansoni
47Department of Physics, Nanjing University, Jiangsu, China
47,
C Santoni
C Santoni
34National Institute of Physics and Nuclear Engineering, Bucharest, Romania
34,
R Santonico
R Santonico
133Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM USA
133,
H Santos
H Santos
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
I Santoyo Castillo
I Santoyo Castillo
149INFN Sezione di Pavia, Pavia, Italy
149,
K Sapp
K Sapp
125National Research Nuclear University MEPhI, Moscow, Russia
125,
A Sapronov
A Sapronov
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
J G Saraiva
J G Saraiva
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
B Sarrazin
B Sarrazin
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
O Sasaki
O Sasaki
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
Y Sasaki
Y Sasaki
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
K Sato
K Sato
160Departamento de Fisica, Universidade do Minho, Braga, Portugal
160,
G Sauvage
G Sauvage
5Istanbul Aydin University, Istanbul, Turkey
5,
E Sauvan
E Sauvan
5Istanbul Aydin University, Istanbul, Turkey
5,
G Savage
G Savage
77Department of Physics, Hampton University, Hampton, VA USA
77,
P Savard
P Savard
158Department of Physics, University of Coimbra, Coimbra, Portugal
158,
C Sawyer
C Sawyer
131INFN Sezione di Napoli, Naples, Italy
131,
L Sawyer
L Sawyer
79Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
79,
J Saxon
J Saxon
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
C Sbarra
C Sbarra
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
A Sbrizzi
A Sbrizzi
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
T Scanlon
T Scanlon
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
D A Scannicchio
D A Scannicchio
163Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
163,
M Scarcella
M Scarcella
150Dipartimento di Fisica, Università di Pavia, Pavia, Italy
150,
V Scarfone
V Scarfone
37West University in Timisoara, Timisoara, Romania
37,
J Schaarschmidt
J Schaarschmidt
172INFN Sezione di Roma Tre, Roma, Italy
172,
P Schacht
P Schacht
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
D Schaefer
D Schaefer
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
R Schaefer
R Schaefer
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
J Schaeffer
J Schaeffer
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
S Schaepe
S Schaepe
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
S Schaetzel
S Schaetzel
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
U Schäfer
U Schäfer
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
A C Schaffer
A C Schaffer
117INFN Sezione di Milano, Milano, Italy
117,
D Schaile
D Schaile
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
R D Schamberger
R D Schamberger
148Department of Physics, Oxford University, Oxford, UK
148,
V Scharf
V Scharf
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
V A Schegelsky
V A Schegelsky
123P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
123,
D Scheirich
D Scheirich
129Nagasaki Institute of Applied Science, Nagasaki, Japan
129,
M Schernau
M Schernau
163Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
163,
C Schiavi
C Schiavi
50Physics Department, Tsinghua University, Beijing, 100084 China
50,
C Schillo
C Schillo
48School of Physics, Shandong University, Shandong, China
48,
M Schioppa
M Schioppa
37West University in Timisoara, Timisoara, Romania
37,
S Schlenker
S Schlenker
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
K Schmieden
K Schmieden
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
C Schmitt
C Schmitt
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
S Schmitt
S Schmitt
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
S Schmitt
S Schmitt
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
B Schneider
B Schneider
159Centro de Física Nuclear da Universidade de Lisboa, Lisboa, Portugal
159,
Y J Schnellbach
Y J Schnellbach
74SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
74,
U Schnoor
U Schnoor
44Departamento de Física, Universidad Técnica Federico Santa María, Valparaiso, Chile
44,
L Schoeffel
L Schoeffel
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
A Schoening
A Schoening
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
B D Schoenrock
B D Schoenrock
90Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
90,
E Schopf
E Schopf
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
A L S Schorlemmer
A L S Schorlemmer
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
M Schott
M Schott
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
D Schouten
D Schouten
159Centro de Física Nuclear da Universidade de Lisboa, Lisboa, Portugal
159,
J Schovancova
J Schovancova
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
S Schramm
S Schramm
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
M Schreyer
M Schreyer
174Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies-Université Hassan II, Casablanca, Morocco
174,
C Schroeder
C Schroeder
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
N Schuh
N Schuh
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
M J Schultens
M J Schultens
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
H-C Schultz-Coulon
H-C Schultz-Coulon
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
H Schulz
H Schulz
16Department for Physics and Technology, University of Bergen, Bergen, Norway
16,
M Schumacher
M Schumacher
48School of Physics, Shandong University, Shandong, China
48,
B A Schumm
B A Schumm
137Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
137,
Ph Schune
Ph Schune
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
C Schwanenberger
C Schwanenberger
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
A Schwartzman
A Schwartzman
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
T A Schwarz
T A Schwarz
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
Ph Schwegler
Ph Schwegler
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
H Schweiger
H Schweiger
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
Ph Schwemling
Ph Schwemling
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
R Schwienhorst
R Schwienhorst
90Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
90,
J Schwindling
J Schwindling
136Department of Physics, Northern Illinois University, DeKalb, IL USA
136,
T Schwindt
T Schwindt
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
F G Sciacca
F G Sciacca
17Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA USA
17,
E Scifo
E Scifo
117INFN Sezione di Milano, Milano, Italy
117,
G Sciolla
G Sciolla
23Department of Physics, Dogus University, Istanbul, Turkey
23,
F Scuri
F Scuri
124Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
124,
F Scutti
F Scutti
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
J Searcy
J Searcy
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
G Sedov
G Sedov
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
E Sedykh
E Sedykh
123P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
123,
P Seema
P Seema
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
S C Seidel
S C Seidel
105Louisiana Tech University, Ruston, LA USA
105,
A Seiden
A Seiden
137Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
137,
F Seifert
F Seifert
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
J M Seixas
J M Seixas
24INFN Sezione di Bologna, Bologna, Italy
24,
G Sekhniaidze
G Sekhniaidze
104Department of Physics and Astronomy, University College London, London, UK
104,
K Sekhon
K Sekhon
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
S J Sekula
S J Sekula
40Department of Physics, Carleton University, Ottawa, ON Canada
40,
D M Seliverstov
D M Seliverstov
123P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
123,
N Semprini-Cesari
N Semprini-Cesari
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
C Serfon
C Serfon
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
L Serin
L Serin
117INFN Sezione di Milano, Milano, Italy
117,
L Serkin
L Serkin
164Czech Technical University in Praha, Praha, Czech Republic
164,
T Serre
T Serre
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
M Sessa
M Sessa
134Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
134,
R Seuster
R Seuster
159Centro de Física Nuclear da Universidade de Lisboa, Lisboa, Portugal
159,
H Severini
H Severini
113Department of Physics, McGill University, Montreal, QC Canada
113,
T Sfiligoj
T Sfiligoj
75II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
75,
F Sforza
F Sforza
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
A Sfyrla
A Sfyrla
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
E Shabalina
E Shabalina
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
M Shamim
M Shamim
116Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
116,
L Y Shan
L Y Shan
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
R Shang
R Shang
165Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
165,
J T Shank
J T Shank
22Department of Physics Engineering, Gaziantep University, Gaziantep, Turkey
22,
M Shapiro
M Shapiro
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
P B Shatalov
P B Shatalov
97Physics Department, Lancaster University, Lancaster, UK
97,
K Shaw
K Shaw
164Czech Technical University in Praha, Praha, Czech Republic
164,
S M Shaw
S M Shaw
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
A Shcherbakova
A Shcherbakova
146Graduate School of Science, Osaka University, Osaka, Japan
146,
C Y Shehu
C Y Shehu
149INFN Sezione di Pavia, Pavia, Italy
149,
P Sherwood
P Sherwood
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
L Shi
L Shi
151Department of Physics, University of Pennsylvania, Philadelphia, PA USA
151,
S Shimizu
S Shimizu
67Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
67,
C O Shimmin
C O Shimmin
163Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
163,
M Shimojima
M Shimojima
102School of Physics and Astronomy, Queen Mary University of London, London, UK
102,
M Shiyakova
M Shiyakova
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
A Shmeleva
A Shmeleva
96Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
96,
D Shoaleh Saadi
D Shoaleh Saadi
95Department of Physics, Kyushu University, Fukuoka, Japan
95,
M J Shochet
M J Shochet
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
S Shojaii
S Shojaii
91KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
91,
S Shrestha
S Shrestha
111CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
111,
E Shulga
E Shulga
98INFN Sezione di Lecce, Lecce, Italy
98,
M A Shupe
M A Shupe
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
S Shushkevich
S Shushkevich
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
P Sicho
P Sicho
127Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
127,
P E Sidebo
P E Sidebo
147Department of Physics, University of Oslo, Oslo, Norway
147,
O Sidiropoulou
O Sidiropoulou
174Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies-Université Hassan II, Casablanca, Morocco
174,
D Sidorov
D Sidorov
114School of Physics, University of Melbourne, Melbourne, VIC Australia
114,
A Sidoti
A Sidoti
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
F Siegert
F Siegert
44Departamento de Física, Universidad Técnica Federico Santa María, Valparaiso, Chile
44,
Dj Sijacki
Dj Sijacki
13Institute of Physics, Azerbaijan Academy of Sciences, Baku, Azerbaijan
13,
J Silva
J Silva
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
Y Silver
Y Silver
153INFN Sezione di Pisa, Pisa, Italy
153,
S B Silverstein
S B Silverstein
146Graduate School of Science, Osaka University, Osaka, Japan
146,
V Simak
V Simak
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
O Simard
O Simard
5Istanbul Aydin University, Istanbul, Turkey
5,
Lj Simic
Lj Simic
13Institute of Physics, Azerbaijan Academy of Sciences, Baku, Azerbaijan
13,
S Simion
S Simion
117INFN Sezione di Milano, Milano, Italy
117,
E Simioni
E Simioni
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
B Simmons
B Simmons
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
D Simon
D Simon
34National Institute of Physics and Nuclear Engineering, Bucharest, Romania
34,
P Sinervo
P Sinervo
158Department of Physics, University of Coimbra, Coimbra, Portugal
158,
N B Sinev
N B Sinev
116Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
116,
M Sioli
M Sioli
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
G Siragusa
G Siragusa
174Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies-Université Hassan II, Casablanca, Morocco
174,
A N Sisakyan
A N Sisakyan
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
S Yu Sivoklokov
S Yu Sivoklokov
99Dipartimento di Matematica e Fisica, Università del Salento, Lecce, Italy
99,
J Sjölin
J Sjölin
146Graduate School of Science, Osaka University, Osaka, Japan
146,
T B Sjursen
T B Sjursen
14Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
14,
M B Skinner
M B Skinner
72High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
72,
H P Skottowe
H P Skottowe
57Marian Smoluchowski Institute of Physics, Jagiellonian University, Kraków, Poland
57,
P Skubic
P Skubic
113Department of Physics, McGill University, Montreal, QC Canada
113,
M Slater
M Slater
18Department of Physics, Humboldt University, Berlin, Germany
18,
T Slavicek
T Slavicek
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
M Slawinska
M Slawinska
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
K Sliwa
K Sliwa
161Departamento de Fisica Teorica y del Cosmos and CAFPE, Universidad de Granada, Granada, Spain
161,
V Smakhtin
V Smakhtin
172INFN Sezione di Roma Tre, Roma, Italy
172,
B H Smart
B H Smart
46Department of Modern Physics, University of Science and Technology of China, Anhui, China
46,
L Smestad
L Smestad
14Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
14,
S Yu Smirnov
S Yu Smirnov
98INFN Sezione di Lecce, Lecce, Italy
98,
Y Smirnov
Y Smirnov
98INFN Sezione di Lecce, Lecce, Italy
98,
L N Smirnova
L N Smirnova
99Dipartimento di Matematica e Fisica, Università del Salento, Lecce, Italy
99,
O Smirnova
O Smirnova
81ZITI Institut für technische Informatik, Ruprecht-Karls-Universität Heidelberg, Mannheim, Germany
81,
M N K Smith
M N K Smith
35Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj Napoca, Romania
35,
R W Smith
R W Smith
35Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj Napoca, Romania
35,
M Smizanska
M Smizanska
72High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
72,
K Smolek
K Smolek
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
A A Snesarev
A A Snesarev
96Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
96,
G Snidero
G Snidero
76Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
76,
S Snyder
S Snyder
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
R Sobie
R Sobie
169Dipartimento di Fisica, Sapienza Università di Roma, Roma, Italy
169,
F Socher
F Socher
44Departamento de Física, Universidad Técnica Federico Santa María, Valparaiso, Chile
44,
A Soffer
A Soffer
153INFN Sezione di Pisa, Pisa, Italy
153,
D A Soh
D A Soh
151Department of Physics, University of Pennsylvania, Philadelphia, PA USA
151,
G Sokhrannyi
G Sokhrannyi
75II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
75,
C A Solans
C A Solans
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
M Solar
M Solar
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
J Solc
J Solc
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
E Yu Soldatov
E Yu Soldatov
98INFN Sezione di Lecce, Lecce, Italy
98,
U Soldevila
U Soldevila
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
A A Solodkov
A A Solodkov
130Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
130,
A Soloshenko
A Soloshenko
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
O V Solovyanov
O V Solovyanov
130Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
130,
V Solovyev
V Solovyev
123P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
123,
P Sommer
P Sommer
48School of Physics, Shandong University, Shandong, China
48,
H Y Song
H Y Song
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
N Soni
N Soni
1Department of Physics, University of Adelaide, Adelaide, Australia
1,
A Sood
A Sood
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
A Sopczak
A Sopczak
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
B Sopko
B Sopko
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
V Sopko
V Sopko
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
V Sorin
V Sorin
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
D Sosa
D Sosa
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
M Sosebee
M Sosebee
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
C L Sotiropoulou
C L Sotiropoulou
124Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
124,
R Soualah
R Soualah
164Czech Technical University in Praha, Praha, Czech Republic
164,
A M Soukharev
A M Soukharev
109Institut für Physik, Universität Mainz, Mainz, Germany
109,
D South
D South
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
B C Sowden
B C Sowden
77Department of Physics, Hampton University, Hampton, VA USA
77,
S Spagnolo
S Spagnolo
73II Physikalisches Institut, Justus-Liebig-Universität Giessen, Giessen, Germany
73,
M Spalla
M Spalla
124Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
124,
M Spangenberg
M Spangenberg
170INFN Sezione di Roma Tor Vergata, Roma, Italy
170,
F Spanò
F Spanò
77Department of Physics, Hampton University, Hampton, VA USA
77,
W R Spearman
W R Spearman
57Marian Smoluchowski Institute of Physics, Jagiellonian University, Kraków, Poland
57,
D Sperlich
D Sperlich
16Department for Physics and Technology, University of Bergen, Bergen, Norway
16,
F Spettel
F Spettel
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
R Spighi
R Spighi
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
G Spigo
G Spigo
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
L A Spiller
L A Spiller
88University of Iowa, Iowa City, IA USA
88,
M Spousta
M Spousta
129Nagasaki Institute of Applied Science, Nagasaki, Japan
129,
T Spreitzer
T Spreitzer
158Department of Physics, University of Coimbra, Coimbra, Portugal
158,
R D St Denis
R D St Denis
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
S Staerz
S Staerz
44Departamento de Física, Universidad Técnica Federico Santa María, Valparaiso, Chile
44,
J Stahlman
J Stahlman
122Group of Particle Physics, University of Montreal, Montreal, QC Canada
122,
R Stamen
R Stamen
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
S Stamm
S Stamm
16Department for Physics and Technology, University of Bergen, Bergen, Norway
16,
E Stanecka
E Stanecka
39Cavendish Laboratory, University of Cambridge, Cambridge, UK
39,
C Stanescu
C Stanescu
134Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
134,
M Stanescu-Bellu
M Stanescu-Bellu
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
M M Stanitzki
M M Stanitzki
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
S Stapnes
S Stapnes
119B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
119,
E A Starchenko
E A Starchenko
130Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
130,
J Stark
J Stark
55Dipartimento di Fisica, Università della Calabria, Rende, Italy
55,
P Staroba
P Staroba
127Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
127,
P Starovoitov
P Starovoitov
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
R Staszewski
R Staszewski
39Cavendish Laboratory, University of Cambridge, Cambridge, UK
39,
P Stavina
P Stavina
144Center for High Energy Physics, University of Oregon, Eugene, OR USA
144,
P Steinberg
P Steinberg
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
B Stelzer
B Stelzer
142Department of Physics, Oklahoma State University, Stillwater, OK USA
142,
H J Stelzer
H J Stelzer
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
O Stelzer-Chilton
O Stelzer-Chilton
159Centro de Física Nuclear da Universidade de Lisboa, Lisboa, Portugal
159,
H Stenzel
H Stenzel
52Nevis Laboratory, Columbia University, Irvington, NY USA
52,
G A Stewart
G A Stewart
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
J A Stillings
J A Stillings
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
M C Stockton
M C Stockton
87Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
87,
M Stoebe
M Stoebe
87Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
87,
G Stoicea
G Stoicea
26Physikalisches Institut, University of Bonn, Bonn, Germany
26,
P Stolte
P Stolte
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
S Stonjek
S Stonjek
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
A R Stradling
A R Stradling
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
A Straessner
A Straessner
44Departamento de Física, Universidad Técnica Federico Santa María, Valparaiso, Chile
44,
M E Stramaglia
M E Stramaglia
17Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA USA
17,
J Strandberg
J Strandberg
147Department of Physics, University of Oslo, Oslo, Norway
147,
S Strandberg
S Strandberg
146Graduate School of Science, Osaka University, Osaka, Japan
146,
A Strandlie
A Strandlie
119B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
119,
E Strauss
E Strauss
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
M Strauss
M Strauss
113Department of Physics, McGill University, Montreal, QC Canada
113,
P Strizenec
P Strizenec
144Center for High Energy Physics, University of Oregon, Eugene, OR USA
144,
R Ströhmer
R Ströhmer
174Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies-Université Hassan II, Casablanca, Morocco
174,
D M Strom
D M Strom
116Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
116,
R Stroynowski
R Stroynowski
40Department of Physics, Carleton University, Ottawa, ON Canada
40,
A Strubig
A Strubig
106Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
106,
S A Stucci
S A Stucci
17Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA USA
17,
B Stugu
B Stugu
14Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
14,
N A Styles
N A Styles
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
D Su
D Su
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
J Su
J Su
125National Research Nuclear University MEPhI, Moscow, Russia
125,
R Subramaniam
R Subramaniam
79Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
79,
A Succurro
A Succurro
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
Y Sugaya
Y Sugaya
118Dipartimento di Fisica, Università di Milano, Milano, Italy
118,
C Suhr
C Suhr
108Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
108,
M Suk
M Suk
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
V V Sulin
V V Sulin
96Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
96,
S Sultansoy
S Sultansoy
4Department of Physics, Ankara University, Ankara, Turkey
4,
T Sumida
T Sumida
68Section de Physique, Université de Genève, Geneva, Switzerland
68,
S Sun
S Sun
57Marian Smoluchowski Institute of Physics, Jagiellonian University, Kraków, Poland
57,
X Sun
X Sun
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
J E Sundermann
J E Sundermann
48School of Physics, Shandong University, Shandong, China
48,
K Suruliz
K Suruliz
149INFN Sezione di Pavia, Pavia, Italy
149,
G Susinno
G Susinno
37West University in Timisoara, Timisoara, Romania
37,
M R Sutton
M R Sutton
149INFN Sezione di Pavia, Pavia, Italy
149,
S Suzuki
S Suzuki
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
M Svatos
M Svatos
127Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
127,
M Swiatlowski
M Swiatlowski
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
I Sykora
I Sykora
144Center for High Energy Physics, University of Oregon, Eugene, OR USA
144,
T Sykora
T Sykora
129Nagasaki Institute of Applied Science, Nagasaki, Japan
129,
D Ta
D Ta
90Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
90,
C Taccini
C Taccini
134Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
134,
K Tackmann
K Tackmann
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
J Taenzer
J Taenzer
158Department of Physics, University of Coimbra, Coimbra, Portugal
158,
A Taffard
A Taffard
163Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
163,
R Tafirout
R Tafirout
159Centro de Física Nuclear da Universidade de Lisboa, Lisboa, Portugal
159,
N Taiblum
N Taiblum
153INFN Sezione di Pisa, Pisa, Italy
153,
H Takai
H Takai
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
R Takashima
R Takashima
69INFN Sezione di Genova, Genova, Italy
69,
H Takeda
H Takeda
67Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
67,
T Takeshita
T Takeshita
140Faculty of Science, Okayama University, Okayama, Japan
140,
Y Takubo
Y Takubo
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
M Talby
M Talby
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
A A Talyshev
A A Talyshev
109Institut für Physik, Universität Mainz, Mainz, Germany
109,
J Y C Tam
J Y C Tam
174Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies-Université Hassan II, Casablanca, Morocco
174,
K G Tan
K G Tan
88University of Iowa, Iowa City, IA USA
88,
J Tanaka
J Tanaka
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
R Tanaka
R Tanaka
117INFN Sezione di Milano, Milano, Italy
117,
S Tanaka
S Tanaka
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
B B Tannenwald
B B Tannenwald
111CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
111,
N Tannoury
N Tannoury
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
S Tapprogge
S Tapprogge
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
S Tarem
S Tarem
152National Research Centre ‘Kurchatov Institute’ B.P.Konstantinov Petersburg Nuclear Physics Institute, St. Petersburg, Russia
152,
F Tarrade
F Tarrade
29Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
29,
G F Tartarelli
G F Tartarelli
91KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
91,
P Tas
P Tas
129Nagasaki Institute of Applied Science, Nagasaki, Japan
129,
M Tasevsky
M Tasevsky
127Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
127,
T Tashiro
T Tashiro
68Section de Physique, Université de Genève, Geneva, Switzerland
68,
E Tassi
E Tassi
37West University in Timisoara, Timisoara, Romania
37,
A Tavares Delgado
A Tavares Delgado
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
Y Tayalati
Y Tayalati
135Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
135,
F E Taylor
F E Taylor
94Kyoto University of Education, Kyoto, Japan
94,
G N Taylor
G N Taylor
88University of Iowa, Iowa City, IA USA
88,
W Taylor
W Taylor
159Centro de Física Nuclear da Universidade de Lisboa, Lisboa, Portugal
159,
F A Teischinger
F A Teischinger
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
M Teixeira Dias Castanheira
M Teixeira Dias Castanheira
76Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
76,
P Teixeira-Dias
P Teixeira-Dias
77Department of Physics, Hampton University, Hampton, VA USA
77,
K K Temming
K K Temming
48School of Physics, Shandong University, Shandong, China
48,
D Temple
D Temple
142Department of Physics, Oklahoma State University, Stillwater, OK USA
142,
H Ten Kate
H Ten Kate
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
P K Teng
P K Teng
151Department of Physics, University of Pennsylvania, Philadelphia, PA USA
151,
J J Teoh
J J Teoh
118Dipartimento di Fisica, Università di Milano, Milano, Italy
118,
F Tepel
F Tepel
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
S Terada
S Terada
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
K Terashi
K Terashi
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
J Terron
J Terron
82Faculty of Applied Information Science, Hiroshima Institute of Technology, Hiroshima, Japan
82,
S Terzo
S Terzo
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
M Testa
M Testa
47Department of Physics, Nanjing University, Jiangsu, China
47,
R J Teuscher
R J Teuscher
158Department of Physics, University of Coimbra, Coimbra, Portugal
158,
T Theveneaux-Pelzer
T Theveneaux-Pelzer
34National Institute of Physics and Nuclear Engineering, Bucharest, Romania
34,
J P Thomas
J P Thomas
18Department of Physics, Humboldt University, Berlin, Germany
18,
J Thomas-Wilsker
J Thomas-Wilsker
77Department of Physics, Hampton University, Hampton, VA USA
77,
E N Thompson
E N Thompson
35Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj Napoca, Romania
35,
P D Thompson
P D Thompson
18Department of Physics, Humboldt University, Berlin, Germany
18,
R J Thompson
R J Thompson
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
A S Thompson
A S Thompson
53Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
53,
L A Thomsen
L A Thomsen
176Faculté des Sciences Semlalia, Université Cadi Ayyad, LPHEA-Marrakech, Marrakech, Morocco
176,
E Thomson
E Thomson
122Group of Particle Physics, University of Montreal, Montreal, QC Canada
122,
M Thomson
M Thomson
28Department of Physics, Brandeis University, Waltham, MA USA
28,
R P Thun
R P Thun
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
M J Tibbetts
M J Tibbetts
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
R E Ticse Torres
R E Ticse Torres
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
V O Tikhomirov
V O Tikhomirov
96Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
96,
Yu A Tikhonov
Yu A Tikhonov
109Institut für Physik, Universität Mainz, Mainz, Germany
109,
S Timoshenko
S Timoshenko
98INFN Sezione di Lecce, Lecce, Italy
98,
E Tiouchichine
E Tiouchichine
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
P Tipton
P Tipton
176Faculté des Sciences Semlalia, Université Cadi Ayyad, LPHEA-Marrakech, Marrakech, Morocco
176,
S Tisserant
S Tisserant
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
K Todome
K Todome
157Faculdade de Ciências, Universidade de Lisboa, Lisboa, Portugal
157,
T Todorov
T Todorov
5Istanbul Aydin University, Istanbul, Turkey
5,
S Todorova-Nova
S Todorova-Nova
129Nagasaki Institute of Applied Science, Nagasaki, Japan
129,
J Tojo
J Tojo
70Dipartimento di Fisica, Università di Genova, Genova, Italy
70,
S Tokár
S Tokár
144Center for High Energy Physics, University of Oregon, Eugene, OR USA
144,
K Tokushuku
K Tokushuku
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
K Tollefson
K Tollefson
90Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
90,
E Tolley
E Tolley
57Marian Smoluchowski Institute of Physics, Jagiellonian University, Kraków, Poland
57,
L Tomlinson
L Tomlinson
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
M Tomoto
M Tomoto
103Department of Physics, Royal Holloway University of London, Surrey, UK
103,
L Tompkins
L Tompkins
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
K Toms
K Toms
105Louisiana Tech University, Ruston, LA USA
105,
E Torrence
E Torrence
116Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
116,
H Torres
H Torres
142Department of Physics, Oklahoma State University, Stillwater, OK USA
142,
E Torró Pastor
E Torró Pastor
138Department of Physics, New York University, New York, NY USA
138,
J Toth
J Toth
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
F Touchard
F Touchard
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
D R Tovey
D R Tovey
139Ohio State University, Columbus, OH USA
139,
T Trefzger
T Trefzger
174Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies-Université Hassan II, Casablanca, Morocco
174,
L Tremblet
L Tremblet
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
A Tricoli
A Tricoli
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
I M Trigger
I M Trigger
159Centro de Física Nuclear da Universidade de Lisboa, Lisboa, Portugal
159,
S Trincaz-Duvoid
S Trincaz-Duvoid
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
M F Tripiana
M F Tripiana
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
W Trischuk
W Trischuk
158Department of Physics, University of Coimbra, Coimbra, Portugal
158,
B Trocmé
B Trocmé
55Dipartimento di Fisica, Università della Calabria, Rende, Italy
55,
C Troncon
C Troncon
91KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
91,
M Trottier-McDonald
M Trottier-McDonald
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
M Trovatelli
M Trovatelli
169Dipartimento di Fisica, Sapienza Università di Roma, Roma, Italy
169,
P True
P True
90Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
90,
L Truong
L Truong
164Czech Technical University in Praha, Praha, Czech Republic
164,
M Trzebinski
M Trzebinski
39Cavendish Laboratory, University of Cambridge, Cambridge, UK
39,
A Trzupek
A Trzupek
39Cavendish Laboratory, University of Cambridge, Cambridge, UK
39,
C Tsarouchas
C Tsarouchas
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
J C-L Tseng
J C-L Tseng
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
P V Tsiareshka
P V Tsiareshka
92Graduate School of Science, Kobe University, Kobe, Japan
92,
D Tsionou
D Tsionou
154Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
154,
G Tsipolitis
G Tsipolitis
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
N Tsirintanis
N Tsirintanis
9Department of Physics, University of Arizona, Tucson, AZ USA
9,
S Tsiskaridze
S Tsiskaridze
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
V Tsiskaridze
V Tsiskaridze
48School of Physics, Shandong University, Shandong, China
48,
E G Tskhadadze
E G Tskhadadze
51Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
51,
I I Tsukerman
I I Tsukerman
97Physics Department, Lancaster University, Lancaster, UK
97,
V Tsulaia
V Tsulaia
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
S Tsuno
S Tsuno
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
D Tsybychev
D Tsybychev
148Department of Physics, Oxford University, Oxford, UK
148,
A Tudorache
A Tudorache
26Physikalisches Institut, University of Bonn, Bonn, Germany
26,
V Tudorache
V Tudorache
26Physikalisches Institut, University of Bonn, Bonn, Germany
26,
A N Tuna
A N Tuna
122Group of Particle Physics, University of Montreal, Montreal, QC Canada
122,
S A Tupputi
S A Tupputi
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
S Turchikhin
S Turchikhin
99Dipartimento di Matematica e Fisica, Università del Salento, Lecce, Italy
99,
D Turecek
D Turecek
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
R Turra
R Turra
91KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
91,
A J Turvey
A J Turvey
40Department of Physics, Carleton University, Ottawa, ON Canada
40,
P M Tuts
P M Tuts
35Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj Napoca, Romania
35,
A Tykhonov
A Tykhonov
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
M Tylmad
M Tylmad
146Graduate School of Science, Osaka University, Osaka, Japan
146,
M Tyndel
M Tyndel
131INFN Sezione di Napoli, Naples, Italy
131,
I Ueda
I Ueda
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
R Ueno
R Ueno
29Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
29,
M Ughetto
M Ughetto
146Graduate School of Science, Osaka University, Osaka, Japan
146,
M Ugland
M Ugland
14Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
14,
F Ukegawa
F Ukegawa
160Departamento de Fisica, Universidade do Minho, Braga, Portugal
160,
G Unal
G Unal
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
A Undrus
A Undrus
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
G Unel
G Unel
163Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
163,
F C Ungaro
F C Ungaro
48School of Physics, Shandong University, Shandong, China
48,
Y Unno
Y Unno
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
C Unverdorben
C Unverdorben
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
J Urban
J Urban
144Center for High Energy Physics, University of Oregon, Eugene, OR USA
144,
P Urquijo
P Urquijo
88University of Iowa, Iowa City, IA USA
88,
P Urrejola
P Urrejola
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
G Usai
G Usai
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
A Usanova
A Usanova
62Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
62,
L Vacavant
L Vacavant
85Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
85,
V Vacek
V Vacek
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
B Vachon
B Vachon
87Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
87,
C Valderanis
C Valderanis
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
N Valencic
N Valencic
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
S Valentinetti
S Valentinetti
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
A Valero
A Valero
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
L Valery
L Valery
12Physics Department, National Technical University of Athens, Zografou, Greece
12,
S Valkar
S Valkar
129Nagasaki Institute of Applied Science, Nagasaki, Japan
129,
E Valladolid Gallego
E Valladolid Gallego
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
S Vallecorsa
S Vallecorsa
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
J A Valls Ferrer
J A Valls Ferrer
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
W Van Den Wollenberg
W Van Den Wollenberg
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
P C Van Der Deijl
P C Van Der Deijl
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
R van der Geer
R van der Geer
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
H van der Graaf
H van der Graaf
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
N van Eldik
N van Eldik
152National Research Centre ‘Kurchatov Institute’ B.P.Konstantinov Petersburg Nuclear Physics Institute, St. Petersburg, Russia
152,
P van Gemmeren
P van Gemmeren
6Division of Physics, TOBB University of Economics and Technology, Ankara, Turkey
6,
J Van Nieuwkoop
J Van Nieuwkoop
142Department of Physics, Oklahoma State University, Stillwater, OK USA
142,
I van Vulpen
I van Vulpen
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
M C van Woerden
M C van Woerden
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
M Vanadia
M Vanadia
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
W Vandelli
W Vandelli
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
R Vanguri
R Vanguri
122Group of Particle Physics, University of Montreal, Montreal, QC Canada
122,
A Vaniachine
A Vaniachine
6Division of Physics, TOBB University of Economics and Technology, Ankara, Turkey
6,
F Vannucci
F Vannucci
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
G Vardanyan
G Vardanyan
177Faculté des Sciences, Université Mohamed Premier and LPTPM, Oujda, Morocco
177,
R Vari
R Vari
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
E W Varnes
E W Varnes
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
T Varol
T Varol
40Department of Physics, Carleton University, Ottawa, ON Canada
40,
D Varouchas
D Varouchas
80Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
A Vartapetian
A Vartapetian
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
K E Varvell
K E Varvell
150Dipartimento di Fisica, Università di Pavia, Pavia, Italy
150,
F Vazeille
F Vazeille
34National Institute of Physics and Nuclear Engineering, Bucharest, Romania
34,
T Vazquez Schroeder
T Vazquez Schroeder
87Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
87,
J Veatch
J Veatch
7LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
7,
L M Veloce
L M Veloce
158Department of Physics, University of Coimbra, Coimbra, Portugal
158,
F Veloso
F Veloso
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
T Velz
T Velz
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
S Veneziano
S Veneziano
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
A Ventura
A Ventura
73II Physikalisches Institut, Justus-Liebig-Universität Giessen, Giessen, Germany
73,
D Ventura
D Ventura
86Department of Physics, Indiana University, Bloomington, IN USA
86,
M Venturi
M Venturi
169Dipartimento di Fisica, Sapienza Università di Roma, Roma, Italy
169,
N Venturi
N Venturi
158Department of Physics, University of Coimbra, Coimbra, Portugal
158,
A Venturini
A Venturini
23Department of Physics, Dogus University, Istanbul, Turkey
23,
V Vercesi
V Vercesi
121Department of Physics, Massachusetts Institute of Technology, Cambridge, MA USA
121,
M Verducci
M Verducci
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
W Verkerke
W Verkerke
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
J C Vermeulen
J C Vermeulen
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
A Vest
A Vest
44Departamento de Física, Universidad Técnica Federico Santa María, Valparaiso, Chile
44,
M C Vetterli
M C Vetterli
142Department of Physics, Oklahoma State University, Stillwater, OK USA
142,
O Viazlo
O Viazlo
81ZITI Institut für technische Informatik, Ruprecht-Karls-Universität Heidelberg, Mannheim, Germany
81,
I Vichou
I Vichou
165Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
165,
T Vickey
T Vickey
139Ohio State University, Columbus, OH USA
139,
O E Vickey Boeriu
O E Vickey Boeriu
139Ohio State University, Columbus, OH USA
139,
G H A Viehhauser
G H A Viehhauser
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
S Viel
S Viel
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
R Vigne
R Vigne
62Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
62,
M Villa
M Villa
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
M Villaplana Perez
M Villaplana Perez
91KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
91,
E Vilucchi
E Vilucchi
47Department of Physics, Nanjing University, Jiangsu, China
47,
M G Vincter
M G Vincter
29Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
29,
V B Vinogradov
V B Vinogradov
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
I Vivarelli
I Vivarelli
149INFN Sezione di Pavia, Pavia, Italy
149,
F Vives Vaque
F Vives Vaque
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
S Vlachos
S Vlachos
10Department of Physics, The University of Texas at Arlington, Arlington, TX USA
10,
D Vladoiu
D Vladoiu
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
M Vlasak
M Vlasak
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
M Vogel
M Vogel
32Instituto de Fisica, Universidade de Sao Paulo, São Paulo, Brazil
32,
P Vokac
P Vokac
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
G Volpi
G Volpi
124Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
124,
M Volpi
M Volpi
88University of Iowa, Iowa City, IA USA
88,
H von der Schmitt
H von der Schmitt
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
H von Radziewski
H von Radziewski
48School of Physics, Shandong University, Shandong, China
48,
E von Toerne
E von Toerne
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
V Vorobel
V Vorobel
129Nagasaki Institute of Applied Science, Nagasaki, Japan
129,
K Vorobev
K Vorobev
98INFN Sezione di Lecce, Lecce, Italy
98,
M Vos
M Vos
167Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
167,
R Voss
R Voss
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
J H Vossebeld
J H Vossebeld
74SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
74,
N Vranjes
N Vranjes
13Institute of Physics, Azerbaijan Academy of Sciences, Baku, Azerbaijan
13,
M Vranjes Milosavljevic
M Vranjes Milosavljevic
13Institute of Physics, Azerbaijan Academy of Sciences, Baku, Azerbaijan
13,
V Vrba
V Vrba
127Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
127,
M Vreeswijk
M Vreeswijk
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
R Vuillermet
R Vuillermet
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
I Vukotic
I Vukotic
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
Z Vykydal
Z Vykydal
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
P Wagner
P Wagner
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
W Wagner
W Wagner
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
H Wahlberg
H Wahlberg
71E. Andronikashvili Institute of Physics, Iv. Javakhishvili Tbilisi State University, Tbilisi, Georgia
71,
S Wahrmund
S Wahrmund
44Departamento de Física, Universidad Técnica Federico Santa María, Valparaiso, Chile
44,
J Wakabayashi
J Wakabayashi
103Department of Physics, Royal Holloway University of London, Surrey, UK
103,
J Walder
J Walder
72High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
72,
R Walker
R Walker
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
W Walkowiak
W Walkowiak
141Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK USA
141,
C Wang
C Wang
151Department of Physics, University of Pennsylvania, Philadelphia, PA USA
151,
F Wang
F Wang
173Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
173,
H Wang
H Wang
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
H Wang
H Wang
40Department of Physics, Carleton University, Ottawa, ON Canada
40,
J Wang
J Wang
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
J Wang
J Wang
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
K Wang
K Wang
87Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
87,
R Wang
R Wang
6Division of Physics, TOBB University of Economics and Technology, Ankara, Turkey
6,
S M Wang
S M Wang
151Department of Physics, University of Pennsylvania, Philadelphia, PA USA
151,
T Wang
T Wang
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
T Wang
T Wang
35Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj Napoca, Romania
35,
X Wang
X Wang
176Faculté des Sciences Semlalia, Université Cadi Ayyad, LPHEA-Marrakech, Marrakech, Morocco
176,
C Wanotayaroj
C Wanotayaroj
116Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
116,
A Warburton
A Warburton
87Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
87,
C P Ward
C P Ward
28Department of Physics, Brandeis University, Waltham, MA USA
28,
D R Wardrope
D R Wardrope
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
A Washbrook
A Washbrook
46Department of Modern Physics, University of Science and Technology of China, Anhui, China
46,
C Wasicki
C Wasicki
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
P M Watkins
P M Watkins
18Department of Physics, Humboldt University, Berlin, Germany
18,
A T Watson
A T Watson
18Department of Physics, Humboldt University, Berlin, Germany
18,
I J Watson
I J Watson
150Dipartimento di Fisica, Università di Pavia, Pavia, Italy
150,
M F Watson
M F Watson
18Department of Physics, Humboldt University, Berlin, Germany
18,
G Watts
G Watts
138Department of Physics, New York University, New York, NY USA
138,
S Watts
S Watts
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
B M Waugh
B M Waugh
78Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA USA
78,
S Webb
S Webb
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
M S Weber
M S Weber
17Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA USA
17,
S W Weber
S W Weber
174Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies-Université Hassan II, Casablanca, Morocco
174,
J S Webster
J S Webster
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
A R Weidberg
A R Weidberg
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
B Weinert
B Weinert
61DESY, Hamburg and Zeuthen, Germany
61,
J Weingarten
J Weingarten
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
C Weiser
C Weiser
48School of Physics, Shandong University, Shandong, China
48,
H Weits
H Weits
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
P S Wells
P S Wells
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
T Wenaus
T Wenaus
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
T Wengler
T Wengler
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
S Wenig
S Wenig
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
N Wermes
N Wermes
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
M Werner
M Werner
48School of Physics, Shandong University, Shandong, China
48,
P Werner
P Werner
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
M Wessels
M Wessels
58Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
58,
J Wetter
J Wetter
161Departamento de Fisica Teorica y del Cosmos and CAFPE, Universidad de Granada, Granada, Spain
161,
K Whalen
K Whalen
116Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
116,
A M Wharton
A M Wharton
72High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
72,
A White
A White
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
M J White
M J White
1Department of Physics, University of Adelaide, Adelaide, Australia
1,
R White
R White
32Instituto de Fisica, Universidade de Sao Paulo, São Paulo, Brazil
32,
S White
S White
124Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
124,
D Whiteson
D Whiteson
163Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
163,
F J Wickens
F J Wickens
131INFN Sezione di Napoli, Naples, Italy
131,
W Wiedenmann
W Wiedenmann
173Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
173,
M Wielers
M Wielers
131INFN Sezione di Napoli, Naples, Italy
131,
P Wienemann
P Wienemann
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
C Wiglesworth
C Wiglesworth
36University Politehnica Bucharest, Bucharest, Romania
36,
L A M Wiik-Fuchs
L A M Wiik-Fuchs
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
A Wildauer
A Wildauer
101Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
101,
H G Wilkens
H G Wilkens
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
H H Williams
H H Williams
122Group of Particle Physics, University of Montreal, Montreal, QC Canada
122,
S Williams
S Williams
107Fysiska institutionen, Lunds universitet, Lund, Sweden
107,
C Willis
C Willis
90Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
90,
S Willocq
S Willocq
86Department of Physics, Indiana University, Bloomington, IN USA
86,
A Wilson
A Wilson
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
J A Wilson
J A Wilson
18Department of Physics, Humboldt University, Berlin, Germany
18,
I Wingerter-Seez
I Wingerter-Seez
5Istanbul Aydin University, Istanbul, Turkey
5,
F Winklmeier
F Winklmeier
116Department of Physics and Astronomy, Michigan State University, East Lansing, MI USA
116,
B T Winter
B T Winter
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
M Wittgen
M Wittgen
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
J Wittkowski
J Wittkowski
100Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
100,
S J Wollstadt
S J Wollstadt
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
M W Wolter
M W Wolter
39Cavendish Laboratory, University of Cambridge, Cambridge, UK
39,
H Wolters
H Wolters
126D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
126,
B K Wosiek
B K Wosiek
39Cavendish Laboratory, University of Cambridge, Cambridge, UK
39,
J Wotschack
J Wotschack
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
M J Woudstra
M J Woudstra
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
K W Wozniak
K W Wozniak
39Cavendish Laboratory, University of Cambridge, Cambridge, UK
39,
M Wu
M Wu
55Dipartimento di Fisica, Università della Calabria, Rende, Italy
55,
M Wu
M Wu
31Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
31,
S L Wu
S L Wu
173Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
173,
X Wu
X Wu
49Department of Physics and Astronomy, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai, China
49,
Y Wu
Y Wu
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
T R Wyatt
T R Wyatt
84Department of Physics, The University of Hong Kong, Hong Kong, China
84,
B M Wynne
B M Wynne
46Department of Modern Physics, University of Science and Technology of China, Anhui, China
46,
S Xella
S Xella
36University Politehnica Bucharest, Bucharest, Romania
36,
D Xu
D Xu
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
L Xu
L Xu
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
B Yabsley
B Yabsley
150Dipartimento di Fisica, Università di Pavia, Pavia, Italy
150,
S Yacoob
S Yacoob
145LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
145,
R Yakabe
R Yakabe
67Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
67,
M Yamada
M Yamada
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
D Yamaguchi
D Yamaguchi
157Faculdade de Ciências, Universidade de Lisboa, Lisboa, Portugal
157,
Y Yamaguchi
Y Yamaguchi
118Dipartimento di Fisica, Università di Milano, Milano, Italy
118,
A Yamamoto
A Yamamoto
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
S Yamamoto
S Yamamoto
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
T Yamanaka
T Yamanaka
155Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA USA
155,
K Yamauchi
K Yamauchi
103Department of Physics, Royal Holloway University of London, Surrey, UK
103,
Y Yamazaki
Y Yamazaki
67Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
67,
Z Yan
Z Yan
22Department of Physics Engineering, Gaziantep University, Gaziantep, Turkey
22,
H Yang
H Yang
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
H Yang
H Yang
173Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
173,
Y Yang
Y Yang
151Department of Physics, University of Pennsylvania, Philadelphia, PA USA
151,
W-M Yao
W-M Yao
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
Y Yasu
Y Yasu
66INFN Laboratori Nazionali di Frascati, Frascati, Italy
66,
E Yatsenko
E Yatsenko
5Istanbul Aydin University, Istanbul, Turkey
5,
K H Yau Wong
K H Yau Wong
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
J Ye
J Ye
40Department of Physics, Carleton University, Ottawa, ON Canada
40,
S Ye
S Ye
25Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
25,
I Yeletskikh
I Yeletskikh
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
A L Yen
A L Yen
57Marian Smoluchowski Institute of Physics, Jagiellonian University, Kraków, Poland
57,
E Yildirim
E Yildirim
42Enrico Fermi Institute, University of Chicago, Chicago, IL USA
42,
K Yorita
K Yorita
171Dipartimento di Fisica, Università di Roma Tor Vergata, Roma, Italy
171,
R Yoshida
R Yoshida
6Division of Physics, TOBB University of Economics and Technology, Ankara, Turkey
6,
K Yoshihara
K Yoshihara
122Group of Particle Physics, University of Montreal, Montreal, QC Canada
122,
C Young
C Young
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
C J S Young
C J S Young
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30,
S Youssef
S Youssef
22Department of Physics Engineering, Gaziantep University, Gaziantep, Turkey
22,
D R Yu
D R Yu
15Institute of Physics, University of Belgrade, Belgrade, Serbia
15,
J Yu
J Yu
8High Energy Physics Division, Argonne National Laboratory, Argonne, IL USA
8,
J M Yu
J M Yu
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
J Yu
J Yu
114School of Physics, University of Melbourne, Melbourne, VIC Australia
114,
L Yuan
L Yuan
67Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
67,
S P Y Yuen
S P Y Yuen
21Department of Physics, Bogazici University, Istanbul, Turkey
21,
A Yurkewicz
A Yurkewicz
108Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
108,
I Yusuff
I Yusuff
28Department of Physics, Brandeis University, Waltham, MA USA
28,
B Zabinski
B Zabinski
39Cavendish Laboratory, University of Cambridge, Cambridge, UK
39,
R Zaidan
R Zaidan
63Institut für Kern- und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
63,
A M Zaitsev
A M Zaitsev
130Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
130,
J Zalieckas
J Zalieckas
14Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
14,
A Zaman
A Zaman
148Department of Physics, Oxford University, Oxford, UK
148,
S Zambito
S Zambito
57Marian Smoluchowski Institute of Physics, Jagiellonian University, Kraków, Poland
57,
L Zanello
L Zanello
132Dipartimento di Fisica, Università di Napoli, Napoli, Italy
132,
D Zanzi
D Zanzi
88University of Iowa, Iowa City, IA USA
88,
C Zeitnitz
C Zeitnitz
175Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
175,
M Zeman
M Zeman
128Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
128,
A Zemla
A Zemla
38Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
38,
Q Zeng
Q Zeng
143Palacký University, RCPTM, Olomouc, Czech Republic
143,
K Zengel
K Zengel
23Department of Physics, Dogus University, Istanbul, Turkey
23,
O Zenin
O Zenin
130Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
130,
T Ženiš
T Ženiš
144Center for High Energy Physics, University of Oregon, Eugene, OR USA
144,
D Zerwas
D Zerwas
117INFN Sezione di Milano, Milano, Italy
117,
D Zhang
D Zhang
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
F Zhang
F Zhang
173Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
173,
H Zhang
H Zhang
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
J Zhang
J Zhang
6Division of Physics, TOBB University of Economics and Technology, Ankara, Turkey
6,
L Zhang
L Zhang
48School of Physics, Shandong University, Shandong, China
48,
R Zhang
R Zhang
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
X Zhang
X Zhang
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
Z Zhang
Z Zhang
117INFN Sezione di Milano, Milano, Italy
117,
X Zhao
X Zhao
40Department of Physics, Carleton University, Ottawa, ON Canada
40,
Y Zhao
Y Zhao
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
117INFN Sezione di Milano, Milano, Italy
33,117,
Z Zhao
Z Zhao
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
A Zhemchugov
A Zhemchugov
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
J Zhong
J Zhong
120National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
120,
B Zhou
B Zhou
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
C Zhou
C Zhou
45Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
45,
L Zhou
L Zhou
35Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj Napoca, Romania
35,
L Zhou
L Zhou
40Department of Physics, Carleton University, Ottawa, ON Canada
40,
N Zhou
N Zhou
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
C G Zhu
C G Zhu
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
H Zhu
H Zhu
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
J Zhu
J Zhu
89Department of Physics and Astronomy, Iowa State University, Ames, IA USA
89,
Y Zhu
Y Zhu
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
X Zhuang
X Zhuang
33Physics Department, Brookhaven National Laboratory, Upton, NY USA
33,
K Zhukov
K Zhukov
96Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
96,
A Zibell
A Zibell
174Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies-Université Hassan II, Casablanca, Morocco
174,
D Zieminska
D Zieminska
61DESY, Hamburg and Zeuthen, Germany
61,
N I Zimine
N I Zimine
65SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
65,
C Zimmermann
C Zimmermann
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
S Zimmermann
S Zimmermann
48School of Physics, Shandong University, Shandong, China
48,
Z Zinonos
Z Zinonos
54INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
54,
M Zinser
M Zinser
83Department of Physics, The Chinese University of Hong Kong, Shatin, N.T. Hong Kong, China
83,
M Ziolkowski
M Ziolkowski
141Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK USA
141,
L Živković
L Živković
13Institute of Physics, Azerbaijan Academy of Sciences, Baku, Azerbaijan
13,
G Zobernig
G Zobernig
173Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
173,
A Zoccoli
A Zoccoli
20School of Physics and Astronomy, University of Birmingham, Birmingham, UK
20,
M zur Nedden
M zur Nedden
16Department for Physics and Technology, University of Bergen, Bergen, Norway
16,
G Zurzolo
G Zurzolo
104Department of Physics and Astronomy, University College London, London, UK
104,
L Zwalinski
L Zwalinski
30Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
30