Predicting malignancy from mammography findings and image-guided core biopsies

Abstract

The main goal of this work is to produce machine learning models that predict the outcome of a mammography from a reduced set of annotated mammography findings. In the study we used a dataset consisting of 348 consecutive breast masses that underwent image guided core biopsy performed between October 2005 and December 2007 on 328 female subjects. We applied various algorithms with parameter variation to learn from the data. The tasks were to predict mass density and to predict malignancy. The best classifier that predicts mass density is based on a support vector machine and has accuracy of 81.3%. The expert correctly annotated 70% of the mass densities. The best classifier that predicts malignancy is also based on a support vector machine and has accuracy of 85.6%, with a positive predictive value of 85%. One important contribution of this work is that our model can predict malignancy in the absence of the mass density attribute, since we can fill up this attribute using our mass density predictor.

1 Introduction

Mammography is considered the cheapest and most efficient method to detect cancer in a preclinical stage and breast screening programs were created precisely with the objective of detecting cancer in earlier stages. The breast screening programs usually generate a huge amount of data, annotated according to the Breast Imaging Reporting and Data System (BI-RADS) created by the American College of Radiology. The BI-RADS system determines a standard lexicon to be used by radiologists when studying each finding. Although the breast screening programs have helped reducing the number of women with undetected cancer, there is still room for improvement, since recent statistics show that one woman dies of breast cancer every 13 minutes in the US and in 2012, an estimated 39,510 women (15% of all deaths) and 410 men in the US are expected to die from breast cancer. Therefore, it is of utmost importance to improve these numbers and raise the life expectancy in the next years.

We applied machine learning methods to 348 consecutive breast masses that underwent image-guided core biopsies performed between October 2005 and December 2007 on 328 female subjects. These 348 findings are defined by 13 attributes, with one of them indicating if the finding is malignant or benign. Our main objective is to produce models that can have a good performance at predicting malignancy and a good performance at avoiding to expose healthy women to extra surgical or screening procedures. We are also interested in studying the actual relevance of mass density in the findings, since this is one of the attributes that usually is not regarded relevant by physicians. According to physicians, mass density is a feature usually considered to be difficult to annotate, because of the breast tissue, and fat composition. Previous works have shown that mass density can be an important attribute when predicting malignancy (Woods et al., 2010, 2011; Ferreira et al., 2011). The 348 mammography examinations used in this study have annotations of mass density, which allow to (1) investigate in more detail the role played by this feature and (2) produce models to predict this particular feature and help physicians distinguish between high and iso/low densities.

Much work has been done on applying machine learning techniques to the area of breast cancer, one of the most common kinds of cancer in the world. In the University of California, Irvine (UCI) machine learning repository (http://archive.ics.uci.edu/ml/ datasets.html), there are four datasets whose main target of study is breast cancer. One of the first works on applying machine learning techniques to breast cancer data dates from 1990. At this time, the first dataset donated to the UCI repository was created by Wolberg and Mangasarian after their work on a multi-surface method of pattern separation for medical diagnosis applied to breast cytology (Wolberg and Mangasarian, 1990). Most works in the literature applies artificial neural networks to the problem of diagnosing breast cancer (Wu et al., 1993; Abbass, 2002). Others focus on prognosis of the disease using inductive learning methods (Street et al., 1995). More recently, Ayer et al. (2010) have evaluated whether an artificial neural network trained on a large prospectively collected dataset of consecutive mammography findings could discriminate between benign and malignant disease and accurately predict the probability of breast cancer for individual patients. Other works concentrate on the correlation of attributes in the mammograms, for example, the influence of mass density and other features on predicting malignancy (Jackson et al., 1991; Sickles, 1991; Cory and Linden, 1993; Davis et al., 2005; Woods et al., 2010, 2011; Ferreira et al., 2011). Other recent works focus on extracting information from free text that appears in medical records of mammography screenings (Nassif et al., 2009, 2012) and on the influence of age in Ductal Carcinoma In Situ (DCIS) findings (Nassif et al., 2010). Yet other works focus on the mammography images themselves (Lesniak et al., 2011; Samulski and Karssemeijer, 2011). These are orthogonal to the above mentioned and to our own work, whose focus is on the medical reports.

We use the same dataset used by Woods et al. (2011). This dataset is unique in the sense that all findings were retrospectively assessed and all of them have accurate information about the density of the breast masses. In that work, they showed that high breast mass density is a significant predictor of malignancy, even after controlling for other well-known predictors of malignancy such as mass margin and mass shape. The metric used to evaluate performance was inter-observer agreement and they found a moderate k-value for mass density (0.53).

The remaining of this paper is organised as follows. The next section introduces the dataset and the attributes used in this study. We then describe how we performed our experiments. In Section 4, we show results for the best classifiers found to predict mass density and malignancy. Lastly, we present the main contributions of this study and perspectives of future work.

2 Breast cancer data

Our study analyses 348 consecutive breast masses that underwent image guided core biopsies performed between October 2005 and December 2007 on 328 female subjects. Each one of the 348 cases refers to a breast nodule retrospectively classified according to the BI-RADS system. On the other hand, a clinical radiologist assessed (at the time of imaging and without biopsy results) the density of 180 of these masses, in an evaluation that can be considered as ‘performed under stress’ (prospective assessment). Pathology result at biopsy was the study endpoint.

Table 1 shows the main attributes used from these data to learn the models along with their explanations. These attributes were collected by our co-authors who are medical doctors, specialists in mammograms. When learning models to predict malignancy the attribute outcome is the target class. It assumes values malignant and benign and was determined using the results of biopsies. From the 348 cases, 118 are malignant (≈34%), and 84 cases have high mass density (≈24%) retrospectively assessed. Other attributes are mass shape, mass margins, depth, size, among others (see Table 4 for more details). For the purpose of our study, we have two attributes that represent the same characteristics of the finding, but with different interpretations. These are retro_density and density_num. Both represent mass densities that can assume values high or iso/low. Retro_density was retrospectively assessed while density_num was prospectively (at the time of imaging) assessed. These two attributes are our target classes when learning models to predict mass density.

Table 1.

Data attributes

Attribute	Description
age_at_mammo	Age of the patient when the mammogram was taken
clockface_location	Location of the mass
mass_shape	Mass shape descriptor
mass_margins	Classification of the margins of the mass
side	Breast where the mass was found (left or right)
depth	Depth of the mass according to a measure from the skin surface to the centre of the lesion
mass_margins_worst	Most worrisome mass margin descriptor
quadrant_location_def size	Quadrant location of the mass Greatest transverse width of the mass (in mm)
breast_composition	Breast density assessment (e.g., almost entirely fat, scattered fibroglandular densities, heterogeneously dense, extremely dense)
retro_density	Retrospective annotation of mass density
density_num	Prospective annotation of mass density (at the time of imaging)
outcome	Classification of the mass based on the results of the biopsy (malignant or benign)

Table 4.

Dataset attribute values and frequencies for the 348 instances

	Benign(%)	Malignant(%)	Total(%)
N	230(66.09%)	118(33.91%)	348(100%)
Age
(0,35]	12(5.22%)	1(0.85%)	13(3.74%)
(35,45]	81(35.22%)	8(6.78%)	89(25.57%)
(45,55]	58(25.22%)	29(24.58%)	87(25%)
(55,65]	56(24.35%)	29(24.58%)	85(24.43%)
(65,100]	23(10%)	51(43.22%)	74(21.26%)
Clockface location
1.0	34(14.78%)	16(13.56%)	50(14.37%)
2.0	15(6.52%)	4(3.39%)	19(5.46%)
3.0	14(6.09%)	7(5.93%)	21(6.03%)
4.0	12(5.22%)	4(3.39%)	16(4.6%)
5.0	9(3.91%)	1(0.85%)	10(2.87%)
6.0	24(10.43%)	7(5.93%)	31(8.91%)
7.0	9(3.91%)	6(5.08%)	15(4.31%)
8.0	10(4.35%)	2(1.69%)	12(3.45%)
9.0	3(1.3%)	5(4.24%)	8(2.3%)
10.0	13(5.65%)	12(10.17%)	25(7.18%)
11.0	31(13.48%)	24(20.34%)	55(15.8%)
12.0	39(16.96%)	20(16.95%)	59(16.95%)
C	17(7.39%)	10(8.47%)	27(7.76%)
Mass shape
L	32(13.91%)	14(11.86%)	46(13.22%)
O	108(46.96%)	26(22.03%)	134(38.51%)
R	41(17.83%)	11(9.32%)	52(14.94%)
X	19(8.26%)	56(47.46%)	75(21.55%)
Mass margins1
D	92(40%)	14(11.86%)	106(30.46%)
I	36(15.65%)	35(29.66%)	71(20.4%)
M	6(2.61%)	8(6.78%)	14(4.02%)
S	2(0.87%)	29(24.58%)	31(8.91%)
U	45(19.57%)	16(13.56%)	61(17.53%)
Mass margins2
D	87(37.83%)	13(11.02%)	100(28.74%)
I	38(16.52%)	36(30.51%)	74(21.26%)
M	6(2.61%)	8(6.78%)	14(4.02%)
S	2(0.87%)	32(27.12%)	34(9.77%)
U	48(20.87%)	13(11.02%)	61(17.53%)
Mass margins worst
Circumscribed	87(37.83%)	13(11.02%)	100(28.74%)
Indistinct	38(16.52%)	36(30.51%)	74(21.26%)
Microlobulated	6(2.61%)	8(6.78%)	14(4.02%)
Obscured	48(20.87%)	13(11.02%)	61(17.53%)
Spiculated	2(0.87%)	32(27.12%)	34(9.77%)
Side
L	116(50.43%)	44(37.29%)	160(45.98%)
R	114(49.57%)	74(62.71%)	188(54.02%)
Size
(0,5]	21(9.13%)	3(2.54%)	24(6.9%)
(5,10]	94(40.87%)	45(38.14%)	139(39.94%)
(10,15]	56(24.35%)	30(25.42%)	86(24.71%)
(15,20]	37(16.09%)	19(16.1%)	56(16.09%)
(20,200]	21(9.13%)	21(17.8%)	42(12.07%)
Depth
A	63(27.39%)	29(24.58%)	92(26.44%)
M	94(40.87%)	53(44.92%)	147(42.24%)
P	54(23.48%)	29(24.58%)	83(23.85%)
Quadrant
Lower Inner	52(22.61%)	21(17.8%)	73(20.98%)
Lower Outer	8(3.48%)	5(4.24%)	13(3.74%)
Upper Inner	38(16.52%)	21(17.8%)	59(16.95%)
Upper Outer	86(37.39%)	57(48.31%)	143(41.09%)
Breast composition
Almost entirely fat	20(8.7%)	30(25.42%)	50(14.37%)
Extremely dense	21(9.13%)	3(2.54%)	24(6.9%)
Heterogeneously dense	104(45.22%)	31(26.27%)	135(38.79%)
Scattered fibroglandular densities	85(36.96%)	54(45.76%)	139(39.94%)
Retro density
High	25(10.87%)	59(50%)	84(24.14%)
Iso/low	205(89.13%)	59(50%)	264(75.86%)
Density num
High	30(13.04%)	51(43.22%)	81(23.28%)
Iso/low	79(34.35%)	20(16.95%)	99(28.45%)

3 Methodology

The whole dataset (348 findings) was split into two subsets: (1) training set: 180 cases, whose mass densities were classified by a radiologist at the exact time of imaging and (2) test set: 168 cases, whose mass densities were not annotated at the time of imaging, but instead in a reassessment of all the 348 exams performed by a group of experienced physicians. The attribute corresponding to the prediction of mass density by the specialist is density_num. The attribute corresponding to the retrospectively assessed mass density is retro_density. We have values for density_num for only 180 of the cases and have values for retro_density for all 348 cases. With these train and test datasets, we performed several experiments in order to generate models to (1) predict malignancy (outcome) and (2) to predict mass density.

Table 2 shows all experiments performed for each task, according to the attributes used to learn mass density or outcome. The first five experiments were performed with 180 findings (training set) while the remaining were performed with 168 findings (test set). From the first five, the first three predict outcome and the other two predict mass density. In a nutshell, the experiments can be described as follows:

• Experiment E₁ aims at finding a classifier to predict outcome using the attribute mass density that was retrospectively annotated (retro_density). This classifier would be useful to help physicians make decisions on retrospectively studied patients.

• Experiment E₂ aims at finding a classifier to predict outcome from patients whose mass density was prospectively assessed (using the attribute density_num). This classifier would be helpful on the clinical daily routine of a physician.

• Experiment E₃ was performed in order to assess the performance of a classifier trained without any mass density information. This experiment was performed in order to assess the relevance of mass density when predicting the outcome. It can be used on new data without any information about mass density.

• Experiment E₄ generates models to predict mass density based on retrospectively annotated density (i.e. using the attribute retro_density).

• Experiment E₅ generates models to predict mass density based on prospectively annotated density (i.e. using the attribute density_num).

The last two experiments were performed to assess how well an automated classifier can predict the kinds of densities (high or iso/low) when compared to the physician.

Table 2.

Experiments on the training and test sets. In each line, we give the conditions of the experiment. For example, E₁, E₂ and E₃ predict outcome, where E₁ uses mass density as described by the attribute retro_density, E₂ uses mass density as described by the attribute density_num and E₃ does not use any information about mass density

Exp.	outcome	retro_density	density_num	size	output
E 1	class	yes	no	180	classifier for outcome (M1)
E 2	class	no	yes	180	classifier for outcome (M2)
E 3	class	no	no	180	classifier for outcome (M3)
E 4	no	class	no	180	classifier for mass density (M4)
E 5	no	no	class	180	classifier for mass density (M5)
E 6	no	class	no	168	test set with mass density filled up by model M4
E 7	no	no	class	168	test set with mass density filled up by model M5
E 8	class	yes	no	168	prediction of outcome using actual values of retro_density
E 9	class	yes (E6)	no	168	prediction of outcome using test set obtained in E6
E 10	class	no	yes (E7)	168	prediction of outcome using test set obtained in E7
E 11	class	no	no	168	prediction of outcome without mass density

We evaluated several classification algorithms available in WEKA (Hall et al., 2009) and varied their parameters. The experiments were performed with the WEKA’s experimenter module using ten times ten-fold cross-validation on the training dataset. For each algorithm we selected the combination of parameters that produced the best classifiers, and then selected the top three classifiers for generating models: NaiveBayes (John and Langley, 1995), DTNB (a decision table algorithm whose leaves are Bayesian networks) and SMO (a support vector machine (Wang, 2005) implementation (Platt, 1998)). A fourth classifier was selected, J48 (decision tree based on Quinlan’s C4.5 algorithm), due to its ability to produce readable and easily understandable models.

The last six experiments of Table 2 apply the models generated (M₁, M₂, M₃, M₄ and M₅ generated by the first five experiments), to the test set containing 168 cases as follows:

1. Experiment E₆ generates the values for mass density using model M₄ trained with the attribute retro_density as the class variable (obtained by experiment E₄).

2. Experiment E₇ generates the values for mass density using model M₅ trained with the attribute density_num as the class variable (obtained by experiment E₅).

3. Experiment E₈ predicts outcome using model M₁ trained with the attribute retro_density (obtained by experiment E₁) and uses the actual values of the attribute retro_density available in the test set.

4. Experiment E₉ predicts outcome using model M₁ trained with the attribute retro_density (obtained by experiment E₁) and uses the mass density values filled up by experiment E₆ in the test set.

5. Experiment E₁₀ predicts outcome using model M₂ trained with the attribute density_num (obtained by experiment E₂) and uses the mass density values filled up by experiment E₇ in the test set.

6. Experiment E₁₁ predicts outcome with model M₃ that does not use any information about mass density, obtained in experiment E₃. For this experiment, no mass density attribute is used in the test set.

We used the metrics Correctly Classified Instances (CCI, a.k.a. accuracy), F-measure (harmonic mean between Precision and Recall) and Kappa statistics to assess the classifiers. Whenever applicable we performed significance tests using paired t-test (α = 0.05).

4 Results

We first investigated the data and calculated simple frequencies to determine if there was some evidence of relationship between attributes, specially if mass density is related to malignancy.

Table 4 shows the frequencies of attribute values. According to the frequencies of attribute values among the classes, from the 348 breast masses, 118 are malignant (≈34%) and 84 have high mass density (≈24%). If we consider that mass density and malignancy are independent and take 84 cases from the 348 at random, the probability of these being malignant should still be ≈ 34%. However, if it happens that all 84 cases selected at random have high density, then the percentage of malignant cases raises to 70.2% and the probability of this being coincidence is very low. This simple calculation may already imply that high density has some relationship with malignancy. So may the other attributes such as age, mass shape and mass margins. In this work, we do not report on the importance of the other attributes.

4.1 Performance analysis

The best models produced for experiments (E₁), (E₂), (E₃) and (E₄) were obtained with the algorithm SMO, with main parameters: polynomial kernel with exponent E = 1 and complexity constant C = 0.05. For experiment (E₁), the best classifier was obtained with data standardisation (N = 1), while the other three experiments used N = 2 (the training data was not normalised/standardised). The parameter C at SMO controls how soft the class margins are. In practice, it controls how many instances are used as ‘support vectors’ to draw the linear separation boundary in the transformed Euclidean feature space. The fact that C = 0.05 produces better results seems to indicate that the default value (1.0) somehow generates an over-fitted trained classifier, whose performance is not so good on the cross-validation test sets. For experiment (E₅), the best classifier was obtained using the NaiveBayes algorithm with default parameters. Most probably, NaiveBayes performed better with this dataset because this data is noisy containing errors associated to the prospectively annotated density_num attribute.

Table 3 shows, for each experiment E₁ to E₅, the best performance of each algorithm after parameter variation (classifiers are sorted in descending order after CCI). The SMO classifier consistently achieves better results for the training dataset, even when NaiveBayes wins (experiment E₅, note that there is no statistically significant difference between NaiveBayes and SMO with respect to CCI and K).

Table 3.

Classifiers’ performance for each task, for the training data. Values not in bold are statistically significantly worse than the classifier with highest accuracy (using paired t-test with α = 0.05)

Exp.	Algorithm	CCI	K	F	AUROC
E 1	SMO	85.6 ±7.3	0.69 ±0.16	0.80 ±0.11	0.84 ±0.08
E 1	DTNB	81.6 ±8.2	0.60 ±0.18	0.74 ±0.13	0.88 ±0.07
E 1	NaiveBayes	81.3 +9.5	0.61 ±0.20	0.76 ±0.12	0.88 ±0.08
E 1	J48	80.7 ±9.3	0.59 ±0.20	0.75 ±0.13	0.79 ±0.11
E 2	SMO	83.9 ±7.7	0.66 ±0.17	0.78 ±0.11	0.82 ±0.08
E 2	NaiveBayes	80.3 ±9.3	0.59 ±0.19	0.75 ±0.12	0.87 ±0.09
E 2	DTNB	79.8 ±9.5	0.56 ±0.21	0.72 ±0.15	0.86 ±0.09
E 2	J48	75.4 ±9.5	0.47 ±0.21	0.65 ±0.15	0.73 ±0.12
E 3	SMO	83.8 ±7.7	0.65 ±0.17	0.78 ±0.11	0.82 ±0.09
E 3	J48	76.3 ±9.9	0.49 ±0.22	0.67 ±0.15	0.76 ±0.13
E 3	NaiveBayes	76.2 ±9.9	0.51 ±0.20	0.71 ±0.13	0.85 ±0.09
E 3	DTNB	75.7 ±9.0	0.48 ±0.19	0.67 ±0.13	0.81 ±0.10
E 4	SMO	81.3 ±8.2	0.52 ±0.21	0.64 ±0.17	0.75 ±0.11
E 4	J48	74.4 ±8.8	0.32 ±0.24	0.47 ±0.21	0.67 ±0.15
E 4	DTNB	73.5 ±10.0	0.34 ±0.24	0.51 ±0.19	0.76 ±0.12
E 4	NaiveBayes	72.8 ±9.9	0.37 ±0.23	0.56 ±0.18	0.77 ±0.11
E 5	NaiveBayes	67.2 ±12.1	0.33 ±0.25	0.62 ±0.15	0.72 ±0.14
E 5	SMO	66.8 ±10.7	0.31 ±0.22	0.55 ±0.16	0.65 ±0.11
E 5	J48	63.6 ±10.1	0.26 ±0.21	0.56 ±0.15	0.62 ±0.13
E 5	DTNB	62.1 ±11.9	0.22 ±0.24	0.54 ±0.16	0.64 ±0.14

All classifiers behave better when trained on retrospectively annotated data (experiment E₁), which seems to indicate that in practical clinical routine, this would be the best classifier to use. However, since it is hard to obtain retrospectively annotated data, the approach followed in E₂, using prospectively annotated mass density values, can also be used with good results. It is important to notice that the SMO obtained with experiment E₂ has performance only slightly lower than the SMO of experiment E₁ and the difference is not statistically significant.

Experiment E₅ is the most difficult as it consists of predicting mass density from noisy data. It is interesting to note that all algorithms achieve lower performance for this experiment than for the other tasks, with NaiveBayes achieving a performance that is close to that of the physician, who has CCI of 70% when compared with the retrospectively annotated mass density.

All results of Table 3, with exception of AUROC, are higher for the best classifier. The AUROC is higher for algorithms other than the best.

4.2 Training to predict outcome

In the three experiments, (E₁), (E₂) and (E₃), the best classifiers found were based on SMO. First of all, these results show that mass density has some influence on the outcome, specially when mass density is the one observed on the retrospective data (experiment E₁). The classifier trained without mass density has an overall performance of 83.8% while the classifier trained with the retrospectively assessed mass has an overall performance of 85.6%, which is a statistically significant difference of 1.8 (p = 0.05). If we look at the K value, we can confirm that the relation between mass density and outcome is not by chance, given the relatively high observed agreement between the real data and the classifier’s predicted values. The F-measure balances the values of Precision and Recall and also indicates that the classifiers are behaving reasonably well.

The results obtained with experiments (E₁), (E₂) and (E₃) confirm findings in the literature regarding the relevance of mass density (Davis et al., 2005, 2007; Ferreira et al., 2011; Woods et al., 2010, 2011), and also show that good classifiers can be obtained to predict outcome (with a high percentage of correctly classified instances and reasonable values of precision and recall, according to F).

Another evidence that mass density is somehow related to malignancy are the decision trees (Figures 1(a) and 1(b)) generated by the J48 algorithm, in which retro_ density and density_num were chosen as the most important attributes appearing in the top of the trees. Despite the fact that J48 was not the best classifier to predict outcome, this fact reveals that the attribute mass density has some influence over all the remaining features. Another important fact to note is that, according to J48, the second most important attribute that helps discriminating between malignant and benign cases is mass_margins.

Figure 1.

Decision trees and mass density

4.3 Training to predict mass density

Our set of experiments E₄ and E₅ are related to predicting mass density. As the dataset has two annotated mass densities, one for the prospective study and another one for the retrospective study, we generated two classifiers: one is trained on the prospective values of mass density (density_num) and another one is trained on the retrospective (retro_density) values of mass density. Once more, we used the 180 cases as training set and ten times ten-fold cross-validation. The best classifier for predicting retro_density was SMO and the best to predict density_num was NaiveBayes.

During the prospective study, the radiologist predicted 70% of masses on the 180 findings compared with the annotated masses of the retrospective study. The SMO classifier predicted 81.3% of correct instances when training on the retrospective annotated mass (retro_density) and NaiveBayes predicted 67.2% of correct instances when training on prospective masses annotated by the radiologist. These results are quite good and indicate that either the SMO or the Bayesian classifier generated in this study can be well applied as a support tool to help physicians/radiologists to classify mass density in mammograms.

The values of K and F-measure for this experiment are not so good as the ones obtained with the classifiers that predict outcome. The K value, once more, indicates that both NaiveBayes and SMO have a moderate level of agreement.

4.4 Performance summary

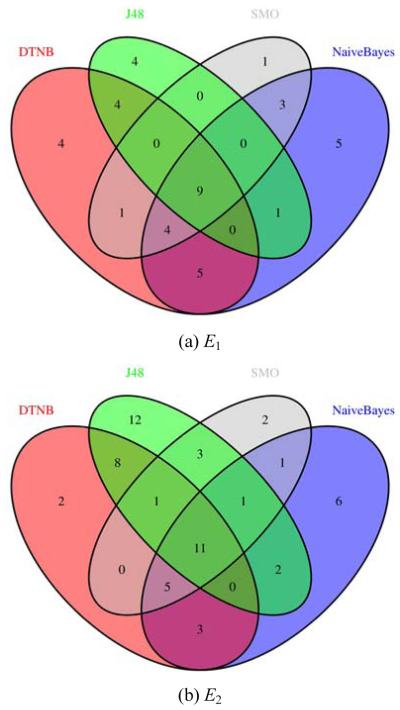
Figure 2 shows the errors associated to the different algorithms for experiments E₁ to E₅, in terms of numbers of common misclassified examples. From each one of the Venn diagrams, we can identify the total number of misclassified examples and the actual examples that are being misclassified by the several algorithms. From the experiments to predict outcome, the one that produces the lowest error rate is E₁ with 41 misclassified examples. This is also one of the two experiments that has lower error rate for all classifiers (only nine examples are commonly misclassified by all algorithms). The experiment that produces the highest error rate is E₅, with all classifiers commonly misclassifying 16 instances.

Figure 2.

Errors of the classifiers on the 180 cases (see online version for colours)

It is interesting to note that some classifiers make mistakes in completely different parts of the dataset. For example, SMO, DTNB and J48 do not have any intersection in experiment E₅.

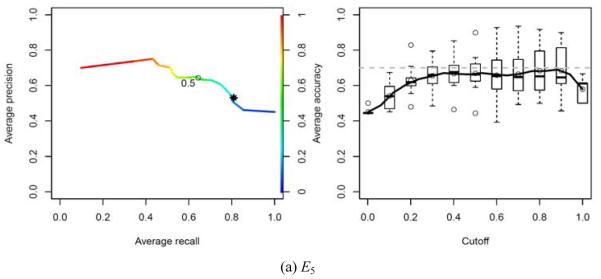
We plotted Precision-Recall curves and CCI curves according to the predicted probabilities of the SMO algorithms for experiments E₁ to E₄ and of NaiveBayes for experiment E₅. The Precision-Recall and CCI curves give a good overview of how well the classifiers behave when one needs a cut-off point.

When predicting mass density, our classifiers ( M ₄ in Figure 3(d) and M ₅ in Figure 4(a)) produce results comparable with the ones obtained by the physician (the physician’s result is plotted with a star symbol). These curves show the performance of the classifiers for predicting malignancy (E₁ to E₃) and high density masses (E₄ and E₅).

Figure 3.

Precision-Recall curves and CCI according to cut-off (SMO based models). The dotted grey line and star on the graphics of (see online version for colours)

Figure 4.

Precision-Recall curves and CCI according to cut-off (NaiveBayes based model). The dotted grey line and star on the graphics indicate the performance of the physician (see online version for colours)

4.5 Performance of the best classifiers on unseen data

Table 5 summarises the results of predicting outcome on the 168 unseen cases as well as the results of filling up the attribute mass density in the test set.

Table 5.

Classifiers’ performance for the test set

	Algorithm	CCI	K	F	AUROC
E 6	SMO	84.52	0.46	0.55	0.74
E 7	NaiveBayes	75.60	0.35	0.49	0.81
E 8	SMO	80.95	0.50	0.63	0.74
E 9	SMO	80.36	0.49	0.62	0.73
E 10	SMO	80.95	0.52	0.65	0.76
E 11	SMO	76.19	0.42	0.58	0.71

The first two lines of Table 5 refer to experiments to fill up values of the attribute mass density in the test set. The CCI indicates how well models M₄ and M₅ , obtained respectively with experiments E₄ and E₅, performed on filling up those values, when compared with the actual values of retro_density available in the test set. The SMO classifier, which had a very good performance on the training set (CCI = 81.3%), behaves even better when filling up values for retro_density, making mistakes in only 15% of the actual masses. The NaiveBayes classifier ( M ₅ ), obtained with experiment E₅ , which had CCI = 67.2% in the training set, performed very well in the task of filling up the missing values of density_num, correctly classifying 75.6% of the instances. A result that surpasses the result obtained by the specialist, which is 70%.

For the tasks of predicting outcome, the classifiers also perform very well, with the worst predictions being produced by model M₃ , which does not use any information about mass density. This result confirms once more the relevance of mass density on predicting outcome. In the absence of this information, the data could be filled up by M ₄ or M ₅ , that, as mentioned, have a good performance on performing this job.

4.6 MammoClass application

The best models were integrated into an online application (called MamoClass). It allows a practitioner to quickly and easily assess mammograms by obtaining a prediction for mass density and/or classify a mammography given a reduced set of mammography findings. The application is freely available at http://cracs.fc.up.pt/mammoclass. This application will start to be used at Hospital São João in Porto, Portugal, and at the Medical School, in the University of Wisconsin, Madison, USA, by our collaborators.

5 Conclusions and future work

In this work, we were provided with 348 cases of patients who went through mammography screening and biopsies. The objective of this work was twofold: (i) find non-trivial relations among attributes by applying machine learning techniques to these data and (ii) learn models that could help medical doctors to quickly assess mammograms. The best models to predict outcome were obtained with Support Vector Machines (SVM), implemented in WEKA’ SMO algorithm, with the parameters polynomial kernel with exponent E =1 and complexity constant C = 0.05. The fact that C =0.05 produces better results seems to indicate that the default value (1.0) somehow generates an over-fitted trained classifier, whose performance is not so good on the cross-validation test sets.

The best model to predict mass density based on retrospective data was also based on SVM. The best model to predict mass density based on prospective data is based on the naive Bayes algorithm with default parameters. The higher levels of noise in the data used for predicting mass density, that results from the errors associated to the prospectively annotated density_num attribute, must have contributed to the better performance of naive Bayes (which is known to be robust to noise).

In general, SVM classifiers showed to be the best for predicting both malignancy and mass density with the retrospective data. The experiments that use the retrospective data are the ones that generate classifiers with the lowest error rate. Predicting malignancy using the models that can fill up missing values of mass density seem to work very well in the test set. An analysis of precision-recall curves and errors indicate that choosing a good threshold, one can have good classifiers, with an acceptable false positive rate and good recall, in all experiments.

We plan to extend this work to larger datasets, and apply other machine learning techniques based on statistical relational learning, since classifiers that fall in this category provide a good explanation of the predicted outcomes as well as can consider the relationship among mammograms of the same patient. We would also like to investigate how other attributes can affect malignancy or are related to the other attributes.

Biographies

Pedro Ferreira received his MSc in Computer Science in 2010 from the University of Porto, Portugal. Currently he is a Project Researcher at the Center for Research in Advanced Computing Systems (CRACS), Portugal. His research interests are data analysis and medical informatics.

Nuno A. Fonseca received the PhD degree in Computer Science from the Faculty of Science of the University of Porto in 2006. Currently, he is a research scientist at the European Bioinformatics Institute (EMBL). His research interests encompass bio-informatics, machine learning and high performance computing.

Inês Dutra received her PhD in Computer Science at the University of Bristol, England. Currently she is a Lecturer at University of Porto, in the Department of Computer Science, Porto, Portugal and a member of the Center for Research in Advanced Computing Systems (CRACS). Her research interests include logic programming, inductive logic programming, machine learning and parallel processing.

Ryan Woods, MD, MPH, is currently a 4th year radiology resident at the Johns Hopkins Hospital in Baltimore, MD. He received his MD degree from the University of Wisconsin School of Medicine and Public Health in 2008, and his MPH from Boston University in 2004. His research interests include breast imaging and informatics.

Elizabeth Burnside is currently an Associate Professor of Radiology in the University of Wisconsin School of Medicine and Public Health. She got her MD degree combined with master’s in Public Health as well as a master’s degree in Medical Informatics. As a result her research investigates the use of artificial intelligence methods to improve decision-making in the domain of breast imaging in the pursuit of improving the population based screening and diagnosis of breast cancer.