FRACTURE-RESISTANT MONOLITHIC DENTAL CROWNS

Abstract

Objective

To quantify the splitting resistance of monolithic zirconia, lithium disilicate and nanoparticle-composite dental crowns.

Methods

Fracture experiments were conducted on anatomically-correct monolithic crown structures cemented to standard dental composite dies, by axial loading of a hard sphere placed between the cusps. The structures were observed in situ during fracture testing, and critical loads to split the structures were measured. Extended finite element modeling (XFEM), with provision for step-by-step extension of embedded cracks, was employed to simulate full failure evolution.

Results

Experimental measurements and XFEM predictions were self consistent within data scatter. In conjunction with a fracture mechanics equation for critical splitting load, the data were used to predict load-sustaining capacity for crowns on actual dentin substrates and for loading with a sphere of different size. Stages of crack propagation within the crown and support substrate were quantified. Zirconia crowns showed the highest fracture loads, lithium disilicate intermediate, and dental nanocomposite lowest. Dental nanocomposite crowns have comparable fracture resistance to natural enamel.

Significance

The results confirm that monolithic crowns are able to sustain high bite forces. The analysis indicates what material and geometrical properties are important in optimizing crown performance and longevity.

1. Introduction

Monolithic all-ceramic crowns are increasingly favored over traditional prostheses with porcelain veneers, minimizing issues associated with complex fabrication, presence of residual stresses, and delamination from an inner core [1–4]. Dense zirconia and lithium disilicate glass-ceramics are prime candidates, for their relatively high modulus and fracture resistance along with ever-improving esthetics [5–15]. A stiff all-ceramic crown shields the inner dentin–pulp region by absorbing the bulk of occlusal stresses. However, brittleness remains a concern—failures for monolithic ceramic systems have been reported [16–18]. These failures are sometimes described as ‘abrupt’, with complete cracking of the crown and sometimes of the entire tooth. But little attempt has been made to examine how cracks evolve in relation to material properties. One effort has been made to elucidate the mechanics of the less disruptive fracture mode of edge chipping in monolithic ceramics [3], but while such studies are useful for quantifying crack resistance properties of the crown material, they do not address the more serious issue of total crown failure.

An alternative, more recent approach to crown restoration is to fabricate monolith prostheses from particle-filled resins [19–21]. While much more compliant and therefore less protective of the underlayer, dental composite crowns are seemingly less prone to fracture, if not to deformation. They appeal to the practicing dentist because of their ease of fabrication and installation. However, their capacity to sustain high bite forces and to avoid debonding is in question. Again, little attempt has been made to determine the mechanics of failure in composite restorations.

Clues to the modes of potential crown failure can be drawn from recent studies of fracture in natural teeth. Apart from incidental edge chipping [3,22], extensive experimental testing and theoretical fracture mechanics analysis of tooth breakdown under occlusal loading reveals a common mode of fracture in human teeth to be longitudinal cracking from the bite surface to the tooth base (or vice versa) [23–29]. Longitudinal cracks start from ‘tuft’-like defects in the enamel close to the junction with dentin and run to the surface before vertical extension along the tooth walls [30,31]. They can remain fully contained as visible ‘lamellae’ within the enamel, and can even heal to some extent, without causing immediate failure—the fracture to that point is ‘contained’. Longitudinal cracks can also act as precursors to whole tooth splitting through the dentin to the root, at which point the tooth is lost [22,32,33]. The question arises as to whether similar fracture processes operate in monolithic crown restorations and, if so, which are the best materials to contain them?

This study addresses these questions, first by conducting in vitro laboratory axial-loading fracture tests on manufactured model zirconia, lithium disilicate and dental nanocomposite crown specimens, and then by extending earlier fracture mechanics computations to analyze the fracture modes. The study focuses on anatomically-correct molars, centrally loaded with a hard spherical indenter to wedge open adjacent cusps and thereby split the crown along a fissure plane. However, the conclusions drawn have a broader reach to other tooth forms. Particular attention is given to the role of crown material properties, notably toughness and modulus, as well as to key geometrical variables such as tooth dimensions and sphere radius. The manner in which cracks progress from the occlusal surface to the enamel/cementum junction will be elucidated. It will be confirmed that monolith ceramics are capable of providing long-lasting crown restorations, provided due caution is exercised in fabrication and cementation procedure.

2. Materials and methods

2.1 Crown preparation and testing

Three candidate restorative materials for monolithic dental crowns were selected for study, each procured in the form of commercially available CAD/CAM blocks: (i) high translucency zirconia, 3 mol% Y-TZP (LAVA Plus, 3M ESPE, St Paul, MN); machinable lithium disilicate glass-ceramic (IPS e.max CAD, Ivoclar-Vivadent, Amherst, NY); and resin-based composite with nanoparticle ceramic filler (LAVA Ultimate Restorative, 3M ESPE, St Paul, MN). Six blocks of each material were machined into anatomically-correct mandibular first molar crowns by inputting scanned profiles of standard dental composite dies (Filtek Z100, 3M ESPE, St Paul, MN) into the following machining systems: Lava Milling System (3M ESPE, St Paul, MN) for zirconia and resin-based nanocomposite, and CEREC System (Sirona, Charlotte, NC) for lithium disilicate. The ensuing occlusal crown thickness was 1.0 mm for zirconia and 2.0 mm for lithium disilicate and nanocomposite, with a common proximal wall thickness 1.5 mm. Allowance was made for a cementation thickness 50 μm in all cases. The dies were engineered to provide common external crown dimensions for all materials, specifically tooth radius 5.0 mm (one quarter of sum of maximum buccal/lingual and mesial/distal widths) and tooth height 7.0 mm (average occlusal to enamel/cementum junction distance over all cusps).

Values of representative mechanical properties of the three crown materials in their finished states are given in Table 1, drawn from manufacturers specifications. The Z100 die material used as substrate in the crown fabrication has near-identical filler content to that of the LAVA Ultimate dental nanocomposite, and is therefore taken to have similar properties. For comparison, some values for enamel and dentin are included in the table. Uncertainties in the values presented, from variations in published literature properties, are estimated at a nominal ~ 20%.

Table 1.

Representative properties of crown materials. Data compiled from manufacturer’s specifications and previous studies [3]. Uncertainties in property values are typically ~ 20%.

Material	Modulus E (GPa)	Poissons ratio	Toughness T (MPa·m1/2)	Strength S (MPa)
Zirconia (Lava Plus)	210	0.30	4.0	1200
Lithium disilicate (IPS e.max CAD)	95	0.23	1.5	376
Resin composite (Lava Ultimate)	13	0.35	2.0	200
Enamel	90	0.22	1.0	–
Dentin	18	0.35	3.0	–

After milling, the crowns were processed as follows. The surfaces of the zirconia and lithium disilicate crowns were glazed at elevated temperatures and times according to manufacturers’ recommendations. The intaglio surfaces of zirconia were sandblasted (aluminum oxide particles, 50 μm at pressure 2 bars, 100 mm standoff distance) to promote a mechanically adherent bond, while those of lithium disilicate were acid-etched (5% HF for 20 s). As-machined resin-based nanocomposite crowns were polished (1 μm diamond paste) on their outer surfaces and sandblasted at their intaglio surfaces, taking care to avoid damage to the margins.

The composite dies were aged in distilled water for at least 21 days, then air dried for receipt of the crowns. The zirconia and lithium disilicate crowns were first coated at their intaglio surfaces with a bonding agent (Monobond Plus, Ivoclar Vivadent, Amherst, NY), then cemented onto the dies (Multilink Automix, Ivoclar Vivadent, Amherst, NY). The dental nanocomposite crowns were similarly coated (Scotchbond Universal, 3M ESPE, St Paul, MN) and cemented (RelyX Ultimate, 3M ESPE, St Paul, MN}. After cementation, the mounted specimen crowns were stored in distilled water at 37°C for a minimum of 5 days to allow complete polymerization and hydration of the cement layer prior to mechanical testing.

The crowns were then subjected to failure testing by axial loading with a tungsten carbide sphere located in the central fossa [33]. This particular mode of loading is the easiest way to deliver wedge-opening forces on adjacent cusps, and simulates biting on a hard food object or opposing molar tooth or crown cusp. A sphere radius 3.2 mm was chosen simply because it was convenient to handle in the experiments. The load was applied in a mechanical testing machine (Model 5566, Instron Corp, Norwood, MA) at a crosshead speed of 0.1 mm/min. A video camera was placed to observe the crown side walls during the loading, in order that the failure evolution may be followed in situ.

2.2 Fracture mechanics analysis

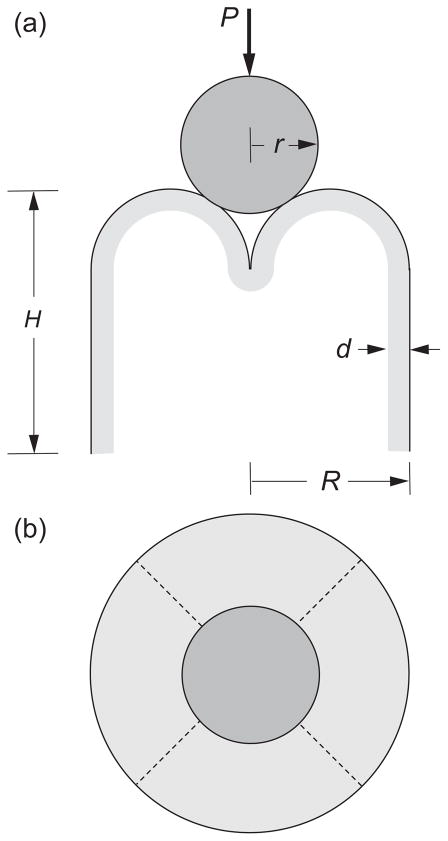
Analysis of the failure evolution was conducted using an extended finite element model (XFEM) package (Abaqus 6.9-EF1, Simulia, Providence, RI), incorporating provision for step-by-step progression of an embedded crack. The model used is depicted in Fig. 1, and is the same as in a preceding article describing the failure of natural molar teeth [33], but with the crown material replacing the enamel shell. It consists of a shell structure with four truncated hemispherical cusps of radius R/2 and uniform thickness d = 1 mm (zirconia) or 2 mm (lithium disilicate and dental nanocomposite) on a cylindrical base of radius R = 5.0 mm and total occlusal-to-margin height H = 7.0 mm, i.e. closely representative of the anatomically-correct crowns. The shell is fully bonded to an interior dentin-like substrate. The presence of an intervening cement layer is considered to have a negligible effect on the fracture mechanics, because of its of thinness (~ 50 μm) and comparable modulus and toughness relative to the dentin-like interior, and was therefore omitted from most computations. Nevertheless, a simple comparative computation with cement layer included was run for confirmation. A vertical load is applied axially onto a rigid sphere of radius r = 3.2 mm in frictionless contact on all four cusps, so that horizontal wedging forces are delivered across symmetry fissure planes (dashed lines in Fig. 1b). Note that these fissure planes are distant from the indenter contact points (Fig. 1a). Input material properties for the crown materials are taken from Table 1.

Fig. 1.

Model for molar tooth fracture, (a) side and (b) top view. Occlusal structure sits atop a cylindrical base of radius R and net height H, with four hemispherical cusps of radius R/2 and thickness d. Cusps are axially loaded with a hard sphere of radius r, generating lateral wedging forces on adjacent cusps and driving splitting fissures along intervening valleys (fossae) between overlapping adjacent cusps (dashed lines).

The XFEM algorithm contains provision for progressive stable growth of an embedded precursor starter crack with increasing load, up to and beyond the point of final failure, corresponding to total splitting of the crown/substrate assembly. Emplacement of the starter crack on a fissure plane and immediately adjacent to the contact points circumvents meshing complexities in the crack initiation region [26], and is tantamount to assuming that the tooth structure contains preexisting cracks. This is justifiable in the case of tooth enamel, in the form of tufts and lamellae [30], but is an assumption that needs to be examined in the case of crown restoratives. Contact with the cusp walls is made by controlling the downward displacement of the indenting sphere in small increments. The outer shell and inner portions of the structure are meshed sufficiently finely that the computations attain convergence. The emplaced crack is allowed to advance mesh cell by cell in accordance with a cohesive zone criterion outlined in detail elsewhere [33], with parameters for the sequential rupture of each cell adjusted to match the appropriate material modulus and toughness. In this way entire progression of the cracks through both the outer shell and inner filler material could be followed.

2.3 Statistical analysis

Experimental critical splitting load data were analyzed by one-way ANOVA. The independent factor was material group (zirconia, lithium disilicate, nanocomposite). The mean critical load and its 95% confidence interval were calculated for each crown group. Post Hoc Tukey HSD test for multiple comparisons was performed to determine which specific groups differed significantly from one other. The significance level was set at p ≤ 0.05 for all analyses.

3. Results

3.1 Experimental data

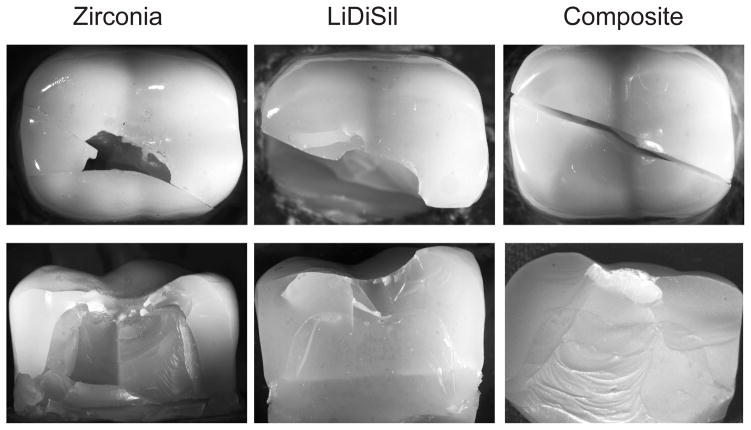
Representative top and side views of failures in each monolithic crown system are shown in Fig. 2. In all cases final fracture occurred by splitting through the dentin to the crown base into two and sometimes more parts. The splits deviated slightly from the symmetry fissure plane between cusps, suggesting that fracture may equally well find a path through part of a cusp, at least for the particular sphere on four-cusp loading configuration investigated here. In all cases the crown failure appeared to be abrupt at the critical load, with no load drop or visible sign of precursor longitudinal or other stable cracking prior to splitting during in situ side wall viewing. This is suggestive of relatively defect-free crown materials where, unlike in enamel, starter cracks must first be initiated before any propagation may ensue. Whereas the section views of the splits in the zirconia and lithium disilicate crowns are ‘clean’ in Fig. 2, indicative of a brittle fracture mode, those in the nanocomposite crown show substantial plastic deformation in the substrate below the occlusal contacts, indicative of a diminished capacity of the composite material to provide adequate support under high loads. Closer fractographic inspection of the broken crown segments confirmed sites of crack initiation to lie in the occlusal region within the crown shell, between the cuspal load points.

Fig. 2.

Contact-induced splits in anatomically correct crowns loaded with tungsten carbide sphere of radius 3.2 mm in a mechanical testing machine, top views (upper) and side views (lower), for zirconia (Y-TZP), lithium disilicate CAD, and resin-based ceramic nanocomposite crowns. Side views are obtained after separating the split fragments. Split paths follow fissure valleys closely, but not exactly.

Experimentally measured critical loads to cause full splits in each monolithic crown system are listed in Table 2, along with mean and standard deviation values (n = 6). Individual experimental data sets in this table follow a normal distribution. One-way ANOVA on the data within individual groups show zirconia to be significantly stronger than the other two materials (p < 0.001), but lithium disilicate not significantly stronger than dental nanocomposite (p = 0.15). The critical loads are all high relative to the most severe bite forces (< 1 kN), at least for the specific loading configuration used in the tests.

Table 2.

Critical splitting loads P_S for anatomically correct monolithic molar crowns on filler resin (Z100) substrates, axially loaded with hard sphere of radius r = 3.2 mm. Evaluations for nominal crown width R = 5.0 mm (one quarter of sum of maximum buccal/lingual and mesial/distal widths), tooth height H = 7.0 mm (average occlusal to margin distance over 4 cusps). Experimental data from ex-vivo splitting tests are means and standard deviations, n = 6 each case. XFEM data are predicted values with uncertainty bounds due to variability in material properties. Coefficients C_S evaluated from eqn. 1 using toughness value T = 2.0 MPa·m^1/2 for composite substrate.

MATERIAL	EXPERIMENT		XFEM
	PS (kN)	CS	PS (kN)	CS
Zirconia	5.78 ± 1.05	3.37 ± 0.61	5.20 ± 1.30	3.03 ± 0.76
Lithium disilicate	3.64 ± 0.33	2.12 ± 0.19	3.65 ± 0.93	2.13 ± 0.54
Dental composite	2.86 ± 0.47	1.67 ± 0.27	2.65 ± 0.66	1.55 ± 0.39

3.2 FEM predictions

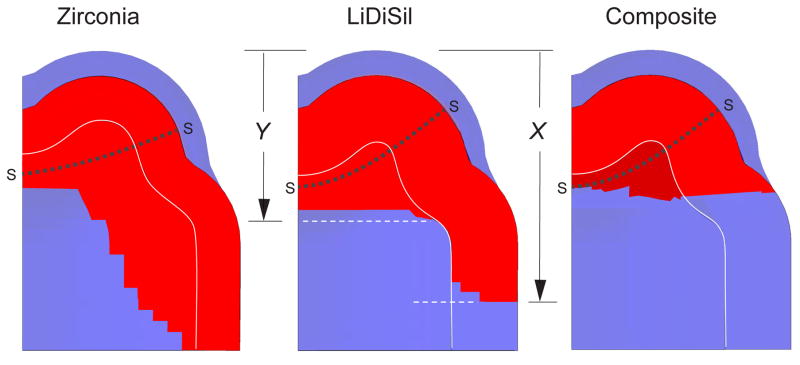
XFEM calculations were made on crown systems with starter cracks using material input parameters from Table 1, for indenting sphere radius r = 3.2 mm. The algorithm enabled extension from the starter cracks to be followed step-by-step along the symmetry fissure plane through the crown shell and composite interior, up to and beyond the point at which the fracture became unstable. Half-section views of the computed crack profiles on the fissure planes between cusps are shown in Fig. 3 for each material at failure. The pixelated crack fronts reflect the discrete mesh configuration. In each case the sections indicate crack growth from starter crack fronts SS, with downward extension measured by crack coordinates X and Y from cusp apex to maximum depth in crown and substrate respectively. XFEM-determined critical loads for each crown system are included in Table 2, with uncertainty bounds assessed from property variability. Consistent with the experimental data, zirconia crowns have the highest failure loads, dental nanocomposite the lowest.

Fig. 3.

XFEM predictions of molar crown splitting for model system in Fig. 1, showing half-sections at point of failure. Calculations made using parameters in Table 1, for crown thicknesses d = 1.0 mm (zirconia) and 2.0 mm (lithium disilicate and dental nanocomposite), base radius R = 5 mm and occlusal-to-margin height H = 7.0 mm, loaded axially with indenting sphere of radius r = 3.2 mm. The sections indicate cracking from starter cracks SS in both the external crown and internal support material, cracks marked in red. Rear cusp lies behind plane of diagram.

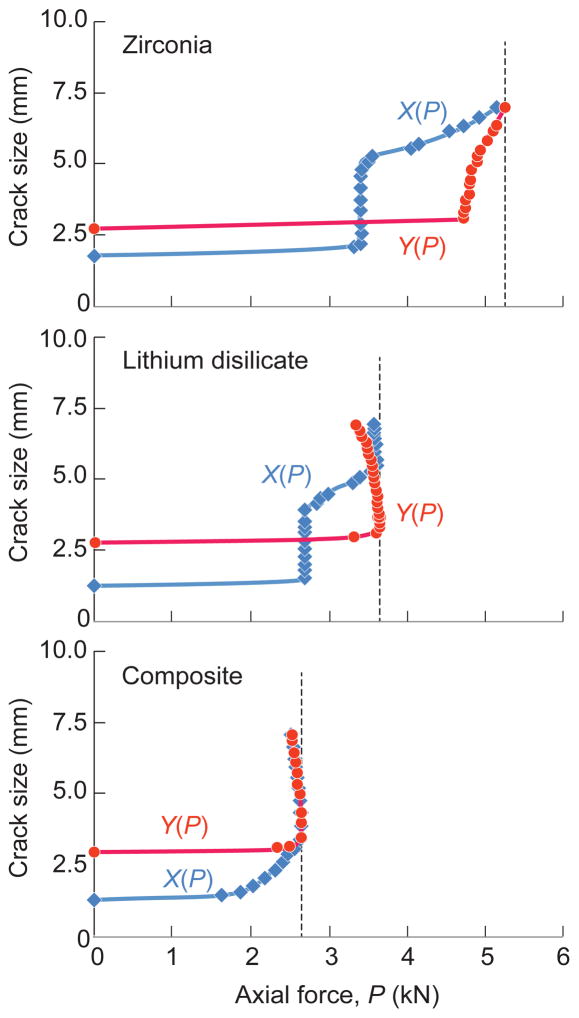
A more detailed account of the cracking sequence is given in Fig. 4, plotting coordinates X and Y as a function of applied load P. In each case crack extension in the substrate is predicted to lag that in the crown shell. This is the case up to the failure load, marked by the vertical dashed lines. Note that for zirconia crowns the X(P) and Y(P) curves have positive slopes, corresponding to stable growth up to the point at which the cracks reach the margins. This stable growth phase means that the failure condition is insensitive to the prescribed size and shape of the starter cracks [26]. For lithium disilicate and nanocomposite, the curves pass through a maximum, indicating instability part way down the tooth wall. (The negative slope beyond the instability point in the latter cases reflects displacement control in the loading algorithm.) Select comparative XFEM runs for the zirconia crown system represented in Fig. 1a, but with a cement layer included, showed no significant difference in the final critical load within the stated bounds of computational uncertainty.

Fig. 4.

XFEM predictions of crack depth X in crown shell and Y in interior filler from cusp height (see Fig. 3) as function of axial load P, for four-cusp molar axially loaded with sphere of radius r = 3.2 mm. Stable crack extension prior to failure is indicated in both crown and substrate in each case. Vertical dashed lines denote instability load, i.e. splitting fracture.

4. Discussion

This study has examined splitting in model anatomically-correct molar restorations, consisting of zirconia, lithium disilicate or filled-resin nanocomposite crowns on dental composite substrates. Splitting was induced by axial loading with a hard sphere of radius r = 3.2 mm wedged between the molar cusps (Fig. 1). Experiments have been run on manufactured crown specimens and critical loads to failure measured (Fig. 2). Analyses of the full fracture evolution have been carried out using extended finite element modeling (XFEM) (Figs. 3 and 4). Critical loads measured experimentally and predicted from XFEM agree within uncertainty bounds (Table 2) and confirm zirconia to be the most split-resistant and dental nanocomposite the least. At very least, the experimental and analytical data provide a quantitative material ranking for prospective strength and longevity.

On an absolute scale, the conditions of testing and analysis are not totally representative of likely clinical conditions. It will be recalled that the critical splitting loads in Table 2 are high compared to maximum biting forces (< 1 kN). Part of the reason for such high loads was the use of a relatively large wedging sphere, i.e. r = 3.2 mm, chosen for experimental expediency. Smaller spheres can dramatically lower the critical loads, by fitting more snugly in the central fossa and thereby enhancing the wedging action [33]. Another experimental expediency was the use of a dental composite (Z100) as a filler substrate for the crowns, whereas dental crowns are generally fitted directly onto stiffer and tougher dentin (Table 1) (except perhaps where the damaged tooth has required ‘build-up’). These factors can be accommodated by an explicit fracture mechanics equation for the critical load P_S to split molars of width R and height H [33]

$$P_{\mathrm{S}}=C_{\mathrm{S}}{\{{(1+2r/R)}^2-1\}}^{1/2}{\mathit{TRH}}^{1/2}$$ (1)

where T is the substrate toughness and C_S is a coefficient dependent on the crown/substrate modulus ratio. The coefficient C_S is subject to approximations in the fracture mechanics analysis, but any uncertainty in its value may be circumvented by ‘calibration’ from eqn. 1 using the data in Table 2. Thus, inserting r = 3.2 mm along with essential tooth dimensions (R = 5.0 mm, H = 7.0 mm) and resin composite toughness (T = 2.0 MPa·m^1/2) from Table 1, we obtain the C_S values for each separate data set listed in Table 2.

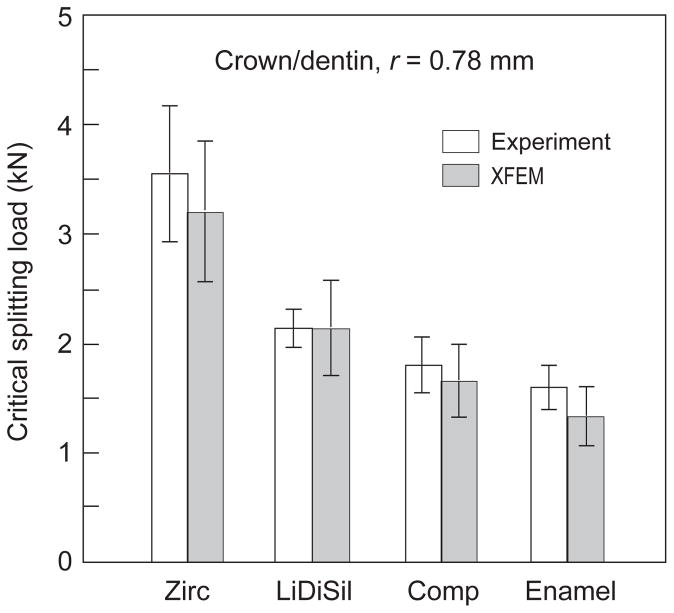
With these evaluations, eqn. 1 may then be used to scale the critical loads in Table 2 to a dentin substrate of toughness (T = 3.0 MPa·m^1/2) and to any contacting sphere radius r. We illustrate here for a sphere size r = 0.78 mm, selected because it is the smallest size for which comparative experimental and analytical data on natural molar teeth are available [33]. Ensuing critical loads are plotted in Fig. 5. The values are still substantial, but closer to the upper limit of bite force, suggesting that even smaller sphere sizes could further reduce the critical loads (although objects that are too small could fit within the cusps without exerting any wedging forces [33]). Note in Fig. 5 that both zirconia and lithium disilicate crowns are more resilient than enamel, and that nanocomposite crowns are comparable. There are other factors that could act to lower the critical loads, such as the incursion of defects from traumatic or cumulative damage, excessive sandblasting or occlusal adjustment prior to placement, development of wear facets or margin chipping (abfraction), and fatigue [2,34–36].

Fig. 5.

Predictions of critical splitting load for crowns, computed for dentin substrates and for sphere size r = 0.78 mm, using data in Table 2 in conjunction with eqn. 1. Data for enamel on dentin from earlier study included at right for comparison.

A feature of the XFEM analysis, apart from affording confirmation of the experimental data trends, is the insight it provides into the splitting evolution. There are stages of crack stability prior to final failure that cannot be inferred from traditional finite element maps of stress distributions alone. The XFEM algorithm enables each stage of crack growth to be followed through the entire fracture process, including any precursor stable phases. Such stable phases have been amply demonstrated in longitudinal cracks from axial loading of actual and simulated tooth structures [23,24,26–29]. And yet in the current experiments on monolithic crown systems, no such stable growth was observed on the outer walls prior to failure. This might be attributed to the difficulty in perceiving any such cracks in the video recording system, but it is more likely that careful fabrication of the zirconia, lithium disilicate and dental composite crowns has precluded the incidence of major starter cracks. In such a case cracks have first to be initiated in order to facilitate immediate stable crack extension. If the initiation load were to be close to the ultimate critical load, the crack would jump abruptly and arrest before final propagation to the tooth base. Such is not the case in natural enamel, where starter cracks abound and where longitudinal cracking is observed around the side walls almost immediately upon loading [24,30,37]. The implication here is that well-prepared, axially-loaded monolithic crowns are unlikely to undergo extensive precursor cracking. If occlusal contact were to be made at the apex of an individual cusp instead of along the tooth axis, especially at a wear facet with attendant surface microcrack damage close to a side wall [38], longitudinal cracks might initiate more easily and grow more steadily; and, moreover, at reduced applied load [29], thereby affording an early warning signal for impending failure.

One issue that deserves justification is the relevance of contact testing methodologies to clinical failures. It has been argued by Kelly and colleagues [39–43] that contact loading with hard spheres does not replicate occlusal loading of dental prostheses in real life. The basis of the objection is that traditional fracture modes beneath hard indenters (cone cracks, radial cracks) are not observed at the occlusal surfaces at failed crowns, and that failure occurs instead by crack initiation at the cementation surface from some intrinsic flaw in the microstructure. However, that argument is not pertinent to the splitting configuration described for molar teeth in the present work, because the fractures in Fig. 2 occur away from the cuspal loading points. The action of any indenting object leading to splitting, be it a foreign food item or opposing tooth/crown cusp, is simply to generate wedging forces on fissure planes between adjacent cusps, not so much to generate cracks at the immediate contact zones. In this context, it has been confirmed that replacement of hard metal indenters with more compliant glass spheres has very little effect on the mechanics of crack evolution in dental-like layer structures [44]. Cuspal contacts are more likely to be implicated in generating wear facets [45–49]. The nature of the contacting item is therefore secondary in determining the mode of ensuing fracture. We have chosen to use hard spheres as contacting agents simply because they are durable and easy to employ experimentally, and are amenable to explicit fracture mechanics analysis.

The utility of analytical modeling of crown fracture, described in Sects. 2.2 and 3.2 and culminating in eqn. 1, is that it quantifies the key material properties that govern criticality. It is substrate toughness that governs the crack resistance in eqn. 1. On the other hand, zirconia, and to a lesser extent lithium disilicate, are strong materials (Table 1), and therefore inhibit longitudinal crack initiation and subsequent propagation in the shell. The crown material plays a further role by providing protection to the tooth substrate, via stress shielding. This is reflected in the material-to-material variation of the modulus-dependent coefficient C_S in Table 2. The increasing values of this quantity in progressing from dental nanocomposite to lithium disilicate to zirconia indicate an increasing shielding capacity, so that higher loads are needed to deliver enough stress to the interior in order to propagate internal fracture. Composite crowns in particular offer little shielding, accounting for the substrate deformation in this material system observed in Fig. 2.

There are some secondary geometrical issues that warrant comment. The fact that the splits in Fig. 2 do not lie exactly along a fissure plane is consistent with earlier findings on fracture of molar teeth [33]. XFEM calculations in that earlier study showed that cracks can sometimes propagate as readily through the cusp apex as through the fissure, especially in those cases involving larger indenting spheres. The crack trajectories depend on the way the tensile stresses distribute themselves in the cuspal region. Variations in the cuspal geometry in molar teeth will inevitably shift the numbers shown in Table 2, as the stress distributions alter. Fracture in different tooth forms, e.g. canines and incisors, can be expected to undergo similar shifts. However, the relative merits of each material type are likely to remain unchanged.

5. Conclusion

Splitting in anatomically-correct molar restorations, consisting of zirconia, lithium disilicate or filled-resin nanocomposite crowns on dental composite substrates, has been evaluated. Splitting is induced by axial loading with a hard indenter wedged between the molar cusps (Fig. 1). Experiments have been run on manufactured crown specimens and critical loads to failure measured (Fig. 2). Analyses of the full fracture evolution have been carried out using extended finite element modeling (XFEM) (Figs. 3 and 4). The entire mechanics of crack evolution to failure is mapped out, from initiation in the crown to penetration into the dentin. Critical loads measured experimentally and predicted from XFEM agree within uncertainty bounds (Table 2).

Zirconia is confirmed to be the most split-resistant and dental nanocomposite the least, with lithium disilicate intermediate. The stiffer and stronger zirconia and lithium disilicate crowns afford superior stress shielding of the tooth interior, and inhibit crack initiation. At the same time, it is cautioned that the integrity of the monolithic crown structure can be readily compromised by fabrication defects and preparation or placement flaws, from inadvertent chipping, excessive sandblasting and drill finishing, and by fatigue.

HIGHLIGHTS.

• Capacity of crown restorations to sustain high bite force has been measured on manufactured, anatomically-correct specimens for three classes of monolithic materials.

• Extended finite element modeling has been used to follow the progression of embedded cracks in the crown/dentin structure, revealing a complex evolution to failure that cannot be inferred from more traditional FEM.

• Zirconia is confirmed to be the most durable of available monolithic ceramics, with lithium disilicate intermediate and dental composite weakest. All perform favorably relative to natural tooth enamel.