Abstract
Near-wall mass transport plays an important role in many cardiovascular processes, including the initiation of atherosclerosis, endothelial cell vasoregulation, and thrombogenesis. These problems are characterized by large Péclet and Schmidt numbers as well as a wide range of spatial and temporal scales, all of which impose computational difficulties. In this work, we develop an analytical relationship between the flow field and near-wall mass transport for high-Schmidt-number flows. This allows for the development of a wall-shear-stress-driven transport equation that lies on a codimension-one vessel-wall surface, significantly reducing computational cost in solving the transport problem. Separate versions of this equation are developed for the reaction-rate-limited and transport-limited cases, and numerical results in an idealized abdominal aortic aneurysm are compared to those obtained by solving the full transport equations over the entire domain. The reaction-rate-limited model matches the expected results well. The transport-limited model is accurate in the developed flow regions, but overpredicts wall flux at entry regions and reattachment points in the flow.
Keywords: mass transport, boundary layer, high Schmidt number, thrombosis, atherosclerosis, wall shear stress, multiscale modeling, advection-diffusion
1 Introduction
Advective and diffusive mass transport between blood and the vessel wall is one of the most fundamental and important processes in cardiovascular biomechanics. Although the large arteries are mostly considered conducting pathways, near-wall transport is of critical importance in the normal function of these vessels, as well as pathological conditions. Examples include the initiation of atherosclerosis by adverse low-density lipoprotein (LDL) and oxygen transport between blood and the vessel wall (Tarbell, 2003), adenosine triphosphate (ATP) and adenosine diphosphate (ADP) control of the vasoregulation of endothelial cells (Burnstock and Kennedy, 1986), and transport of proteins and platelets involved in thrombosis (Hathcock, 2006).
The regions of interest for these problems often have complex geometries and disturbed flow conditions, hindering attempts at analytical solutions. Numerical models have become a favored approach to supplement experimental findings. These models generally solve one or more advection-diffusion-reaction equations, and include various boundary conditions to represent vessel-wall surface effects. For example, previous numerical models of ATP conversion tracked concentrations of ATP and ADP, and included Robin-type boundary conditions to model both the production of ATP by endothelial cells and the enzymatic conversion of ATP to ADP at the vessel wall (John and Barakat, 2001; Boileau et al, 2013). Thrombosis models have represented the tissue factor-induced initiation of coagulation and the deposition of platelets on the vessel wall with both Dirichlet-type (Biasetti et al, 2012) and Robin-type (Sorensen et al, 1999; Leiderman and Fogelson, 2010) boundary conditions. These models generally track the transport and reaction of platelets and dozens of proteins, although recent work has suggested that this level of complexity may not be necessary to model the initial phases of thrombin production (Wagenvoord et al, 2006; Papadopoulos et al, 2014). In models of LDL and oxygen transport, Dirichlet-type (Kaazempur-Mofrad et al, 2005; Iori et al, 2015) and Robin-type (Fazli et al, 2011; Lantz and Karlsson, 2012) boundary conditions have been used to model transport into the vessel wall.
Computational modeling of these types of mass transport problems is challenging (Ethier, 2002), however, and often under-resolved in large-artery flows. Transport in the large arteries is characterized by large Péclet and Schmidt numbers (Pe ~ 107, Sc ~ 104). Representative Schmidt numbers imply the presence of micron-scale concentration boundary layers near the vessel walls, demanding high mesh resolution in these regions, while a flow solve in the entire domain is required to accurately capture the velocity field. The steep gradients innate to advection-dominated large-Péclet-number flows require stabilization schemes to avoid oscillations in the solution, despite the fact that the areas of interest are typically in the diffusion-dominated near-wall region. Due to these numerical challenges, few if any previous works have achieved a fully-resolved, patient-specific, three-dimensional, time-dependent computational model of transport in the large arteries, despite the importance of each of these aspects to the transport problem.
As an alternative to numerical models, other researchers have used simplifying assumptions to develop analytical models of cardiovascular mass transport near a reactive surface (David, 2003; Plank et al, 2006). These analyses, however, were limited to two-dimensional, steady flow conditions, and not applicable to complex, patient-specific geometries or time-dependent problems.
In some areas of fluid mechanics, particularly boundary layer theory, success has been obtained by integrating over one spatial direction to reduce the topological dimensionality of a problem (von Kármán, 1921). In this work, such an approach is taken to develop a multiscale model in which the fluid mechanics in the full domain are coupled to a newly-proposed transport model that lies on a codimension-one vessel-wall surface. Thrombin and oxygen transport within a previously-considered abdominal aortic aneurysm geometry are used as test cases, and the results are compared to those obtained by solving the full transport equations in the complete volumetric domain.
2 Methods
2.1 Model development
We consider the problem in which a concentration C of a dilute species with uniform, isotropic diffusivity and no internal sources is transported throughout a domain Ω with surface ∂Ω, some region of which contains a reactive surface ∂Ωr ∈ ∂Ω. This transport problem is governed for x ∈ Ω by the advection-diffusion (AD) equation
| (1) |
where D is the species diffusivity, u(x, t) is fluid velocity, and c(x, t) = C0 − C is the species concentration scaled such that the inflow concentration has a value of c = 0. Assuming a first-order surface reaction with rate k, the boundary condition for x ∈ ∂Ωr is
| (2) |
where n is the inward-normal vector to the domain.
An intrinsic orthonormal frame is chosen relative to ∂Ω such that s1, s2, and n are the two tangent coordinates and the inward-normal coordinate, respectively, and n = 0 corresponds to the location of the surface. To map the transport problem onto the surface, Eq. (1) is integrated over a constant normal distance δ chosen such that δ is outside the concentration boundary layer:
| (3) |
Assuming ∂Ω is stationary and δ is constant, the order of integration and differentiation on the left-hand side can be interchanged:
| (4) |
If δκ ≪ 1, where κ is the maximum curvature of ∂Ω (i.e. the surface is locally flat relative to concentration boundary layer length scale), the advective term becomes
| (5) |
where the s subscript represents a surface-tangent vector: as = a − a·en for any vector a. No-penetration at the vessel wall and the boundary layer assumption give
| (6) |
and Eq. (5) reduces to
| (7) |
Likewise, the diffusive term becomes
| (8) |
The boundary layer assumption gives ∂c/∂n = 0 at n = δ, and the last term reduces to
| (9) |
where q(s1, s2, t) is the flux into the domain at the wall. Substituting into Eq. (8) gives
| (10) |
Define φ as
| (11) |
and substitute Eq. (7) and Eq. (10) into Eq. (3):
| (12) |
This is the transport equation for the new surface variable φ.
In order to calculate φ based on surface quantities alone, the integral in Eq. (12) must be evaluated. Assuming the concentration boundary layer is much smaller than the momentum boundary layer, the Lévêque (1928) approximation applies and
| (13) |
where τw (s1, s2, t) is the wall shear stress. Eq. (12) then becomes
| (14) |
To evaluate the integral of cn, a functional profile must be assigned for c(n). As one approximation, it can be assumed that c takes the shape of the solution to the steady two-dimensional Graetz-Lévêque problem for flow over a reactive surface. This problem is governed by
| (15a) |
| (15b) |
| (15c) |
Ghez (1978) defined a non-dimensional axial distance equivalent to (where Γ(a) is the gamma function)
| (16) |
and showed that asymptotic solutions exist in the limits ξ ≪ 1 and ξ ≫ 1, corresponding to the reaction-rate-limited and transport-limited cases, respectively. These solutions are used below to develop surface transport equations for each limit.
2.1.1 Reaction-rate-limited solution
Defining dimensionless variables x = μk3X/τwD2 and y = kY/D, and the constant α = 3⅙[Γ(⅓)]2/2π, the solution to Eq. (15) for ξ ≪ 1 is given by Ghez (1978) as
| (17) |
where Γ(a, x) is the upper incomplete gamma function. Integrating with respect to y, letting Y = n, and using the definition of φ,
| (18) |
This gives an expression for x in terms of φ:
| (19) |
The integral of cy can also be found analytically:
| (20) |
By substituting Eq. (19) into Eq. (20), the integral can be eliminated from Eq. (14):
| (21) |
where
| (22) |
The wall flux is given by q = k(C0 − cw), where the wall concentration cw is found by substituting Eq. (19) into Eq. (17) and setting y = 0:
| (23) |
Equation (21) becomes the reduced-dimensional model for near-wall transport in reaction-rate-limited applications. This equation is similar to a standard advection-diffusion-reaction equation, except that velocity is replaced by wall shear stress, the advective term is nonlinear in φ, and the reactive-surface boundary condition appears instead as a source term.
2.1.2 Transport-limited solution
The ξ ≪ 1 solution to Eq. (15) is also given by Ghez (1978), as
| (24) |
Using an identical analysis as in the rate-limited case, it can be shown that
| (25) |
Equation (14) thus becomes
| (26) |
where
| (27) |
In this case, the value of cw is identically equal to C0 to first order. To find q, we instead calculate D ∂c/∂n = D ∂c/∂Y directly by taking the derivative of Eq. (24):
| (28) |
Note that k does not appear in this formulation. The first-order solution essentially assumes an infinite reaction rate, i.e. the reaction is transport-limited.
2.1.3 Advective term modification
The advective terms in Eq. (21) and Eq. (26) require extra attention. Using Eq. (21) as an example, the chain rule gives
| (29) |
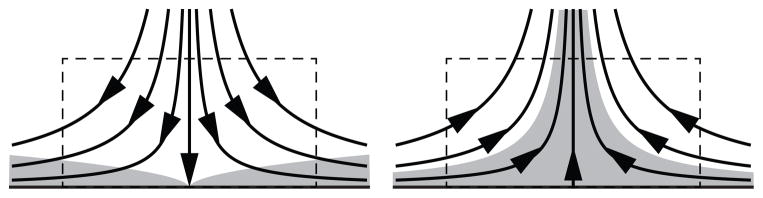
The first term on the right-hand side has the appearance of a typical advective term in an incompressible fluid, except that velocity is replaced by wall shear stress and it is nonlinear in φ. The second term, however, represents the “compressibility” of τw, and is not present in the incompressible transport equations. In regions where ∇s·τw is positive, often corresponding to reattachment points in the flow (Surana et al, 2006), this term becomes a sink and physically represents the replacement of fluid in the boundary layer with fluid from the free stream. In regions where ∇s·τw is negative, corresponding to separation points in the flow, this term becomes a source.
To help understand this behavior, we consider control volumes surrounding forward and reverse stagnation points (Fig. 1), corresponding to positive and negative values of ∇s·τw, respectively. In both flows, the flux through the side of the control volume is described by the ∇s·τw term in the surface transport model. In the reverse stagnation point flow, however, there is an additional flux through the top of the control volume. Wall-normal transport becomes important in such regions, but this behavior cannot be captured with a surface model and instead yields an aphysical source. To help reconcile this anomaly, we note that in the steady case this wall-normal flux and the source due to negative ∇s·τw should balance. Therefore, in order to make the model tractable, we assume that this approximation holds for the general unsteady case as well, and the source is ignored. From Eq. (21), the final form of the transport equation becomes
Fig. 1.
Forward and reverse stagnation point flows, with concentration boundary layer shaded. In the reverse stagnation point flow there is a flux through the top of the control volume that cannot be described by the surface model
| (30) |
A similar form follows from Eq. (26) for the transport-limited case:
| (31) |
2.2 Test cases
Numerical results using the surface transport model were compared to those obtained by solving the full AD equation in two unsteady, axisymmetric validation cases corresponding to the two limits of ξ. The first test case investigated a reaction-rate-limited problem representative of the initiation phase of thrombin production on an prothrombotic surface, and was solved using Eq. (30) for the surface model. The second test case investigated a transport-limited problem representative of oxygen transport into a vessel wall, and was solved using Eq. (31).
The reaction-rate-limited case used the simplified model of Papadopoulos et al (2014) to model the conversion of prothrombin (II) into thrombin (IIa) in the presence of tissue factor. The presence of platelets was excluded as only the initiation phase of thrombin production was considered. The surface reaction rate was set to kIIa = 9.75 × 10−6 cm/s to match a representative value for an atherosclerotic surface (Papadopoulos et al, 2014). Diffusivity was set to DIIa = 2×10−6 cm2/s to approximate the shear-enhanced diffusivity level for thrombin in the presence of red blood cells (Sorensen et al, 1999). Although the transport equations were solved for prothrombin concentration, all results are presented in terms of thrombin concentration. The reactive surface was considered to be the wall of the aneurysmal region (z = 7 cm to z = 15 cm).
In the oxygen transport case, the reaction rate represents the permeability of the vessel wall surface rather than an actual chemical reaction. Values of kO2 = 2 × 10−3 cm/s and D O2 = 1 × 10−5 cm2/s were chosen to match those used by Kolandavel et al (2006). Again, the reaction was applied only on the aneurysm wall.
2.3 Numerics
Both tests were conducted in an idealized abdominal aortic aneurysm geometry (Fig. 2) chosen to match that presented by Biasetti et al (2012). Triangular computational meshes were created using Gmsh (Geuzaine and Remacle, 2009). Mesh size was set to 500 μm globally and refined to 10 μm near the vessel wall based on the results of a mesh-convergence study.
Fig. 2.
Idealized axisymmetric abdominal aortic aneurysm geometry, taken from Biasetti et al (2012)
The finite element method was used for all computations. Custom code for this purpose was written using the FEniCS package (Logg et al, 2012). FEniCS was chosen because of its built-in capability to automate the surface derivatives necessary to solve the surface transport equation (Rognes et al, 2013). A second-order implicit time-stepping scheme was used for all cases, with a timestep of 1 ms chosen based on the results of convergence studies.
2.3.1 Computational fluid dynamics
The incompressible Navier-Stokes equations,
| (32a) |
| (32b) |
were solved using a streamline upwind/Petrov-Galerkin (SUPG) formulation (Brooks and Hughes, 1982). Blood was assumed to be a Newtonian fluid with ρ =1.06 g/cm3 and ν = 3.8 cSt. The flow rate data from Biasetti et al (2009) was mapped to a Womersley velocity profile at the vessel inlet. A boundary condition of ur = n · ∇uz = n · ∇p = 0 was applied on the symmetry plane, ur = uz = n · ∇p = 0 was applied at the walls, and p = n · ∇ur = n · ∇uz = 0 was applied at the outlet. The flow problem was solved until pressure and velocity fields reached periodic convergence. Both fields converged within five cardiac cycles (5 s); the velocity and wall shear stress fields from the fifth cycle were applied periodically for subsequent calculations using the full and reduced-order transport models.
2.3.2 Full advection-diffusion model
For the full AD model, Eq. (1) was solved using SUPG stabilization (Bazilevs et al, 2007) with quadratic elements. Boundary conditions were set to Eq. (2) on the reactive aneurysmal surface, n · ∇c = 0 on the non-reactive and symmetry surfaces, and c = 0 on the inflow and outflow surfaces. Although the Dirichlet boundary condition at the outlet is physically unrealistic, it was applied to avoid numerical problems during periods of backflow, and is expected to have little effect on results in the interior of the domain for advection-dominated simulations such as this. An initial condition of c = 0 was applied throughout the domain, and simulations were run until peak concentration values reached periodic convergence (cf. Tab. 1).
Table 1.
The number of cardiac cycles required for periodic peak value convergence to within 0.01%
| Test case | Model | Cardiac cycles |
|---|---|---|
| Reaction-rate-limited | Full AD | 151 |
| Surface | 77 | |
| Transport-limited | Full AD | 51 |
| Surface | 34 |
2.3.3 Surface transport model
Equations (30) and (31) were solved on the extracted vessel wall surface from the same mesh used for the computational fluid dynamics and AD computations. Rather than adding stabilization, diffusion was increased to D = 2 × 10−3 cm2/s in the transport equations but not in the calculation of β. This had the effect of adding diffusion in the streamwise direction only, which is the goal of most advection stabilization schemes. This additional diffusion was found to have negligible effect on the results while eliminating numerical oscillations. Boundary conditions were set to φ = 0 at the inflow and outflow points, with the same justification as given for the full AD model. Again, a value of φ = 0 was applied as an initial condition, and peak values of φ were allowed to reach periodic convergence. In the oxygen transport case, boundary and initial conditions were set to a small value near machine precision to avoid divide-by-zero errors in calculating the source term; results did not depend on the choice of this value. Motivated by previous work that has shown that near-wall transport is a quasi-steady phenomenon for high Schmidt numbers (Ma et al, 1994), a quasi-steady solution for each case was also calculated. To achieve this, Eqs. (30) and (31) were solved by setting ∂c/∂t to zero and τw to the time-averaged wall shear stress vector field obtained from the unsteady Navier-Stokes solution.
3 Results
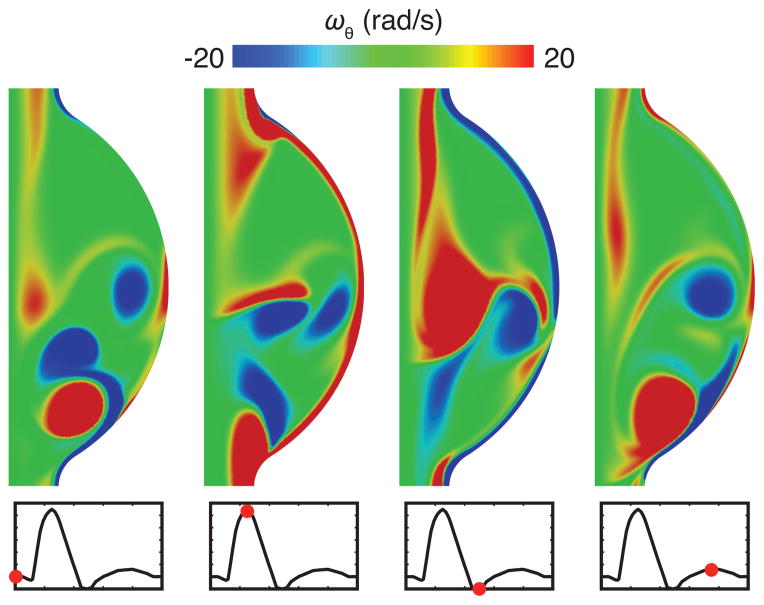
The time-dependent velocity field results are shown in the form of azimuthal vorticity within the aneurysm in Fig. 3. The calculated flow field was characterized by the separation of a vortex from the proximal end of the aneurysm during systole, followed by impingement on the distal end during mid-diastole. This complex, separated flow led to a wall shear stress field that varied in both space and time, especially near the separation and reattachment regions (Fig. 4).
Fig. 3.
Azimuthal vorticity ωθ in the aneurysm at end of diastole (t = 0 s), peak systole (t = 0.25 s), end of systole (t = 0.5 s), and mid-diastole (t = 0.75 s)
Fig. 4.
Wall shear stress τΩ in the aneurysm over one cardiac cycle. The wall shear stress was highly variable in both space and time, especially in the vicinity of the proximal separation and distal reattachment regions
All transport models were run until peak values of c reached periodic convergence to within 0.01% of the previous cardiac cycle. Time to convergence for each case is shown in Table 1. Results for the transport-limited case converged two to three times faster than those for the reaction-rate-limited case, and the surface model converged in approximately half the time of the full AD model.
Representative results for thrombin concentration obtained with the reaction-rate-limited model are shown in Fig. 5. As expected, the highest values are confined to a thin near-wall boundary layer, and results in the interior of the domain are two to three orders of magnitude smaller. The interior boundary layers typical to high Péclet number flows are also apparent.
Fig. 5.
Thrombin concentration at the end of diastole, normalized to the peak value on the wall. Levels in the interior of the domain were two to three orders of magnitude lower than those in the thin near-wall boundary layer region
The time-averaged value and intracycle range for thrombin concentration on the aneurysm wall is shown in Fig. 6. These results indicate that near-wall transport is a quasi-steady process, even though the flow field is complex and time-dependent.
Fig. 6.
Shaded region shows intracycle variation of thrombin concentration [IIa] on the aneurysm wall taken from the full-AD-model results, demonstrating that near-wall transport is quasi-steady. Results from the oxygen transport case were comparable
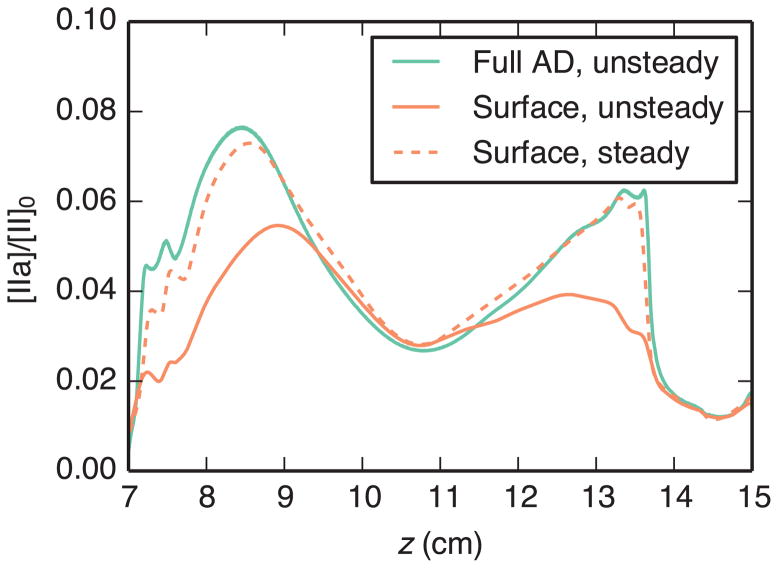
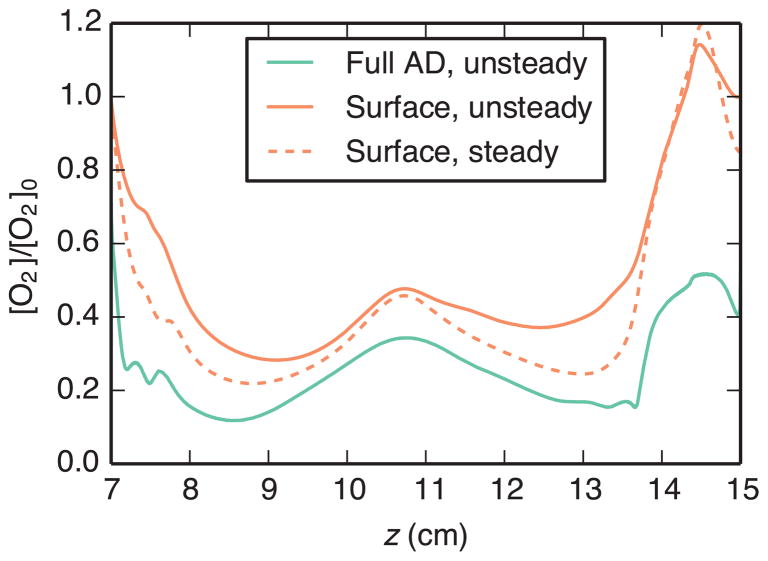
Time-averaged results obtained using the full AD model, unsteady surface model, and steady surface model are compared in Fig. 7 and Fig. 8. Both figures show wall concentration of the quantity of interest. For the reaction-rate-limited surface model, this concentration is calculated directly from Eq. (23). For the transport-limited surface model, wall flux is calculated from Eq. (28), then an equivalent concentration is calculated according to C = q/k. The steady surface model matched the full-AD-model results better than the unsteady surface model for both cases. In the reaction-rate-limited case (Fig. 7), these results matched well over the entire aneurysm surface. The transport-limited case (Fig. 8) also demonstrated relatively good agreement, except in regions of flow separation or reattachment (cf. Fig. 4). Although qualitative features were similar between the two methods, calculated oxygen concentration levels were higher with the surface model, especially in the vicinity of the distal impingement point.
Fig. 7.
Comparison of time-averaged thrombin concentration [IIa] on the aneurysm wall, normalized by the inlet prothrombin concentration [II]0, using the full AD model and reaction-rate-limited surface models
Fig. 8.
Comparison of time-averaged oxygen concentration [O2] on the aneurysm wall, normalized by the inlet oxygen concentration [O2]0, using the full AD model and transport-limited surface models. For the surface models, plotted concentration is the equivalent concentration required for the calculated flux, i.e. C = q/k
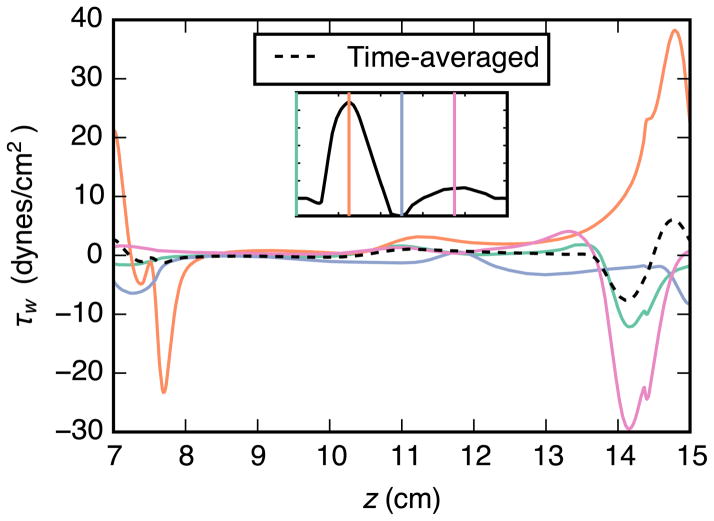
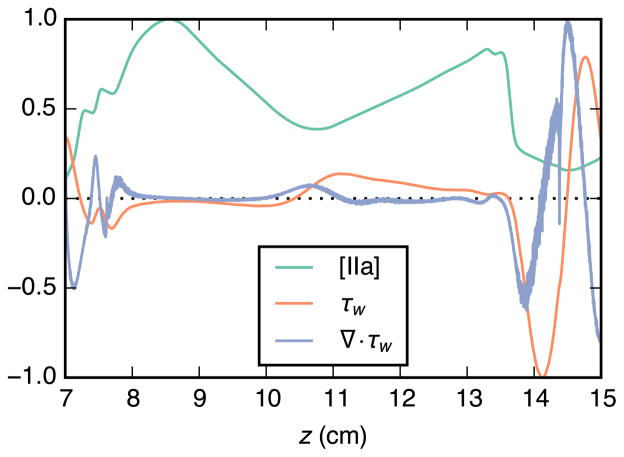
Normalized time-averaged values for wall thrombin concentration, wall shear stress, and divergence of wall shear stress are plotted in Fig. 9. Two peaks are apparent in the thrombin concentration curve. Both are in locations where the wall shear stress is near zero and that are adjacent to large regions of low wall shear stress. Thrombin concentration also appears to be reduced in regions where divergence of wall shear stress is positive.
Fig. 9.
Relationship between time-averaged aneurysm-wall thrombin concentration [IIa], wall shear stress τw, and divergence of wall shear stress ∇ · τw. Thrombin concentration is taken from the steady surface-model simulation, all values are normalized to their respective peak values within the aneurysm, and positive τw is in the downstream direction
4 Discussion
For both reaction-rate and transport-limited cases, the steady surface-model results showed the same general qualitative features as the full-AD-model results. In the reaction-rate-limited case, this correlation was very good throughout the entire aneurysm, even near the proximal separation and distal reattachment points where the flow was quite complex. In the transport-limited case, the surface-model results began to diverge from the full-AD-model solution near the distal reattachment point. In fact, the calculated equivalent concentration was above unity, implying that the wall flux was higher than physically possible. The reason for this disparity is in assuming that ξ ≫ 1 over the entire aneurysm. Even if this is true from a global scaling perspective, every domain will contain regions—such as reattachment points or entrance regions—where this assumption is violated. As such, the surface transport model as presented may not be appropriate for transport-limited problems under complex aneurysmal flow. However, it should be noted that this is only a consequence of the analytical solution used to develop this model. Construction of a solution that is uniformly valid across all ξ could solve this problem, which is the aim of future work.
The steady surface-model results, using the time-averaged wall shear stress field, were better than the time-dependent surface-model results for both cases. This is likely due to the advective term modification, which removed the contribution of positive wall shear stress divergence (Section 2.1.3). In regions where ∇ ·τw is oscillatory in time, this modification will skew the results toward the negative contribution, causing an artificial sink. This is consistent with the results, which showed lower values of cw in the unsteady surface-model simulations. However, this effect was mitigated using the time-averaged wall shear stress field, in which case positive and negative divergence during the cycle tend to cancel. Moreover, this choice is justified. Fluid velocities within the concentration boundary layers of high-Schmidt-number flows are so small that fluid parcels remain effectively stationary over the course of one cardiac cycle, which is the time scale of flow unsteadiness herein. Because of this, advection in these regions due to a time-varying velocity field is equivalent to that due to the time-averaged velocity field, and the near-wall transport problem can be considered quasi-steady. This was confirmed by the full-AD-model results, which showed very little intracycle variation in concentration at the wall even though the flow field itself was highly time-dependent.
The use of the time-averaged wall shear stress field is appealing for numerical efficiency, which is an important advantage of this framework. By reducing the transport problem to the region in which the results are quasi-steady, the time-dependent transport problem is reduced to one that can be solved in steady state, even if the flow field is time-dependent. It is important to note that such saving is not readily accessible using the full transport model. This was was verified by using time-averaged velocity fields in the full transport model, which produced erroneous results.
This model has the potential to significantly reduce computational cost in boundary-layer-type near-wall transport problems. First, the dimensionality of the problem is decreased by one, reducing the computational mesh from a volume to a surface. Second, because the boundary layer behavior is modeled analytically rather than calculated explicitly, the need for a finely resolved mesh in the wall-normal direction is eliminated. Finally, as noted above, cases for which the full transport equations require tens to hundreds of cardiac cycles to converge can be solved as steady-state problems using the cycle-averaged wall shear stress field. The computational savings in solving the transport problem are highly significant, especially in three-dimensional, patient-specific geometries. For example, in one tested patient-specific model of the abdominal aorta and surrounding vasculature, at least
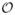 (10M) elements were required to properly resolve the problem, while the surface problem required only
(10M) elements were required to properly resolve the problem, while the surface problem required only
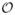 (100k) elements. Simulation of hemodynamics on grids of tens of millions of elements over hundreds of cardiac cycles is not routine, nor viable in most practical settings, and this model offers a feasible alternative.
(100k) elements. Simulation of hemodynamics on grids of tens of millions of elements over hundreds of cardiac cycles is not routine, nor viable in most practical settings, and this model offers a feasible alternative.
The surface transport model can also be used to help elucidate the relationship between wall shear stress and transport in cardiovascular flows. Previous studies have provided mixed and often contradictory links between wall-shear-stress-based metrics and phenomena such as thrombus formation (Arzani et al, 2014) and atherosclerosis (Peiffer et al, 2013). A better understanding of the influence of wall shear stress on near-wall transport may help provide insight into why this is the case, and aid in the development of improved diagnostic metrics.
This model is valid for flows in which the concentration boundary layer is small compared to the momentum boundary layer; otherwise the Lévêque approximation no longer applies and the complex flow features in the interior of the domain become important. Using scaling arguments, the thickness of the momentum boundary layer in a Womersley-type flow is δm ~ α−1R (Fung, 1997), where α is Womersley number and R is vessel radius, and the thickness of a developing concentration boundary layer is δc ~ Re−½Sc−⅓ L (Truskey et al, 2004), where Re is Reynolds number, Sc is Schmidt number, and L is a length scale. The boundary layer thickness restriction is therefore equivalent to
| (33) |
where ω is the angular frequency of the pulsatile flow and U is a velocity scale. Unlike the restriction in ξ, which is only a limitation of the analytical solution presented herein, this is a firm restriction: after this point the transport problem becomes fully three-dimensional and a reduction to a surface model is not feasible. Table 2 contains estimates for valid length scales under this criterion, and indicates that this assumption generally holds true over the typical length scales of diseased vascular regions in the large arteries.
Table 2.
Maximum valid length scale L for the use of the surface transport model throughout the arterial tree, assuming the dimensionless parameter in Eq. (33) must be less than 0.25 (i.e. the concentration boundary layer is one-quarter the size of the momentum boundary layer) and angular frequency is ω = 2π rad/s (60 BPM). Thrombin and oxygen transport cases are represented by Sc = 19000 and Sc = 3800, respectively, and estimates for diameter D and velocity scale U are taken from Goldsmith and Turrito (1986) and Cheng et al (2003)
| Vessel | D(cm) | U (cm/s) | Sc | L(cm) |
|---|---|---|---|---|
| Infrarenal aorta | 2.0 | 4.8 | 19000 | 34 |
| 2.0 | 4.8 | 3800 | 12 | |
| Common carotid | 0.59 | 19 | 19000 | 130 |
| 0.59 | 19 | 3800 | 46 | |
| Small arteries | 0.03 | 5.0 | 19000 | 35 |
| 0.03 | 5.0 | 3800 | 12 | |
| Arterioles | 0.0025 | 0.5 | 19000 | 3.5 |
| 0.0025 | 0.5 | 3800 | 1.2 |
The effective diffusivity of large proteins and platelets in blood is augmented by red-blood-cell-enhanced mixing, which may be dependent on the local shear rate. Enhanced diffusion was included for the thrombin generation case, however it was assumed to be uniform and isotropic. This is consistent with previous models that have assumed uniform enhanced diffusivity due to inconsistencies that arise in the shear-rate-dependent case (Folie and McIntire, 1989; Sorensen et al, 1999). This is a modeling assumption, however, and the effect of nonuniform red-blood-cell-enhanced mixing on near-wall transport should be investigated further in future work.
Finally, although this work was presented in the context of cardiovascular mass transport, its usefulness is not limited to this application. Reactive surface problems arise in many fields of science and engineering, and this model is applicable to any problem that falls within the previously discussed flow regimes. Additionally, although the thermal boundary layers in heat transfer problems are often too large for such a surface model to be applied, high enough Prandtl numbers do arise in some areas—for example geophysical flows—where this technique may be of use.
5 Conclusion
A model was developed that reduced the advection-diffusion equation to a codimension-one transport equation for near-wall boundary-layer problems. This equation was based on analytical solutions of the Graetz-Lévêque problem in the reaction-rate-limited and transport-limited regimes. Biologically relevant test cases were chosen for each of these regimes, and numerical results were compared to those obtained with the full advection-diffusion equation. Results were good for the reaction-rate-limited case, as well as the transport-limited case outside of entry regions and flow reattachment points. This model offers a valid alternative to modeling near-wall transport in cardiovascular applications where the computational burden of solving the full transport equations is prohibitively expensive.
Acknowledgments
This work was supported by the National Heart, Lung, and Blood Institute (Grant No. HL108272) and the National Science Foundation (Grant No. 1354541).
Contributor Information
Kirk B. Hansen, Department of Mechanical Engineering, University of California, Berkeley, Berkeley, CA, USA
Shawn C. Shadden, Email: shadden@berkeley.edu, Department of Mechanical Engineering, University of California, Berkeley, Berkeley, CA, USA
References
- Arzani A, Suh GY, Dalman RL, Shadden SC. A longitudinal comparison of hemodynamics and intraluminal thrombus deposition in abdominal aortic aneurysms. Am J Physiol Heart Circ Physiol. 2014;307(12):H1786–H1795. doi: 10.1152/ajpheart.00461.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bazilevs Y, Calo VM, Tezduyar TE, Hughes TJR. YZβ discontinuity capturing for advection-dominated processes with application to arterial drug delivery. Int J Numer Methods Fluids. 2007;54(6–8):593–608. [Google Scholar]
- Biasetti J, Gasser TC, Auer M, Hedin U, Labruto F. Hemodynamics of the normal aorta compared to fusiform and saccular abdominal aortic aneurysms with emphasis on a potential thrombus formation mechanism. Ann Biomed Eng. 2009;38(2):380–390. doi: 10.1007/s10439-009-9843-6. [DOI] [PubMed] [Google Scholar]
- Biasetti J, Spazzini PG, Swedenborg J, Gasser TC. An integrated fluid-chemical model toward modeling the formation of intraluminal thrombus in abdominal aortic aneurysms. Front Phys. 2012;3:266. doi: 10.3389/fphys.2012.00266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boileau E, Bevan R, Sazonov I, Rees M, Nithiarasu P. Flow-induced ATP release in patient-specific arterial geometries – a comparative study of computational models. Int J Numer Methods Biomed Eng. 2013;29(10):1038–1056. doi: 10.1002/cnm.2581. [DOI] [PubMed] [Google Scholar]
- Brooks AN, Hughes TJ. Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations. Comput Methods Appl Mech Eng. 1982;32(1–3):199–259. [Google Scholar]
- Burnstock G, Kennedy C. A dual function for adenosine 5′-triphosphate in the regulation of vascular tone: Excitatory cotransmitter with noradrenaline from perivascular nerves and locally released inhibitory intravascular agent. Circ Res. 1986;58(3):319–330. doi: 10.1161/01.res.58.3.319. [DOI] [PubMed] [Google Scholar]
- Cheng CP, Herfkens RJ, Taylor CA. Comparison of abdominal aortic hemodynamics between men and women at rest and during lower limb exercise. Journal of Vascular Surgery. 2003;37(1):118–123. doi: 10.1067/mva.2002.107. [DOI] [PubMed] [Google Scholar]
- David T. Wall shear stress modulation of ATP/ADP concentration at the endothelium. Ann Biomed Eng. 2003;31(10):1231–1237. doi: 10.1114/1.1615574. [DOI] [PubMed] [Google Scholar]
- Ethier CR. Computational modeling of mass transfer and links to atherosclerosis. Ann Biomed Eng. 2002;30(4):461–471. doi: 10.1114/1.1468890. [DOI] [PubMed] [Google Scholar]
- Fazli S, Shirani E, Sadeghi M. Numerical simulation of LDL mass transfer in a common carotid artery under pulsatile flows. J Biomech. 2011;44(1):68–76. doi: 10.1016/j.jbiomech.2010.08.025. [DOI] [PubMed] [Google Scholar]
- Folie BJ, McIntire LV. Mathematical analysis of mural thrombogenesis. Concentration profiles of platelet-activating agents and effects of viscous shear flow. Biophys J. 1989;56(6):1121–1141. doi: 10.1016/S0006-3495(89)82760-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fung YC. Biomechanics. Springer; New York, NY: 1997. [Google Scholar]
- Geuzaine C, Remacle JF. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int J Numer Methods Eng. 2009;79(11):1309–1331. [Google Scholar]
- Ghez R. Mass transport and surface reactions in Lévêque’s approximation. Int J Heat Mass Transp. 1978;21(6):745–750. [Google Scholar]
- Goldsmith HL, Turrito VT. Rheological aspects of thrombosis and haemostasis: basic principles and applications. ICTH-Report–Subcommittee on Rheology of the International Committee on Thrombosis and Haemostasis. Thrombosis and Haemostasis. 1986;55(3):415–435. [PubMed] [Google Scholar]
- Hathcock JJ. Flow effects on coagulation and thrombosis. Arter Thromb Vasc Biol. 2006;26(8):1729–1737. doi: 10.1161/01.ATV.0000229658.76797.30. [DOI] [PubMed] [Google Scholar]
- Iori F, Grechy L, Corbett RW, Gedroyc W, Duncan N, Caro CG, Vincent PE. The effect of in-plane arterial curvature on blood flow and oxygen transport in arteriovenous fistulae. Phys Fluids. 2015;27(3):031,903. doi: 10.1063/1.4913754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- John K, Barakat AI. Modulation of ATP/ADP concentration at the endothelial surface by shear stress: effect of flow-induced ATP release. Ann Biomed Eng. 2001;29(9):740–751. doi: 10.1114/1.1397792. [DOI] [PubMed] [Google Scholar]
- Kaazempur-Mofrad M, Wada S, Myers J, Ethier C. Mass transport and fluid flow in stenotic arteries: Axisymmetric and asymmetric models. Int J Heat Mass Transp. 2005;48(21–22):4510–4517. [Google Scholar]
- von Kármán T. Über laminare und turbulente Reibung. Z Angew Math Mech. 1921;1(4):233–252. [Google Scholar]
- Kolandavel MK, Fruend ET, Ringgaard S, Walker PG. The effects of time varying curvature on species transport in coronary arteries. Ann Biomed Eng. 2006;34(12):1820–1832. doi: 10.1007/s10439-006-9188-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lantz J, Karlsson M. Large eddy simulation of LDL surface concentration in a subject specific human aorta. J Biomech. 2012;45(3):537–542. doi: 10.1016/j.jbiomech.2011.11.039. [DOI] [PubMed] [Google Scholar]
- Leiderman K, Fogelson AL. Grow with the flow: A spatial-temporal model of platelet deposition and blood coagulation under flow. Math Med Biol. 2010;28(1):47–84. doi: 10.1093/imammb/dqq005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lévêque M. Les lois de la transmission de chaleur par convection. Ann Mines. 1928;13:201–239. [Google Scholar]
- Logg A, Mardal KA, Wells G, editors. Lecture Notes in Computational Science and Engineering. Vol. 84. Springer; Berlin, Heidelberg: 2012. Automated Solution of Differential Equations by the Finite Element Method. [Google Scholar]
- Ma P, Li X, Ku DN. Heat and mass transfer in a separated flow region for high Prandtl and Schmidt numbers under pulsatile conditions. Int J Heat Mass Transp. 1994;37(17):2723–2736. [Google Scholar]
- Papadopoulos KP, Gavaises M, Atkin C. A simplified mathematical model for thrombin generation. Med Eng Phys. 2014;36(2):196–204. doi: 10.1016/j.medengphy.2013.10.012. [DOI] [PubMed] [Google Scholar]
- Peiffer V, Sherwin SJ, Weinberg PD. Does low and oscillatory wall shear stress correlate spatially with early atherosclerosis? A systematic review. Cardiovasc Res. 2013;99:242–250. doi: 10.1093/cvr/cvt044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plank M, Comerford A, David T, Wall D. Concentration of blood-borne agonists at the endothelium. Proc R Soc A Math Phys Eng Sci. 2006;462(2066):671–688. [Google Scholar]
- Rognes ME, Ham DA, Cotter CJ, McRae ATT. Automating the solution of PDEs on the sphere and other manifolds in FEniCS 1.2. Geosci Model Dev. 2013;6(6):2099–2119. [Google Scholar]
- Sorensen EN, Burgreen GW, Wagner WR, Antaki JF. Computational simulation of platelet deposition and activation: I. Model development and properties. Ann Biomed Eng. 1999;27(4):436–448. doi: 10.1114/1.200. [DOI] [PubMed] [Google Scholar]
- Surana A, Grunberg O, Haller G. Exact theory of three-dimensional flow separation. Part 1. Steady separation. J Fluid Mech. 2006;564:57–103. [Google Scholar]
- Tarbell JM. Mass transport in arteries and the localization of atherosclerosis. Annu Rev Biomed Eng. 2003;5(1):79–118. doi: 10.1146/annurev.bioeng.5.040202.121529. [DOI] [PubMed] [Google Scholar]
- Truskey GA, Yuan F, Katz DF. Transport Phenomena in Biological Systems. Pearson/Prentice Hall; Upper Saddle River, NJ: 2004. [Google Scholar]
- Wagenvoord R, Hemker PW, Hemker HC. The limits of simulation of the clotting system. J Thromb Haemost. 2006;4(6):1331–1338. doi: 10.1111/j.1538-7836.2006.01967.x. [DOI] [PubMed] [Google Scholar]