Modeling the training-performance relationship using a mixed model in elite swimmers

Abstract

Purpose

The aim of this study was to model the relationship between training and performance in 13 competitive swimmers, over 3 seasons, and to identify individual and group responses to training.

Methods

A linear mixed model was used as an alternative to the Banister model. Training effect on performance was studied over 3 training periods: short-term, the average of training load accomplished during the 2 weeks preceding each performance of the studied period; mid-term, the average of training load accomplished during weeks 3, 4 and 5 before each performance; and long-term, weeks 6, 7 and 8.

Results

Cluster analysis identified 4 groups of subjects according to their reactions to training. The first group corresponded to the subjects who responded well to the long-term training period, the second group to the long- and mid-term period, the third to the short- and mid-term period, and the fourth to the combined periods. In the model, the inter-subject differences and the evolution over the 3 seasons were statistically significant for the identified groups of swimmers. Influence of short-term training was negative on performance in the 4 groups while mid- and long-term training had, on the average, a positive effect in 3 groups out of 4. Between seasons 1 and 3, the effect of mid-term training declined, while the effect of long-term training increased. The fit between real and modeled performances was significant for all swimmers (0.15 ≤ r² ≤ 0.65; P ≤ 0.01).

Conclusion

The mixed model described a significant relationship between training and performance both for individuals and for groups of swimmers. This relationship was different over the 3 years. Personalized training schedules could be prescribed on the basis of the model results.

The training-performance relationship is particularly important for elite sports coaches who search for reproducible phenomena useful for organizing the athlete’s training program. Many authors have studied the relative influence of training (7, 22, 23, 27) and found that reactions to training depend on volume, intensity and frequency of the training sessions (7, 16, 23). Others have reported divergent results (4, 9), perhaps related to the fact that delayed effects and inter–individual differences were not taken into account.

For individual swimmers, mathematical models have been developed to describe the dynamic aspect of training and the consequences of succession of training loads over time (2). The Banister model (2, 3, 4) and its modifications (5, 6) are based on two antagonistic functions, both calculated from the training impulse. Studies on cellular adaptability reactions to exercise (3) have demonstrated that the negative function can be assimilated to a fatiguing impulse. The positive function can be compared to a fitness impulse resulting from the organism’s adaptation to training. Expressed as an exponential, the functions account for the decreasing impact of the training effect. When iterative training sessions are considered, the time course of performance is described by:

$$p_t=p_0+k_a\sum _{s=0}^{t-1}{e}^{-(t-s)/{\tau }_a}{w}_s-k_f\sum _{s=0}^{t-1}{e}^{-(t-s)/{\tau }_f}{w}_s$$

where p_t is the known performance at week (or day) t; w_s is the known training load per week (or day) from the first week of training to the week (or day) preceding performance p_t; k_a, k_f are the fitness and fatigue multiplying factors, respectively; τ_a, τ_f are the fitness and fatigue decay time constants, respectively; p₀ corresponds to an initial basic level of performance.

There is no clear consensus on just how many data points are needed per parameter to ensure a stable solution in a regression analysis. Proposals reported in the literature have ranged from 5 to 50. Stevens (26) recommends a nominal number of 15 observations per parameter (except the intercept parameter) for a multiple linear regression. But since the Banister model is a non-linear model, inference is based on asymptotic theory (10), which implies more data points per parameter than for a linear regression model. This means a large number of observations would be required to obtain precise results and enable pertinent statistical analysis. The Banister model also assumes the parameters remain constant over time, an assumption which is not consistent with observed time-dependent alterations in response to training (3, 4, 6, 22).

When few repeated measurements are available for several subjects, mixed models provide an attractive solution (29). Instead of constructing a personal model for each subject, a model of popular behavior is constructed, allowing parameters to vary from one individual to another, to take into account the heterogeneity between subjects. Particular care in characterizing random variation in the data is required to recognize two levels of variability: random variation among measurements within a given individual (intra-individual variation) and random variation among individuals (inter-individual variation) (10). In addition, mixed models analyze responses corresponding to different dose inputs (10), a common situation in swimming since training loads differ with age, specialty, and/or competition level (7, 23).

The aim of the present study was to investigate the effect of training on performance of 13 elite swimmers taking into account A) individual profiles; B) sub population profiles; and C) time effect over 3 seasons.

METHODS

Subjects

Thirteen national and international level French swimmers were studied (6 females, 7 males). Their mean (±SD) age, height, and weight were 22±3 yr, 177±7 cm, and 66±10 kg, respectively. Other population characteristics can be found in Table 1. Written informed consent was obtained from the subjects before entering the study. Approval for the project was obtained from the Saint-Etienne University Committee on Human Research. Each swimmer trained according to the program prescribed by the two-team coaches independently of the authors of the present study. Performances were measured during real competitions and expressed as a percentage of the personal record performed by each swimmer during the studied period. The total number of performances was 302, and the mean number of performances per season was 9.5±2.4 (over a total of 13 subjects and 3 seasons). P_ij designated the j^th percentage for the i^th individual, j = 1,…,n_i; i = 1,…,N; n_i the number of performances for the i^th individual; N = 13, number of subjects in the study. A percentage increment indicated a faster performance. Inversely, when percentage decreased, the performance was lower.

TABLE 1.

Population characteristics.

Subjects	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10	S11	S12	S13
Sex	F	M	M	M	F	M	M	F	F	M	F	M	F
Distance	200	200	200	400	400	100	100	100	200	100	100	200	200
Style	FS	ME	FS	FS	FS	BR	BR	FS	BR	BR	BU	BR	BU

Sex: M (Male), F (Female). Distance values are expressed in m. Style: FS (Freestyle), ME (Medley), BR (Breaststroke), BU (Butterfly).

Quantification of the training load

For workouts in water, intensity levels were evaluated using the method proposed by Mujika et al. (22). A progressive test was performed at the beginning of the first season to determine blood lactate concentration. During the test, each swimmer performed 200-m swims at a progressively increased percentage of his/her own best competition time in that distance, until exhaustion (failure to follow the required pace). Blood lactate concentration was determined from blood samples taken from a fingertip during the 1-min recovery periods separating the 200-m swims. According to the individual results obtained during this test, all the training performed in water was divided into five intensity levels. Intensities Z1, Z2, and Z3 represented swimming speeds below (≈2 mmol·l⁻¹), equal to (≈4 mmol·l⁻¹) and slightly above (≈6 mmol·l⁻¹) the onset of blood lactate accumulation, respectively. High intensity swimming that elicits blood lactate levels of ≈10 mmol·l⁻¹ was defined as intensity Z4 and maximal intensity swimming as intensity Z5. Intensity levels were modified according to the training distances and rest duration (25). The measurements were repeated 4 times during the season, and training intensity was adjusted to the swimmer’s response to training. Workout in the water was quantified in km per week (km·wk⁻¹).

Two dry land intensity levels were defined. Maximal strength exercises, Z6, consisted of exercises performed between 70% and 100% of the maximal strength measured for each exercise. Endurance exercises, Z7, included exercises between 40% and 70% and/or exercises performed with a number of repetitions greater than 20. Dry land workout was quantified in min per week (min·wk⁻¹).

Weekly volumes for each intensity level of every two groups where compared using Friedman analysis of variance (ANOVA).

For each swimmer each intensity level was then expressed as a percentage of the maximal intensity recorded during the study. This normalization allowed training loads of different units or intensities to be compared using the same scale of values. The global weekly training load, w, was the mean of normalized weekly training intensities.

In swimming, training time and quantity are considerably different for different training regimes. In our study, the quantitative relationship between Z5 training and Z1 training was, approximately, 1 to 40 fold. Thus if the data are not normalized zone by zone, training sessions with a lower quantitative level would be overpowered by training sessions with a higher quantitative level. Other options are possible to consider this fact: Mujika et al. (22) condensed all variables for the different training loads to a more comparable level by multiplying them by their coefficients of energetic intensity. Since it was decided not to make any preliminary hypotheses concerning the impact of training charges, this mode of normalization was preferred.

Definition of variables

The total training load of the 8 weeks preceding the performance was taken into account: w₀, w₋₁, w₋₂, w₋₃, w₋₄, w₋₅, w₋₆, w₋₇. Three variables were defined: X₁, short-term training, was the average of w₀ and w₋₁; X₂, mid-term training, was the average of w₋₂, w₋₃ and w₋₄; and X₃, long-term training, was the average of w₋₅, w₋₆ and w₋₇. Variables were denoted X_1ij, X_2ij, X_3ij, to indicate the j^th observation for the i^th subject of aforementioned variables, j = 1,…,n_i; i = 1,…,N.

Definition of covariates

Two covariates were chosen to take into account 1) the evolution over the 3 seasons of the relationship between training and performance and 2) some reactions to training. The covariate «season» indicated whether the observation belonged to the first, second or third season. It was parameterized by two indicator variables. A1_ij and A2_ij were defined to be «1» if the observation j of subject i belonged to the first season or the second season, respectively, and «0» otherwise.

The covariate «group» stemmed from a classification study. Firstly, correlation values of short-, mid- and long-term training periods with performance were used to achieve a Principal Component Analysis (PCA) and, then, investigate distances between subjects. Four kinds of reactions to training classes appeared accounting for the first and the second principal component factors. Secondly, the hypothesis of 4 well-distinguished classes were tested and significantly accepted (P < 0.05) from a Cluster Analysis according to the k-means method. The 4 groups were interpreted (relating each group to the others, not in absolute meaning) as follows: 1. Poor responders to the short- or mid-term training and neutral to the long-term training: PN (S6, S7, S10); 2. Good responders to the short- or mid-term training as well as to the long-term training: GG (S4, S5, S13); 3. Good responders to the short- or mid-term training and neutral to the long-term training: GN (S9, S11); 4. Neutral responders to the short- or mid-term training and good to the long-term training: NG (S1, S2, S3, S8, S12). «Neutral response» expressed a dispersed reaction into the group or a slight effect of the factor. This covariate was parameterized by three indicator variables. G1_i, G2_i and G3_i are defined to be «1» if the subject i belonged to PN, or GG, or GN, respectively, and «0» otherwise.

The mixed model

A linear mixed-effects model is any model that satisfies (29): Y_i = X_i β + Z_i b_i + ε_i with b_i ~ N(0, D), ε_i ~ N(0, Σ_i) and b_i’s independent of ε_i’s. Y_i represents the performances of subject i. X_iβ is the common to the population part of the model, Z_ib_i is the specific to each subject part of the model, and ε_i is the random sampling error of the model. β (the fixed effects) represent the population regression coefficients that are applied to X_i, the whole set of variables and covariates (training variables, and season and group covariates) of subject i. b_i (the random effects) represent the personal regression coefficients for subject i that are applied to Z_i, the subset of variables and covariates that present a specific-subject profile. b_i are regarded as the subject’s random deviation from the population mean. They are taken to be normally distributed with covariance matrix D. ε_i can be thought of as sampling error, or random perturbations, it is also taken to be normally distributed with an autoregressive covariance matrix, Σ_i. This covariance structure supposes that two observations taken close in time within an individual are more closely correlated than two observations taken far apart in the same individual. D models the between-subject variance, while Σ_i models the within-subject variance.

Summarizing, the main ideas and hypotheses of mixed-effects modeling that are used in this study are:

1. Mixed effect models have two levels: one level corresponding to the popular behavior and a second level corresponding to the individual behavior. All data are used to construct the common to the population part of the model, but only the observations specific to each individual are used to construct the personal part of the model. The contribution of population information is higher when the individual information is poor, and inversely.

2. Two levels of variability corresponding to the popular and the individual levels are characterized: the intra-individual and the inter-individual variability.

3. Intra-individual modeling takes into account the closeness in time of performances.

Mathematical descriptions of the particular linear mixed model explaining the relationship between training and performance can be found in the appendix.

Fitting the model

For fitting the model and testing suitable hypotheses the SAS 8.1 MIXED procedure was employed. Estimates and standard errors (SE) for all fixed effects and all variance components were computed. Parameters were calculated from the restricted maximum likelihood estimates, to take into account the loss of the degrees of freedom involved in estimating the fixed effects (29).

Hypotheses about the mean structure had to be tested. These hypotheses concerned, first, the influence of training variables, covariate of evolution through seasons and covariate of reaction to training, and second, differences between every 2 classes of covariates «season» and «group». Pertinence of hypotheses about the variance structure had to be tested too. These hypotheses concerned, first, the shape of matrix D and Σ_i, and lastly, the assumption of variability in all subject specific intercepts and slopes.

For each hypothesis, an appropriate statistical test was available in the MIXED procedure (29). For the assumptions of the mean structure, an approximate F-Test, using the containment method to compute degrees of freedom, and the sandwich estimate of variance, to ensure robustness, were used. Results were used to reduce the original model to a more parsimonious model. This was done in a hierarchical way, starting with highest P–value term and comparing the model with and without the term. If the presence of the term did not imply a significant improvement in the model, it was deleted. The obtained final model assumed no effect of season on basic level nor on near training.

With regard to variance structure, a Likelihood Ratio Test for nonstandard testing situations was used for testing the need of random effects. The presence of random effects was clearly necessary. Finally, Akaike Information Criteria and Schwarz Information Criteria discriminated between different non-nested models of structure of variance. The greatest amount of information was given by models with an auto regressive error covariance. This can be explained since, in addition to seasonal evolution, a continuous evolution through time, caused by a progressive adaptation to training, is likely.

RESULTS

Training volume and intensity

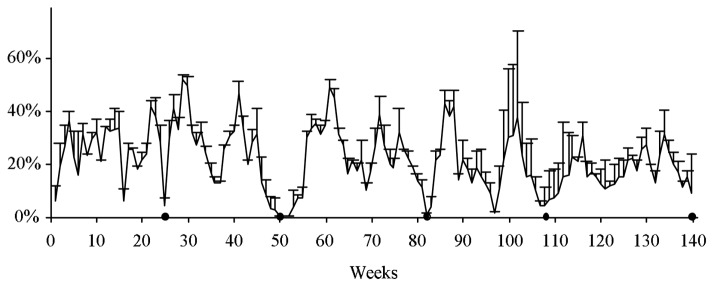
Global training load changed through the studied period according to a wave pattern of 4 macro-cycles in each season training plan (Figure 1). Each macro-cycle consisted of a high-load phase, whereby total training load was gradually increased alternating with regeneration phases (weeks 16, 37, 69, 97, 122) and competition periods: national events (weeks 25, 82, 140), European events (week 50) and Olympic games (week 108).

FIGURE 1.

Global weekly training load (the mean of the 7 intensity levels expressed in percentage of their maxima) for all the subjects, over the 3 seasons. Values are mean (SE). Discs in horizontal axis indicate main competitions. Over the 3 seasons, the 100% value was not attempted: there is no week in which the 100% value was attempted for all intensity levels and for all subjects.

PN was the group with the highest Z3, Z4, Z6 and Z7 volumes. GG was the group with the highest Z2 volume, and the lowest Z4 and Z5 volumes. GN was the group with the lowest dry land intensity level volumes. Finally, NG was the group with the highest Z1 volume and the second highest Z2, Z3, Z4, Z6 and Z7 volumes (Table 2). Weekly Z2 and Z4 volumes were not significantly different between groups. For the other intensity levels, there were some significant differences between some groups.

TABLE 2.

Weekly training volume (including rest periods) for each intensity level and group.

Intensity Level	PN			GG			GN			NG
	GG	GN	NG	PN	GN	NG	PN	GG	NG	PN	GG	GN
Z1	*	*	**	*	-	-	*	-	-	**	-	-
(km· wk−1)	13543 (7529)			15785 (9477)			15725 (7624)			16201 (8407)
Z2	-	-	-	-	-	-	-	-	-	-	-	-
(km· wk−1)	17488 (13120)			19018 (16447)			17262 (11857)			17847 (13748)
Z3	**	-	**	**	**	-	-	**	-	**	-	-
(km· wk−1)	3065 (2507)			2249 (2130)			2033 (2061)			2474 (2132)
Z4	-	-	-	-	-	-	-	-	-	-	-	-
(km· wk−1)	663 (541)			572 (652)			586 (492)			623 (510)
Z5	**	-	*	**	**	*	-	**	-	*	*	-
(km· wk−1)	613 (460)			443 (408)			667 (383)			535 (451)
Z6	-	**	*	-	**	*	**	**	**	*	*	**
(min· wk−1)	4.8 (14.2)			3.5 (13.2)			1.4 (12)			3.9 (14.6)
Z7	**	**	-	**	**	**	**	**	**	-	**	**
(min· wk−1)	6.4 (15.4)			2.13 (7.5)			0 (0)			5.9 (17.5)

Values are mean (SD).

^*Significant difference of the 1st line group from the 2nd line group, for each intensity level (P ≤ 0.05).

^**Significantly different (P ≤ 0.01).

-Not significantly different.

Cluster Analysis and PCA

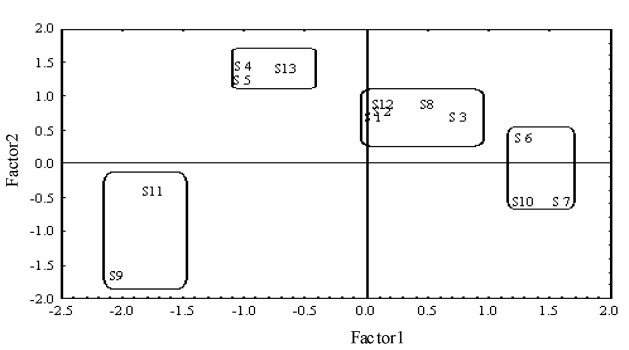
PCA results are shown in Table 3. Only factors with eigenvalues greater than 1 were retained. Factor 1 accounted for 56% of the total variance. This factor was highly negatively related to the short- and mid-term training period (r = −0.91; r = −0.92, respectively). Factor 1 is represented in Figure 2 by the horizontal axis. Subjects S6, S7 and S10, on the right, for whom X₁ and X₂ exerted a negative influence, were separated from subjects S9 and S11, on the left, for whom X₁ and X₂ exerted a positive influence.

TABLE 3.

Results of PCA. Weights of principal factors and explained variance.

	ρ1	ρ2	ρ3	EV	%EV
Factor 1	*−0.91	*−0.92	−0.02	1.68	0.56
Factor 2	−0.28	0.25	*0.99	1.12	0.37

ρ_i correlation between X_i and performance, i=1,2,3. EV, explained variance.

^*Significant value (P ≤ 0.05).

FIGURE 2.

Geometric representation of subjects (from S1 to S13) from the PCA. Factor 1 was negatively related to correlation between the short- and mid-term training periods with performance. Factor 2 was positively related to correlation between the long training period and performance. Groups: Poor responders to the short- or mid-term training and neutral to the long-term training (PN); Good responders to the short-, mid- and long-term training (GG); Good responders to the short- or mid-term training and poor to the long-term training (GN); Neutral responders to the short- or mid-term training and good to the long-term training (NG).

Factor 2 accounted for 37% of the total variance. This factor was highly positively related to long training period (r = 0.99). Factor 2 is represented in Figure 2 by the vertical axis. Subjects S4, S5, and S13, at the top, for whom X₃ exerted a positive influence, were separated from subjects S11 and S9, at the bottom, for whom X₃ exerted a negative influence. For subjects S1, S2, S3, S8, and S12, situated in the middle of the figure, X₃ exerted a positive influence and X₁ and X₂ exerted a neutral influence. Cluster analysis divided the swimmers into 4 statistically different groups.

Fitted model analysis

After testing, the model was modified and reduced (mathematical descriptions can be found in the appendix). Random effects reflect how much the subject-specific profiles deviates from the overall average profile. In the initial model, 4-dimensional random effects were taken into account: the first element was associated with basic level, the second, third and fourth elements were associated with training variables X₁, X₂, X₃, respectively. Nevertheless, tests showed that, even though every combination of two random effects was significant, more than two effects were not necessary. Thus, short-, mid-, and long-term training varied from a subject to another, but this variation was mainly provided by 2 variables. A supplementary variable did not contribute significantly to describe the subject-specific profiles. So, to ensure a parsimonious model, only random effects providing the most of the information were kept in the final model: random effect associated with basic level and to long-term training. This could mean that groups were homogeneous enough to account for a great part of the behavior of each swimmer. Only little complementary information was needed to describe individual profiles.

From parameter estimates of the mean structure, it was possible to compute each group’s parameter, for each variable X₁, X₂, X₃, and the basic level. Also, parameters assigned to each of the 3 seasons and to their average were computed, when effect of the season was significant. Results are given in Table 4. The higher basic level, 98.7%, belonged to the group PN and the lower, 95.4%, belonged to GG. Short-term training was negative on performance for all the groups (PN: −1.02; GG: −0.74; GN: −0.29; NG: −1.04). Mid-term training was negative for PN and positive for the others (PN: −0.35; GG: 0.63; GN: 0.93; NG: 0.41). Finally, long-term training was negative for GN and positive for the others (PN: 0.60; GG: 0.69; GN: −0.05; NG: 0.54).

TABLE 4.

Weights for basic level, X₁, X₂, and X₃, for each group and season.

		Group
		PN	GG	GN	NG
BL	-	98.70	95.40	97.31	97.52
X1	-	−1.02	−0.74	−0.29	−1.04
X2	1st	−0.11	0.87	1.17	0.66
	2nd	−0.16	0.82	1.12	0.61
	3rd	−0.78	0.20	0.49	−0.02
	AV	−0.35	0.63	0.93	0.41
X3	1st	0.17	0.26	−0.48	0.12
	2nd	0.59	0.68	−0.07	0.53
	3rd	1.04	1.13	0.39	0.99
	AV	0.60	0.69	−0.05	0.54

All values are % of the personal record. BL, basic level. AV, average of seasonal values.

-Not significant difference between seasons.

The effect of the seasons was not significant for short-term training while for mid- and long-term training, it was statistically different. For mid-term training, the effect of seasons was significantly negatively decreasing on PN (−0.11, −0.16, −0.78, for the first, second and third seasons, respectively). For GG and GN, the effect was significantly positively decreasing and for NG, the effect was significantly decreasing from positive to negative values (GG: 0.87, 0.82, 0.20; GN: 1.17, 1.12, 0.49; NG: 0.66, 0.61, −0.02, for the first, second and third seasons, respectively). For long-term training, the effect was significantly positively increasing for all the groups, except GN. For this group, the effect was significantly increasing from negative to positive values (PN: 0.17, 0.59, 1.04; GG: 0.26, 0.68, 1.13; GN: −0.48, −0.07, 0.39; NG: 0.12, 0.53, 0.99).

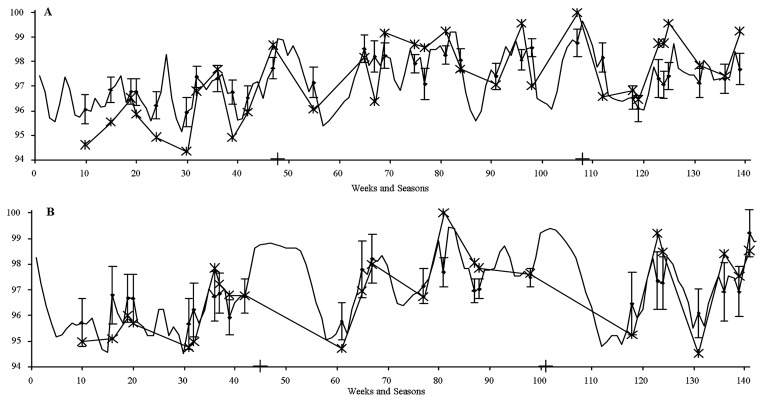
Table 5 presents r² and average standard error values (ASE) for all subjects. The average r² was 37.7%, range 15.1%–65.5%. The mean ASE was 0.33, range 0.15–0.55. Figure 3 shows real and modeled performance for subject 1 (A) and subject 7 (B). For subject 1, ASE was 0.27, this value indicated an error of 0.32 s for a 200 m event performed in less than 2 min. For subject 7, optimal modeled performance was situated shortly after the main seasonal competition, corresponding to the last event of the first and second season.

TABLE 5.

r² and average SE for predicted values of each subject.

Subject	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10	S11	S12	S13
r2 (%)	46.5	26.0	40.0	43.1	20.1	46.5	51.7	15.1	31.0	27.4	65.5	57.5	20.6
ASE for prediction	0.27	0.28	0.44	0.23	0.34	0.38	0.44	0.32	0.15	0.55	0.17	0.38	0.32

ASE, average standard error expressed in % of the personal record.

FIGURE 3.

Real and modeled performance for subject 1 (A) and subject 7 (B). Performance in vertical axis is expressed in % of the personal record. Time in horizontal axis is expressed in weeks and seasons (crosses separate 1^st from 2^nd and 2^nd from 3^rd seasons). Real performance is indicated with stars linked by straight lines. Modeled performance is indicated by an irregular prediction curve and by diamonds for weeks where an actual performance took place. The 95% confidence intervals for the last case are also represented. For subject 1, the pattern of modeled performance is similar to that of real performance. Inversely, for subject 7, optimal modeled performance was situated shortly after the main seasonal competition, corresponding to the last event of the first and second season (weeks 40 and 98), indicating probably the need of a longer recovery.

DISCUSSION

The main findings of this study are that:

1. Reactions to the short-, mid- and long-term training periods (X₁, X₂ and X₃, respectively) were significantly different for swimmers when divided into 4 groups. Interpretation of groups was based on terms of relative (to the other groups) good, poor or neutral reaction to training. Swimmers reacting poorly to the short- or mid- and reacting neutrally to the long-term training period (PN) composed the first group. The second group was composed by those reacting well to the three training periods (GG). The third group was composed by those reacting well to the short- or mid- period and neutrally to the long-term training period (GN). Swimmers reacting neutrally to the short- and mid- period and well to the long-term training period composed the fourth group (NG). This classification of swimmers from cluster and principal component analyses was incorporated into the mixed model.

2. The impact of training on performance changed significantly from the first to the third season, for the mid- and long-term training period. For X₂, the effect decreased, inversely for X₃.

3. Proposed model fitted significantly training and performance data for all the subjects.

Specific adaptations to training for each group

Reactions to training periods were significantly different according to the 4 clusters. These responses were independent of training load differences which were integrated into the model (10). Differences between athletes’ reactions to the same training program matched previous studies (23). Some swimmers are more tolerant to the training than others (7). The 4 different adaptation groups found in the present study confirmed studies by Hohmann (16), that differentiated athletes reacting «early» to training from others reacting «late».

Effect of short-term training period

Training exerted a negative effect on PN, GG, GN and NG, which is consistent with taper studies. Morton et al. (19) and Mujika et al. (22) proposed a 2–3 week taper duration, on average. Taper allows for the recovery of previous accumulated fatigue, and the conservation of acquired capacities over such a period (17, 22).

Training exerted the slightest effect on GN. This group was composed by the 2 youngest females, with the lowest performance level of swimmers in the study. These swimmers performed the lowest volume of dry land training that implies a lower muscular fatigue (7). Furthermore, optimal recovery length seems to be longer for elite athletes than for sedentary subjects performing a moderate endurance training (5). In addition, adolescents rely less on glycolytic metabolism than adults during intense training (15), implying less fatigue and, so, shorter taper (27).

Effect of mid-term training period

Mid-term training had a negative influence on PN and a mean positive influence on the other groups. Several studies (4, 11, 20, 21) confirm the importance of this period during which the increase in training load volume and intensity creates a powerful training impulse and a differed stimulation of biological adaptations through an overcompensation process (11, 20, 27). Nevertheless, there is a threshold to the impact of training loads on the organism. Furthermore, for certain loads, a greater amount of training implies the risk of overtraining (20, 21).

PN was composed by 3 older male sprinters, specialized in breaststroke (Table 1). For these swimmers, cumulative effects of high Z3, Z4, Z5, and Z6 volumes implies, in all likelihood, a severe impact on the organism and a longer recovery period (7, 23). In addition, energy consumption in breaststroke is very high (28), probably causing more fatigue and longer recovery (8). Also, adaptation capacity seems to decrease with age (14).

Mid-term training had a positive influence on GG. Some studies point out the interest of increasing training volume and aerobic loads for this type of swimmer (7). Coyle (9) observed that maximal O₂ uptake, which is the most solicited quality for distance swimmers (28), declined by 7% during the first 3 weeks of inactivity.

Training had a moderate mean positive effect on NG. This group was composed by 200-m swimmers: 1 female (S1) and 3 male swimmers (S2, S3, S12), and a female 100-m swimmer (S8). NG had a slight mean weekly Z2, Z3, Z4, Z6 and Z7 volume. Two hundred meter races have been described as maximal aerobic and anaerobic metabolism solicitation (28). For this group, aerobic (Z1, Z2), maximal oxygen consumption (Z3), anaerobic (Z4) and dry land (Z6, Z7) training should probably be maintained for a sufficiently long period, before competition, to avoid detraining (24). On the other hand, a sufficiently long taper is needed to recover from the cumulative effect of these high training loads, generating severe fatigue and «overreaching» risks (18, 21). In this respect, optimal training duration ensures overcompensation without the downfall of overstraining manifestations (11).

Effect of long-term training period

Training had a positive effect on PN, GG and NG. A high training volume has to be maintained over this period to develop main qualities for further specific training periods (8, 9). Weeks 5 to 12 before the performance are the most suitable weeks for hard training (4, 19, 20). Training had a slight mean negative effect on GN. These results emphasized that, for athletes with a short-term training background, schedules based on a regular and continuous distribution of training loads are more efficient than schedules based on the amount of hard training units, when comparing overcompensation (27).

Influence of the season on the effect of training

Subject reactions to mid- and long-term training were significantly modified between the first and third season. This result confirmed that swimmer reaction to training changes when identical training load is reiteratively applied through time (4, 6, 8). Busso et al. (6) suggested that variations over time in the model parameters appear with training. In the present study, response variations as a function of time were similar to the one found by Busso et al. (6). The application of the same training load through time leads to a negligible decrease of performance, in the mid period (2 to 3 weeks), and a bigger decrease in the long training period (4 to 6 weeks). First, repeated training through time would cause accumulated effects that improve performance (4, 6, 7, 8). On the other hand, performance through years would be improved by a progressive increase of volume and intensity of training (6, 12, 21). Elite athletes would need to train more than untrained athletes to maintain the same progression (2). Conversely, they need a longer recovery time (19).

Finally, different reactions to training between different groups of subjects are known to be highly individualized (23). These differences can be attributed to genetic factors (30), individual training background (17, 22), psychological factors (2) and technical factors (28). Thus, these results suggest that major personalization of the training programs has to be prescribed for each individual swimmer, depending on age, specialty, training background and individual profiles.

Fitting the model

Results of fitting showed that the proposed mathematical model was a correct method to describe the relationship between training and performance. For 13 elite swimmers over 3 different training seasons, including rest time, the fit between actual and modeled performance was statistically significant. The average r² was 37.7%, with extreme values ranging from 15.1% to 65.5%. The mean average standard error for estimated performances was 0.33, with extreme values 0.15 and 0.55. From a practical point of view, these values are accurate (for subject 1, ASE was 0.32 s for a 200 m event performed in less than 2 min).

Although transformations through the seasons and common and individual variability were taken into account, r² were lower than data reported in swimming (22, 23) or other sports (4, 19). Interpreting and comparing different r² is difficult. Indeed, the sample size can have a marked effect on the calculated value of the determination coefficient. For small samples, the mean r² may assume a high value even though there is no relationship between predictor and response variables (1). A longer period of study could also explain these lower fitting values. In addition, even if r² is one of the most important measures of the adequacy of prediction equations, a high value of r² does not necessarily guarantee accurate prediction (13). A complementary measure, (like confidence interval used in the present study), is needed to indicate accuracy and sensitivity. Furthermore, classification in 7 intensity levels may be insufficient when compared to the high number of different training variables used by the coaches in their programs (6, 22, 23). Psychological, nutritional (2, 19) and technical factors (28) are related to performance. Hence, the long-term and cumulative effects of training, that may be evidenced some macro-cycles after, may not have been taken into account (8).

CONCLUSION

Modeling relationships between training and performance by a linear mixed model has made contributions to the Banister model. Identification of immediate and delayed reactions to training for each group as well as individual reactions help to improve the personalized distribution of training load through the 8 weeks preceding competitions. Evidence of the different evolutions through the training seasons suggests that multi-annual planning must be made most carefully. The graphical representation of the real performance versus modeled performance may estimate, with a fixed confidence interval, the athlete’s responses to training load, week after week. A supplementary study, with a larger number of subjects would be necessary to generalize these results.

TABLE 6.

Individual coefficients and SE for the two considered random effects.

Subject	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10	S11	S12	S13
b0i (%)	−0.10	0.07	0.21	0.11	0.22	−0.29	−0.07	−0.10	−0.03	0.16	0.03	−0.22	−0.15
SE	0.28	0.28	0.30	0.29	0.29	0.30	0.30	0.30	0.32	0.31	0.32	0.30	0.30
b3i (%)	−0.01	0.07	0.16	0.14	0.13	−0.21	−0.08	−0.05	−0.03	0.13	0.03	−0.11	−0.10
SE	0.15	0.14	0.14	0.15	0.14	0.14	0.14	0.14	0.16	0.15	0.16	0.14	0.14

All values are expressed in % of the personal record. b_0i and b_3i reflect deviation of the individual profiles from the population profile.

APPENDIX

The linear mixed model explaining, in particular, the relationship between training and performance, taking into account training variables and season and group covariates can be expressed as follows:

• 1)P_ij = (β₀₀ + β₀₁G1_i + β₀₂G2_i + β₀₃G3_i + β₀₄A1_ij + β₀₅A2_ij) + (β₁₀ + β₁₁G1_i + β₁₂G2_i + β₁₃G3_i + β₁₄A1_ij + β₁₅A2_i) X_1ij + (β₂₀ + β₂₁G1_i + β₂₂G2_i + β₂₃G3_i + β₂₄A1_ij + β₂₅A2_ij) X_2ij + (β₃₀ + β₃₁G1_i + β₃₂G2_i + β₃₃G3_i + β₃₄A_i + β₃₅A2_ij) X_3ij + b_0i + b_1iX_1ij + b_2iX_2ij + b_3iX_3ij + ε_ij
• 2)b_i = (b_0i, b_1i, b_2i, b_3i)′ ~ N(0, D) and ε_i = (ε_i1,ε_i2,…,ε_ini)′ ~ N(0, Σ_i)

  D is a diagonal matrix: D = diag [σ_b0², σ_b1², σ_b2², σ_b3²]

  Σ_i is an autoregressive matrix Σ_i (k, l) = σ² ρ^|k−j|, k, l = 1,…,n_i,.

  j = 1,…,n_i, i = 1,…,N.

After fitting and testing, the model was modified and reduced to:

• 3)P_ij = (97.52 + 1.18 G1_i − 2.12 G2_i − 0.20 G3_i) + (−1.04 + 0.02 G1_i + 0.30 G2_i + 0.76 G3_i) X_1ij + (−0.02 − 0.77 G1_i + 0.22 G2_i + 0.51 G3_i + 0.67 A1_ij + 0.62 A2_ij) X_2ij + (0.99 + 0.06 G1_i + 0.15 G2_i − 0.60 G3_i − 0.87 A1_ij − 0.46 A2_ij) X_3ij + b_0i + b_3i X_3ij +ε_ij

  j =1,…, n_i; i =1, …,N

• 4)b_i = (b_0i, b_3i)′ ~ N(0, D) and ε_i = (ε_i1,ε_i2,…,ε_{i ni})′ ~ N(0, Σ_i)

  where D = diag [0.11, 0.03] and Σ_i (k, l) = 2.04· 0.51 ^|k−j|.

Individual coefficients and the associated standard errors are given in Table 6 for the two considered random effects.