Abstract
Spirals or scroll waves pinned to heterogeneities in cardiac tissues may cause lethal arrhythmias. To unpin these life-threatening spiral waves, methods of wave emission from heterogeneities (WEH) induced by low-voltage pulsed DC electric fields (PDCEFs) and circularly polarized electric fields (CPEFs) have been used in two-dimensional (2D) cardiac tissues. Nevertheless, the unpinning of scroll waves in three-dimensional (3D) cardiac systems is much more difficult than that of spiral waves in 2D cardiac systems, and there are few reports on the removal of pinned scroll waves in 3D cardiac tissues by electric fields. In this article, we investigate in detail the removal of pinned scroll waves in a generic model of 3D excitable media using PDCEF, AC electric field (ACEF) and CPEF, respectively. We find that spherical waves can be induced from the heterogeneities by these electric fields in initially quiescent excitable media. However, only CPEF can induce spherical waves with frequencies higher than that of the pinned scroll wave. Such higher-frequency spherical waves induced by CPEF can be used to drive the pinned scroll wave out of the cardiac systems. We hope this remarkable ability of CPEF can provide a better alternative to terminate arrhythmias caused by pinned scroll waves.
Spiral waves are typical self-organized structures that exist in various systems including chemical media1,2, aggregations of Dictyostelium discoideum amoebae3, and cardiac tissues4,5. Scroll waves are three-dimensional (3D) extensions of spiral waves, which rotate around one-dimensional singularities known as their filaments6,7,8,9,10,11,12. Spiral and scroll waves can also be pinned (anchored) to localized heterogeneities, giving rise to sustained periodic or quasiperiodic activity13,14,15,16,17,18,19,20,21,22,23,24. Pinning is believed to play a crucial role in maintaining abnormal high frequency heart rhythms, including ventricular tachycardia and fibrillation, the main causes of sudden cardiac death4,5.
Better than the traditional but side-effect therapy of applying a high-voltage electric shock globally, the effect of unpinning by a series of electric pulses, i.e. antitachycardia pacing (ATP)25,26, is confirmed in both chemical and cardiac systems27,28,29,30,31. Theoretical analyses are introduced recently to explain its mechanism32,33. However, the efficiency of a successful unpinning by ATP requires more and better locations of electrodes, and these requirements are not easily accomplished for now.
To overcome the limitations of ATP, a new method using wave emission from heterogeneities (WEH) induced by low-voltage pulsed DC electric fields (PDCEFs) provides a better alternative to terminate arrhythmias34,35,36. This method relies on the effect of the response of cardiac tissue to an external electric field that modifies the membrane potential distribution near the heterogeneities. In hearts, as in many other systems, e.g. nervous network systems37,38, the complicated nature largely comes from heterogeneities, such as complex anatomical structures, blood vessels, and even tissue damage36. If the electric field strength exceeds the excitable threshold, a wave can be nucleated near the heterogeneity. This phenomenon in cardiology is known as virtual electrodes or secondary sources39,40,41,42,43,44,45. Using this strategy, unpinning of spiral waves is possible in cardiac tissues by the interaction between the newly generated waves and the anchored spirals46,47,48,49,50,51. Recently, the circularly polarized electric field (CPEF) has shown its unique ability to control spirals and turbulence52,53,54 in chemical media, and has been verified experimentally in the Belousov-Zhabotinsky (BZ) reaction by applying two ACs onto two pairs of field electrodes perpendicular to each other55. In ref. 56, we study the mechanism of WEH induced by CPEF in cardiac tissues, and find its ability to successfully unpin anchored spirals is better than that of PDCEF at higher success rate and in larger application scope.
Most of previous works regarding the unpinning only considered two-dimensional (2D) systems, while actually the heart is a 3D object. And the unpinning of scroll waves in 3D systems is much more difficult than that of spiral waves in 2D systems. For 2D systems, after a successful unpinning, the spiral wave will remain free as long as the distance between the obstacle boundary and the spiral tip is larger than the core size of its own46,47,48,49,50,51. For 3D systems, the filament of scroll wave may undergo a deformation in the neighborhood of the obstacle and detach from the obstacle after a suitable electric field is applied, which is similar to the case of spiral wave in 2D systems. However, if we switch off the electric field, the filament would be straightened and re-pinned back to the obstacle again as a result of the positive tension of the filament.
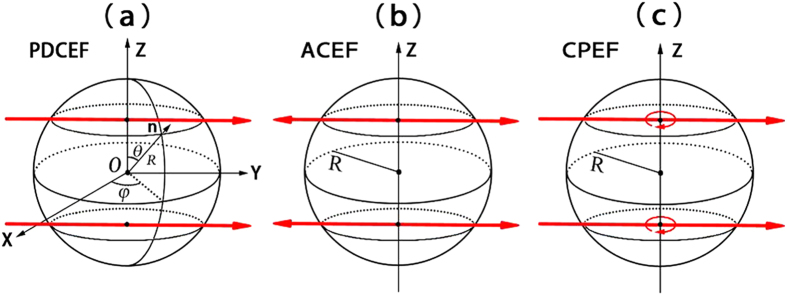
Though unpinning of scroll waves in 3D chemical systems has been investigated57,58 at present, there are few reports on the removal of pinned scroll waves in 3D cardiac tissues. In this paper, we will focus on removing pinned scroll waves in 3D cardiac tissues using external electric fields in a generic model of excitable media. These electric fields include PDCEF, AC electric field (ACEF) and CPEF, which are shown in Table 1 and Fig. 1. We respectively study the WEH induced by these three forms of external electric fields. We find all of them can induce spherical waves near the obstacles in initially quiescent excitable media. Only CPEF can induce spherical waves whose frequencies are higher than that of the pinned scroll wave. Such higher-frequency spherical waves induced by CPEF may have a unique ability to drive the pinned scroll wave out of the cardiac systems.
Table 1. Three forms of external electric fields.
| PDCEF |
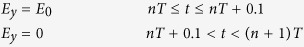 
|
| ACEF | 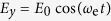 |
| CPEF | 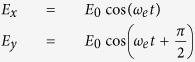 |
Figure 1. Three forms of external electric fields.
The spheres with radius R represent the obstacles in cardiac tissues. The red straight arrows represent the directions of PDCEF in (a), ACEF in (b), and CPEF in (c). The red curved arrow in (c) means CPEF can rotate horizontally around the z-axis.
Results
To describe the electrical activities of cardiac tissues, we use the general Barkley model59, a simplified mono-domain model:
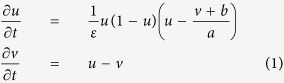 |
where u is the fast variable corresponding to membrane potential, and v is a slow variable corresponding to a recovery process. The parameters a, b and ε are fixed at 0.9, 0.08 and 0.02, respectively. When we choose such parameter configurations, the spiral undergoes rigid rotation and the scroll wave filament has positive tension, which corresponds to the “collapsing scroll rings” region in the parameter space of the Barkley model9.
In mono-domain models, the general effect of an external electric field on an obstacle can be expressed as a Neumann boundary condition50,51,60:
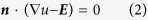 |
where n is a local unit vector perpendicular to the obstacle boundary, and E is the external electric field which represents PDCEF, ACEF or CPEF in this paper. When we apply these three forms of electric fields to a 3D cardiac system, the electric fields will change the membrane potential around the obstacle, respectively (see Fig. 1).
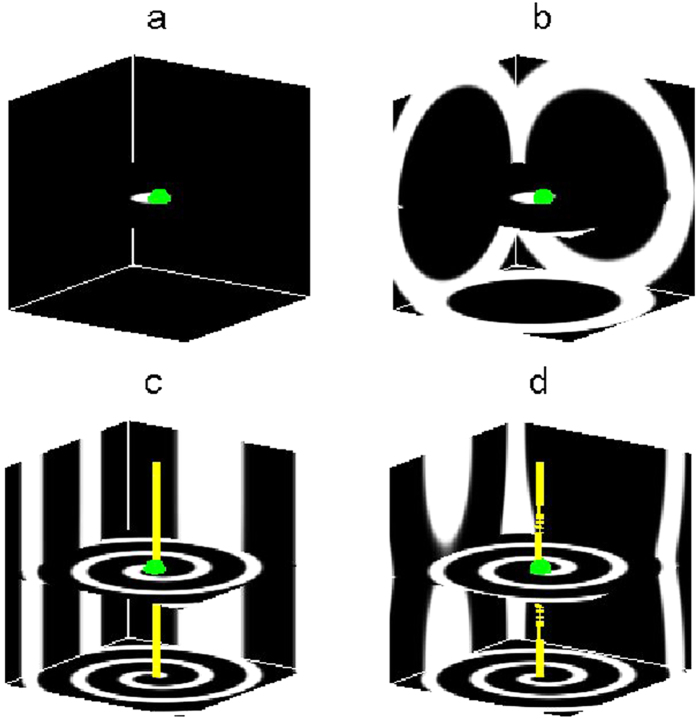
Firstly, we study the effect of PDCEF on an initially quiescent excitable medium with an obstacle. By applying PDCEF to the initially quiescent excitable medium, as shown in Fig. 1a, the membrane potential around the obstacle will be redistributed. The de-polarized and hyper-polarized regions are induced on opposite sides of the obstacle respectively, similarly as those in Fig. 1b,d in ref. 56. If the electric field strength is large enough, a wave can be emitted from the de-polarized region and then gradually form a spherical wave near the obstacle, as shown in Fig. 2a. And with the continued effect of the electric field, the spherical wave detaches from the obstacle and propagates outward, then the second spherical wave ensues, and next the third one. Finally, the medium will be dominated by spherical waves, as shown in Fig. 2b.
Figure 2. WEH induced by PDCEF.
The strength and the frequency of PDCEF are E0 = 2.0, ωe = 3.75, respectively.The central green spheres denote the obstacles with radius 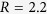 . The yellow line, i.e., the filament, represents the rotation center of the scroll wave. (a,b) show PDCEF induces spherical waves from the obstacle in a quiescent medium. (c,d) show the unsuccessful unpinning of the scroll wave by PDCEF.
. The yellow line, i.e., the filament, represents the rotation center of the scroll wave. (a,b) show PDCEF induces spherical waves from the obstacle in a quiescent medium. (c,d) show the unsuccessful unpinning of the scroll wave by PDCEF.
Now we consider the case that there is a scroll wave initially pinned to the obstacle, as shown in Fig. 2c. By employing the same PDCEF to the system, it is shown that spherical waves cannot be nucleated around the obstacle due to the preceding existence of the pinned scroll wave, as shown in Fig. 2d. That is, the scroll wave is still anchored to the obstacle. Although PDCEF is able to induce spherical waves near the obstacle in a quiescent state, it cannot remove the pinned scroll wave.
Considering that PDCEF cannot induce spherical waves with the presence of pinned scroll waves, one may guess that the frequency 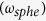 of the induced spherical waves is lower than the frequency
of the induced spherical waves is lower than the frequency 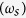 of the pinned scroll wave. So next we will measure the values of
of the pinned scroll wave. So next we will measure the values of 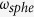 and
and 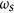 , and verify the above suppose. Since the frequency of the generated spherical waves
, and verify the above suppose. Since the frequency of the generated spherical waves 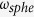 depends on the frequency of electric fields
depends on the frequency of electric fields 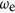 , we can obtain a series of spherical waves with different frequencies in a quiescent medium by varying
, we can obtain a series of spherical waves with different frequencies in a quiescent medium by varying 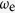 . And we find that if
. And we find that if 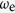 is lower than 2.5, the electric field cannot induce a sound spherical wave initially near the obstacle and these waves may break up subsequently. To study the relation between
is lower than 2.5, the electric field cannot induce a sound spherical wave initially near the obstacle and these waves may break up subsequently. To study the relation between 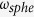 and
and 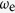 , we gradually increase
, we gradually increase 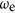 from 2.5 which can be seen as a minimum. Specifically, for a PDCEF with strength
from 2.5 which can be seen as a minimum. Specifically, for a PDCEF with strength 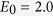 and pulse duration of 0.1 in Fig. 3a, it is shown that no matter how to choose the frequency of PDCEF, it cannot induce spherical waves with frequencies higher than that of the pinned scroll wave. Furthermore, when we increase the pulse duration to 0.2 as shown in Fig. 3b, the results are similar to the case of the pulse duration of 0.1. That is, PDCEF with pulse duration of 0.2 also cannot induce spherical waves whose frequencies are higher than that of the pinned scroll wave. Note that if the pulse duration is 0.05, spherical waves cannot nucleate near the obstacle. On the other hand, changing the strength of PDCEF to 7.0 as shown in Fig. 3c, we cannot get spherical waves with frequencies higher than that of the pinned scroll wave either.
and pulse duration of 0.1 in Fig. 3a, it is shown that no matter how to choose the frequency of PDCEF, it cannot induce spherical waves with frequencies higher than that of the pinned scroll wave. Furthermore, when we increase the pulse duration to 0.2 as shown in Fig. 3b, the results are similar to the case of the pulse duration of 0.1. That is, PDCEF with pulse duration of 0.2 also cannot induce spherical waves whose frequencies are higher than that of the pinned scroll wave. Note that if the pulse duration is 0.05, spherical waves cannot nucleate near the obstacle. On the other hand, changing the strength of PDCEF to 7.0 as shown in Fig. 3c, we cannot get spherical waves with frequencies higher than that of the pinned scroll wave either.
Figure 3. The relationship between the frequencies of the induced spherical wave and of PDCEF.
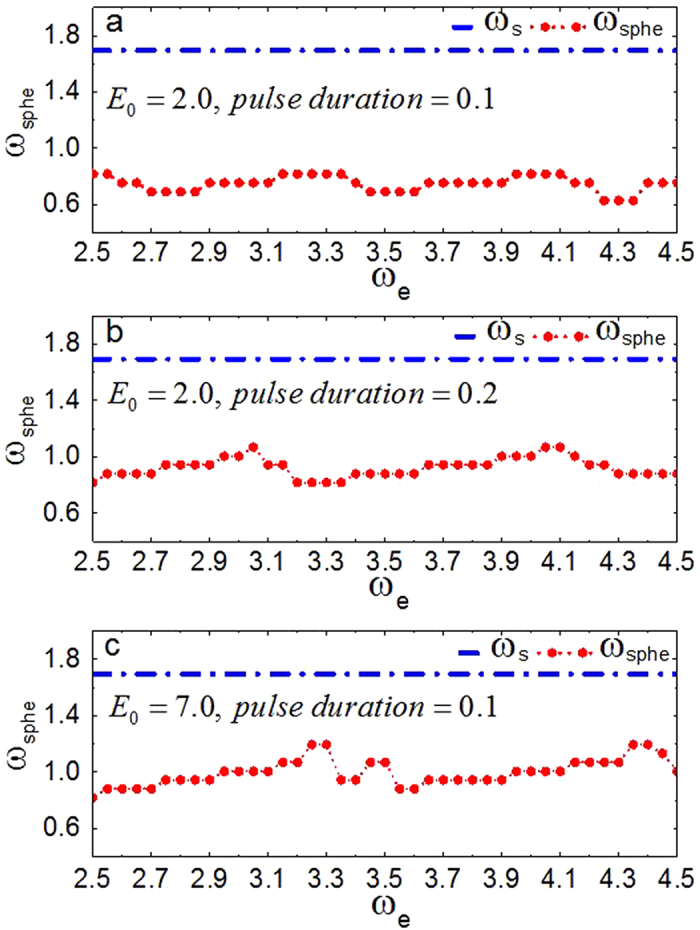
The pulse duration and the strength of PDCEF vary in different subgraphs. (a) E0 =2.0 and pulse duration is 0.1, (b) E0 = 2.0 and pulse duration is 0.2 and (c) E0 =7.0 and pulse duration is 0.1. The dashed line with solid circles represents the frequency of the induced spherical wave 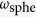 in a quiescent medium. The dash-dotted line represents the frequency of the pinned scroll wave
in a quiescent medium. The dash-dotted line represents the frequency of the pinned scroll wave 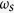 .
.
From the above discussion, we can conclude that PDCEF, even with different strength and pulse duration, is not able to induce spherical waves with frequencies higher than that of the pinned scroll wave; thus it cannot remove the pinned scroll wave out of the medium.
In the next, we study the medium responding to the other two forms of external electric fields: ACEF and CPEF. For ACEF as shown in Fig. 1b, with the effect of the electric field, the induced de-polarized and hyper-polarized regions are no longer steadily distributed but alternately appeared on opposite sides of the obstacle; thus the waves can be emitted equally on both sides of the obstacle. Although the frequencies of the formed spherical waves induced by ACEF can be higher than those of the spherical waves induced by PDCEF, they are still lower than that of the pinned scroll wave, as shown in Fig. 4a. Even if we increase the strength of ACEF to 4.0 and 7.0, it also cannot induce the spherical waves with frequencies higher than that of the pinned scroll wave. While, if we apply a suitable CPEF, it is capable to obtain higher-frequency spherical waves than that of the pinned scroll wave, as shown in Fig. 4b. This may owe to the unique ability of CPEF: compared to PDCEF and ACEF, the de-polarized and hyper-polarized regions induced by CPEF can rotate around z-axis, as shown in Fig. 1c (similarly as those in Fig. 1ac in ref. 56). Moreover, we test some other values of parameters a and b within the “collapsing scroll rings” region in the parameter space of the Barkley model9, and find that CPEF can also induce higher-frequency spherical waves than that of the pinned scroll wave.
Figure 4. The relationship between the frequencies of spherical waves and of electric fields.
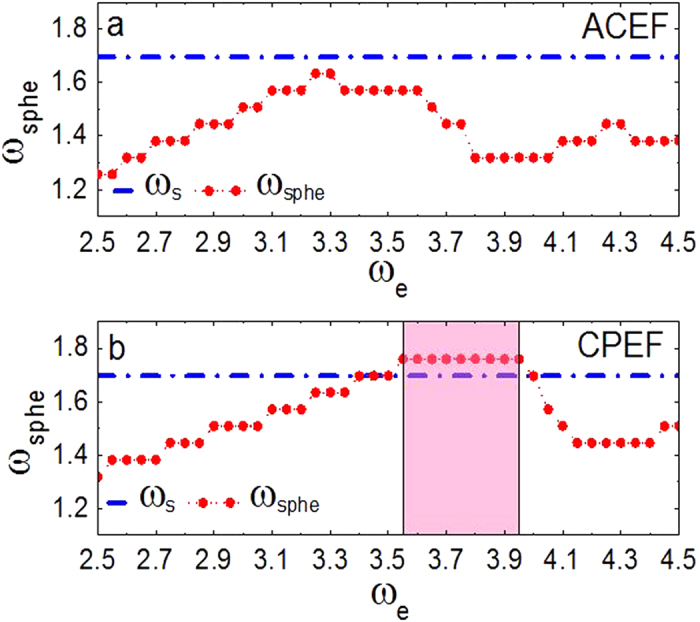
The forms of external electric field vary in different subgraphs. (a) ACEF and (b) CPEF. The strength 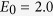 . The dashed line with solid circles represents the frequencies of the induced spherical waves
. The dashed line with solid circles represents the frequencies of the induced spherical waves 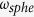 in a quiescent state. The dash-dotted line represents the frequency of the pinned scroll wave
in a quiescent state. The dash-dotted line represents the frequency of the pinned scroll wave 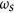 .
.
So far, we have shown that spherical waves can be induced from the obstacle by PDCEF, ACEF and CPEF. But only CPEF can induce spherical waves with frequencies higher than that of the pinned scroll wave. Next, we will give a further discussion on the membrane potential under the influence of these three different electric fields according to Eq. (2). The effect of electric fields on the membrane potential u at the boundary of the obstacle can be written as 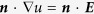 . That is, the value of
. That is, the value of  affects the distribution of membrane potential u at the boundary of the obstacle. And for any point at the boundary of the spherical obstacle, the local unit vector perpendicular to the obstacle boundary can be expressed as
affects the distribution of membrane potential u at the boundary of the obstacle. And for any point at the boundary of the spherical obstacle, the local unit vector perpendicular to the obstacle boundary can be expressed as 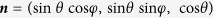 in spherical coordinates (see Fig. 1a). Then we can calculate the value of
in spherical coordinates (see Fig. 1a). Then we can calculate the value of  , as shown in Table 2. In detail, for PDCEF and ACEF, since they are applied merely in one direction, the extremum of
, as shown in Table 2. In detail, for PDCEF and ACEF, since they are applied merely in one direction, the extremum of  are still relied on θ and φ. While CPEF can rotate horizontally around the z-axis, so the extremum of
are still relied on θ and φ. While CPEF can rotate horizontally around the z-axis, so the extremum of  no longer has a dependency on φ. And the effect of CPEF on the membrane potential at the boundary of the spherical obstacle is more remarkable than those of PDCEF and ACEF, which to some extent may explain the reason why CPEF can generate spherical waves with frequencies higher than that of the pinned scroll wave.
no longer has a dependency on φ. And the effect of CPEF on the membrane potential at the boundary of the spherical obstacle is more remarkable than those of PDCEF and ACEF, which to some extent may explain the reason why CPEF can generate spherical waves with frequencies higher than that of the pinned scroll wave.
Table 2. The effects of electric fields on the membrane potential.
 |
Extremums of 
|
|
|---|---|---|
| PDCEF | 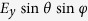 |
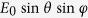 |
| ACEF | 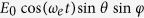 |
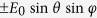 |
| CPEF | 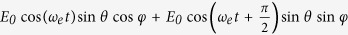 |
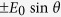 |
In view of the promising findings elucidated above in which the frequency of spherical wave 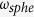 induced by CPEF can be higher than that of the pinned scroll wave
induced by CPEF can be higher than that of the pinned scroll wave 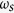 , we believe these higher-frequency spherical waves are capable of unpinning the anchored scroll waves and of driving them away out of the medium. We use the same initial state as that in Fig. 2c, and apply a CPEF with
, we believe these higher-frequency spherical waves are capable of unpinning the anchored scroll waves and of driving them away out of the medium. We use the same initial state as that in Fig. 2c, and apply a CPEF with 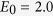 ,
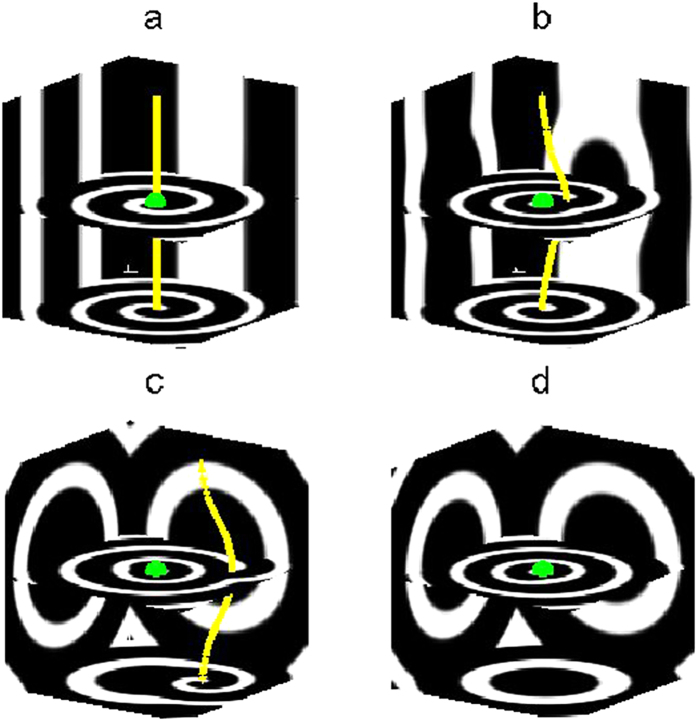
, 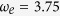 (such a CPEF can induce spherical waves with frequency higher than that of the pinned scroll wave, as shown in Fig. 4b) to the medium. After 30 time units, the filament of scroll wave undergoes a deformation in the neighborhood of the obstacle and then detaches from it (see the yellow line in Fig. 5b). This suggests that the initial unpinning of scroll waves can be obtained due to the interaction between the newly generated waves and the filament. However, if we switch off CPEF at this moment, the filament will be straightened and re-pinned back to the obstacle again as a result of the positive tension of the filament. This is quite different from the unpinning of spirals in 2D systems46,47,48,49,50,51: after a successful unpinning, the spiral wave will remain free as long as the distance between the obstacle boundary and the spiral tip is larger than the core size of its own. Therefore, it is much easier for 2D systems to realize unpinning. As for scroll waves in 3D systems, to achieve definite unpinning, it requires sustainable effects of the CPEF, which can induce higher-frequency spherical waves. As shown in Fig. 5c, scroll wave filament has been driven away far from the obstacle by the higher-frequency outward-propagating spherical waves. Finally, after 380 time units, the scroll wave has been completely swept away out of the medium boundary, and the medium is dominated by spherical waves (see Fig. 5d). When we turn off CPEF at this time, no new spherical waves can be induced near the obstacle afterwards and the remaining spherical waves will move out of the boundary. In the end, the system converts into the quiescent state (
(such a CPEF can induce spherical waves with frequency higher than that of the pinned scroll wave, as shown in Fig. 4b) to the medium. After 30 time units, the filament of scroll wave undergoes a deformation in the neighborhood of the obstacle and then detaches from it (see the yellow line in Fig. 5b). This suggests that the initial unpinning of scroll waves can be obtained due to the interaction between the newly generated waves and the filament. However, if we switch off CPEF at this moment, the filament will be straightened and re-pinned back to the obstacle again as a result of the positive tension of the filament. This is quite different from the unpinning of spirals in 2D systems46,47,48,49,50,51: after a successful unpinning, the spiral wave will remain free as long as the distance between the obstacle boundary and the spiral tip is larger than the core size of its own. Therefore, it is much easier for 2D systems to realize unpinning. As for scroll waves in 3D systems, to achieve definite unpinning, it requires sustainable effects of the CPEF, which can induce higher-frequency spherical waves. As shown in Fig. 5c, scroll wave filament has been driven away far from the obstacle by the higher-frequency outward-propagating spherical waves. Finally, after 380 time units, the scroll wave has been completely swept away out of the medium boundary, and the medium is dominated by spherical waves (see Fig. 5d). When we turn off CPEF at this time, no new spherical waves can be induced near the obstacle afterwards and the remaining spherical waves will move out of the boundary. In the end, the system converts into the quiescent state ( ). Note that, our further studies show that CPEF with
). Note that, our further studies show that CPEF with 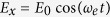 ,
, 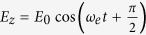 and with
and with 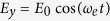 ,
, 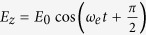 also can remove the pinned scroll wave out of the medium under the same above strength and frequency of CPEF.
also can remove the pinned scroll wave out of the medium under the same above strength and frequency of CPEF.
Figure 5. The evolution process for the removal of a pinned scroll wave by CPEF.
(a), t = 0. (b), t = 30. (c), t = 160. (d), t = 380. The obstacle radius 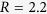 , and the frequency of the pinned scroll wave
, and the frequency of the pinned scroll wave 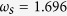 . The strength and the frequency of CPEF are
. The strength and the frequency of CPEF are 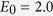 ,
, 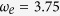 , respectively.
, respectively.
Parameter region of the removal of pinned scroll waves as a function of external field amplitude E0 and frequency 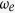 is given in Fig. 6. Specifically, for simplicity we define a box containing the obstacle in its center with a grid size of
is given in Fig. 6. Specifically, for simplicity we define a box containing the obstacle in its center with a grid size of 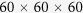 . If the scroll wave filament is swept away out of this box by CPEF within 500 time units, we treat it as a successful removal and denote it by a triangle; otherwise, for unsuccessful removal, denote it by a square. From Fig. 6, in particular, we find that when
. If the scroll wave filament is swept away out of this box by CPEF within 500 time units, we treat it as a successful removal and denote it by a triangle; otherwise, for unsuccessful removal, denote it by a square. From Fig. 6, in particular, we find that when 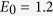 , it begins to exist a range of
, it begins to exist a range of 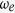 that can lead to successful removal. When we increase the strength E0 to 1.8, such a “successful removal” range of
that can lead to successful removal. When we increase the strength E0 to 1.8, such a “successful removal” range of 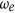 becomes larger as well, which corresponds to the shaded region in Fig. 4b. However, further increasing E0 makes no contribution to enlarge “successful removal” range any more.
becomes larger as well, which corresponds to the shaded region in Fig. 4b. However, further increasing E0 makes no contribution to enlarge “successful removal” range any more.
Figure 6. Parameter region of the removal of pinned scroll waves as a function of E0 and ωe.
The triangles denote the successful removal by CPEF; the squares the unsuccessful.
In conclusion, we have demonstrated that, spherical waves can be induced near the obstacle in initially quiescent cardiac tissues by PDCEF, ACEF and CPEF in a generic model of 3D excitable media. The frequencies of all the spherical waves generated by PDCEF are lower than that of the pinned scroll wave. Though the frequencies of the spherical waves induced by ACEF can be higher than those of the spherical waves induced by PDCEF, they are still lower than that of the pinned scroll wave. Only CPEF can induce spherical waves whose frequencies are higher than that of the pinned scroll wave, and these higher-frequency spherical waves can drive the pinned scroll wave out of the medium. The main difference of CPEF from PDCEF and ACEF is the rotation. Because of the rotation of CPEF, the medium will be affected by both de-polarization and hyper-polarization. Note that the model used in this paper is too simple for simulating actual cardiac systems. In order to give some more useful instruction for practical cardiac arrhythmias termination, further investigation taking into account more realistic cardiac activities is needed. On the other hand, CPEF can be easily realized in cardiac tissues by replacing DCs with ACs in the experimental preparation of Fig. 5d in ref. 35, which is similar to the case of the BZ reaction in ref. 55. In this sense, we hope the remarkable ability of CPEF to unpin scroll waves can be verified in cardiac tissues.
Methods
To add the introduced boundary condition into the spherical boundary of the obstacle in Cartesian coordinates, we adopt the phase field method50,51,60. Considering the effects of an external electric field on the obstacle, Eq. (1) can be adapted as
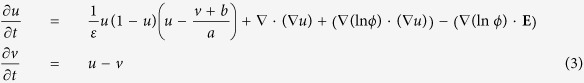 |
In Cartesian coordinates, Eq. (3) are integrated on a grid size of  medium with no-flux boundary condition via Euler method, and the central difference method is applied to compute the Laplacian term
medium with no-flux boundary condition via Euler method, and the central difference method is applied to compute the Laplacian term 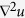 and the gradient terms
and the gradient terms 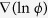 ,
,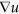 . The space and the time steps are
. The space and the time steps are 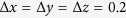 and
and 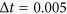 , respectively.
, respectively.
Additional Information
How to cite this article: Pan, D.-B. et al. Removal of pinned scroll waves in cardiac tissues by electric fields in a generic model of three-dimensional excitable media. Sci. Rep. 6, 21876; doi: 10.1038/srep21876 (2016).
Acknowledgments
This work was supported by the National Natural Science Foundation of China under Grants No. 11275167, No. 11447026, and No. 11505151, and the Fundamental Research Funds for the Central Universities. We thank Guo-Ning Tang for his useful discussions.
Footnotes
Author Contributions H.Z. conceived the concept of using CPEF to unpin scroll waves. D.-B.P., X.F., X.G. and J.-T.P. developed this approach and performed numerical simulations and data analysis. X.G., X.F., D.-B.P., J.-T.P. and H.Z. contributed to the discussions about unpinning mechanisms by CPEF. D.-B.P., X.F., X.G., J.-T.P. and H.Z. wrote the manuscript with input from all authors.
References
- Winfree A. T. Spiral waves of chemical activity. Science 175, 634–636 (1972). [DOI] [PubMed] [Google Scholar]
- Jakubith S., Rotermund H. H., Engel W., von Oertzen A. & Ertl G. Spatiotemporal concentrtion patterns in a surface-reaction: propagating and standing waves, rotating spiral, and turbulence. Phys. Rev. Lett. 65, 3013–3016 (1990). [DOI] [PubMed] [Google Scholar]
- Sawai S., Thomason P. A. & Cox E. C. An autoregulatory circuit for long-range self-organization in Dictyostelium cell populations. Nature 433, 323–326 (2005). [DOI] [PubMed] [Google Scholar]
- Davidenko J. M., Pertsov A. V., Salomonsz R., Baxter W. & Jalife J. Stationary and drifting spiral waves of excitation in isolated cardiac-muscle. Nature 355, 349–351 (1992). [DOI] [PubMed] [Google Scholar]
- Gray R. A., Pertsov A. M. & Jalife J. Spatial and temporal organization during cardiac fibrillation. Nature 392, 75–78 (1998). [DOI] [PubMed] [Google Scholar]
- Winfree A. T. Scroll-shaped waves of chemical activity in three dimensions. Science 181, 937–939 (1973). [DOI] [PubMed] [Google Scholar]
- Keener J. P. The dynamics of three-dimensional scroll waves in excitable media. Physica D 31, 269–276 (1988). [Google Scholar]
- Biktashev V. N., Holden A. V. & Zhang H. Tension of organizing filaments of scroll waves. Phil. Trans. R. Soc.Lond. A 347, 611–630 (1994). [Google Scholar]
- Alonso S., Sagués F. & Mikhailov A. S. Taming Winfree turbulence of scroll waves in excitable media. Science 299, 1722–1725 (2003). [DOI] [PubMed] [Google Scholar]
- Zhang H., Cao Z. J., Wu N. J., Ying H. P. & Hu G. Suppress Winfree turbulence by local forcing excitable systems. Phys. Rev. Lett. 94, 188301 (2005). [DOI] [PubMed] [Google Scholar]
- Bánsági T. & Steinbock O. Negative filament tension of scroll rings in an excitable system. Phys. Rev. E 76, 045202 (2012). [DOI] [PubMed] [Google Scholar]
- Dierckx H., Verschelde H., Selsil Ö. & Biktashev V. N. Buckling of scroll waves. Phys. Rev. Lett. 109, 174102 (2012). [DOI] [PubMed] [Google Scholar]
- Steinbock O. & Müller S. C. Light-controlled anchoring of meandering spiral waves. Phys. Rev. E 47, 1506–1509 (1993). [DOI] [PubMed] [Google Scholar]
- Zou X., Levine H. & Kessler D. A. Interaction between a drifting spiral and defects. Phys. Rev. E 47, R800–R803 (1993). [DOI] [PubMed] [Google Scholar]
- Bär M., Gottschalk N., Eiswirth M. & Ertl G. Spiral waves in a surface reaction: Model calculations. J. Chem. Phys. 100, 1202–1214 (1994). [Google Scholar]
- Xie F., Qu Z. L. & Garfinkel A. Dynamics of reentry around a circular obstacle in cardiac tissue. Phys. Rev. E 58, 6355–6358 (1998). [Google Scholar]
- Jalife J. Ventricular fibrillation: mechanisms of initiation and maintenance. Annu. Rev. Physiol. 62, 25–50 (2000). [DOI] [PubMed] [Google Scholar]
- Pertsov A. M., Wellner M., Vinson M. & Jalife J. Topological constraint on scroll wave pinning. Phys. Rev. Lett. 84, 2738–2741 (2000). [DOI] [PubMed] [Google Scholar]
- Wang X., Lu Y., Jiang M. & Ouyang Q. Attraction of spiral waves by localized inhomogeneities with small-world connections in excitable media. Phys. Rev. E 69, 056223 (2004). [DOI] [PubMed] [Google Scholar]
- Pazó D. et al. Pinning force in active media. Phys. Rev. Lett. 93, 168303 (2004). [DOI] [PubMed] [Google Scholar]
- Jiménez Z., Marts B. & Steinbock O. Pinned scroll rings in an excitable system. Phys. Rev. Lett. 102, 244101 (2009). [DOI] [PubMed] [Google Scholar]
- Biktashev V. N., Barkley D. & Biktasheva I. V. Orbital motion of spiral waves in excitable media. Phys. Rev. Lett. 104, 058302 (2010). [DOI] [PubMed] [Google Scholar]
- Zemlin C. W. & Pertsov A. M. Anchoring of drifting spiral and scroll waves to impermeable inclusions in excitable media. Phys. Rev. Lett. 109, 038303 (2012). [DOI] [PubMed] [Google Scholar]
- Jiménez Z. A. & Steinbock O. Stationary vortex loops induced by filament interaction and local pinning in a chemical reaction-diffusion system. Phys. Rev. Lett. 109, 098301 (2012). [DOI] [PubMed] [Google Scholar]
- Krinsky V. I. & Agladze K. I. Interaction of rotating waves in an active chemical medium. Physica D 8, 50–56 (1983). [Google Scholar]
- Hayes D. L., Asirvatham S. J. & Friedman P. A. Cardiac Pacing, Defibrillation and Resynchronization: A Clinical Approach (Wiley-Blackwell, Hoboken, NJ, 2012). [Google Scholar]
- Fu Y. Q., Zhang H., Cao Z. J., Zheng B. & Hu G. Removal of a pinned spiral by generating target waves with a localized stimulus. Phys. Rev. E 72, 046206 (2005). [DOI] [PubMed] [Google Scholar]
- Agladze K., Kay M. W., Krinsky V. & Sarvazyan N. Interaction between spiral and paced waves in cardiac tissue. Am. J. Physiol. Heart Circ. Physiol. 293, H503–H513 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isomura A., Hörning M., Agladze K. & Yoshikawa K. Eliminating spiral waves pinned to an anatomical obstacle in cardiac myocytes by high-frequency stimuli. Phys. Rev. E 78, 066216 (2008). [DOI] [PubMed] [Google Scholar]
- Tanaka M. et al. Unpinning of a spiral wave anchored around a circular obstacle by an external wave train: Common aspects of a chemical reaction and cardiomyocyte tissue. Chaos 19, 043114 (2009). [DOI] [PubMed] [Google Scholar]
- Hörning M., Isomura A., Jia Z., Entcheva E. & Yoshikawa K. Utilizing the eikonal relationship in strategies for reentrant wave termination in excitable media. Phys. Rev. E 81, 056202 (2010). [DOI] [PubMed] [Google Scholar]
- Pumir A. et al. Wave-train-induced termination of weakly anchored vortices in excitable media. Phys. Rev. E 81, 010901 (R) (2010). [DOI] [PubMed] [Google Scholar]
- Gao X. & Zhang H. Mechanism of unpinning spirals by a series of stimuli. Phys. Rev. E 89, 062928 (2014). [DOI] [PubMed] [Google Scholar]
- Pumir A. et al. Wave emission from heterogeneities opens a way to controlling chaos in the heart. Phys. Rev. Lett. 99, 208101 (2007). [DOI] [PubMed] [Google Scholar]
- Fenton F. H. et al. Termination of atrial fibrillation using pulsed low-energy far-field stimulation. Circulation 120, 467–476 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luther S. et al. Low-energy control of electrical turbulence in the heart. Nature 475, 235–239 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yilmaz E., Baysal V., Ozer M. & Perc M. Autaptic pacemaker mediated propagation of weak rhythmic activity across small-world neuronal networks. Physica A 444, 538–546 (2016). [Google Scholar]
- Ma J., Song X. L., Tang J. & Wang C. N. Wave emitting and propagation induced by autapse in a forward feedback neuronal network. Neurocomputing 167, 378–389 (2015). [Google Scholar]
- Sepulveda N. G., Roth B. J. & Wikswo J. P. Current injection into a two-dimensional anisotropic bidomain. Biophys. J. 55, 987–999 (1989). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sobie E. A., Susil R. C. & Tung L. A generalized activating function for predicting virtual electrodes in cardiac tissue. Biophys. J. 73, 1410–1423 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fishler M. G. Syncytial heterogeneity as a mechanism underlying cardiac far-field stimulation during defibrillation-level shocks. J. Cardiovasc. Electr. 9, 384–394 (1998). [DOI] [PubMed] [Google Scholar]
- Fast V. G., Rohr S., Gillis A. M. & Kléber A. G. Activation of cardiac tissue by extracellular electrical shocks: Formation of ‘secondary sources’ at intercellular clefts in monolayers of cultured myocytes. Circ. Res. 82, 375–385 (1998). [DOI] [PubMed] [Google Scholar]
- Trayanova N. & Skouibine K. Modeling defibrillation-Effects of fiber curvature. J. Electrocardiol. 31, 23–29 (1998). [DOI] [PubMed] [Google Scholar]
- Hooks D. A. et al. Cardiac microstructure: Implications for electrical propagation and defibrillation in the heart. Circ. Res. 91, 331–338 (2002). [DOI] [PubMed] [Google Scholar]
- Woods M. C. et al. Virtual electrode effects around an artificial heterogeneity during field stimulation of cardiac tissue. Heart Rhythm 3, 751–752 (2006). [DOI] [PubMed] [Google Scholar]
- Pumir A. & Krinsky V. Unpinning of a rotating wave in cardiac muscle by an electric field. J. Theor. Biol. 199, 311–319 (1999). [DOI] [PubMed] [Google Scholar]
- Takagi S. et al. Unpinning and removal of a rotating wave in cardiac muscle. Phys. Rev. Lett. 93, 058101 (2004). [DOI] [PubMed] [Google Scholar]
- Ripplinger C. M., Krinsky V. I., Nikolski V. P. & Efimov I. R. Mechanisms of unpinning and termination of ventricular tachycardia. Am. J. Physiol. Heart Circ. Physiol. 291, H184–H192 (2006). [DOI] [PubMed] [Google Scholar]
- Cysyk J. & Tung L. Electric field perturbations of spiral waves attached to millimeter-size obstacles. Biophys. J. 94, 1533–1541 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bittihn P. et al. Far field pacing supersedes anti-tachycardia pacing in a generic model of excitable media. New J. Phys. 10, 103012 (2008). [Google Scholar]
- Bittihn P. et al. Phase-resolved analysis of the susceptibility of pinned spiral waves to far-field pacing in a two-dimensional model of excitable media. Phil. Trans. R. Soc. A 368, 2221–2236 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai M. C., Pan J. T. & Zhang H. Electric-field-sustained spiral waves in subexcitable media. Phys. Rev. E 86, 016208 (2012). [DOI] [PubMed] [Google Scholar]
- Li B. W., Deng L. Y. & Zhang H. Chiral symmetry breaking in a reaction-diffusion system. Phys. Rev. E 87, 042905 (2013). [DOI] [PubMed] [Google Scholar]
- Li B. W., Cai M. C., Zhang H., Panfilov A. V. & Dierckx H. Chiral selection and frequency response of spiral waves in reaction-diffusion systems under a chiral electric field. J. Chem. Phys. 140, 184901 (2014). [DOI] [PubMed] [Google Scholar]
- Ji L., Zhou Y., Li Q., Qiao C. & Ouyang Q. Experimental evidence of using a circularly polarized electric field to control spiral turbulence. Phys. Rev. E 88, 042919 (2013). [DOI] [PubMed] [Google Scholar]
- Feng X., Gao X., Pan D. B., Li B. W. & Zhang H. Unpinning of rotating spiral waves in cardiac tissues by circularly polarized electric fields. Sci. Rep. 4, 04831 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiménez Z. A., Zhang Z. H. & Steinbock O. Electric-field-controlled unpinning of scroll waves. Phys. Rev. E 88, 052918 (2013). [DOI] [PubMed] [Google Scholar]
- Das N. P., Mahanta D. & Dutta S. Unpinning of scroll waves under the influence of a thermal gradient. Phys. Rev. E 90, 022916 (2014). [DOI] [PubMed] [Google Scholar]
- Barkley D. A model for fast computer simulation of waves in excitable media. Physica D 49, 61–70 (1991). [Google Scholar]
- Bittihn P. Complex Structure and Dynamics of the Heart (Springer International Publishing, 2014). [Google Scholar]