FETI Methods for the Simulation of Biological Tissues

Summary

In this paper we describe the application of finite element tearing and interconnecting methods for the simulation of biological tissues, as a particular application we consider the myocardium. As most other tissues, this material is characterized by anisotropic and nonlinear behavior.

1 Modeling Biological Tissues

In this paper we consider the numerical simulation of biological tissues, that can be described by the stationary equilibrium equations

$$\text{div}\sigma (u,x)+f(x)=0\text{for}x\in \Omega \subset {\mathbb{R}}^3,$$ (1)

to find a displacement field u where we have to incorporate boundary conditions to describe the displacements or the boundary stresses on Γ = ∂Ω.

In the case of biological tissues the material is assumed to be hyperelastic, i.e. we have to incorporate large deformations and a non-linear stress-strain relation. For the derivation of the constitutive equation we introduce the strain energy function Ψ (C) which represents the elastic stored energy per unit reference volume. From this we obtain the constitutive equation as in [1]

$$\sigma =J^{-1}\mathrm{F}\frac{\partial \Psi (\mathrm{C})}{\partial \mathrm{C}}{\mathrm{F}}^{⊺},$$

where J = det F is the Jacobian of the deformation gradient F = ∇φ, and C = F^⊤ F is the right Cauchy-Green tensor. In what follows we make use of the Rivlin-Ericksen representation theorem to find a representation of the strain energy function Ψ in terms of the principal invariants of C = F^⊤ F.

The cardiac muscle, the so-called myocardium, is the most significant layer for the modeling of the elastic behavior of the heart wall. Muscle fibers are arranged in parallel, in different sheets within the tissue. Although this fiber type is predominant, we have also collagen that is arranged in a spatial network connecting the muscle fibers. We denote by f₀ the fiber axis which is referred to as the main direction of the cardiac muscle fibers. The sheet axis s₀ is defined to be perpendicular to f₀ in the plane of the layer. This direction coincides with the collagen fiber orientation. As many other biological tissues we treat the myocardium as a nearly incompressible material. It shows a highly nonlinear and, due to the muscle and collagen fibers, an anisotropic behavior.

To capture the specifics of this fiber-reinforced composite, Holzapfel and Ogden proposed a strain-energy function Ψ that is decomposed into a volumetric, an isotropic and an anisotropic part, which consists of a transversely isotropic and an orthotropic response, see [7, 11],

$$\Psi (\mathrm{C})={\Psi }_{\text{vol}}(J)+{\Psi }_{\text{iso}}(\mathrm{C})+{\Psi }_{\text{trans}}(\mathrm{C},{\mathbf{f}}_0)+{\Psi }_{\text{trans}}(\mathrm{C},{\mathbf{s}}_0)+{\Psi }_{\text{ortho}}(\mathrm{C},{\mathbf{f}}_0,{\mathbf{s}}_0).$$ (2)

Following [11], we describe the volume changing part by

$${\Psi }_{\text{vol}}\left(J\right)=\frac{\kappa }{2}{\left(\log J\right)}^2.$$ (3)

The bulk modulus κ > 0 serves as a penalty parameter to enforce the (almost) incompressibility constraint. To model the isotropic ground substance we use a classical exponential model, see [2],

$${\Psi }_{\text{iso}}\left(\mathrm{C}\right)=\frac{a}{2b}\left\{\exp \left[b\right(J^{-2∕3}{I}_1-3\left)\right]-1\right\},$$ (4)

where a > 0 is a stress-like and b is a dimensionless material parameter. I₁ = tr(C) is the first principal invariant of the right Cauchy-Green tensor C. In (2), Ψ_trans is associated with the deformations in direction of the fiber directions. Following [7] we describe the transversely isotropic response by using

$$\begin{array}{cc}\hfill {\Psi }_{\text{trans}}\left(\mathrm{C},{\mathbf{f}}_0\right)& =\frac{a_f}{2b_f}\left\{\exp [b_f{(J^{-2∕3}{I}_{4f}-1)}^2]-1\right\},\hfill \\ \hfill {\Psi }_{\text{trans}}\left(\mathrm{C},{\mathbf{s}}_0\right)& =\frac{a_s}{2b_s}\left\{\exp [b_s{(J^{-2∕3}{I}_{4s}-1)}^2]-1\right\},\hfill \end{array}$$ (5)

with the invariants I_4f := f₀ · (Cf₀) and I_4s := s₀ (Cs₀) and the material parameters a_f, b_f, a_s and a_f which are all assumed to be positive. It is worth to mention, that in this model the transversely isotropic responses Ψ_trans only contribute in the cases I_4f > 1, I_4s > 1, respectively. This corresponds to a stretch in a fiber direction, and this is explained by the wavy structure of the muscle and collagen fibers. In particular, the fibers are not able to support compressive stress. Moreover, the fibers are not active at low pressure, and the material behaves isotropically in this case. In contrast, at high pressure the collagen and muscle fibers straighten and then they govern the resistance to stretch of the material. This behavior of biological tissues was observed in experiments and this is fully covered by the myocardium model as described above. The stiffening effect at higher pressure also motivates the use of the exponential function in the anisotropic responses of the strain energy Ψ.

Finally a distinctive shear behavior motivates the inclusion of an orthotropic part in the strain energy function in terms of the invariant I_8fs = f₀ · (Cs₀)

$${\Psi }_{\text{ortho}}\left(\mathrm{C}\right)=\frac{a_{\mathit{fs}}}{2b_{\mathit{fs}}}\left\{\exp \left(b_{\mathit{fs}}{J}^{-2∕3}{I}_{8\mathit{fs}}^2\right)-1\right\}.$$ (6)

Here a_fs > 0 is a stress-like and b_fs > 0 a dimensionless material constant.

Note that the material parameters can be fitted to an experimentally observed response of the biological tissue. In the case of the myocardium, experimental data and, consequently, parameter sets are very rare. Following [7] and [11], we use the slightly adapted material parameters to be found in Table 1.

Table 1.

Material parameters used in the numerical experiments [7, 11].

κ = 3333.33 kPa,	a = 33.445 kPa,	b = 9.242 (−),
af = 18.535 kPa,	bs = 10.446 (−),	bf = 15.972 (−),
afs = 0.417 kPa,	as = 2.564 kPa,	bfs = 11.602 (−).

Note that similar models can also be used for the description of other biological materials, e.g., arteries, cf. [6, 8].

2 Finite Element Approximation

In this section we consider the variational formulation of the equilibrium equations (1) with Dirichlet boundary conditions u = g_D on Γ_D, Neumann boundary conditions t := σ (u)n = g_N on Γ_N, $\Gamma ={\overline{\Gamma }}_D\cup {\overline{\Gamma }}_N$, Γ_D ∩ Γ_N = θ and n is the exterior normal vector of Γ = ∂Ω. In particular we have to find u ∈ [H¹(Ω)]³, u = g_D on Γ_D, such that

$$a\left(u,v\right)≔{\int }_{\Omega }\sigma \left(u\right):\mathrm{e}\left(v\right)\mathit{dx}={\int }_{\Omega }f\cdot v\mathit{dx}+{\int }_{{\Gamma }_N}{g}_N\cdot v{\mathit{ds}}_x≕F\left(v\right)$$ (7)

is satisfied for all v ∈ [H¹(Ω)]³, v = 0 on Γ_D.

By introducing an admissible decomposition of the computational domain Ω into tetrahedra and by using piecewise quadratic basis functions φ_ℓ, the Galerkin finite element discretization of the variational formulation (7) results in a nonlinear system of algebraic equations, to find u_h satisfying an approximate Dirichlet boundary condition u_h = Q_hg_D on Γ_D, and

$$K_{\ell }\left(u_h\right)={\int }_{\Omega }\sigma \left(u_h\right):\mathrm{e}\left({\phi }_{\ell }\right)\mathit{dx}={\int }_{\Omega }f\cdot {\phi }_{\ell }\mathit{dx}+{\int }_{{\Gamma }_N}{g}_N\cdot {\phi }_{\ell }{\mathit{ds}}_x=F_{\ell }.$$ (8)

For the solution of the nonlinear system (8), i.e. of G(u_h) := K(u_h) − F = 0, we apply Newton’s method to obtain the recursion

$$u_h^{k+1}=u_h^k+\Delta u_h^k,{\mathrm{G}}_h^{\prime }\left(u_h^k\right)\Delta u_h^k=-G\left(u_h^k\right),$$

or, by using the definition of G(·),

$$u_h^{k+1}=u_h^k+\Delta u_h^k,{\mathrm{K}}_h^{\prime }\left(u_h^k\right)\Delta u_h^k=-K\left(u_h^k\right).$$ (9)

For the computation of the linearized stiffness matrix ${\mathrm{K}}_h^{\prime }\left(u_h^k\right)$ we need to evaluate the derivative of the nonlinear material model as described in the previous section. For a detailed presentation how to compute ${\mathrm{K}}_h^{\prime }\left(u_h^k\right)$ in this particular case, see [5].

3 Finite Element Tearing and Interconnecting

For the parallel solution of (9) we will use a finite element tearing and interconnecting approach [4], see also [8, 14] and references given therein. For a bounded domain $\Omega \subset {\mathbb{R}}^3$ we introduce a non-overlapping domain decomposition

$$\overline{\Omega }=\bigcup _{i=1}^p{\overline{\Omega }}_i\text{with}{\Omega }_i\cap {\Omega }_j=\varnothing \text{for}i\ne j,{\Gamma }_i=\partial {\Omega }_i.$$ (10)

The local interfaces are given by Γ_ij := Γ_i ∩ Γ_j for all i < j. The skeleton of the domain decomposition (10) is denoted as

$${\Gamma }_C≔\bigcup _{i=1}^p{\Gamma }_i=\Gamma \cup \bigcup _{i<j}{\overline{\Gamma }}_{\mathit{ij}}.$$

Instead of the global problem (1) we now consider local subproblems to find the local restrictions u_i = u_∣Ωi satisfying partial differential equations

$$\text{div}\left(\sigma \left(u_i\right)\right)+f\left(x\right)=0\text{for}x\in {\Omega }_i,$$

the Dirichlet and Neumann boundary conditions u_i = g_D on Γ_i ∩ Γ_D, σ (u_i)n_i = g_N on Γ_i ∩ Γ_N, and the transmission conditions u_i = uj, t_i + tj = 0 on Γ_ij, where t_i = σ (u_i)n_i is the local boundary stress, and n_i is the exterior normal vector of the local subdomain boundary Γ_i = ∂Ω_i. Note that the local stress tensors σ (u_i) are defined locally by using the stress-strain function Ψ as introduced in Sect. 1, and by using localized parameters κ,k₁,k₂,c and fiber directions β₁, β₂. Hence, by reordering the degrees of freedom, the linearized system (9) can be written as

$$\left(\begin{array}{cccc}\hfill {\mathrm{K}}_{11}^{\prime }\left(u_{1,h}^k\right)\hfill & \hfill \hfill & \hfill \hfill & \hfill {\mathrm{K}}_{1C}^{\prime }\left(u_{1,h}^k\right){\mathrm{A}}_1\hfill \\ \hfill \hfill & \hfill \cdot \hfill & \hfill \hfill & \hfill \cdot \hfill \\ \hfill \hfill & \hfill \hfill & \hfill K_{\mathit{pp}}^{\prime }\left(u_{p,h}^k\right)\hfill & \hfill {\mathrm{K}}_{\mathit{pC}}^{\prime }\left(u_{p,h}^k\right){\mathrm{A}}_p\hfill \\ \hfill {\mathrm{A}}_1^{⊺}{\mathrm{K}}_{C1}^{\prime }\left(u_{1,h}^k\right)\hfill & \hfill \cdot \hfill & \hfill {\mathrm{A}}_p^{⊺}{\mathrm{K}}_{\mathit{Cp}}^{\prime }\left(u_{p,h}^k\right)\hfill & \hfill \sum _{i=1}^p{\mathrm{A}}_i^{⊺}{\mathrm{K}}_{\mathit{CC}}^{\prime }\left(u_{i,h}^k\right){\mathrm{A}}_i\hfill \end{array}\right)\left(\begin{array}{c}\hfill \Delta {\mathbf{u}}_{1,I}^k\hfill \\ \hfill \cdot \hfill \\ \hfill \Delta {\mathbf{u}}_{p,I}^k\hfill \\ \hfill \Delta {\mathbf{u}}_C^k\hfill \end{array}\right)=-\left(\begin{array}{c}\hfill {\mathrm{K}}_1\left(u_{1,h}^k\right)\hfill \\ \hfill \cdot \hfill \\ \hfill {\mathrm{K}}_p\left(u_{p,h}^k\right)\hfill \\ \hfill \sum _{i=1}^p{\mathrm{A}}_i^{⊺}{\mathrm{K}}_C\left(u_{i,h}^k\right)\hfill \end{array}\right),$$

where the increments $\Delta {\mathbf{u}}_{i,I}^k$ correspond to the local degrees of freedom within the subdomain Ω_i, and $\Delta {\mathbf{u}}_C^k$ is related to all global degrees of freedom on the coupling boundary Γ_C. By introducing the tearing

$${\mathbf{w}}_i=\left(\begin{array}{c}\hfill \Delta {\mathbf{u}}_{i,I}^k\hfill \\ \hfill {\mathrm{A}}_i\Delta {\mathbf{u}}_C^k\hfill \end{array}\right),{\mathrm{K}}_i^{\prime }=\left(\begin{array}{cc}\hfill {\mathrm{K}}_{\mathit{ii}}^{\prime }\left(u_{i,h}^k\right)\hfill & \hfill {\mathrm{K}}_{\mathit{iC}}^{\prime }\left(u_{i,h}^k\right)\hfill \\ \hfill {\mathrm{K}}_{\mathit{Ci}}^{\prime }\left(u_{i,h}^k\right)\hfill & \hfill {\mathrm{K}}_{\mathit{CC}}^{\prime }\left(u_{i,h}^k\right)\hfill \end{array}\right),{\mathbf{f}}_i=-\left(\begin{array}{c}\hfill {\mathrm{K}}_i\left(u_{i,h}^k\right)\hfill \\ \hfill {\mathrm{K}}_C\left(u_{i,h}^k\right)\hfill \end{array}\right),$$

by applying the interconnecting $\sum _{i=1}^p{\mathrm{B}}_i{\mathbf{w}}_i=0$, and by using discrete Lagrange multipliers, we finally have to solve the system

$$\left(\begin{array}{cccc}\hfill {\mathrm{K}}_1^{\prime }\hfill & \hfill \hfill & \hfill \hfill & \hfill {\mathrm{B}}_1^{⊺}\hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill ⋮\hfill \\ \hfill \hfill & \hfill \hfill & \hfill {\mathrm{K}}_p^{\prime }\hfill & \hfill {\mathrm{B}}_p^{⊺}\hfill \\ \hfill {\mathrm{B}}_1\hfill & \hfill \cdots \hfill & \hfill {\mathrm{B}}_p\hfill & \hfill \hfill \end{array}\right)\left(\begin{array}{c}\hfill {\mathbf{w}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{w}}_p\hfill \\ \hfill \lambda \hfill \end{array}\right)=\left(\begin{array}{c}\hfill {\mathbf{f}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{f}}_p\hfill \\ \hfill 0\hfill \end{array}\right).$$ (11)

For the solution of the linear system (11) we follow the standard approach of tearing and interconnecting methods. In the case of a floating subdomain Ω_i, i.e. Γ_i ∩ Γ_D = θ, the local matrices ${\mathrm{K}}_i^{\prime }$, are not invertible. Hence we introduce the Moore-Penrose pseudo inverse ${\mathrm{K}}_i^{†}$ to represent the local solutions as

$${\mathbf{w}}_i={\mathrm{K}}_i^{†}({\mathbf{f}}_i-{\mathrm{B}}_i^{⊺}\lambda )+\sum _{k=1}^6{\gamma }_{k,i}{\mathbf{v}}_{k,i},$$ (12)

where v_k,i ∈ ker ${\mathrm{K}}_i^{\prime }$ correspond to the rigid body motions of elasticity. Note that in this case we also require the solvability conditions

$$({\mathbf{f}}_i-{\mathrm{B}}_i^{⊺}\lambda ,{\mathbf{v}}_{k,i})=0\text{for}i=1,\dots ,6.$$

In the case of a non-floating subdomain, i.e. ker K_i = θ, we may set ${\mathrm{K}}_i^{†}={\mathrm{K}}_i^{-1}$. As in [10] we may also consider an all-floating approach where also Dirichlet boundary conditions are incorporated by using discrete Lagrange multipliers.

In general, we consider the Schur complement system of (11) to obtain

$$\sum _{i=1}^p{\mathrm{B}}_i{\mathrm{K}}_i^{†}{\mathrm{B}}_i^{⊺}\lambda -\sum _{i=1}^p\sum _{k=1}^6{\gamma }_{k,i}{\mathrm{B}}_i{\mathbf{v}}_{k,i}=\sum _{i=1}^p{\mathrm{B}}_i{\mathrm{K}}_i^{†}{\mathbf{f}}_i,({\mathbf{f}}_i-{\mathrm{B}}_i^{⊺}\lambda ,{\mathbf{v}}_{k,i})=0,$$

which can be written as

$$\left(\begin{array}{cc}\hfill \mathrm{F}\hfill & \hfill -\mathrm{G}\hfill \\ \hfill {\mathrm{G}}^{⊺}\hfill & \hfill \hfill \end{array}\right)\left(\begin{array}{c}\hfill \lambda \hfill \\ \hfill \gamma \hfill \end{array}\right)=\left(\begin{array}{c}\hfill \mathbf{d}\hfill \\ \hfill \mathbf{e}\hfill \end{array}\right)$$ (13)

with

$$\mathrm{F}=\sum _{i=1}^p{\mathrm{B}}_i{\mathrm{K}}_i^{†}{\mathrm{B}}_i^{⊺},\mathrm{G}=\sum _{i=1}^p\sum _{k=1}^6{\mathrm{B}}_i{\mathbf{v}}_{k,i},\mathbf{d}=\sum _{i=1}^p{\mathrm{B}}_i{\mathrm{K}}_i^{†}{\mathbf{f}}_i,e_{k,i}=\left({\mathbf{f}}_i,{\mathbf{v}}_{k,i}\right).$$

For the solution of the linear system (13) we use the projection P^⊤ := I−G(G^⊤G)⁻¹G^⊤ and it remains to consider the projected system

$${\mathrm{P}}^{⊺}\mathrm{F}\lambda ={\mathrm{P}}^{⊺}\mathbf{d}$$ (14)

which can be solved by using a parallel GMRES method with suitable preconditioning. Note that the initial approximate solution λ⁰ satisfies the compatibility condition G^⊤ λ⁰ = e. In a post processing we finally recover γ = (G^⊤ G)⁻¹G^⊤ (Fλ − d), and subsequently the desired solution (12).

Following [3] we are going to apply either the lumped preconditioner

$${\mathrm{PM}}^{-1}≔\sum _{i=1}^p{\mathrm{B}}_i{\mathrm{K}}_i^{\prime }{\mathrm{B}}_i^{⊺},$$ (15)

or the Dirichlet preconditioner

$${\mathrm{PM}}^{-1}≔\sum _{i=1}^p{\mathrm{B}}_i\left(\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathrm{S}}_i\hfill \end{array}\right){\mathrm{B}}_i^{⊺},$$ (16)

where

$${\mathrm{S}}_i={\mathrm{K}}_{\mathit{CC}}^{\prime }\left(u_{i,h}^k\right)-{\mathrm{K}}_{\mathit{Ci}}^{\prime }\left(u_{i,h}^k\right){\mathrm{K}}_{\mathit{ii}}^{\prime -1}\left(u_{i,h}^k\right){\mathrm{K}}_{\mathit{iC}}^{\prime }\left(u_{i,h}^k\right)$$

is the Schur complement of the local finite element matrix ${\mathrm{K}}_i^{\prime }$. Alternatively, one may also use the scaled hypersingular boundary integral operator preconditioner as proposed in [9].

4 Numerical Results

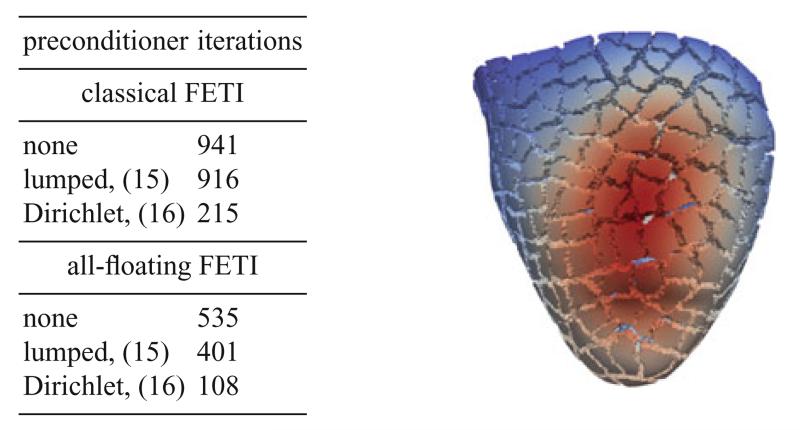
In this section we present some examples to show the applicability of the FETI approach for the simulation of the myocardium, see Fig. 3. We consider a mesh of the left and the right ventricle of a rabbit heart with given fiber and sheet directions, see Fig. 1, which is decomposed in 480 subdomains, see Fig. 2. To describe the anisotropic and nonlinear cardiac tissue, we use the material model (2) with the parameters given in Table 1. Dirichlet boundary conditions are imposed on the top of the myocardium mesh. The interior wall of the right ventricle is exposed to the pressure of 1 mmHg which is modeled with Neumann boundary conditions. Although this pressure is rather low, the material model as used is orthotropic. To simulate a higher pressure, an appropriate time stepping scheme has to be used. However, this does not affect the number of local iterations significantly. The local Moore Penrose pseudo inverse matrices are realized with a sparsity preserving regularization and the direct solver package Pardiso [12, 13]. The global nonlinear finite element system with 12.188.296 degrees of freedom is solved by a Newton scheme, where the FETI approach is used in each Newton step. For this specific example the Newton scheme needed six iterations. Due to the non-uniformity of the subdomains the efficiency of a global preconditioner becomes more important. We consider both the classical FETI approach, as well as the all–floating formulation. Besides no preconditioning we use the simple lumped preconditioner (15) and the Dirichlet preconditioner (16). It turns out that the number of iterations for the all–floating formulation is approximately half the number of iterations for the standard approach. Moreover, the Dirichlet preconditioner within the all–floating formulation requires only 108 iterations, with a computing time of approximately 5 min. All computations were done at the Vienna Scientific Cluster (VSC2).

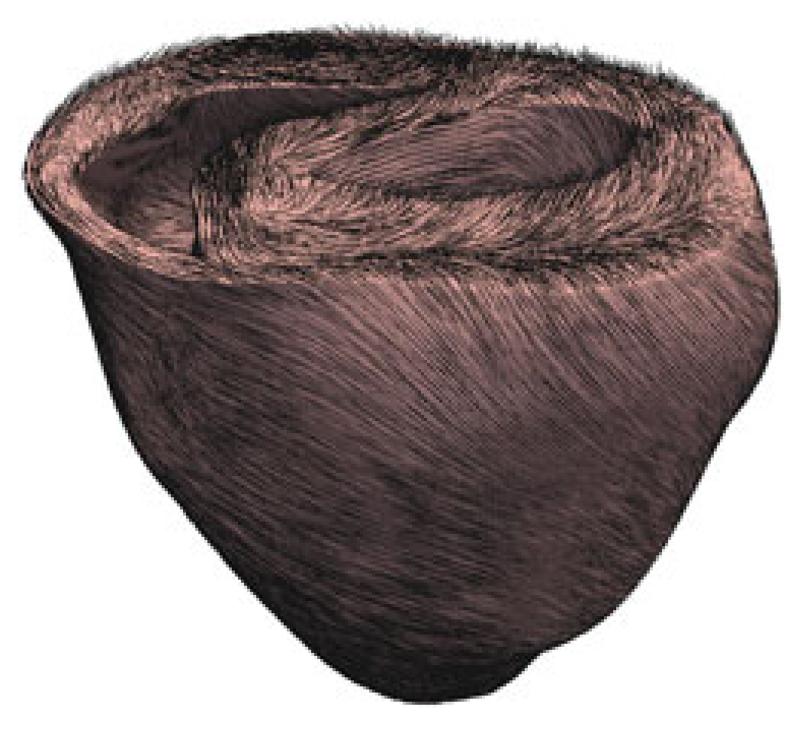
Fig. 1.

Left and right ventricle of the rabbit heart. Mesh consists of 3.073.529 tetrahedrons and 547.680 vertices. Black lines indicate fiber directions f₀. Point of view is from above showing the interior of the left and right ventricle

Fig. 2.

The picture shows the displacement field of the rabbit heart with pressure applied in the right ventriculum. Point of view is from below showing the apex of the heart at the bottom. In the table the iteration numbers of the global GMRES method for different preconditioners are given

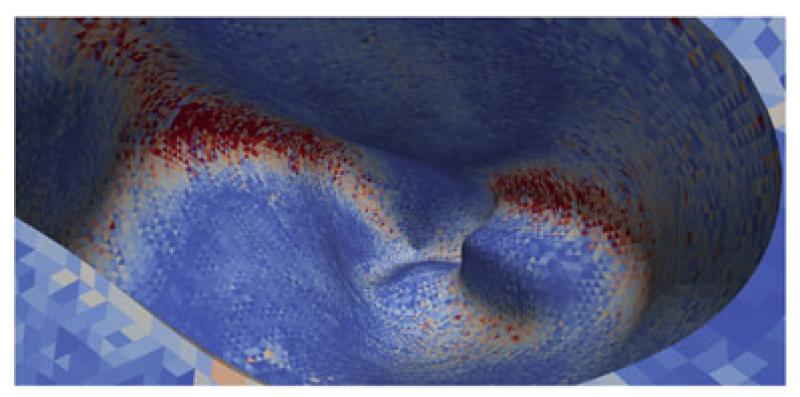
Fig. 3.

Von Mises stress in the right ventricle. Point of view is from above looking inside the right ventricle