Correcting for Brain Swelling’s Effects on Infarct Volume Calculation After Middle Cerebral Artery Occlusion in Rats

Abstract

Evaluating infarct volume is the primary outcome for experimental ischemic stroke studies and is a major factor in determining translation of a drug into clinical trials. Numerous algorithms are available for evaluating this critical value, but a major limitation of current algorithms is that brain swelling is not appropriately considered. The model by Lin et al. is widely used, but overestimates swelling within the infarction, yielding infarct volumes which do not reflect the true infarct size. Herein, a new infarct volume algorithm is developed to minimize the effects of both peri-infarct and infarct core swelling on infarct volume measurement. 2,3,5-Triphenyl-2H-tetrazolium chloride-stained brain tissue of adult rats subjected to middle cerebral artery occlusion was used for infarct volume analysis. When both peri-infarct swelling and infarction core swelling are removed from infarct volume calculations, such as accomplished by our algorithm, larger infarct volumes are estimated than those of Lin et al.’s algorithm. Furthermore, the infarct volume difference between the two algorithms is the greatest for small infarcts (<10 % of brain volume) when peri-infarct swelling is the greatest. Finally, using data from four published studies, our algorithm is compared to Lin et al.’s algorithm. Our algorithm offers a more reliable estimation of the infarct volume after ischemic brain injury, and thus may provide the foundation for comparing infarct volumes between experimental studies and standardizing infarct volume quantification to aid in the selection of the best candidates for clinical trials.

Introduction

Preclinical studies investigating potential therapeutics for stroke critically rely on infarct volume quantification to justify advancing to clinical trials [1, 2]. To date, a variety of methods have been developed for evaluating the sizes of infarctions in experimental stroke models [3–11]; the most popular method is histological analysis, such as staining with 2,3,5-triphenyl-2H-tetrazolium chloride (TTC). TTC is one of the most commonly used stains for infarction visualization and relies on an algorithm to calculate infarct volume.

While a number of algorithms exist for measuring the infarct size of TTC-stained brains, the gold standard is the algorithm by Lin et al. [12]. Their algorithm utilizes the difference between the areas of the non-infarcted ipsilesional hemisphere and the contralesional hemisphere to correct for brain swelling [12]. However, Lin et al. base their swelling correction on the assumption that swelling occurs only in the infarcted tissue [12]. Thus, it follows that if only the infarct swells, then the non-ischemic ipsilesional tissue is the true size, so the difference between the contralesional tissue and non-ischemic ipsilesional tissue yields the size of the infarct devoid of swelling. Yet, this assumption makes Lin et al.’s algorithm vulnerable to artifacts, the most salient of which is changes in ipsilesional hemisphere swelling.

Brain swelling accompanies infarction, beginning within hours of infarct appearance [13–15], and is known to affect the apparent volume of infarction, accounting for up to 30 % of the observed infarct volume [16]. Additionally, drugs which are purported to reduce infarction size may actually decrease swelling via edema reduction, thus seemingly producing smaller infarcts. Therefore, is it critical for an infarct volume algorithm to adequately remove the effects of cerebral swelling on infarct estimation. While current algorithms remove the effects of infarct core swelling, peri-infarct swelling is not adequately considered.

Herein, we develop a novel algorithm for calculating infarct volume which (1) relaxes the assumptions of previous algorithms and (2) reduces the effects of brain swelling on infarct volume measurement. Our algorithm relies on the ratio of infarction to the ipsilesional hemisphere, then adjusted using the area of the contralesional hemisphere, to minimize the effects of peri-infarct and infarct core swelling on infarction calculation. Our algorithm is compared to the algorithm by Lin et al. [12] using brain tissue samples from rats subjected to middle cerebral artery occlusion. The use of our algorithm is also investigated using four previously published studies to identify differences in the reported effects of the therapeutics examined. Additionally, the advantages, applications, and limitations of our algorithm are discussed. Finally, the potential of our algorithm to change basic science translational studies, as well as selection of drug candidates for clinical trials, is considered.

Materials and Methods

All experiments were approved by Loma Linda University Institutional Animal Care and Use Committee. One hundred one adult male Sprague-Dawley rats (270–310 g) were subjected to middle cerebral artery occlusion (MCAO, n=101).

Middle Cerebral Artery Occlusion Model

Adult male Sprague-Dawley rats were subjected to 2 h of middle cerebral artery occlusion as previously described [17]. Animals were anesthetized with an intraperitoneal injection mixture of ketamine (80 mg/kg) and xylazine (20 mg/kg). After reaching an adequate plane of anesthesia, determined by loss of paw pinch reflex, surgery began.

Briefly, animals were placed supine, then the right common, internal, and external carotid arteries were surgically exposed and isolated. The external carotid artery was ligated leaving a 3–4-mm stump. The pterygopalatine artery was ligated close to its origin with the internal carotid artery, then a vascular clip was placed on the internal carotid artery and another was placed on the common carotid artery. The stump of the external carotid artery was reopened and a 4.0 monofilament nylon suture with a rounded tip was inserted up through the internal carotid artery and stopped when resistance was felt. The suture remained in place for 2 h, after which the suture was removed, beginning reperfusion. The stump of the external carotid artery was then ligated, and the skin was sutured.

Twenty-four hours after reperfusion, deeply anesthetized animals were sacrificed and the brains were removed, sectioned into 2-mm-thick slices, and placed into 2 % TTC for 15 min at room temperature. TTC-stained slices were photographed.

Quantifying Ipsilesional Swelling

Twenty-four hours after MCAO, ipsilesional hemisphere swelling can be found by analyzing the difference between the ipsilesional and contralesional hemisphere volumes [18–20], or

$$\text{Ipsilateral Hemispheric Volume}(\%)=\left(\frac{\sum _i(I_i-C_i)}{\left(\sum _i{C}_i\right)}\right)100,$$ (1)

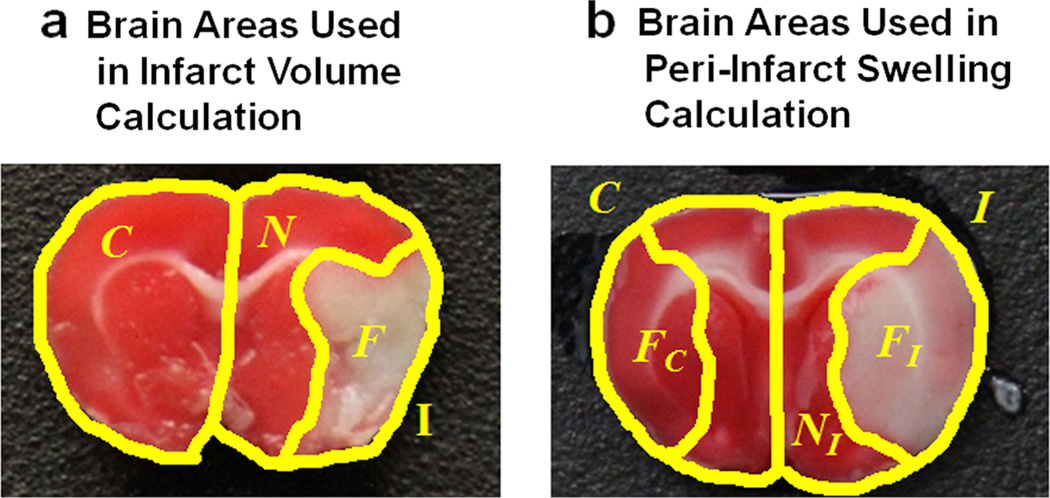
where I_i is the ipsilesional area of slice i and C_i is the contralesional area of slice i (Fig. 1a).

Fig. 1.

Representative brains showing the areas used in infarct volume and ipsilesional swelling calculations. a The areas of the contralesional hemisphere (C), ipsilesional hemisphere (I), non-infarcted ipsilesional hemisphere (N), and the infarcted ipsilesional hemisphere (F) which are used in infarct volume calculation are shown. b The areas of the contralesional hemisphere (C), ipsilesional hemisphere (I), non-infarcted ipsilesional hemisphere (N_I), and the infarcted ipsilesional hemisphere (F_I) which are used in peri-infarct swelling calculation are shown. Also shown is the area of the contralesional hemisphere which corresponds to the non-ischemic ipsilesional tissue (N_C) and the corresponding infarct (devoid of swelling) (F_C). When there is no peri-infarct swelling, then N_C=N_I and F_C<F_I. When peri-infarct swelling occurs, then N_C≠N_I

Evaluating Peri-infarct Swelling via the Difference in the Non-ischemic Hemisphere Volumes

In order to determine if peri-infarct swelling occurs within the non-ischemic tissue of the ipsilesional hemisphere, we compared the observed non-ischemic ipsilesional hemisphere tissue to a region reflected onto the contralesional hemisphere which represents the non-ischemic ipsilesional hemisphere area.

First, following Lin et al. ‘s algorithm development [12], we assumed that if no peri-infarct swelling occurs within the ipsilesional hemisphere tissue, then all of the ipsilesional swelling is associated with the infarction only. Second, we assumed that the contralesional tissue is its true size. In other words, the contralesional tissue is unaffected by either the infarction or swelling. Thus, the contralesional hemisphere offers ground truths for the true hemisphere areas/volume.

Therefore, following the above two assumptions, there exists two areas on the contralesional hemisphere which correspond to areas on the ipsilesional hemisphere. The first contralesional region corresponds to the non-ischemic ipsilesional hemisphere tissue. The second contralesional region corresponds to the infarct area which is devoid of all swelling. This logic follows that of Lin et al.’s infarct algorithm [12].

Since swelling is assumed to be only within the infarction, and no peri-infarct swelling exists, then the area/volume of the non-ischemic ipsilesional hemisphere (N_I) should equal the corresponding area/volume of the contralesional hemisphere (N_C), or N_C=N_I also follows the same logic as outlined by Lin et al. If the non-ischemic ipsilesional hemisphere contains peri-infarct swelling, then N_C≠N_I. Therefore, comparing the area/volume of the non-ischemic ipsilesional hemisphere to the corresponding contralesional hemisphere area/volume, the presence or absence of peri-infarct swelling can be determined.

The contralesional tissue corresponding to the nonischemic ipsilesional tissue is

$$N_C=\sum _i{C}_i-\sum _i{F}_{Ci}$$ (2)

where N_C is the volume of the contralesional tissue which corresponds to the non-ischemic ipsilesional area of slice i, C_i is the contralesional area of slice i, and F_Ci is the area of the corresponding infarct, without swelling, of slice i (Fig. 1b). While the contralesional areas are known, the area of the contralesional hemisphere which corresponds to the infarct without swelling is unknown, but can be determined assuming the ratio of the infarct to the ipsilesional hemisphere is unaffected by swelling, or

$$F_{Ci}=\left(\frac{I_i-N_i}{I_i}\right)C_i.$$ (3)

Therefore, Eq. 2 becomes

$$N_C=\sum _i{C}_i-\sum _i\left(\right(\frac{I_i-N_i}{I_i}\left)C_i\right).$$ (4)

To determine if peri-infarct swelling is present, the percent difference between the volumes of the non-ischemic ipsilesional hemisphere and that of the corresponding contralesional hemisphere is assessed, or

$$\text{Non-ischemic Volume}(\%\text{Difference})=\left(\frac{N_I-N_C}{N_C}\right)100$$ (5)

where N_I is the volume of the non-ischemic ipsilesional hemisphere and N_C is the volume of the contralesional hemisphere which correlates to that of the non-ischemic ipsilesional hemisphere and adjusted for volume differences. N_I is the sum of the non-ischemic ipsilesional areas within the ipsilesional hemisphere. If peri-infarct swelling is not present, then Eq. 5 will be zero.

Next, ipsilesional hemisphere swelling was separated into the amount of peri-infarct swelling and the amount of infarct core swelling. To determine the amount of swelling which is associated with the peri-infarct region and that which is associated with the infarction, the volumes of the non-ischemic ipsilesional tissue and the infarction were corrected and then used within the ipsilesional swelling model (Eq. 1).

To identify the amount of peri-infarct swelling, the ipsilesional hemisphere area (I_i in Eq. 1) is equal to the sum of the observed non-ischemic ipsilesional hemisphere area (in which swelling is present) and the corrected infarct area. For infarct core swelling, the ipsilesional hemisphere area is equal to the sum of the corrected non-ischemic ipsilesional hemisphere area (in which swelling is removed) and the observed infarct area. Peri-infarct swelling and infarct core swelling, respectively, are computed using

$$\text{Peri-infarct Swelling}(\%)=\left(\frac{\sum _i\left(\right(N_i+F_i^{’})-C_i)}{\sum _i{C}_i}\right)100$$ (6)

$$\text{Infarct Core Swelling}(\%)=\left(\frac{\sum _i\left(\right(N_i^{’}+F_i)-C_i)}{\sum _i{C}_i}\right)100$$ (7)

where C_i is the contralesional area of slice i, N_i is the observed non-ischemic ipsilesional area of slice i, and $N_i^{’}$ is the corrected non-ischemic ipsilesional area of slice i, F_i is the observed infarct area of slice i, and $F_i^{’}$ is the corrected infarct area of slice i. The ipsilesional area corrected for peri-infarct swelling, so that only infarct core swelling remains, is $(N_i^{’}+F_i)$. The ipsilesional area corrected for infarct core swelling, so that only peri-infarct edema remains, is $(N_i+F_i^{’})$. The corrected areas for the nonischemic ipsilesional and infarct areas, respectively, are

$$N_i^{’}=\left(\frac{N_i}{I_i}\right)C_i$$ (8)

and

$$F_i^{’}=\left(\frac{F_i}{I_i}\right)C_i$$ (9)

where F_i can be computed by taking the difference between the ipsilesional hemisphere and the non-ischemic area of the ipsilesional hemisphere, or (F_i=I_i–N_i).

Ipsilesional Swelling Statistical Analysis

The differences between the non-ischemic volume of the ipsilesional hemisphere and the corresponding adjusted non-ischemic volume of the contralesional hemisphere were presented as the mean±standard deviation (SD) and grouped based on infarct volume range. The infarct volume ranges, based on the infarct volumes computed using Lin et al.’s algorithm, were 0–10 % (n=25), 10–15 % (n=22), 15–20 % (n=20), 20–25 % (n=14), 25–30 % (n=13), and 30–40 % (n=7). The data was analyzed using one-way ANOVA with a Tukey post hoc test (GraphPad Prism 6, La Jolla, CA, USA).

The peri-infarct and infarct core swelling are presented as mean±SD and grouped based on infarct volume range [0–10 % (n=25), 10–15 % (n=22), 15–20 % (n=20), 20–25 % (n=14), 25–30 % (n=13), and 30–40 % (n=7)]. The data was analyzed using two-way ANOVA with a Sidak post hoc test [factor 1, infarct size; factor 2, swelling (peri-infarct vs. infarct core)] (GraphPad Prism 6, La Jolla, CA, USA).

Quantifying Infarct Volume

Lin et al.’s Algorithm for Calculating Infarct Volume

The indirect method for infarct volume of Lin et al.’s algorithm utilizes the area of the contralesional hemisphere, C_i, the area of the non-ischemic (healthy) tissue of the ipsilesional hemisphere, N_i, and the thickness of each brain slice, d. The infarct volume, expressed as a percent of the contralesional hemisphere volume, is [12]

$$\text{Infarct Volume}(\%)=\left(\frac{d\sum _i(C_i-N_i)}{d\sum _i{C}_i}\right)100,$$ (10)

where (C_i–N_i) is the swelling-corrected infarct area for slice i, $(d\sum _i(C_i-N_i))$ is the swelling-corrected infarct volume for the whole ipsilesional hemisphere, and $\left(d\sum _i{C}_i\right)$ is the volume of the contralesional hemisphere. Since the contralesional hemisphere is assumed to be the same size as the ipsilesional hemisphere before injury, the contralesional hemisphere is used to determine the percent of the hemisphere volume that is occupied by the infarction.

Typically, the thickness of each slice is equivalent for a given method, thus Eq. 10 can be reduced to

$$\text{Infarct Volume}(\%)=\left(\frac{\sum _i(C_i-N_i)}{\left(\sum _i{C}_i\right)}\right)100.$$ (11)

A slight modification of Lin et al. ‘s algorithm was made to compare the infarct volume to the whole brain, $\left(2\sum _i{C}_i\right)$, rather than a single hemisphere. This correction results in the version of Lin et al.’s algorithm which is utilized hereafter:

$$\text{Infarct Volume}(\%)=\left(\frac{\sum _i(C_i-N_i)}{2\sum _i{C}_i}\right)100.$$ (12)

Using the photographs of TTC-stained brain slices, the areas of the contralesional, C_i, ipsilesional, I_i, and nonischemic ipsilesional hemispheres, N_i, were traced (ImageJ 1.48, NIH) and the infarct volume from Lin et al.’s algorithm was computed (Eq. 12).

Development of Our Infarct Volume Algorithm

To better correct for the effects of brain hemisphere volume changes on infarct volume estimation, a new algorithm is developed. This algorithm relies on the ratio of the infarction to the whole ipsilesional hemisphere as an estimation of the infarct area.

First, the infarct area is calculated by taking the difference in the area of the ipsilesional hemisphere and the non-infarcted ipsilesional hemisphere tissue, N_i, for slice i, or (I_i-N_i). Taking this difference removes bias of the analyzer towards the infarct area. This difference (infarct area) is then normalized to the area of the ipsilesional hemisphere for slice i, yielding the fractional amount of the ipsilesional hemisphere which is infarcted per slice, or

$$\text{Fractional Amount of Infarcted Tissue per Slice}=\frac{I_i-N_i}{I_i},$$ (13)

where I_i is the ipsilesional hemisphere for slice i, N is the non-infarcted ipsilesional hemisphere tissue for slice i, and (I_i–N_i) is the infarct area for slice i.

To obtain the corrected area of the infarct, the fractional amount of infarcted tissue (Eq. 13) is multiplied by the area of the contralesional hemisphere for slice i (C_i), or

$$\text{Corrected Infarct Area per Slice}=\left(\frac{I_i-N_i}{I_i}\right)C_i.$$ (14)

The corrected infarct area is then summed over all slices and multiplied by the thickness of each slice, d. This yields the infarct volume, or

$$\text{Infract Volume}=d\sum _i\left(\right(\frac{I_i-N_i}{I_i}\left)C_i\right).$$ (15)

To determine the percentage of the whole brain which is infarcted, the infarct volume (Eq. 15) is divided by two times the volume of the contralesional hemisphere. Following the same logic as Lin et al.’s algorithm, since the thickness of each slice is typically the same, the thickness term in the numerator and denominator cancel out. After these modifications, the novel algorithm for computing infarct volume is

$$\text{Infarct Volume}(\%)=\left(\frac{\sum _i\left(\right(\frac{I_i-N_i}{I_i}\left)C_i\right)}{2\sum _i{C}_i}\right)100.$$ (16)

Using the photographs of TTC-stained brain slices, the areas of the contralesional, C_i, ipsilesional, I_i, and nonischemic ipsilesional hemispheres, N_i, were traced (ImageJ 1.48, NIH) and the infarct volume from our algorithm was computed (Eq. 16).

Infarct Volume Statistical Analysis

Data is presented as mean±SD. To analyze the infarct volumes computed for Lin et al.’s and our algorithms, the infarct volumes were grouped into infarct volume ranges [0–10 % (n=25), 10–15 % (n=22), 15–20 % (n=20), 20–25 % (n=14), 25–30 % (n=13), and 30–40 % (n=7)]. For each subject within these infarct volume ranges, our algorithm was used to estimate the infarcts. Two-way repeated measures ANOVA with Sidak post hoc test (factor 1, infarct size; factor 2, algorithm) was used to identify significance between the infarct volume ranges (intra-algorithm difference for the infarct volume ranges) and between the two algorithms used for computing infarct volume (inter-algorithm difference for each infarct volume range) (GraphPad Prism 6, La Jolla, CA, USA).

Bland-Altman plots were used to qualitatively examine the differences between the two algorithms for the infarct volume difference and the infarct volume ratio. The first Bland-Altman plot was created for the infarct volume difference between our algorithm and Lin et al.’s algorithm,

$$\text{Infarct Volume Difference}(\%)=(\text{Our Algorithm’s Infarct Volume}-\text{Lin et al.’s Algorithm’s Infarct Volume}),$$ (17)

and plotted against the average infarct volume between the two algorithms, or Average Infarct Volume (%)

$$\text{Average Infarct Volume}(\%)=\frac{(\text{Our Algorithm’s Infarct Volume}+\text{Lin et al.’s Algorithm’s Infarct Volume})}{2}.$$ (18)

A second Bland-Altman plot was created to examine the infarct volume ratio, Infarct Volume Ratio

$$\text{Infarct Volume Ratio}=\left(\frac{\text{Our Algorithm’s Infarct Volume}}{\text{Lin et al.’s Algorithm’s Infarct Volume}}\right).$$ (19)

The mean values of the infarct volume difference and the mean values of the infarct ratio were both determined for each infarct volume range. These were used to determine the mean value curve for the entire infarct volume spectrum using non-linear regression of the mean values (of infarct volume difference and of infarct ratio) for each infarct volume range (TableCurve 2D; Systat Software, San Jose, CA, USA). In a similar manner, the mean 95 % agreements (of infarct volume difference and of infarct ratio) were determined for each infarct volume range. These mean 95 % agreement values were used to determine the 95 % agreement curve for the entire infarct volume spectrum using non-linear regression of the mean values (of 95 % agreement for infarct volume difference and of 95 % agreement for infarct ratio) for each infarct volume range (TableCurve 2D; Systat Software, San Jose, CA, USA). One way-ANOVAs with Tukey post hoc tests were used to analyze the infarct volume difference and infarct volume ratio for the infarct volume ranges.

Published Data Used to Compare Our Algorithm and Lin et al.’s Algorithm

A PubMed search was performed to identify publications for which the data could be used as a comparison between Lin et al.’s algorithm and our algorithm. The search terms were “middle cerebral artery occlusion” AND “rats” with a publication date “2014” to “2015”. The search, performed on January 21, 2015, yielded 544 hits, of which 13 satisfied the inclusion criteria: adult Sprague-Dawley rats given food and water ad libitum, 2 h of MCAO using the intraluminal suture model, animals sacrificed 24 h post-ictus, TTC-stained brain slices, and infarct quantification using the indirect method of Lin et al. [12]. Of the 13 publications, four were chosen and used to compare our algorithm with that of Lin et al. [21–24].

All four publications reported the infarct volumes as a percent of the contralesional hemisphere, so each mean and SD or standard error of the mean (SEM) were adjusted to reflect the infarct volume as a percentage of the whole brain (i.e., the infarct volume and SD or SEM were divided by 2). For the publications in which SEM was reported, the SD was calculated. The mean, SD, and animal number (n) for each group were used in a random number generator to produce representative datasets of each group which had the same mean, SD, and n as those in the original publications. The generated datasets, which represent the infarct volumes computed by Lin et al.’s algorithm, were verified for published statistical significance following the statistical analysis methods reported within each study.

To estimate the value that the infarct volumes would have been if our algorithm was used in the publications, the infarct volume difference (Eq. 17, Fig. 3b, Table 2) was added to each infarct volume of the generated data depending on the range which the infarct volume belonged to (i.e., for the generated infarct volumes which were between 0 and 10 %, the mean infarct volume difference observed between the two algorithms for the infarct volume range of 0–10 % was added to those generated infarct volumes). Data is presented as mean± SD. Two-way ANOVAs with Sidak post hoc tests were performed (factor 1, injury; factor 2, algorithm) for the data of each study.

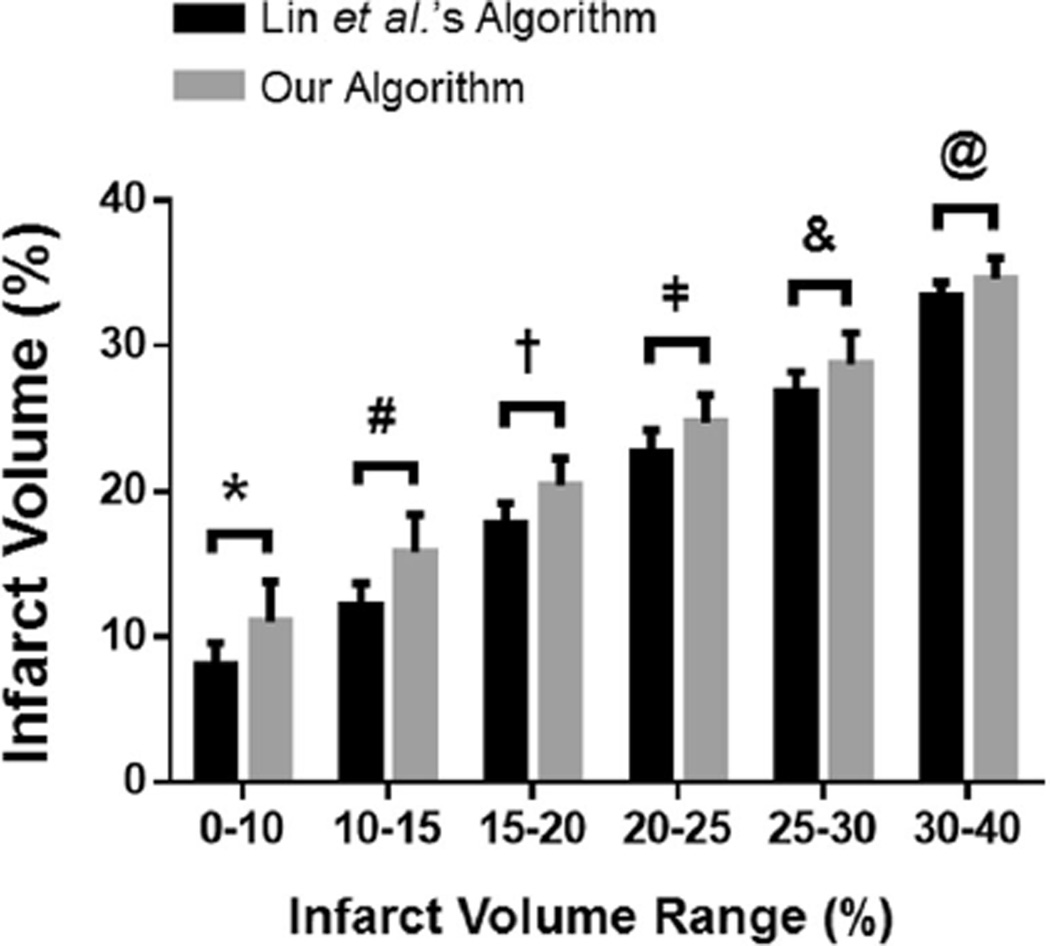
Fig. 3.

Comparison of our algorithm to Lin et al.’s algorithm. The infarct volumes (%) 24 h post-MCAO in rats were grouped based on the infarct volume range (based on the infarct volumes computed using Lin et al.’s algorithm) to determine the difference between our algorithm and Lin et al.’s algorithm for infarct volume calculation. For all infarct volume ranges, our algorithm computes a larger infarct volume than that of Lin et al.’s algorithm. All infarct volume ranges are significantly different from each other for both Lin et al.’s algorithm and our algorithm (i.e., intra-algorithm significance for all infarct volume range comparisons). *p<0.05 for 0–10 % between the two algorithms, ^#p<0.05 for 10–15 % between the two algorithms, ^†p<0.05 for 15–20 % between the two algorithms, p<0.05 for 20–25 % between the two algorithms, &p<0.05 for 25–30 % between the two algorithms, ^@p<0.05 for 30–40 % between the two algorithms. n=7–25/group

Table 2.

Bland-Altman comparison of the differences between our algorithm and Lin et al.’s algorithm for infarct volume difference (Eq. 17) and infarct volume ratio (Eq. 19)

Infarct volume range (%)a	Differences in infarct volume (%)		Infarct volume ratio
	Mean±SD	95 % Agreement (lower, upper)	Mean±STD	95 % Agreement (lower, upper)
0–10	3.0±2.12	−1.16, 7.16	1.39±0.293	0.816, 1.964
10–15	3.6±1.95	−0.22, 7.42	1.30±0.170	0.967, 1.633
15–20	2.6±1.33	−0.01, 5.15	1.15±0.079# †	0.995, 1.305
20–25	2.1±1.45†	−0.74, 4.84	1.09±0.063# †	0.967, 1.213
25–30	1.9±1.16†	−0.37, 4.10	1.07±0.044# †	0.984, 1.156
30–40	1.2±0.63†	−0.03, 2.36	1.04±0.018# †	1.005, 1.075

The means and standard deviations are computed using the individual data points within each infarct volume range. The 95 % agreements are computed based on the method of Bland and Altman [49]. n=7–25/group.

^#p<0.05 vs. 0–10 % infarct volume range,

^†p<0.05 vs. 10–15 % infarct volume range

^aThe infarct volume range is based on infarct volumes computed using Lin et al. ‘s algorithm

Results

Peri-infarct Brain Swelling

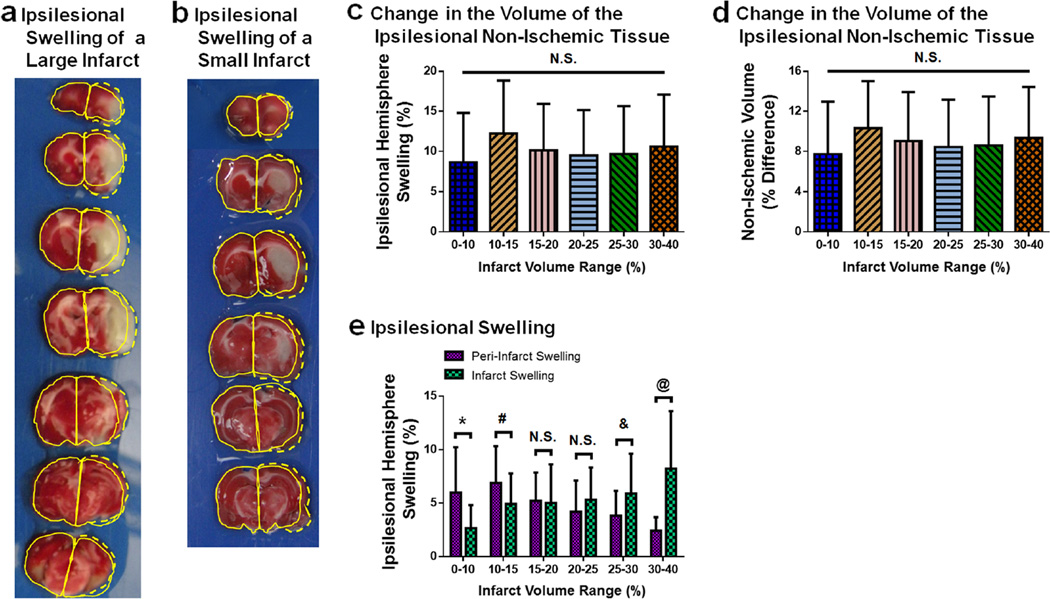
Significant ipsilesional brain swelling occurs 24 h after MCAO in rats and is a combination of peri-infarct swelling and infarct core swelling (Fig. 2). The differences between the non-ischemic ipsilesional volume and the corresponding volume of the contralesional hemisphere are non-zero for all size infarctions due to the presence of significant peri-infarct swelling within the non-ischemic ipsilesional tissue (Fig. 2d). This difference remains the same for all size infarctions (p>0.05 for all group comparisons).

Fig. 2.

Ipsilesional swelling is a combination of infarct core and peri-infarct swelling 24 h after MCAO. a A representative image of TTC-stained brain slices which have a large infarction and ipsilesional swelling. The contralesional hemisphere areas are outlined (solid yellow curves) for each slice and reflected on the ipsilesional hemisphere areas. The reflected outlines display the difference in the areas between the two hemispheres caused by swelling (dashed yellow curves). Table 1 contains the values of the areas and infarction calculations. b A representative image of TTC-stained brain slices have a small infarction. The contralesional hemisphere areas are outlined (solid yellow curves) for each slice and reflected on the ipsilesional hemisphere areas. The reflected outlines display the difference in the areas between the two hemispheres caused by swelling (dashed yellow curves). Table 1 contains the values of the areas and infarction calculations. c Ipsilesional hemisphere swelling (%, Eq. 1) for each infarct volume range (based on the infarct volumes computed using Lin et al.’s algorithm). n=7–25/group. d The change in the volumes of the ipsilesional non-ischemic tissue are plotted for each infarct volume range. The non-ischemic tissue of the ipsilesional hemisphere was determined from image analysis. This area was reflected into the contralesional hemisphere and corrected for peri-infarct swelling. The percent difference between the reflected and ipsilesional non-ischemic tissues are plotted. n=7–25/group. e Ipsilesional swelling is separated into that which occurs in the peri-infarct region and infarction. Peri-infarct swelling (%) and infarct core swelling (%) are plotted for each infarct volume range. n=7–25/group. *p<0.05 for 0–10 % between peri-infarct swelling and infarct swelling, ^#p<0.05 for 10–15 % between peri-infarct swelling and infarct swelling, &p<0.05 for 25–30 % between peri-infarct swelling and infarct swelling, ^@p<0.05 for 30–40 % between peri-infarct swelling and infarct swelling. N.S. denotes lack of statistical significance

When the swelling associated with the peri-infarct region is separated from that of the infarction, the peri-infarct swelling decreases as the volume of infarction increases, while the infarct core swelling increases as infarct volume increases (Fig. 2e). For infarctions with a volume less than 15 %, the amount of peri-infarct swelling is significantly greater than that of the infarct (p<0.05 between peri-infarct and infarct swelling for 0–10 %, p<0.05 between peri-infarct and infarct swelling for 10–15 %). For infarction volumes between 15 and 25 %, the amount of peri-infarct swelling and infarct swelling is indistinguishable (p>0.05 between peri-infarct and infarct swelling for 15–20 %, p>0.05 between peri-infarct and infarct swelling for 20–25 %). For infarct volumes greater than 25 %, the amount of peri-infarct swelling is significantly lower than that of the infarct (p<0.05 between peri-infarct and infarct swelling for 0–10 %, p<0.05 between peri-infarct and infarct swelling for 10–15 %).

Effects of Peri-infarct Swelling on the Infarct Volume Computed by Lin et al.’s Algorithm

The presence of peri-infarct swelling can cause the infarct volumes by Lin et al.’ algorithm to be estimated as smaller than the true infarction. When significant peri-infarct swelling is present within a TTC-stained brain slice, the infarct area of that particular slice can yield a negative value (Table 1). For animals with large infarctions, for which peri-infarct swelling is less prominent than infarct swelling, the amount of computed negative infarct areas is minimized (Table 1 Animal 1). Table 1 contains a representative animal with a large infarction (Table 1 Animal 1) which has a total infarct volume of 128.3 mm³ when Lin et al.’s algorithm is used, for which one of the seven slices yields a negative infarct area of −2.7 mm².

Table 1.

Negative infarct areas caused by peri-infarct swelling

		Contralesional area (mm2)	Non-injured ipsilesional area (mm2)	Infarct area (mm2)
				Lin et al.’s algorithm	Our algorithm
Animal 1	Slice 1	23.4	18.9	4.5	9.4
	Slice 2	45.9	25.0	20.9	24.8
	Slice 3	57.8	18.0	39.8	41.6
	Slice 4	62.4	26.5	35.9	39.1
	Slice 5	65.5	40.5	25.0	28.6
	Slice 6	64.3	67.0	−2.7	0.0
	Slice 7	53.9	49.0	4.9	3.0
	Total	373.2	244.9	128.3	164.5
Animal 2	Slice 1	24.6	26.2	−1.6	0.0
	Slice 2	53.1	33.0	20.1	20.2
	Slice 3	59.0	52.7	6.3	14.4
	Slice 4	57.1	63.3	−6.2	6.9
	Slice 5	63.9	64.2	−0.3	0.1
	Slice 6	64.6	74.6	−10.0	0.2
	Total	322.3	314	8.3	41.8

Infarct area analysis per slice of two TTC-stained brains from animals subjected to 2 h of MCAO and sacrificed 24 h after reperfusion (Fig. 2a, b). The infarct area for each slice calculated via Lin et al.’s algorithm uses the numerator in Eq. 12, (C_i–N_i). The infarct area for each slice calculated via the developed algorithm uses the numerator in Eq. 16, $\left(\right(\frac{I_i-N_i}{I_i}\left)C_i\right)$. For Animal 1 (Fig. 2a), the infarct volume is 17.2 % using Lin et al.’s algorithm and 22.0 % using our algorithm. The amount of peri-infarct swelling is 4.9 %, while the infarct swelling is 5.6 %. For Animal 2 (Fig. 2b), the infarct volume is 1.3 % using Lin et al.’s algorithm and 6.5 % using our algorithm. The amount of peri-infarct swelling is 10.3 %, while that of infarct swelling is 1.4 %

For animals with small infarctions, peri-infarct swelling can cause the calculated infarct volume to be vastly different from its true value due to computed negative infarcts for some slices (Table 1 Animal 2). This causes the infarcts to be significantly smaller than the true infarct size. The representative animal for a small infarct (Table 1 Animal 2) contains a total infarct volume of 8.3 mm³ when Lin et al. ‘s algorithm is used compared to our algorithm’s infarct volume of 41.8 mm³. The infarct volume estimation by Lin et al.’s algorithm is five times less than that of our algorithm because Lin et al.’s algorithm contains two slices which have positive infarct areas and four slices which have negative infarct areas.

Infarct Volume After Middle Cerebral Artery Occlusion in Rats

The infarct volumes, computed by Lin et al.’s algorithm, for each infarct volume range are significantly different from each other (for Lin et al.’s algorithm—p<0.05 for 0–10 vs. 10–15, 15–20, 20–25, 25–30, and 30–40 %; p<0.05 for 10–15 vs. 15–20, 20–25, 25–30, and 30–40 %; p<0.05 for 15–20 vs. 20–25, 25–30, and 30–40 %; p<0.05 for 20–25 vs. 25–30 and 30–40 %; p<0.05 for 25–30 vs. 30–40 %). Similarly, for our algorithm, the infarct volumes in each infarct volume range are significantly different from one another (our algorithm— p<0.05 for 0–10 vs. 10–15, 15–20, 20–25, 25–30, and 30–40 %; p<0.05 for 10–15 vs. 15–20, 20–25, 25–30, and 30–40 %; p<0.05 for 15–20 vs. 20–25, 25–30, and 30–40 %; p<0.05 for 20–25 vs. 25–30 and 30–40 %; p<0.05 for 25–30 vs. 30–40 %) (Fig. 3).

For our algorithm, the infarct volumes for each infarct volume range are significantly higher than their corresponding infarct volumes calculated by Lin et al.’s algorithm (p<0.05 for the 0–10 % infarct volume range between the two algorithms, p<0.05 for the 10–15 % infarct volume range between the two algorithms, p<0.05 for the 15–20 % infarct volume range between the two algorithms, p<0.05 for the 20–25 % infarct volume range between the two algorithms, p<0.05 for the 25–30 % infarct volume range between the two algorithms, p<0.05 for the 30–40 % infarct volume range between the two algorithms) (Fig. 3).

Infarct Volume Differences Between the Two Algorithms

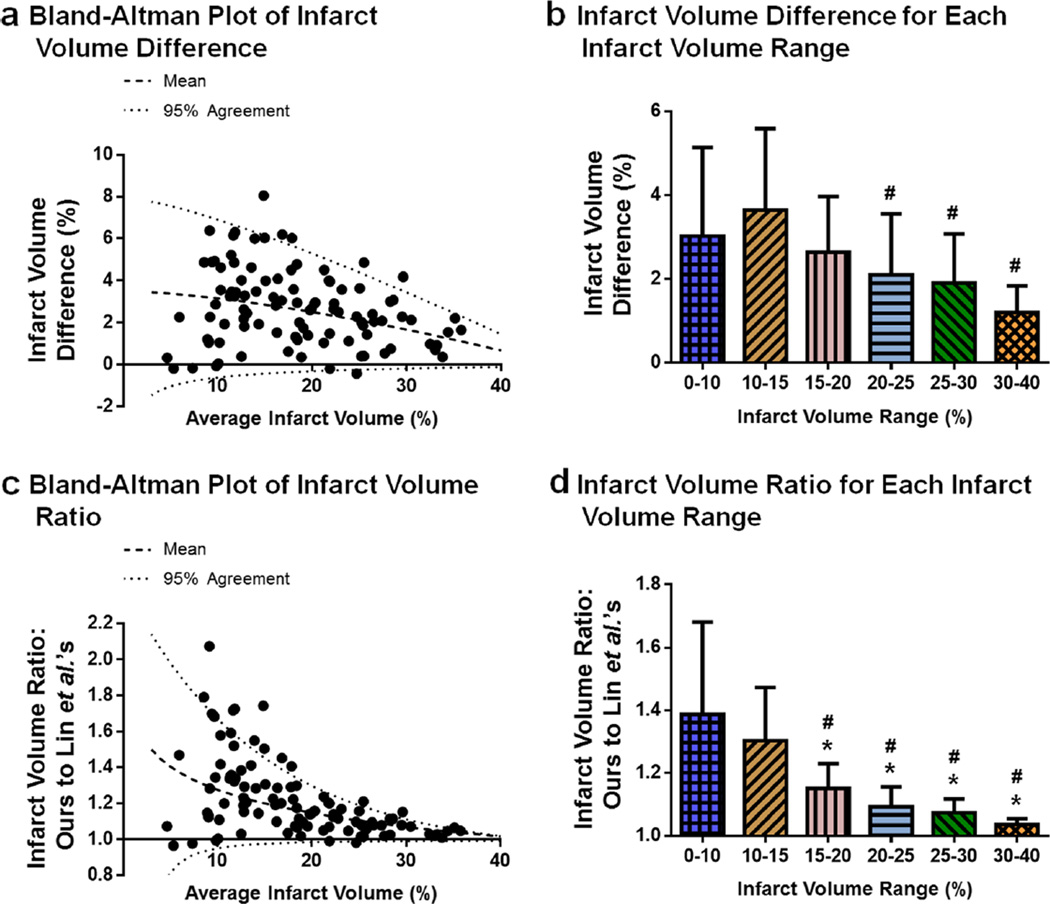
For each brain sample, the infarct volume differences between our algorithm and Lin et al.’s algorithm were determined. A Bland-Altman plot of the infarct volume difference (our algorithm’s infarct minus Lin et al.’s algorithm’s infarct) displays a greater difference between the two algorithms for the smaller infarctions than large infarctions; as infarct size increases, the difference between the two algorithms decreases. In a similar manner, the infarct difference values for which the two algorithms have a 95 % agreement that approaches each other as the infarct volume increases (Fig. 4a). The mean difference in infarct volume between the two algorithms is quantified and grouped into the infarct volume ranges. As infarct volume increases, the difference between the algorithms decrease (p<0.05 for 10–15 vs. 20–25, 25–30, and 30–40 %) (Fig. 4b, Table 2).

Fig. 4.

Infarct volume difference between our algorithm and Lin et al.’s algorithm decreases as the infarct volume range increases. Differences between the two algorithms for infarct volume estimation are examined using rat brains 24 h post-MCAO. a Bland-Altman plot of infarct volume difference. The infarct volume difference (%, Eq. 17) between the two algorithms decreases as the average infarct volume (%, Eq. 18) increases. n=101. b Infarct volume difference for each infarct volume range. The infarct volume difference (%) between our algorithm and Lin et al.’s algorithm decreases as the infarct volume range (%) increases. n=7–25/group. c Bland-Altman plot of infarct volume ratio. The infarct volume ratio (Eq. 19) decreases as the average infarct volume (%) increases. n=101. d Infarct volume ratio for each infarct volume range. The infarct volume ratio of the two algorithms decreases as the infarct volume range (%) increases. n=7–25/group. Bland-Altman plots (a, c): the mean values (dashed lines) and the values for which 95 % agreement (dotted lines) is observed between the two algorithms are plotted. Bar graphs (b, d): *p<0.05 vs. 0–10 %, ^#p<0.05 vs. 10–15 %. Infarct volume ranges are based on the infarct volumes computed using Lin et al.’s algorithm

The ratio of our algorithm’s infarct volume to that of Lin et al.’s algorithm were determined for each brain sample. A Bland-Altman plot of the infarct volume ratio shows the ratio between the two algorithms is the greatest for small infarctions and approaches 1 as infarct volume increases. The 95 % agreement for the infarct volume ratio between our algorithm and Lin et al.’s algorithm also converges on 1 as the infarct increases (Fig. 4c). Grouping the infarct volume ratios into the infarct volume ranges demonstrates that the significant reduction in the infarct volume ratio as the infarct volume increases (p<0.05 for 0–10 vs. 15–20, 20–25, 25–30, and 30–40 %; p<0.05 for 10–15 vs. 15–20, 20–25, 25–30, and 30–40 %) (Fig. 4d, Table 2).

Effect of Our Algorithm on the Infarct Volumes for Published Studies

A PubMed search of middle cerebral artery occlusion in rats from the years 2014–2015 was performed. Five hundred forty-four hits were found, but only 13 of them satisfied the inclusion criteria, of which four were chosen to compare the two algorithms.

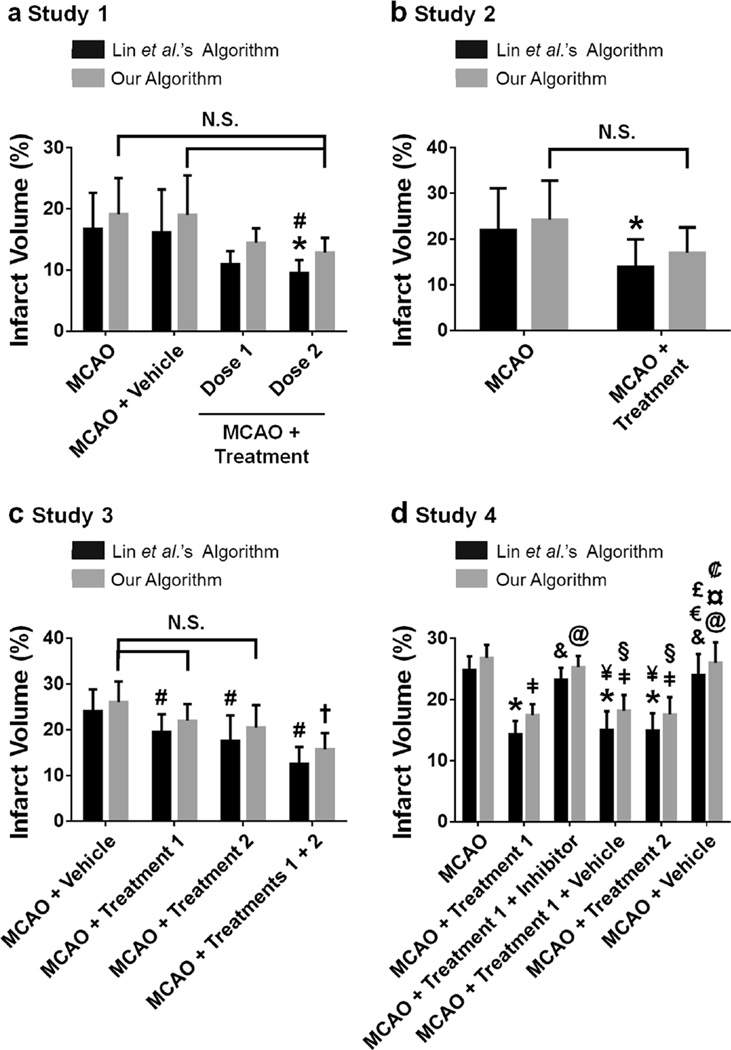
Study 1 examines two different doses of a treatment for reducing infarction [22]. When Lin et al.’s algorithm is used for calculating the infarct volumes, the MCAO+Treatment Dose 2 group has a significantly smaller infarct volume than both the MCAO and MCAO+Vehicle groups (p<0.05 for MCAO+Treatment Dose 2 vs. MCAO and MCAO+Vehicle). However, when our algorithm is used to estimate the infarct volumes, there is no statistically significant difference between the MCAO+Treatment Dose 2 group and either the MCAO or the MCAO+Vehicle groups (p>0.05 for all group pairings) (Fig. 5a).

Fig. 5.

Effect of our algorithm on infarct volume analysis for published data. Algorithm differences are examined using four published studies which utilized Lin et al.’s algorithm for estimating infarct volume in TTC-stained brain tissue of adult Sprague-Dawley rats subjected to 2 h MCAO and sacrificed 24 h after MCAO. a Study 1. Lin et al.’s algorithm’s infarct volumes display statistical significance between the MCAO+Treatment Dose 2 and the MCAO groups and the MCAO+ Treatment Dose 2 and the MCAO+Vehicle groups. The infarct volumes computed using our algorithm are increased more for the smaller infarct volumes (MCAO+Treatment Dose 1 and MCAO+Treatment Dose 2). Our algorithm’s infarct volumes are not statistically different from one another. n=6/group [22]. b Study 2. When Lin et al.’s algorithm is used, the MCAO+Treatment group is significantly lower than the MCAO group. When our algorithm is used, no significance is observed between the two groups. n=8/group [21]. c Study 3. The infarct volumes computed using Lin et al.’s algorithm displays statistical significance for all three treatment groups versus the Vehicle group. Our algorithm’s infarct volumes for the MCAO+Treatment 1 and the MCAO+Treatment 2 groups are not significantly different from the MCAO+Vehicle group. However, the combined treatment group (MCAO+Treatments 1+2) is statistically different from the MCAO+ Vehicle group. n=6/group [23]. d Study 4. All inter-group statistical significance for Lin et al.’s algorithm’s infarct volumes are identical to that of our algorithm’s. n=6/group [24]. All graphs: *p<0.05 vs. MCAO for Lin et al.’s algorithm, ^#p<0.05 vs. MCAO+Vehicle for Lin et al.’s algorithm, ^†p<0.05 vs. MCAO+Vehicle for our algorithm, p<0.05 vs. MCAO for our algorithm, &p<0.05 vs. MCAO+Treatment 1 for Lin et al.’s algorithm, ^@p<0.05 vs. MCAO+Treatment 1 for our algorithm, ¥<0.05 vs. MCAO+Treatment 1+Inhibitor for Lin et al.’s algorithm, ^§p<0.05 vs. MCAO+Treatment 1+Inhibitor for our algorithm, ^€p<0.05 vs. MCAO+Treatment 1+Vehicle for Lin et al.’s algorithm, ^£p<0.05 vs. MCAO+Treatment 2 for Lin et al.’s algorithm, ^¤p<0.05 vs. MCAO+ Treatment 1 +Vehicle for our algorithm, p<0.05 vs. MCAO+Treatment 2 for our algorithm. N.S. denotes lost statistical significance when our algorithm is used rather than Lin et al.’s algorithm

Study 2 examines a single treatment on reducing infarction [21]. The infarct volume, computed by Lin et al.’s algorithm, is significantly reduced in the MCAO+Treatment group compared to that of the MCAO group (p<0.05 for MCAO vs. MCAO+Treatment). However, the significant difference between these two groups is lost when our algorithm’s infarct volumes are analyzed (p>0.05 for MCAO vs. MCAO+Treat-ment) (Fig. 5b).

Study 3 examines the infarct reduction for two treatments and a combined treatment [23]. For Lin et al.’s algorithm, the infarct volume of the MCAO+Vehicle group is significantly reduced by treatments 1 and 2 and the combined treatment (p<0.05 for MCAO+Vehicle vs. MCAO+Treatment 1, MCAO+Treatment 2, and MCAO+Treatments 1+2). However, for our algorithm, the infarct volumes of the MCAO+ Treatment 1 and MCAO+Treatment 2 groups are statistically indistinguishable from that of the MCAO+Vehicle group (p>0.05 for MCAO+Vehicle vs. MCAO+Treatment 1 and MCAO+Treatment 2). Yet, identical to Lin et al.’s algorithm, when our algorithm is used, the infarct volume of the MCAO+Treatments 1+2 group is significantly lower than that of the MCAO+Vehicle group (p<0.05) (Fig. 5c).

Study 4 examines the effects of two treatments and an inhibitor on infarction reduction [24]. Using the infarct volumes calculated by Lin et al.’s algorithm, the infarct volume is statistically lower in the MCAO+Treatment 1, MCAO+Treatment 1+Vehicle, and MCAO+Treatment 2 groups compared to that of the MCAO, MCAO+Treatment 1+Inhibitor, and MCAO+Vehicle groups (p<0.05 for MCAO vs. MCAO+Treatment 1, MCAO+Treatment 1+Vehicle, and MCAO+Treatment 2; p<0.05 for MCAO+Treatment 1+In-hibitor vs. MCAO+Treatment 1, MCAO+Treatment 1+Ve-hicle, and MCAO+Treatment 2; p<0.05 for MCAO+Vehicle vs. MCAO+Treatment 1, MCAO+Treatment 1+Vehicle, and MCAO+Treatment 2). The infarct volumes, calculated by our algorithm, had identical statistical significance as that observed when Lin et al.’s algorithm is used (p<0.05 for MCAO vs. MCAO+Treatment 1, MCAO+Treatment 1+Vehicle, and MCAO+Treatment 2; p<0.05 for MCAO+Treatment 1+In-hibitor vs. MCAO+Treatment 1, MCAO+Treatment 1+Ve-hicle, and MCAO+Treatment 2; p<0.05 for MCAO+Vehicle vs. MCAO+Treatment 1, MCAO+Treatment 1+Vehicle, and MCAO+Treatment 2) (Fig. 5d).

Discussion

Herein, peri-infarct swelling was found to be a significant contributor to the overall ipsilesional hemisphere swelling in rats after MCAO. An algorithm was developed to minimize the effects of both types of brain swelling on infarct volume calculation. Our algorithm was used to evaluate infarct volume after experimental ischemic stroke, and we validated its difference in infarct volume calculation using MCAO data as well as previously published studies. Our algorithm relaxes the assumptions and removes several limitations of Lin et al.’s algorithm, thereby providing an estimation of infarct size which is independent of brain swelling’s effects. Herein, data from rats subjected to MCAO was analyzed using Lin et al.’s algorithm and our algorithm and, for all samples, our algorithm estimated larger infarct volumes than those of Lin et al.’s algorithm. Furthermore, the infarct volume difference between our algorithm and Lin et al.’s algorithm is the greatest for small infarcts and converges at large infarcts. Finally, our algorithm was used to analyze several published studies; in three of the studies, our algorithm displayed different statistical significance than when Lin et al.’s algorithm was used.

A Brief History of Infarct Volume Algorithms

Despite the vast amount of research on experimental models of ischemic stroke [25–28], it was not until 1984 that an algorithm was developed for infarct quantification [9]. Jones and Coyle developed the first algorithm which measured infarction on whole brains, utilizing curvature correction factors to compute the infarct surface area [9], but this method only lasted a few years [29, 30].

Simultaneous to the development of the Jones and Coyle model, Bederson et al. created an alternative algorithm which directly calculated infarct area by outlining the infarct in several brain slices and normalizing them to the area of the coronal section [3, 4]. This direct method of infarct size estimation was more widely accepted, leading to the direct method of infarct volume by Osborne et al. [20]. Although the direct infarct volume algorithm was used for several years, it did not yield a true measurement of infarct volume due to swelling of the ipsilesional hemisphere.

In 1990, Swanson et al. recognized that the direct method for infarct volume could be severely affected by brain swelling [3, 4, 20], thus the indirect infarct volume algorithm was developed [31]. The method by Swanson et al. utilized pixel density analysis of eight to nine slices of stained brain tissue. The authors examined four stains and found that the ischemic tissue had a similar staining to that of white matter. The conclusion was that any stain for which differences in staining intensity was observed between the ischemic and non-ischemic tissue was ideal. Since the stains used by Swanson et al. did not stain ischemic tissue nor did it stain white matter, their algorithm relied on the pixel intensities of healthy gray matter tissue for infarct volume estimation [31]. Although the algorithm by Swanson et al. yielded a much better estimate of the infarct volume, reducing the effect of brain edema on infarct volume by up to 22 % [31], it was modified shortly after.

In 1993, Lin et al. modified the model by Swanson et al. to use the non-ischemic tissue volume in the ipsilesional hemisphere and total volume of the ipsilesional hemisphere, and although Lin et al. reported direct infarct volumes [12], it led to an indirect version.

Since Lin et al.’s indirect algorithm was published, several additional algorithms have been developed [32, 33]. Yet despite these recent algorithms, the indirect Lin et al. algorithm remains the gold standard for infarct volume.

Assumptions of Lin et al.’s Algorithm

As with any algorithm, the development of Lin et al.’s algorithm makes several assumptions. The first assumption is that the contralesional hemisphere is unaffected by infarction and brain swelling. This implies that the measured volume of the contralesional hemisphere is the true volume. This assumption is typically valid and therefore is assumed by most infarct volume algorithms.

The second assumption is that swelling occurs only in the infarcted tissue. Thus, it follows that if swelling only occurs in the infarct, the area/volume of the non-ischemic ipsilesional tissue is unaffected (i.e., the healthy ipsilesional tissue is its true size). This assumption makes Lin et al.’s algorithm vulnerable to artifacts due to volume changes in the ipsilesional hemisphere since significant peri-infarct edema may occur.

Our Algorithm and its Assumptions

The new algorithm developed to estimate the infarct volume utilizes the ratio of the infarcted tissue area to the entire ipsilesional area to correct for brain swelling. Normalizing the infarct area to that of the ipsilesional hemisphere allows for the amount of infarcted tissue to be determined as a percent of the hemisphere. This ratio is then multiplied by the area of the contralesional hemisphere; the effects of swelling are minimized since swelling does not occur in the contralesional hemisphere, yielding an estimate of the true infarct size (Eq. 16).

First, identical to the assumption made for Lin et al.’s algorithm, the contralesional hemisphere is assumed to be unaffected by brain swelling, or the area of the contralesional hemisphere is the true value. While the first assumption is shared between the two algorithms, the second assumption makes our algorithm unique. Our algorithm assumes that swelling is not confined to the infarction, but rather peri-infarct edema may be present in the ipsilesional hemisphere. This assumption relaxes the constraint of swelling being restricted to only the infarct, made for Lin et al.’s algorithm, which caused a majority of Lin et al.’s algorithm’s artifacts to exist.

Advantages of Our Algorithm

Our infarct volume algorithm offers several advantages to Lin et al.’s algorithm. First, our algorithm removes the effects of cerebral swelling on infarct volume which allows for an estimation of the true infarct size. This is achieved by utilizing the ratio of the infarct to the ipsilesional hemisphere. Second, our algorithm allows experimental studies to examine the effects of a drug on solely infarction, rather than its effects on the swollen infarction. Lin et al.’s algorithm is unable to uncouple the effect of peri-infarct swelling from that of infarct core, so drugs which display a decreased infarct volume may decrease the infarction, decrease swelling within the infarction, or both. The third advantage of our algorithm is that the infarct volume can be standardized. Evaluation of the true infarct permits comparison of the effects on infarction of the same drug from different laboratories, adhering to the recommendations of the STAIR meetings [34]. Finally, standardization of infarct volume calculation will aid future clinical trials in candidate selection. With respect to infarct volume, each promising drug can be directly compared to all others. This will not only help translation but may also improve the success rate of clinical trials.

Application of Our Algorithm to Other Methods of Infarct Visualization

This study investigated our algorithm for the swelling correction of infarction estimation using TTC-stained brains. TTC staining of brain tissue is the gold standard for infarct visualization and can be used up to 3 days post-MCAO. However, for animals sacrificed more than 3 days post-ictus, Nissl or hematoxylin and eosin stains are commonly used. Infarctions visualized using TTC are reported to be identical to those shown by Nissl [35] as well as hematoxylin and eosin stains [3]. Additionally, Lin et al.’s algorithm has been used to evaluate infarct size for all three stains [12, 31]. Thus, our algorithm may also be used for infarct volume estimation for Nissl and hematoxylin and eosin stains, in addition to TTC.

Comparison of Our Algorithm to Other Infarct Volume Algorithms

Although measurement of infarction volume is essential for understanding a treatment’s benefits following stroke, no single algorithm has been adopted by all experimental studies [12, 31, 32, 36–39]. Each algorithm developed relies on a different set of assumptions, resulting in infarct values which are algorithm dependent [12, 31, 32, 36–39]. Infarct volume can be evaluated as a direct [30, 36, 37, 39] or an indirect measurement [12, 31, 32, 38], and may be normalized to hemisphere or whole brain volumes. Direct infarct measurements yield values with physical units (i.e., square millimeters for area and cubic millimeters for volume), while indirect infarct measurements yield dimensionless values (typically percent). Each of these infarct estimation methods produces a different interpretation regarding the effectiveness of novel drugs on infarction, ultimately making the comparison of infarct volumes between studies nearly impossible.

The discrepancy in infarct volume calculations leads to standalone basic science studies that cannot be compared to one another for drug efficacy not only affecting basic science research but also clinical trials. Since the most promising drugs in experimental studies become clinical trial candidates, for which infarct volume is one of the primary selection factors [40–42], it is of the highest importance to standardize infarct volume calculations. Yet, the various infarct volume algorithms available confound the results of experimental studies, which may be partially responsible for the failure of many drugs translated to clinical trials.

The algorithm developed within may provide the foundation for standardization of infarct volume measurement. Herein, our algorithm was shown to provide a more realistic calculation of infarction size than Lin et al.’s algorithm, but our algorithm is also likely to be more robust than other algorithms.

Lin et al., confirmed by Jin et al. [43], found that the algorithm by Lin et al. is superior to the direct measurement of infarct volume for a variety of reasons, including reduced swelling effects and constant infarction size estimation over 3 days post-MCAO [12]. Yet despite the disadvantages of the direct method for infarct estimation, it is still being utilized [44]. Since our algorithm was found to be more robust than Lin et al.’s algorithm, it is likely also superior to the direct infarct measurement.

Another model developed for brain swelling correction is that of Belayev et al. [32]. To date, no studies have been conducted to determine the advantage of their model over Lin et al.’s method. However, the model of Belayev et al. has not been widely adopted. Future studies can compare the model of Belayev et al. to our algorithm as well as Lin et al.’s algorithm.

Limitations of Our Algorithm

Our algorithm assumes that cerebral swelling is not confined to the infarction, but rather extends beyond the infarct core into the peri-infarct zone in the ipsilesional hemisphere [45]. This assumption relaxes the constraint of only infarct swelling, made in Lin et al.’s algorithm, which caused infarct volume to be estimated as smaller than the true infarct size. A limitation, unique to our algorithm, arises from this assumption. While our algorithm can yield information about the amount of peri-infarct swelling and infarct core swelling, the swelling gradient that likely exists is not defined. Although this limitation does not affect the calculation of infarct volume (i.e., our algorithm estimates the true infarct volume), studying the roles of peri-infarct swelling and swelling within the infarct core, as well as the swelling gradient, will improve our understanding of stroke pathophysiology. The most likely scenario is that a gradient in swelling exists for which swelling is at a maximum in the ischemic core and/or penumbra and decreases as the distance from the infarction increases. Incorporating this phenomenon into an infarct volume algorithm would result in a unique infarct volume algorithm for each animal. Until an automatic method which evaluates and corrects for the effects of a brain swelling gradient on infarct volume exists, the assumption that swelling exists within the infarct as well as in the peri-infarct region provides the best platform for development of an infarct volume algorithm.

Impact of Our Algorithm on Clinical Trial Drug Candidates

The recommendations from the STAIR meetings highlight the importance of preclinical studies being mindful in designing experiments, including carefully defining primary and secondary endpoints [1, 34, 46, 47]. However, choosing methods for data analysis should be given the same amount of care since clinical trials for ischemic stroke depend on infarct reduction as a major factor in identifying potential therapeutic candidates. The numerous algorithms for quantifying infarct volume, leading to disparate experimental studies, implies that we have not been as meticulous as we should be about choosing the method used for infarct size measurement. Therefore, standardizing infarct volume computation is of the utmost importance.

Despite the differences in assumptions and limitations for infarct volume algorithms, a decrease in the infarct size by 20– 40 % has been suggested as a threshold for clinical translation [2, 48]. A major concern of this threshold for infarct volume reduction is that each algorithm can yield vastly different measurements of infarction. The study by Lin et al. identified such differences between the direct and indirect methods [12], and although swelling was purported to be the cause, there may also be differences between distinct indirect algorithms, such as observed in the current study.

Comparison of the Infarct Volume Reduction Between Our Algorithm and Lin et al.’s Algorithm for the Four Published Studies

When Lin et al.’s algorithm is used in the four published studies examined herein [21–24], statistical significance is achieved for the treatment groups when the infarct volumes are reduced by a minimum of 20 %. However, when our algorithm is used, for statistical significance to be observed between the treated and untreated groups, the infarctions must be reduced by a minimum of 32 %. Based on this finding, the infarct volume reduction threshold for a drug to be considered for clinical trials should be no less than 30 %. At first glance, the difference between a 20 and 30 % infarct reduction might not seem like a lot; however, if the effects of peri-infarct swelling are removed (accomplished with our algorithm), then the 10 % difference represents solely preserved tissue rather than a combination of swollen healthy tissue and swollen injured tissue.

Towards a Standardized Algorithm for Infarct Volume

One of the major concerns when computing infarction size is the effect of brain swelling. While Lin et al.’s algorithm was developed to correct for swelling [12], it overestimates the effect of cerebral swelling on infarct size. Peri-infarct swelling causes the estimated infarct to be aggrandized since the swollen healthy tissue will be larger than its true size. By incorporating the ratio of the infarction to the ipsilesional hemisphere, the effect of both peri-infarct swelling and swelling associated with the infarct core can be minimized in the calculation of infarct volume. Our algorithm relies on this swelling correction to provide a more robust estimation of infarct volume.

A standardized model which removes the effects of cerebral swelling, as well as removing analyzer bias towards the infarcted tissue, will provide experimental studies with an in-farct volume which can be compared between studies to identify the most promising drugs for clinical trials. Furthermore, the value of basic science studies will be improved as a standardized infarct volume algorithm allows for direct comparison with other drugs to their molecular pathways. This may lead to identification of the most salient molecular pathways of stroke pathophysiology. Finally, a standardized infarct equation will bridge the gap between clinical and basic research since miscalculation of infarction volume may be one of the potential weaknesses that mislead clinicians to begin trials.

Conclusions

Herein, we developed a new algorithm for quantifying infarct volume which better corrects for brain swelling than gold standard algorithm by Lin et al. The major limitation of our model is it does not provide any information as to the localization of peri-infarct swelling, but this can be experimentally verified in future studies. Ultimately, standardizing infarct volume quantification will allow for comparison between experimental studies and may lead to more stringent criteria for advancing therapeutics to clinical trials.