Abstract
Background and Aims Root diameter, especially apical diameter, plays an important role in root development and function. The variation in diameter between roots, and along roots, affects root structure and thus the root system’s overall foraging performance. However, the effect of diameter variation on root elongation, branching and topological connections has not been examined systematically in a population of high-order roots, nor along the roots, especially for mature plants grown in the field.
Methods A method combining both excavation and analysis was applied to extract and quantify root architectural traits of adult, field-grown maize plants. The relationships between root diameter and other root architectural characteristics are analysed for two maize cultivars.
Key Results The basal diameter of the lateral roots (orders 1–3) was highly variable. Basal diameter was partly determined by the diameter of the bearing segment. Basal diameter defined a potential root length, but the lengths of most roots fell far short of this. This was explained partly by differences in the pattern of diameter change along roots. Diameter tended to decrease along most roots, with the steepness of the gradient of decrease depending on basal diameter. The longest roots were those that maintained (or sometimes increased) their diameters during elongation. The branching density (cm–1) of laterals was also determined by the diameter of the bearing segment. However, the location of this bearing segment along the mother root was also involved – intermediate positions were associated with higher densities of laterals.
Conclusions The method used here allows us to obtain very detailed records of the geometry and topology of a complex root system. Basal diameter and the pattern of diameter change along a root were associated with its final length. These relationships are especially useful in simulations of root elongation and branching in source–sink models.
Keywords: Lateral roots, branching order, root diameter, branching density, root length, growth potential, root system architecture, maize.
INTRODUCTION
Root elongation and branching are iterative processes in root development (Malamy and Benfey, 1997; Nibau et al., 2008; Atkinson et al., 2014). Variations in the attributes of elongation and branching create morphological differences in the lengths, numbers and diameters of different-order roots within the root system (Fitter, 1987; Gruber et al., 2013).
To understand the resulting root-system architecture, records of root diameters – especially of their younger parts (the tip or apical diameters) – is a key trait for several reasons. From an economic point of view, root diameter relates directly to the investment by a plant of biomass in its roots (Eissenstat, 1992), because, to a first approximation, the biomass of a given length of root varies with the square of its diameter. Therefore, for a given investment of carbohydrate, root diameter affects the possible lengths × numbers of the roots in the system (Bidel et al., 2000). As expected, many plant species have root system architectures with a majority of very fine roots. These tend to optimize the ratio of root length (and hence root surface area for uptake) to root weight (investment). However, decreased root diameter limits root penetration through the soil (Materechera et al., 1992; Clark et al., 2008), and roots must also develop internal structures dedicated to water and nutrient transport (Jordan et al., 1993; Jaramillo et al., 2013). From a developmental point of view, apical diameter reflects the size of the apical meristem. In many species, a positive relationship has been found between the size of the root meristem (and hence apical diameter) and several important developmental characteristics, including: elongation rate (Cahn et al., 1989; Thaler and Pagès, 1996a), growth duration (Cahn et al., 1989; Pregitzer et al., 1993; Pagès, 1995; Wells and Eissenstat, 2001) and gravitropism (Oyanagi et al., 1993; Abe and Morita, 1994; Singh et al., 2011).
There are several other allometric relationships within a root system that affect its function. The range of variation of root diameter within a root system is also variable (Pagès, 1995; Thaler and Pagès, 1996a; Wu et al., 2014) and this can be of prime importance for foraging performance, as shown by Pagès (2011). A root system is also a sap-conducting network, sometimes with a high number of branching orders (e.g. up to four, or even five) (Wu and Guo, 2014). Hydraulic and nutritional constraints may also influence root diameter and the relative arrangement of anatomical characteristics (North and Nobel, 1991; Steudle, 2000; Fan et al., 2003; Saengwilai et al., 2014; Lynch et al., 2014) and hence the topological relationships between diameters. Thus, the precise relationship between diameter and elongation attributes on the one hand and the topological connections of roots of different diameter on the other are important questions we seek to address for field-grown maize plants.
Most work on the developmental consequences of root diameter on root growth has assumed (often implicitly) that root diameter at emergence (basal diameter) remains constant throughout root development (Hackett, 1969; Cahn et al., 1989). However, this simplistic view is worth further examination. Several authors have recently shown that root apical diameter can fluctuate during elongation or is not uniform along some roots (Pagès, 1995; Thaler and Pagès, 1996a; Wu et al., 2014). This possibility would offer additional degrees of freedom for root growth. With some species, temporal variations in assimilate availability have been shown to synchronize with root diameter variations (Thaler and Pagès, 1996a, b) and hence can introduce multiple patterns of elongation (Thaler and Pagès, 1996a). This factor will make developmental models more complicated, but also more adaptive, as root diameter can readjust during root elongation. Nevertheless, the generality of some of these findings is worth assessing with other species and should also be evaluated under field conditions. It should be recalled that time variations in root diameter were first recorded by monitoring the apical diameter of individual roots through observation windows (Pagès, 1995; Thaler and Pagès, 1996a). While this method gives direct access to the dynamics of root diameter, it is very constraining and requires special equipment, rendering measurement under more natural soil conditions impossible. In monocotyledonous species, where no secondary root growth modifies root diameter, it is possible to substitute time-monitoring of diameter by a study of the longitudinal profile of root diameter along an excavated root. This method should be applied promptly to carefully excavated roots before any degradation of diameter occurs due to senescence following injury.
Branching density is also an important component of root-system architecture, and it is possible that this could be related to root diameter (Draye, 2002; Lecompte and Pagès, 2007; Bécel et al., 2012). However, the branching/root diameter relationship remains uncertain, with contradictory results even in the same species (Draye, 2002; Lecompte and Pagès, 2007). It remains difficult to determine from the literature the extent to which these differences are due to species diversity, and that to which they are due to environmental diversity. Because of longitudinal variations in both root diameter and branching density (Lecompte et al., 2005), to further elucidate this important new aspect of root development, it is proposed to consider these relationships at the scale of the root segment, instead of at that of the whole root, as is more usual (Draye, 2002; Lecompte and Pagès, 2007; Bécel et al., 2012).
Thus, our study relies on analysis of large numbers of roots and of several orders of branching in field-grown maize plants. We also use two genotypes in the same season, and one genotype over two seasons, to better assess the generality of our results. The plants were very carefully excavated with a custom device described in a preceding paper (Wu and Guo, 2014). The main objectives were to characterize: (1) the distribution of root diameters within the system, by studying diameter relationships through branch points (lateral diameter versus parents diameter) and longitudinal diameter variation along individual roots; (2) the relationship between root diameter and total root length, considering both the basal (initial) diameter and possible longitudinal variation; and (3) the relationship between diameter and branching density at the local, root-segment, scale, to test for the existence of a positive relationship, or a distinct distribution of branching density along roots. Specifically, we tested the hypothesis that the final length of a lateral root (LR) was associated with the size of the basal root and the extent of diameter change along the root.
MATERIALS AND METHODS
Field experiments
Field experiments were carried out at the Shangzhuang Experimental Station, China Agricultural University, Beijing, China (40°8′N, 116°10′E). The soil type is an aquic cambisol with a sandy clay loam texture (FAO). Two maize hybrids (Zea mays L.), ‘ND108’ and ‘ZD958’, were used. ‘ND108’ and ZD958 successively had the largest planting acreage as a commercial hybrid in China in recent years. In 2009, both hybrids were sown on 8 May. In 2011, only ‘ZD958’ was used and it was sown on 15 May. Plant density was 5·8 plants m−2 with inter-row and intra-row spacing of 60 and 30 cm, respectively (each block 16 × 6·5 m, east–west × north–south). The experimental design was a randomized block, with two block replications. To avoid the potential effect of returned cut straw on root growth, the straw was removed from the field after harvest in the previous years. Fifteen days before sowing, flooding irrigation was applied.
Based on local practice for maize, a base fertilizer of 120 kg P2O5 ha−1 (superphosphate) and 100 kg K2O ha−1 (potassium sulphate) was spread before sowing. This was incorporated into the upper 0–15 cm of the soil by a mouldboard plough and rotary tiller. A total of 120 kg N ha−1 was applied to both cultivars; 30 % of total N as urea was spread as a topdressing at the four-leaf stage with 5 mm irrigation using a microspray belt, and 70 % of total N as urea was spread at the 11-leaf stage. Weeds were removed by hand to avoid herbicide influence on crop growth.
Root sampling in the field
The root systems of individual maize plants were sampled at the grain-filling stage. Plant screening was conducted before sampling. Each sampled plant was selected from a group of nine plants (3 rows × 3 plants in the row). Row and plant spacing between neighbouring plants in each group should be in the range 58–62 and 28–32 cm, respectively. The plants in each group were of similar height, ear height and basal internode thickness. The root system sampled was that of the plant situated in the centre of the group.
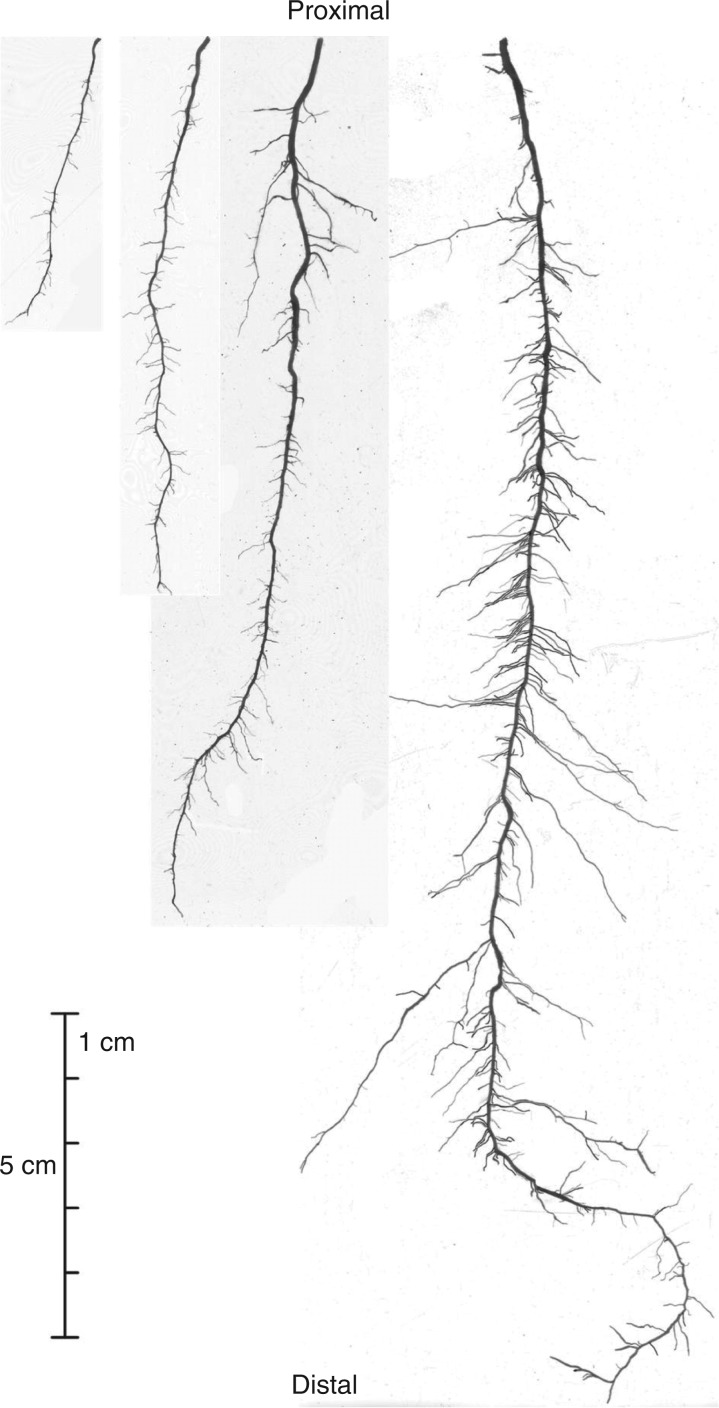
In 2009, four root systems of ‘ZD958’ (Z09) and ‘ND108’ (N09) were sampled 24 and 27 d after silking, respectively. To sample the roots, the shoot was first cut off. Next, a custom ‘sector sampler’ was made up, comprising two demountable parts. First, a sheet of 4-mm mild steel (70 × 50 cm) was folded across its long axis to create a ‘V’ blade with central angle of 120°, and sides 35 cm wide (radius) and 50 cm high (depth). To this ‘V’ was wired, with 3-mm soft-iron wire, an outer panel made up of a sheet of 5-mm mild steel (105 × 50 cm) curved to form a smooth arc which just touched the edges of the ‘V’ blade at right angles. The two components included flanges welded along their abutting edges to assist assembly. The sector sampler was placed on the soil surface with its long axis vertical, and aligned such that its apex just included the maize stump (with a gap of about 5 cm). Root samples of the selected plants were collected in the inter-row and inner-row directions, respectively. The sector sampler was then hammered into the soil using a horizontal wooden block and a sledge hammer. The surrounding soil was progressively excavated to facilitate insertion. When the sampler had been driven to its full depth (approx. 50 cm), and the surrounding soil was fully excavated, two steel ropes were attached to welded lugs on the sampler and it and the wedge-shaped monolith of soil it contained were carefully lifted out. Next, the tangential steel sheets were removed and replaced by a coarse steel-wire mesh (10 × 10 mm) to minimize root breakage during subsequent washing out of the soil monolith, using fine water jets. After washing, the soil-free root system sector was stored in a cool room at 3 °C. Because of the shape and size of the sector sampler, it was inevitable that some nodal roots intersected the angled sides and so these were cut. Hence, there was a limited number of intact nodal roots in each monolith.
In 2011, three root systems of ‘ZD958’ (Z11) were sampled 19 d after silking. To increase the efficiency of root sampling, and to obtain a more complete root system, a new sampling system was developed (Wu and Guo, 2014). The new system used a mild steel tube (4 mm thickness; 50 cm diameter, 55 cm high) made up of two demountable half-tubes, bolted together. The sampling tube was placed on the soil surface, coaxially with the maize stump and a cross-bearing was attached to the top. An electric hammer was then used to force the sampling cylinder into the soil to the desired depth (approx. 50 cm). The sampling tube together with its cylindrical soil monolith was then lifted from the soil using a chain block linked to a steel portal frame. The two half-tubes were then removed and the soil monolith was washed out using fine water jets. To minimize root breakage, a steel tube (50 cm diameter, 10 cm high) made up of two demountable half-tubes was fastened around the base of the root core, and the angles and pressures of the jets were optimized. Detailed information of the root sampling system are given in Wu and Guo (2014).
Root separation and scanning
Only two root systems were analysed after a simple visual comparison of the root shape among the three root systems. Each nodal root dissected from the sampled root system was stored in a separate plastic box. There were up to seven whorls of nodal roots in each root system. Only nodal roots arising from the 4th to the 7th nodal-root whorls were comparatively intact and suitable for measurement. Nodal roots from each of the whorls were then grouped according to their visual similarity (i.e. the diameter and length of their axile roots, the length of the unbranched zones, the numbers and lengths of the first-order LRs). The representative nodal roots in each group were selected for further analysis.
The branching zone of the axile root of each of the selected nodal roots was cut into 5-cm sections. Three different scanning strategies were applied according to the complexity of the axile branching sections. For sections of low complexity, the axile branching section was scanned directly including its LRs. For sections of medium complexity, the first-order LRs were cut from the axile root and then scanned together. For sections of high complexity, the first-order LRs were first cut from the axile root and then each LR was cut into a number of parts. After these processes, LRs were spread out by hand before scanning to minimize root overlap. All roots were scanned with a flatbed scanner (i800 Plus, Microtek, Shanghai, China) at a resolution of 400 d.p.i.
Image and data processing
A WinRHIZO Pro 2009b (Régent Instruments Inc., Québec City, Canada) image-analysis system was used to analyse the scanned root images. Noise in the original images was removed using the erasing tool of the software. Pale roots not recognized by the software were emphasized using the filling tool. Incorrect topological connections were also identified and rectified. The developmental segment-ordering system (Berntson, 1997) was used to record root topology. A ‘link’, being defined as a linear (unbranched) portion of a root section bounded at each end either by another root section or by a root tip, was regarded as the basic unit for measurement using the WinRHIZO software. Contiguous groups of links of the same order were treated as an axis (Berntson, 1997). The software organizes the geometry (length and diameter) and topological connection (branching order, axis sequence, link sequence on current axis, its mother axis sequence) of individual links. An LR unit (LRU), a first-order LR with higher-order LRs, was used as a unit to group data derived from the same first-order LR.
Corresponding to the three different root-scanning strategies, corresponding strategies were applied for analysing the images using WinRHIZO. For an axile section with low complexity, the entire axile root section was selected and marked. For an axile section of medium complexity, each first-order root was selected and marked with sequential numbers. For an LRU of high complexity, the successive parts of each cut first-order LR were marked with sequential numbers. After analysis of a scanned image, the data were output to a text file by the software. A script based on the Visual Basic Application (VBA) language embedded in Microsoft Excel was used to batch the files to extract the topological connections and geometrical data of individual LRUs (Wu and Guo, 2014). For an LRU of high complexity, which had been cut into pieces for scanning, these pieces were sequentially merged to reconstitute the complete LRU by the script. Finally, the script exported a file containing comma-separated values for individual nodal roots. Detailed information on the script can be found in Wu and Guo (2014).
Calculations
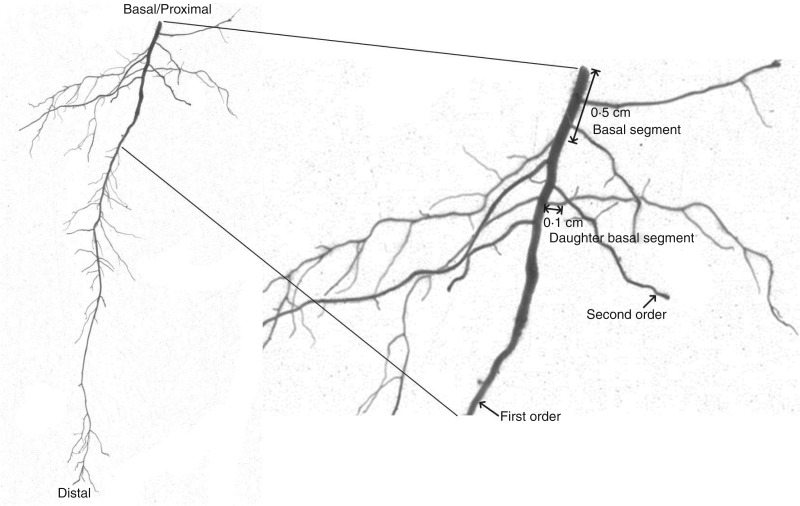
A total of 25 nodal roots of N09, 19 of Z09 and 28 of Z11 were scanned. Altogether, there were 22 880 first-order, 144 624 second-order, 25 650 third-order and 1941 fourth-order LRs. Each LR was divided into 1-mm-long segments using linear interpolation, and the diameter of each was equal to the diameter of its link. Basal diameters of first-order LRs were referred to the diameters of the basal root segment with length being at most 0·5 cm long, and the length of the basal segment for higher-order LRs was 0·1 cm (Fig. 1). The R software (R Development Core Team, 2014) was used for data analysis in which the ggplot2 package (http://ggplot2.org/) was used for data visualization.
Fig. 1.
Scheme for describing the terminology of roots and the definition of root traits.
RESULTS
Variation of diameters and topological connections of diameters within the root system
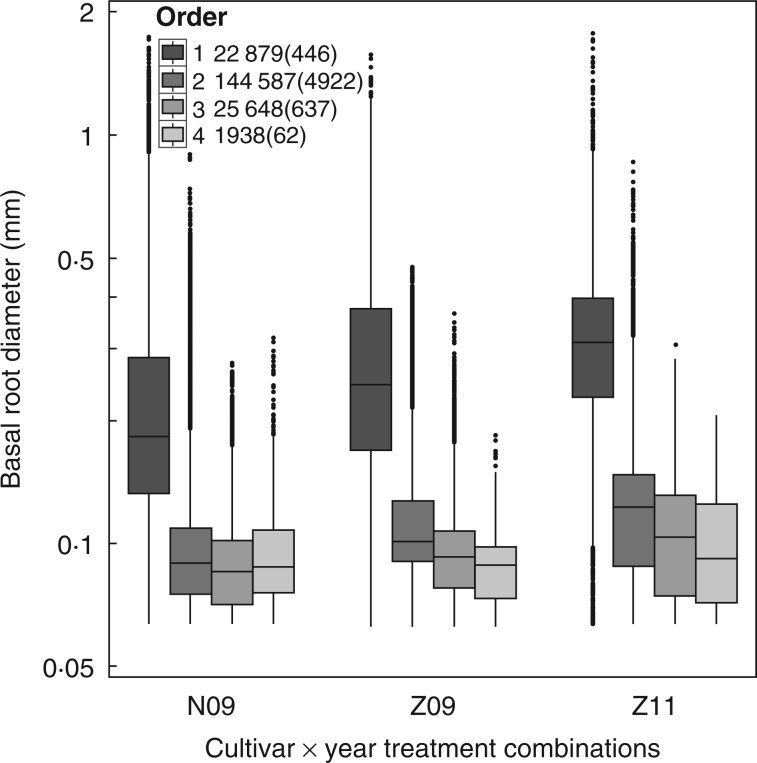
Median basal diameter decreased with increasing branching order. The exception to this was for fourth-order LRs of N09 (Fig. 2). The median basal diameters of the first-order LRs were substantially greater than of the second-order LRs, while the differences in median basal diameter among the other-order LRs were much smaller. The variations in diameter also decreased with increasing branching order. This effect was still distinguishable at a logarithmic scale. However, the diameter variations did not differ very much for the two cultivars in the same season (Z09 and N09) nor for the same cultivar in the two different seasons (Z09 and Z11).
Fig. 2.
Basal diameter variation of different-order lateral roots of maize cultivar × year treatment combinations. N09, Z09 and Z11 indicate ‘ND108’ in 2009, ‘ZD958’ in 2009 and ‘ZD958’ in 2011, respectively. Medians (solid, horizontal thick lines), means (dashed horizontal lines), and 25 and 75 % quartiles (lower and upper margins of the boxes) of diameters of different-order laterals are shown. The upper/lower whiskers extend from the hinge to the highest/lowest value that is within 1·5 × IQR (inter-quartile range) of the hinge, where IQR is the distance between the first and third quartiles. Outliers are any data lying beyond the end of the whiskers. The y-axis scale is logarithmically transformed. The total number of roots and outliers (in parentheses) of each LR order are given in the key.
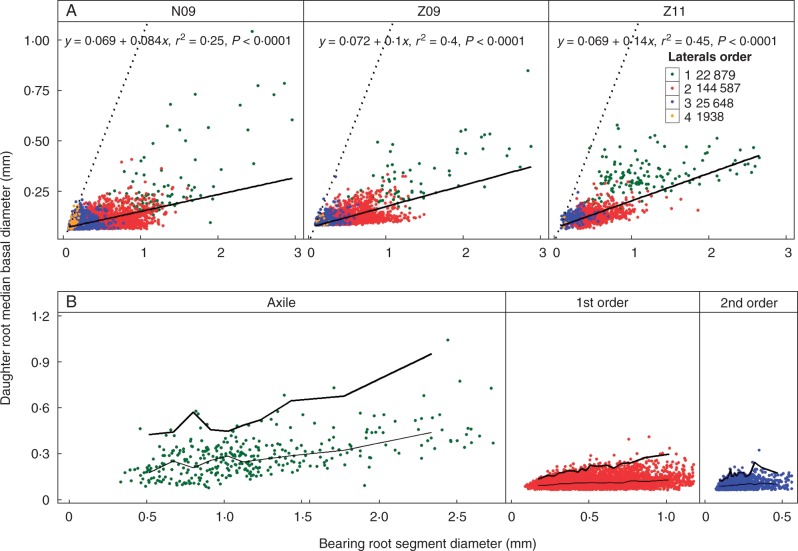
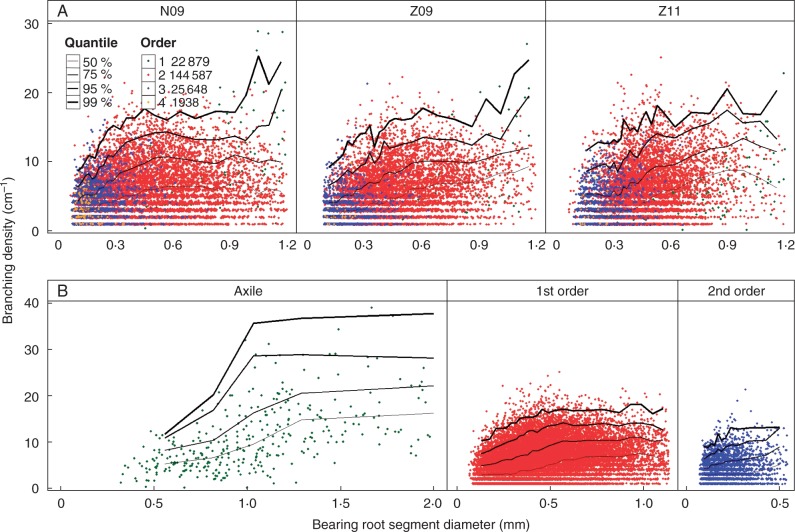
In Fig. 3 we present the relationship between the median diameter of the LRs and the diameter of the bearing segment, for the three treatment combinations separately, and also pooling all root orders. The correlations were highly significant but lower for cultivar N (R2 = 0·26 for N09) than for cultivar Z (R2 = 0·4 for Z09 and R2 = 0·45 for Z11). Both the intercepts and the slopes were not significantly different for the three treatment combinations. The position of the points depended on the root order, especially those for the first-order laterals, which tended to be above the common regression lines. For this reason, we re-analysed the relationship for distinct root orders, mixing the three treatment combinations. These correlations were significant but were high only for the axile-bearing segments (R2 = 0·35 for the axile roots and R2 < 0·1 for the second- and third-order LRs). Thus, a simple linear regression did not satisfactorily describe the relationship due to the large variation of daughter root diameter for a given diameter class. Instead, we calculated and plotted quantiles of the median basal diameter of the daughter roots based on its bearing diameter classes (Fig. 3B). The highest curve (the 99 % quantile) defined the potential median basal diameter of the daughter roots for a given bearing diameter. With increasing bearing root diameter, the increase in the potential diameter of daughter roots was steeper than for the median diameter. For similar bearing diameter ranges, lower-order roots tended to give daughter roots with larger potential basal diameters.
Fig. 3.
Relationship between the basal diameter of daughter roots and the diameter of bearing root segments. Different criteria were set for the length of bearing root segment and its branching number: length of axile root segment was 5 cm; length of first-order LR segment was 2 cm and its branching number was not less than 4; length of second-order LR segment was 1 cm and its branching number was not less than 2. (A) Different branching-order LRs were pooled for each treatment combination. (B) For each branching order, pooling the three treatment combinations. Curves of different thickness indicate the 50 % (thin) and 99 % (thick) quantile curves. The total number of roots for each-order LRs is given in the key.
Relationships between diameter and final individual root length
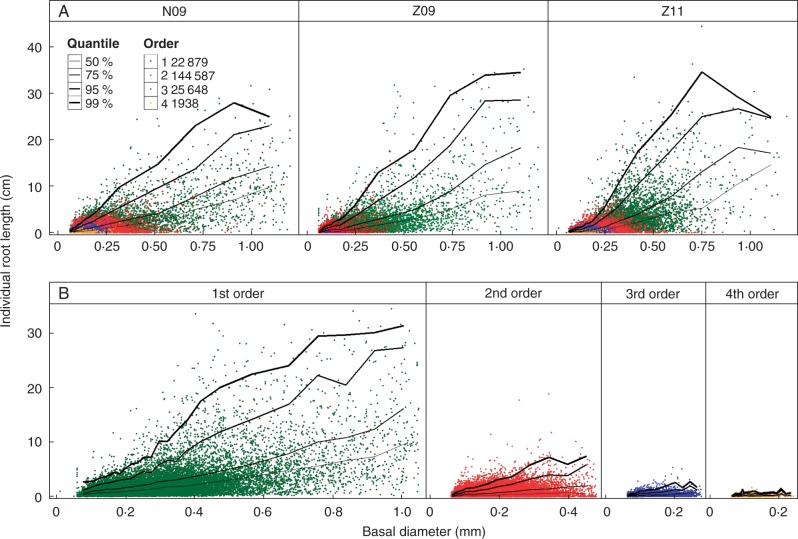
Root length tended to increase with basal diameter (Fig. 4). The correlations between these variables were significant for all treatment combinations (P < 0·0001), and the coefficients of determination (R2) were always greater than 0·39. The variation of the intercepts (−0·46 to −0·86 mm) and slopes (83 to 96) of the regression lines of the three treatment combinations were small. As the length variations were high for each diameter class, we calculated and plotted quantiles of length for diameter classes (Fig. 4). The curves joining these quantiles increased, particularly in the range 0–0·9 mm, and then stabilized to a plateau from 25 to 35 cm (Fig. 4A). The higher curves (the 95 and 99 % quantiles) defined a potential length for a given diameter. As the regression lines and the variations of the quantile curves were similar for the three treatment combinations, the data for the three treatment combinations were pooled and examined for distinct orders (Fig. 4B). Within the same basal diameter range, roots of lower order had greater root lengths. However, with increasing basal diameter, the increased rate in potential length was lower for roots with larger diameter, above 0·6 mm (Fig. 4A).
Fig. 4.
Relationships between lengths and basal diameters of different-order LRs. Basal diameters were divided into 25 classes. (A) Pooling the branching orders for each treatment combination. (B) For each order of roots, pooling the three treatment combinations. The total number of roots for each LR order is given in the key.
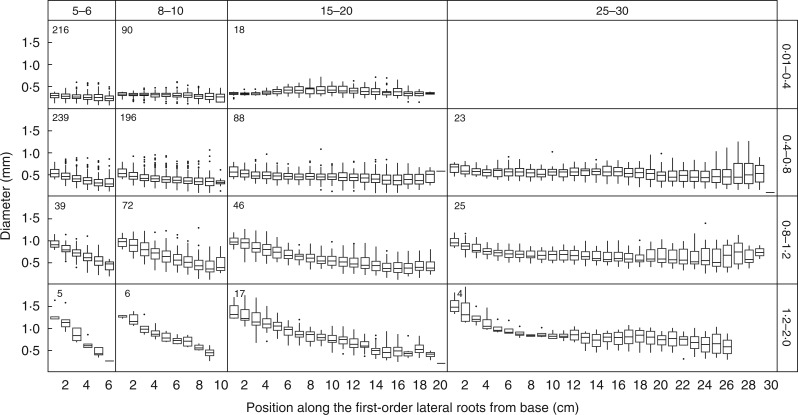
We observed that diameter varied along the first-order LRs (Supporting Information, Fig. S1). Therefore, we made a more systematic examination of the diameter change pattern of first-order LRs for different classes of length and basal diameter (Fig. 5). For a large majority of roots, the diameter decreased from the proximal to the distal end. It is also clear that variations of basal diameter were much larger than those of distal diameter. Distal diameter remained in the range 0·25–0·55 mm for the median values. For the same length class, roots with a greater basal diameter showed a steeper diameter decrease. This indicates that, for a given length class, diameter change is related to basal diameter. Moreover, for each basal diameter class, this decrease was steeper for short roots. Conversely, the long roots tended to maintain their larger diameters better. Root diameter even increased in intermediate position for roots in the small diameter class (0·01–0·4 mm) but having greater length (15–20 cm). Hence, the pattern of diameter change along the roots was related to basal diameter and length and the diameter decrease rate was related to the final length.
Fig. 5.
Diameter variations along first-order LRs for different classes of length and basal diameter. The length classes were 5–6, 8–10, 15–20 and 25–30 cm and the diameter classes were 0·01–0·4, 0·4–0·8, 0·8–1·2 and 1·2–2·0 mm. For each position (every 1 cm) along the root, the boxplot shows the 50 % (line), 25 % and 75 % (box margins) values. The meaning of whiskers and outliers is as in Fig. 2. The number of roots used in each panel is given in the upper left.
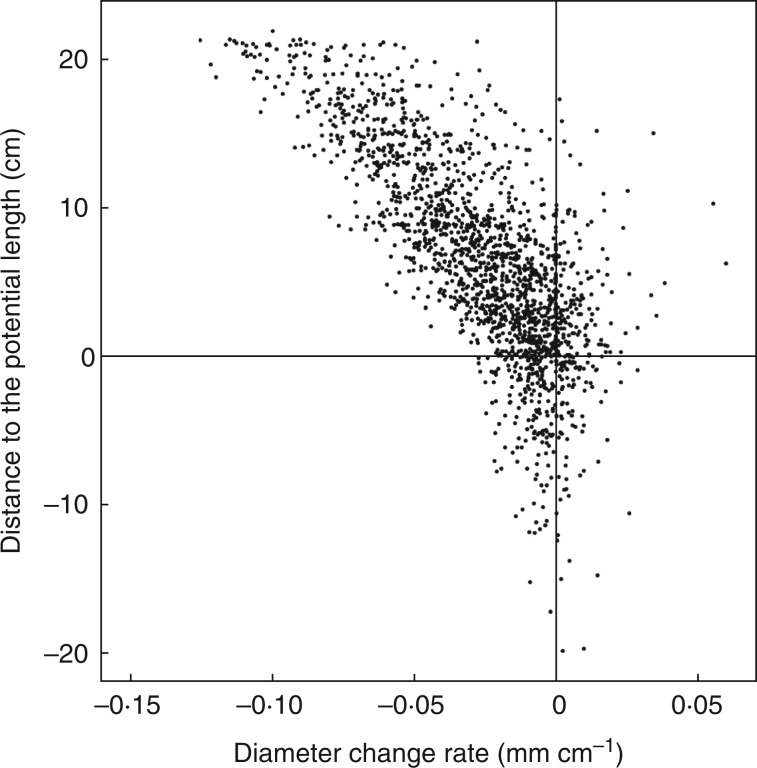
To understand this trend from a more synthetic view, we plotted the distance to the potential length (95 % quantile) versus the diameter change rate for each basal diameter class (Fig. 6). The distance to the potential length is calculated for individual roots as the potential length minus the observed length. The diameter change rate is calculated as the difference between the distal diameter and the basal diameter, divided by the length. First-order roots greater than 5 cm were included, irrespective of their classification based on length and basal diameter. The left-hand side of Fig. 6 confirms the phenomenon shown in Fig. 5 – i.e. the lower the rate of diameter decrease, the closer a root is to its potential length (for its basal diameter class). In contrast, the right-hand side does not show an obvious trend. The lower, right-hand part of the figure shows roots that increased their diameters and reached lengths higher than expected, while the upper right-hand part shows roots that increased their diameters but whose lengths were very different from their potential lengths. We hypothesize that the roots in the upper right-hand part may have encountered a volume of compacted soil (having low penetrability), as their growth stopped and their apical diameters increased (Fig. S2). Some of these roots have also produced thick LRs (Fig. S2).
Fig. 6.
Distance to the potential length versus diameter change rate of different basal diameter classes of first-order LRs. Diameter change rate is calculated as: the distal diameter minus the basal diameter, divided by the length. Potential length indicates the length within the 95 % quantile. Distance to the potential length is calculated as: the potential length minus the length of an individual root. Roots <5 cm long were not included in this calculation.
The relationships between diameter and branching density at the root segment scale
The relationships between the number of daughter roots and diameters of their bearing root segments are presented in Fig. 7. Correlations were significant (P < 0·0001) for the three treatment combinations, but the coefficients of determination were low (R2 < 0·16). Again, we used the curves joining the quantiles to help interpret these loose relationships (Fig. 7). Branching density increased with bearing root segment diameter, especially for low values of segment diameter, i.e. below 0·5 mm (Fig. 7A). Above this value, the increase was null or moderate. The potential branching density (represented by the 95 and 99 % quantiles) was reached for intermediate diameter roots. Branching density was also analysed by branching order (Fig. 7B). According to these graphs, branching density was dependent on branching order. Branching density was higher for lower-order bearing roots of the same diameter range. The plateau was reached by thicker bearing roots (1 mm for axile roots, 0·5 mm for first-order LRs and 0·3 mm for second-order LRs).
Fig. 7.
Relationship between branching density and diameter of root segments of different orders. Unbranched segments were not included in the figures. Different criteria were set for the length of bearing root segment and its branching number, as in Fig. 3. (A) Pooling the branching orders for each treatment combination; basal diameters were divided into 25 classes. (B) For each branching order, pooling the three treatment combinations; basal diameters were divided into five classes for axile roots and into 25 classes for LRs. The total number of roots for each LR order are given in the key.
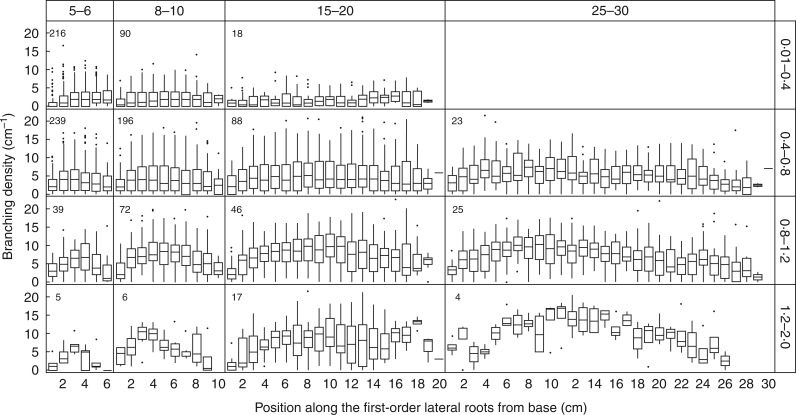
We further analysed the pattern of variation in branching density as it relates to the categories of length and basal diameter (Fig. 8). In the small-diameter class (0·01–0·4 mm), branching density did not vary consistently along the roots whatever their length. However, for larger-diameter classes, branching density increased from the base and reached its highest values at intermediate positions. The thicker and longer the root, the stronger was this trend. In both Fig. 7 and Fig. 8, the relationship between diameter and branching density was distorted by the location of this segment along the root. Indeed, thick segments near the proximal part of the root did not branch as densely. This ‘position’ effect partly explains the loose relationship between branching density and the diameter of the bearing segment.
Fig. 8.
Branching density variation along first-order LRs for different classes of length and basal diameter. The length classes were 5–6, 8–10, 15–20 and 25–30 cm and the diameter classes were 0·01–0·4, 0·4–0·8, 0·8–1·2 and 1·2–2·0 mm. For each position (every 1 cm) along the root, the boxplot shows the 50 % (line), 25 % and 75 % (box margins) values. The meaning of whiskers and outliers is as in Fig. 2. The number of roots used in each panel is given in the upper left.
DISCUSSION
In this study, we applied a custom root sampling method and a combined image processing procedure and data analysis program to study root diameter and branching at the root segment scale in mature, field-grown maize plants. This combined method allows very detailed examination of the geometry and topology of the root systems of mature, field-grown plants, such as maize. A simple scheme was used to illustrate the common structure of roots having increasing basal diameter (Fig. 9). Roots with larger basal diameters tended to grow longer, and to have more branches of larger basal diameters and greater lengths. In spite of large variations in their basal diameters, their distal diameters did not vary very much. However, some distinct branching patterns did occur. In this study, we found that first-order LRs with similar basal diameters had multiple patterns of diameter change, resulting in different root lengths. Basal diameter further determined the extent of diameter change. Specifically, for roots having the same length classification, those having larger basal diameters showed a greater rate of diameter decrease along the roots; meanwhile for roots having the same diameter classification, those having longer roots show a smaller rate of diameter decrease (Fig. 5). The variation of the diameter of root segments thus affected the basal diameter and the number of daughter roots (Figs 3 and 7). The relationships between diameter, length and branching density and their hierarchical connections are discussed below.
Fig. 9.
Four scanned first-order roots with increasing basal diameter, length and branching density but with similar distal diameters.
The positive correlation between daughter root diameter and mother root diameter has been already noted and quantified for several species (Bouma et al., 2001; Lecompte et al., 2005; Bécel et al., 2012; Pagès et al., 2013, 2014). However, in these studies the sampling methods and definitions of daughter root and bearing root diameter were mostly different from those used here. The earlier studies normally linked the median apical diameter of the daughter roots in a whole or a distal bearing root to the apical or average diameter of the bearing root for various dicotyledonous and monocotyledonous species (Lecompte et al., 2005; Bécel et al., 2012; Pagès et al., 2013, 2014). To account for the change in diameter along the bearing roots, which were not considered in previous studies, we linked the median basal diameters of daughter roots in successive bearing root segments to the diameters of these segments for axile roots and higher-order LRs (Fig. 3A). The relationship between daughter root diameter and mother root diameter shows that a significant part of the variation of basal diameter can be explained by the diameter of the bearing segment. The distribution of the diameters of daughter roots in each diameter class of bearing roots was simply described using quantile curves with different probability values (Fig. 3B). Thicker bearing root segments had larger variations in the diameters of daughter roots. This may indicate that the daughter roots of a thick bearing root segment have a greater capacity to respond to the local soil environment, or to the overall condition of the plant. This capacity is important if plants are to expand and refine their exploration of the soil. Thus, roots with large basal diameters will have a greater capacity both to grow longer (to reach more distant resources) (Fig. 4) and to generate more abundant and higher-order branches (to increase soil contact area) (Figs 3 and 7). The converse is also true. Small root basal diameter allows the effective uptake of local resources and will minimize the investment needed to build and maintain the root system, to allow other parts of the root system to exploit the soil’s external resources (water, minerals, etc.) more effectively.
The relationship between basal diameter and final root length of different-order roots indicates that only roots with large basal diameters have a chance to become long (Fig. 4). This relationship has been confirmed and refined in earlier studies with maize, on correlations between root apical diameter and growth rate and growth duration (Cahn et al., 1989). In our study, however, we observed very large variations in root length (especially for thick roots) which were not considered by Cahn et al. (1989), and most roots do not reach their potential length. Several previous studies have recorded temporal variations in apical diameter (Pagès, 1995; Thaler and Pagès, 1996a, b; Lecompte et al., 2001). These found that apical diameter was not a fixed attribute of the root and could vary in parallel with growth rate during the elongation of an individual root. Such fluctuations in apical diameter and growth rate were related to variations in assimilate availability (Pagès, 1995; Thaler and Pagès, 1996a, b; Lecompte et al., 2001). Monocot roots do not grow radially, so the time variation of apical diameter is represented in a root’s proximal–distal diameter profile. Of course local variations in soil factors, such as penetrability, will also influence this pattern of longitudinal diameter (Bécel et al., 2012). According to the diameter profile of first-order LRs with various basal diameter (0–2 mm) (Fig. 5), we found most roots decreased in diameter, while others increased, and then decreased in diameter. This phenomenon has also been observed in dicot seedlings (e.g. in oak and rubber trees) for roots with a small basal diameter range (0·4–0·8 mm) (Pagès, 1995; Thaler and Pagès, 1996a). We found that the structured diameter change along a root also induced length variation (Figs 5 and 6). For a given basal diameter, those roots which become long were also able somehow to maintain their diameters. This property was similar to that observed in tree seedlings (Pagès, 1995). Nevertheless, increasing apical diameter did not always result in increased root length, as soil physical characteristics can induce increases in diameter for distal parts of roots while, at the same time, hindering their elongation (Fig. S2). This phenomenon has been observed previously (Atwell, 1993; Croser et al., 2000; Bengough et al., 2006). Basal diameter did not only affect final root length (Fig. 4) nor the longitudinal pattern of diameter variation (Fig. 5). For a given length, roots having larger basal diameters had steeper longitudinal diameter decreases. Morphologically, both the basal diameter and the pattern of diameter change determined final root length. In addition to the effects of root diameter, several external factors have also been shown to affect root growth rate and root growth duration, and thus final root length. These external factors include soil temperature (Tardieu and Pellerin, 1991; Nagel et al., 2009), soil penetrability (Bécel et al., 2012), global nutrient availability and nutrient patchiness (Yu et al., 2015). In spite of the large variation in basal diameter and the discernible pattern of diameter change among first-order LRs, distal diameter was much less variable. This seems to imply the existence of a minimum threshold for distal diameter.
There were large variations in branching density, especially along the axile roots. The highest branching density along axile root segments was almost 45 cm−1 in the 5-cm segments (Fig. 7). This is higher than observed in field-grown maize (35 cm−1 in 2-cm segments) (Pagès and Pellerin, 1994), in pot-grown maize seedlings (30 cm−1 in 5-cm segments) (Varney et al., 1991) and in banana (20 cm−1 in 2-cm segments) (Lecompte and Pagès, 2007). The highest branching density of our first-order LR segments was 24 cm−1 (Fig. 7). This is not very different from the highest values of 23 cm−1 in banana (Lecompte and Pagès, 2007). Contrasting with the consensus view that a positive relationship exists between daughter-root diameter and bearing-root diameter, there are contradictory understandings of the relationship between branching density and bearing-root diameter. Bécel et al. (2012) observed decreases in branching density with decreasing mean bearing-root diameter in peach. Lecompte and Pagès (2007) also found in banana that first-order LRs of smaller diameters tended to have higher branching densities than axile roots of larger diameter. For banana, Draye (2002) also observed for axile roots that branching density increased with increasing apical diameter. These different relationships observed in banana may be attributed to the different elongation rate among root orders, which can cause differences in daughter-root spacing along the protoxylem-based files and also variation in the number of protoxylem poles (Draye, 2002; Lecompte and Pagès, 2007). The decrease in branching density along nodal roots has been observed in field-grown maize (Pagès and Pellerin, 1994). As diameter decreases along a nodal root, it can be inferred that branching density decreases with decreasing root diameter. In our study, we divided the bearing root into successive segments so the variation in branching density in different parts of a bearing root could be recorded. We observed that branching density increased with bearing root segment diameter for all root orders. The relationship was relatively tight for axile roots, although an early plateau was reached by axile root segments of intermediate diameters (Fig. 7). Most researchers have measured branching density in young plants (Varney et al., 1991; Lecompte et al., 2005; Ito et al., 2006) while our study considers the nodal roots of high whorls on mature plants. It has already been shown that diameter decrease is much steeper on nodal roots originating from the higher whorls (Wu et al., 2014). The proximity to the root base, and hence the (presumably) abundant carbohydrate supply from the shoot, may enable the large, basal axile root segments to burst more daughter roots, these still mostly having large basal diameters. The phenomenon that axile root segments generally have greater numbers of daughter roots, with large basal diameters, does not fit with the idea of a trade-off between the numbers and diameters of daughter roots of young seedlings (Lecompte et al., 2005; Pagès, 2014). The contrary observation of these authors may relate to a limitation of assimilate supply from the small above-ground shoots of their plants. Hence, the axile roots, emerging at different stages of growth, could well have different branching characteristics.
Compared with axile roots, the branching density along LRs has received generally less attention (Lecompte et al., 2005; Ito et al., 2006; Gaudin et al., 2011; Gruber et al., 2013). The structured profile of branching density along first-order LRs is a new finding (Fig. 8). Although the potential branching density of root segments of maize may usually be related to their diameter, the largest number of daughter roots was often found in intermediate positions and with roots of intermediate diameter. This was especially true for the thick, first-order LRs. The diameter normally decreases sharply in the proximal part, while the protoxylem poles decrease at a moderate rate (Draye, 2002). The longitudinal spacing of daughter roots within protoxylem-based files was found to be positively correlated with apical diameter (Draye, 2002). The decrease in protoxylem poles may cause the decrease in branching density, while the decrease in longitudinal spacing within protoxylem-based files may cause an increase in branching density (Draye, 2002). When the decrease in the longitudinal spacing within protoxylem-based files exceeds the decrease in protoxylem poles, it will probably result in an increase in branching density with apical diameter decrease. Hence, the highest branching density can often be found in the middle and/or proximal part of a root. With increasing distance to the root base (also to the assimilate source), the assimilate supply from the above-ground shoot may not satisfy the demand for increasing branching density, induced by the progressive reductions in both apical diameter and elongation rate. Thus, branching density tends to decrease in the distal part of the root. The variation in branching density can also be attributed to soil factors, such as to gradients in soil bulk density (Konôpka et al., 2009), in soil moisture (Johnson and Aguirre, 1991; Ito et al., 2006), in soil temperature (Sattelmacher et al., 1990) and in soil nutrients (Gruber et al., 2013), including as roots traverse nutrient patches (Hodge, 2004; Yu et al., 2014). However, as these first-order LRs are located at different positions along the nodal roots, and the nodal roots from higher whorls exhibit steeper root angles, so that they penetrate the soil more vertically, the first-order LRs will experience a diversity of local soil environments, so being more likely to be affected by a range of soil factors. In spite of the effects of these factors, the profile of branching density on the first-order LRs is relatively stable. Hence, the profile of branching density on first-order LRs is determined by both their basal diameter and their elongation and may be an inherent feature of maize plants.
Detailed root traits have been extracted mostly for seedling root systems, using recently developed automated/semi-automated methods in two or three dimensions (Iyer-Pascuzzi et al., 2010; Clark et al., 2011, 2012; Mairhofer et al., 2012; Nagel et al., 2012; Tracy et al., 2012). These results, combined with root function studies, facilitate the parameterization of root architectural models used to simulate the whole root systems of young plants. In contrast, these detailed results on adult root architecture, especially of plants grown in the field, are still largely lacking (Fiorani and Schurr, 2013). The most detailed measurements of mature root systems in the field were the trajectories of axile roots in two/three dimensions (Tardieu and Pellerin, 1990; Wu et al., 2014). The diameters along the axile roots were also measured with the trajectory (Wu et al., 2014). In contrast, information on root branching was particularly lacking, even for the branching of axile roots (Pagès and Pellerin, 1994; Pagès, 2014; Wu and Guo, 2014). In this research, we started from an analysis of the branching of first-order LRs of field-grown maize plants, including their diameter variations. Root diameter is an indispensable morphological parameter in a root architectural model (Dunbabin et al., 2013). To simplify computation in most root models, LR diameter has usually been assumed to be constant for young plants, as the diameters of fine LRs do not vary greatly (Fig. 5). For simulations of adult root systems, the diameter variation along axile roots and along first-order LRs cannot be ignored (Pagès, 1995; Thaler and Pagès, 1996a; Wu et al., 2014) as this diameter variation correlates strongly with anatomical features, the diameters and numbers of the daughter laterals (Fig. 3 and Fig. 7), and thus their life spans and functions in resource absorption. The relationships of branching characteristics obtained in this research did not exclude the effects of external factors on branching, such as the availability of N and P (Postma et al., 2014), nutrient patchiness (Yu et al., 2015) and soil penetrability (Bécel et al., 2012), as large variations in branching density did, indeed, exist among roots even in the same groupings (Fig. 8). In spite of this, the general branching patterns should be a primary guide for obtaining root morphological parameters for root models used to simulate large root systems.
SUPPLEMENTARY DATA
Supplementary data are available online at www.aob.oxfordjournals.org and consist of the following. Fig. S1: Diameter change along a small sample of first-order LRs for different classes of length and basal diameter. Fig. S2: Roots that may have encountered an obstruction (e.g. a volume of low-penetrability soil) have increased their apical diameters and produced thicker LRs.
ACKNOWLEDGEMENTS
This work was supported by the National Natural Science Foundation of China (41471235) and the China Postdoctoral Science Foundation (2015M571167). We thank Jie Zhou and Kai Bai for their help on conducting the experiments and Dr Sandy Lang for his valuable comments on the manuscript.
LITERATURE CITED
- Abe J, Morita S. 1994. Growth direction of nodal roots in rice: its variation and contribution to root system formation. Plant and Soil 165: 333–337. [Google Scholar]
- Atkinson JA, Rasmussen A, Traini R, et al. 2014. Branching out in roots: uncovering form, function, and regulation. Plant Physiology 166: 538–550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atwell BJ. 1993. Response of roots to mechanical impedance. Environmental and Experimental Botany 33: 27–40. [Google Scholar]
- Bécel C, Vercambre G, Pagès L. 2012. Soil penetration resistance, a suitable soil property to account for variations in root elongation and branching. Plant and Soil 353: 169–180. [Google Scholar]
- Bengough AG, Bransby MF, Hans J, McKenna SJ, Roberts TJ, Valentine TA. 2006. Root responses to soil physical conditions; growth dynamics from field to cell. Journal of Experimental Botany 57: 437–447. [DOI] [PubMed] [Google Scholar]
- Berntson GM. 1997. Topological scaling and plant root system architecture: developmental and functional hierarchies. New Phytologist 135: 621–634. [Google Scholar]
- Bidel LPR, Pagès L, Rivière LM, Pelloux G, Lorendeau JY. 2000. MassFlowDyn I: a carbon transport and partitioning model for root system architecture. Annals of Botany 85: 869–886. [Google Scholar]
- Bouma TJ, Nielsen KL, Van Hal J, Koutstaal B. 2001. Root system topology and diameter distribution of species from habitats differing in inundation frequency. Functional Ecology 15: 360–369. [Google Scholar]
- Cahn M, Zobel R, Bouldin D. 1989. Relationship between root elongation rate and diameter and duration of growth of lateral roots of maize. Plant and Soil 119: 271–279. [Google Scholar]
- Clark LJ, Price AH, Steele KA, Whalley WR. 2008. Evidence from near-isogenic lines that root penetration increases with root diameter and bending stiffness in rice. Functional Plant Biology 35: 1163–1171. [DOI] [PubMed] [Google Scholar]
- Clark RT, MacCurdy RB, Jung JK, et al. 2011. Three-dimensional root phenotyping with a novel imaging and software platform. Plant Physiology 156: 455–465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark RT, Famoso AN, Zhao K, et al. 2012. High-throughput two-dimensional root system phenotyping platform facilitates genetic analysis of root growth and development. Plant, Cell & Environment 36: 454–466. [DOI] [PubMed] [Google Scholar]
- Croser C, Bengough AG, Pritchard J. 2000. The effect of mechanical impedance on root growth in pea (Pisum sativum). II. Cell expansion and wall rheology during recovery. Physiologia Plantarum 109: 150–159. [Google Scholar]
- Draye X. 2002. Consequences of root growth kinetics and vascular structure on the distribution of lateral roots. Plant, Cell & Environment 25: 1463–1474. [Google Scholar]
- Dunbabin VM, Postma JA, Schnepf A, et al. 2013. Modelling root–soil interactions using three–dimensional models of root growth, architecture and function. Plant and Soil 372: 93–124. [Google Scholar]
- Eissenstat DM. 1992. Costs and benefits of constructing roots of small diameter. Journal of Plant Nutrition 15: 763–782. [Google Scholar]
- Fan M, Zhu J, Richards C, Brown KM, Lynch JP. 2003. Physiological roles for aerenchyma in phosphorus-stressed roots. Functional Plant Biology 30: 493 – 506. [DOI] [PubMed] [Google Scholar]
- Fiorani F, Schurr U. 2013. Future scenarios for plant phenotyping. Annual Review of Plant Biology 64: 267–291. [DOI] [PubMed] [Google Scholar]
- Fitter AH. 1987. An architectural approach to the comparative ecology of plant root systems. New Phytologist 106: 61–77. [Google Scholar]
- Gaudin ACM, Mcclymont SA, Holmes BM, Lyons E, Raizada MN. 2011. Novel temporal, fine-scale and growth variation phenotypes in roots of adult-stage maize (Zea mays L.) in response to low nitrogen stress. Plant, Cell & Environment 34: 2122–2137. [DOI] [PubMed] [Google Scholar]
- Gruber BD, Giehl RFH, Friedel S, von Wirén N. 2013. Plasticity of the Arabidopsis root system under nutrient deficiencies. Plant Physiology 163: 161–179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hackett C. 1969. Quantitative aspects of the growth of cereal root systems. In: WJ Wittington, ed. Root growth. London: Butterworth & Co, 134–147. [Google Scholar]
- Hodge A. 2004. The plastic plant: root responses to heterogeneous supplies of nutrients. New Phytologist 162: 9–24. [Google Scholar]
- Ito K, Tanakamaru K, Morita S, Abe J, Inanaga S. 2006. Lateral root development, including responses to soil drying, of maize (Zea mays) and wheat (Triticum aestivum) seminal roots. Physiologia Plantarum 127: 260–267. [Google Scholar]
- Iyer-Pascuzzi AS, Symonova O, Mileyko Y, et al. 2010. Imaging and analysis platform for automatic phenotyping and trait ranking of plant root systems. Plant Physiology 152: 1148–1157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaramillo RE, Nord EA, Chimungu JG, Brown KM, Lynch JP. 2013. Root cortical burden influences drought tolerance in maize. Annals of Botany 112: 429–437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson DA, Aguirre L. 1991. Effect of water on morphological development in seedlings of three range grasses: root branching patterns. Journal of Range Management 44: 355–360. [Google Scholar]
- Jordan M-O, Harada J, Bruchou C, Yamazaki K. 1993. Maize nodal root ramification: absence of dormant primordia, root classification using histological parameters and consequences on sap conduction. Plant and Soil 153: 125–143. [Google Scholar]
- Konôpka B, Pagès L, Doussan C. 2009. Soil compaction modifies morphological characteristics of seminal maize roots. Plant Soil Environment 55: 1–10. [Google Scholar]
- Lecompte F, Pagès L. 2007. Apical diameter and branching density affect lateral root elongation rates in banana. Environmental and Experimental Botany 59: 243–251. [Google Scholar]
- Lecompte F, Ozier-Lafontaine H, Pagès L. 2001. The relationships between static and dynamic variables in the description of root growth. Consequences for field interpretation of rooting variability. Plant and Soil 236: 19–31. [Google Scholar]
- Lecompte F, Pagès L, Ozier-Lafontaine H. 2005. Patterns of variability in the diameter of lateral roots in the banana root system. New Phytologist 167: 841–850. [DOI] [PubMed] [Google Scholar]
- Lynch JP, Chimungu JG, Brown KM. 2014. Root anatomical phenes associated with water acquisition from drying soil: targets for crop improvement. Journal of Experimental Botany 65: 6155–6166. [DOI] [PubMed] [Google Scholar]
- Mairhofer S, Zappala S, Tracy SR, et al. 2012. RooTrak: automated recovery of three-dimensional plant root architecture in soil from x-ray microcomputed tomography images using visual tracking. Plant Physiology 158: 561–569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malamy JE, Benfey PN. 1997. Organization and cell differentiation in lateral roots of Arabidopsis thaliana. Development 124: 33–44. [DOI] [PubMed] [Google Scholar]
- Materechera SA, Alston AM, Kirby JM, Dexter AR. 1992. Influence of root diameter on the penetration of seminal roots into a compacted subsoil. Plant and Soil 144: 297–303. [Google Scholar]
- Nagel KA, Kastenholz B, Jahnke S, et al. 2009. Temperature responses of roots: impact on growth, root system architecture and implications for phenotyping. Functional Plant Biology 36: 947–959. [DOI] [PubMed] [Google Scholar]
- Nagel KA, Putz A, Gilmer F, et al. 2012. GROWSCREEN-Rhizo is a novel phenotyping robot enabling simultaneous measurements of root and shoot growth for plants grown in soil-filled rhizotrons. Functional Plant Biology 39: 891–904. [DOI] [PubMed] [Google Scholar]
- Nibau C, Gibbs DJ, Coates JC. 2008. Branching out in new directions: the control of root architecture by lateral root formation. New Phytologist 179: 595–614. [DOI] [PubMed] [Google Scholar]
- North GB, Nobel PS. 1991. Changes in hydraulic conductivity and anatomy caused by drying and rewetting roots of Agave deserti (Agavaceae). American Journal of Botany 78: 906–915. [Google Scholar]
- Oyanagi A, Nakamoto T, Morita S. 1993. The gravitropic response of roots and the shaping of the root system in cereal plants. Environmental and Experimental Botany 33: 141–158. [Google Scholar]
- Pagès L. 1995. Growth patterns of the lateral roots of young oak (Quercus robur) tree seedlings relationship with apical diameter. New Phytologist 130: 503–509. [DOI] [PubMed] [Google Scholar]
- Pagès L. 2011. Links between root developmental traits and foraging performance. Plant, Cell & Environment 34: 1749–1760. [DOI] [PubMed] [Google Scholar]
- Pagès L. 2014. Branching patterns of root systems: quantitative analysis of the diversity among dicotyledonous species. Annals of Botany 114: 591–598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pagès L, Pellerin S. 1994. Evaluation of parameters describing the root system architecture of field grown maize plants II. Density, length, and branching of first-order lateral roots. Plant and Soil 164: 169–176. [Google Scholar]
- Pagès L, Xie J, Serra V. 2013. Potential and actual root growth variations in root systems: modeling them with a two-step stochastic approach. Plant and Soil 373: 723–735. [Google Scholar]
- Pagès L, Bécel C, Boukcim H, Moreau D, Nguyen C, Voisin A-S. 2014. Calibration and evaluation of ArchiSimple, a simple model of root system architecture. Ecological Modelling 290: 76–84. [Google Scholar]
- Postma JA, Dathe A, Lynch J. 2014. The optimal lateral root branching density for maize depends on nitrogen and phosphorus availability. Plant Physiology 166: 590–602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pregitzer KS, Hendrick RL, Fogel R. 1993. The demography of fine roots in response to patches of water and nitrogen. New Phytologist 125: 575–580. [DOI] [PubMed] [Google Scholar]
- R Development Core Team. 2014. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. [Google Scholar]
- Saengwilai P, Nord EA, Chimungu JG, Brown KM, Lynch JP. 2014. Root cortical aerenchyma enhances nitrogen acquisition from low-nitrogen soils in maize. Plant Physiology 166: 726–735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sattelmacher B, Marschner H, Kühne R. 1990. Effects of the temperature of the rooting zone on the growth and development of roots of potato (Solanum tuberosum). Annals of Botany 65: 27–36. [Google Scholar]
- Singh V, van Oosterom EJ, Jordan DR, Hunt CH, Hammer GL. 2011. Genetic variability and control of nodal root angle in sorghum. Crop Science 51: 2011. [Google Scholar]
- Steudle E. 2000. Water uptake by roots: effects of water deficit. Journal of Experimental Botany 51: 1531. [DOI] [PubMed] [Google Scholar]
- Tardieu F, Pellerin S. 1990. Trajectory of the nodal roots of maize in fields with low mechanical constraints. Plant and Soil 124: 39–45. [Google Scholar]
- Tardieu F, Pellerin S. 1991. Influence of soil temperature during root appearance on the trajectory of nodal roots of field grown maize. Plant and soil 131: 207–214. [Google Scholar]
- Thaler P, Pagès L. 1996a. Root apical diameter and root elongation rate of rubber seedlings (Hevea brasiliensis) show parallel responses to photoassimilate availability. Physiologia Plantarum 97: 365–371. [Google Scholar]
- Thaler P, Pagès L. 1996b. Periodicity in the development of the root system of young rubber trees (Hevea brasiliensis Müell. Arg.): relationship with shoot development. Plant, Cell & Environment 19: 56–64. [Google Scholar]
- Tracy SR, Black CR, Roberts JA, et al. 2012. Quantifying the impact of soil compaction on root system architecture in tomato (Solanum lycopersicum) by X-ray micro-computed tomography. Annals of Botany 110: 511–519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varney G, Canny M, Wang X, McCully M. 1991. The branch roots of Zea. I. First order branches, their number, sizes and division into classes. Annals of Botany 67: 357. [Google Scholar]
- Wells CE, Eissenstat DM. 2001. Marked differences in survivorship among apple roots of different diameters. Ecology 82: 882–892. [Google Scholar]
- Wu J, Guo Y. 2014. An integrated method for quantifying root architecture of field-grown maize. Annals of Botany 114: 841–851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu J, Pagès L, Wu Q, Yang B, Guo Y. 2014. Three-dimensional architecture of axile roots of field-grown maize. Plant and Soil 387: 363–377. [Google Scholar]
- Yu P, White PJ, Hochholdinger F, Li C. 2014. Phenotypic plasticity of the maize root system in response to heterogeneous nitrogen availability. Planta 240: 667–678. [DOI] [PubMed] [Google Scholar]
- Yu P, Hochholdinger F, Li C. 2015. Root-type-specific plasticity in response to localized high nitrate supply in maize (Zea mays). Annals of Botany 116: 751–762. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.