Data-driven Temporal Prediction of Surgical Site Infection

Abstract

Analysis of data from Electronic Health Records (EHR) presents unique challenges, in particular regarding nonuniform temporal resolution of longitudinal variables. A considerable amount of patient information is available in the EHR - including blood tests that are performed routinely during inpatient follow-up. These data are useful for the design of advanced machine learning-based methods and prediction models. Using a matched cohort of patients undergoing gastrointestinal surgery (101 cases and 904 controls), we built a prediction model for post-operative surgical site infections (SSIs) using Gaussian process (GP) regression, time warping and imputation methods to manage the sparsity of the data source, and support vector machines for classification. For most blood tests, wider confidence intervals after imputation were obtained in patients with SSI. Predictive performance with individual blood tests was maintained or improved by joint model prediction, and non-linear classifiers performed consistently better than linear models.

Introduction

When using observational data from secondary sources such as the Electronic Health Record (EHR) one needs to take into account that the information is rarely recorded in a systematic way. Indeed, the data are often sparse, and gathered at a clinician’s discretion. For example, blood tests are taken at a mixture of predefined stages in a patient pathway and clinically driven sampling. Thus, if predictive analytics relies on regularly sampled data, imputation methods need to be employed such that regular sampling is simulated. However, in the case of very irregular sampling a classical imputation approach may not be sufficient. In this paper we study prediction models for real time evaluation of patients admitted for gastrointestinal surgery with respect to surgical site infections (SSI) post-operatively.

SSIs are among the most common hospital-acquired infections. In fact, they represent up to 30% of all hospital acquired infections.^1,2 SSIs are associated with considerable morbidity and mortality. A mortality rate of 3%, prolonged stay up to 10 days and a significant decrease in quality of life, are reported. Similarly, readmissions related to SSIs are associated with a considerable increase in healthcare cost, up to 27,000 USD per readmission.³ This persistent in-hospital morbidity is particularly associated with surgery for colorectal cancer.^4–6

The American College of Surgeons Surgical Quality Improvement Program (ACS-NSQIP) and The Centers for Disease Control and Prevention divide SSI into three subtypes based on the anatomical location of the infection, i.e. superficial, deep incisional and organ space.⁴ Superficial infections can usually be cured with oral antibiotics and surgical debridement. In contrast, deep and organ space SSI require intravenous antibiotics, percutaneous drainage and lapratomies.

The patient specific risk factors for SSI are well documented and reported. A recent study by Lawson et al.⁴ identified open surgery, ulcerative colitis, older age, overweight, smoking, disseminated cancer and prolonged operation time as factors contributing to an increased risk of SSI. However, they found that different risk factors were associated with superficial and deep SSI. High Body Mass Index (BMI) and revision of an osteomy were associated with superficial SSI, whereas prolonged operation time and perioperative transfusions were associated with organ space SSI.^4,6

Using blood test results as predictive features in a data-driven decision support system is useful since these are performed relatively often with little burden to the patient. Therefore it is possible to estimate the expected information content of a blood test at stages in a patient trajectory.⁷ However, combining different tests performed at different stages in the trajectory, a necessity when observational data are used, presents challenges that we address here. The information from tests may be further combined with other data such as textual features that are predictive of complications.⁸

For the purpose of this manuscript we denote the sparsity of the clinical data as missing data. Missing data percentages are even larger for some studies such as clinical laboratory measurements or biomarkers. Despite of the efforts made to develop statistical methods for handling missing data, there is no global best approach because they inevitably depend on stated assumptions.

In this work we present methods for predictive modeling in a context of features that have strongly irregular sampling patterns. We analyze different smoothing and interpolation/imputation techniques and different input spaces to predict SSI using blood tests. Finally we look at linear and non-linear classifiers to do the predictive modeling. Figure 1 shows an overview of the data-driven decision support system used in this work for SSI prediction.

Figure 1:

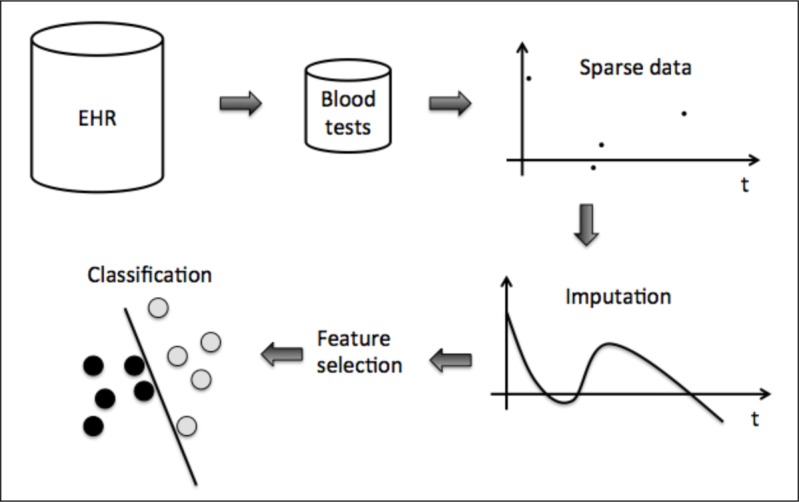
Overview of the processing pipeline.

Methods

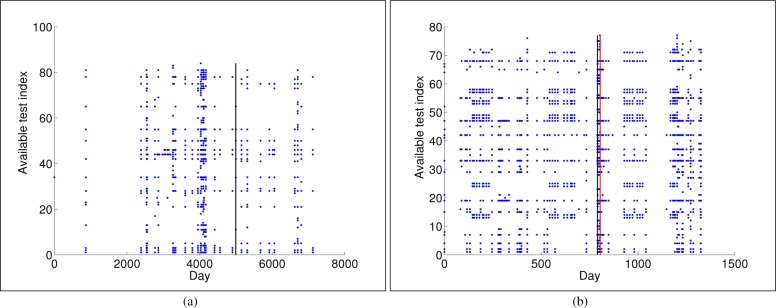
We extracted a cohort of patients based on relevant International Classification of Diseases (ICD10) or NOMESCO Classification of Surgical Procedures (NCSP) codes related to severe post-operative complications, and in particular to surgical site infections, from the EHR of the Department of Gastrointestinal Surgery at the University Hospital of North Norway. The selection of codes was guided by input from clinicians at the hospital. The cohort identified as control was matched with patients that did not have any of these codes but were otherwise similar in terms of which blood tests were performed. Additionally, a text search was performed to ensure that the controls did not have the word “infection” in any of their post-operative text documents. This resulted in a cohort of 101 cases and 904 matched controls. Patients with codes indicating superficial infections were excluded. A set of 10 different types of blood tests were defined as clinically relevant and extracted for all patients from their EHRs. All tests were not available every day, which results in a high percentage of missing values when analyzing data on that scale, yielding to a nonuniform time sampling description for each patient (Fig. 2). The data matrix is hence sparse over lab tests and time, therefore constituting a challenging data set to work on. A method denoted bootstrap nonparametric resampling^9,10 was designed to statistically describe the influence of imputation. Thus, the population mean and corresponding 95% CI was computed on a daily basis for each test, obtaining an averaged trend.

Figure 2:

Available laboratory test measurements for one control (a) and another infected (b) patient. The y-axis shows the available tests for a patient, with no specific order, as each patient can have different number of tests. The x-axis represents the day when each test was recorded, being t = 0 the day when the first test was recorded. Vertical black line indicates the surgery day, whereas red line indicates the infection day.

The data represent a diverse group of patients undergoing gastrointestinal surgery such that results can generalize across this group. The basic demographics of the cohort are given in Table 1.

Table 1:

Demographic characteristics of the patient groups.

	Overall	Controls	Cases
Female (%)	477 (47.4)	441 (48.7)	36 (35.6)
Age [Mean±SD]	57.0 ± 20.7	56.9 ± 21.2	57.4 ± 15.2

Feature extraction for sparse clinical data

Working with complete datasets is the standard scenario for most statistical and machine learning methods. In the literature, there are works that simply omit patients with any missing data. However, discarding patients with missing data may lead to incorrect assessments or prognostics. To avoid this situation, different methods have been proposed to deal with observations at non regular sampling. These methods can be categorized into:¹¹ (1) smoothing or interpolation techniques; (2) spectral analysis tools such as wavelets or Lomb-Sargle Periodogram; and (3) kernel methods.

Regarding interpolation methods, the well-known Last Observation Carried Forward (LOCF) scheme imputes the last non-missing value for the following missing values. Some works support that LOCF should not be considered as the primary approach to the treatment of missing data.¹² Alternatively, Lasko et al.¹³ suggest using Gaussian Process (GP) followed by a warped function,¹³ and we follow this approach in this paper. The warped function is intended to adjust for the fact that rapid changes in temporal variables in connection with active treatment is often followed by long periods of apparent stability leading to highly nonstationary processes. The time warping function can be constructed as

$$d^{\prime }=d^{1/\alpha }+\beta$$ (1)

where d is the original distance between two adjacent observations, and α and β are free parameters to be tuned. This function converts non-stationary clinical data into a stationary process which allows the use of a GP to deal with sparsity.

A random process f(t) is a Gaussian process if, for any finite set of values of t₁, t₂, …, t_k, the variables of the corresponding random vector f = f(t₁), f(t₂), …, f(t_k) are jointly normal (Gaussian). Element K_ij of the covariance matrix K of f is k[f(t_i), f(t_j)] where k[·,·] is a covariance (kernel) function, such as the radial basis function, or the squared exponential function. Using Bayes theorem, the posterior density function for an (unseen) random variable f_★ = f(t_★) conditioned on the observed f becomes

$$\mathbf{P}(f_{★}|\mathbf{f})=\frac{1}{\sqrt{2\pi {\widehat{\sigma }}^2}}\exp \left[-\frac{{\left(f_{★}-\widehat{f}\right)}^2}{2{\widehat{\sigma }}^2}\right],$$ (2)

where the posterior mean value is given by $\widehat{f}={\mathrm{k}}^T{\mathbf{K}}^{-1}\mathbf{f}$; and the posterior variance is ${\widehat{\sigma }}^2=\kappa -{\mathbf{k}}^T{\mathbf{K}}^{-1}\mathbf{k}$. In this expression, element i of the vector k is k[f(t), f(t_i)], i = 1, …, k, and κ = k[f(t_i), f(t_i)]. In Gaussian process regression, $\widehat{f}$ is used as the estimate, or prediction, of f_★, while ${\widehat{\sigma }}^2$ provides the level of confidence in the prediction. Thus, we use this approach in this manuscript to deal with sparse data.

Prediction Analytics

The SSI prediction is performed from a data-driven approach based on machine learning techniques. These techniques learn the underlying predictive model from a set of d-dimensional examples known as training set, where d corresponds to the number of features which are supposed to be relevant to the predictive task. The generalization of the model is estimated using an independent set of examples known as test set. Among the plethora of machine learning techniques proposed in the literature, Support Vector Machines (SVM) have shown to provide good generalization capabilities, and they have been considered in this work. We next briefly describe linear and non-linear SVM classifiers as well as the feature selection (FS) methods used in this work.

Linear and non-linear SVM

The data model for a linear classifier is given by y = 〈x, w〉 + b, where x is the feature vector, w is the weight vector of the linear model, b is the bias term, y is the classification output and 〈·,·〉, denotes the inner product. We focus on the Support Vector Machine (SVM) classifier,^14,15 with a regularization term such that model complexity is controlled, and the upper bound of the generalization error is minimized. These theoretical properties make the SVM an attractive approach for predictive modeling.

Denote $D={\left\{{\mathrm{x}}_i,y_i\right\}}_{i=1}^n$ as a binary labeled training set, where x_i ∈ ℝ^d and y_i ∈ {−1, +1}. The SVM classifier seeks the separating hyperplane with the largest margin between the two classes. The hyperplane optimally separating data is defined from a subset of training data named support vectors (SV), and it is obtained by minimizing ║w║², as well as the classification losses in terms of a set of slack variables ${\left\{{\xi }_i\right\}}_{i=1}^n$. Considering the ν-SVM introduced by Schölkopf et al.¹⁶ and a potential non-linear mapping ϕ(·), the ν-SVM classifier solves

$$\underset{\mathbf{w},\left\{{\xi }_i\right\},b.\rho }{\min }\left\{\frac{1}{2}{\Vert \mathbf{w}\Vert }^2+\nu \rho +\frac{1}{n}{\displaystyle \sum _{i=1}^n{\xi }_i}\right\}$$ (3)

subject to:

$$y_i\left(\langle \varphi ({\mathbf{x}}_i),\mathbf{w}\rangle +b\right)\ge \rho -{\xi }_i,\rho \ge 0,\text{and}{\xi }_i\ge 0\forall i=1,\dots ,n.$$ (4)

The variable ρ adds another degree of freedom to the margin, and the margin size linearly increases with ρ. The parameter ν ∈ [0, 1] acts as an upper bound on the fraction of margin errors, and it is also a lower bound on the fraction of SVs. An appropriate choice of non-linear mapping ϕ guarantees that the transformed input vectors are more likely to be linearly separable in the (higher dimensional) feature space.

The primal problem in Eq. (3) can be solved using its dual formulation, yielding¹⁵ $\mathbf{w}={\displaystyle {\sum }_{i=1}^n{y}_i{\alpha }_i\varphi ({\mathbf{x}}_i)}$, where α_i are Lagrange multipliers corresponding to constraints in Eqs. (3–4). Thus, the decision function for any test vector x_* is given by

$$f({\mathbf{x}}_{\ast })\left({\displaystyle \sum _{i=1}^n{y}_i{\alpha }_{i}K({\mathbf{x}}_i,{\mathbf{x}}_{\ast })+b}\right)$$ (5)

In order to predict the label of x_*, the sign of f(x_*) is used. The so-called SV are those training samples x_i with corresponding Lagrange multipliers α_i ≠ 0. The bias term b is calculated by using the unbounded Lagrange multipliers as $b=1/k{\displaystyle {\sum }_{i=1}^k(y_i-\langle \varphi ({\mathbf{x}}_i,\mathbf{w}\rangle )}$, where k is the number of non-null and unbounded Lagrange multipliers.

The use of Mercer kernels allows to handle the non-linear algorithm implementations as K(x_i, x_*) = 〈ϕ(x_i), ϕ(x_*)〉. In this work, we use two well-known Mercer kernels: the linear kernel K(x, z) = 〈x, z〉, and the Radial Basis Function (RBF) kernel $K(\mathbf{x},\mathbf{z})=\exp \left(-\frac{{\Vert \mathbf{x}-\mathbf{z}\Vert }^2}{2{\sigma }^2}\right)$, where σ is the width parameter, to be tuned together with ν free parameter.

SVM Feature Selection

Feature Selection (FS) strategies have been widely studied in the machine learning literature.^17–19 The purpose of FS is to choose a subset of features that are relevant for classification or regression tasks, while at the same time maintain or improve the performance of the learning method in comparison of using the whole set of available features. Regarding FS for SVM linear classifiers, the Recursive Feature Elimination (RFE) method¹⁷ has been shown to compare very favorably to many of the classical FS methods. Improved versions of SVM FS methods that included non-linear kernel functions have been described.^17,20,21

Results

In this section, we evaluate the capabilities of different ways to deal with sparse data and show the effects on performance results. Furthermore, linear and non-linear classifiers are benchmarked to predict SSI when using data from different laboratory tests obtained from the EHR. Firstly, each laboratory test was used separately to predict SSI using linear and non-linear classifiers after dealing with sparse data. Secondly, we analyzed the use of multiple blood tests to check the impact of combining them as well as the temporal-feature relative importance.

Our database was imbalanced, with 101 and 904 cases in the positive and negative classes, respectively. This is a common situation for clinical databases, where different number of patients are assigned to each class. Though previous studies have demonstrated that balanced classes in the training set often improve the overall classification performance.²² We used an undersampling strategy (discarding samples from the majority class), such that the training set was built by enforcing balanced classes. In order to represent correctly the population, we selected a different number S of subsets of the negative class with 101 samples in each, and computed classification performances in terms of the mean and the standard deviation of the results for each subset.

We used a cross-validation strategy to ensure the generalizability of the prediction analytics. First, we balanced the classes and then we split the data into training and tests subsets (80%–20%). A leave-one-out (LOO) cross-validation was carried out on the training subset of the balanced set for selecting the classifier free parameters. Thus, the SVM classifier was retrained R times, where R is the number of cases per class for balanced classes (R = 101 in this work). In this work, accuracy was considered as performance measurement for free parameter tuning.²³

Effect of the imputation methods on performance

Two different strategies, namely, LOCF and warped-GP, were considered to deal with the extreme sparsity present in the input space as given by different tests measured in a patient at different days.

Last observation carried forward (LOCF)

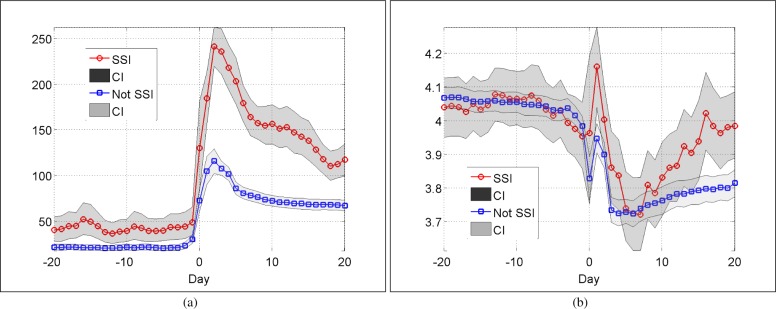
The last observed non-missing value was used to fill in the missing values into a regular time sampling grid with a daily time basis, i.e., if we have a missing value, we consider instead the previous value if it exists. A nonparametric resampling method to represent the averaged trend was applied to statistically describe the influence of imputation. See two examples in Fig. 3(a) for C-Reactive Protein (CRP) and Fig. 3(b) Potassium tests. It is well known that CRP is a good predictor for complications after colorectal surgery.²⁴ We note that our pattern of CRP levels following surgery is consistent with that observed by Singh et al.²⁴ Note that the higher mean CRP levels before surgery reflects the smaller group size and thus larger variance in this case, not a real difference between the groups.

Figure 3:

Population mean and corresponding 95% CI per day for CRP (a) and Potassium (b) tests. LOCF imputation and a nonparametric resampling strategy have been used.

For most blood tests, wider confidence interval (CI) after LOCF imputation were obtained for patients with SSI. Specifically, the data recorded at the day of surgery are highly noisy, as it can be seen in Fig. 3. For this reason, we excluded these values from our analysis, and we focused only on pre-operative and post-operative periods.

Warped function and GP

Using the time warped function Eq. (1), for each test we selected values of α and β parameters which maximize the accuracy of the predictive system. For this purpose, we used a grid search over values α ∈ [1, 10] and β ∈ [0, 100]. A LOO strategy was considered to ensure generalizability. The use of GP regression allows us to transform a set of finite measurements contained in the EHR from each blood tests into a continuous longitudinal function. In this way, missing values are inferred, allowing pre-operative and post-operative feature extraction.

Prediction of SSI

Table 2 shows the pre-operative and post-operative classification performance in terms of accuracy (mean and 95% CI) for each blood test individually when considering a LOCF strategy and warped function with GP methodology. Pre-operative stage was defined as four days before surgery, and four days immediately after surgery were considered in the post-operative stage (i.e., d = 4). We considered linear and non-linear SVM classifiers for the prediction of SSI, and we benchmarked results with a simpler logistic regression classifier.²⁵ Results suggest the presence of strong non-linear relationship among input features for the analyzed tests, as given by consistently achieving the best performances when a non-linear SVM was considered. Note also that the post-operative predictive power is in general higher than pre-operative, which is to be expected.

Table 2:

Pre-operative and post-operative prediction results in terms of accuracy (mean and 95% CI) for each test individually and different classifiers: Logistic regression (first row), linear SVM (second row), and non-linear SVM (third row). The best accuracy values for pre-operative and post-operative are shown in bold.

	LOCF		Warped-GP
Lab test	Pre-operative	Post-operative	Pre-operative	Post-operative
Hemoglobin	0.48 [0.43, 0.53]	0.47 [0.44, 0.75]	0.60 [0.54, 0.64]	0.60 [0.54, 0.64]
	0.58 [0.50, 0.69]	0.62 [0.51, 0.69]	0.52 [0.40, 0.62]	0.55 [0.46, 0.63]
	0.70 [0.56, 0.84]	0.89 [0.77, 0.95]	0.71 [0.64, 0.81]	0.79 [0.65, 0.85]
Leucocytes	0.50 [0.43 0.56]	0.47 [0.43, 0.51]	0.54 [0.48, 0.59]	0.54 [0.48, 0.59]
	0.50 [0.38, 0.59]	0.61 [0.50, 0.71]	0.45 [0.30, 0.55)]	0.53 [044, 0.65]
	0.75 [0.62, 0.85]	0.77 [0.65, 0.85]	0.75 [0.61, 0.87]	0.81 [0.73, 0.93]
CRP	0.49 [0.44, 0.55]	0.48 [0.44, 0.54]	0.62 [0.51, 0.73]	0.44 [0.41, 0.50]
	0.51 [0.43, 0.60]	0.79 [0.71, 0.87]	0.50 [0.39, 0.67]	0.60 [0.47, 0.71]
	0.61 [0.52, 0.69]	0.90 [0.84, 0.94]	0.79 [0.66, 0.94]	0.79 [0.67, 0.88]
Potassium	0.48 [0.44, 0.54]	0.47 [0.44, 0.54]	0.52 [0.49, 0.60]	0.48 [0.51, 0.44]
	0.58 [0.49, 0.66]	0.64 [0.46, 0.72]	0.59 [0.52, 0.69]	0.53 [0.63, 0.43]
	0.73 [0.60, 0.84]	0.88 [0.77, 0.95]	0.66 [0.60, 0.83]	0.74 [0.64, 0.86]
Sodium	0.48 [0.44, 0.54]	0.47 [0.44, 0.54]	0.49 [0.45, 0.57]	0.48 [0.42, 0.53]
	0.53 [0.43, 0.68]	0.55 [0.34, 0.73]	0.54 [0.42, 0.70]	0.52 [0.46, 0.58]
	0.66 [0.56, 0.74]	0.76 [0.67, 0.89]	0.71 [0.55, 0.90]	0.68 [0.63, 0.79]
Creatinine	0.46 [0.40, 0.53]	0.46 [0.44, 0.50]	0.49 [0.47, 0.57]	0.41 [0.34, 0.45]
	0.55 [0.46, 0.62]	0.61 [0.44, 0.67]	0.50 [0.36, 0.59]	0.52 [0.38, 0.64]
	0.79 [0.73, 0.86]	0.69 [0.56, 0.82]	0.68 [0.55, 0.74]	0.75 [0.69, 0.83]
ALAT	0.50 [0.44, 0.53]	0.49 [0.44, 0.53]	0.57 [0.49, 0.64]	0.54 [0.48, 0.58]
	0.61 [0.53, 0.69]	0.54 [0.43, 0.66]	0.63 [0.56, 0.59]	0.49 [0.40, 0.59]
	0.69 [0.50, 0.82]	0.61 [0.47, 0.71]	0.76 [0.63, 0.88]	0.67 [0.63, 0.75]
Thrombocytes	0.57 [0.48, 0.63]	0.56 [0.470.62]	0.57 [0.49, 0.65]	0.57 [0.54, 0.60]
	0.56 [0.45, 0.70]	0.66 [0.59, 0.73]	0.61 [0.40, 0.75]	0.49 [0.43, 0.56]
	0.73 [0.62, 0.83]	0.73 [0.66, 0.89]	0.65 [0.58, 0.70]	0.68 [0.58, 0.74]
Albumin	0.53 [0.41, 0.65]	0.50 [0.41, 0.64]	0.56 [0.52, 0.60]	0.47 [0.42, 0.50]
	0.55 [0.40, 0.66]	0.70 [0.44, 0.84]	0.79 [0.55, 0.92]	0.63 [0.54, 0.69]
	0.71 [0.48, 0.89]	0.82 [0.69, 0.93]	0.91 [0.88, 0.92]	0.83 [0.77, 0.92]
ALP	0.49 [0.38, 0.54]	0.49 [0.41, 0.53]	0.41 [0.36, 0.54]	0.33 [0.31, 0.36]
	0.55 [0.43, 0.67]	0.58 [0.53, 0.65]	0.69 [0.64, 0.75]	0.55 [0.44, 0.71]
	0.69 [0.50, 0.84]	0.63 [0.47, 0.76]	0.69 [0.44, 0.87]	0.74 [0.69, 0.79]

CRP: C-Reactive Protein; ALAT: Alanine aminotransferase; ALP: Alkaline phosphatase

Table 2 also shows that performance depend on the method used to deal with sparsity. In general, the combination of warped function and GP improved results, however, it can be seen that for some tests LOCF is better.

Feature selection

The results in Table 2 suggest that a non-linear classifier provides a better prediction of SSI. Taking that into account, we obtained the accuracy using a non-linear SVM classifier both for pre-operative and post-operative stages. First, we considered all blood tests together, i.e., d = 40 (first row in Table 4) and then we applied the FS method denoted as RBF RFE (second row in Table 3). Table 3 shows the mean and 95% CI accuracy when using both schemes. Comparison of Table 2 and Table 3 shows that the model built with all tests provide higher accuracy. Note also that a similar or tending to higher accuracy is obtained with the FS method, so it is appropriate for addressing the interpretation of the relevance and meaning of the input space.

Table 3:

Joint pre-operative and post-operative accuracy (mean and 95% CI) with a RBF RFE FS method.

	LOCF		Warped-GP
	Pre-operative	Post-operative	Pre-operative	Post-operative
All tests	0.81 [0.76,0.86]	0.89 [0.92,0.97]	0.88 [0.79,0.92]	0.90 [0.87,0.92]
FS	0.83 [0.67,0.90]	0.91 [0.90,0.92]	0.87 [0.76,0.94]	0.92 [0.90,0.94]

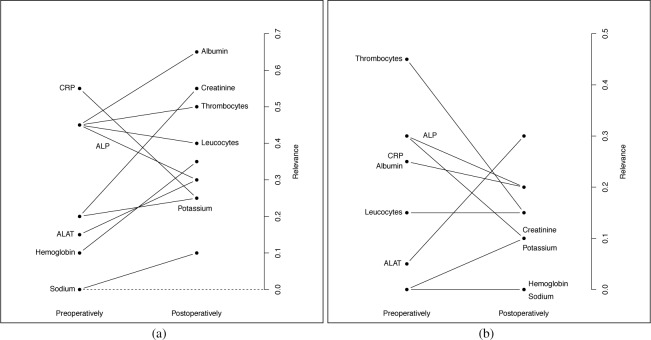
Figure 4 summarizes the results of FS with non-linear SVM (with RBF kernel) in terms of relevance of blood tests. Towards that end, we calculated how many times every feature is selected (frequency of relevance), separately for the pre-operative and post-operative stages. From these values, a relevance index for each blood test is obtained as the normalization of the cumulative frequency of relevance by number of features per day (d = 4) times the number of subsets (S = 5). Note that a comparison with baseline level is remarkable for all tests (excepts sodium), indicating the relevance of the intra-patient pre-operative levels on each test. In general terms, thrombocytes reached the highest prediction information, together with ALP, CRP, albumin, creatinine and leukocytes, most of them being consistent with previous results. Although less relevant in the pre-operative state, the other tests (potassium, ALAT, and hemoglobin) also included highly relevant information in the post-operative state.

Figure 4:

Pre-operative and post-operative relevance index for each blood test using LOCF (a) and Warped-GP (b).

Discussion

The results clearly demonstrate the utility of blood tests for predicting SSIs both pre- and post-operatively. These results will potentially be useful as part of a data-driven online clinical decision support system that can enable clinicians to improve post-surgical recovery rates. With proper warning necessary actions such as closer follow up and risk stratification can be performed.

We chose to generate the cohort in a way that may open the problem to being in a sense “too easy”. Since our emphasis was on methodology development, we chose to generate a cohort where the testing patterns were similar in the negative and positive classes. This aids the algorithmic development, but opens the possibility that the problem does not entirely reflect the clinical scenario since many in the negative class would not be suspected of having SSIs. Nevertheless, this does not invalidate the methodology development or the results. Indeed, if the envisioned decision support system is thought of as a warning system flagging patients at risk, the cohort reflects well the actual clinical setting.

Testing is often done at the discretion of the clinician, and often not driven by formulaic rules. This is part of the reason for the irregular sampling in the data, leading to the problem formulation in this paper. Thus, the testing pattern for patients in inpatient care itself may be an informative feature of post-operative complications independent of the test results. By generating the cohort by matching testing patterns, this information is largely lost and only the test results remain as the informative features.

In retrospective EHR studies there is inevitably the chance of a censoring effect where a test result informs the clinician of a possible complication and the clinician takes appropriate and successful action to avoid the complication. Then the pattern for complication will be present, but not the complication itself, which leads to effectively mislabeled data, known as confounding medical interventions.²⁶ In our case this is unlikely to be a large issue since there is little information to act on to avoid a SSI such that most cases are likely to be correctly coded.

Using ICD10 and NCSP codes to phenotype a cohort there is a significant chance of miscoding leading to labeling errors. However, there is a far greater chance of false negatives (i.e., missing coding) than false positives. In this case, the positive class will be correct while the negative class may contain erroneous labels. When generating the cohort by matching we alleviate this since a minority of patients get SSIs, and additionally we check for the Norwegian equivalent of the word “infection” in the post-operative notes, which would almost surely appear if the patient actually got an SSI.

In the literature several approaches for reducing SSI have recently been described. Wick et al, used a multidisciplinary approach to reduce SSI and showed that formation of small groups of front line providers to address SSIs reduced SSIs by 33%.²⁷ One of the most popular existing risk models for SSI is the National Nosocomial Infection Surveillance (NNIS) Basic SSI Risk Index.²⁸ Also, recently, a logistic regression model for predicting SSIs was developed by van Walraven et al.²⁹ A more data driven approach has been used by Gbegon et al. predicting SSIs in real time within 30 days of the operation³⁰. However, these studies rely on clinical data, demographic and other information but do not take blood tests into account. There exists validated risk assessment tools for post-operative complications, including the Surgical AGPAR Score³¹ and the POSSUM score.³² Both of them assess the immediate post-operative risk based on a number of variables. The American College of Surgeons’ NSQIP risk calculator was developed as a preoperative risk stratification tool.³³

In this context our work presents a path forward to combine clinical variables along with demographic and other data with test results that can be updated in real-time and provide a live assessment of a patient’s progression.

Conclusion

We have shown that our model has a potential for real time prediction and identification of patients at risk for developing SSI. This can give decision support to clinicians, and treatment plans can be adjusted taking into account the identified increased risk.

Appropriately adjusting the temporal structure of blood tests can dramatically improve the system accuracy. This can provide the basis for a future on-line system that alerts clinicians to patients at risk for complications, such that appropriate action can be taken. With early identification of these patients, improved clinical outcomes, reduced readmissions and cost savings are likely.