A hybrid manifold learning algorithm for the diagnosis and prognostication of Alzheimer’s disease

Abstract

The diagnosis of Alzheimer’s disease (AD) requires a variety of medical tests, which leads to huge amounts of multivariate heterogeneous data. Such data are difficult to compare, visualize, and analyze due to the heterogeneous nature of medical tests. We present a hybrid manifold learning framework, which embeds the feature vectors in a subspace preserving the underlying pairwise similarity structure, i.e. similar/dissimilar pairs. Evaluation tests are carried out using the neuroimaging and biological data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) in a three-class (normal, mild cognitive impairment, and AD) classification task using support vector machine (SVM). Furthermore, we make extensive comparison with standard manifold learning algorithms, such as Principal Component Analysis (PCA), Principal Component Analysis (PCA), Multidimensional Scaling (MDS), and isometric feature mapping (Isomap). Experimental results show that our proposed algorithm yields an overall accuracy of 85.33% in the three-class task.

Introduction

Alzheimer’s disease (AD) is a genetically complex, progressive and fatal neurodegenerative disease, which leads to memory impairment and other cognitive problems¹. There currently is no effective treatment that delays the onset or slows the progression of AD. According to the 2010 World Alzheimer report, there are an estimated 35.6 million people worldwide living with dementia at a total cost of over US$600AD billion in 2010, and the incidence of AD throughout the world is expected to double in the next 20 years¹. Therefore, there is an increasing demand for diagnosing and treating AD. This paper focuses on the application of machine learning algorithms for Alzheimer’s disease diagnosis.

The diagnosis of AD is complex involving a variety of medical tests. These may include physical exam, neurological exam, mental status tests, and brain imaging, which will be used as a whole to assess memory impairment, judge functional abilities, and identify behavior changes, while ruling out other conditions that may cause symptoms similar to Alzheimer’s disease. Current diagnosis of Alzheimer’s relies largely on assessments of cognition and behavior, e.g. memory loss and behavior disorder, which start to decline in the later disease stages^1,3. It is very difficult to treat neurological damage in current medical technology. Therefore, early detection of AD is of vital importance. Early detection of AD allows early treatment and thus help to delay the onset of AD symptoms, which could greatly improve the daily livings of patients.

There are many challenges in the early detection of AD. For example, it is very difficult to distinguish it from other types of dementia that begin in middle age, such as Pick disease. Another important thing that has to be mentioned is feature selection. A large amount of factors (e.g. biomarkers, metal status tests, etc.) contributes to the diagnosis of AD. It is very difficult to obtain the optimal set of discriminant features, which can best identify Alzheimer’s disease patients from healthy people or further classify different stages of AD. In this paper, we propose a hybrid manifold learning framework to embed multivariate feature vectors into a manifold, which preserves the pairwise similarity relationship. Some preliminary results are given. Generally speaking, our proposed algorithm consists of two parts, metric learning and manifold learning. Firstly, we utilize metric learning algorithm, i.e. Probabilistic Global Distance Metric Learning (PGDM)¹⁵, to construct a similarity matrix, which is then passed to isometric feature mapping (Isomap)⁴ to construct a manifold, which shows better discriminant property for Alzheimer’s disease recognition (i.e. disease diagnosis).

The remainder of this paper is structured as follows. In the Background section, we present a general review of the application of machine learning algorithms in Alzheimer’s disease diagnosis. Then, we narrow down to manifold learning algorithms. In the Methods section, we describe our proposed approach in detail, together with necessary supporting information. Detailed experiment setup is also given in this section. In the Results and Analysis section, extensive evaluation tests are presented to show the performance of our method. Furthermore, comparison is made with a wide range of modern manifold learning algorithms, i.e. as Principal Component Analysis (PCA), Multidimensional Scaling (MDS)⁵, and isometric feature mapping (Isomap)¹⁵. Finally, we draw conclusion and discuss about future work in the last section.

Background

Conventional manifold learning refers to “nonlinear dimensionality reduction methods based on the assumption that [high-dimensional] input data are sampled from a smooth manifold” so that one can embed these data into the [low dimensional] manifold while preserving some structural (or geometric) properties that exist in the original input space^{6, 7}. Manifold learning is usually based on certain objective function. For example, PCA is designed to find the subspace with each dimension pointing to the direction with largest variance. By designing an appropriate objective function, it is possible to find a suitable manifold for AD diagnosis.

A large amount of work has been done on the application of manifold learning algorithms in the diagnosis of Alzheimer’s disease. The general idea is to design a manifold, which possesses more discriminant power in terms of classification tasks. Based on the whether a training set is needed, those approaches can be divided into two broad categories, i.e. unsupervised approach and supervised approach. For unsupervised algorithms, principal component analysis (PCA) was applied to the ADNI dataset for the early detection of AD in Lopez et al.’s work⁸. Yang and coworkers utilized independent component analysis (ICA) to the MRI data in 2011⁹. In 2011, Park proposed to use Multidimensional Scaling (MDS) to discriminate shape information between AD from normal controls¹⁰. For supervised approach, it has begun to draw more attention due to its promising performance. It is usually formulated as prior information about the patient clusters, e.g. similar/dissimilar training set, which is similar to Xing et al.’s algorithm¹⁵. Examples of this category are Wolz et al.’s neighborhood embedding approach¹¹ and Shen et al.’s sparse Bayesian learning approach¹⁴.

The progressive structural damage caused by AD can be noninvasively assessed by using magnetic resonance imaging (MRI) to measure cerebral atrophy or ventricular expansion³. Therefore, many researchers have been focusing on MRI images, leading to massive application of image processing algorithms. Keraudren et al. proposed to localize the fetal brain in MRI using Scale-Invariant Feature Transform (SIFT) features¹². Suk et al. proposed a deep learning-based feature representation with a stacked auto-encoder, which combines latent information with the original low-level features¹³.

Recently, researchers begin to use hybrid manifold learning algorithm to improve system performance. For example, Gray et al. reported to use the random forest algorithm together with MDS for multi-modal classification of Alzheimer’s disease³ in 2013. The algorithm introduced in this paper belongs to this category. Manifold learning algorithms are usually based on certain similarity metric. For example, the classical MDS was based on the distance matrix derived from L2 norm. Therefore, designing a proper similarity metric is of vital importance in the algorithm (Isomap for our proposed algorithm, and MDS for Gray et al.’s algorithm³). Gray et al. improved the algorithm by utilizing the random forest algorithm as the first step to generate a better similarity metric, which is then passed to MDS for manifold construction. Random forest is based on decision tree, which is a ‘general purpose’ classification algorithm. The objective function is to maximize the classification accuracy but not to improve the similarity performance. In our proposed algorithm, we utilize Xing et al.’s metric learning algorithm¹⁵ to obtain an optimal Mahalanobis distance based on pairwise similarity prior knowledge. In other words, the learned distance yields small value for similar pairs and large value for dissimilar pairs, which is the optimization criteria of the algorithm. On the other hand, Isomap is developed based on the similarity graph of the data, which means the performance is highly dependent on the similarity measure. Therefore, an extra optimization step for optimal similarity measure is a straight forward approach to improve system performance.

Methods

In order to enact the model, we follow the description of our proposed algorithm below in Figure 1. Our proposed algorithm is developed based on Isomap. In contrast to other nonlinear dimensionality reduction algorithms, Isomap can efficiently computes a globally optimal solution⁴. Moreover, Isomap is based on the similarity graph calculated using certain similarity metric, which can be perfectly combined with metric learning algorithm. It’s because the direct input of Isomap is the optimal metric, which is different from many other algorithms. For example, PCA looks for the direction for maximum variance span of the high dimensional data, and ICA finds independent directions of the input data ²⁰.

Figure 1.

Schematic overview of the proposed methodology.

In classical Isomap⁴, the Euclidean or Mahalanobis distance is used to construct the similarity graph, which is then used to construct the manifold. Therefore, an appropriate similarity measure is of vital importance. The probabilistic global distance metric learning (PGDM) algorithm¹⁵ is utilized to learn a robust metric, which is then used to construct a neighborhood graph. Then, the Isomap algorithm is utilized to learn the underlying global geometry of the data set. Finally, a support vector machine (SVM) classifier is trained for a three-class classification task.

Similarity metric learning

Distance metric learning^7,15,21 aims to learn a distance metric (parameters) for the input data space from a collection of similar/dissimilar points that preserves the distance relation among the training data. In our present implementation, the probabilistic global distance metric learning (PGDM) algorithm¹⁵ is adopted. It is designed to learn a Mahalanobis distance which satisfies¹⁵,

$$\begin{array}{l}{\min }_A{\Sigma }_{(x_i,x_j)\in S}{\Vert x_i-x_j\Vert }_A^2\\ s.t.{\Sigma }_{(x_i,x_j)\in D}{\Vert x_i-x_j\Vert }_A\ge 1,A\ge 0\end{array}$$ (1)

where ‖·‖_A stands for the Mahalanobis distance; A is the Mahalanobis distance matrix; S and D are the similar and dissimilar training sets, respectively.

In our present implementation, we only study a simplified scenario, where A is diagonal. Then, Equation (1) can be solved by using the equivalent form¹⁵,

$$g(A)={\Sigma }_{(x_i,x_j)\in S}{\Vert x_i-x_j\Vert }_A^2-log({\Sigma }_{(x_i,x_j)\in D}{\Vert x_i-x_j\Vert }_A).$$ (2)

We can thus use Newton-Raphson method to efficiently solve Equation (2)¹⁵.

It has to be noted that the Mahalanobis distance gives different weight to different dimensions, which is equivalent to feature selection. Lower weight indicates lower impact on the final result, i.e. similarity measure.

Manifold learning

The isometric feature mapping (Isomap) is a nonlinear dimensionality reduction method, which is also a low-dimensional embedding method⁴. Isomap is used for computing a quasi-isometric, low-dimensional embedding of a set of high-dimensional data points⁴. The algorithm provides a simple method for estimating the intrinsic geometry of a data manifold based on a rough estimate of each data point’s neighbors on the manifold⁴.

As shown in Figure 2, the raw feature vectors are firstly transformed into similarity distance matrix (equivalent to neighborhood graph). According to the Isomap algorithm, the traditional MDS is then applied to the matrix to construct a manifold.

Figure 2.

Embedding multivariate medical records into a manifold.

SVM Classification

In our present implementation, a support vector machine (SVM) classifier is utilized. It has to be noted that our focus is the construction of a better manifold which is more suitable for diagnosis. SVM is only implemented for demonstration purposes, whoch can be replaced by other algorithms, such as Neural Networks, nearest neighbor, etc.

An SVM is a high-dimensional pattern classification algorithm, which constructs a hyperplane or set of hyperplanes in a high- or infinite-dimensional space, which can be used for classification, regression, or other tasks¹⁶. The data points are mapped so that the examples of the separate categories are divided by a clear gap that is as wide as possible. SVM can be formulated as

$$\begin{array}{l}arg\underset{(w,b)}{\min }\frac{1}{2}{\Vert w\Vert }^2\\ s.t.y_i(w_i-b)\ge 1\end{array}$$

where w is the normal vector to the hyperplane; The parameter $\frac{b}{\Vert w\Vert }$ determines the offset of the hyperplane from the origin along w.

Results and Analysis

In this section, we first discuss the dataset that was used in the analysis. Then, we present the detailed experimental results for our proposed algorithm.

Data acquisition and pre-processing

Data used in the preparation of this article were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year publicprivate partnership. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD). Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials^3,22.

The Principal Investigator of this initiative is Michael W. Weiner, MD, VA Medical Center and University of California – San Francisco. ADNI is the result of efforts of many co-investigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the U.S. and Canada²². The initial goal of ADNI was to recruit 800 subjects but ADNI has been followed by ADNI-GO and ADNI-2. To date these three protocols have recruited over 1500 adults, ages 55 to 90, to participate in the research, consisting of cognitively normal older individuals, people with early or late MCI, and people with early AD. The follow up duration of each group is specified in the protocols for ADNI-1, ADNI-2 and ADNI-GO. Subjects originally recruited for ADNI-1 and ADNI-GO had the option to be followed in ADNI-2²². For up-to-date information, see www.adni-info.org.

We obtained MRI image data and diagnosis information from the ADNI database. We applied the proposed methodology to neuroimaging and biological data from 822 ADNI participants (229 normal patient, 405 MCI patients, and 188 AD patients). Each patient has three different high dimensional vectors of medical test data, corresponding to three distinct visits to the hospital. For example, for each visit there is a N-dimensional vector, corresponding to all the tests (totally N) done at that time. All MRIs were sagittal T1-weighted scans. The scans were collected using a 1.5 T GE Signa scanner with an MR-RAGE acquisition sequence.

We excluded all invalid records (with missing feature entries), resulting in totally 2158 high dimensional data points. Direct recognition using the 2158 raw data points based on the MRI images is very challenging, since it is very difficult to identify importance features. Therefore, instead of using the raw images, the MRI images are preprocessed by the CIVET software to get the brain volume information, such as volume for 3rd ventricle, 4th ventricle, right/left brain fornix, right/left frontal, right/left globus pallidus, right/left occipital, etc. A complete list of features used in this paper is given at my personal website¹⁷.

Experiment setup

As described in previous section, there are totally 2158 data points, with 586 normal records, 1006 MCI records, and 416 AD records. We randomly select 50 normal, 50 CI, and 50 AD data points as the testing set, leaving the rest (i.e. 536 normal, 956 MCI, 366 AD) as the training set (2008 training points and 150 testing points).

The training/testing set preparation process is repeated 10 times, which leads to 10 training/testing set combinations. For each training/testing set, our proposed algorithm is applied to construct a manifold, which is then passed to a SVM classifier for a three-class recognition task (Normal, MCI, and AD). Therefore, there are totally 10 set of recognition results. We use the sample code at the corresponding authors’ website for Isomap and PGDM implementation²³. Relative improvement is defined as

$$R_{im}=\frac{r_p-r_t}{r_t}\times 100\%$$

where R_im is the relative improvement; r_p is the recognition rate of our proposed algorithm; r_t is the recognition rate of the comparison target.

Experimental results

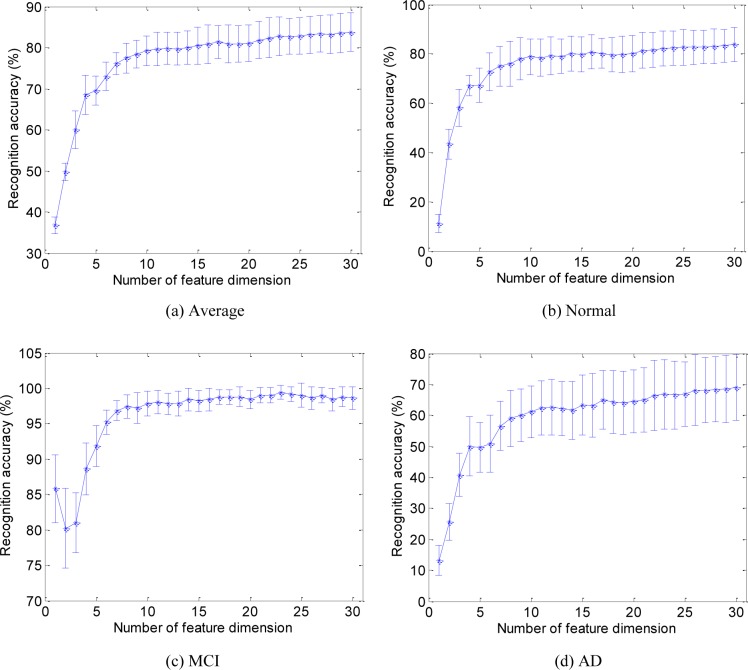
Figure 3 gives the error bar plot of experimental results for different conditions, i.e. average of 3 classes, normal, MCI, and AD. In order to eliminate the bias caused by training/testing set partition, we take the mean and variance of the recognition results. The error bars are calculated from the mean and variance of the recognition results from ten training/testing sets.

Figure 3.

Recognition results for different conditions.

It can be seen that as the dimension of the manifold increases the recognition rate increases significantly. For example, in the 3-class recognition task, shown in Figure 3(a), the recognition rate increases from 33% at 1 dimensional feature to around 83% at 27 dimensional (or more) feature. Furthermore, at lower dimension (e.g. <10), the change of dimension number gives more impact on the final result, while at high dimension (e.g. >10) the performance improvement resulting from feature dimension increase becomes very small. As feature dimension changes from 1 to 10, the recognition rate increases by around 40% (from 34% to 80%). However, as feature dimension (i.e. the number of features) further increases, the recognition rate increases only 4% with fluctuation.

Based on one’s objectives, the optimal dimension number may vary. For example, if the objective is to classify if the patient is MCI, the optimal feature dimension can be chosen to 10. However, if recognition accuracy is the main concern, the optimal feature dimension would be around 25. In our present work, the optimal dimension is chosen to be 15 for a balance between recognition rate and efficiency.

Another thing that has to be mentioned is that the recognition results for MCI are much better than Normal and AD. This is due to the fact that we possess more MCI training materials (956 feature vectors) compared to 536 normal feature vectors and 366 AD feature vectors. More training materials yield better recognition results, which are consistent with the results in Figure 3. The Normal training records are more than AD, corresponding to higher recognition rate for Normal. The amount of training materials can be arranged according to special application purposes.

Table 1 gives the confusion matrix based on the experimental results in Figure 3. It can be seen that for MCI patients our proposed algorithm yields a very promising recognition rate, 98.4%, which means high sensitivity. However, the misclassification rate (false positive) is also very high, i.e. low accuracy. This means our propose algorithm tend to misclassify other category as MCI (1 − 67.86% = 32.14%). The physical meaning is that for a patient with MCI our proposed algorithm can probably recognized the patient as MCI (98.4%, high sensitivity). However, if our propose algorithm classify the patient as MCI, there is 32.22% chance that the diagnosis is incorrect. In this case, 10.76% chance the patient is actually Normal, and 21.38% chance the patient is AD. For the other two categories (Normal and AD), the false positive rates are low. However, the recognition rates drop to 84% and 68.8%, respectively. This means if the recognition result is Normal or AD, it is very likely (> 98%) that the diagnosis is correct. However, there is less chance the algorithm will go to this category i.e. low sensitivity. On average, the proposed algorithm shows better performance at classifying Normal (high sensitivity 84% and high accuracy 98.59%).

Table 1.

Confusion Matrix, feature dimension is chosen to be 30.

		Predicted Class			Rate (sensitivity)
		Normal	MCI	AD
Actual Class	Normal	420	78	2	84%
	MCI	5	492	3	98.4%
	AD	1	155	344	68.8%
Rate (accuracy)		98.59%	67.86%	98.57%

Comparison with other manifold learning algorithm

Extensive comparison is made state of the art manifold learning algorithms, i.e. PCA, MDS, and Isomap. Here, Isomap utilizes the L2 norm to construct the neighborhood graph. We also give the recognition result based on the original feature vectors, denoted as Original in Table 2. The raw data vectors are processed by mean and variance normalization before processed by each of the above mentioned algorithms. Table 2 gives the experimental results for all the comparison targets.

Table 2.

Recognition results for comparison targets (%).

	Proposed	Isomap	PCA	MDS	Original
Recognition accuracy	83.83	82.83	83.00	82.67	74.66
Relative Improvement	–	1.21	1.00	1.40	12.28

It can be seen that our proposed algorithm yields much better results than all the comparison targets. The relative improvements are 1.21% over Isomap, 1.00% over PCA, 1.40% over MDS, and 12.28% over Original. The detailed recognition results for different conditions are visualized in Figure 4. Our proposed algorithm shows consistently better results than all the comparison targets. Since we have more MCI training materials, the corresponding MCI results are much better than the others, followed by Normal and AD.

Figure 4.

Recognition results for different feature dimension.

Conclusion and future work

In this paper we propose a general framework for embedding multivariate medical records into a low dimensional manifold which possesses better discriminative property. This proposed algorithm is designed by the combination of two algorithms. We first construct a neighborhood graph based on a robust similarity metric, which is then used for manifold learning. It has to be noted that the PGDM algorithm is used to learn a Mahalanobis distance, which assigns different weights to different dimensions. This is equivalent to performing feature selection on the whole feature set. For example, in our present, the 23th feature (i.e. right globus pallidus volume) is given very low weight, which indicates that right globus pallidus volume is not suitable for the proposed classification task.

Our present study focuses mainly on the diagnosis of Alzheimer’s disease. We utilize all the features as a whole for the recognition task. However, it would be better if we can identify which feature is more important in identifying AD. The application of feature selection algorithms will help to further improve the performance of the proposed algorithm. Furthermore, our present work cannot predict the future tendency of a patient. Risk analysis of a patient in terms of developing Alzheimer’s disease will be our next step.