Examining the Distribution, Modularity, and Community Structure in Article Networks for Systematic Reviews

Abstract

Systematic reviews (SRs) provide high quality evidence for clinical practice, but the article screening process is time and labor intensive. As SRs aim to identify relevant articles with a specific scope, we propose that a pre-defined article relationship, using similarity metrics, could accelerate this process. In this study, we established the article relationship using MEDLINE element similarities and visualized the article network with the Force Atlas layout. We also analyzed the article networks with graph diameter, closeness centrality, and module classes. The results revealed the distribution of articles and found that included articles tended to aggregate together in some module classes, providing further evidence of the existence of strong relationships among included articles. This approach can be utilized to facilitate the articles selection process through early identification of these dominant module classes. We are optimistic that the use of article network visualization can help better SR work prioritization.

Introduction

Systematic reviews (SR) provide a summary of evidence from high quality studies for a specific research question. They are regularly used in health care^1–3 and for health policy making⁴. Evidence-based Medicine (EBM) relies heavily on the use of synthesized, up-to-date research evidence to make decisions. SRs are considered the highest quality source of evidence for EBM⁵.

SR is commonly conducted by domain experts who are able to draft SR scopes, retrieve relevant citations, assess study quality, and synthesize evidence. Expert researchers first identify the SR scope and research questions, and then generate search strategies to explore related databases (e.g. MEDLINE). The search result is a list of citations, which are usually organized in reference management software (e.g. Endnote, Ref-Works). Before synthesizing relevant evidences, expert researchers need to classify articles based on the title and abstract. Then through the triage (or article selection) process, included articles will proceed to the full-text level⁶. In most SRs, expert researchers include only 2% to 30% of citations at the title and abstract level triage, and 1.6% to 27% gets to be included at the full-text level. In other words, expert researchers spend most of their effort excluding non-relevant or low quality studies. As the classification of articles is one of the most resource and time intensive steps, such workload and resource challenges can limit the tractability of an individual review, the ability to fund a review, and also the ability to respond to new evidence that may require an update to an existing review. To accelerate this process, several machine learning (ML) approaches (i.e. Naïve Bayes and Support Vector Machine)^6–10 were proposed to facilitate and enhance the title and abstract level triage, abstracts screening¹¹, or “article selection”.

As SRs aim to identify, appraise, select and synthesize high quality research evidence relevant to the research questions with a well-designed SR scope, we propose a new approach to pre-define the article relationship with similarity metrics in SR reports. The similarity metric is calculated using several MEDLINE elements¹², such as title, abstract, MeSH, author, and publication type. We hypothesized that relevant (or included) articles should be more similar to each other than to the excluded ones. We could illustrate such an article relationship as an article network. Each article represents as a node and the relationship (similarity) between two articles represents as an edge connecting them. We hypothesize that with article network visualization, we could detect groups or clusters in the article network, especially for relevant (included) articles in a SR report.

Through our research, we have demonstrated the visualization of article relationships using similarity metrics, and discovered community structures for article networks using 20 completed SR reports. Communities are densely connected groups of vertices, with only sparser connections between groups^13–15. Communities reveal a non-trivial internal organization of the network, and allow people to infer special relationships among nodes. Communities have been shown to have significant real-world meaning¹³.

We visualized article networks using a force-directed graph algorithm, which is commonly used for generating network graph where pair-wise geometric distances between the drawn vertices match graph theoretic pairwise distances. Because of the SR article screening process, articles can be classified into three categories: excluded, half-included (articles included at the title/abstract level, but excluded at the full-text level) and included (articles included at both the title/abstract level and the full-text level). We evaluated the distributions of articles from these three categories (excluded, half-included, and included) using graph diameter, closeness centrality, and module classes (communities). Our research questions included: (1) do included articles tend to aggregate together? (2) with a community detection algorithm, do included articles cluster in the same communities (module classes)?

Methods

We used 20 completed SRs: 15 SR reports were produced by the Drug Effectiveness Review Project team (DERP; www.ohsu.edu/drugeffectiveness), the data was made publicly available from Cohen^6,16, and 5 SR reports^17–21 were produced by the Cochrane Collaboration²². These 20 SRs were completed by experienced and knowledgeable human expert researchers, with inclusion and exclusion decisions made by at least two expert researchers. Table 1 shows the number and percentage of articles included at 1) abstract level decision and 2) full-text level decision. For instance, the review for ACE Inhibitors has a total of 2544 citations. Based on the abstracts, 183 (7.19%) were included; after full-text reading, 41 (1.61%) were included in the ACE Inhibitor SR report. The final inclusion rates range from 0.55% to 27.04%.

Table 1.

Twenty SR reports’ total article numbers and rate of inclusion

	Total	Abstract N (%)	Full-text N (%)
ACE Inhibitors16	2544	183  (7.19%)	41    (1.61%)
ADHD16	851	84    (9.87%)	20    (2.35%)
Antihistamines16	310	92    (29.68%)	16    (5.16%)
Atypical Antipsychotics16	1120	363  (32.41%)	146  (13.04%)
Beta Blockers16	2072	302  (14.58%)	42    (2.03%)
Calcium Channel Blockers16	1218	279  (22.91%)	100  (8.21%)
Estrogens16	368	80    (21.74%)	80    (21.74%)
NSAIDS16	393	88    (22.39%)	41    (10.43%)
Opioids16	1915	48    (2.51%)	15    (0.78%)
Oral Hypoglycemics16	503	139  (27.63%)	136  (27.04%)
Proton Pump Inhibitors16	1333	238  (17.85%)	51    (3.83%)
Skeletal Muscle Relaxants16	1643	34    (2.07%)	9      (0.55%)
Statins16	3465	173  (4.99%)	85    (2.45%)
Triptans16	671	218  (32.49%)	24    (3.58%)
Urinary Incontinence16	327	78    (23.85%)	40    (12.23%)
Antibiotic17	412	74    (17.96%)	10    (2.43%)
Antineoplastic18	1294	N/A  N/A	19    (1.47%)
Antiretrovirals19	749	N/A  N/A	38    (5.07%)
Hearing Loss20	467	13    (2.78%)	3      (0.64%)
Leukaemia21	328	11    (3.35%)	7      (2.13%)

Please note that for SRs from DERP¹⁶ (the first 15 SRs in Table 1), full references in MEDLINE format were downloaded using explicit PubMed Identifiers (PMID). For SRs from Cochrane library (The last 5 SRs in Table 1), references in MEDLINE format were retrieved using the established search strategy on PubMed, references from other databases (i.e. EMBASE/Ovid) were not used.

Again, based on the SR article screening process, articles were classified into three categories: excluded, half-included (articles included at the title/abstract level, but excluded at the full-text level) and included (articles included at both the title/abstract level and the full-text level).

MEDLINE Elements

In order to establish the relationship among articles, we used MEDLINE elements to create the similarity metrics. MEDLINE elements are the fields in the MEDLINE format, that document the major pieces of information of a publication (article)²³. The MEDLINE display format is used in PubMed MEDLINE records. As the most informative elements, title (TI), abstract (AB) and MeSH (MH) elements are widely used in related work to build feature spaces for ML algorithms. Publication type (PT) is also selected by some studies^10,24 as it may be a key factor for inclusion or exclusion decisions. In our preliminary work, we found that author information also had some predictive value in the article selection process. Therefore, in this study, we used TI, AB, MH, PT and author (AU) element in our experiments.

Similarity Score

We calculated the similarity using Cosine similarity²⁵. Cosine similarity is widely applied to text mining and measures the cosine of the angle between a pair of vectors. It is a common and efficient measure for text comparison, especially for large datasets^26,27. Cosine similarity reflects the degree of similarity based on the presence and frequency of words or terms in each text. For every pair of AUs, PTs and MHs, we simply compared them by exact string matching, because a minor difference may completely alter the outcome. For example, even if two authors’ names are very similar, they may be two different people. However, TI and AB are free text. To calculate the similarity between two TIs and between two ABs, we pre-processed TIs and ABs by removing some common words (such as “the”, “is”, “are”, etc.) that appear frequently in text, stemming each word by the classic Porter Stemmer algorithm²⁸. This approach, named alphabetic features, also has been verified to be an effective method to represent an article²⁹. The resulting similarity score ranges from 0 to 1 for each element, where 0 indicates independence and 1 means exactly the same. In summary, the similarity score is the equally weighted sum of the MEDLINE element(s) similarity, ranging from 0 to 5.

Network Visualization

Force-directed graph drawing algorithms assign forces among the set of edges and the set of nodes of a graph drawing. Spring-like attractive forces are typically used to attract pairs of endpoints of the graph’s edges towards each other, while simultaneously electrical repulsive force are used to separate each pair of nodes. In balanced states, the edges tend to have uniform length, and nodes that are not connected by an edge tend to be drawn further apart. Graphs drawn with these algorithms tend to be aesthetically pleasing, exhibit symmetries, and tend to produce crossing-free layouts for planar graphs^30,31.

We used Force Atlas layout³² to visualize article networks. In this graphic layout, each article was represented as a node and the edge connecting a pair of nodes had an edge weight, which was the similarity score of any paired articles. The initial article network was a complete network with $\frac{n\left(n-1\right)}{2}$ edges. Large complete networks are usually complex and unreadable. To provide a more readable network, we filtered edges with lower similarity scores (in this study, the threshold was 1.0). After the filtering, the largest connected network was generated to represent the relationships among most articles. In the Force Atlas algorithm model, the pair-wise geometric distances between the drawn vertices match the graph theoretic pairwise distances. In our results, similar nodes (articles) tended to aggregate together after implementing the algorithm. Adjacent nodes represented articles with more similarities.

Evaluation Measures

Graph Diameter and Closeness Centrality

To mathematically represent the distribution of articles in the force atlas layout and then topologically study the aggregation/clustering of the included articles, we took graph diameter and closeness centrality as the evaluation measures.

In connected graphs, there is a natural distance metric between all pairs of nodes, defined by the length of their shortest paths. Graph diameter is the length of the shortest path between the most distanced nodes. In other words, a graph’s diameter is the largest number of vertices needed to travel from one vertex to another when paths which backtrack, detour, or loop are excluded from consideration³³. A disconnected graph has infinite diameter. As the graph diameter is the maximum eccentricity of any vertex in the graph, it is widely used to measure the topology and concentration/centralization of a graph. A more concentrated graph comes with a smaller diameter. In this study, we examined the graph diameter of the largest connected network as well as the sub-graphs from the subsets of articles (included, half-included, and excluded).

Closeness centrality measures the farness from one node to all other nodes. The more central a node, the lower its total distance to all other nodes. Closeness can be considered as a measure of how long it will take to spread information from a node to all other nodes sequentially^34,35. In our study, each node had a closeness centrality value. We used the distribution of closeness centrality as a measure to evaluate the network centralization.

Modularity

Modularity (community detection) is a measure of network structure. It was designed to measure the strength of division of a network into modules. Networks with high modularity have dense connections between the nodes within modules but sparse connections between nodes in different modules. Although a diversity of community detection algorithms have been proposed, the quality of community detection is usually measured by modularity and also some benchmark graphs.

We used modularity to examine resulted communities (also called module classes) in article networks. In this study, the implemented community detection algorithm was a modularity optimization based heuristic method for fast uncovering of communities in large networks. It was first published in Blondel 2008³⁶. This algorithm (also called Louvain method³⁶) has several advantages, such as easy implementation, fast computation speed, and the capability to handle large and weighted networks.³⁶ More importantly, comparing to other methods^14,36, Blondel’s algorithm has demonstrated to provide higher quality results for community detection.

While working on several commonly used test-case networks with size ranges from 34 to 118 million, Blondel’s algorithm performs the best in modularity and efficiency while compared to three other algorithms^37–39. In addition, this algorithm has also been successfully tested on the commonly applied Girvan and Newman (GN) benchmarks¹⁵ and Lancichinetti and Fortunato and Radicchi (LFR) benchmarks⁴⁰. The performance of Blondel’s algorithm is among the best when considering more than 10 popular community detection algorithms, including Rosvall 2008⁴¹ and Newman’s works^15,38. Blondel’s algorithm has also been applied to some popular social networks with millions of nodes like LinkedIn and Twitter^42,43. Therefore, we implemented the Blondel’s algorithm, available in Gephi, to examine the article networks in the SR reports.

Networks Implementation in Gephi

Gephi⁴⁴ is an open source software for graph and network analysis. It provides an interactive visualization and exploration platform for all kinds of networks and complex systems, dynamic and hierarchical graphs. It supports Blondel’s algorithm as the modularity function. We used Gephi version 0.8.2 to examine our article networks. There are three parameters for this modularity function, including resolution, randomization, and weight. We used the original modularity function in Blondel’s algorithm. In Gephi, the parameters were adjusted to use “resolution=1.0” and “randomize”. This is also resulted from the nature of Blondel’s algorithm that a random node order is selected for iteration rather than an unnecessarily fixed order. Although different runs might bring slightly different results, the differences are trivial and the overall structure remains the same. In addition, our article networks used article similarities as edge weights, so the “use weight” option was applied.

Result

We examined 20 SR reports, evaluated their graph diameter, closeness centrality, and modularity, and visualized article networks using Force Atlas layout. To provide a readable article network visualization, edges with a weight less than 1.0 were filtered. After filtering, the largest connected network was generated to represent the relationships among most articles, averaging 92.07% of all articles.

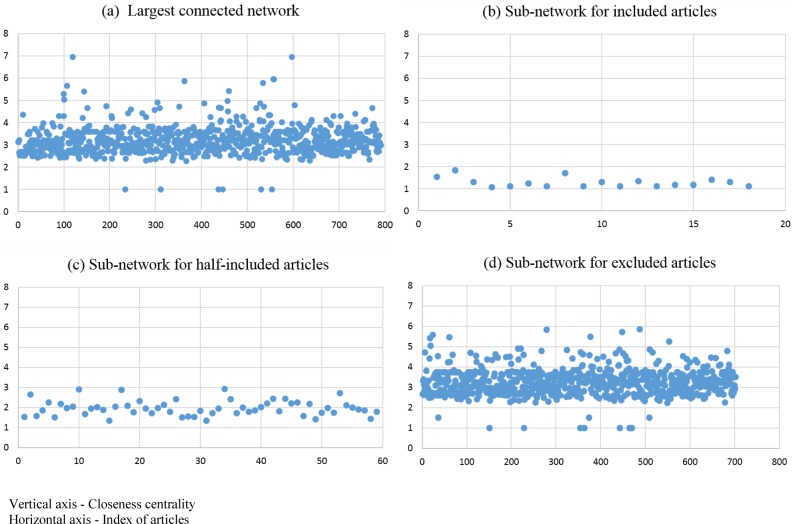
To illustrate the article network graph, we used ADHD report as an example to demonstrate the graphical topology and corresponding evaluation measures. Figure 1 shows the article network graphs for ADHD report. The ADHD report had a total of 851 articles; among which, 84 articles were included at the title/abstract level and 20 articles were included at the full-text level. In Figure 1, nodes were colored by inclusion/exclusion classes. Therefore, 20 nodes (included articles) were labeled in green, 64 nodes (half-included articles) were labeled in yellow, and 767 nodes (excluded articles) were labeled in red. To examine the article distribution, we measured the graph diameter of the largest connected network, which was 10; the graph diameter of the sub-network for included articles (green nodes) was 2; the graph diameter of the sub-network for half-included articles (yellow) was 4; and the graph diameter of the sub-network for excluded articles (red) was 9. The graph diameter demonstrated that included articles were similar to each other.

Figure 1.

Sample article network graphs from ADHD report. Nodes colored by inclusion/exclusion classes (green= included articles; yellow= half-included articles; red= excluded articles.

The distribution of closeness centrality for the largest connected network and sub-networks are shown in Figure 2. The closeness centrality of the largest connected network ranges from 1 to 7 (Figure 2a); but the closeness centrality of the sub-network for included articles, ranges from 1 to 2 (Figure 2b). The higher the closeness centrality score is, the more distance the node is to other nodes (less similar). Only if a node was isolated because of the filtering process (edges weighted <1 were eliminated), the closeness centrality score is 0.

Figure 2.

The distribution of closeness centrality for ADHD report

In summary, the sub-network of included articles had a smaller graph diameter and relatively smaller closeness centrality values than the largest connected network. We can conclude that included articles tend to have strong relationships (high similarities in MEDLINE elements). Similarly, the sub-network of the included articles also had a smaller graph diameter and closeness centrality values comparing to the sub-network of the half-included articles.

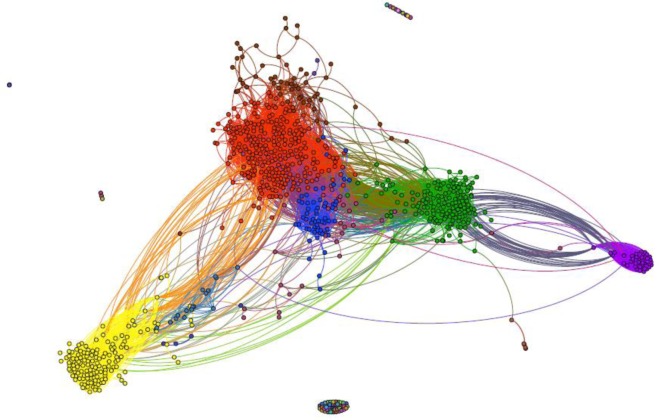
In Figure 3, it shows the same network graph as Figure 1, but with a different coloring scheme. Here, nodes are colored based on module classes using Blondel’s algorithm. A total of 73 module classes were found. Eight out of 73 modules contain more than 17 nodes, which is 2% of all articles in the ADHD report. The rest of 65 modules were considered minor communities with only a small amount of nodes or even one single node inside. The top three modules, which contain 31.02%, 18.21% and 17.04% of all articles, were colored in red, green, and yellow (in Figure 3) respectively. With this partition, we observed that 18 out of 20 included articles tended to aggregate in the green module class, with the exception of two articles. In other words, the green module class in Figure 3 covers 90% of included articles. The included articles in this green module class (18/155=11.61%), are much higher than those in the entire network (20/851=2.35%). The findings again confirmed our hypothesis that included articles tend to cluster together because of their high similarities to each other. With this scenario, if the article screening process can begin with this community, we could rapidly identify 90% (18 out of 20) relevant articles.

Figure 3.

Sample article network graphs from ADHD report. Nodes colored by module classes. A total of 73 module classes were found.

Graph diameter and closeness centrality

To evaluate the graph centralization of the sub-network for included articles, we calculated its graph diameter and closeness centrality range and compared them with the largest connected network (Table 2). Because Skeletal Muscle Relaxants report has the graph diameter of 1, which is not meaningful for calculation, it was not included in the following analysis due to its fracture network. For the remaining 19 SR reports, the average value of largest connected networks’ diameter was 8.26 (SD = 1.76), while the average graph diameter value of the sub-network for included articles was only 3.84 (SD = 1.54). The results show that the graph diameter of the sub-network of included articles was significantly smaller than that of the largest connected network (paired-t test, p<0.001). And for the closeness centrality range of the largest connected network, the largest one was 1~9 while the smallest one was 1~4. The largest closeness centrality range of the sub-network for included articles was 1~5 while the smallest one was only 1~2.

Table 2.

Graph diameter and closeness centrality

	Largest connected network		Sub-network of included articles
	GD	CCR	GD	CCR
ACE Inhibitors	7	1~5	3	1~3
ADHD	10	1~7	2	1~2
Antihistamines	8	1~6	3	1~3
Atypical Antipsychotics	8	1~6	7	1~5
Beta Blockers	8	1~6	4	1~4
Calcium Channel Blockers	8	1~6	7	1~5
Estrogens	7	1~5	6	1~4
NSAIDS	11	1~9	3	1~3
Opioids	7	1~5	3	1~3
Oral Hypoglycemics	5	1~4	5	1~4
Proton Pump Inhibitors	8	1~7	3	1~3
Skeletal Muscle Relaxants	13	1~9	1a	1~1
Statins	9	1~6	4	1~4
Triptans	10	1~7	5	1~4
Urinary Incontinence	8	1~6	4	1~3
Antibiotic	6	1~5	3	1~3
Antineoplastic	9	1~7	4	1~3
Antiretrovirals	6	1~5	3	1~3
Hearing Loss	11	1~8	2	1~2
Leukemia	11	1~8	2	1~2
Average	8.26	1~6	3.84*	1~3

GD = Graph Diameter; CCR= Closeness Centrality Range.

^a=Fracture network, only 2 out of 9 nodes are connects. Therefore, the report was not included in the average value.

^*Significant smaller than the largest connected network (p<0.001)

In summary, the graph diameter of the sub-network for included articles was smaller than the graph diameter of the largest connected network. More than half of the SR reports even have less than a half size of the graph diameter. Besides, the closeness centrality range also shows a smaller value and tighter distribution in the sub-network of included articles comparing to the largest connected network, (1~3 vs. 1~6). The results confirmed that included articles tend to aggregate into a few small areas, and these generate “communities” cover 93.75% included articles in average from 19 SR reports in our study.

Module Classes

Table 3 shows modularity results on module classes after the implementation of modularity function (community detection function) for the 20 SRs. We used the number of modules (M), the number of modules with included articles (Mi), and the number of dominant modules with more than 10% included articles (DMi). We also reported the top two modules, which contain most included articles.

Table 3.

Modularity and detected module classes

	Modularity			Module1				Module2
	M	Mi	DMi	articles covered		included articles covered		articles covered		included articles covered
				#	%a	#	%b	#	%a	#	%b
ACE Inhibitors	72	2	1	707	27.97%	40	97.56%	796	31.29%	1	2.44%
ADHD	73	3	1	159	18.68%	18	90%	50	5.88%	1	5%
Antihistamines	43	4	3	83	26.77%	9	56.25%	74	23.87%	3	18.75%
Atypical Antipsychotics	83	8	4	187	16.7%	50	34.25%	200	17.86%	45	30.82%
Beta Blockers	89	4	2	400	19.26%	26	61.90%	476	22.97%	12	28.57%
Calcium Channel Blockers	68	5	3	274	22.5%	36	36%	333	27.34%	32	32%
Estrogens	42	6	3	75	20.38%	34	42.5%	66	17.93%	24	30%
NSAIDS	44	3	2	78	19.85%	32	78.05%	42	10.69%	7	17.07%
Opioids	90	3	2	298	15.56%	11	73.33%	592	30.91%	3	20%
Oral Hypoglycemics	31	7	3	161	32.01%	66	48.53%	146	29.03%	33	24.26%
Proton Pump Inhibitors	51	6	2	449	33.68%	37	72.55%	405	30.38%	7	13.73%
Skeletal Muscle Relaxants	322	3	2	826	50.27%	6	66.67%	184	11.20%	2	22.22%
Statins	191	4	2	1384	39.95%	67	78.82%	1160	33.49%	14	16.47%
Triptans	43	2	2	205	30.55%	17	70.83%	183	27.27%	7	29.17%
Urinary Incontinence	57	7	1	67	20.49%	30	75%	18	5.5%	3	7.5%
Antibiotic	25	3	3	45	10.92%	6	60%	125	30.34%	3	30%
Antineoplastic	195	5	3	144	11.13%	9	47.37%	191	14.76%	4	21.05%
Antiretrovirals*	13	1	1	331	44.19%	38	100%	–	–	–	–
Hearing Loss	87	2	2	116	24.84%	2	66.67%	100	21.41%	1	33.33%
Leukaemia*	92	1	1	80	24.39%	7	100%	–	–	–	–
Average	86	4	2	303	25.50%	27	67.81%	286	21.78%	11	21.24%

M= number of modules; Mi= number of modules that contain included articles; DMi= number of dominant modules with more than 10% included articles;

^*The SR report has only one module that contains included articles. Therefore, there is no Module2.

^a= percentage of articles covered in the module;

^b= percentage of included articles covered in the module

Although a large number of modules are detected for the largest connected network (average M = 86), included articles were only found in a few modules (average Mi = 4), and even less were classified into the dominant modules (average DMi = 2). This implies that included articles have strong similarity which tends to cluster in the same module classes. Moreover, the number of included articles found in Module1 (the top module for each report) provides additional aggregation evidence. In average, Module1 covers 25.5% articles overall, but 67.81% included articles. With Module1 and Module2 together, they total cover 89.03% (67.81%+21.24%=89.03%) included articles. Due to the space limitation, we only report the top two modules in Table 3. However, other modules except dominant modules contain very few included articles. In many cases, there was only one included article in a module.

Discussion

The use of article network visualization for SR

In this study, we used the visualization approach to demonstrate article relationships. While article networks bring a more intuitive view of article distribution, the use of graph measures also provides mathematical support for our hypotheses. The aggregation of included articles confirms the feasibility of utilizing article relationships (similarity) to facilitate the article selection process for SR. We believe the visualization approach can be a powerful tool in assisting SR researchers for article screening. Taking the ADHD report as an example (Figure 3), we can rapidly identify included articles if we start the article screening in the green module. 90% (18 out of 20) included articles could be found earlier before screening in other areas, thus significant workload would likely to be saved.

The article network visualization can be applied to (1) identify multiple key communities when the topic of articles is diversified; (2) assign high priority to communities with relevant articles and screen articles from the closet neighbors; (3) assign low priority to communities that contain several known irrelevant articles to save unnecessary workload; (4) customize the network structure with different similarity calculation for edge weights that align to specific sub-aims of a SR scope, e.g. authorship, publication type, keywords; (5) provide potential knowledge discovery from unexpected module classes. Our future work has planned to develop such an article network visualization application to assist SR.

The limitation of force-directed algorithm

Although the basic force-directed approach performs well for small graphs, the results are poor for graphs with more than one or two thousands vertices. This is mainly resulted from the obstacles to scalability and resolution. To be specific, the minimum vertex separation tends to be very small for large graphs, which leads to unreadable drawings. In addition, the typical force-directed algorithms are considered to have a time complexity equivalent to O(n³), thus the running time could be very long for large graphs. Due to this limitation, the SRs we applied in our study had no more than 4000 articles. Algorithms and layouts like T-SNE⁴⁵ which supports implicit structure and dimensionality reductions could be considered for larger SRs in future works.

Future direction

As most included articles exhibiting a tendency to aggregate to a specific graphic region, we demonstrated the existence of such dominant module classes that cover a high percentage of included articles. Screening articles within these module classes first will likely accelerate the speed of discovering relevant articles. For our future work, we plan to work on early identification of the dominant module classes by integrating SR expert researchers’ knowledge on SR scopes and research questions. With the external information, we are able to generate virtual article(s) representing ideal articles for inclusion. Virtual article(s) are likely to be located in the dominant module classes in the article network.

Conclusion

We demonstrated visualizing article relationships for SR with MEDLINE similarity in force layout. We used measures: graph diameter, closeness centrality, and module classes from the perspective of graph theory, to evaluate the centrality and communities of generated article networks. The sub-networks of included articles have a significantly smaller graph diameter than those of the largest connected network (3.84 vs. 8.26, p<0.001), and a smaller distribution in closeness centrality (1~3 vs. 1~6). Although a large number of modules were detected for the largest connected network (n=86) after the implementation of modularity function, included articles only cluster into a few communities (n=4), and are found in even fewer dominant communities (n=2). More importantly, the top two modules covered 89.03% included articles.

Since most included articles in our research cohort exhibited a tendency to aggregate to specific regions, early identifying and exploring of these regions will likely accelerate the discovery of relevant articles for a SR We conclude that while relevant articles in SRs share common features and strong relationships (similarities), the article similarity can be utilized to facilitate the article selection process thus shortening and facilitating the most labor intensive aspect of the SR. which is the most intensive job in SR. Besides, through the visualization of article networks, we demonstrated viewing article relationships in a more intuitive way. We also discovered other advantages of visualizing article networks that are infeasible from the common text comparison approach. For example, if there are multiple major aggregated regions in an article network, a branching of SR scopes may be needed. Integrating article network visualization as a decision support tool in the SR process will enable SR researchers to discover particular patterns or communities; thus accelerating the SR production.