Abstract
The rapid growth of digital health databases has attracted many researchers interested in using modern computational methods to discover and model patterns of health and illness in a research program known as computational phenotyping. Much of the work in this area has focused on traditional statistical learning paradigms, such as classification, prediction, clustering, pattern mining. In this paper, we propose a related but different paradigm called causal phenotype discovery, which aims to discover latent representations of illness that are causally predictive. We illustrate this idea with a two-stage framework that combines the latent representation learning power of deep neural networks with state-of-the-art tools from causal inference. We apply this framework to two large ICU time series data sets and show that it can learn features that are predictively useful, that capture complex physiologic patterns associated with critical illnesses, and that are potentially more clinically meaningful than manually designed features.
1 Introduction
The increasing volume, detail, and availability of stored digital health data offers an unprecedented opportunity to learn richer, data-driven descriptions of health and illness.1 This principle has driven the rapid development of computational phenotyping, a broad field encompassing a variety of efforts to apply modern computational methods to increasingly large and complex medical data sets. These efforts are further unified by a common goal: to not only build successful predictive models but also to learn and recognize clinically meaningful descriptors of health. Computational phenotyping has attracted many researchers in machine learning and data mining, who apply many different techniques (ranging from Gaussian processes to tensor factorization) to extract meaningful representations from a variety of data sources and types (e.g., clinical time series, text, event counts, etc.).1;2;3;4;5;6;7
Some of the most interesting phenotyping work involves phenotype discovery, i.e., learning latent representations that capture structure in data and may represent real patterns of illness. Such techniques have the potential to become powerful tools for clinical research. For example, Schulam, Wigley, and Saria used a Bayesian framework to find patient clusters that may represent previously unknown subtypes of Scleroderma.6 However, phenotype discovery from physiologic data poses significant challenges because human physiology is immensely complex and nonlinear, and illnesses often span a large number of body systems and processes. Acute respiratory distress syndrome (ARDS), for example, involves an acute failure of the respiratory system but may manifest with circulatory, excretory, and even neurological symptoms. What is more, its causes range from injury from inhalants to infection to overdose of antidepressants.8 This complexity suggests that such diseases have many latent factors of variation, and modeling and disentangling these factors is essential to successful analysis.9 One potential solution to this problem is deep learning (e.g., multilayer neural networks), which has led to major breakthroughs in speech recognition10 and computer vision11.
However, despite rapid advances in methods12 and software,13;14;15;16 there has been comparatively little formal research on interpretation of deep learning architectures.17;18 This becomes an especially critical question when applying deep learning to health and medicine. Neural networks are classically viewed as “black box” models that may achieve high predictive accuracy but are uninterpretable by humans and unsafe for use on clinical problems. One solution for unraveling the complex representations produced by deep learning to apply ideas and tools from causal inference.19 Feed-forward architectures are in fact directed acyclic graphs (DAGs), in which inputs cause higher layer activations, which in turn cause outputs. Thus, they may be thought of as causal models, which makes them amenable to causal analysis. This likewise provides an motivation for phenotype discovery, in which we seek to learn representations that are potential causes of outcomes, rather than merely correlated or predictive.
There is a growing body of research on discovering causal relationships among variables from observational data under a variety of assumptions and settings.20;21;22 In particular, we can identify potential causal relationships among the variables if noise is not Gaussian distributed.21;22 This is frequently the case for neural networks with, e.g., sigmoid hidden units and binary outcomes. In this paper, we present a first step toward automatic discovery of causal phenotypes and for cracking open the black box of neural networks, making them more readily applicable to medical data. Our frame is a two-stage process. First, we use a simple deep neural network architecture to learn latent representations of physiology from clinical time series. Then we use a state-of-the-art causal inference algorithm called Pairwise LiNGAM22 to analyze the relationships between these learned phenotypes and patient outcomes and diseases of interest. Finally, we use common deep learning heuristics to visualize and interpret the learned phenotypes. We show that this algorithm discovers intuitive patterns of physiology known to be associated with acute illnesses. We also propose an informal causality-based framework for measuring the causal power of learned representations.
1.1 Related Work
While a young field (at least by that name), computational phenotyping is advancing rapidly, spurred on by the increased adoption of electronic health records (EHRs) and the growing interest from data mining and machine learning researchers. There is already a large body of excellent research, much of it published in just the last five years or so.
One popular approach to computational phenotyping is to construct a large multi-dimensional array (i.e., matrix or tensor) view of clinical data and then apply dimensionality reduction or feature selection techniques to learn a lower-dimensional set of latent bases that can be treated as phenotypes. Each basis can be seen as a combination of observations (from the original tensor), while each patient becomes a sparse set of coefficients representing her projection onto the phenotype bases. Such work can be seen as a much more powerful generalization of classic techniques such as principal components analysis. Two primary examples of this paradigm include Zhou, et al.,4 and Ho, Ghosh, and Sun,5 which apply such frameworks to outpatient disease data and medicare claims, respectively, with very interesting results. Such an approach could be applied to physiologic time series, as well.
An alternative phenotyping paradigm includes probabilistic models, which assume a generative process and then fit the model to data using, e.g., maximum a posteriori inference. Such models can be robust to uncertainty, noise, and some types of missing values and are often interpretable. Marlin, et al., used a Gaussian mixture model with a temporal smoothness kernel prior to discover meaningful physiologic patterns (or physiomes) in multivariate time series from acute care settings similar to ours.1 Saria, et al., proposed a Time Series Topic Model (TSTM) that can learn bag-of-AR (autoregressive linear models) representations from dense time series (e.g., ECG waveforms) and has been used to develop a novel severity of illness score for neonatal patients.7 Schulam, Wigley, and Saria recently proposed the Probabilistic Subtyping Model, a Bayesian framework that combines splines and Gaussian processes to cluster longitudinal data from chronic Scleroderma patients and discover potentially novel subtypes.6
To our knowledge, work by Lasko, Denny, and Levy represents one of the first applications of modern deep learning to clinical time series.3 They train stacked autoencoders on 30-day windows of uric acid readings to learn features that are competitive with expert-designed features for classifying gout versus leukemia. They handle irregular, biased sampling by warping their time series and then sampling from a fitted Gaussian process. This framework successfully learns time series features that are both visually intuitive and useful for discerning the two phenotypes. Kale, et al., and Che, et al., recently demonstrated that neural networks (unsupervised and supervised) can be used to discover and detect interpretable subsequences in multivariate physiologic time series that are useful for classifying acute illnesses.23;24 Given that deep learning approaches have achieved breakthrough results in language modeling,25 speech recognition,10 and music transcription,26 we expect similar results (with time and effort) in health and medicine.
In deep learning research, feature analysis is often secondary to, e.g., prediction performance, and focuses on visualization. Strategies include sampling from generative models and optimizing (using, e.g., stochastic gradient ascent) over inputs rather than parameters.17 Each method has strengths and weaknesses (e.g., simplicity, computational efficiency, local optima), but they share several properties: they work best for data that are easily interpreted by human beings (e.g., images27); they employ heuristics and approximations; and they analyze each hidden unit independently. However, recent research has begun to provide a more rigorous understanding of the representations learned by deep architectures. Szegedy, et al., showed that the semantics encoded by hidden unit activations in one layer are preserved when projected onto random bases, instead of the next layer’s bases.28 This implies that the practice of interpreting individual units can be misleading and that the behavior of deep models may be more complex than previously believed.29
One solution for unraveling the complex representations produced by deep learning is to apply ideas and tools from causal inference.19 Chalupka, Perona, and Eberhart recently proposed a theoretical framework that reformulates image classification as a causality problem (i.e., an image causes an agent to label it as a 7 or 9) and uses active learning to perform interventions that can separate causal features from spurious correlations.30 This idea offers a partial solution to the problems described above28 but requires the ability to perform interventions that may not be possible in clinical data analysis. Alternatively, there is a growing body of research on discovering causal relationships among variables from observational data under a variety of assumptions and settings,20;21;22 which we discuss in detail later.
2 Methods
In this section we describe our two-stage framework for discovery and analysis of causal phenotypes from clinical time series data uses deep neural networks. We first describe the background of feature (i.e., phenotype) extraction from time series in Section 2.1. We then demonstrate how deep neural networks can be used to perform both unsupervised (Section 2.2) and supervised (Section 2.3) discovery of latent representations of physiology (i.e., phenotypes) from clinical time series. Finally, we show in Section 2.4 how state-of-the-art causal inference algorithms can be used to analyze the learned phenotypes and to identify potential causal relationships between phenotypes and critical illness.
2.1 Background: feature extraction from time series
Given a multivariate time series with P variables and length T, we can represent it as a matrix X ∈ ℝP×T. We denote the time series of the pth variable as a row vector xp,. ∈ ℝT and the tth time as a column vector x.,t ∈ ℝP. A feature map for time series X is a function f : ℝP×T ↦ℝD that maps X into a D-dimensional feature space, which can be used for machine learning tasks like classification, segmentation, and indexing.31 In a medical context, we can think of features as phenotypes. These can take the form of extreme measurements (as in severity of illness scores), thresholds, or important patterns. In multivariate time series, features become increasingly complex to design, so automated feature discovery is an attractive proposition. Given the recent success of deep learning in a variety of applications, it is natural to investigate its effectiveness for feature learning from clinical time series data.
2.2 Deep unsupervised autoencoders for phenotyping clinical time series
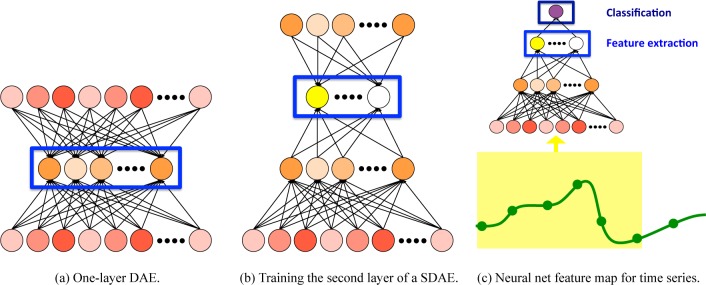
We explore several deep neural network architectures for automatic discovery and detection of important physiologic patterns. We begin with a simple denoising autoencoder (DAE).32 This is a one layer unsupervised model that simultaneously learns paired encoding and decoding functions, similar to sparse coding but easier to optimize and incorporate into deep architectures. Figure 1a shows a simple illustration of the DAE.
Figure 1:
Deep neural networks for phenotyping from clinical time series.
We encode and decode x using rules similar to making a prediction using a logistic function:
where h ∈ [0, 1]D′ is the latent representation, is the reconstruction, and g and g′ are elementwise nonlinearities (a common choice is the sigmoid function g(z) = 1/(1 + exp{−z}). The choice of g′ depends on the type of input x. As described later, in this work we scale all variables to fall between 0 and 1, so we can use a sigmoid for decoding as well. As is typical, we also tie the weights, letting W′ = W⊤. Finally, in DAEs we actually add random corruption to the input before encoding, sampling . In our case, Pcorr applies a binary masking to x, zeroing out each entry independently with some probability p.
We train the weights by minimizing the reconstruction loss for each training example. For [0, 1] inputs, we use cross entropy loss
where xd is the dth dimension of x. Note that for a DAE, , i.e., the reconstruction of the corrupted input . We use standard (stochastic) gradient methods to minimize the reconstruction error with respect to W, b and b′ for all training examples.
We can construct a deep autoencoder by stacking multiple DAEs, forming a stacked denoising autoencoder (SDAE).33 SDAEs are typically trained using greedy layer-wise training,(34) as shown in Figure 1b. Once the weights for layer ℓ have been trained, we can map each training example into its feature space, producing h(ℓ). This then becomes the input for training the (ℓ + 1)th layer. Note that h(0) = x, the input.
In our setting, x = vec(X), a vectorization of our P × T time series. We can then use an SDAE of any number of layers as a feature map f for time series, as shown in Figure 1c. Each element of h(ℓ) is a nonlinear function of the SDAE’s inputs, meaning that it can capture complex correlations across both time and variables. This makes it well-suited tool for phenotyping from clinical time series, especially when working with relatively small data sets with few or unreliable labels.3
2.3 Deep supervised neural networks for phenotyping clinical time series
We can convert a deep autoencoder into a deep feed-forward neural network by adding an additional output layer to make predictions, as shown in Figure 1c. For binary classification, we typically use a sigmoid nonlinearity applied to a linear activation, i.e., a logistic regression:
where yk is the kth output unit and h are the hidden unit activations (we omit the bias for brevity). Neural networks lend themselves naturally to multi-output prediction problems (also called multi-label or multi-task learning), and training such neural networks can often improve prediction performance by enabling the neural network discover shared features that are useful across a range of tasks. In a medical context, this approach can be used to train a single model to predict multiple outcomes or diagnoses.
A neural network with L hidden layers and an output layer has hidden layer parameters and output parameters for D(L) hidden units in the Lth layer and K outputs. For K binary classification tasks, the loss function during supervised training also uses cross-entropy but with the true labels (vs. reconstruction, as in the SDAE):
where h(L) = g(W (L)h(L−1)+b(L)) and h(0) = x. Again, we minimize the loss with respect to all model parameters using (stochastic) gradient descent and backpropagation.
2.4 Discovery of causal phenotypes from clinical time series
One of the main advantages of deep learning is its ability to disentangle factors of variation that are present in the data but unobserved.9 This makes subsequent learning (i.e., training a classifier) much easier since it counteracts the curse of dimensionality.35 In addition, knowledge about one factor usually improves estimation about another.36
However, it can often be difficult to analyze and understand the learned latent representations and to understand whether the model is learning truly important relationships or spurious correlations. One way to explore and demonstrate this fact is to perform causal analysis of the features extracted by the hidden layers of a deep neural network. Disentangled representations should have clearer and stronger causal relationships with other variables of interest (e.g., mortality) than raw outputs and other choices of features. Additionally, causality is of primary interest in medicine and health, especially if analytics will contribute to decisions about treatment and care, which can significantly impact patient lives and outcomes. Thus, discerning correlation from true causal relationships is of vital importance.
Given a set of features denoted by and a response variable y, we investigate the causal relationship between each feature hj, j = 1, …, D(L), and the response variable y. There are two options: either the direction of the edge is from feature to the response variable hj → y or vice versa hj ← y. We are interested only in the former case where the features are causally predictive of the response variable. Thus, we need to use a causality discovery procedure to find the direction of causation between the features and the response variable.
Classic causal inference algorithms require a set of causal priors to be available for the variable to be able to cancel out the impact of spurious causation paths.19 While we often do not have such priors available for our outputs, we can still identify causation among the variables if they are not distributed according to a Gaussian distribution.20;21;22 Binary labels (e.g., mortality prediction) satisfy the requirements of many causal inference frameworks. We apply a state-of-the-art causal inference algorithm Pairwise LiNGAM 22, based on DirectLiNGAM, in order to discover the causal edges between each feature and response variable. The key idea of this algorithm is to compute the likelihood ratio of the two models hj → y and hj ← y for j = 1, …, D(L) and select the direction that makes the log-likelihood ratio positive. In particular, we have
where n denotes the number of observations. The log-likelihood values are computed using the non-parametric entropy estimation techniques. Pairwise LiNGAM requires that the two variables be non-Gaussian distributed, which makes it especially useful for analyzing deep neural networks with nonlinear activation functions in hidden layers and logistic outputs. This is the case in our setting.
It is important to emphasize that causal inference algorithms do not necessarily select those features that are most correlated with the response or most useful in predicting it. Our goal in causal analysis, rather, is to discover a subset of features that are the best candidates to be true causes of the response and which may provide insight (not necessarily more predictive power).
Next we propose an informal method for quantifying the causal power of features (derived or learned). After learning the causal features, we follow the recommendation22, we fit a logistic regression model to the features selected by the causality discovery algorithm as follows:
where represent the set of features selected by the causality discovery algorithm and α, α0 denote the prediction vector and the intercept, respectively. We treat the resulting weights as the magnitude of each variable’s causal relationship. Finally, we use the L2 norm of the regression coefficient vector ∥α∥2 to quantify the overall causal power of the features being analyzed. We can use this to compare the causal power of different representations.
3 Experiments
In order to demonstrate the effectiveness of our framework, we performed a series of phenotype experiments using two clinical time series data sets collected during the delivery of care in intensive care units (ICUs) at large hospitals. After describing our data and experimental set up, we briefly present quantitative results for several classification tasks, in order to demonstrate the predictive power of features discovered by neural networks (Section 3.1). Then in Section 3.2, we apply causal inference tools to the learned features in order to discover the most clinically meaningful features and to analyze the quality of the learned phenotypes. We also provide example visualizations of causal features learned by neural networks that capture clinically significant physiologic patterns.
Physionet Challenge 2012 Data
The first data set comes from PhysioNet Challenge 2012 website37 which is a publicly available collection of 8000 multivariate clinical time series from one ICU and three specialty units, including coronary care and cardiac and general surgery recovery units. As with the competition, we focus on mortality prediction (from the first 48 hours of each episode) as our main prediction task. This is a challenging problem: no competition entry scored precision or recall higher than 0.53. We used both Training Subsets (A and B) for any unsupervised training but only the labeled Training Subset A for supervised training and evaluation (to our knowledge, labels are not available for Subset B). Each episode is a multivariate time series of roughly 48 hours and containing over 30 variables. While each episode also has a variety of static variables available (e.g., age, weight, gender), we focus our experiments on just the time series. In all supervised learning experiments, we use label stratified 10-folds cross validation when estimating performance scores.
PICU Data
The second data set consists of ICU clinical time series extracted from the electronic health records (EHRs) system from Children’s Hospital LA (CHLA), previously described in Marlin, et al, and Kale and Che, et al.1;38 The original data set includes roughly ten thousand episodes of varying lengths, but we exclude episodes shorter than 24 hours, yielding a data set of roughly 8500 multivariate time series of thirteen physiologic variables. Each episode has zero or more associated diagnostic codes from the Ninth Revision of the International Classification of Diseases (ICD-9).39 We aggregate the five-digit ICD-9 codes according to the standard seventeen broad category codes (e.g., 460-519 for respiratory diseases) and supplementary V and E groups. We then treat predicting each category code as a distinct binary classification task. The sparse multi-label nature of these data prevents us from applying cross-validation; we instead create five 80/20 random splits of the data, ensuring that each split has a minimum number of positives examples for each ICD-9 label.
Preprocessing
We perform three steps of preprocessing to both data sets before analysis. First, we scale each variable to a [0, 1] range. Where variables have known ranges (e.g., Total Glasgow Coma Scale or binary variables), we use those. Otherwise, we treat the 1st and 99th percentiles of all measurements of a variable as its minimum and maximum values. Outliers are truncated to 0 or 1. This is applied to both time series and static variables. Next, we resample all time series to a fixed hourly sampling rate using a simple bucketing procedure: we divide each time series into 48 non-overlapping hour-long windows. When a window includes more than one measurement, we take the mean. Where this creates missing values, we propagate forward the previous measurement. This makes a reasonable assumption that each time series is relatively stable and that important changes are observed and recorded. Finally, we handle entirely missing time series (e.g., a patient may have zero measurements of end-tidal CO2 if she is not ventilated) by imputing a “normal” value. For variables without known normals, we use the median of all measurements in the data set. This strategy the fact that missing time series are typically not missing-at-random but rather are missing because clinical staff decided not to measure a particular variable. Often this is because they also assume it is normal.
Neural network training
We implemented all neural networks in Theano13 as variations of a multilayer perceptron with 3–5 hidden layers (of the same size) of sigmoid units. The input layer has PT input units for P variables and T time steps, while the output layer has one sigmoid output unit per label. We initialize each neural network by training it as an unsupervised stacked denoising autoencoder (SDAE). We found this helps significantly because our data sets are relatively small and our labels are quite sparse. We use minibatch stochastic gradient descent to minimize cross-entropy loss during unsupervised pretraining and logistic loss during supervised finetuning. We use ten-fold cross validation, and both neural networks and classifiers are not trained on the test folds. Additionally, we use grid search and one training fold to tune parameters (e.g., the strength of the L1 penalty).
3.1 Classification performance
We first present a quantitative evaluation of the predictive performance of different types of features, both hand-designed and learned, on the Physionet Challenge 2012 data set. To ensure a fair comparison, we use the same type of classifier in all experiments: a linear support vector machine (SVM) with hinge loss and a L1 regularization penalty.40 We do not use our neural networks to make predictions. We select the strength of the L1 penalty by performing a grid search over the range [10−2, 102] and choosing the value that maximizes the Area Under the Precision-Recall Curve (AUPRC) on a held-out subset of our training data. We report both Area Under the Receiver Operator Curve (AUROC) and AUPRC, as well as the Precision when Recall is 90%. All three metrics are more robust to the class imbalance of our label than accuracy and give us an idea of the trade-off between false negatives and false positives.37
Our baselines include the raw data and hand-designed features that capture the extremes, central tendency, variation, and trends within the entire time series. While relatively simple from a machine learning perspective, these features are often quite effective for clinical predictive modeling and similar to those used in classic severity of illness scores.(41;42) Table 1 shows the mortality prediction performance for the Physionet Challenge 2012 data for our best-performing baselines and neural network features. We see that features learned using a 3-layer neural network beat the raw data fairly substantially and are competitive with the hand-designed features. Given the success of neural networks in other domains, it is somewhat disappointing that the learned features do not beat the hand-engineered features soundly. However, we offer several observations to temper this disappointment: first, we invested minimal time in tuning hyperparameters of the neural network, including hidden layer sizes, learning rate, and early stopping criteria. Additional experiments (not reported here) suggest that our neural network underfit the training data due to insufficient size and training epochs.
Table 1:
Classification performance on the Physionet Challenge 2012 data set. We report mean and standard deviation (across 10 folds) for each metric. We use the following abbreviations: R: raw time series, H: hand-designed features, NNet(I,L): L-layer neural network with input I
| AUROC | AUPRC | Precision@90%Recall | |
|---|---|---|---|
| Raw Time Series (R) | 0.786848 ± 0.028957 | 0.407419 ± 0.042878 | 0.221303 ± 0.017106 |
| Hand-designed Features (H) | 0.828652 ± 0.021065 | 0.467742 ± 0.047852 | 0.259324 ± 0.049400 |
| NNet(R,3) | 0.820760 ± 0.021021 | 0.444315 ± 0.032367 | 0.255792 ± 0.030306 |
| H+R | 0.822907 ± 0.018251 | 0.438160 ± 0.035444 | 0.255608 ± 0.031871 |
| H+NNet(R,3) | 0.845015 ± 0.016525 | 0.486791 ± 0.047373 | 0.291411 ± 0.033500 |
Second, as shown in the bottom two rows of Table 1, we found that we could substantially improve performance by combining the neural net and hand-engineered features. This suggests that in fact the neural net learns features that contain information that does not overlap that captured by the hand-engineered features and may capture different physiologic patterns. What is more, as shown in Section 3.2, they have increased causal power.
Interestingly, we found minimal difference between the performance of features learned using unsupervised and supervised neural networks. We speculate that this has two causes. The principle reason, we speculate, is the class imbalance in our labels, which we did not attempt to handle in any way during neural network training. Second, mortality prediction from early admission data is a difficult problem, and it may not be possible to do substantially better (our results are similar to those from the competition).
3.2 Causal analysis
Next, we perform causal inference on the hand-designed and learned features using the framework described in Section 2.4. Table 2 shows the per-feature causal power (i.e., the L1 norm of the coefficient vector divided by the number of features with nonzero weights) of the raw data, hand-designed features, and neural network features for Acute Respiratory Distress Syndrome (ARDS) in the PICU data. We see the the neural network features have, on average, a much larger magnitude than either of the baselines.
Table 2:
Magnitude of causal relationships of differents with ARDS in PICU data.
| Raw Time Series | Hand-designed Features | NNet(R,3) |
|---|---|---|
| 0.013 ± 0.0063 | 0.093 ± 0.058 | 0.25 ± 0.27 |
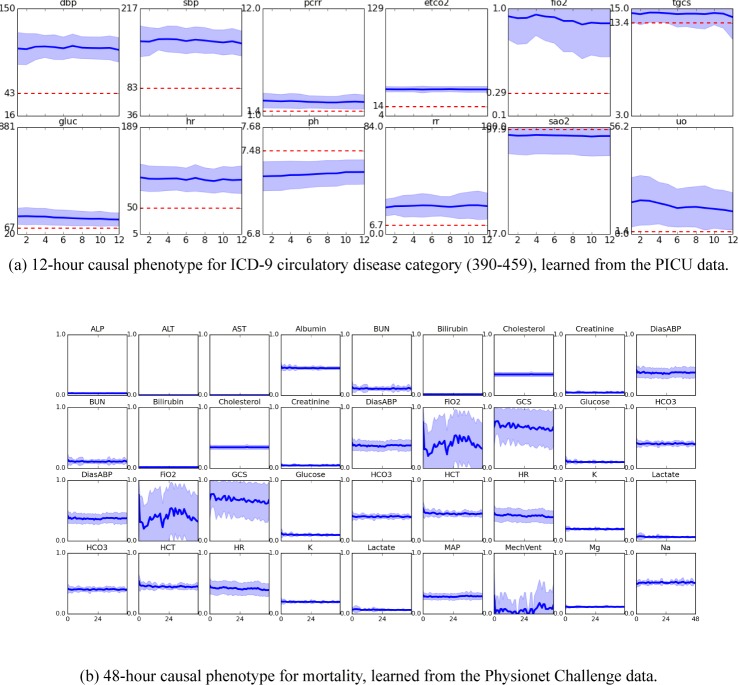
Figure 2 shows visualizations of two the significant physiologic patterns learned by the neural networks. For each we used causal inference to discover the subset of features with the strongest causal relationship with our outcome of interest. Then we found the 50 input subsequences with the highest activations in those units and plotted the mean trajectories for some or all physiologic variables. Figure 2a visualizes features that were found to be causally related to the ICD-9 circulatory disease category from the PICU data. We see these features detect highly elevated blood pressure and heart rate, as well as depressed pH. The features also detect elevated end-tidal CO2 (ETCO2) and fraction-inspired oxygen (FIO2), which likely indicate ventilation and severe critical illness. Interesting, these features also detect elevated urine output, and thus it is not surprising that these features are also correlated with diagnostic labels related to urinary disorders. Figure 2b visualizes the First-48-hour physiologic patterns detected by features that are causal of mortality in the Physionet Challenge 2012 data.
Figure 2:
Causal features learned from ICU time series.
4 Discussion and Conclusion
We have presented a simple, two-stage framework for discovering latent phenotypes from clinical time series that have strong causal relationships with patient outcomes and critical illness. Our framework combines feature learning using neural networks with causal inference tools to discover latent phenotypes that are causally predictive of clinical outcomes. While our results are preliminary, we believe that this general line of research will help us discover more clinically meaningful representations of health and illness and to eventually develop tools for automatic discovery of causal phenotypes.
Acknowledgments
David Kale was supported by the Alfred E. Mann Innovation in Engineering Doctoral Fellowship, and the VPICU was supported by grants from the Laura P. and Leland K. Whitter Foundation. Mohammad Taha Bahadori was supported by NSF award number IIS-1254206. Yan Liu was supported by NSF IIS-1134990 and IIS-1254206 awards. The views and conclusions are those of the authors and should not be interpreted as representing the official policies of the funding agency, or the U.S. Government.
References
- [1].Marlin BM, Kale DC, Khemani RG, Wetzel RC. Unsupervised Pattern Discovery in Electronic Health Care Data Using Probabilistic Clustering Models; Proceedings of the 2Nd ACM SIGHIT International Health Informatics Symposium. IHI '12; pp. 389–398. [Google Scholar]
- [2].Xiang T, Ray D, Lohrenz T, Dayan P, Montague PR. Computational Phenotyping of Two-Person Interactions Reveals Differential Neural Response to Depth-of-Thought. PLoS Computational Biology. 2012;12;8(12):e1002841. doi: 10.1371/journal.pcbi.1002841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Lasko TA, Denny JC, Levy MA. Computational Phenotype Discovery Using Unsupervised Feature Learning over Noisy, Sparse, and Irregular Clinical Data. PLoS ONE. 2013 Jun;8(6):e66341. doi: 10.1371/journal.pone.0066341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Zhou J, Wang F, Hu J, Ye J. From Micro to Macro: Data Driven Phenotyping by Densification of Longitudinal Electronic Medical Records; Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. KDD '14; pp. 135–144. [Google Scholar]
- [5].Ho JC, Ghosh J, Sun J. Marble: High-throughput Phenotyping from Electronic Health Records via Sparse Non-negative Tensor Factorization; Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. KDD '14; pp. 115–124. [Google Scholar]
- [6].Schulam P, Wigley F, Saria S. Clustering Longitudinal Clinical Marker Trajectories from Electronic Health Data: Applications to Phenotyping and Endotype Discovery. AAAI Conference on Artificial Intelligence. 2015 [Google Scholar]
- [7].Saria S, Rajani AK, Gould J, Koller D, Penn AA. Integration of early physiological responses predicts later illness severity in preterm infants. Science translational medicine. 2010;2(48):48ra65–48ra65. doi: 10.1126/scitranslmed.3001304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].The ARDS Definition Task Force* Acute respiratory distress syndrome: The berlin definition. JAMA. 2012;307(23):2526–2533. doi: 10.1001/jama.2012.5669. [DOI] [PubMed] [Google Scholar]
- [9].Bengio Y, Courville A, Vincent P. Representation Learning: A Review and New Perspectives. IEEE Trans Pattern Anal Mach Intell. 2013;35(8):1798–1828. doi: 10.1109/TPAMI.2013.50. [DOI] [PubMed] [Google Scholar]
- [10].Dahl GE, Yu D, Deng L, Acero A. Context-dependent pre-trained deep neural networks for large-vocabulary speech recognition. Audio, Speech, and Language Processing, IEEE Transactions on. 2012;20(1):30–42. [Google Scholar]
- [11].Oquab M, Bottou L, Laptev I, Sivic J. CVPR. 2014. Learning and transferring mid-level image representations using convolutional neural networks. [Google Scholar]
- [12].Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R. Dropout: A simple way to prevent neural networks from overfitting. The Journal of Machine Learning Research. 2014;15(1):1929–1958. [Google Scholar]
- [13].Bergstra J, Breuleux O, Bastien F, Lamblin P, Pascanu R, Desjardins G, et al. Theano: a CPU and GPU Math Expression Compiler; Proceedings of the Python for Scientific Computing Conference (SciPy); 2010. p. 3. Oral Presentation. Available from: http://deeplearning.net/software/theano/ [Google Scholar]
- [14].Goodfellow IJ, Warde-Farley D, Lamblin P, Dumoulin V, Mirza M, Pascanu R, et al. Pylearn2: a machine learning research library. 2013. arXiv preprint arXiv: 13084214. Available from: http://arxiv.org/abs/1308.4214.
- [15].Jia Y, Shelhamer E, Donahue J, Karayev S, Long J, Girshick R, et al. Caffe: Convolutional Architecture for Fast Feature Embedding. 2014. arXiv preprint arXiv: 14085093. [Google Scholar]
- [16].Collobert R, Kavukcuoglu K, Farabet C. Torch7: A matlab-like environment for machine learning; BigLearn, NIPS Workshop. EPFL-CONF-192376; p. 2011. [Google Scholar]
- [17].Erhan D, Bengio Y, Courville A, Vincent P. Visualizing higher-layer features of a deep network. Dept IRO, Université de Montréal, Tech Rep; 2009. [Google Scholar]
- [18].Erhan D, Courville A, Bengio Y. Understanding representations learned in deep architectures. Vol. 2010. Dept Inf Res Oper, Univ Montréal, Montréal, QC, Canada, Tech Rep; p. 1355. [Google Scholar]
- [19].Pearl J. Causality: models, reasoning and inference. Cambridge Univ Press; 2009. [Google Scholar]
- [20].Shimizu S, Hoyer PO, Hyvärinen A, Kerminen A. A linear non-Gaussian acyclic model for causal discovery. The Journal of Machine Learning Research. 2006;7:2003–2030. [Google Scholar]
- [21].Shimizu S, Inazumi T, Sogawa Y, Hyvärinen A, Kawahara Y, Washio T, et al. DirectLiNGAM: A direct method for learning a linear non-Gaussian structural equation model. The Journal of Machine Learning Research. 2011;12:1225–1248. [Google Scholar]
- [22].Hyvärinen A, Smith SM. Pairwise likelihood ratios for estimation of non-Gaussian structural equation models. The Journal of Machine Learning Research. 2013;14(1):111–152. [PMC free article] [PubMed] [Google Scholar]
- [23].Kale DC, Che Z, Liu Y, Wetzel R. Computational discovery of physiomes in critically ill children using deep learning; DMMI Workshop, AMIA Annual Symposium; 2014. [Google Scholar]
- [24].Che* Z, Kale* DC, Li W, Bahadori MT, Liu Y. Deep Computational Phenotyping; Proceedings of the 21st ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; 2015. [Google Scholar]
- [25].Mikolov T, Deoras A, Kombrink S, Burget L, Cernockỳ J. Empirical Evaluation and Combination of Advanced Language Modeling Techniques. INTERSPEECH. 2011;s 1:605–608. [Google Scholar]
- [26].Boulanger-Lewandowski N, Bengio Y, Vincent P. In: Langford J, Pineau J, editors. Modeling Temporal Dependencies in High-Dimensional Sequences: Application to Polyphonic Music Generation and Transcription; Proceedings of the 29th International Conference on Machine Learning (ICML-12). ICML '12; New York, NY, USA: Omnipress; 2012. pp. 1159–1166. [Google Scholar]
- [27].Le QV. Building high-level features using large scale unsupervised learning; Acoustics, Speech and Signal Processing (ICASSP), 2013 IEEE International Conference on. IEEE; 2013. pp. 8595–8598. [Google Scholar]
- [28].Szegedy C, Zaremba W, Sutskever I, Bruna J, Erhan D, Goodfellow I, et al. Intriguing properties of neural networks; International Conference on Learning Representations; 2014. [Google Scholar]
- [29].Ian J, Goodfellow CS, Jonathon Shlens. Explaining and Harnessing Adversarial Examples; International Conference on Learning Representations; 2015. [Google Scholar]
- [30].Chalupka K, Perona P, Eberhardt F. Visual Causal Feature Learning Uncertainty in Artificial Intelligence. 2015 [Google Scholar]
- [31].Domingos P. A Few Useful Things to Know About Machine Learning. Commun ACM. 2012 Oct;55(10):78–87. Available from: http://doi.acm.org/10.1145/2347736.2347755. [Google Scholar]
- [32].Vincent P, Larochelle H, Bengio Y, Manzagol PA. Extracting and composing robust features with denoising autoencoders; Proceedings of the 25th international conference on Machine learning; ACM; 2008. pp. 1096–1103. [Google Scholar]
- [33].Vincent P, Larochelle H, Lajoie I, Bengio Y, Manzagol PA. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. The Journal of Machine Learning Research. 2010;11:3371–3408. [Google Scholar]
- [34].Bengio Y, Lamblin P, Popovici D, Larochelle H. In: Schölkopf B, Platt JC, Hoffman T, editors. Greedy Layer-Wise Training of Deep Networks; Advances in Neural Information Processing Systems 19; MIT Press; 2007. pp. 153–160. [Google Scholar]
- [35].Bengio Y, Mesnil G, Dauphin Y, Rifai S. Better mixing via deep representations; Proceedings of the 30th International Conference on Machine Learning (ICML-13); 2013. [Google Scholar]
- [36].Reed S, Sohn K, Zhang Y, Lee H. Learning to disentangle factors of variation with manifold interaction; Proceedings of the 31st International Conference on Machine Learning (ICML-13); 2014. [Google Scholar]
- [37].Silva I, Moody G, Scott DJ, Celi LA, Mark RG. Predicting in-hospital mortality of ICU patients: The physioNet/computing in cardiology challenge 2012. Computing in cardiology. 2012;39:245. Available from: http://physionet.org/challenge/2012/ [PMC free article] [PubMed] [Google Scholar]
- [38].Kale* DC, Gong* D, Che* Z, Liu Y, Medioni G, Wetzel R, et al. An Examination of Multivariate Time Series Hashing with Applications to Health Care. Proceedings of the 2014 IEEE International Conference on Data Mining. ICDM '14; pp. 260–269. [Google Scholar]
- [39].Organization WH. International statistical classification of diseases and related health problems. Vol. 1. World Health Organization; 2004. [Google Scholar]
- [40].Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, et al. Scikit-learn: Machine Learning in Python. Journal of Machine Learning Research. 2011;12:2825–2830. Available from: http://scikit-learn.org/ [Google Scholar]
- [41].Knaus W, Draper E, Wagner D, Zimmerman J. APACHE II: a severity of disease classification system. Critical Care Medicine. 1985 Oct;13(10):818–29. [PubMed] [Google Scholar]
- [42].Pollack MM, Patel KM, Ruttimann UE. PRISM III: an updated Pediatric Risk of Mortality score. Critical Care Medicine. 1996;24(5):743–752. doi: 10.1097/00003246-199605000-00004. [DOI] [PubMed] [Google Scholar]