Abstract
Operating rooms (ORs) are one of the most expensive and profitable resources within a hospital system. OR managers strive to utilize these resources in the best possible manner. Traditionally, surgery durations are estimated using a moving average adjusted by the scheduler (adjusted system prediction or ASP). Other methods based on distributions, regression and data mining have also been proposed. To overcome difficulties with numerous procedure types and lack of sufficient sample size, and avoid distributional assumptions, the main objective is to develop a hybrid method of duration prediction and demonstrate using a case study.
Keywords: Classification, prediction, hybrid method, regression, surgery times
1. Introduction
Accurate prediction of the duration of surgical procedures is necessary to meet the needs of stakeholders. The duration of the procedure is critical in determining optimal schedules, and to reduce delays for patients and providers as well as reducing overtime and under-utilization of operating rooms (ORs) for administration. As surgeries get scheduled, the surgery duration is estimated and an appropriate day is selected to schedule the surgery. Currently most hospitals use software designed by commercial surgical scheduling systems from EMR vendors such as Cerner, Epic, etc. Both traditional method of surgery prediction and those used by commercial software used in most hospitals is based upon a moving average of previous cases, based on surgeon and procedure codes. This warrants the need for a scientific method to predict duration. With the increasing amount of data in healthcare and the need for making improvements in healthcare industry, it is critical to use more efficient methods of surgery prediction that can improve system performance and encourage physicians and hospital staff to not only think about the success of their own practice as an individual surgeon but also think of improving the performance of the hospital as a system. In this study, we consider data from a large hospital and propose a hybrid method for predicting surgery duration times. Our method is consisting of two steps 1) classification and 2) prediction. In prediction portion, we explore two different methods and discuss the performance of each method.
2. Literature Review
To provide a more scientific mechanism for prediction, various approaches have been proposed. While predicting surgical durations, there are two main streams of research. The first stream attempts to find the best fit among known distributions (most commonly normal [1] and lognormal [2]–[6]) and use these fitted distributions in order to characterize variability in surgical procedures and predict durations. In the second approach, researchers build statistical models to predict surgical procedure durations and identify critical factors that influence variability in these durations.
Among those studies relating to distributions, Strum et. al. analyzed a large dataset of clinical cases and concluded that fitting a log-normal model for each Current Procedural Terminology (CPT) code-anesthesia combination provides accurate predictions for procedure duration [7]. In a follow-up study, Strum et. al. showed that the lognormal distribution provides a better fit than normal distributions for modeling procedure durations having exactly two CPT codes [8]. With such an approach, the distribution is used in scheduling instead of a single value. This approach is good because it considers stochasticity by using distribution, however it is clear that there is a lot of variability within procedures of a certain CPT code in terms of complexity and that the single criteria CPT code is not an accurate indicator of surgery prediction. Relying on the lognormality assumption for procedure durations, Dexter, and Ledolter develop a Bayesian method to calculate prediction bounds for procedure durations [9]. Stepaniak et. al. use a three-parameter lognormal model for predicting the procedure durations of CPT-anesthesia combinations including surgeon effects and show that their model can significantly reduce prediction errors and therefore operating room (OR) inefficiency [10].
On the other hand, with model building, due to the large number of CPT codes, Strum et. al. built a separate five-factor main-effects linear model for each CPT code [11] using logarithm of surgical time (i.e., the time from incision to closure) or the logarithm of total procedure time (i.e., the time from when the patient enters the OR until he/she emerges from anesthesia) as the response variable and surgeon, anesthesia type, American Society of Anesthesiologist (ASA) risk class, patient gender, and patient age as the explanatory variables. Eijkemans et. al. developed a regression-based prediction model with the logarithm of the total OR time, defined as the time from patient entry into the OR room until the patient is moved out of the OR, as the response variable [12]. Besides the surgeon’s estimate, they considered a large set of additional factors, divided into three classes, including operation characteristics (e.g., the number of separate procedures and whether it is a laparoscopic procedure), team characteristics (e.g., number and experience of the surgical team), and patient characteristics (e.g., age, sex, body mass index, previous hospital admissions) and determined their significance when added as a single factor to the base model, which only included the procedure type as a random effect. Motivated by the fact that CPT codes are among the factor with the highest predictive power for procedure durations, Li et. al. developed a general regression-based predictive model with multiple CPT codes as dependent variables [13]. They developed a grouping procedure to identify CPT codes that always appear together in order to construct a full-ranked design matrix for the regression model. Kayis et. al. developed a regression model, which adjusts a commonly used base estimation method using procedure-surgeon specific last five cases, using operational (e.g., order of surgery, OR assignment, surgical staff) and temporal factors (e.g., day, month, time of day) [14]. Due to the larger number of explanatory variables, they used an elastic-net regularized generalized linear model. Their model results in improved mean absolute deviation, especially for cases with long durations.
Some authors investigated use of data mining techniques to predict procedure durations. Combes et. al. proposed a knowledge discovery in databases (KDD) framework. Within the data mining step of this framework, they developed and compared two data mining methodologies, namely rough sets and neural networks, using patient related factors (e.g., administrative data, previous medical history) and surgical environment (e.g., surgeon, type of anesthesia) as explanatory variables [15]. Based on factors related, the patient and surgical environment (including patient age, experience of surgical staff, type of anesthesia) within an ophthalmology department, Devi et. al. developed and compared the performance of three methods: 1) adaptive neuro fuzzy inference systems (ANFIS), 2) artificial neural networks (ANN), and 3) multiple linear regression [16]. Using duration estimates, they solved a mixed-integer programming problem to optimize surgery schedules with an objective of minimizing overall completion time (i.e., make span). Their numerical experiments indicated that ANFIS outperforms other methods. Instead of predicting duration of individual surgical procedures, some authors study the completion time of a series of surgical procedures (also referred to as operating list) in the same operating room on a given day. Dexter et. al. proposed a regression model to predict the completion time of a list with the number of surgeon-procedure combinations with the list as independent variables [17]. Pandit and Carey used a questionnaire of surgical staff (including surgeons, anesthetists, and senior nurses) to estimate the duration of procedures and subsequently applied the average of these estimates to predict the completion time of historical lists. They concluded that even though estimates from surgical staff are accurate in predicting the completion time of operating lists, a substantial number of lists were overbooked [18]. In a related work, Pandit and Tavare developed a method for calculating the probability that a list will finish within its scheduled time [19].
3. Method and Case Study
As previous research suggests there are several factors that impact surgical times. In this study we received data from a large hospital system. The data includes several fields including some general fields and some patient specific information (we discuss the details related to the data in next section). One of the fields that show to be impacting surgery duration is procedure code. Our data shows the record of 2000 procedure codes during the study period. Therefore, the first step in our proposed method is to statistically reduce the number of sub factors for this field. Our proposed method consists of two steps as part of the model and an evaluation to assess the performance of the model (as shown in Figure 1). In first step, we use classification to group procedure codes and to reduce the number of sub-factors for the field of procedure code. The next step is prediction; in this step we develop two separate regression models for procedure duration prediction using classical least square linear regression with main factors included (LIN) and stepwise regression (STEP) where main factors and second level interactions are included (we note that the stepwise with more levels of interaction did not add value, therefore were not considered). We then evaluate the model by comparing prediction results from LIN and STEP against the baseline. The hospital system prediction (baseline) currently uses the moving average of 5 to 10 previous cases of same surgeon for that procedure code. The system then allows the scheduler to adjust this value. Therefore, the recorded value for procedure time in the system is the adjusted system prediction (ASP) and that is the value we use as baseline. The adjustment scheduler makes to the moving average value is reflected by clinical situation of patient (such as preexisting conditions, etc.,) and the complexity of the surgery which we do not have any fields available for that in electronic data. This may seem that we set an unfair baseline to compare with. However, we feel confident that if our model can outperform this baseline, then with additional data fields that will be added in future, our model can perform even better.
Figure 1.
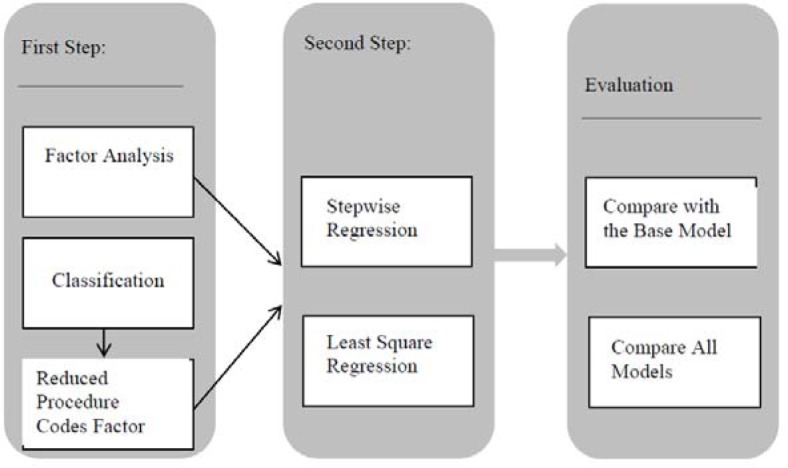
Research Method
3.1. Data Structure
A total of 63,254 surgical procedures performed by 234 surgeons over 39 months at a large academic health system with a total of 60 ORs were included. The data fields that show to impact surgery times and are included as part of the electronic data records are specialty, priority, ASA class (American Society of Anesthesiologists score – preoperative evaluation of patient physical status), age, encounter class, and procedure code. We also use fields such as actual surgery start and stop times, actual OR start and stop times, and scheduled OR start and stop times for evaluation purposes. Tables 1 and 2 show how the patients are distributed in relation to factors priority class and ASA code. We also note that there are total of 2000 procedure codes, and 30 specialties associated with the data. The patient class consist of 41% inpatient and 59% outpatient cases. Figure 2 shows how patients were distributed among different age groups.
Table 1.
Cases by Priority Class
| Priority Class | Number of Cases | % of Cases |
|---|---|---|
| Emergent | 1886 | 2.97 |
| Immediate | 960 | 1.51 |
| Organ Donor | 50 | 0.08 |
| Urgent | 1634 | 2.58 |
| Elective | 58873 | 92.86 |
Table 2.
Cases by ASA Class
| ASA Class | Number of Patients |
|---|---|
| 1 | 11856 |
| 2 | 25066 |
| 3 | 21473 |
| 4 | 4704 |
| 5 | 254 |
| 6 | 50 |
Figure 2.
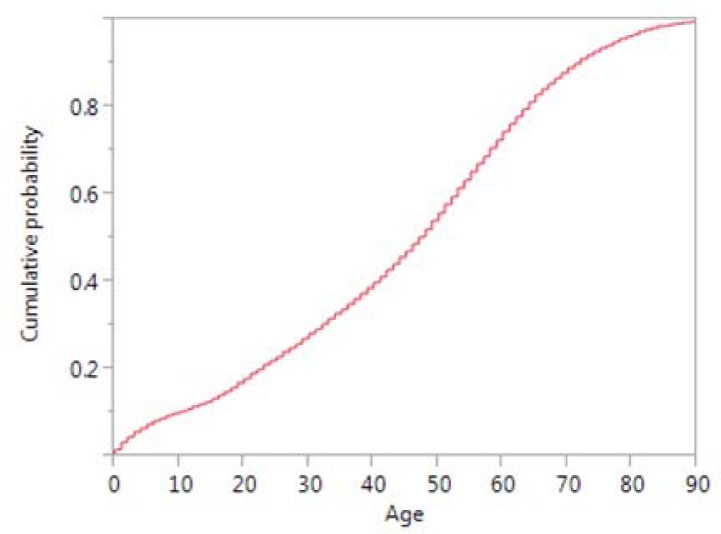
Patient Age Distribution
Although surgeon name was available as part of the data, however, this field was not considered as a factor, because a surgeon based model makes the model not to be used for surgeons who just join the practice or those who start performing a new surgery. Data was split with 85 percent for training and the remaining for the test set. The analysis was performed using JMP PRO 10 software. We also note that all time units throughout the paper are in minutes.
3.2. Classification
The dataset shows record of 2000 different procedure codes performed over the period of 39 months. The analysis indicates that procedure code is highly significant factor in both surgery time (ST) and ASP. However, some of the procedure codes are very rare and there are not enough records of these surgery types available. Also there are procedure codes that are very similar in terms of duration. In order to consider the effect of procedure code while fixing some of the issues with rare cases, we decide to define a new variable based on the grouped procedure codes. In order to do that, we use data mining technique, particularly classification to categorize the 2000 different procedure types in new groups. Classification or decision tree is a platform that recursively partitions data according to a relationship between certain independent and dependent variables, creating a tree of partitions. It finds a set of cuts or groupings of independent variables that best predict a dependent variable. These splits of data are done recursively forming a tree of decisions until the desired fit is reached. There are several heuristic algorithms used to build classification and decision trees [21,22]. Some of these algorithms are ID3, and CART [21]; in this study we used CART. The proposed work uses classification to group different procedure codes based on their length of OR time. This allows reduction of the number of categories of procedure codes. This reduction needs to be validated by using cross-validation. We use a 10 fold cross validation to validate the categorization at 95% confidence. The new categorization then can replace the variable procedure code in our regression model. This new variable called adjusted procedure code. The classification method categorizes 2000 procedure types to 49 distinct groups. Therefore, nominal variable adjusted procedure code has 49 levels instead of the initial 2000 levels. The R2 value for the classification is 0.65. We apply Tukey Kramer HSD test with α=.05 to test that these categories represent statistically different groups in terms of mean procedure times. The results of this test are very lengthy and therefore are omitted.
3.3. Prediction
Once the procedure category variable is created, regression models are developed to predict the duration. A multi regression is a regression with more than one independent variable or factor and is one of the common methods of prediction. The two of the most common techniques used in multiple regressions are least square regression and stepwise regression. These methods are applied to predict surgery duration. We note that the stepwise regression and linear least square regression are very similar in nature. The difference is mainly in the way significant variables selected. For stepwise regression we use the combination of backward elimination and forward selection.
According to the Gauss–Markov theorem, there are a few conditions to be satisfied such that the least square estimator will be the best linear unbiased estimator. We notice that validation of these conditions is often ignored in many previous studies, resulting in poor or invalid outcomes. In practice, there are rarely situations that all these conditions hold; therefore, there is often need for adjustments and changes in the data that can help to satisfy these. These conditions are:
Relationship between dependent and independent variables should be linear
The residuals are normally distributed with mean close to zero
There is no heteroscedasticity which means that residuals have a constant variance
There is no autocorrelation, that is successive residuals are not correlated
There is no multi-colinearity
In preparation for use of regression model, all above assumptions have been verified. Due to the length of results related to these assumptions, here only the method that applied to test each of the assumptions has been listed in Table 3.
Table 3.
List of Assumptions
| Assumption | Method to Verify |
|---|---|
| 1 | Looking for un even distribution of standardized residuals as function of standardized predicted value around zero horizontal line |
| 2 | Distribution of residuals |
| 3 | Applying white’s test |
| 4 | Applying Durbin Watson test |
| 5 | Calculating correlation between response and the factors (for age) and visual examination of graph of response by factor (for factors other than age) |
Also regression factor statistical analysis indicates that all main factors shown in Table 4 are significant factors for least square prediction model with p-value<0.0001. Although we admit that these are not the only factors influencing OR times however the statistical results show that all of these factors significantly affect OR times. For the stepwise regression we not only consider these main factors but also the two level interactions of these factors to start the stepwise regression. The stepwise method however enters only those factors that have a significant impact on the result. We also tested the stepwise with three levels of interaction; however, no improvement has been reported from this model compared to the model with only two levels of interaction. Therefore, in result section only the stepwise method with two levels of interaction has been discussed.
Table 4.
Description of Variables
| Independent Variables (Factors) | Type | Number of Levels |
|---|---|---|
| Priority Class | Nominal | 5 |
| Procedure Category | Nominal | 49 |
| ASA Class | Nominal | 6 |
| Age | Continuous | – |
| Patient Class | Nominal | 2 |
| Specialty | Nominal | 30 |
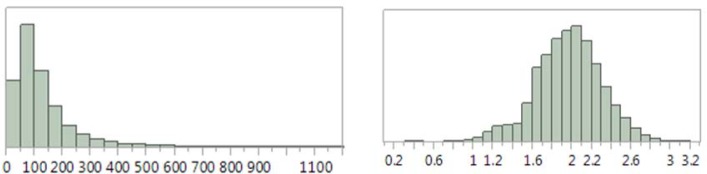
As we are predicting duration of times, we also need to make sure that the values reported as output of the regression model are greater than zero. Plotting the distribution of duration of surgeries, it could be seen that the distribution is very much skewed to the left. We expect this to cause the prediction values to occasionally get values of zero or even negative. To prevent that, we use log transformation as predictor in regression model. This transformation has been widely used in literature to prevent the output of time predictions from falling to negative numbers. After applying the regression model, inverse transformation needs to be applied before statistical results are gathered. Figure 3 shows the distribution of case durations in train set before and after transformation.
Figure 3.
Case Distribution Before and After Transformation
4. Results
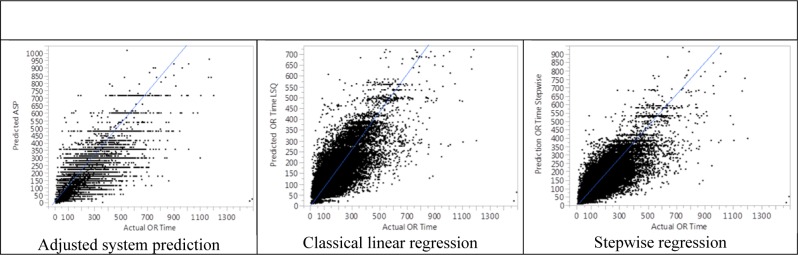
The results of the three predictions (ASP, LIN, and STEP) are compared against each other. Multiple performance measures such R2, RASE, and AAE which are coefficient of determination, root square average error, and average absolute error respectively, are reported for both train and test sets (due to respective strengths [23, 24) ]. Table 5 shows the comparison statistics of the three methods. As can be seen, STEP prediction is better than LIN, and each outperforms ASP
Table 5.
Comparison of Results
| Train Set | Test Set | |||||
|---|---|---|---|---|---|---|
| Predictor | R2 | RASE | AAE | R2 | RASE | AAE |
| ASP | 0.6375 | 59.26 | 37.7017 | 0.652 | 57.3641 | 37.4473 |
| LIN | 0.6598 | 57.4116 0.678 | 34.0933 | 0.678 | 55.1816 | 34.3059 |
| STEP | 0.6838 | 55.3505 | 33.0578 | 0.6822 | 54.8274 | 34.0446 |
Table 6 shows the comparison of the three prediction values by specialty, for most frequent specialties with at least 100 cases. STEP is the best model for the most frequent specialties (orthopedics and general surgeries, surgical oncology). LIN is better for urology, ophthalmology, thoracic, vascular, GYN oncology, and gynecology. ASP outperforms both STEP and LIN for otolaryngology, plastic, and GYN oncology procedures. Neuro surgery, obstetrics, and acute care procedures have mixed results. For Psychosurgery cases, the R2 values for ASP and LIN are negative (these values for psychology is not shown in table as this specialty did not have many cases), suggesting that the mean of the group is a better representative of the predicted values. Even though the R2 values for STEP is positive (yet very small), none of the prediction models can accurately estimate the procedure durations of this specialty. The t-test performed with alpha=0.05, suggests that LIN and STEP are significantly different from ASP in terms of the mean residuals.
Table 6.
Comparison by Specialty
| Specialty | Predictor | R-Square | RMSE | MAE | Frequency |
|---|---|---|---|---|---|
| Orthopedics | ASP | 0.5257 | 57.9685 | 39.9777 | |
| LIN | 0.5755 | 54.8451 | 36.1095 | 34.2% | |
| STEP | 0.5828 | 54.3689 | 35.9546 | ||
| General | ASP | 0.3729 | 55.0437 | 37.3926 | |
| LIN | 0.4697 | 50.616 | 33.7518 | 14.6% | |
| STEP | 0.4965 | 49.3186 | 32.7425 | ||
| Otolaryngology | ASP | 0.7319 | 51.7225 | 32.9076 | |
| LIN | 0.7126 | 53.5506 | 32.2944 | 11.3% | |
| STEP | 0.7189 | 52.9621 | 32.0055 | ||
| Urology | ASP | 0.7272 | 46.7483 | 30.5251 | |
| LIN | 0.7733 | 42.614 | 26.7203 | 7.8% | |
| STEP | 0.7709 | 42.8332 | 26.9698 | ||
| Ophthalmology | ASP | 0.2313 | 35.9271 | 22.6226 | |
| LIN | 0.5206 | 28.3732 | 17.5264 | 6.3% | |
| STEP | 0.4968 | 29.0675 | 17.6161 | ||
| Neuro Surgery | ASP | 0.5946 | 81.0404 | 54.9013 | |
| LIN | 0.5947 | 81.0349 | 52.2301 | 5.1% | |
| STEP | 0.5893 | 81.5648 | 52.1195 | ||
| Surgical Oncology | ASP | 0.6781 | 54.9955 | 32.3168 | |
| LIN | 0.691 | 53.8794 | 31.6966 | 4.6% | |
| STEP | 0.7119 | 52.0292 | 30.4564 | ||
| Plastic | ASP | 0.7299 | 78.7518 | 54.2446 | |
| LIN | 0.6102 | 94.609 | 58.9855 | 4.0% | |
| STEP | 0.6412 | 90.7662 | 58.5443 | ||
| Thoracic | ASP | 0.5998 | 99.1005 | 66.6381 | |
| LIN | 0.7161 | 83.4766 | 59.6474 | 2.8% | |
| STEP | 0.6775 | 88.958 | 60.5216 | ||
| Vascular | ASP | 0.6072 | 60.2528 | 40.1038 | |
| LIN | 0.7247 | 50.4412 | 35.8458 | 2.0% | |
| STEP | 0.7008 | 52.5839 | 37.4437 | ||
| Obstetrics | ASP | 0.6049 | 34.3594 | 26.9036 | |
| LIN | 0.6995 | 29.9654 | 20.1546 | 1.8% | |
| STEP | 0.673 | 31.2549 | 19.1835 | ||
| Psychosurgery | ASP | −2.2645 | 7.9547 | 4.5975 | |
| LIN | −0.0481 | 4.5072 | 3.3032 | 1.7% | |
| STEP | 0.0009 | 4.4006 | 3.2347 | ||
| Acute Care Surgery | ASP | 0.2728 | 51.8505 | 38.2971 | |
| LIN | 0.3784 | 47.9386 | 31.887 | 1.5% | |
| STEP | 0.3583 | 48.7057 | 31.8369 | ||
| GYN Oncology | ASP | 0.6277 | 56.7332 | 35.9823 | |
| LIN | 0.6227 | 57.1121 | 36.812 | 1.2% | |
| STEP | 0.6144 | 57.7381 | 36.4322 | ||
| Gynecology | ASP | 0.5071 | 52.1249 | 37.6535 | |
| LIN | 0.6241 | 45.5197 | 30.9478 | 1.1% | |
| STEP | 0.6195 | 45.7996 | 31.8781 |
5. Discussion
Both LIN and STEP show moderate improvement over ASP. This is not surprising since ASP prediction is often adjusted by the scheduler and/or the surgeon. These adjustments are typically based on intuitive consideration of patient characteristics and clinical factors and surgery complexity (12). There is no indication in the data set of any of these variables however about how often the moving average has been adjusted and by how much to determine reported scheduled duration. We believe that additional factors such as those considered by scheduler to adjust the value of the moving average if available can potentially make LIN and STEP even more accurate. The STEP regression model includes two-level interactions (inclusion of three-level interactions gives only slight improvement). The performance of LIN and STEP is dependent on the choice of independent variables and the size of the data set. While having additional factors and interaction of factors can potentially increase R2 value in the training set indicating a better model, corresponding performance in the test set needs to be evaluated.
The independent variables considered in this study are general factors available across all specialties, and hence ensures ease of scalability. If more clinical factors are added to the model, then the interaction of factors will add more value to the accuracy of the prediction. These clinical factors however may not be available in structured data format. In some situations these factors could be observed by applying text mining on pre and post diagnostic notes if these notes are recorded electronically in unstructured form. However, in some situations such data is not available electronically. In such case there is need for manual observation of factor from notes by reading hand written charts by experts. We also note that each specialty has several meaningful variables which are specific to their practice, to add all these factors into a single model, care needs to be taken since this will create an uneven spread of factors among data due to the fact that some practices perform more surgeries than others. For instance, our data shows an indication that there is more of general and orthopedic surgery compared with other specialties; this however should not be used against accuracy of the prediction of duration of specialties with lesser number of cases. Further, individual specialties tend to show variation in performance based on the type of regression. STEP performs best with fewer specialties but those that account for more than half of the procedures. LIN performs best with specialties that account for a third of the procedures. Psychosurgery as a specialty is not predicted well by any of the models, and hence needs further investigation.
6. Conclusion
Prediction of OR times is very important as these times are used to assign time and day of the surgery. Accurate predictions are necessary to prevent over- and under-utilization. We proposed and evaluated a hybrid method with two steps 1) creation of a new variable to categorize procedures across all specialties and 2) development of regression models to predict procedure duration using the procedure category variable from the first step along with other factors. Evaluation shows that both regression models (LIN and STEP) result in better predictions compared to the current state-of-the-practice. The hybrid method with STEP regression gives a better prediction for orthopedics and general surgeries and surgical oncology specialties, which constitute more than half of the procedures. The proposed hybrid method can effectively deal with the heterogeneity problem, and further improvements can be obtained through inclusion of additional clinical factors.
Figure 4.
Scatter Plot for Prediction
References
- 1.Barnoon S, Wolfe H. Scheduling a multiple operating room system: A simulation approach. Health services research. 1968;3(4):272. [PMC free article] [PubMed] [Google Scholar]
- 2.Hancock WM, Walter PF, More RA, Glick ND. Operating room scheduling data base analysis for scheduling. Journal of medical systems. 1988;12(6):397–409. doi: 10.1007/BF00992688. [DOI] [PubMed] [Google Scholar]
- 3.Robb DJ, Silver EA. Scheduling in a Management Context: Uncertain Processing Times and Non-Regular Performance Measures. Decis Sci. 1993;24(6):1085–108. [Google Scholar]
- 4.Strum D, May J, Vargas L. Surgical procedure times are well modeled by the lognormal distribution. Anesthesia & Analgesia. 1998;86(2S):47S. [Google Scholar]
- 5.May JH, Strum DP, Vargas LG. Fitting the Lognormal Distribution to Surgical Procedure Times*. Decision Sciences. 2000;31(1):129–48. [Google Scholar]
- 6.Spangler WE, Strum DP, Vargas LG, May JH. Estimating procedure times for surgeries by determining location parameters for the lognormal model. Health care management science. 2004;7(2):97–104. doi: 10.1023/b:hcms.0000020649.78458.98. [DOI] [PubMed] [Google Scholar]
- 7.Strum DP, May JH, Vargas LG. Modeling the uncertainty of surgical procedure times: comparison of log-normal and normal models. Anesthesiology. 2000;92(4):1160–7. doi: 10.1097/00000542-200004000-00035. [DOI] [PubMed] [Google Scholar]
- 8.Strum DP, May JH, Sampson AR, Vargas LG, Spangler WE. Estimating times of surgeries with two component procedures: comparison of the lognormal and normal models. Anesthesiology. 2003;98(1):232–40. doi: 10.1097/00000542-200301000-00035. [DOI] [PubMed] [Google Scholar]
- 9.Dexter F, Ledolter J. Bayesian prediction bounds and comparisons of operating room times even for procedures with few or no historic data. Anesthesiology. 2005;103(6):1259–167. doi: 10.1097/00000542-200512000-00023. [DOI] [PubMed] [Google Scholar]
- 10.Stepaniak PS, Heij C, Mannaerts GH, de Quelerij M, de Vries G. Modeling procedure and surgical times for current procedural terminology-anesthesia-surgeon combinations and evaluation in terms of case-duration prediction and operating room efficiency: a multicenter study. Anesthesia & Analgesia. 2009;109(4):1232–45. doi: 10.1213/ANE.0b013e3181b5de07. [DOI] [PubMed] [Google Scholar]
- 11.Strum DP, Sampson AR, May JH, Vargas LG. Surgeon and type of anesthesia predict variability in surgical procedure times. Anesthesiology. 2000;92(5):1454–66. doi: 10.1097/00000542-200005000-00036. [DOI] [PubMed] [Google Scholar]
- 12.Eijkemans MJ, van Houdenhoven M, Nguyen T, Boersma E, Steyerberg EW, Kazemier G. Predicting the unpredictable: a new prediction model for operating room times using individual characteristics and the surgeon’s estimate. Anesthesiology. 2010;112(1):41–9. doi: 10.1097/ALN.0b013e3181c294c2. [DOI] [PubMed] [Google Scholar]
- 13.Li Y, Zhang S, Baugh RF, Huang JZ. Predicting surgical case durations using ill-conditioned CPT code matrix. IIE Transactions. 2009;42(2):121–35. [Google Scholar]
- 14.Kayis E, Wang H, Patel M, Gonzalez T, Jain S, Ramamurthi R, et al. Improving Prediction of Surgery Duration using Operational and Temporal Factors. AMIA Annual Symposium Proceedings. 2012;2012:456. [PMC free article] [PubMed] [Google Scholar]
- 15.Dexter F, Traub RD, Qian F. Comparison of statistical methods to predict the time to complete a series of surgical cases. Journal of clinical monitoring and computing. 1999;15(1):45–51. doi: 10.1023/a:1009999830753. [DOI] [PubMed] [Google Scholar]
- 16.Pandit J, Carey A. Estimating the duration of common elective operations: implications for operating list management. Anaesthesia. 2006;61(8):768–76. doi: 10.1111/j.1365-2044.2006.04719.x. [DOI] [PubMed] [Google Scholar]
- 17.Pandit JJ, Tavare A. Using mean duration and variation of procedure times to plan a list of surgical operations to fit into the scheduled list time. European Journal of Anaesthesiology (EJA) 2011;28(7):493–501. doi: 10.1097/EJA.0b013e3283446b9c. [DOI] [PubMed] [Google Scholar]
- 18.Hancock T, Jiang T, Li M, Tromp J. Lower bounds on learning decision lists and trees. Information and Computation. 1996;126(2):114–22. [Google Scholar]
- 19.Zantema H, Bodlaender HL. Finding small equivalent decision trees is hard. International Journal of Foundations of Computer Science. 2000;11(02):343–54. [Google Scholar]
- 20.Quinlan JR. Induction of decision trees. Machine learning. 1986;1(1):81–106. [Google Scholar]
- 21.Breiman L, Friedman J, Stone CJ, Olshen RA. Classification and regression trees. CRC press; 1984. [Google Scholar]
- 22.Anguita D, Ghelardoni L, Ghio A, Oneto L, Ridella S. The ‘K’in K-fold Cross Validation. [Google Scholar]
- 23.Willmott CJ, Matsuura K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. CLIMATE RESEARCH. 2005 Dec 19;30:79–82. [Google Scholar]
- 24.Chai T, Draxler RR. Model Dev. Discuss. with version 4.1 of the LATEX class copernicus discussions.cls. ed2014. Root mean square error (RMSE) or mean absolute error (MAE)? – Arguments against avoiding RMSE in the literature. Manuscript prepared for Geosci. [Google Scholar]