Abstract
Modeling and clustering medical inpatient journeys is useful to healthcare organizations for a number of reasons including inpatient journey reorganization in a more convenient way for understanding and browsing, etc. In this study, we present a probabilistic model-based approach to model and cluster medical inpatient journeys. Specifically, we exploit a Bayesian Hidden Markov Model based approach to transform medical inpatient journeys into a probabilistic space, which can be seen as a richer representation of inpatient journeys to be clustered. Then, using hierarchical clustering on the matrix of similarities, inpatient journeys can be clustered into different categories w.r.t their clinical and temporal characteristics. We evaluated the proposed approach on a real clinical data set pertaining to the unstable angina treatment process. The experimental results reveal that our method can identify and model latent treatment topics underlying in personalized inpatient journeys, and yield impressive clustering quality.
1. Introduction
In recent years, healthcare process management is increasingly being used in healthcare organizations to provide standardized and normalized health services in medical inpatient journeys [1, 2]. Different from common business processes in commercial and industrial environments, healthcare processes are highly dynamic, context sensitive, event driven, and knowledge intensive such that they often bear no relation to the ideal as envisaged by the designers of healthcare processes [3]. To this end, healthcare organizations need to analyze and improve healthcare processes continuously [4].
Regarding healthcare process analysis and improvement, process mining, as a valuable set of techniques in business process management, has achieved emerging attention in clinical settings [3, 5, 6]. Process mining techniques use event logs to record business process execution information, to mine the actual behaviors in business processes, and to discover business process models from event logs [7]. Shifting to clinical settings, process mining can be an objective way of analyzing healthcare processes as it is not biased by perceptions or normative behaviors [5]. Applying process mining in clinical settings, non-trivial information about healthcare processes can be extracted from electronic medical records (EMRs) that contains the execution results of inpatient journeys, such as latent treatment patterns [3], treatment performance metrics [8], and performance characteristics [9], etc.
However, the diversity of treatment behaviors in healthcare processes is far higher than that of common business processes [5]. Healthcare processes are typically dynamic, complex, and loosely-structured, such that traditional process mining techniques have many problems and challenges when applied for healthcare process analysis and improvement [3, 10]. In fact, the diversity of healthcare processes, i.e. each inpatient journey has different kind of treatment events as well as difficult sequences of treatment events, causes the mining results often complicated and difficult to understand.
As a fundamental research problem, clustering actual medical inpatient journeys plays an important role in assisting healthcare process analysis and improvement. Indeed, a key step for healthcare process analysis is to cluster similar inpatient journeys into homogeneous subsets (clusters) [5, 11]. This helps clinical analysts locate treatment information of interest and capture an overview of healthcare processes easily and quickly. It must mention that, in contrast to static health data clustering, the clustering of medical inpatient journeys needs to be performed for each type of healthcare processes and be limited to the number of patients following a particular healthcare process protocol (e.g., a specific clinical guideline or pathway to a specific disease, etc.). This adds extra requirements to clustering, i.e., the clustering algorithm should group similar inpatient journeys together, and separate relevant inpatient journeys from irrelevant ones in order to support medical staff to efficiently understand and browse these journeys for the further tasks on healthcare process analysis and improvement.
The requirements above in general introduce several challenges to modeling and clustering of medical inpatient journeys. In contrast to structured business process execution traces, an inpatient journey is described as a series clinical epochs/stages in the patient’s hospitalization, and each epoch consists of a set of treatment events which may occur arbitrarily without a particular order [12]. Thus, one has to incorporate such loosely-structured treatment event sequence in the clustering process for good similarity measure. To the best of our knowledge, most of the approaches developed so far try to modify the existing algorithms to handle sequential business process data [6, 13, 14]. In order to have benefits, the data sources should be in fine structures. Unfortunately, such types of data sources are not available or rich enough for healthcare processes [5, 6].
In consideration of informal structures and the modelling of non-stationary data on inpatient journeys, we present a new approach for modeling and clustering medical inpatient journeys in this article. The proposed approach combines the model-based method provided by a well-known Bayesian Hidden Markov Model (B-HMM) [15] and a hierarchical clustering procedure. More specifically, we develop a clustering process that incorporates the medical behavior dependency observed in inpatient journeys and transforms inpatient journeys into a probabilistic space, where a symmetric similarity between inpatient journeys can be measured. Then, we resort to hierarchical clustering on the matrix of similarity in order to cluster the data sequences into homogenous groups according to both their characteristics and dynamics. In this sense, our approach provides an intuitive organization of the inpatient journey repository. Experiments on a real clinical data set collected from a Chinese hospital show that our proposal outperforms traditional approaches on medical inpatient journey modeling and clustering.
2. Methods
This section introduces a probabilistic model-based approach for medical inpatient journey modeling and clustering. The proposed approach combines both model-based and hierarchical clustering procedures, as shown in Figure 1. We first introduce the basic concepts and notations.
Figure.1.
The proposed approach for medical inpatient journey clustering.
2.1 Representation of a Medical Inpatient Journey
In this study, we make an assumption that treatment events in medical inpatient journeys are regularly recorded in EMRs, which effectively reflects real executing conditions in inpatient journeys Each treatment event refers to a well-defined step in inpatient journeys. Additional information such as the occurring time-stamp of the event is used in this study. To explain the kind of input needed for the proposed approach, we first define the following concepts.
Let A be a finite set of treatment event identifiers (clinical terms describing activities), and T the time domain set (set of time point primitives). A treatment event e is a pair e = (a, t) where a ∈ A and t ∈ T. We denote by ε = A × T the set of all valid events of a particular domain. Note that treatment events could be characterized by various properties, e.g., an event has an occurring time stamp, it corresponds to an event type, it is executed for a particular patient, has associated cost, etc. We do not impose a specific set of properties, however, given the focus of this study, we assume that the event type and occurring time stamp of the event are present. For convenience, let e. a and e. t denote the event type and occurring time stamp of e, respectively. For example, e = (admission, 1) is a treatment event where e. a = admission is the admission type, and e. t = 1 is the occurring time of the event. A medical inpatient journey is a series of treatment events σ = 〈e1, e2,⋯, en〉, observed on a particular patient in his/her hospitalization.
For a particular medical inpatient journey σ = 〈e1, e2, …,en〉, we have e1. t ≤ e2.t ≤ … < en.t. In general, an inpatient journey consists of different categories of treatment events, and certain temporal dependencies exist between the events for a particular inpatient journey. Figure 2 depicts examples of medical inpatient journeys.
Figure.2.
Examples of medical inpatient journeys
2.2 Medical inpatient journey modeling
In this section, we present a probabilistic model to recognize medical inpatient journeys by considering the sequential and dependency characteristics of treatment information in the journeys. As we mentioned above, inpatient journeys are dynamic, flexible, and loosely-structured. Although there are temporal dependencies between some critical events in different clinical epochs of inpatient journeys treatment events in one time epoch might occur arbitrarily without a strict order. In this sense, we segment an inpatient journey σ as a series of M clinical epochs σ = 〈σ(1), σ(2), …, σ(M)〉, and each epoch has a specific time duration, e.g., a hospitalization day1, etc. For example, inpatient journey σ1, shown in Figure 2 consists of 5 epochs sequentially, in which each epoch records typical treatment events occurring on a particular hospitalization day. For example, the first clinical epoch of σ1 consists of 26 treatment events, i.e., σ1(1) = {(A0,1), (A1,1), (A2,1),…}, and the last epoch of σ1 has one treatment event, i.e., σ1(5) = {(A17,5)}, etc.
In addition, we assume that each clinical epoch of a particular inpatient trajectory has a specific treatment topic (e.g., “Admission”, “Prepare Surgery”, “Surgery”, “Post-surgery recovery”, etc.). Formally, we use zσ(t) to denote the underlying treatment topic in the tth epoch σ(t) of a particular inpatient journey σ. Thus the objective of inpatient journey modeling is to identify the latent treatment topics and their transitions in a particular inpatient journey.
To this end, we propose a Bayesian Hidden Markov Model (B-HMM) [15] based medical inpatient journey model (IJM) to identify inpatient journeys. The proposed IJM has the structure of a standard HMM that contains symmetric Dirichlet priors over the transition and emission distributions for modeling the sequential treatment information in an individual inpatient journey. Formally, given an inpatient journey σ = 〈σ(1), σ(2), …, σ(M)〉 with a series of M clinical epochs, the dependency relationships of IJM are represented as follows:
| (1) |
;
| (2) |
| (3) |
;
| (4) |
Where means zσ(t) follows multinomial distribution is the topic transition distribution over the tth clinical epoch σ(t) when the treatment topic of the previous journey epoch σ(t − 1) is zσ(t−1). zσ(t) indicates the treatment topic in σ(t). eti is the ith treatment event recorded in σ(t), and is the emission distribution of treatment events in σ(t). Particularly, Θ and Φ follow the Dirichlet distribution with parameters α and β. Figure 3 shows the graphical representation of IJM.
Figure 3.
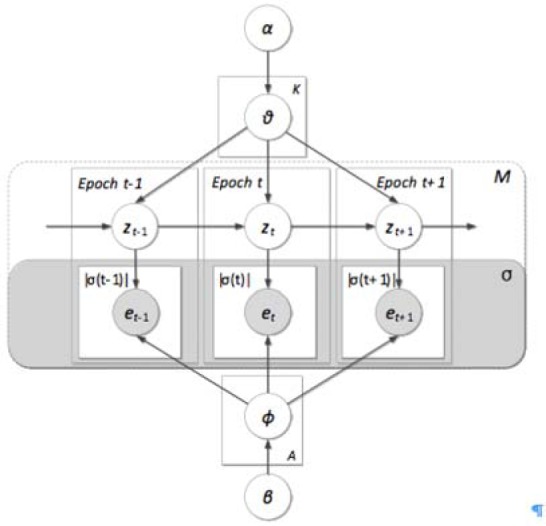
The proposed medical inpatient journey model
In summary, the processed IJM assumes the following generative process for an inpatient journey σ:
Draw treatment topic proportions θz ~ Dirichlet(α)
For each treatment topic z = 1, …, K, draw treatment event probability ϕz ~ Dirichlet(β);
- For each clinical epoch t = 1,…,M of σ:
- 3.1 Draw treatment topic Zσ(t) from w.r.t the previous treatment topic Zσ(t−1),
- 3.2 For each treatment event eti ∈ σ(t), i = 1, …, |σ(t) |, draw .
Given the generative process of IJM, we can calculate the joint distribution of all observations and hidden variables in IJM by the following equation:
| (5) |
Therefore, the likelihood of a medical inpatient journey σ can be calculated as follows:
| (6) |
We developed a Gibbs sampling based approach to get the to maximize the likelihood in Equation (6), with the time complexity for a particular inpatient journey σ being 0 (LKM), where L is the number of iterations, K is the number of treatment topics, and M is the number of clinical epochs in σ.
2.3 Medical inpatient journey clustering
The second step of our hybrid clustering method exploits the information provided by the probabilistic space obtained in the first step to define the clusters of medical inpatient journeys characterized by similar treatment behaviors. Based on the generated IJM models of inpatient journeys, we measure the similarity between the journeys. Specifically, we use Monte Carlo sampling to compare two IJM models. Formally, let and , be the learned IJM for inpatient journeys σi and σj, respectively. The similarity between any two IJM models is defined as
| (13) |
Where land are a measure of how well model matches observations generated by model , relative to how well matches the observations generated by itself. and are in the same spirit and make the similarity symmetric. Equation (13) can be rewritten in terms of inpatient journeys as
| (14) |
Where σj(t) is the t-th clinical epoch in σj, σi(t) is the t-th clinical epoch in σi, and the log-likelihood for each inpatient journey given the IJM can be obtained from Equation (8). This similarity measure is well suited to large collection of inpatient journeys, as it only requires the storage of the IJM parameters for each piece rather than the original patient’s EMR data itself.
In order to make no assumption on the number of medical inpatient journey clusters that are to be extracted, we use hierarchical clustering, which builds a hierarchy of clusters rather than treating all clusters as distinct, equal entities, such as in K-Means clustering.
A reasonable similarity measure Sim(σi,σj) for medical inpatient journeys σi and σj is critical for inpatient journey clustering, In Equation (15), we have presented how to measure Sim(σi,σj) between inpatient journeys σi and aj, which defines the similarity matrix used for grouping the collected journeys into a tree of clusters through the hierarchical clustering procedure [16]: the dendrogram is achieved starting from C clusters, one for each inpatient journey σ, and iteratively aggregating pairs of clusters until one single clusters is obtained. This agglomerate strategy is defined using complete linkage, i.e., similarity between clusters is measured on the basis of the similarity between the two furthest data points in two clusters. The hierarchical clustering allows us to easily obtain an informative data structure without having to specify a priori the number of clusters.
3. Experiments
In this case study, a collection of EMRs consisting of 9944 medical inpatient journeys following the unstable angina treatment process (from 2004 to 2013) was extracted from hospital information systems of Chinese PLA General Hospital to demonstrate the feasibility of the proposed approach. The collected data-set have 704004 treatment events within 606 event types. The average length of stay (LOS) recorded in the collection of EMRs is 8.30 days, which some inpatient journeys take a very short time, e.g., only 1 day in hospital, and other trajectories take much longer, e.g., more than 3 months in the hospital, which implicitly indicates the diversity of inpatient journeys in the unstable angina treatment process.
The case study was performed in the Cardiology Department at the Chinese PLA General Hospital. Prior approval was obtained from the data protection committee of the hospital to conduct the study. We state that the patient data was anonymized in this study and in this paper. All experiments were performed on a Lenevo Compatible PC with an Intel Pentium IV CPU 2.8 GHz, 4G byte main memory running on Microsoft Windows 8.1. The algorithm was implemented using Microsoft C#.
To evaluate the proposed IJM, we also developed a traditional sequence alignment based inpatient journey clustering method, and a variation HMM to model and cluster inpatient journeys. For the variation HMM, it can label the t-th clinical epoch of a particular inpatient journey
| (15) |
Based on the suggestion of our clinical collaborators, the number of latent treatment topics for both IJM and HMM was chosen as 5, which is the general number of clinical stages of the unstable angina treatment process. For the other parameters of the proposed IJM, we used the following values: α = 0.1, β = 0.01, and the number of Gibbs iterations L=1000.
Modeling performance
In this subsection, we evaluate the proposed IJM on modeling medical inpatient journeys. To this end, we randomly picked up 10 sample inpatient journeys from the collected dataset, as shown in Figure 2. Since the whole time period of the collected EMRs is across 10 years (i.e., from 2004 to 2013), we randomly selected one piece of EMRs in the dataset segment of a particular year. Each selected sample records typical treatment behaviors occurred in a particular inpatient journey.
To investigate the problem of how to know the learned treatment topics are meaningful or not for a given medical inpatient journey, we adopted a hypothesis testing in which we used the derived treatment topics to describe each clinical epoch of an inpatient journey, and then conducted statistical tests to know whether the derived treatment topics from IJM can better represent the treatment topical information of a particular clinical epoch than that of the variation HMM on a given inpatient journey. The null hypothesis assumes that “both IJM and HMM have no difference in treatment topical representation in inpatient journeys”. The process to test the significance of violating the null hypothesis is given as follows:
Firstly, we labeled each clinical epoch σ(t), (1 ≤ t ≤ M) of a sample inpatient journey σ with the recognized treatment topic z which is derived from either IJM or HMM. In particular, we chose the treatment event types e. a with P(e.a|z)> 0.01 to represent the derived treatment topic z.
-
Secondly, we asked 3 clinicians from the Cardiology department of the hospital to evaluate that to what extend the derived treatment topic correctly represents the actual treatment information in each clinical epoch of a sample inpatient journey. To ensure the evaluation quality, we did not inform evaluators that a given learnt treatment topic is learned by which model. The answer was given on a particular label, i.e., “Bad”, “Fair” or “Good” (i.e., “Bad” represents “does not represent at all”, “Fair” represents “fairly represent the treatment information in a specific clinical epoch”, and “Good” represents “perfectly represent the treatment information in a specific clinical epoch”, respectively). Note that we obtained the evaluation result of 3 evaluators based on a major voting strategy.
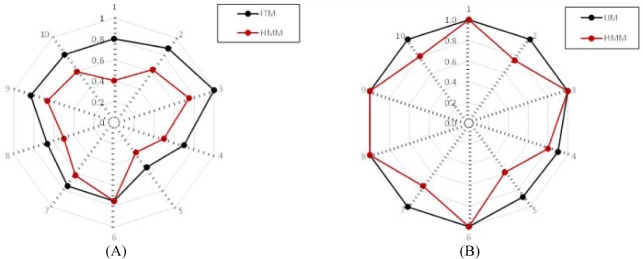
Figure 4 shows the results of human judgment for both IJM and HMM. From Figure 4, we can observe that the proposed IJM outperforms HMM in terms of “Good” cases and positive cases (“Good” + “Fair”), which indicates that treatment topics learned by our IJM is more reasonable because our model can represent loosely-structured inpatient journeys into the learning process.
We performed both cohen’s Kappa test and t-test on the human evaluation results for both IJM and HMM. (i) The Kappa test is used to calculate inter-judge reliability between IJM and HMM. For the good cases, the obtained kappa value for Kappa test is 0.053, which is slightly larger than 0 and indicates the poor agreement between IJM and HMM. For the positive cases, the obtained kappa value for Kappa test is 0.167, indicating slight agreement between IJM and HMM. (ii) The t-test is used to evaluate the human understandings on the derived treatment topics and their assignments on clinical epochs of medical inpatient journeys. For the good cases, the obtained t statistic is 6.020, which is larger than 3.250 (the confidence value of 99.5%). It indicates that the proposed IJM achieves the better understanding of human evaluators on the discovered treatment topics and their assignments on clinical epochs of inpatient journeys than that of HMM. For the positive cases, the obtained t statistic is 2.756, which is less than 3.250 (the confidence value of 99.5%), and indicates that there are statistically no differences between IJM and HMM on positive cases.
Figure.4.
Spherical comparison in terms of human evaluation. (A) Percentage of good cases; (B) Percentage of positive cases.
To illustrate the quality of inpatient journey modeling more intuitively, we take the inpatient journeys σ1 and σ2 (as shown in Figure 2) as examples. In particular, we manually checked the learned treatment topics with their representative treatment events for σ1 and σ2. In consideration of treatment topic and their transitions for both examples, clinical evaluators think that all these transitions are reasonable and easy to understand.
For example, the patient with σ1 is an aged male patient. He has high-risk level of unstable angina and his LOS is 5 days. With IJM, a typical treatment topic transition pattern for the unstable angina treatment process is generated:
Topic 1 (Admission, day 1)→Topic 2 (Prepare surgery, day 2)→Topic 3 (Surgery, day 3)→Topic 4 (Post-surgery recovery, day 4)→Topic 5 (Discharge, day 5)
To look insight into the learned treatment topics, clinical evaluators think that most of treatment event types of each learned topic underlying in σ1 are reasonable, except for one irrelevant treatment event type in the learned topic “Prepare surgery“ of σ1, which is shown in bold in Table 1. As a result, 4 out of 5 clinical epochs are labeled as “Good” and 1 clinical epoch (t = 2) is labeled as “Fair”.
Table.1.
The generated treatment topics with their representative treatment activities for the selected inpatient journey examples σ1 and σ2, as shown in Figure 2.
| σ1 | |
|---|---|
| Topic 1 | Admission, Routine urine test, Blood typing, Routine stool test, Calcium channel blockers, Routine blood test, Blood serum test, Ultrasonography examination, ECG examination, Cardiovascular treatment, Antianginal treatment, Biochemical examination, Antiplatelet treatment, β-adrenergic receptor blockers, Lipid regulation, Anticoagulation treatment, Angiotensin-converting enzyme inhibitors, Angiotensin receptor antagonists, Proton pump inhibitors, Peripheral vasodilator, Thyroid function tests, X-ray, Occult blood test, Coagulation examination, Radiographic examination, Blood sugar regulation |
| Topic 2 | Cardiovascular treatment, Anticoagulation treatment, Antiplatelet treatment, β-adrenergic receptor blockers, Antianginal treatment, Oxygen inhalation, Proton pump inhibitors, Lipid regulation, Angiotensin-converting enzyme inhibitors, Calcium channel blockers, X-ray, Angiotensin receptor antagonists, Peripheral vasodilator |
| Topic 3 | Cardiovascular treatment, Anticoagulation treatment, Antiplatelet treatment, β-adrenergic receptor blockers, Antianginal treatment, Lipid regulation, Angiotensin-converting enzyme inhibitors, Anesthesia, Coronary angiography, Stent implantation, Proton pump inhibitors, Calcium channel blockers, Angiotensin receptor antagonists, Peripheral vasodilator |
| Topic 4 | Cardiovascular treatment, Anticoagulation treatment, Antiplatelet treatment, β-adrenergic receptor blockers, Antianginal treatment, Oxygen inhalation, Lipid regulation, Angiotensin-converting enzyme inhibitors, Proton pump inhibitors, Calcium channel blockers, Angiotensin receptor antagonists, Multifunctional monitors |
| Topic 5 | Antianginal treatment, Discharge |
| σ2 | |
|---|---|
| Topic 1 | Admission, Routine stool test, Routine urine test, Blood typing, Routine care, Routine blood test, Blood serum test, Specific meal, Ultrasonography examination, Cardiovascular treatment, Anticoagulation treatment, Antiplatelet treatment, β-adrenergic receptor blockers, Antianginal treatment, Second-level care, Lipid regulation, Occult blood test, Coagulation examination, Blood sugar regulation, Consultation |
| Topic 2 | Cardiovascular treatment, Anticoagulation treatment, Antiplatelet treatment, β-adrenergic receptor blockers, Antianginal treatment, Lipid regulation, Blood sugar regulation, Troponin T |
| Topic 3 | Cardiovascular treatment, Anticoagulation treatment, Antiplatelet treatment, β-adrenergic receptor blockers, Antianginal treatment, Lipid regulation, Blood sugar regulation, Anti-diabetes treatment |
| Topic 4 | Cardiovascular treatment, Anticoagulation treatment, Antiplatelet treatment, β-adrenergic receptor blockers, Antianginal treatment, Lipid regulation, Anesthesia, Coronary angiography, Stent implantation, PTCA, Local anesthesia, Blood sugar regulation, Anti-diabetes treatment |
| Topic 5 | Cardiovascular treatment, Anticoagulation treatment, Antiplatelet treatment, β-adrenergic receptor blockers, Antianginal treatment, Lipid regulation, Coagulation examination, Discharge, Anti-diabetes treatment |
The patient with σ2 is an aged female unstable angina patient. Her LOS is 8 days. This patient also has a common comorbidity of unstable angina, i.e., “Diabetes”, such that anti-diabetes treatments, e.g., “Diabetes check”, “Glucose regulating treatment”, etc., were performed during her LOS (shown in bold in Table 1). In clinical practice, conservative treatments are performed in σ2. The proposed IJM generates the following treatment topic transition pattern:
Topic 1 (Admission, day 1)→Topic 2 (day 2)→Topic 3 (day 3)→Topic 4 (Surgery, day 4)→Topic 3 (days 5–7)→Topic 5 (Discharge, day 8)
To look insight into the learned treatment topics of σ2, clinical evaluators find that most of treatment event types in the derived topics of σ2 are reasonable. In particular, they point out that our approach cannot only discover typical medical interventions on unstable angina treatment and therapy, but also disclose typical medical interventions on Diabetes treatment for the patient, such as “Blood sugar regulation”, and “Anti-diabetes treatment”, etc., as shown in the derived topics of σ2. Regarding discovered topics for each clinical epoch, clinical evaluators think it would be better to label the third clinical epoch of σ2 as “Topic 2” than “Topic 3”. As a result, clinical evaluators labeled 7 clinical epochs as “Good”, and the other one as “Fair” for σ2.
Clustering performance
The hierarchical clustering on the experimental dataset was performed based on the similarity matrix using Equation (14). Since the similarity measure is the key of clustering techniques, we compared the presented IJM-based similarity measure with the variation HMM-based similarity measure, and the classical sequence-alignment-based (SA) similarity measure [16].
To evaluate the proposed approach in a quantitative manner, we measured the cluster homogeneity, which is a widely used measure for the quality evaluation of clustering [22, 43]. A classical definition of cluster homogeneity is as follows:
| (16) |
Where is the number of inpatient journeys in cluster , and sim(σi,σj) is the similarity between any two inpatient journeys σi and σj in . The higher the homogeneity value, the better the quality of clustering results.
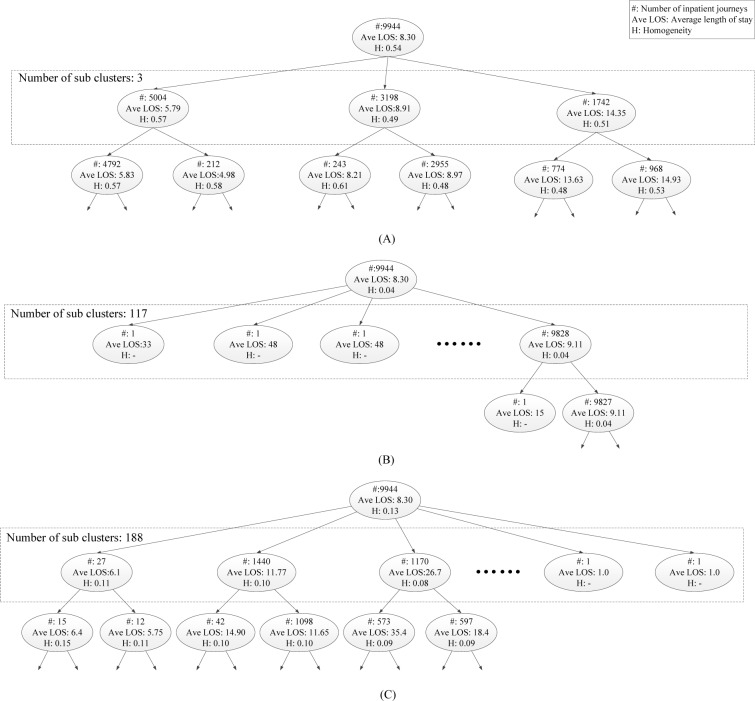
Figure 5 shows parts of the cluster hierarchies we obtained by applying the proposed IJM, HMM, and SA, respectively, on the experimental dataset. The structure of the hierarchies and the content of the resulting clusters are very different between the proposed approach and the baseline methods. As shown in Figure 5(B) and (C) the hierarchies built by both HMM and SA are a bit friable: the root node has a lot of children. It indicates that both HMM and SA resort to a large amount of clusters (117 and 188 for HMM and SA, respectively). In addition, the generated hierarchies by both HMM and SA are very unbalanced: one of these children corresponds to a very big cluster, while the others contain only one or just a few inpatient journeys. In comparison with the benchmark methods, the hierarchy generated by our approach is not sparse, and each node is normally split into few clusters of more comparable dimensions (cc. Figure 5(A)).
Figure.5.
Part of the cluster hierarchies obtained by applying the proposed IJM (A), a variation HMM (B), and sequence alignment (C). Every node represents a cluster and reports the number of traces in the cluster itself, and their average normalized similarity (in brackets).
In addition, the average homogeneity H were calculated on the obtained clusters from data to assess its quality [11]. Average cluster homogeneity allows to compare the output of different clustering techniques on the same dataset. Figure 5(A) shows that the proposed approach had an average homogeneity of 0.54. On the other side, using HMM and sequence alignment, they reached an average homogeneity of 0 04 and 0.13, respectively. These indicate that the proposed method outperforms the benchmark methods on medical inpatient journey clustering.
As shown in Figure 5(A), three clusters in the second level generated by our approach define the cut of the cluster tree that corresponds to the maximum split between clusters, which allow us to obtain some relevant insights on the dynamics of the unstable angina treatment process:
Cluster 1, which corresponds to 50.3% inpatient journeys, collects typical treatment behavior of unstable angina patients who have been performed PCI surgery in their treatment processes. A closer analysis shown on Table 2 indicates that cluster 1 contains typical treatment interventions (e.g., “Coronary angiography”, “Stent implantation”, etc.) for unstable angina. There is little variation occurred and common treatment events are carried out smoothly. In clinical practice, patients who are categorized into cluster 1 have shorter LOS (on average 5.79 days) than the others.
Table 2.
Clustering results on the unstable angina dataset using IJM. 25 top-ranked treatment activities are listed to refer to clusters at level 2 in the hierarchies. Unique treatment activities of each cluster are marked with bold type.
| Cluster | Cluster description |
|---|---|
| 1 | Antiplatelet treatment, Antianginal treatment, Routine blood test, Anticoagulation treatment, Ultrasonography examination, Lipid regulation, Biochemical examination, Discharge, Routine urine test, Admission, Routine stool test, Blood serum test, ECG examination, Coronary angiography, Blood typing, Calcium channel blockers, β-adrenergic receptor blockers, Anesthesia, Coagulation examination, Occult blood test, Angiotensin receptor antagonists, Radiographic examination, Stent implantation, Troponin T, PTCA |
| 2 | Antianginal treatment, Routine blood test, Biochemical examination, Ultrasonography examination, Hypnotic sedative and anxiolytic, Diuretics, Antiplatelet treatment, Glucose regulating treatment, ECG examination, Routine urine test, Calcium channel blockers, Routine stool test, Lipid regulation, Anticoagulation treatment, Discharge, Coagulation examination, Admission, Electrolyte regulating treatment, Analysis of blood plasma, Blood serum test, Blood sugar regulation, β-adrenergic receptor blockers, Occult blood test, Angiotensin receptor antagonists, Radiographic examination |
| 3 | Ultrasonography examination, CT examination, Antianginal treatment, Routine blood test, Biochemical examination, Routine urine test, Routine stool test, Admission, Lipid regulation, Discharge, Coagulation examination, Glucose regulating treatment, Calcium channel blockers, Blood serum test, Antiplatelet treatment, Occult blood test, Radiographic examination, Blood typing, ECG examination, Peripheral vasodilator, Anticoagulation treatment, Tumor markers checks, Analysis of blood plasma, Consultation, Transfer |
Cluster 2, which collects about 32.2% samples, contains typical conservative treatments of unstable angina. In clinical practice, patients in cluster 2 have either low risks or specific physical problems, e.g., coronary stenosis such that they prefer conservative treatments instead of PCI surgery. As a result, the average LOS of patients in cluster 2 (i.e., 8.91 days as shown in Figure 5(A)) is longer than patients in cluster 1.
Cluster 3 has captured typical treatment behaviors of unstable angina patients who have more complex conditions than others such that many treatments on the comorbidities of the patients, e.g., “Glucose regulating treatment”, “Tumor markers checks”, “Consultation”, etc., can be found in this cluster (as shown in Table 2). Note that several patients in cluster 3 are transferred to Cardiac Surgery department for the further surgical thoracotomy, such as “Coronary artery bypass graft (CABG)”, etc. Note that this variant cluster is a bit normal in the unstable angina treatment process (17.5% patients in the collections of EMRs). The average LOS of patients in cluster 3 is about 14.35 days, which is much longer than the other clusters.
4. Conclusions
In this paper, we propose a novel approach for medical inpatient journey modeling and clustering, which first collects critical treatment events in inpatient journeys from EMRs, and then develop a probabilistic model-based approach to group inpatient journeys characterized by similar treatment behaviors. To this end, we present a Bayesian HMM-based representation method, i.e., inpatient journey model, to transform the collection of medical inpatient journeys into a probabilistic space defined by the estimated posterior probabilities without losing information related to the dynamics and dependency in the data. Based on the constructed probabilistic space, similarities between inpatient journeys are calculated and the homogenous ones are grouped into the same cluster.
Footnotes
In this study, we set the time range of each clinical epoch in an inpatient journey σ as a hospitalization day, which records a set of treatment events observed on a particular day in the patient’s length of stay.
References
- 1.Muluk SC, Painter L, Sile S, Rhee RY, Makaroun MS, Steed DL, Webster MW. Utility of clinicalpathway and prospective case management to achieve cost and hospital stay reduction for aortic aneurysm surgery at a tertiary care hospital. Journal of Vascular Surgery. 1997;25(1):84–93. doi: 10.1016/s0741-5214(97)70324-0. [DOI] [PubMed] [Google Scholar]
- 2.Hunter B, Segrott J. Re-mapping client journeys and professional identities: A review of the literature on clinical pathways. International Journal of Nursing Studies. 2008;45:608–625. doi: 10.1016/j.ijnurstu.2007.04.001. [DOI] [PubMed] [Google Scholar]
- 3.Huang Z, Dong W, Bath P, Ji L, Duan H. On mining latent treatment patterns from electronic medical records. Data Mining and Knowledge Discovery. 2014:1–36. [Google Scholar]
- 4.Lenz R, Reichert M. IT support for healthcare processes-premises, challenges, perspectives. Data & Knowledge Engineering. 2007;61(1):39–58. [Google Scholar]
- 5.Rebuge A, Ferreira DR. Business process analysis in healthcare environments: A methodology based on process mining. Information Systems. 2012;37(2):99–116. [Google Scholar]
- 6.Peleg M. Computer-interpretable clinical guidelines: A methodological review. Journal of Biomedical Informatics. 2013;46(4):744–763. doi: 10.1016/j.jbi.2013.06.009. [DOI] [PubMed] [Google Scholar]
- 7.van der Aalst WMP, Weijters AJMM, Maruster L. Workow Mining: Discovering process models from event logs. IEEE Transactions on Knowledge and Data Engineering. 2004;16(9):1128–1142. [Google Scholar]
- 8.Montani S, Leonardi G, Quaglini S, Cavallini A, Miciel G. Improving structural medical process comparison by exploiting domain knowledge and mined information. Artificial Intelligence in Medicine. 2014;62(1):33–45. doi: 10.1016/j.artmed.2014.07.001. [DOI] [PubMed] [Google Scholar]
- 9.Lakshmanan GT, Rozsnyai S, Wang F. Investigating clinical care pathways correlated with outcomes. In: Daniel Florian, Wang Jianmin, Weber An Barbara., editors. Business Process Management, volume 8094 of Lecture Notes in Computer Science. Springer Berlin; Heidelberg: 2013. pp. 323–338. [Google Scholar]
- 10.Lenz R, Reichert M. IT support for healthcare processes-premises, challenges, perspectives. Data & Knowledge Engineering. 2007;61(1):39–58. [Google Scholar]
- 11.Montani S, Leonardi G. Retrieval and clustering for supporting business process adjustment and analysis. Information Systems. 2014;40(0):128–141. [Google Scholar]
- 12.Huang Z, Lu X, Duan H, Fan W. Summarizing clinical pathways from event logs. Journal of Biomedical Informatics. 2013;46(1):111–127. doi: 10.1016/j.jbi.2012.10.001. [DOI] [PubMed] [Google Scholar]
- 13.Huang Z, Lu X, Duan H. On mining clinical pathway patterns from medical behaviors. Artificial Intelligence in Medicine. 2012;56(1):35–50. doi: 10.1016/j.artmed.2012.06.002. [DOI] [PubMed] [Google Scholar]
- 14.Ferreira DR, Zacarias M, Malheiros M, Ferreira P. Approaching process mining with sequence clustering: experiments and findings. In: Alonso G, Dadam P, Rosemann M, editors. Lecture Notes in Computer Science. Vol. 4714. Springer; Berlin/Heidelberg: 2007. pp. 360–374. [Google Scholar]
- 15.Goldwater S, Griffiths T. A fully Bayesian approach to unsupervised part-of-speech tagging. Annual Meeting: Association for Computational Linguistics. 2007;45:744. [Google Scholar]
- 16.Mirkin B. Mathematical Classification and Clustering. Springer; 1996. [Google Scholar]