Abstract
Motivation: Despite ongoing cancer research, available therapies are still limited in quantity and effectiveness, and making treatment decisions for individual patients remains a hard problem. Established subtypes, which help guide these decisions, are mainly based on individual data types. However, the analysis of multidimensional patient data involving the measurements of various molecular features could reveal intrinsic characteristics of the tumor. Large-scale projects accumulate this kind of data for various cancer types, but we still lack the computational methods to reliably integrate this information in a meaningful manner. Therefore, we apply and extend current multiple kernel learning for dimensionality reduction approaches. On the one hand, we add a regularization term to avoid overfitting during the optimization procedure, and on the other hand, we show that one can even use several kernels per data type and thereby alleviate the user from having to choose the best kernel functions and kernel parameters for each data type beforehand.
Results: We have identified biologically meaningful subgroups for five different cancer types. Survival analysis has revealed significant differences between the survival times of the identified subtypes, with P values comparable or even better than state-of-the-art methods. Moreover, our resulting subtypes reflect combined patterns from the different data sources, and we demonstrate that input kernel matrices with only little information have less impact on the integrated kernel matrix. Our subtypes show different responses to specific therapies, which could eventually assist in treatment decision making.
Availability and implementation: An executable is available upon request.
Contact: nora@mpi-inf.mpg.de or npfeifer@mpi-inf.mpg.de
1 Introduction
Cancer is not only a very aggressive but also a very diverse disease. Therefore, a number of approaches aim to identify subtypes of cancer in a specific tissue, where subtypes refer to groups of patients with corresponding biological features or a correlation in a clinical outcome, e.g. survival time or response to treatment. Nowadays, most of these methods utilize single data types (e.g. gene expression). However, subtypes that are merely based on information from one level can hardly capture the subtleties of a tumor. Therefore, huge efforts are made to improve the comprehensive understanding of tumorigenesis in the different tissue types. Large-scale projects, e.g. The Cancer Genome Atlas (TCGA) (The Cancer Genome Atlas, 2008), provide a massive amount of data generated by diverse platforms such as gene expression, DNA methylation and copy number data for various cancer types. Still, we require computational methods that enable the comprehensive analysis of these multidimensional data and the reliable integration of information generated from different sources.
One simple and frequently applied method to combine biological data consists of clustering the samples using each data type separately and subsequently integrating the different cluster assignments. The latter step can be performed either manually or automatically, e.g. using consensus clustering (Monti et al., 2003). Manual integration tends to be biased, leading to inconsistent results. However, both manual and automatic integration cannot capture correlated information between the data types because low signals might already vanish during the initial clustering. Therefore, more advanced approaches bring forward the step of data integration to make use of weak but concordant structures in different data sources. Shen et al. (2009, 2012) introduced iCluster, which allows for data integration and dimensionality reduction at the same time. The basis is a Gaussian latent variable model with regularization for sparsity, in which the cluster assignment can be derived from the latent variable vector. Because of the high computational complexity of this approach, preselection of the features is necessary, so the clustering result strongly depends on this preprocessing step. An approach that tackles both the problem of how to use correlation between the data types and the problem of feature preselection is Similarity Network Fusion (SNF) (Wang et al., 2014). First, a similarity network of the samples is constructed from each input data type. These networks are then fused into one combined similarity network using an iterative approach based on message passing. This way, the networks are updated in each iteration such that they become more similar to each other, until the process converges. The resulting network is then clustered by Spectral Clustering (von Luxburg, 2007). An approach that uses the same clustering algorithm is Affinity Aggregation for Spectral Clustering (Huang et al., 2012). Here, the main idea is to extend Spectral Clustering to allow for several affinity matrices as input. The matrices are fused using a linear combination, with weights being optimized using multiple kernel learning.
2 Approach
We propose to apply and extend multiple kernel learning for data integration and subsequently perform cancer subtype identification. To this end, we adopt the multiple kernel learning for dimensionality reduction (MKL-DR) framework (Lin et al., 2011) that enables dimensionality reduction and data integration at the same time. This way, the samples are projected into a lower dimensional, integrated subspace where they can be analyzed further. We show that this representation captures useful information that can be used for clustering samples, but other follow-up analyses are also possible from this data representation. Compared to previous approaches, this procedure offers several advantages: The framework provides high flexibility concerning the choice of the dimensionality reduction method, i.e. not only unsupervised but also supervised and semi-supervised methods can be adopted. Furthermore, the framework provides high flexibility concerning the input data type, i.e. since the first step is a kernelization of the input matrices, these can be of various formats, such as sequences or numerical matrices. Moreover, in case one does not have enough information from which to choose the best kernel function for a data type or the best parameter combination for a given kernel beforehand, it is possible to input several kernel matrices per data type, based on different kernel functions or parameter settings. The multiple kernel learning approach will automatically upweight the matrices with high information content while downweighting those with low information content. To avoid overfitting, especially in the scenario with many distinct input matrices, we extend the MKL-DR approach by adding a regularization term.
We use five different cancer sets for the evaluation of our method. The resulting clusterings reflect characteristics from distinct input data types and reveal differences between the clusters concerning their response to specific treatments. Furthermore, we show that kernel matrices with less information have less influence on the final result. A comparison of the P values for survival differences between our clusters and the SNF clusters shows that our method yields comparable results while offering a lot more flexibility.
3 Methods
To integrate several data types, we utilize multiple kernel learning, extending the MKL-DR approach (Lin et al., 2011). This method is based, on the one hand, on multiple kernel learning, and, on the other hand, on the graph embedding framework for dimensionality reduction. We add a constraint that leads to the regularization of the vector controlling the kernel combinations, which, to our knowledge, is the first time this has been done for unsupervised multiple kernel learning. We call this method regularized multiple kernel learning for dimensionality reduction (rMKL-DR) in the following discussion.
3.1 Multiple kernel learning
In general, multiple kernel learning optimizes the weights β that linearly combine a set of input kernel matrices to generate a unified kernel matrix K, such that
| (1) |
Here, each input data type is represented as an individual kernel matrix. Therefore, this approach can be used for data having different feature representations.
3.2 Graph embedding
MKL-DR is described upon the graph embedding framework for dimensionality reduction (Yan et al., 2007), which enables the incorporation of a large number of dimensionality reduction methods. In this framework, the projection vector v (for the projection into a one-dimensional subspace) or the projection matrix V (for the projection into higher dimensions) is optimized based on the graph-preserving criterion:
| (2) |
| (3) |
| (4) |
with v being the projection vector, W a similarity matrix with entries wij and D (or ) a constraint matrix to avoid the trivial solution. The choice of the matrices W and D (or W and ) determines the dimensionality reduction scheme to be implemented. It also depends on this scheme whether the first or the second constraint is used. In the following, we will focus on the optimization problem with Constraint (3), but the constructions are analogous when using Constraint (4).
3.3 Multiple kernel learning for dimensionality reduction
The kernelized version of the constrained optimization problem (2) can be derived using an implicit feature mapping of the data to a high-dimensional Hilbert space . Additionally, it can be shown that the optimal projection vector v lies in the span of the data points xi, thus . Together with the kernel function and Formula (1), this yields the following optimization problem:
| (5) |
| (6) |
| (7) |
where
| (8) |
| (9) |
| (10) |
Since we are applying several kernels and want to avoid overfitting, we add the constraint . Had we added the constraint , this would amount to an Ivanov regularization. The corresponding Tikhonov regularization would be to directly add the regularization term to the minimization problem. The full optimization problem for rMKL-DR is then:
| (11) |
| (12) |
| (13) |
| (14) |
The optimization problem can easily be extended to the projection into more than one dimension. In that case, a projection matrix A is optimized instead of the single projection vector . Then, A is optimized at the same time as the kernel weight vector according to a chosen dimensionality reduction method. Since the simultaneous optimization of these two variables is difficult, coordinate descent is employed, i.e. A and are iteratively optimized in an alternating manner until convergence or a maximum number of iterations is reached. One can start either with the optimization of A, then is initialized to equal weights for all kernel matrices summing up to one or with the optimization of , then AAT is initialized to I.
Using this framework, we apply the dimensionality reduction algorithm Locality Preserving Projections (LPP) (He and Niyogi, 2004). This is an unsupervised local method that aims to conserve the distances of each sample to its k nearest neighbors. The neighborhood of a data point i is denoted as . For LPP, the matrices W and D are then defined as
| (15) |
| (16) |
The rMKL-DR approach with LPP will be called rMKL-LPP from now on. The clustering process is performed using k-means. For the evaluation of the clusterings, we use the silhouette width (Rousseeuw, 1987), a measure that indicates, for each data point, how well it fits into its own cluster, compared to how well it would fit into the best other cluster. When averaged over all data points, the resulting mean silhouette value gives a hint on how coherent a clustering is and how well the clusters are separated.
The running time of the whole algorithm can be separated into the dimensionality reduction step and the k-means clustering. The dimensionality reduction is performed by iteratively updating the projection matrix A and the kernel weight vector . The optimization of uses semidefinite programming where the number of constraints is linear in the number of input kernel matrices and the number of variables is quadratic in the number of input kernel matrices. However, if , the bottleneck is the optimization of A. This involves solving a generalized eigenvalue problem that has a complexity of .
3.4 Leave-one-out cross-validation
To assess the stability of the resulting clusterings, we applied a leave-one-out cross-validation approach, i.e. we apply the pipeline consisting of dimensionality reduction and subsequent clustering to a reduced dataset that does not include patient i. The projection of the left-out sample can be calculated using = A, and this patient is assigned to the cluster with the closest group mean in the dimensionality reduced space. Finally, we compare this leave-one-out clustering to the clustering of the full dataset using the Rand index (Rand, 1971).
3.5 Materials
We used data from five different cancer types from TCGA (The Cancer Genome Atlas, 2008), preprocessed and provided by Wang et al. (2014). The cancer types comprise glioblastoma multiforme (GBM) with 213 samples, breast invasive carcinoma (BIC) with 105 samples, kidney renal clear cell carcinoma (KRCCC) with 122 samples, lung squamous cell carcinoma (LSCC) with 106 samples and colon adenocarcinoma (COAD) with 92 samples. For each cancer type, we used gene expression, DNA methylation and miRNA expression data in the clustering process. For the survival analysis, we used the same quantities as were used in Wang et al. (2014), this means, we used the number of days to the last follow-up, where available. For COAD, these were combined with the number of days to last known alive because of many missing values in the number of days to the last follow-up data.
4 Results and discussion
We applied rMKL-LPP to five cancer datasets. For each dataset, we ran the algorithm with both possible initializations, either starting with the optimization of A or with the optimization of . For both dimensionality reduction results, the integrated data points were then clustered using k-means with . We chose the optimal number of clusters using the average silhouette value of the clustering result. This criterion was then also utilized to select the best clustering among the two different initializations. In most cases, initializing led to slightly better silhouette values, although the final results for both initializations were highly similar concerning the number of identified clusters and the cluster assignment.
As a consequence, the method has only two free parameters, the number of neighbors used in the dimensionality reduction method LPP and the number of dimensions of the projection subspace. Our initial analyses showed that the clusterings are fairly stable when choosing the number of nearest neighbors between 5 and 15 (data not shown). We chose 9 for all datasets to show the robustness of this parameter, although specific optimization would be feasible in terms of running time and memory requirements. The number of dimensions to project into was fixed to 5 for two reasons. First, because of the curse of dimensionality, samples with many dimensions tend to lie far apart from each other, leading to sparse and dispersed clusterings. Second, we wanted only a medium number of subtypes, such that very high dimensionality was not necessary.
4.1 Comparison to state-of-the-art
For each data type, we used the Gaussian radial basis kernel function to calculate the kernel matrices and normalized them in the feature space. To investigate how well the method is able to handle multiple input kernels for single data types, we generated two scenarios. The first contained one kernel matrix per data type where γ1 was chosen according to the rule of thumb , with d being the number of features of the data. Since this results in three kernels, the scenario is called 3K. For Scenario 2, we generated five kernel matrices per data type by varying the kernel parameter γ such that , where . This scenario is called 15K, consequently.
We compared the resulting clusterings with the results of SNF in Table 1 . Considering the P value for the log-rank test of the Cox regression model (Hosmer et al., 2011), rMKL-LPP with one kernel per data type has a comparable performance to SNF. Only for KRCCC, the result was not significant when using one fixed value for γ (significance level ). As can be seen in the last column, the significance for four out of the five datasets increased when using a set of different values for the kernel parameter γ, indicating that the method is able to capture more information if provided. A further observation when moving from one to five different γ values is the increase of the optimal number of clusters. A possible explanation for this could be that more detailed information is contributed by the different kernel matrices because, depending on the parameter setting, similarities between particular groups of patients can appear stronger while others diminish. Overall, the performance of rMKL-LPP with five kernel matrices was best. The median P value for this approach was 2.4E-4, whereas it was 0.0011 for SNF and 0.028 for rMKL-LPP with one kernel per data type. The product of all P values of each method showed a similar trend (rMKL-LPP 15K: 5.9E-19, SNF: 1.1E-13, rMKL-LPP 3K: 1.9E-10). Note that the higher number of clusters of rMKL-LPP is controlled in the calculation of the log-rank test P value by the higher number of degrees of freedom of the distribution.
Table 1.
Survival analysis of clustering results of similarity network fusion (SNF) and rMKL-LPP with one and five kernels per data type
| Cancer type | SNF | rMKL-LPP | |
|---|---|---|---|
| 3K | 15K | ||
| GBM | 2.0E-4 (3) | 4.5E-2 (5) | 6.5E-6 (6) |
| BIC | 1.1E-3 (5) | 3.0E-4 (6) | 3.4E-3 (7) |
| KRCCC | 2.9E-2 (3) | 0.23 (6) | 4.0E-5 (14) |
| LSCC | 2.0E-2 (4) | 2.2E-3 (2) | 2.4E-4 (6) |
| COAD | 8.8E-4 (3) | 2.8E-2 (2) | 2.8E-3 (6) |
The numbers in brackets denote the number of clusters. For SNF, these are determined using the eigenrotation method (Wang et al., 2014), and for rMKL-LPP, by the silhouette value.
A further advantage of the rMKL-LPP method with five kernels per data type is that one does not have to decide on the best similarity measure for the data type beforehand, which makes this method more applicable out of the box. Additionally, the results suggest that it might even be beneficial in some scenarios to have more than one kernel matrix per data type to capture different degrees of similarity between data points (patients in this application scenario).
As shown in Wang et al. (2014), the running time of iCluster scales exponentially in the number of genes, which makes the analysis of the cancer datasets infeasible if no gene preselection is performed. For SNF, this preprocessing step is not necessary, and it is significantly faster than iCluster. We compared the run time for the data integration in SNF and rMKL-LPP (15K), which precedes the clustering step in both methods. The SNF approach with the standard parameter settings completes the network fusion procedure for each cancer type within a few seconds, whereas the data integration with rMKL-LPP (15K) was slightly slower with running times up to one minute. However, just like SNF, rMKL-LPP does not require a gene preselection, which suggests that using datasets with a higher number of samples and including more kernel matrices should be feasible in terms of running times.
4.2 Contribution of individual kernel matrices to the combined kernel matrix
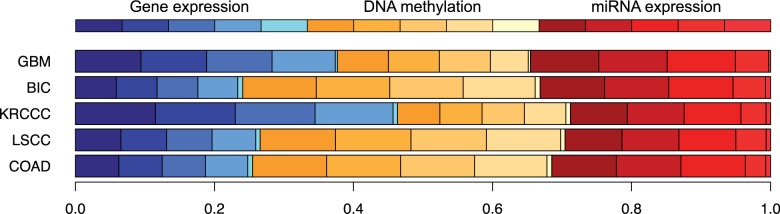
For rMKL-LPP with five kernels per data type, Figure 1 shows the influence of every kernel matrix on the final integrated matrix. The top bar shows what the graphic would look like for an equal contribution of all kernel matrices. In comparison to this, we can see that kernel matrices using high values for the parameter have a very low impact for all cancer types. These results agree with the rule of thumb that γ should be chosen in the order of magnitude of or lower, which was used for the choice of γ1 (Gärtner et al., 2002). Furthermore, all data types contribute to the combined kernel matrix, and we can observe differences for the individual cancer types, e.g. for BIC, DNA methylation data has a higher impact, whereas for KRCCC, there is more information taken from the gene expression data.
Fig. 1.
Contribution of the different kernel matrices to each entry in the unified ensemble kernel matrix. The three colors represent gene expression (blue), DNA methylation (yellow) and miRNA expression (red). The intensities represent the kernel parameter γ, starting from (high intensity) to (low intensity)
4.3 Robustness analysis
To assess the robustness of the approach to small changes in the dataset, we performed a leave-one-out cross-validation approach (cf. Section 3.4). Figure 2 shows the stability of the clustering when using one kernel matrix per data source (Scenario 1) and five kernel matrices per data source (Scenario 2). Although we can observe for GBM and LSCC almost no perturbation in cluster structure in Scenario 1, for the other three cancer types, there is some deviation to the full clustering and some variance among the leave-one-out results. Especially for the COAD dataset, we observed for a number of leave-one-out clusterings that, compared with the full clustering, one of the clusters was split up into two distinct groups, which increases the overall number of clusters from two to three and leads to a decrease in the Rand index. The opposite happens for BIC, where we have a full clustering consisting of six groups, while in some of the leave-one-out runs, two of the groups are collapsed, resulting in five different clusters and, therefore, a lowered Rand index. However, when using five kernel matrices per data source, the results seem to be more stable, which appears, on the one hand, in the increased agreement with the full clustering and, on the other hand, in the reduced variance among the leave-one-out results.
Fig. 2.
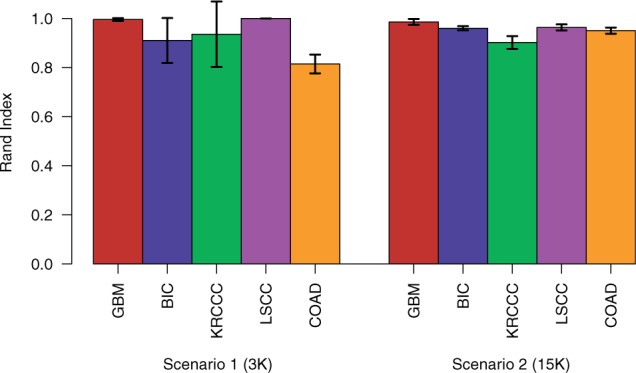
Robustness of clustering for leave-one-out datasets measured using Rand index. Each patient is left out once in the dimensionality reduction and clustering procedure and afterwards added to the cluster with the closest mean based on the learned projection for this data point, which is given by = A. The resulting cluster assignment is then compared with the clustering of the whole dataset. The error bars represent one standard deviation
To further investigate the impact of the regularization constraint, we compared the robustness of the results obtained using rMKL-LPP to the robustness of the results from MKL-LPP. In general, overfitting is expected especially for datasets with a small number of samples or a high number of predictors. Therefore, we generated from each cancer dataset smaller datasets using 50% of the samples. In this setting, the unregularized MKL-LPP showed some instabilities for GBM and KRCCC, with an increased variance among the clustering results compared to rMKL-LPP for most cancer types (cf. Fig. 3). This trend continued when the number of samples was further reduced, as shown in Figure 4. Although the results without regularization seem robust when using the complete dataset for each cancer type, we could observe that the robustness decreased when the number of samples decreased. The regularized approach, however, showed only a slight decrease in robustness when half the samples of each dataset were deleted and remained at this level when only one third or one quarter of the data were used. This suggests that rMKL-LPP has advantages in scenarios where MKL-LPP would overfit, while being comparable when no regularization is required.
Fig. 3.
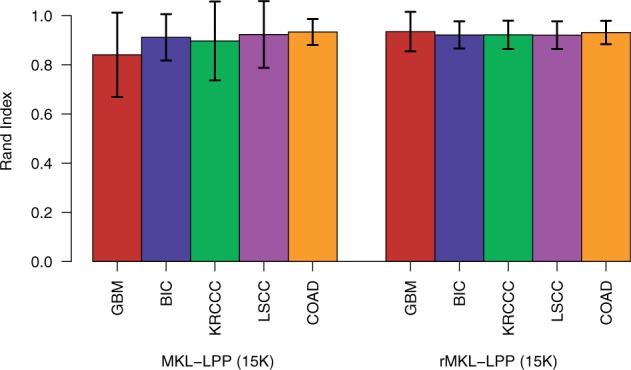
Robustness of clustering for leave-one-out cross-validation applied to reduced sized datasets measured using Rand index. For each cancer type, we sampled 20 times half of the patients and applied leave-one-out cross-validation as described in Section 3.4. The error bars represent one standard deviation
Fig. 4.
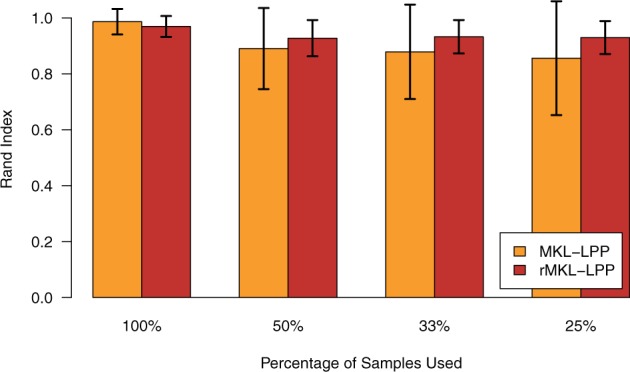
Comparison of the robustness of the clustering generated with and without regularization averaged over all cancer types for datasets of different sizes. The percentage on the x-axis denotes, how many patients were used for generating a smaller dataset on which leave-one-out cross-validation was performed. For each cancer type and each fraction of patients, we repeated the process 20 times. The error bars represent one standard deviation
4.4 Comparison of clusterings to established subtypes
In the following, we look further into the results generated by the use of five kernel matrices per data type (Scenario 2) for the GBM dataset. For this cancer type, there exist four established subtypes determined by their gene expression profiles (Verhaak et al., 2010) as well as one subtype called Glioma-CpG island methylator phenotype (G-CIMP), which is one out of three groups that emerged from a clustering of DNA methylation (Noushmehr et al., 2010). The comparison of our GBM clustering to these existing subtypes (cf. Table 2) shows that our method does not only reflect evidence from one data type, but finds a clustering that takes both gene expression and DNA methylation information into account.
Table 2.
Comparison of clusters identified by rMKL-LPP to gene expression and DNA methylation subtypes of GBM (Rand indices of 0.75 and 0.64, respectively)
| rMKL-LPP clusters | Gene expression subtypes (Verhaak et al., 2010) | DNA methylation subtypes (Noushmehr et al., 2010) | |||||
|---|---|---|---|---|---|---|---|
| Classical | Mesenchymal | Neural | Proneural | G-CIMP+ | #2 | #3 | |
| #1 | 0 | 36 | 5 | 1 | 0 | 7 | 37 |
| #2 | 31 | 7 | 13 | 2 | 0 | 46 | 6 |
| #3 | 1 | 0 | 1 | 15 | 16 | 1 | 1 |
| #4 | 1 | 1 | 5 | 22 | 0 | 13 | 27 |
| #5 | 9 | 8 | 2 | 3 | 0 | 19 | 18 |
| #6 | 6 | 1 | 2 | 9 | 3 | 7 | 9 |
We can observe that Cluster 1 is strongly enriched for the mesenchymal subtype, whereas Cluster 2 contains mainly samples that belong to the classical and the neural subtype. Samples of the proneural subtype are mainly distributed over Cluster 3 and Cluster 4, where these two clusters also reflect the G-CIMP status. While Cluster 3 consists almost only of G-CIMP positive samples, Cluster 4 contains samples that belong to the proneural subtype but are G-CIMP negative. This shows that in this scenario, evaluating expression and DNA methylation data together can be very beneficial since an analysis based on gene expression data alone would have probably led to a union of Cluster 3 and Cluster 4.
4.5 Clinical implications from clusterings
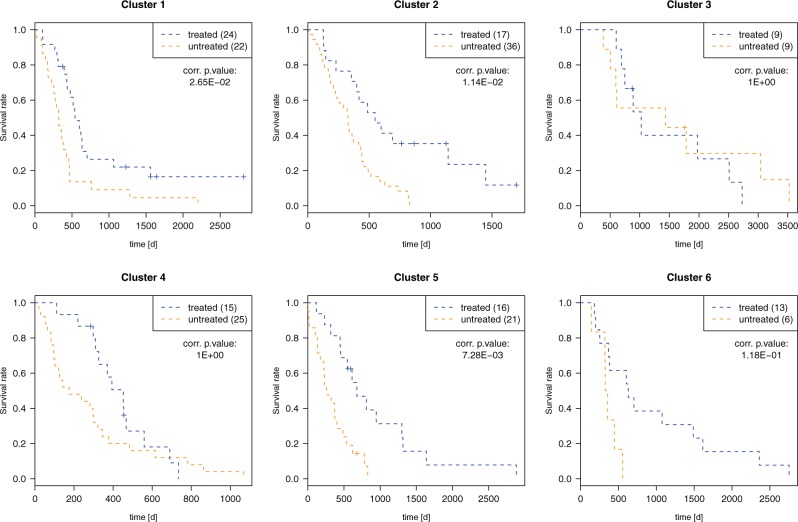
To gain further insights into the biological consequences of the identified clusters, we have investigated how patients of the individual clusters respond to different treatments. Of the 213 glioblastoma patients, 94 were treated with Temozolomide, an alkylating agent which leads to thymine mispairing during DNA replication (Patel et al., 2014). Figure 5 shows for each cluster the survival time of patients treated versus those not treated with this drug. We can see that this treatment was effective only in a subset of the identified groups. Patients belonging to Cluster 5 had a significantly increased survival time when treated with Temozolomide (P value after Bonferroni correction ). For Cluster 1 and Cluster 2, we can see a weaker tendency of treated patients living longer than untreated ones (P value after Bonferroni correction ), whereas for the other clusters, we did not detect significant differences in survival time between treated and untreated patients after correcting for multiple testing. Survival analysis for other medications could show their effectiveness in different groups.
Fig. 5.
Survival analysis of GBM patients for treatment with Temozolomide in the different clusterings. The numbers in brackets denote the number of patients in the respective group; the specified P values are corrected for multiple testing using the Bonferroni method
Cluster 3 consists mainly of patients belonging to the proneural expression subtype and the G-CIMP methylation subtype. Patients from this cluster show in general an increased survival time; however, they do not benefit significantly from the treatment with Temozolomide. We have determined differentially expressed genes between these patients and all other patients using the Kruskal–Wallis rank sum test. Table 3 (column 1) shows the top 15 terms of a Gene Ontology enrichment analysis of the set of overexpressed genes. The results are very similar to those found by Noushmehr et al. (2010) for their identified G-CIMP positive subtype. In addition, we found the set of underexpressed genes to be highly enriched for processes associated to the immune system and inflammation [cf. Table 3 (column 2)]. Since chronic inflammation is generally related to cancer progression and is thought to play an important role in the construction of the tumor microenvironment (Hanahan and Weinberg, 2011), these downregulations might be a reason for the favorable outcome of patients from this cluster.
Table 3.
Top 15 enriched GO terms (FDR q value ≪ 0.001) from the category biological process of differentially expressed genes of Cluster 3
| GO enrichment of overexpressed genes | GO enrichment of underexpressed genes |
|---|---|
| Nucleic acid metabolic process | Immune system process |
| RNA biosynthetic process | Defense response |
| Transcription, DNA templated | Response to external stimulus |
| Nucleic acid templated transcription | Response to stress |
| RNA metabolic process | Extracellular matrix organization |
| Regulation of cellular macromolecule biosynthetic process | Extracellular structure organization |
| Cellular macromolecule biosynthetic process | Regulation of immune system process |
| Nucleobase-containing compound metabolic process | Positive regulation of immune system process |
| Nucleobase-containing compound biosynthetic process | Inflammatory response |
| Regulation of RNA metabolic process | Positive regulation of response to stimulus |
| Regulation of transcription, DNA-templated | Response to external biotic stimulus |
| Regulation of nucleic acid-templated transcription | Regulation of response to stimulus |
| Regulation of macromolecule biosynthetic process | Response to biotic stimulus |
| Macromolecule biosynthetic process | Cell activation |
| Regulation of RNA biosynthetic process | Leukocyte migration |
5 Conclusion
Because of the large amount of different biological measurements, it is now possible to study diseases on many different levels such as comparing differences in DNA methylation, gene expression or copy number variation. For the unsupervised analysis of samples to detect interesting subgroups, it is not in general clear how to weight the importance of the different types of information. In this work, we have proposed to use unsupervised multiple kernel learning in this setting. For patient data from five different cancers, we have shown that our approach can find subgroups that are more interesting according to the log-rank test than are the ones found by state-of-the-art methods. Furthermore, we have demonstrated that we can even utilize several kernel matrices per data type, not only to improve performance but also to remove the burden of selecting the optimal kernel matrix from the practitioner. The visualizations of the contributions of the individual kernels suggest that using more than one kernel matrix per data type can even be beneficial, and the stability analysis shows that the method does not overfit when more kernels are added. In contrast to the unregularized MKL-DR, rMKL-DR remains stable also for small datasets. For a wide applicability of the method, this is especially important, since in many potential application scenarios the number of available samples is smaller than in this study. Furthermore, as we used the graph embedding framework, it is straightforward to perform semi-supervised learning (e.g. use the treatment data as labels where available and evaluate how unlabeled data points distribute over the different clusters). The clustering of GBM patients displayed concordance to previous clusterings based on expression as well as on DNA methylation data, which shows that our approach is able to capture this diverse information within one clustering. For the same clustering, we also analyzed the response of the patients to the drug Temozolomide, revealing that patients belonging to specific clusters significantly benefit from this therapy while others do not. The GO enrichments for the interesting clusters of the GBM patient samples showed, on the one hand, similar results to what was known from the biological literature and, on the other hand, down-regulation of the immune system in the subgroup of cancer patients who survived longer. This suggests that down-regulation of parts of the immune system could be beneficial in some scenarios. Further follow-up studies on the results of the different clusterings are necessary to assess their biological significance and implications.
Acknowledgement
The authors wish to thank Thomas Lengauer for helpful remarks and discussions during the course of this work.
Conflict of Interest: none declared.
References
- Gärtner T., et al. (2002) Multi-instance kernels. In: Sammut C., Hoffmann A.G. (eds), Proceedings of the 19th International Conference on Machine Learning Morgan Kaufmann, San Francisco, USA, pp. 179–186 [Google Scholar]
- Hanahan D., Weinberg R.A. (2011) Hallmarks of cancer: the next generation. Cell, 144, 646–674. [DOI] [PubMed] [Google Scholar]
- He X., Niyogi P. (2004) Locality preserving projections. In: Thrun S., et al. (eds.) Advances in Neural Information Processing Systems 16. MIT Press, Cambridge, MA, pp. 153–160. [Google Scholar]
- Hosmer D.W., Jr., et al. (2011) Applied Survival Analysis: Regression Modeling of Time to Event Data. Wiley, New York. [Google Scholar]
- Huang H.-C., et al. (2012) Affinity aggregation for spectral clustering. In: Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). IEEE Computer Society, Washington DC, USA, pp. 773–780. [Google Scholar]
- Lin Y.-Y., et al. (2011) Multiple kernel learning for dimensionality reduction. IEEE Trans. Pattern Anal. Machine Intell., 33, 1147–1160. [DOI] [PubMed] [Google Scholar]
- Monti S., et al. (2003) Consensus clustering—a resampling-based method for class discovery and visualization of gene expression microarray data. In: Machine Learning, Functional Genomics Special Issue. Kluwer Academic Publishers, Hingham, MA, USA, pp. 91–118. [Google Scholar]
- Noushmehr H., et al. (2010) Identification of a CpG island methylator phenotype that defines a distinct subgroup of glioma. Cancer Cell, 17, 510–522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patel M.A., et al. (2014) The future of glioblastoma therapy: synergism of standard of care and immunotherapy. Cancers, 6, 1953–1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rand W.M. (1971) Objective criteria for the evaluation of clustering methods. J. Am. Stat. Assoc., 66, 847–850. [Google Scholar]
- Rousseeuw P.J. (1987) Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math., 20, 53–65. [Google Scholar]
- Shen R., et al. (2009) Integrative clustering of multiple genomic data types using a joint latent variable model with application to breast and lung cancer subtype analysis. Bioinformatics, 25, 2906–2912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen R., et al. (2012) Integrative subtype discovery in glioblastoma using iCluster. PloS One, 7, :e35236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The Cancer Genome Atlas Network. (2006) The Cancer Genome Atlas. http://cancergenome.nih.gov/.
- Verhaak R.G.W., et al. (2010) Integrated genomic analysis identifies clinically relevant subtypes of glioblastoma characterized by abnormalities in PDGFRA, IDH1, EGFR, and NF1. Cancer Cell, 17, 98–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- von Luxburg U. (2007) A tutorial on spectral clustering. Stat. Comput., 17, 395–416. [Google Scholar]
- Wang B., et al. (2014) Similarity network fusion for aggregating data types on a genomic scale. Nat. Methods, 11, 333–337. [DOI] [PubMed] [Google Scholar]
- Yan S., et al. (2007) Graph embedding and extensions: a general framework for dimensionality reduction. IEEE Trans. Pattern Anal. Machine Intell., 29, 40–51. [DOI] [PubMed] [Google Scholar]