cNMA: a framework of encounter complex-based normal mode analysis to model conformational changes in protein interactions

Abstract

Motivation: It remains both a fundamental and practical challenge to understand and anticipate motions and conformational changes of proteins during their associations. Conventional normal mode analysis (NMA) based on anisotropic network model (ANM) addresses the challenge by generating normal modes reflecting intrinsic flexibility of proteins, which follows a conformational selection model for protein–protein interactions. But earlier studies have also found cases where conformational selection alone could not adequately explain conformational changes and other models have been proposed. Moreover, there is a pressing demand of constructing a much reduced but still relevant subset of protein conformational space to improve computational efficiency and accuracy in protein docking, especially for the difficult cases with significant conformational changes.

Method and results: With both conformational selection and induced fit models considered, we extend ANM to include concurrent but differentiated intra- and inter-molecular interactions and develop an encounter complex-based NMA (cNMA) framework. Theoretical analysis and empirical results over a large data set of significant conformational changes indicate that cNMA is capable of generating conformational vectors considerably better at approximating conformational changes with contributions from both intrinsic flexibility and inter-molecular interactions than conventional NMA only considering intrinsic flexibility does. The empirical results also indicate that a straightforward application of conventional NMA to an encounter complex often does not improve upon NMA for an individual protein under study and intra- and inter-molecular interactions need to be differentiated properly. Moreover, in addition to induced motions of a protein under study, the induced motions of its binding partner and the coupling between the two sets of protein motions present in a near-native encounter complex lead to the improved performance. A study to isolate and assess the sole contribution of intermolecular interactions toward improvements against conventional NMA further validates the additional benefit from induced-fit effects. Taken together, these results provide new insights into molecular mechanisms underlying protein interactions and new tools for dimensionality reduction for flexible protein docking.

Availability and implementation: Source codes are available upon request.

Contact: yshen@tamu.edu

1 Introduction

Proteins participate in many important cellular processes through interactions with proteins, nucleic acids, small molecules and so on. These interactions often occur with protein motions and unbound-to-bound conformational changes which might exist at different space scales but are often found to be directly relevant to protein functions (Bahar et al., 2010). Although it remains a fundamental challenge to fully understand and correctly anticipate these conformational changes, theoretical models describing protein–protein or protein–ligand interactions have been proposed beyond the traditional ‘key-and-lock’ model where proteins are treated rigid. In particular, the theory of conformational selection treats protein flexibility and motions as pre-existing conformational ensembles which originate from proteins’ intrinsic flexibility, whereas the theory of induced fit emphasizes an effect from the binding partner (Goh et al., 2004; Nussinov and Ma, 2012). Following the theory of conformational selection, methods such as molecular dynamics (MD) simulation (Karplus and McCammon, 2002) and normal mode analysis (NMA, Brooks and Karplus, 1985; Gibrat and Go, 1990; Harrison, 1984) have been developed to sample conformational space which reflects intrinsic flexibility and covers potential conformational changes.

NMA based on various elastic network models including anisotropic network model (ANM) and Gaussian network model (Atilgan et al., 2001) has been found to be able to quickly generate low-frequency normal modes that capture proteins’ collective motions often observed in NMR experiments or MD simulations (Doruker et al., 2000) as well as unbound-to-bound conformational changes observed in X-ray crystallography (Bakan and Bahar, 2009; Dobbins et al., 2008; Petrone and Pande, 2006). However, it is unclear how much induced-fit effects contribute to protein conformational changes along with conformational-selection effects, especially when cases have been found where conformational selection alone could not adequately explain conformational changes and induced fit was suggested to distort intrinsic flexibility-driven motions or even introduce new motions (Bakan and Bahar, 2009; Dobbins et al., 2008). Inspired by these studies, here we model protein conformational changes upon associations with the contributions of both intrinsic flexibility and intermolecular interactions. The objectives are not only to develop new insights into mechanisms of conformational changes but also to apply these insights to predicting protein complex structures starting from separate, unbound protein structures (a.k.a. ‘protein docking’). Major challenges in protein docking include the extremely high dimensionality of the space of conformational changes [a protein of n atoms has 3 n – 6 degrees of freedom (DoFs) in theory where n could easily reach thousands for a medium-sized protein] as well as the coupling among conformational variables originating from chemical bonds and non-bonded interactions (Bonvin, 2006). Better capabilities to anticipate conformational changes and reduce dimensionality, possibly with the help from both intrinsic flexibility and partner-specific inter-molecular interactions, would facilitate solving protein docking problems.

Toward the objectives described above, beyond conventional NMA of a single protein (Atilgan et al., 2001) or a straightforward application of conventional NMA to a complex formed through protein–protein interactions (Venkatraman and Ritchie, 2012), we extend ANM to include concurrent but differentiated intra-molecular and intermolecular potentials to treat protein complexes, develop a new theoretical framework of NMA based on the extended ANM, design two classes of methods to extract modes useful for approximating conformational changes and test our work over a large-scale, non-redundant benchmark set of protein conformational changes.

2 Materials and Methods

In this section, we will first give a brief description of conventional NMA based on ANM and then introduce our extended, complex-based ANM (cANM) and the corresponding new framework of NMA (cNMA) including its relationship to conventional NMA (or NMA in short), also shown in Figure 1. We will also describe two methods reflecting two ways of exploiting protein dynamics to extract normal modes and metrics to assess the capabilities of these normal modes to approximate conformational changes. Lastly, we will describe a large-scale dataset of unbound proteins, bound protein complexes and encounter complexes formed during protein–protein associations, against which empirical assessment is performed.

Fig. 1.

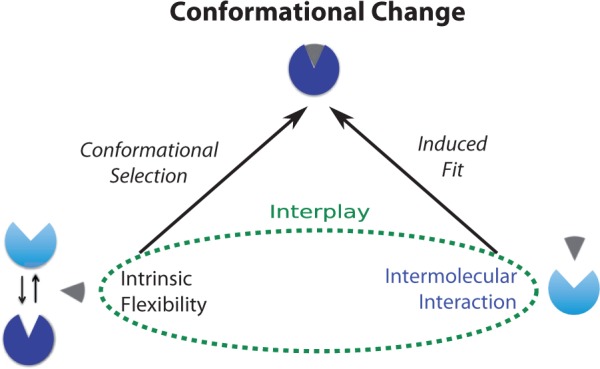
Illustrations of conventional (left arrow) and proposed (both arrows) models for conformational change. A protein illustrated in blue changes its conformation from unbound (light blue) to bound (dark blue) upon interactions with its partner (gray)

2.1 Extended ANM

NMA provides an efficient way to study the dynamics of macromolecules including proteins near an equilibrium state by harmonic approximation of the potential. It was shown that the usually sophisticated semi-empirical molecular potentials such as molecular mechanic potential could be replaced by a simple pairwise Hookean potential at the all-atom (Tirion, 1996) or even the coarse-grained level (C_α atoms only) (Hinsen, 1998) without the loss of capability to replicate low-frequency protein motions. It is noteworthy that the coarse-grained C_α-level model further reduces the dimensionality of conformational space, thus chosen in this study. Correspondingly, nodes and (C_α) atoms will be used interchangeably unless otherwise noted.

The resulting ANM (Atilgan et al., 2001; Doruker et al., 2000) describes a protein as nodes (ranging from all atoms to just C_α atoms) connected to each other through edges with a Hookean potential (or ‘springs’) if pairwise distances fall below a cutoff D:

$$U={\displaystyle \sum _{(i,j)\in N\left(P\right)}\frac{1}{2}}\gamma {(d_{ij}-d_{ij}^0)}^2$$ (1)

where γ is the intramolecular spring constant of the harmonic system and U is summed over all neighboring (i, j) pairs in protein P whose set is denoted by N(P) and depends on D.

When modeling an encounter complex formed through protein–protein associations and consisting of a receptor (R) and a ligand (L) (receptor and ligand here are only used to differentiate two proteins forming a complex and do not bear biological meanings), we introduce concurrent but differentiated intra- and inter-molecular harmonic potentials. As a stepping stone to our goal, here we introduce different parameters (spring constants and distance cutoffs to define node pairs) for the two types of potentials:

$$U\prime ={\displaystyle \sum _{(i,j)\in N\left(R\right)\cup N\left(L\right)}\frac{1}{2}}{\gamma }_1{(d_{ij}-d_{ij}^0)}^2+{\displaystyle \sum _{(i,j)\in N(R,L)}\frac{1}{2}}{\gamma }_2{(d_{ij}-d_{ij}^0)}^2$$ (2)

where N(R, L) denotes the set of intermolecular (i, j) pairs with atom i from the receptor (R) and atom j from the ligand (L). Figure 2 provides an example (PDB code: 1Y64) illustrating the difference between a conventional ANM and our new model cANM.

Fig. 2.

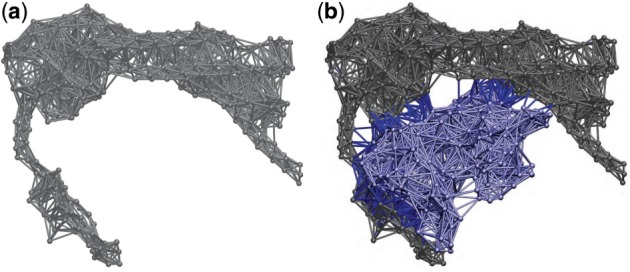
(a) Conventional ANM with intramolecular potentials only (illustrated through gray edges). (b) Complex-based ANM with both intra- (gray and slate blue edges for two individual proteins) and intermolecular potentials (dark blue edges between two proteins)

Throughout this study, the intramolecular parameters are set at default values as in the ProDy computer package (Bakan et al., 2011) (${\gamma }_1=1$ and $D_1=15$Å), whereas the intermolecular ones γ₂ and D₂ are tested at various values.

2.2 Complex-based NMA

Normal modes are the eigenvectors of the Hessian matrix of the potential. The Hessian matrix ${\mathcal{H}}^C$ of $U\prime$ in our cANM is constructed by deriving the second order partial derivatives of $U\prime$. The complex-derived Hessian matrix ${\mathcal{H}}^C$ possesses a special structure of $\left[\begin{array}{cc}{\tilde{\mathcal{H}}}^R& {\mathcal{H}}^{RL}\\ {\mathcal{H}}^{LR}& {\tilde{\mathcal{H}}}^L\end{array}\right]$, also investigated similarly in (Dasgupta et al., 2014). Specifically, ${\mathcal{H}}^C$ [a $3(m+n)\times 3(m+n)$ matrix where m and n are the number of nodes of R(eceptor) and L(igand), respectively] has two diagonal submatrices ${\tilde{\mathcal{H}}}^R$ ($3m\times 3m$) and ${\tilde{\mathcal{H}}}^L$ ($3n\times 3n$) capturing the coupled intramolecular motions of R and L, respectively. The overhead tilde for each submatrix indicates that each differs from the counterpart in conventional NMA, i.e. ${\mathcal{H}}^R$ or ${\mathcal{H}}^L$. The expressions of both submatrices are shown in Tables 1 and 2 with their differences from conventional counterparts highlighted in bold fonts and gray backgrounds. It is noteworthy that only diagonal super-elements of (3 × 3 matrices; see more details in the Appendix) ${\tilde{\mathcal{H}}}^L$ and ${\tilde{\mathcal{H}}}^R$ could differ from their conventional counterparts without consideration of intermolecular interactions. These diagonal super-elements correspond to the coupled DoFs (x, y and z in this case) for the same atom that forms intermolecular interactions and the differences capture the cumulative inter-molecular interactions this atom forms. In addition, ${\mathcal{H}}^C$ has two off-diagonal submatrices describing the couplings between motions of R and L, where ${\mathcal{H}}^{RL}\equiv {({\mathcal{H}}^{LR})}^T$. Their expressions are also given in Table 2.

Table 1.

Partial derivatives for diagonal super-elements of ${\tilde{\mathcal{H}}}^R$ or ${\tilde{\mathcal{H}}}^L$ with additional terms compared with conventional counterparts highlighted in bold fonts and gray backgrounds

Table 2.

Partial derivatives for off-diagonal super-elements of ${\tilde{\mathcal{H}}}^R$ (unchanged from those of ${\mathcal{H}}^R$), as well as those for super-elements of the off-diagonal submatrix ${\mathcal{H}}^{RL}$ newly introduced in cNMA, thus highlighted in bold fonts and gray backgrounds

2.3 Projecting ${\mathcal{H}}^C$

Eigenvectors of ${\mathcal{H}}^C$ include rigid-body motions of individual proteins because of the Eckart body frame (Eckart, 1935) imposed on the protein complex: with the external (rigid-body) motions of the entire complex separated away from its internal motions, the latter motions include internal motions of individual proteins as well as their relative external motions. And here we are interested in the internal motions of each component of a protein complex. Therefore, when applying complex-derived normal modes to model individual proteins’ conformational changes, the rigid-body motions of each protein need to be removed appropriately. This can be accomplished by projecting ${\mathcal{H}}^C$ away from the space of rigid-body motions for a protein under study via the Rayleigh–Ritz procedure (Field, 2007; Saad, 1992). The orthogonal projection procedure calculates approximate eigen pairs of a matrix so that the resulting eigenvectors lie in a subspace following the steps below:

1. Construct six basis vectors for the space of rigid-body motions

2. Orthonormalize the basis set by QR factorization: $[T_x,T_y,T_z,R_x,R_y,R_z]$ ← QR($[{\mathcal{T}}_x,{\mathcal{T}}_y,{\mathcal{T}}_z,{\mathcal{R}}_x,{\mathcal{R}}_y,{\mathcal{R}}_z]$)

3. Define projection matrix P: $P\leftarrow I-R_x{R}_x^T-R_y{R}_y^T-R_z{R}_z^T-T_x{T}_x^T-T_y{T}_y^T-T_z{T}_z^T$

4. Apply projection to the Hessian: ${{\mathcal{H}}^{\prime }}^C\leftarrow P{\mathcal{H}}^C{P}^T$

5. Calculate eigensystem of ${{\mathcal{H}}^{\prime }}^C$.

For instance, to study the internal motions of the receptor, we need to remove trivial modes representing rigid-body motions of the receptor, whereas keeping both internal and external motions of the ligand. This can be achieved by constructing first the projection matrix P^R for the receptor using the procedure above and then the projection matrix $P=\left[\begin{array}{cc}{P}^R& 0\\ 0& I\end{array}\right]$ for the entire complex. Therefore, the new Hessian after projection can be written as

(3)

Structurally, ${{\mathcal{H}}^{\prime }}^C$ contains applying the operation of P^R to ${\tilde{\mathcal{H}}}^R$ whereas keeping ${\tilde{\mathcal{H}}}^L$ unchanged on the diagonal. Consequently, ${{\mathcal{H}}^{\prime }}^C$ contains trivial modes with non-zero values only in the component (the receptor here) specific subvector.

2.4 Approaches to extract normal modes

Two approaches are used to derive normal modes useful for approximating conformational changes of individual proteins. In the first approach, we use the diagonal submatrix ${\tilde{\mathcal{H}}}^R$ or ${\tilde{\mathcal{H}}}^L$ that captures induced motions of each protein without considerations of induced motions of its binding partner or the coupling between the two sets of protein motions. The matrix is projected with the procedure described above [akin to the projection of the covariance matrix in Dasgupta et al. (2013)], and eigenvalues and eigenvectors are calculated with eigenvectors ranked with increasing eigenvalues (six eigenvectors corresponding to zero-valued eigenvalues are trivial normal modes corresponding to rigid-body motions and thus removed). In the second approach, the complex-derived Hessian matrix ${\mathcal{H}}^C$ is used for projection and eigen calculations, and the component of non-trivial normal modes corresponding to a protein under investigation is extracted. We call these two approaches submatrix and subvector correspondingly which are illustrated in Figure 3.

Fig. 3.

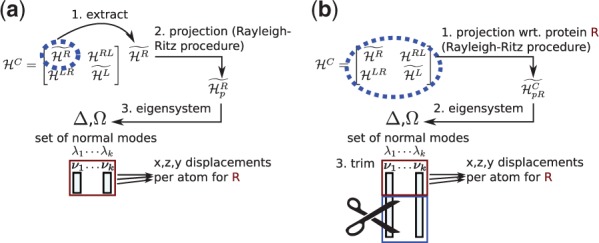
Work flow for (a) submatrix and (b) subvector approaches

2.5 Assessment measures

An unbound-to-bound conformational change can be approximated by a linear combination of the first K normal modes: $d=b-u=r+{\sum }_{j=1}^K{\beta }_j{M}_j$ where d is a vector of conformational change, u a vector representing the unbound structure, b a vector representing the bound structure, M_j the jth normal mode and r residuals of the fit. The optimal coefficients of the first K modes to minimize the magnitude of d are analytically derived as in (Moal and Bates, 2010):

$$\mathbf{\beta }={(M^{T}M)}^{-1}{M}^{T}d$$ (4)

With such an optimal approximation of conformational changes for any given set of K normal modes, the optimal root mean square deviation (RMSD) reduction R(K) is defined as

$$R(K)=1-\frac{\text{RMSD}(u+{\displaystyle \sum _{j=1}^K{\beta }_j}{M}_j,b)}{\text{RMSD}(u,b)}.$$ (5)

Based on the measure above, the average improvement of cNMA compared with the conventional NMA (or NMA in short) is defined by the average of $(\frac{R_{\text{cNMA}}(K)}{R_{\text{NMA}}(K)}-1)*100$, which gives a relative improvement of the optimal RMSD reduction averaged over all cases. And the population improvement (or net success rate) is defined as the percentage with at least 5% relative improvement subtracted by the percentage with at least 5% relative deterioration. Note that a large fraction of comparable results (with neither significant improvement nor deterioration) would penalize net success rate here. All comparisons are based on backbone atoms unless stated otherwise.

In addition, a measure of overlap, as described in Dobbins et al. (2008), is used to calculate the cosine similarity between the vector of conformational change and any given normal mode.

2.6 Test set

The Protein–Protein Docking Benchmark Version 4.0 (http://zlab.umassmed.edu/benchmark/, Hwang et al., 2010) provides a large-scale data set of protein–protein interactions giving a broad coverage of non-redundant sequences and structural folds and thus allowing extrapolation of analytic and empirical results for new, uncharacterized proteins. Specifically, it contains 176 pairs of unbound protein structures and their corresponding bound complexes. With 12 proteins removed due to identical unbound and bound structures, the rest 340 individual proteins are classified into three categories corresponding to the extent of conformational changes as well as the difficulty for protein docking. Specifically, individual proteins are classified as rigid, medium and difficult cases when their unbound-to-bound interface RMSD (iRMSD) values fall below 1 Å, between 1 Å and 2 Å and above 2 Å, respectively.

Conformational change vectors d between unbound and bound proteins are constructed by determining residue-to-residue correspondence and then least-squares fitting. Determining the correspondence is a nontrivial task because of the need for chain-to-chain correspondence for multi-chain proteins and the possible differences in atoms or residues even for corresponding pairs of chains. Therefore, the chain matching problem is formulated as the maximum weight perfect matching in a weighted bipartite graph. Specifically, the two partite sets include chains of unbound and bound structures; edge weights are defined as the average of sequence identity and sequence coverage after pairwise chain alignment. The problem is then solved using an implementation (https://pypi.python.org/pypi/munkres/) of the Kuhn–Munkres algorithm (Kuhn, 1955) (Hungarian algorithm).

Encounter complexes of protein pairs are constructed by two approaches: (i) geometrically fitting unbound proteins to their corresponding bound complex which gives an optimal scenario for rigid, unbound protein docking and (ii) rigidly docking unbound protein pairs, which does not assume any knowledge of bound complexes. For the latter approach, 10 encounter complex structures for each of the 170 protein pairs have been generated by ZDOCK as the top 10 cluster centers (with angular distances instead of RMSD as dissimilarity measure) (Vreven et al., 2013) and kindly provided by the Weng group. The number (10) of distinctive models per protein complex is chosen as it is frequently used in assessing protein docking methods and shown to be enough in most benchmark cases; but it can be adjusted larger with the increase of case difficulty. The statistics for individual components (receptors and ligands) of encounter complexes and category breakdowns are provided in Table 3.

Table 3.

Statistics of the test set

Class	Fit components	Docked components
		iRMSD < 5Å	iRMSD < 10Å	All
Difficult	113	68	253	1130
Medium	185	234	536	1850
Rigid	42	33	132	420
All	340	335	921	3400

Input data for cNMA are just an encounter complex structure consisting of the unbound structure of a protein under study and that of its binding partner. Parameters include distance cutoff and spring constant for intermolecular potentials (D₂ and γ₂, respectively). The bound structure of the protein is only needed for posterior assessment.

3 Results and discussion

In this section, two cNMA approaches (submatrix and subvector) are first compared with conventional NMA empirically for difficult cases (as in Table 3) that involve large-scale conformational changes, a major challenge to protein docking. The submatrix approach only considers induced motions of a protein under study, which involves the diagonal submatrix (${\tilde{\mathcal{H}}}^R$ or ${\tilde{\mathcal{H}}}^L$) of the Hessian matrix for the encounter complex (${{\mathcal{H}}^{\prime }}^C$). The performances of the submatrix approach prompt us to look into induced motions of a protein’s binding partner and the coupling between the two sets of induced motions and to introduce the subvector approach that indeed shows considerable improvement over conventional NMA.

Next, in an effort to isolate the contribution of intermolecular interactions to the improved results, a special case of cNMA with intermolecular potentials removed reveals an overlooked factor of order effect and inspires the development of a re-ranking strategy for the subvector approach. This scheme even improves the performances of the subvector approach and proves the isolated contribution of intermolecular interactions.

Finally, the approximating power of the cNMA modes is investigated against the quality of encounter complexes.

Throughout the section, parameter dependence and mechanistic insights are also reported.

3.1 Submatrix approach

As described in Section 2, the complex-derived Hessian matrix ${\mathcal{H}}^C$ contains diagonal submatrices ${\tilde{\mathcal{H}}}^R$ or ${\tilde{\mathcal{H}}}^L$ describing intra-molecular motions of each component protein. Compared with Hessian matrices calculated on individual proteins without considerations of binding partners (${\mathcal{H}}^R$ and ${\mathcal{H}}^L$), only diagonal 3 × 3 super-elements of these diagonal submatrices could change if the corresponding atoms form intermolecular interactions. It is intriguing that these changes are only for the coupling among the DoFs for the same atom due to its summed intermolecular interactions, which suggests perturbations to intrinsic flexibility due to interactions. We set out to explore whether these submatrices provide normal modes capable of approximating conformational changes better than conventional NMA does with the submatrix approach first.

Figure 4 shows both the average and the population improvements in approximating conformational changes when comparing the submatrix approach against conventional NMA. Here difficult cases with geometrically fit encounter complexes were considered. Both overall conformational changes (top panel) and those at the interface (bottom panel) were studied. The best initial performance was given with intermolecular parameters $D_2=10$Å and ${\gamma }_2=0.25$ (red line). The fact that both values are smaller than those of corresponding intramolecular parameters (D₁ and γ₁, respectively) is intuitively satisfying because non-bonded intermolecular interactions are often assumed to be weaker and in shorter range than intramolecular ones. Although the approach improved the average overall RMSD reduction by orders of magnitude when using the first 1 or 2 normal modes (see Fig. 4a inset), its performance was quickly outperformed by conventional NMA methods until tying it after the number of the slowest normal modes reached 40. The population measure in Figure 4b told a similar story. So were the average and population performance for interface conformational changes (Fig. 4c and d). It is noteworthy that the parameters equalizing intra- and intermolecular interactions (thick dashed line) gave the worst performance, which further proves the importance of differentiating intra- and intermolecular interactions.

Fig. 4.

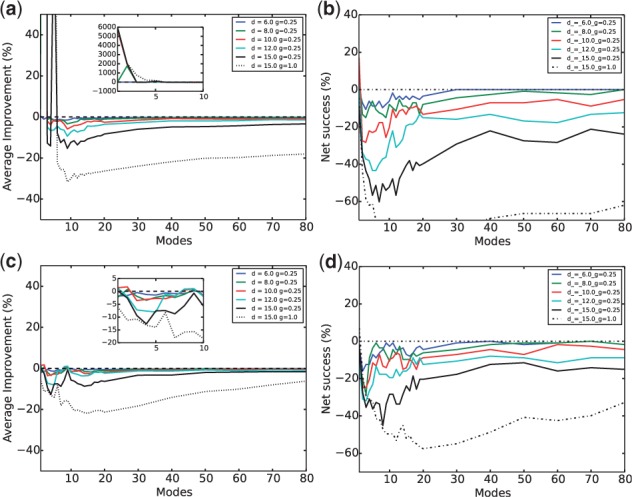
Submatrix approach for proteins in geometrically fit encounter complexes—average improvement against conventional NMA on (a) the whole protein and (c) the interface and population improvement (or net success rates) against conventional NMA on (b) the whole protein and (d) the interface. The same color code is applied here and in Figures 5, 6 and 8: blue, green, red, cyan and black solid curves correspond to $D_2=6$Å, 8 Å, 10 Å, 12 Å and 15 Å, respectively (${\gamma }_2=0.25$ in all cases) and the black dashed curve correspond to $D_2=D_1=15$Å and ${\gamma }_2={\gamma }_1=1$

Considering that these results were derived from fit complexes which were constructed with the information of bound complexes, the performance of submatrix approach was extremely unsatisfying. We also collected the results for docked complexes—apparently with many non-native interactions present in those encounter complexes its performance was even worse (results not shown). This prompted us to propose the subvector approach which looked beyond submatrices and whose results will be reported next.

3.2 Subvector approach

Although submatrix ${\tilde{\mathcal{H}}}^R$ or ${\tilde{\mathcal{H}}}^L$ contains additional information on intermolecular interactions, thus perturbing couplings between DoFs for the same atom, the other diagonal submatrix corresponding to the binding partner as well as the off-diagonal submatrices for coupling between the two proteins were not considered. In contrast, the subvector approach considers not only the induced motions of a protein under study but also those of its binding partner as well as the coupling between the two sets of motions.

Considerable amounts of average and population improvements against conventional NMA using the subvector approach are observed in Figure 5. Again, geometrically fit encounter complexes were used here. First, it is intriguing that the parameters with the best performances (cyan line) still correspond to a small spring constant ${\gamma }_2=0.25$ but a slightly higher distance cutoff $D_2=12$Å for intermolecular interactions (although it is still smaller than the intramolecular distance cutoff $D_1=15$Å). Also, although a $D_2=12$Å (cyan line) gave slightly better initial results between the first 10–20 normal modes, it was then surpassed by $D_2=15$Å (black solid line). These data suggest that although intermolecular interactions, being non-bonded, could act in shorter space scales than intramolecular interactions, considerations of inter-molecular interactions beyond the first layer (typically considered within $6$Å) are still needed for modeling protein–protein interactions. In contrast, a straightforward application of conventional NMA to a protein complex without differentiating intra- and inter-molecular interactions (thick dashed line) produced results far from optimal. From the first 20 normal modes on, our approach improved on average RMSD reduction for both overall and interface conformational changes by around 10%. Considering that the average performance could be misleading with significant outliers, we also looked at the population statistics in Figure 5b and d. With a ± 5% cutoff of improvement or deterioration to define success versus failure, our net success rate (success rate minus failure rate) impressively reached above 30% for the overall and nearly 20% for the interface conformational changes.

Fig. 5.

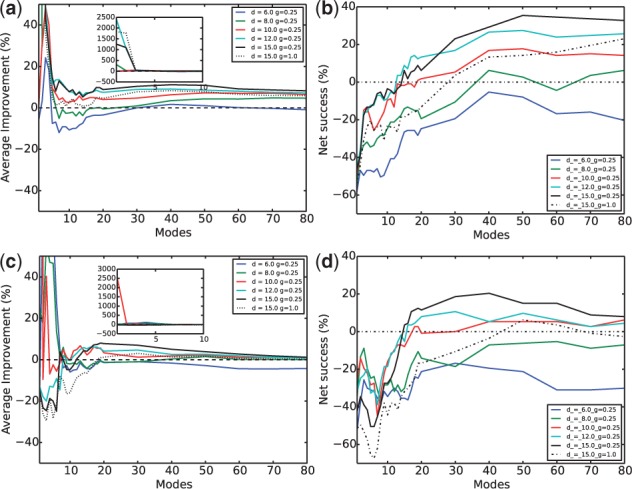
Subvector approach for proteins in geometrically fit encounter complexes—average improvement against conventional NMA on (a) the whole protein and (c) the interface and net success rates against conventional NMA on (b) the whole protein and (d) the interface

Even for the rigidly docked encounter complexes with iRMSD below 10 Å (which is a very loose definition of near-native encounter complexes in the field of protein docking), the same optimal parameter sets (corresponding to cyan and black lines) were found (Fig. 6), indicating that the trends in parameters in the subvector approach were not sensitive to the choice of encounter complexes. More importantly, significant improvements over conventional NMA were still present. The best improvement over average RMSD reduction with the first 30 normal modes was almost 20% for the overall protein and 10% for the interface. The best net success rate was over 40% for the overall and nearly 20% for the interface with the first 30 normal modes. Interestingly, the improvement against conventional NMA in the more realistic case of the docked complexes was even higher than that in the case of fit complexes.

Fig. 6.

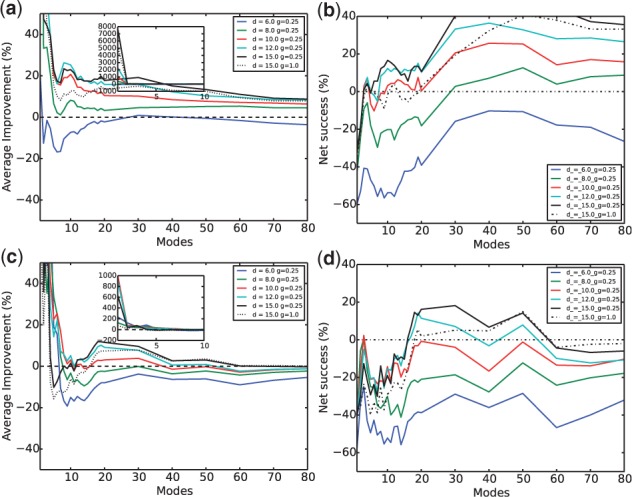
Subvector approach for proteins in rigidly docked encounter complexes—average improvement against conventional NMA on (a) the whole protein and (c) the interface, and net success rates against conventional NMA on (b) the whole protein and (d) the interface

So far, the subvector approach has produced a set of conformational vectors which better and consistently explained conformational changes of difficult proteins by considering induced motions of both binding partners and their couplings in an encounter complex. These results provided additional support to both mechanisms of conformational selection and induced fit. Next, to single out the effects of intermolecular interactions in our approach and evaluate their contributions alone, we proceed to investigate in depth the changes from the conventional NMA to our cNMA with a subvector approach and propose a modification of the subvector method next.

3.3 Order effect

A special case of ${\mathcal{H}}^C$ can be made by creating ${\mathcal{H}}^{C_0}$, a complex-based Hessian without intermolecular interactions as ${\mathcal{H}}^{C_0}=\left[\begin{array}{cc}{\mathcal{H}}^R& 0\\ 0& {\mathcal{H}}^L\end{array}\right]$. Such a block-diagonal matrix essentially contains the unchanged Hessian of the receptor and ligand proteins, the off-diagonal matrices being zero matrices. In such a system, the eigenvalues λ_i of ${\mathcal{H}}^{C_0}$ are the union of the eigenvalues of ${\mathcal{H}}^R$ and ${\mathcal{H}}^L$ (${\lambda }_i^R$ and ${\lambda }_i^L$, respectively). The associated eigenvectors ${\mathit{\mu }}_i^R$ and ${\mathit{\mu }}_i^L$ are also preserved, now being subvectors of eigenvector ${\mathit{\mu }}_i$ of ${\mathcal{H}}^{C_0}$ and having zero elements appended to fill the dimensions corresponding to their binding partners. The eigensystem contains 12 zero-valued eigenvalues, corresponding to the six DoFs for each protein. Applying the projection matrix P from Section 2.3 to ${\mathcal{H}}^{C_0}$ leads to

$${{\mathcal{H}}^{\prime }}^{C_0}=P{\mathcal{H}}^{C_0}{P}^T=\left[\begin{array}{cc}{P}^R{\mathcal{H}}^R{(P^R)}^T& 0\\ 0& {\mathcal{H}}^L\end{array}\right]$$ (6)

Empirically, in our experiments, the resulting matrix ${{\mathcal{H}}^{\prime }}^{C_0}$ after projection was equal to ${\mathcal{H}}^{C_0}$.

In protein docking, deformation directions are often explored along low-frequency normal modes of both component proteins, for instance, alternating between ligand and receptor low-frequency normal modes. However, applying the subvector approach to ${\mathcal{H}}^{C_0}$ does not replicate the alternating strategy. The reason is that the normal modes of component proteins appended with zero elements are now reshuffled in an order corresponding to the mixed and re-sorted eigenvalues from ${\mathcal{H}}^R$ and ${\mathcal{H}}^L$, even though the order among normal modes containing subvectors for the same protein maintains. Figure 7 shows this order effect for the first six slowest modes of ${\mathcal{H}}^{C_0}$ for a random subset of complexes from the test set. It is apparent that the first few normal modes are often not a uniform mixture of those originated from both component proteins, which might originate from their differences in size, shape and flexibility. Examples here include that protein complex 2OT3 had its first six modes solely coming from the receptor component, whereas the complex 2UUY displayed only ligand modes in the first six.

Fig. 7.

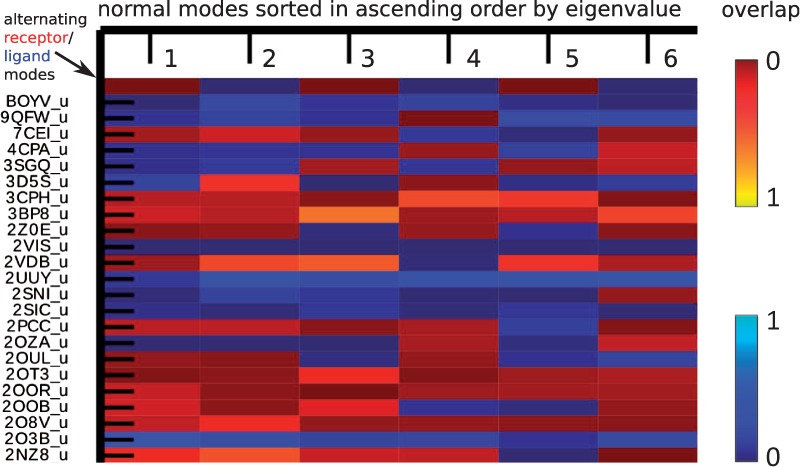
Normal mode spectrum. Each complex-derived mode is shown in a row, with a blue color indicating its origin being the ligand and red the origin being the receptor. The brightness reflects the amount of overlap between this particular mode and the conformational change. Only a subset of protein complexes and their first six non-trivial modes are shown here

3.4 Component-specific re-ranking of complex-based normal modes

A strategy with the goal to dampen the order effect, denoted as λ^R, performs re-ranking of eigenvalues λ_i and corresponding eigenvectors ${\mathit{\mu }}_i$ by re-scaling the eigenvalues with component-specific contributions:

$${\lambda }_i^R=\frac{{\lambda }_i}{\left|\right|{\mathit{\mu }}_i^R|{|}^2}$$ (7)

where ${\mathit{\mu }}_i^R$ is a component-specific subvector of ${\mathit{\mu }}_i$. Through the λ^R re-ranking, normal modes with a relatively small amount of directional contribution to the protein under study get demoted in rank. It does not, per se, imply that complex-based modes with higher magnitudes of corresponding components are indeed more valuable for approximating protein conformational changes. Rather, by re-ranking with λ^R, the re-ordered normal modes can now assess the sole contribution from intermolecular interactions. In particular, if there are no intermolecular interactions present (the case of ${\mathcal{H}}^{C_0}$), this approach produces the exact same set of normal modes in the same order for individual proteins as conventional NMA does.

This re-ordering is invariant to the application of external motions to the system, when for instance superposing unbound and bound proteins (or interfaces). Translations of the system leave both λ_i and ${\mathit{\mu }}_i$ unchanged and rotations change the three-dimensional sub-elements of ${\mathit{\mu }}_i$ by definition in a way that each magnitude is unchanged.

We will next assess normal modes produced by this approach for ${{\mathcal{H}}^{\prime }}^C$ where inter-molecular interactions are present (as opposed to ${{\mathcal{H}}^{\prime }}^{C_0}$).

3.5 Subvector approach with re-ranking to assess the sole contribution of intermolecular interactions

The subvector approach with λ^R re-ranking was applied to the difficult case again, with Figure 8 showing the results calculated using geometrically fit encounter complexes. The optimal parameter set for the subvector approach without re-ranking was still found to give one of the best results (cyan lines) here. This approach produced slightly improved average RMSD reduction compared with the conventional NMA for both overall and interface conformational changes. Moreover, it led to over 15% net success rate for overall and about 20% for interface conformational changes. Similar results (not shown here) can be found for near-native encounter complexes constructed from rigid docking. It is potentially useful for practical purposes that the parameter sensitivity with a λ^R re-ranking is lower than that without re-ranking, which was particularly visible in the curves for net success rates.

Fig. 8.

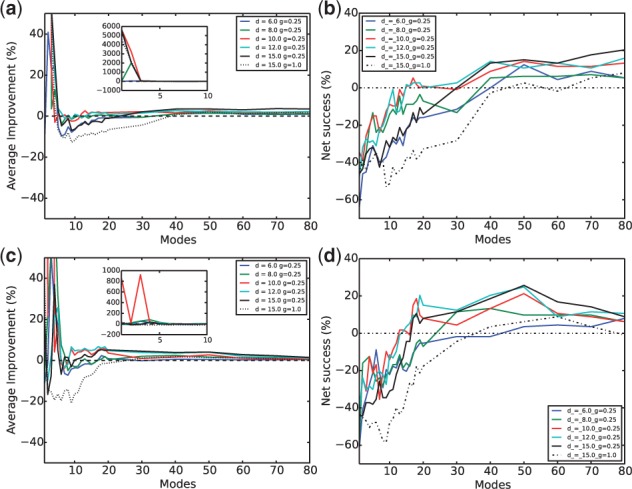
Subvector approach with re-ranking for proteins in geometrically fit encounter complexes—average improvement against conventional NMA on (a) the whole protein and (c) the interface, and net success rates against conventional NMA on (b) the whole protein and (d) the interface

An intriguing fact is that lower D₂ here improved performances compared with the same parameter values in subvector approach without re-ranking (one example is that the blue curves for $D_2=6$ Å here had much better performances than they did in Fig. 5). An explanation can be given through the order effect and interaction effect in tandem. Since the order effect gives rise to modes mainly explaining the collective motions of a counterpart protein in the lower eigenvalue spectrum, subvector approach with a smaller D₂ can possess modes not as relevant to the conformational change among low-frequency modes. In contrast, with a lower D₂, the subvector approach with λ^R re-ranking promoted modes that contain a significant amount of motions for the protein under study and many of such motions were empirically found to be relevant to conformational changes, which is exemplified and visible in Figure 9a ($D_2=15$ Å and ${\gamma }_2=0.25$ without particular optimization). It can be observed that, after the λ^R re-ranking, the slower modes (sorted from afar to near on the y-axis) may have a relatively low level of promotion (indicated by small negative values on the z-axis) compared with some higher-frequency ones toward the near end but many of those slower modes had good resemblance to actual conformational changes.

Fig. 9.

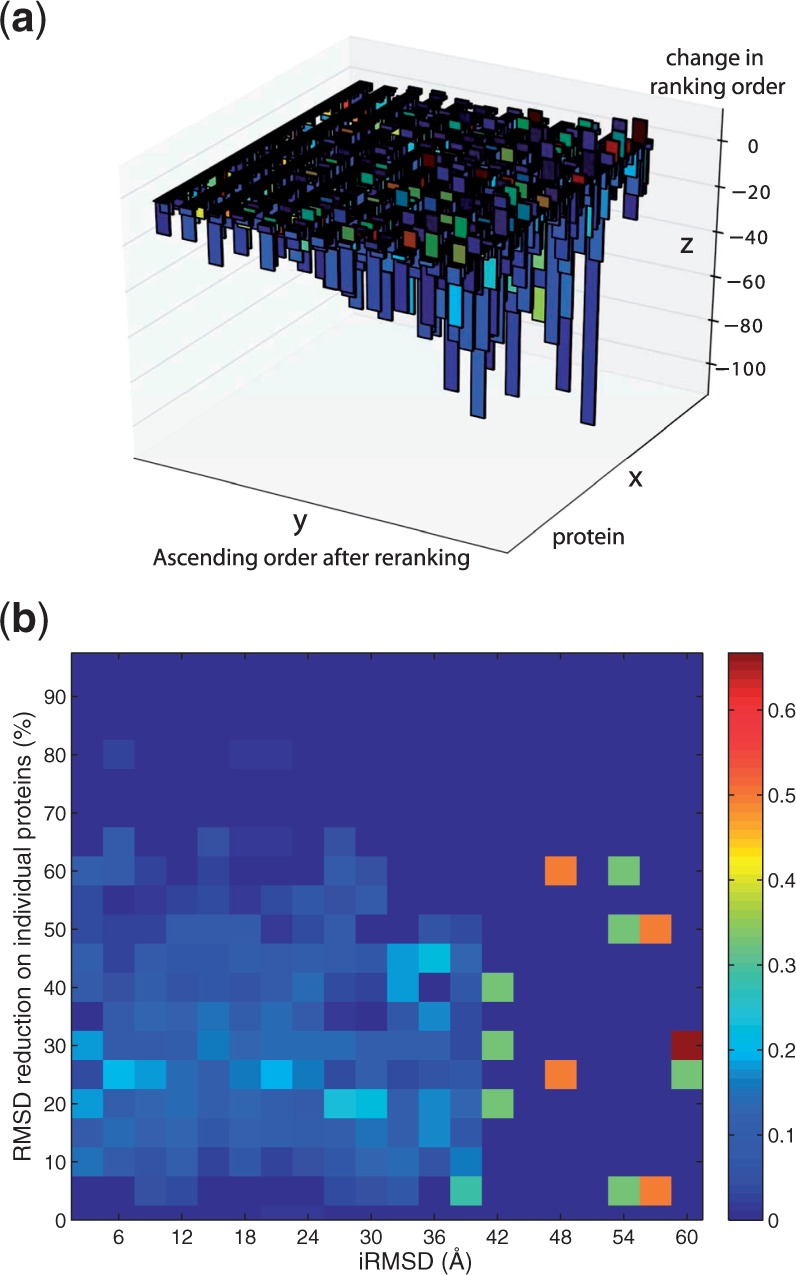
(a) The order of slowest modes after re-ranking is given on the y-axis from afar to near for each protein on the x-axis, with the change in ranking order shown on the z-axis (negative values indicate a promotion in the order of the eigenvector after re-ranking and positive ones indicate a demotion). The colors indicated the overlaps between any given mode and the corresponding actual conformational changes, warmer colors representing higher overlaps. (b) The relationship between the power of cNMA to approximate conformational changes and the quality of encounter complexes as input. Colors in each block represent the conditional probability of RMSD reduction (y-axis) given certain range of iRMSD (x-axis) of docked encounter complexes compared with bound complexes. Calculations were performed using the subvector approach with $D_2=15$Å and ${\gamma }_2=0.25$ at the first 20 modes (these parameters were not particularly optimized)

3.6 Reduction power versus model quality

For the real-world application of protein docking, an important question is how the model quality of an encounter complex (as measured by an interface RMSD value from the bound complex) affects the approximation power of cNMA modes (as measured by the optimal RMSD reduction defined earlier). Figure 9b shows the relationship between the two derived using the subvector approach with the first 20 normal modes. Without counting the statistically insignificant samples with iRMSD > 50 Å, one can observe a clear trend that high level of approximation power (RMSD reduction above 50%) only comes with models of relatively good quality (iRMSD < 30 Å) even though a good-quality model of encounter complex could still lead to large variation in approximation power. We note that iRMSD < 30 Å represents an even larger range than what is typically considered ‘near-native’ hits in protein docking.

4 Conclusion

To decipher and anticipate protein conformational changes, we extended ANM to include concurrent but differentiated intra- and inter-molecular potentials, developed a new framework of complex-based NMA (cNMA) to analyze protein flexibility in the environment of encounter complexes and tested two ways of extracting useful normal modes against a large-scale, nonredundant set of protein conformational changes. It was found important to differentiate intra- and inter-molecular interactions in the model. In particular, parameters defining shorter range (D₂) (but preferably beyond the first-layer interactions) or less strength (γ₂) for intermolecular interactions improved the performance of approximating conformational changes. Apparently, a straightforward application of conventional NMA to an encounter complex does not necessarily improve upon conventional NMA for proteins under study.

Our study provides additional support to both mechanisms of conformational selection and induced fit for protein–protein interactions and calls for more generalized theoretical models [candidates include population shifts (Kumar et al., 2000)]. With contributions from both intrinsic flexibility and intermolecular interactions, our new modeling and analysis framework, cNMA, produced modes better at approximating significant conformational changes than conventional, intrinsic flexibility-driven NMA did. Interestingly, the subvector approach outperformed the submatrix approach thanks to the incorporation of both induced motions of the protein under study and those of its binding partner as well as the couplings between the two sets of motions. The sole contribution of intermolecular interactions toward performance improvement was further dissected and validated with a re-ranking scheme applied to the subvector approach.

Our study also provides new tools for dimensionality reduction of conformational space in flexible protein docking. A successful protein docking method often involves the following critical components that affect each other: reduced and essential representation of conformational space, accurate energy function capable of discriminating native from non-native conformations and effective conformational search or sampling strategy. cNMA focuses on improving conformational representation thus is assessed in a critical way using optimal combination of its modes to isolate this component. In practice, any efficient search strategy under the guidance of a well discriminatory energy function can be applied in the reduced conformational space spanned by cNMA modes to determine weights (or coefficients) for individual modes and to improve protein docking results.

Appendix

${\tilde{\mathcal{H}}}^R$ for R with m nodes consists of m 3 × 3 super elements (each corresponding to one of m nodes or C_α atoms here), i.e.

$${\tilde{\mathcal{H}}}^R=\left[\begin{array}{cccc}{\tilde{\mathcal{H}}}_{11}& {\tilde{\mathcal{H}}}_{12}& \cdots & {\tilde{\mathcal{H}}}_{1m}\\ {\tilde{\mathcal{H}}}_{21}& \ddots & & {\tilde{\mathcal{H}}}_{2m}\\ ⋮& & \ddots & ⋮\\ {\tilde{\mathcal{H}}}_{m1}& \cdots & \cdots & {\tilde{\mathcal{H}}}_{mm}\end{array}\right].$$

Each diagonal super-element contains second order partial derivatives along 3 DoFs (x, y and z here) of an atom (say i), i.e.

$${\tilde{\mathcal{H}}}_{ii}^R=\left[\begin{array}{ccc}\frac{{\partial }^{2}U\prime }{\partial x_i^2}& \frac{{\partial }^{2}U\prime }{\partial x_i\partial y_i}& \frac{{\partial }^{2}U\prime }{\partial x_i\partial z_i}\\ \frac{{\partial }^{2}U\prime }{\partial y_i\partial x_i}& \frac{{\partial }^{2}U\prime }{\partial y_i^2}& \frac{{\partial }^{2}U\prime }{\partial y_i\partial z_i}\\ \frac{{\partial }^{2}U\prime }{\partial z_i\partial x_i}& \frac{{\partial }^{2}U\prime }{\partial z_i\partial y_i}& \frac{{\partial }^{2}U\prime }{\partial z_i^2}\end{array}\right].$$

Each off-diagonal super-element contains second order partial derivatives along DoFs of a pair of atoms (say i and j), i.e.

$${\tilde{\mathcal{H}}}_{ij}^R=\left[\begin{array}{ccc}\frac{{\partial }^{2}U\prime }{\partial x_i\partial x_j}& \frac{{\partial }^{2}U\prime }{\partial x_i\partial y_j}& \frac{{\partial }^{2}U\prime }{\partial x_i\partial z_j}\\ \frac{{\partial }^{2}U\prime }{\partial y_i\partial x_j}& \frac{{\partial }^{2}U\prime }{\partial y_i\partial y_j}& \frac{{\partial }^{2}U\prime }{\partial y_i\partial z_j}\\ \frac{{\partial }^{2}U\prime }{\partial z_i\partial x_j}& \frac{{\partial }^{2}U\prime }{\partial z_i\partial y_j}& \frac{{\partial }^{2}U\prime }{\partial z_i\partial z_j}\end{array}\right].$$

The structures of super-elements in ${\tilde{\mathcal{H}}}^L$ for L are similar to those described above.

The expressions of partial derivatives are given in Tables 1 and 2. Terms different from counterparts of ${\mathcal{H}}^R$ or ${\mathcal{H}}^L$ in conventional NMA are highlighted in bold fonts and gray backgrounds. Note that the expressions are before setting $d_{ij}$ at equilibrium distance $d_{ij}^0$ and those reported in Atilgan et al., (2001) can be regarded as a special case where no intermolecular potentials are present and $d_{ij}=d_{ij}^0$.