Metabolome-scale de novo pathway reconstruction using regioisomer-sensitive graph alignments

Abstract

Motivation: Recent advances in mass spectrometry and related metabolomics technologies have enabled the rapid and comprehensive analysis of numerous metabolites. However, biosynthetic and biodegradation pathways are only known for a small portion of metabolites, with most metabolic pathways remaining uncharacterized.

Results: In this study, we developed a novel method for supervised de novo metabolic pathway reconstruction with an improved graph alignment-based approach in the reaction-filling framework. We proposed a novel chemical graph alignment algorithm, which we called PACHA (Pairwise Chemical Aligner), to detect the regioisomer-sensitive connectivities between the aligned substructures of two compounds. Unlike other existing graph alignment methods, PACHA can efficiently detect only one common subgraph between two compounds. Our results show that the proposed method outperforms previous descriptor-based methods or existing graph alignment-based methods in the enzymatic reaction-likeness prediction for isomer-enriched reactions. It is also useful for reaction annotation that assigns potential reaction characteristics such as EC (Enzyme Commission) numbers and PIERO (Enzymatic Reaction Ontology for Partial Information) terms to substrate–product pairs. Finally, we conducted a comprehensive enzymatic reaction-likeness prediction for all possible uncharacterized compound pairs, suggesting potential metabolic pathways for newly predicted substrate–product pairs.

Contact: maskot@bio.titech.ac.jp

1 Introduction

Understanding cell metabolism is essential in a wide range of fields, e.g. metabolic engineering, synthetic biology, drug discovery and clinical treatments of metabolic disorders (Toya and Shimizu, 2013; Newman and Cragg, 2012; Ramautar et al., 2013). Recent advances in mass spectrometry and related metabolomics technologies have enabled the rapid and comprehensive analysis of numerous metabolites. However, biosynthetic and biodegradation pathways are only known for a small portion of metabolites, with the majority of pathways remaining uncharacterized (Sreekumar et al., 2009). For example, it is estimated that at least 1 060 000 metabolites are produced within all plants, for which most chemical transformations remain to be identified (Afendi et al., 2012). Elucidation of potential metabolic pathways in plants would provide a significant benefit for environmental, agricultural, pharmaceutical and public health matters. Experimental determination of metabolic pathways is difficult, expensive and time consuming (Nakabayashi and Saito, 2013); thus automatic pathway reconstruction on a metabolome scale is a challenging issue in current computational biology.

The traditional in silico method for metabolic pathway reconstruction is the predefined pathway approach, where enzyme-coding genes are mapped onto appropriate positions in the predefined pathway diagrams based on gene-gene sequence similarities (Bono et al., 1998). This method has been used for analyzing metabolic pathways in fully sequenced organisms or in specific conditions of cellular processes (Kanehisa et al., 2014). Another method in the predefined pathway approach is to consider chemical structures for finding pathways that conserve atoms from start to the target compounds in predefined pathway diagrams (Boyer and Viari, 2003; Heath et al., 2010). However, these methods are not applicable to the identification of previously unknown pathways (absent from predefined pathway maps).

Conversely, various de novo pathway reconstruction methods have been developed to elucidate novel reactions based on metabolite chemical structures, known enzymatic reactions and possible chemical transformations. The overall problem resembles that of synthetic organic chemistry (Faulon and Sault, 2001), but few studies have tackled this problem for enzymatic reactions. Previously developed de novo methods can be categorized into either the compound-filling framework (Darvas, 1988; Ellis et al., 2008; Greene et al., 1999; Moriya et al., 2010; Talafous et al., 1994) or the reaction-filling framework (Hatzimanikatis et al., 2005; Nakamura et al., 2012; Tanaka et al., 2009). However, previous methods in both frameworks are not applicable to metabolome-scale compound sets because of prohibitive computational burden.

Recently, de novo pathway reconstruction in the reaction-filling framework has been formulated as a problem of enzymatic reaction-likeness, and an efficient supervised method has been proposed to predict whether the given pairs of metabolites can be chemically interconverted by single enzymatic reactions (Kotera et al., 2013b). With this method, the use of chemical descriptors—binary/integer vectors representing compound chemical characteristics (e.g. chemical substructures) (Steinbeck et al., 2003)—is key for computational efficiency, which enables metabolome-scale application for tens of thousands of metabolites at a time. However, chemical descriptors cannot handle connectivities among substructures in a compound; thus, in theory, it is difficult to distinguish regioisomers (positional isomers), resulting in many false positive predictions in practice. Regioisomers are a group of compounds with the same compositional formula (numbers of respective elements) but are different in connectivity among the substructures. Proper distinction of isomers is required for appropriate interpretation of metabolome data (Mitchell et al., 2014). Thus, there is a strong need to develop an efficient approach that can deal with regioisomers, thus strengthening the de novo pathway reconstruction study.

In this study, we developed a novel method for supervised de novo metabolic pathway reconstruction with an improved graph alignment-based approach in the reaction-filling framework. We propose a novel chemical graph alignment algorithm, which we called PACHA (Pairwise Chemical Aligner), in order to detect regioisomer-sensitive connectivities between the aligned substructures of two compounds. Unlike other existing graph alignment methods [such as SIMCOMP (Hattori et al., 2003)], PACHA can efficiently detect only one common subgraph between two compounds. Our results show that the proposed method outperforms previous descriptor-based methods or existing graph alignment-based methods in the enzymatic reaction-likeness prediction for isomer-enriched reactions. It is also useful for reaction annotation that assigns potential reaction characteristics such as EC (Enzyme Commission) numbers (McDonald and Tipton, 2014) and PIERO (Enzymatic Reaction Ontology for Partial Information) terms (Kotera et al., 2014) to substrate–product pairs. Finally, we conducted a comprehensive enzymatic reaction-likeness prediction for all possible uncharacterized compound pairs, suggesting potential metabolic pathways for newly predicted substrate–product pairs.

2 Materials

2.1 Chemical structures of compounds

Chemical structures of metabolic compounds were retrieved from the KEGG LIGAND database (Kanehisa et al., 2014). MDL molfiles, which are the de facto standard of chemical structure format files, were converted to the KEGG Chemical Function (KCF) format (Hattori et al., 2003). In KCF, atoms (with the exception of hydrogen atoms) and bonds were represented as vertices and edges, respectively. Each vertex was given three labels representing the different levels of physicochemical properties, e.g. ‘C’ for a carbon atom, ‘C1’ for an sp3 carbon and ‘C1a’ for a methyl carbon (CH₃-). Hydrogen atoms were not explicitly represented as vertices but were implicitly represented in the attached atoms (see http://www.genome.jp/kegg/reaction/KCF.html). In this study, the one-letter label (e.g. C), two-letter label (e.g. C1) and three-letter label (e.g. C1a) were referred to as the primary, secondary and tertiary labels, respectively.

2.2 Substrate–product pair datasets

Substrate–product relationships were retrieved from KEGG RPAIR and used as the positive examples of enzymatic reaction likeness. Different reaction directions were dealt as different pairs (e.g. ‘L-Arginine - L-Ornithine’ and ‘L-Ornithine - L-Arginine’) in order to not miss the similarity between the forward direction of a reaction and the reverse of another reaction.

Known substrate–product pairs were regarded as positive examples, whereas the remaining compound pairs were regarded as negative examples. To a certain extent, substrate–product pairs share common structures, therefore, chemical similarity is one of the efficient measures to distinguish positive and negative examples. In this study, we focused on dealing with similar pairs (Jaccard coefficient > 0.5), which are more difficult and realistic condition. The numbers of positive examples and negative examples are 10 852 and 518 854, respectively, which is referred to as the ‘all’ dataset.

From the all dataset, the positive and negative pairs were grouped by the same compositional formulas (i.e. the compound on one side of a pair is a regioisomer of the compound on the same side of another pair). The groups were then removed if there were less than four positive or negative pairs within a group. The set of the remaining compound pairs was referred to as the ‘isomer-enriched’ dataset. The numbers of positives and negatives in the isomer-enriched dataset were 1632 and 53 046, respectively. Note that the isomer-enriched dataset is more difficult than the ‘all’ dataset in terms of enzymatic reaction-likeness prediction because of the issue of regioisomers.

2.3 Chemical descriptors

Chemical structures of compounds were represented by high-dimensional chemical descriptors, which are the binary/integer vectors representing the chemical structural characteristics of metabolites. We tested CDK Extended fingerprint, CDK GraphOnly fingerprint, CDK Hybridization fingerprint (Steinbeck et al., 2003), EState fingerprint (Hall and Kier, 1995), KlekotaRoth fingerprint (Klekota and Roth, 2008), MACCS fingerprint (Durant et al., 2002), PubChem fingerprint (Chen et al., 2009), the atomic environment (AE) descriptor (Nakamura et al., 2012) and KCF-S descriptor (Kotera et al., 2013a). For example, KCF-S descriptors represent the number of biochemical substructures, e.g. methyl, n-butyl, benzene and adenine residue. AE and KCF-S descriptors were calculated by our in-house program, whereas the other descriptors were generated using the Chemistry Development Kit (Steinbeck et al., 2003).

2.4 Manually curated reaction annotations

EC numbers and PIERO terms were retrieved from KEGG and GenomeNet, respectively. EC numbers represent the hierarchical enzyme classification based on the full reaction equation (McDonald and Tipton, 2014). EC sub-subclasses (upto the third digit of the EC numbers) were used as the reaction annotation by EC. PIERO is a collection of terminology annotating substrate–product relationships in enzymatic reactions (Kotera et al., 2014).

3 Methods

3.1 Chemical graph alignment problem

We address the problem of chemical graph alignment using a simple example. Figure 1 shows two compounds of n-butylamine (compound A) and methyl-n-propylamine (compound B) that are regioisomers (positional isomers). Figure 1(a) shows the atom–atom mapping by the chemical graph alignment of the two compounds, which detects the preserved substructure in a putative reaction and the changed chemical bonds. In this example, four vertices are preserved, two of which changed labels; an edge labeled ‘C1a-C1b’ is eliminated and an edge labeled ‘C1a-N1b’ is generated. To characterize reactions and distinguish regioisomers, it is crucial to detect type of bond that has changed and the position where it has changed.

Fig. 1.

(a) Graph alignment-based vector proposed in this study. Graph alignment yields atom–atom mapping (represented by dashed lines). Subsequently, the number of atom–atom pairs in the alignment (e.g. the column labeled ‘a:C1a = C1a’ in the white boxes on the left), the number of eliminated bonds (e.g. the column labeled ‘e:C1a-C1b’ in the gray boxes in the middle) and the number of generated bonds (e.g. column labeled ‘g:C1a-N1b’ in the gray boxes on the right) were represented as a vector. The symbols ‘=’ and ‘−’ represent the atom–atom mapping and the chemical bond, respectively. (b) Descriptor-based vectors in the previous studies (e.g. KCF-S). Each compound vector represents chemical characteristics (e.g. number of substructures). The feature vector for the compound pair consists of three parts: common features between the two compounds (in the white boxes on the left), excess number of features in the left compound (in the gray boxes in the middle) and right compound (in the gray boxes on the right)

Since the two compounds are regioisomers, no differences would be detected by counting the elements (C, H and N). Figure 1(b) shows a feature vector representation of the compound pairs, such as, using KCF-S descriptors representing the number of substructures, e.g. methyl (C1a-), ethyl (C1a-C1b-) and n-propyl (C1a-C1b-C1b-), etc. The feature vector detects preserved (common) and changed (decreased and increased) chemical characteristics. However, the descriptor-based feature vector does not necessarily reflect the exact chemical changes that actually occur in the reaction. For example, although the feature vector indicates that vertex C1a is preserved in two compounds, the C1a vertices do not form an atom–atom pair in the graph alignment. Thus, it is very difficult for descriptor-based methods to capture the chemically important characteristics of reactions.

In this study, we propose a novel method for chemical graph alignment that can handle the issue of regioisomers and show the potential of the proposed method for applications to the enzymatic reaction likeness prediction and reaction annotation on a metabolome-scale. The details of the proposed method are explained below.

3.2 Pairwise chemical aligner (PACHA)

We propose a novel, efficient algorithm named PACHA for chemical graph alignments. We represent each compound chemical structure G by a labeled graph defined as $G=(V,E,L)$, where V is the set of vertices (i.e. atoms in this study), E is the set of undirected edges (i.e. bonds in this study) and $L:V\to \Sigma$ is a function that assigns labels from an alphabet Σ to vertices (i.e. primary, secondary or tertiary labels in this study). Let $s:V\times V\to \mathcal{R}$ be a similarity function between a vertex pair (i.e. an atom–atom pair in this study) and returns $-\infty$ if the vertex pair is unmatched. The function s will be detailed in the next subsection.

Suppose we are given two chemical graphs $G=(V,E,L)$ and $G\prime =(V\prime ,E\prime ,L\prime )$. We formulate the graph alignment as the problem of finding a set of matching vertex pairs $M\subseteq V\times V\prime$ that maximizes the summation of vertex similarities $s(v,v\prime )$ for $(v,v\prime )\in M$ as follows:

$$\underset{M\subseteq V\times V\prime }{\max }{\displaystyle \sum _{(v,v\prime )\in M}s}(v,v\prime ),$$ (1)

under the following two constraints:

1. If $(v,v\prime )\in M$, then $(v,z)\notin M$ for all $z\in V\prime$ and $(z,v\prime )\notin M$ for all $z\in V$, i.e. a vertex in V can be matched to at most one vertex in $V\prime$.

2. The matching vertices in M of G (respectively, $G\prime$) and edges $E\prime$ (respectively, $E\prime$) form connected subgraphs, i.e. there is a pass from any vertex to the other vertices in G (respectively, $G\prime$).

Note that constraint (ii) is absent from existing graph alignment methods such as SIMCOMP (Hattori et al., 2003), which causes the generation of many (possibly small) subgraph matches, thus preventing the sensitive detection of regioisomers.

Because computing the exact solution for the graph alignment is intractable, we solved it using a greedy strategy. To efficiently select vertex pairs with the highest similarity in order, we propose to use the priority queue PQUEUE that stores vertex pairs $(v,v\prime )\in V\times V\prime$ and their similarities $S(v,v\prime )$. PQUEUE supports the following operations:

• Insert: insert a vertex pair $(v,v\prime )\in V\times V^{\prime }$ and its similarity $s(v,v\prime )$ into PQUEUE.

• Get: get the vertex pair $(v,v\prime )$ with the highest similarity in PQUEUE.

• Pop: delete the vertex pair $(v,v\prime )$ with the highest similarity from PQUEUE.

We propose the following algorithm. We initialize PQUEUE as a vertex pair $(v,v\prime )\in V\times V\prime$ with the highest similarity and its similarity $s(v,v\prime )$. The algorithm iterates as follows. We first get the vertex pair $(v,v\prime )$ with the highest similarity in PQUEUE and delete it from PQUEUE. We then insert the vertex pair $(v,v\prime )$ into a set M^c. Let N(v) be a set of vertices adjacent to $v\in V$. We next insert all combinations of vertex pairs adjacent to v and $v\prime$, i.e. $(x,x\prime )\in N(v)\times N(v\prime )$, into PQUEUE, which is necessary to satisfy constraint (ii) in the graph alignment. Considering constraint (i), we insert only vertex pairs $(x,x\prime )\in N(v)\times N(v\prime )$ into PQUEUE such that $(x,z)\notin M^c$ for all $z\in V\prime$ and $(z,x\prime )\notin M^c$ for all $z\in V$. When PQUEUE is empty, the algorithm stops. For accurate alignments, the algorithm restarts from each vertex pair chosen among those with top-k highest similarities, where k is a user defined parameter; k is set to 10 in this study. The algorithm finally returns the set of vertex pairs with the highest summation of similarities in M^c. The pseudocode of the algorithm is presented in Algorithm 1.

Algorithm 1 Chemical graph alignment for two compounds.

1: function PACHA($G,G\prime$)

2:  Set $K\subseteq V\times V\prime$ as a set of k vertex pairs with the top-k highest vertex similarities

3:  for each $(v,v\prime )\in K$ do

4:    Insert $(v,v\prime )$ and $s(v,v\prime )$ into PQUEUE

5:    $M^c\leftarrow \varphi$ ▹ Initialize M^c

6:    while PQUEUE is not empty do

7:     Get $(v,v\prime )$ from PQUEUE and pop PQUEUE

8:     $M^c\leftarrow M^c\cup (v,v\prime )$

9:     for each $(x,x\prime )\in N(v)\times N(v\prime )$ do

10:      if $(x,z)\notin M^c$ for $\forall z\in V\prime$ and $(z,x\prime )\notin M^c$ for $\forall z\in V$ then

11:       Insert $(x,x\prime )$ and $s(x,x\prime )$ into PQUEUE if $s(x,x\prime )\ne -\infty$

12:   $M\leftarrow M^c$ if the score ${\displaystyle \sum _{(v,v\prime )\in M^c}s}(v,v\prime )$ is at its highest ever

13:  return M

3.3 Vertex similarity function based on fingerprints

We propose to evaluate the similarity of each vertex pair in a graph by computing the similarity between two fingerprints of the vertices using the Weisfeiler–Lehman (WL) procedure (Shervashidze et al., 2011). A fingerprint defined as a binary vector is conceptually equivalent to the set that contains elements i if the ith bit of the fingerprint is 1, thus we use the set representation of fingerprints in this paper.

Suppose we are given a chemical graph $G=(V,E,L)$. The first fingerprint of a vertex $v\in V$ is obtained by collecting vertex labels from N(v), adjacent vertices of v, to create a string. The string is then converted into a unique integer using a hash function, and it is added to the fingerprint as a new element. The integer is also assigned to a new vertex label for v. The same procedure is repeated T times. As a consequence, we obtain a fingerprint of T elements per vertex. The pseudocode of the WL procedure is presented in Algorithm 2.

Algorithm 2 WL procedure for computing fingerprints for vertices in a graph. T is a user-defined parameter for deciding the number of iterations. $g:{\Sigma }^{*}\to \Sigma$ is a hash function that maps a string $s_h(v)$ to an integer such that $g(s_h(v))=g(s_h(w))$ if and only if $s_h(v)=s_h(w)$.

1: function WLprocedure(G)

2:  $W(v)\leftarrow \varphi$ for all $v\in V$

3:  Initialize ${\ell }_0(v)$ to v’s vertex label L(v) for all $v\in V$

4:  for $h=1,\dots ,T$ do

5:   for each $v\in V$ do

6:    Assign a multi-label $M_h(v):=\{{\ell }_{h-1}(u);u\in N(v)\}$ to v

7:    Sort elements in $M_h(v)$ in the ascending order of vertex labels and concatenate them into a string $s_h(v)$

8:    Set ${\ell }_h(v):=g(s_h(v))$ as a new vertex label of v

9:    $W(v)\leftarrow W(v)\cup \{{\ell }_h(v)\}$

10:  return $\{W(v);v\in V\}$

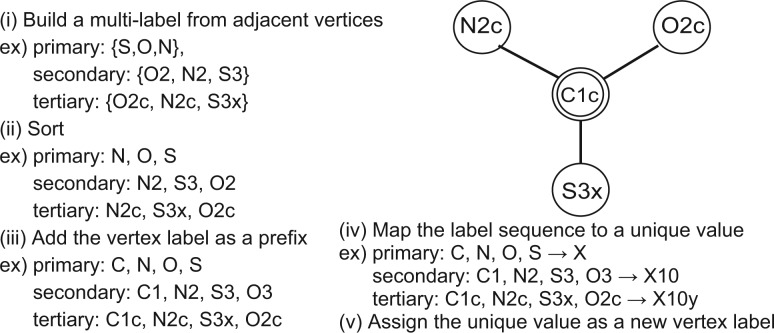
Each vertex in the chemical graph has three types of labels: primary, secondary and tertiary labels in this study. We apply the WL procedure to each label. Figure 2 shows an illustration of the WL procedure. The fingerprint for a vertex v is defined as W(v), which is the union of the resulting fingerprints for three labels.

Fig. 2.

Updating a node label surrounded by double circle by aggregating with neighboring labels in the WL procedure. The WL procedure is applied to each label class of primary, secondary and tertiary labels

Given two compound chemical graphs $G=(V,E,L)$ and $G\prime =(V\prime ,E\prime ,L\prime )$, we propose the following similarity function $s:V\times V\prime \to \mathcal{R}$ for a vertex pair $(v,v\prime )$ using the corresponding fingerprints W(v) and $W(v\prime )$ generated by the WL procedure:

$$s(v,v\prime ):=\{\begin{array}{ll}\frac{|W(v)\cap W(v\prime )|}{|W(v)\cup W(v\prime )|}& \text{if\hspace{0.5em}}v\prime \text{s\hspace{0.5em}primary\hspace{0.5em}label\hspace{0.5em}is\hspace{0.5em}identical\hspace{0.5em}to}\\ & v\prime \text{s\hspace{0.5em}primary\hspace{0.5em}label},\\ -\infty & \text{otherwise}.\end{array}$$

The vertex similarity is computed by the Tanimoto (also known as Jaccard) coefficient of fingerprints W(v) and $W(v\prime )$ if v’s primary label is identical to $v\prime$’s primary label. Otherwise, the vertex similarity is set to $-\infty$, which forces atom pairs with different primary labels to be unmatched in the graph alignment between two compounds.

3.4 Graph alignment-based feature vector

The PACHA-based graph alignment enables us to assign one of three alignment states: ‘aligned’, ‘generated’ and ‘eliminated’ to each vertex pair, defined as follows: (i) aligned: v is aligned to $v\prime$ if $(v,v\prime )\in M$; (ii) generated: z is generated from $v\prime$ if $\exists z,v\prime \in V\prime$ s.t. $z\in N(v\prime ),(v,v\prime )\in M$ for any $v\in V$; (iii) eliminated: z is eliminated from v if $\exists z,v\in V$ s.t. $z\in N(v),(v,v\prime )\in M$ for any $v\prime \in V\prime$. Figure 1(a) shows an example of the three alignment states.

We represent a compound pair $(G,G\prime )$ as a D-dimensional non-negative integer vector ${\Phi }_{\text{pacha}}(G,G\prime )\in {\mathcal{N}}^D$ using matching vertex pairs in M. Considering the three alignment states, we define ${\Phi }_{\text{pacha}}(G,G\prime )$ as a combination of three sub-vectors: the aligned sub-vector ${\Phi }^a(G,G\prime )$, the generated sub-vector ${\Phi }^g(G\prime )$ and the eliminated sub-vector ${\Phi }^e(G)$.

The aligned sub-vector ${\Phi }^a(G,G\prime )$ counts the number of vertices v aligned to vertices $v\prime$ for each pair of labels L(v) and $L\prime (v\prime )$. Let $F^a(v,v\prime )$ be a local vector for ${\Phi }^a(G,G\prime )$ and each element of $F^a(v,v\prime )$ be the following indicator function:

$$f^a(v,v\prime ):=\{\begin{array}{ll}1& \text{if\hspace{0.5em}}v\text{\hspace{0.5em}is\hspace{0.5em}aligned\hspace{0.5em}to\hspace{0.5em}}v\prime \text{\hspace{0.5em}with\hspace{0.5em}}L(v)\text{\hspace{0.5em}and\hspace{0.5em}}L(v\prime ),\\ 0& \text{otherwise}.\end{array}$$

The aligned sub-vector is defined as ${\Phi }^a(G,G\prime )=\sum _{(v,v\prime )\in V\times V\prime }{F}^a(v,v\prime )$.

The generated sub-vector ${\Phi }^g(G\prime )$ counts the number of vertices z generated from vertices $v\prime$ for each pair of labels $L\prime (z)$ and $L\prime (v)$. Let $F^g(z,v\prime )$ be a local vector for ${\Phi }^g(G,G\prime )$ and each element of $F^g(z,v\prime )$ be the following indicator function:

$$f^g(z,v\prime ):=\{\begin{array}{ll}1& \text{\hspace{0.5em}if\hspace{0.5em}}z\text{\hspace{0.5em}is\hspace{0.5em}generated\hspace{0.5em}from\hspace{0.5em}}v\prime \text{\hspace{0.5em}with\hspace{0.5em}}L\prime (z)\text{\hspace{0.5em}and\hspace{0.5em}}L\prime (v\prime ),\\ 0& \text{\hspace{0.5em}otherwise}.\end{array}\text{\&}$$

The generated sub-vector is defined as ${\Phi }^g(G\prime )=\sum _{(z,v\prime )\in V\prime \times V\prime }{F}^g(z,v\prime )$.

The eliminated sub-vector ${\Phi }^e(G)$ counts the number of vertices z eliminated from vertices v for each pair of labels L(z) and L(v). Let $F^e(z,v)$ be a local vector for ${\Phi }^e(G)$ and each element of $F^g(z,v)$ be the following indicator function:

$$f^e(z,v):=\{\begin{array}{ll}1& \text{\hspace{0.5em}if\hspace{0.5em}}z\text{\hspace{0.5em}is\hspace{0.5em}eliminated\hspace{0.5em}from\hspace{0.5em}}v\text{\hspace{0.5em}with\hspace{0.5em}}L(z)\text{\hspace{0.5em}and\hspace{0.5em}}L(v),\\ 0& \text{\hspace{0.5em}otherwise}.\end{array}$$

The eliminated sub-vector is defined as ${\Phi }^e(G)=\sum _{(z,v)\in V\times V}{F}^e(z,v)$.

Finally, ${\Phi }_{\text{pacha}}\text{(}G,G\prime )$ is constructed as ${\Phi }_{\text{pacha}}(G,G\prime )={({\Phi }^a{(G,G\prime )}^{⊺},{\Phi }^g{(G\prime )}^{⊺},{\Phi }^e{(G)}^{⊺})}^{⊺}$, which is referred to as ‘PACHA descriptor’ in this study. We built the PACHA descriptors using 68 tertiary labels, resulting in 3567-dimensional integer vectors. Figure 1a represents an example of the PACHA descriptor.

3.5 Predictive models for metabolic pathway reconstruction

We propose to apply the above PACHA descriptor to the enzymatic reaction-likeness prediction and reaction annotation, which are important applications for metabolic pathway reconstruction.

Given two compound chemical graphs G and $G\prime$, we consider a predictive model defined as the linear function $f(G,G\prime )=w^{⊺}{\Phi }_{\text{pacha}}(G,G\prime )$, where $w\in {\mathcal{R}}^D$ is a weight vector. In the case of enzymatic reaction-likeness prediction, the weight vector $w$ is estimated such that it can correctly predict the enzymatic reaction-likeness of compound-compound pairs. In the case of reaction annotation, the weight vector $w$ is estimated such that it can correctly predict a specific reaction annotation class (i.e. EC sub-subclass or PIERO term in this study) of the compound-compound pairs.

Given a collection of compound-compound pairs and their labels $({\Phi }_{\text{pacha}}(G_i,G_j),y_{ij})$, where $y_{ij}\in \{+1,-1\}(i=1,\dots ,n,j=1,\dots ,n,i\ne j)$ and n is the number of compounds in the learning set, we optimize the weight vector $w$ by L₁-regularized linear support vector machine (L1SVM) formulated as

$$\underset{w}{\min }\left|\right|w|{|}_1+C{\displaystyle \sum _{i=1}^n\{{\displaystyle \sum _{j=1}^{i-1}{P}_{ij}}+{\displaystyle \sum _{j=i+1}^n{P}_{ij}}\}},$$

where $P_{ij}=\max {\{1-y_{ij}{w}^{⊺}{\Phi }_{\text{pacha}}(G_i,G_j),0\}}^2$, C is a hyper-parameter and $\left|\right|·|{|}_1$ is L₁ norm (the sum of absolute values in the vector). L₁-regularization has an effect of making the weights of uninformative features zeros without loss of classification accuracy, which enables to extract important features characteristic of each task.

4 Results

4.1 Performance evaluation of the enzymatic reaction-likeness prediction

We tested the proposed PACHA descriptor for its ability to predict enzymatic reaction-likeness of compound-compound pairs from their chemical structure data. We compared this with previously developed chemical descriptors and graph alignment methods: CDK Extended fingerprint, CDK GraphOnly fingerprint, CDK Hybridization fingerprint, EState fingerprint, KlekotaRoth fingerprint, MACCS fingerprint, PubChem fingerprint, AE descriptor, KCF-S descriptor and SIMCOMP alignment (see Section 2 for more details). First, we focused on analysis of the isomer-enriched reaction data to validate the ability of PACHA to solve the issue of regioisomers.

We performed the following five-fold cross-validation. First, we randomly split the compound-compound pairs in the gold standard reaction data into five subsets of roughly equal sizes, where known substrate–product pairs were regarded as positive examples and the other compound-compound pairs were regarded as negative examples. Second, we took each subset as a test set and the remaining four subsets as a training set. Third, we learned a predictive model based only on the training set. Finally, we evaluated the prediction accuracy based on the prediction scores of compound–compound pairs in the test set over the 5-folds.

We evaluated the prediction performance using the receiver operating characteristic (ROC) curve, which is a plot of true-positive rates as a function of false-positive rates, and the precision-recall (PR) curve, which is a plot of precision (positive predictive value) as a function of recall (sensitivity). We summarized the performance by the area under the ROC curve (AUC) score, where 1 is perfect inference and 0.5 is random inference, and the area under the PR curve (AUPR) score, where 1 is perfect inference and the ratio of positive examples in the gold standard data is random inference.

The third column of Table 1 shows the resulting AUC and AUPR scores and their standard deviations (SDs) in performing 5-fold cross-validation experiments for the isomer-enriched reaction data. It was observed that PACHA worked best among the graph alignment-based methods and KCF-S worked the best among the descriptor-based methods. In total, PACHA outperformed the previously developed methods in terms of higher AUC and AUPR scores. These results suggest that PACHA can capture the important features of isomer-related chemical changes in reactions, while other methods can not capture isomer-specific chemical changes.

Table 1.

Performance evaluation of the enzymatic reaction-likeness prediction for isomer-enriched reaction data and all reaction data

Method	Input feature vector		Isomer-enriched reaction data		All reaction data
	Descriptor based	Graph alignment based	AUC ± SD	AUPR ± SD	AUC ± SD	AUPR ± SD
Random	—	—	0.5000	0.0306	0.5000	0.0204
CDK extended	Yes	—	0.7112 ± 0.0065	0.0840 ± 0.0021	0.6918 ± 0.0042	0.0594 ± 0.0001
CDK graph-only	Yes	—	0.7243 ± 0.0080	0.0842 ± 0.0042	0.7158 ± 0.0002	0.0614 ± 0.0005
CDK hybridization	Yes	—	0.7061 ± 0.0055	0.0792 ± 0.0026	0.7013 ± 0.0010	0.0502 ± 0.0006
E-state	Yes	—	0.5455 ± 0.0021	0.0607 ± 0.0057	0.6046 ± 0.0012	0.0346 ± 0.0002
KlekotaRoth	Yes	—	0.5702 ± 0.0011	0.0512 ± 0.0013	0.6028 ± 0.0029	0.0354 ± 0.0001
MACCS	Yes	—	0.7001 ± 0.0033	0.0750 ± 0.0007	0.6830 ± 0.0004	0.0504 ± 0.0006
PubChem	Yes	—	0.6945 ± 0.0018	0.0744 ± 0.0028	0.7199 ± 0.0008	0.0538 ± 0.0001
AE	Yes	—	0.8476 ± 0.0012	0.1521 ± 0.0033	0.8853 ± 0.0001	0.2110 ± 0.0004
KCF-S	Yes	—	0.9340 ± 0.0013	0.2815 ± 0.0062	0.9654 ± 0.0006	0.4050 ± 0.0060
SIMCOMP	—	Yes	0.9222 ± 0.0018	0.2533 ± 0.0014	0.9470 ± 0.0001	0.3127 ± 0.0004
PACHA	—	Yes	0.9401 ± 0.0004	0.3205 ± 0.0052	0.9617 ± 0.0001	0.3880 ± 0.0005
PACHA + KCF-S	Yes	Yes	0.9454 ± 0.0006	0.3224 ± 0.0044	0.9741 ± 0.0003	0.4711 ± 0.0061

Next, we tested the PACHA descriptor on its ability to predict enzymatic reaction-likeness using the ‘all’ reaction data that contains not only isomer-enriched reactions but also other enzymatic reactions. We performed Five-fold cross-validation experiments in a similar manner as the previous experiments.

The fourth column of Table 1 shows the resulting AUC and AUPR scores and their SDs in performing the Five-fold cross-validation experiments of the enzymatic reaction-likeness prediction for all reactant pair data. It was also observed that PACHA worked the best among graph alignment-based methods and KCF-S worked the best among the descriptor-based methods. Thus, we attempted to combine PACHA and KCF-S by vector concatenation, which we call ‘PACHA + KCF-S’. As a result, PACHA + KCFS worked much better than other individual methods, implying that descriptor- and graph alignment-based methods are complementary to each other and the integration of both approaches is useful in practice.

4.2 Analysis of chemical changes in isomer-related reactions

We examined the detailed prediction results of the cross-validation experiments and analyzed the relationship with chemical changes in isomer-related reactions. We then compared PACHA (the best among graph alignment-based methods) and KCF-S (the best among descriptor-based methods).

Figure 3 shows some examples of the predicted chemical transformations grouped by isomeric compounds. Most positive examples (a1, b1 and c1) were predicted correctly by KCF-S and PACHA, whereas some negative examples (a2, a3, b2, b3, c2 and c3) were predicted differently. Pairs a2, b2 and c2 were predicted as negative by KCF-S and positive by PACHA. Although these pairs were not known substrate–product pairs, these chemical changes were already known in other compounds, which occurs only once in each pair. Therefore, we can conclude that these pairs represent potential reactions that are likely to occur.

Fig. 3.

Examples of predicted chemical transformations grouped by isomeric compounds, with compositional formula (a) C₁₀H₁₆O - C₁₀H₁₄O, (b) C₁₅H₁₀O₅ - C₂₁H₂₀O₁₀ and (c) C₂₀H₁₂ - C₂₀H₁₂O. Vertically aligned compounds, e.g. C11938, C11415 and C11491 in (a), are regioisomers. Pairs a1, b1 and c1 are known substrate–product pairs for which the predictions were correct for KCF-S and PACHA. Pairs a2, b2 and c2 are negative examples and were predicted negative by KCF-S and positive by PACHA. Pairs a3, b3 and c3 are also negative examples and were predicted negative by PACHA and positive by KCF-S

Conversely, pairs a3, b3 and c3 were predicted negative by PACHA and positive by KCF-S. If these chemical conversions were to occur, at least two reactions would be needed for each pair. Pair a3, representing the chemical change from pinocarveol (C11941) to myrtenal (C11939), would require dehydroxylation and hydroxylation reactions and the isomerization of the pi-conjugated system. Pair b3, genistein (C06563) and vitexin (C01460), would require not only C-glycosylation but also in the rearrangement of the ring attachment. Pair c3, benzo[e]pyrene (C14435) and benzo[a]pyrene-7,8-epoxide (C14850), would also require at least two reactions, not only an epoxydation but also the rearrangement of the ring structure. Thus, we can conclude that these pairs do not represent single reactions.

4.3 Performance evaluation of reaction annotation and extraction of reaction class-specific features

We investigated the usefulness of the proposed PACHA descriptor for reaction annotation. As enzymatic reaction characteristics, we used EC sub-subclasses and PIERO terms. Reaction annotation is generally performed by predicting potential EC sub-subclasses or PIERO terms directly from differential chemical structures of compound–compound pairs, which is referred to as ‘direct approach’. Here, we proposed a two-step approach that first performs enzymatic reaction-likeness prediction for compound–compound pairs, followed by the reaction annotation for only the predicted substrate–product pairs, which is referred to as the ‘filtering approach’. Because PACHA + KCF-S worked the best in the cross-validation experiments for enzymatic reaction-likeness prediction, we focused on the use of PACHA + KCF-S and made a performance comparison between the previous direct approach and our proposed filtering approach.

We performed the following Five-fold cross-validation. First, we randomly split compound–compound pairs in the gold standard reaction data with an EC sub-subclass (respectively, PIERO term) into five subsets of roughly equal sizes, where compound–compound pairs with the EC sub-subclass (respectively, PIERO term) were regarded as positive examples and other compound–compound pairs were regarded as negative examples. Second, we took each subset as a test set and the remaining four subsets as a training set. Third, we learned an EC-specific (respectively, PIERO-specific) predictive model based only on the training set. Fourth, we evaluated the prediction accuracy based on the prediction scores of compound–compound pairs in the test set over the Five-folds. Finally, we repeated the above processes for all EC sub-subclasses (respectively, all PIERO terms).

Figures 4 show the resulting AUC and AUPR scores for EC sub-subclasses and PIERO terms, respectively. In both cases, our proposed filtering approach outperformed the previous direct approach in terms of higher AUC and AUPR scores. These results suggest that, in practice, comprehensive filtering of compound-compound pairs by enzymatic reaction-likeness is useful for more accurate reaction annotation. and 5

Fig. 4.

AUC and AUPR scores for EC sub-subclasses using previous direct approach and our proposed filtering approach

Fig. 5.

AUC and AUPR scores for PIERO terms using previous direct approach and our proposed filtering approach

Table 2 shows the examples of respective reaction annotations predicted by the direct and filtering approaches. The filtering approach worked better than the direct approach in terms of AUC and AUPR. The best performance was achieved for EC1.3.5 ‘oxidoreductase reactions acting on the CH-CH group of donors with a quinone or related compound as an acceptor’ as EC sub-subclasses and ‘diesterification’ as PIERO. Regardless of AUC or AUPR, the predictive values were generally higher in PIERO than in EC. This result reflects the fact that EC numbers were given to full reaction equations, whereas PIERO terms were given to substrate–product pairs.

Table 2.

Examples of correctly assigned reaction annotations

	Direct		Filtering
	AUC	AUPR	AUC	AUPR
EC sub-subclasses
EC1.3.5	0.9317	0.7782	0.957	0.8364
EC5.1.3	0.9988	0.7673	0.9982	0.808
EC1.8.1	0.965	0.7564	0.9906	0.7626
EC2.7.4	0.997	0.605	0.9982	0.7302
EC6.2.1	0.9852	0.6583	0.9916	0.715
PIERO terms
Diesterification	0.9912	0.3795	0.9989	0.8496
Transacylation	0.9983	0.6753	0.9989	0.8467
Sulfonation	0.9978	0.6545	0.9986	0.8301
Diphosphorylation	0.995	0.4714	0.9987	0.7836
Lipoxygenation	0.9973	0.6307	0.9985	0.7522

The EC and PIERO annotations are listed in the descending order of the AUPR scores by the filtered approach.

Table 3 shows several examples of the extracted vector features in PACHA and KCF-S that are significant to EC and PIERO. Note that the predictive model used in this study (i.e. L1SVM) has the ability of feature extraction. Interestingly, the extracted PACHA features correspond to the chemical changes that occurred in the preserved atoms. For example, the feature ‘a:O2x = O7x’ represents the preserved oxygen atom that changes from a cyclic ether to a cyclic ester, which is one of the typical EC1.1.1 reactions that causes dehydrogenation of sugars to yield lactone sugars. This feature was a reasonably important and characteristic feature of EC1.1.1 and ‘dehydrogenation’. Conversely, the extracted features from descriptors-based methods (e.g. KCF-S) were generally difficult to interpret because descriptor-based methods cannot distinguish the relationships between preserved atoms and their chemical changes. All results can be found at http://www.bioreg.kyushu-u.ac.jp/labo/systemcohort/pacha/.

Table 3.

Examples of extracted vector features significant to respective annotations

	Subvector	Feature	Weight
EC sub-subclasses and PACHA
EC1.1.1	Aligned	a:O2x = O7x	2.5502
EC1.4.3	Aligned	a:C1b = C4a	2.1923
EC3.1.3	Aligned	a:O1a = O2b	1.9833
EC3.5.1	Aligned	a:C5a = C6a	1.8904
EC4.1.1	Generated	g:C6a-C8y	1.8426
PIERO terms and PACHA
Dehydrogenation	Eliminated	e:C1z-O7x	2.4881
Dehydrogenation	Aligned	a:O2x = O7x	2.4666
Dehydrogenation	Generated	g:C1z-O7x	2.4621
Monooxygenation	Eliminated	e:C1b-C8x	2.0967
Deamination	Aligned	a:C1b = C4a	2.0079
EC sub-subclasses and KCF-S
EC1.2.7	Common	C1c-O1a	1.7583
EC3.1.2	Decreased	O-C-S	1.3214
EC4.2.1	Increased	C8y-C8x-N4x	1.2998
EC1.14.13	Common	C8y-O7x	1.196
EC2.5.1	Common	C1b-C1b-N1a	1.0245
PIERO terms and KCF-S
Hydration	Common	C1y-C1b-O2b	1.5443
Oxidoreduction	Increased	C2b-C1b-S2a	1.4682
Oxidoreduction	Increased	C1y-N1b-C2c	1.3741
Decarboxylation	Decreased	C1a-C1c-N1a	1.2947
Oxidoreduction	Decreased	C2c-C1b-O1a	1.2013

4.4 Novel prediction

Finally, we conducted a comprehensive prediction of enzymatic reaction-likeness for all possible compound pairs, with the exception of known substrate–product pairs. We trained a predictive model using all known substrate–product pairs in the gold standard data (10 852 pairs retrieved from KEGG as of December 2012) and applied the model to all possible uncharacterized compound-compound pairs (30 719 540 pairs) for which pathways and reaction characteristics were not known. PACHA and PACHA + KCFS predicted 54 919 and 28 192 compound pairs as potential substrate–product pairs, respectively. We confirmed the validity of 672 compound pairs predicted by PACHA and 683 compound pairs predicted by PACHA + KCF-S using independent resources such as recent scientific literatures and the latest databases (KEGG as of December 2014).

Figure 6 shows an example of the newly predicted pathways by PACHA and PACHA + KCF-S methods, which are supported by the latest database information. Note that the reactions in the pathway were not used in the learning set for constructing the predictive model. These reactions and compounds were not in the January 2014 release of KEGG but were recently added to the December 2014 release. This pathway represents the biosynthesis of brassinosteroids, important steroid hormones that regulate plant development and physiology (Ohnishi et al., 2006). This pathway was successfully reconstructed by our proposed methods but was not reconstructed by previous methods.

Fig. 6.

One of the newly predicted pathway supported by both PACHA and PACHA + KCF-S, as well as the recent KEGG release

5 Discussion

We developed a novel method for supervised de novo metabolic pathway reconstruction with an improved graph alignment algorithm called PACHA. Our proposed PACHA enabled us to detect regioisomer-sensitive connectivities between aligned substructures of two compounds. The novelty of our proposed method lies in the detection of a unique graph alignment, scalability for analyzing a vast amount of compounds on a metabolome-scale and applicability to many tasks in metabolic pathway reconstruction. We showed the usefulness of the PACHA descriptors for enzymatic reaction-likeness prediction and reaction annotation with a sparsity-induced classifier.

This study addressed the importance of the distinction of regioisomers for metabolic pathway analysis. Although a popular approach for representing compounds is to use chemical descriptors that deal with many small chemical substructures, they cannot correctly consider the substructure connectivity. Thus, the comparison of two chemical descriptors is insufficient to generate atom–atom mapping, which makes it impossible for all descriptor-based methods to describe sensitive chemical changes in a single enzymatic reaction, as illustrated in Figure 1.

SIMCOMP (Hattori et al., 2003), the most related previous graph-based method, was designed for searching similar compounds in databases by allowing some small common substructures. The common procedure in SIMCOMP and PACHA is to generate an association graph, where the vertices (association nodes) represent the atom–atom pairs of two compounds and obtain common subgraph(s) considering adjacency. The difference between SIMCOMP and PACHA lies in the definition of ‘adjacency’ in the association graph. PACHA defines the association nodes as being adjacent to each other only when the corresponding atoms are adjacent in both compounds; therefore, only one common subgraph occurs and the second common subgraph is not allowed. SIMCOMP defines the association nodes to be adjacent either when the corresponding atoms are adjacent in both compounds or when they are not adjacent in both compounds. The adjacency in the SIMCOMP association graph often generates multiple common subgraphs, which are integrated afterwards; however, in some cases, the integrated subgraph contains many gaps.

Having such gaps is not an issue when finding similar compounds, e.g. for pharmaceutical purposes. However, it is of crucial importance for metabolic pathway analysis, because most reactions generate or eliminate only a few chemical bonds. Therefore, the number of gaps affects the prediction accuracy of enzymatic reaction-likeness. Our proposed PACHA algorithm solved this problem successfully as demonstrated by significant improvement of the de novo pathway reconstruction, especially in the analysis of isomer-enriched data. Future extensions would involve the detection of frequent substructure changes and stereoinversions, which requires more sophisticated tuning of PACHA.

Funding

This work was supported by MEXT/JSPS Kakenhi (25108714 and 24700140) and the JST PRESTO program (MEXT: the Ministry of Education, Culture, Sports, Science and Technology of Japan; JSPS: the Japan Society for the Promotion of Science; JST: the Japan Science and Technology Agency). This work was also supported by the JST/MEXT Program to Promote the Tenure Track System and Kyushu University Interdisciplinary Programs in Education and Projects in Research Development.

Conflict of Interest: none declared.