A hierarchical Bayesian model for flexible module discovery in three-way time-series data

Abstract

Motivation: Detecting modules of co-ordinated activity is fundamental in the analysis of large biological studies. For two-dimensional data (e.g. genes × patients), this is often done via clustering or biclustering. More recently, studies monitoring patients over time have added another dimension. Analysis is much more challenging in this case, especially when time measurements are not synchronized. New methods that can analyze three-way data are thus needed.

Results: We present a new algorithm for finding coherent and flexible modules in three-way data. Our method can identify both core modules that appear in multiple patients and patient-specific augmentations of these core modules that contain additional genes. Our algorithm is based on a hierarchical Bayesian data model and Gibbs sampling. The algorithm outperforms extant methods on simulated and on real data. The method successfully dissected key components of septic shock response from time series measurements of gene expression. Detected patient-specific module augmentations were informative for disease outcome. In analyzing brain functional magnetic resonance imaging time series of subjects at rest, it detected the pertinent brain regions involved.

Availability and implementation: R code and data are available at http://acgt.cs.tau.ac.il/twigs/.

Contact: rshamir@tau.ac.il

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Identifying modules of elements acting in concert is a fundamental paradigm in interpreting, visualizing and dissecting complex biomedical data. For two-dimensional data (e.g. genes versus conditions), clustering is the simplest way to group the elements of one dimension (Hartigan, 1972). Biclustering seeks row and column subsets that manifest similarity (Cheng and Church, 2000; Hartigan, 1972; Madeira and Oliveira, 2004). Such analysis has become standard in computational biology (Mitra et al., 2013; Oghabian et al., 2014). Algorithms for finding biclusters differ in how they define (and identify) biclusters (Madeira and Oliveira, 2004). For example, biclusters were defined as sub-matrices with constant values (Hartigan, 1972), row or column additive or multiplicative values (Lazzeroni and Owen, 2002) and submatrices with order preserving values (Ben-Dor et al., 2003).

Recent studies have extended the idea of biclustering to more complex input structures beyond the standard row–column data (Mitra et al., 2013). Meng et al. (2009) extended the classic Iterative Signature Algorithm (ISA) (Bergmann et al., 2003) to analyze a single matrix of time series data together with prior knowledge on gene function to detect temporal transcription modules that are biologically meaningful. Li and Tuck (2009) introduced an algorithm for joint analysis of ChIP-chip and gene expression data to find biclusters that are likely to be regulated by similar transcription factors. Waltman et al. (2010) and Dede and Ogul (2013) proposed three-way clustering of gene-condition-organism data. The algorithm of Waltman et al. (2010) uses sequence information to integrate data across species, and a post-processing step allows detection of species-specific information. Gerber et al. (2007) cluster tissues hierarchically and then find the representative gene set of each tissue cluster in the hierarchy.

A common data source that calls for three-way analysis is a collection of gene expression profiles measured for a set of subjects over a series of time points. Hence, the data are represented by a gene × subject × time 3D matrix (i.e. a tensor of order 3) (Mankad and Michailidis, 2014; Zhao and Zaki, 2005). For such matrices, Supper et al. (2007) presented EDISA, an extension of ISA that handles a time-course vector for each gene–subject pair instead of a single scalar. Extant models are limited in their ability to detect a signal that is specific to a particular subject. For example, the set of genes active under one subject in a module may only partially overlap with the gene set of other subjects. Another limitation is the assumption of synchronicity of time points across subjects. Although this assumption is valid for technical repeats or well-tailored experiments, it is less plausible in other situations, e.g. samples taken from patients over time, due to possible heterogeneity in the response of different patients.

Here, we introduce a new, flexible definition of a module suitable for three-way data where subjects have entities (e.g. genes) measured over time, but time courses are unsynchronized among the subjects. A core module is defined by a subset of the subjects and a subset of the entities, along with subject-specific subset of the time points. In addition, subjects may have private modules that only partially coincide with the core set of entities. The assumption is that the resulting submatrices will show values markedly different from the whole matrix. A toy example is shown in Figure 1A.

Fig. 1.

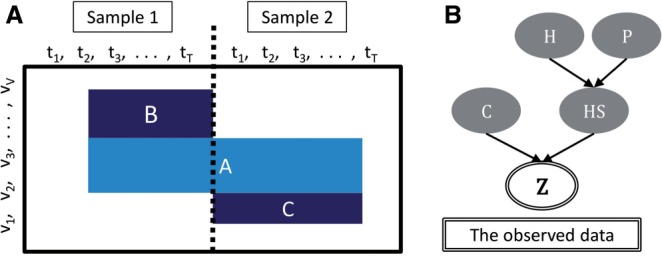
Overview of the model. (A) A toy example of a core module (A) and its private modules (B, C). (B) An overview of the dependencies in the hierarchical model. P is the vector of subject-specific probabilities P_s

We developed a statistical framework and algorithm for analyzing such data. Our framework can detect core modules and for each subject in a core module, a private module with relevant time points. We developed a hierarchical Bayesian generative model for the data and a procedure that aims to fit model parameters for a given dataset. Our algorithm uses a regular biclustering solution as a starting point and then performs iterative improvement using a Gibbs sampling procedure. The algorithm is called TWIGS (three-way module inference via Gibbs sampling). In simulations, we show that TWIGS outperforms standard algorithms even when the core modules have no additional subject-specific signal. When subject-specific signals exist, the ability of extant algorithms to detect the core modules declines markedly, whereas the performance of TWIGS remains high.

We demonstrate the advantage of our framework on experimental data from two different domains: gene expression and brain functional magnetic resonance imaging (fMRI) signals. We first analyzed whole blood expression profiles, taken daily for 5 days from 14 patients after septic shock (Parnell et al., 2013). TWIGS detected two core modules of up-regulated genes, showing enrichment for different immune system processes. The first was related to response to bacteria, whereas the second was related to regulation of T-cells. Analysis of the subject-specific private modules revealed multiple enrichments that illustrate patient-specific-activated biological processes. Hence, our analysis produced both shared and subject-specific insights, highlighting biological pathways that repeatedly emerge as up-regulated after septic shock, together with additional biological functions particular to each patient. We also analyzed fMRI readings for 20 subjects at rest (Vaisvaser et al., 2013). The data for each subject are a matrix of 464 brain regions (parcels) measured over 94 time points at 3 s intervals. Each value in the matrix is the parcel’s average blood-oxygen-level-dependent (BOLD) contrast. These levels are indicators of the activity at that region. TWIGS revealed several core modules of highly activated bi-lateral brain regions. Reassuringly, the detected modules were enriched with regions that are known to be active during rest. This analysis shows that our framework is able to detect large functional networks that reappear as activated across subjects and also highlight subject-specific activation patterns.

2 Methods

2.1 The probabilistic model

The input for our problem is summarized as a 3D matrix Z where $Z_{v,t,s}$ is the activity level of the measured object $v\in 1,\dots ,V$, at time $t\in 1,\dots ,T$, for subject $s\in 1,\dots ,S$. We will say that v and t represent the rows and columns of the matrix and s represents layers. In gene expression data, v represents genes, whereas in fMRI, data v represents brain regions (parcels or voxels). For uniformity, from now on we use for v the term row or voxel. Here, we describe a hierarchical probability model for generating a single module from the distribution of $Z$.

We assume that there is a set of voxels $\mathcal{V}\subset \{1,\dots ,V\}$ that tend to have high values jointly in a subset of the subjects. $\mathcal{V}$ is specified by the indicator vector $H=(H_1,\dots ,H_V)$, through the relation $\mathcal{V}=\{v:H_v=1\}$. We assume that $H_v\sim \text{Bernoulli}({\pi }^{VC})$. Although H marks the rows of the core module, the signal in each specific subject might change. The subject-specific voxel sets are specified by the matrix $HS=\{H{S}_{1,1},\cdots ,H{S}_{V,S}\}$, where $H{S}_{v,s}=1$ specifies that voxel v participates in the module of subject s. The relation between $H$ and $HS$ is as follows: if H_v = 1 then $H{S}_{v,s}\sim \text{Bernoulli}(p_s)$, otherwise $H{S}_{v,s}\sim \text{Bernoulli}(p_0)$.

We next model the time-series relations. $C=C_{t,s}\in \{0,1\}$ indicates whether the voxel set of subject s is active at time t. We assume $\mathrm{Pr}(C_{1,s}=1)={\pi }^{1,1}$. The activity at time $t=2,\dots ,T$, depends on the time window of size $w\ge 1$ before t. In times $t=2,\dots ,w$, the time window is $1\cdots t-1$. Let $C{\prime }_{t,s}=1$, if the time window of subject s right before time point t contains at least one active time point and set $C{\prime }_{t,s}=0$ otherwise. We assume that $\mathrm{Pr}(C_{t,s}=1|C{\prime }_{t,s}=0)={\pi }^{1|0}$ and $\mathrm{Pr}(C_{t,s}=1|C{\prime }_{t,s}=1)={\pi }^{1|1}$.

Finally, we assume that for v, t, s for which $C_{t,s}=1$ and $H{S}_{v,s}=1,Z_{v,t,s}\sim F_1$, otherwise $Z_{v,t,s}\sim F_0$. An overview of the model hierarchy is shown in Figure 1B. We assume that all hyper-parameters above have Beta prior distributions: ${\pi }^{VC}\sim \text{Beta}(a_1,b_1),p_s\sim \text{Beta}(a_2,b_2),p_0\sim \text{Beta}(a_3,b_3),{\pi }^{1,1}\sim \text{Beta}(a_4,b_4),{\pi }^{1|1}\sim \text{Beta}(a_5,b_5)$, ${\pi }^{1|0}\sim \text{Beta}(a_6,b_6)$.

2.2 The Gibbs sampling algorithm

Our algorithm starts from a solution produced using a standard biclustering algorithm and then applies iterative improvement steps. In each step, all parameters are fixed except a single one that is sampled according to its conditional probability. The order of parameters matches the subsections below. This order is repeated cyclically k times. The output of the process is the set of sampled values for each parameter in all iterations. We then extract the core modules and the subject-specific modules from this output.

• (1) As H_v are Bernoulli realizations with success probability π^VC:

  $${\pi }^{VC}|\cdots \sim \text{Beta}(a_1+\left|\right\{v:H_v=1\left\}\right|,b_1+\left|\right\{v:H_v=0\left\}\right|).$$

Similarly:

$$\begin{array}{l}{p}_s|\cdots \sim \text{Beta}(a_2+\left|\right\{v:H{S}_{v,s}=1,H_v=1\left\}\right|,\\ b_2+\left|\right\{v:H{S}_{v,s}=0,H_v=1\left\}\right|).\\ p_0|\cdots \sim \text{Beta}(a_3+\left|\right\{v,s:H{S}_{v,s}=1,H_v=0\left\}\right|,\\ b_3+\left|\right\{v,s:H{S}_{v,s}=0,H_v=0\left\}\right|),\\ {\pi }^{1,1}|\cdots \sim \text{Beta}(a_4+\left|\right\{s:C_{1,s}=1\left\}\right|,\\ b_4+\left|\right\{s:C_{1,s}=0\left\}\right|),\end{array}$$

$$\begin{array}{l}{\pi }^{1|1}|\cdots \sim \text{Beta}(a_5+\left|\right\{t,s:C{\prime }_{t,s}=1,C_{t,s}=1\left\}\right|,\\ b_5+\left|\right\{t,s:C{\prime }_{t,s}=1,C_{t,s}=0\left\}\right|),\\ {\pi }^{1|0}|\cdots \sim \text{Beta}(a_6+\left|\right\{t,s:C{\prime }_{t,s}=0,C_{t,s}=1\left\}\right|,\\ b_6+\left|\right\{t,s:C{\prime }_{t,s}=0,C_{t,s}=0\left\}\right|)\end{array}$$

• (2) H_v is affected by π^VC, and it affects the values of $H{S}_{v,s}$ for each s:

  $$\begin{array}{c}\mathrm{Pr}(H_v=1,H{S}_{v,s}=1|\cdots )={\pi }^{VC}·p_s,\\ \mathrm{Pr}(H_v=1,H{S}_{v,s}=0|\cdots )={\pi }^{VC}·(1-p_s),\\ \mathrm{Pr}(H_v=0,H{S}_{v,s}=1|\cdots )=(1-{\pi }^{VC})·p_0,\\ \mathrm{Pr}(H_v=0,H{S}_{v,s}=0|\cdots )=(1-{\pi }^{VC})·(1-p_0).\end{array}$$

Thus,

$$\begin{array}{l}\mathrm{Pr}(H_v=1,H{S}_{v,*}|\cdots )={\pi }^{VC}·p_s^{{\sum }_{s}H{S}_{v,s}}\\ ·(1-p_s{)}^{{\sum }_s(1-H{S}_{v,s})},\\ \mathrm{Pr}(H_v=0,H{S}_{v,*}|\cdots )=(1-{\pi }^{VC})·p_0^{{\sum }_{s}H{S}_{v,s}}\\ ·(1-p_0{)}^{{\sum }_s(1-H{S}_{v,s})}.\end{array}$$

Therefore, the conditional posterior of H_v is:

$$\mathrm{Pr}(H_v=1|\cdots )=\frac{\mathrm{Pr}(H_v=1,H{S}_{v,*}|\cdots )}{\mathrm{Pr}(H_v=1,H{S}_{v,*}|\cdots )+\mathrm{Pr}(H_v=0,H{S}_{v,*}|\cdots )}$$

• (3) Given $C_{t,s}$, only the value of $H{S}_{v,s}$ affects the distribution of $Z_{v,t,s}$. Assume for now, that we condition on H_v = 1, then:

  $$\begin{array}{l}\mathrm{Pr}(Z_{v,t,s},H{S}_{v,s}=0|C_{t,s}=0,\cdots )=(1-p_s)f_0(Z_{v,t,s}),\\ \mathrm{Pr}(Z_{v,t,s},H{S}_{v,s}=1|C_{t,s}=0,\cdots )=p_s·f_0(Z_{v,t,s}),\\ \mathrm{Pr}(Z_{v,t,s},H{S}_{v,s}=0|C_{t,s}=1,\cdots )=(1-p_s)·f_0(Z_{v,t,s}),\\ \mathrm{Pr}(Z_{v,t,s},H{S}_{v,s}=1|C_{t,s}=1,\cdots )=p_s·f_1(Z_{v,t,s}).\end{array}$$

From the above, it is clear that when $C_{t,s}=0$:

$$\begin{array}{l}\mathrm{Pr}(H{S}_{v,s}=1|C_{t,s}=0,H_v=1,Z_{v,t,s},\cdots )=p_s,\\ \mathrm{Pr}(H{S}_{v,s}=0|C_{t,s}=0,H_v=1,Z_{v,t,s},\cdots )=1-p_s.\end{array}$$

Therefore, a time point t in which $C_{t,s}=0$ will not affect the marginal distribution of $H{S}_{v,s}$. Let $T{\prime }_s=\{t:C_{t,s}=1\}$, then:

$$\begin{array}{l}\mathrm{Pr}(H{S}_{v,s}=1,Z_{v,*,s}|H_v=1,\cdots )\\ =p_s·{\displaystyle {\prod }_{t\in T{\prime }_s}{f}_1}(Z_{v,t,s}),\\ \mathrm{Pr}(H{S}_{v,s}=0,Z_{v,*,s}|H_v=1,\cdots )\\ =(1-p_s)·{\displaystyle {\prod }_{t\in T{\prime }_s}{f}_0}(Z_{v,t,s}).\end{array}$$

On the basis of the equations above, we can calculate the conditional posterior of $H{S}_{v,s}$, given that H_v = 1, through:

$$\begin{array}{l}\mathrm{Pr}(H{S}_{v,s}=1|H_v=1,\cdots )\\ =\frac{\text{Pr}(H{S}_{v,s}=1,Z_{v,*,s}|H_v=1,\cdots )}{\text{Pr}(H{S}_{v,s}=0\vee H{S}_{v,s}=1,Z_{v,*,s}|H_v=1,\cdots )}\end{array}$$

Similarly, the conditional posterior of $H{S}_{v,s}$ given that H_v = 0 can be calculated by replacing every p_s with p₀ in the formulas above.

• (4) As the value of $C_{1,s}$ affects the value of the time window $C_{2,s},\dots ,C_{w+1,s}$ and the values of $Z_{v,1,s}$ with $H{S}_{v,s}=1$:

  $$\begin{array}{l}\mathrm{Pr}(C_{1,s}=1,C_{2,s},\cdots ,C_{w+1,s},Z_{*,1,s}|\cdots )\\ ={\pi }^{1,1}·{\pi }^{1|1}{}^{{\displaystyle \sum _{k=2}^{w+1}{C}_{k,s}}}·(1-{\pi }^{1|1}{)}^{\sum _{k=2}^{w+1}(1-C_{k,s})}·{\displaystyle \prod _{v:H{S}_{v,s}=1}{f}_1}(Z_{v,1,s})\end{array}$$

Unlike the equation above, calculating the probability of $C_{1,s}=0$ requires breaking the window into two parts. Assume that the time window contains at least one active cell. Let l be the first time point of $C_{2,s},\dots ,C_{w+1,s}$ that changes from 0 to 1. Thus:

$$\begin{array}{l}\mathrm{Pr}(C_{1,s}=0,C_{2,s},\cdots ,C_{w+1,s},Z_{*,1,s}|\cdots )\\ =(1-{\pi }^{1,1})·\left[{\displaystyle \prod _{k=2}^{l-1}(1-{\pi }^{1|0})}\right]·{\pi }^{1|0}·{\pi }^{1|1}{}^{{\displaystyle \sum _{k=2}^{w+1}{C}_{k,s}}}·\\ (1-{\pi }^{1|1}{)}^{{\displaystyle \sum _{k=2}^{w+1}(1-C_{k,s})}}·{\displaystyle \prod _{v:H{S}_{v,s}=1}{f}_0}(Z_{v,1,s})\end{array}$$

If there are no active cells in $C_{2,s},\cdots ,C_{w+1,s}$, then the calculation reduces to:

$$\begin{array}{l}\mathrm{Pr}(C_{1,s}=0,C_{2,s},\cdots ,C_{w+1,s},Z_{*,1,s}|\cdots )\\ =(1-{\pi }^{1,1})·(1-{\pi }^{1|0}{)}^w·{\displaystyle \prod _{v:H{S}_{v,s}=1}{f}_0}(Z_{v,1,s})\end{array}$$

Finally, the conditional of $C_{1,s}$ can be calculated by:

$$\begin{array}{l}\mathrm{Pr}(C_{1,s}=1|C_{2,s},\cdots ,C_{w+1,s},Z_{*,1,s},\cdots )\\ =\frac{\mathrm{Pr}(C_{1,s}=1,C_{2,s},\cdots ,C_{w+1,s},Z_{*,1,s}|\cdots )}{\mathrm{Pr}(C_{2,s},\cdots ,C_{w+1,s},Z_{*,1,s}|\cdots )}\end{array}$$

The conditional probability of the event $C_{1,s}=0$ is computed in the same way.

• (5) For $t\in 2,\dots ,T-1$, the value of $C_{t,s}$ is affected by the value of $C{\prime }_{t,s}$, and it affects the value of $C_{t,s},\dots ,C_{\text{min}(w+t,T),s}$, and the values of $Z_{v,t,s}$ with $H{S}_{v,s}=1$. Thus:

  $$\begin{array}{l}\mathrm{Pr}(C_{t,s}=1,C_{*,s},Z_{*,t,s}|\cdots )\\ ={{\pi }^{1|1}}^{C_{t,s}^{\prime }}·{{\pi }^{1|0}}^{1-C_{t,s}^{\prime }}·{\pi }^{1|1}{}^{{\displaystyle \sum _{k=t+1}^{\text{min}(w+t,T)}{C}_{k,s}}}\\ ·(1-{\pi }^{1|1}{)}^{{\displaystyle \sum _{k=t+1}^{\text{min}(w+t,T)}(1-C_{k,s})}}·{\displaystyle \prod _{v:H{S}_{v,s}=1}{f}_1}(Z_{v,t,s})\end{array}$$

  $$\begin{array}{l}\mathrm{Pr}(C_{t,s}=0,C_{*,s},Z_{*,t,s}|\cdots )\\ ={\displaystyle \prod _{k=t}^{\text{min}(t+w,T)}{{\pi }^{1|1}}^{C_{k,s}·C_{k,s}^{\prime }}}·{{\pi }^{1|0}}^{C_{k,s}·(1-C_{k,s}^{\prime })}\\ ·{\displaystyle \prod _{k=t}^{\text{min}(t+w,T)}{(1-{\pi }^{1|1})}^{(1-C_{k,s})·C_{k,s}^{\prime }}}\\ ·{\displaystyle \prod _{k=t}^{\text{min}(t+w,T)}{(1-{\pi }^{1|0})}^{(1-C_{k,s})·(1-C_{k,s}^{\prime })}}\\ ·{\displaystyle \prod _{v:H{S}_{v,s}=1}{f}_0}(Z_{v,t,s})\end{array}$$

Thus, $\mathrm{Pr}(C_{t,s}=1|\cdots )$ can be calculated similarly to the calculations in the previous section.

2.3 Setting f₀ and f₁

Here, we discuss two options for setting f₀ and f₁ and their hyper-parameters: (i) a Bernulli-Beta model for binary data and (ii) a Normal-Gamma model for normal distributions. Let A be the cells within the module (including the core and private parts): $A=\{Z_{v,t,s}:C_{t,s}=1\wedge H{S}_{v,s}=1\}$. Let B be the cells outside the module: $B=\{Z_{v,t,s}:C_{t,s}=0\vee H{S}_{v,s}=0\}$

For binary data, we assume that $Z_{v,t,s}\in \{0,1\},f_0=\text{Bernoulli}({\pi }^{C0})$ and $f_1=\text{Bernoulli}({\pi }^{C1})$. Thus, our model learns the background probability ${\pi }^{C0}$ of observing a value of 1 and the probability ${\pi }^{C1}$ of observing 1 within the module. In this model, ${\pi }^{C0}$ and ${\pi }^{C1}$ follow Beta posterior distributions:

$$\begin{array}{c}{\pi }^{C0}|\cdots \sim \text{Beta}(a_7+\left|\right\{i:B_i=1\left\}\right|,b_7+\left|\right\{i:B_i=0\left\}\right|)\\ {\pi }^{C1}|\cdots \sim \text{Beta}(a_7+\left|\right\{i:A_i=1\left\}\right|,b_7+\left|\right\{i:A_i=0\left\}\right|)\end{array}$$

In the continuous case, we assume that f₀ is $N({\mu }_0,{\sigma }_0)$ and f₁ is $N({\mu }_1,{\sigma }_1)$. Under the Normal-Gamma model, the prior distribution for the mean μ and the standard deviation σ of a normal distribution $N(\mu ,\sigma )$ is:

$$\begin{array}{c}1/\sigma \sim \text{Gamma}\left(\frac{v_0}{2},\frac{S{S}_0}{2}\right)\\ \mu \sim N\left(m_0,\frac{1}{p_0}\right)\end{array}$$

The conditional posteriors for $Y=(y_1,\dots ,y_n)$ where for each i, $y_i\sim N(\mu ,\sigma )$ are:

$$\begin{array}{l}1/\sigma |Y\sim \text{Gamma}(1/2·(v_0+n),\\ 1/2·\left(S{S}_0+{\displaystyle \sum _{i=1}^n{(y_i-\overline{y})}^2}+\frac{n·p_0}{n+p_0}·{(\overline{y}-m_0)}^2)\right)\\ \mu |Y,\sigma \sim N\left(\frac{m_0{p}_0+n\overline{y}}{n+p_0},\frac{\sigma }{p_0+n}\right)\end{array}$$

Thus, we apply the model above for A and B, thereby modeling f₀ and f₁ as normal distributions.

2.4 Finding multiple modules

To find a single module, we use a standard biclustering algorithm to produce an initial solution and then use the Gibbs sampler to improve it. The biclustering algorithm is applied on a 2D matrix M obtained by concatenating the layers in Z, i.e. $M_{v,i}=Z_{v,t,s}$, where $i=(s-1)S+t$. In this study, we tested Bimax (Prelic et al., 2006) and ISA (Bergmann et al., 2003) as the base algorithms. To binarize real-valued data Z to run Bimax, we use a threshold τ: we set every value $Z_{v,t,s}\ge \tau$ ($<\tau$) to 1 (0). By default, we set τ to be the 0.9 quantile of the values in Z. After running the Gibbs sampler, we take the mode of H, HS and C as the solution. By default, all hyperparameters of the Gibbs sampler are set to non-informative priors. This means that the algorithm infers these parameters and thus no tunning is required.

To find multiple modules, we tested two previously used heuristics (Serin and Vingron, 2011; Shabalin et al., 2009). In the first (Cheng and Church, 2000), which we call masker, we run the algorithm iteratively on the residual matrix of Z. The residual matrix is calculated by going over all cells in the module and updating their values in Z. In the binary model, the update rule is to change all module cells to zero. In the normal model, we subtract the mean of f₁ from the value of each cell.

The second heuristic, called filter, takes a set of biclusters U as input and produces a reduced set. It first uses the overlap reduction method of Serin and Vingron (2011): initially $U\prime =\varnothing$, then the largest module in U is added to $U\prime$ and all remaining modules with a large overlap with it (we used Jaccard index $\ge 0.5$) are removed from U. The process is repeated until U is empty. Next, we run the Gibbs sampler on the original matrix Z starting with each module in $U\prime$. The result is a set of new modules $U″$. Finally, as different modules in $U\prime$ might converge into similar modules in $U″$, the overlap removal process is used again, taking $U″$ as input.

For both heuristics, we define when to add a module to the final output. When using masker, we add modules until the first time a module is rejected. A module is accepted if it is large enough and the difference $|f_1-f_0|$ for it is large enough. In the binary case, we set ${\pi }^{C1}>0.5$ and in the normal case we set $\mu >0.3$. Setting the minimal module size depends on the application and on the size of the input data. By default, we set the minimal size of a core module to 5 rows and 5 time points (combining all subjects).

2.5 Performance measures

In the results below, we compare algorithms on simulated data. In each case, we compare the known H, HS, C to the algorithm output $H\prime ,HS\prime ,C\prime$ using the Jaccard coefficient. For example, the Jaccard score of H and $H\prime$ is:

$$J(H,H\prime )=\frac{\left|\right\{i;H_i\wedge H{\prime }_i\left\}\right|}{\left|\right\{i;H_i\vee H{\prime }_i\left\}\right|}$$

When the data contain more than one module we use the running max average of all pairwise Jaccard scores. Given the known solution $H=(H_1,\dots ,H_{k_1})$ and the algorithm output $H\prime =(H{\prime }_1,\dots ,H{\prime }_{k_2})$ the running max average score is:

$$\frac{{\displaystyle \sum _{i\in 1,\dots ,k_1}\left(\underset{j\in 1,\dots ,k_2}{\max }J(H_i,H{\prime }_j)\right)}+{\displaystyle \sum _{j\in 1,\dots ,k_2}\left(\underset{i\in 1,\dots ,k_1}{\max }J(H_i,H{\prime }_j)\right)}}{k_1+k_2}$$

The same method is used for HS and C.

3 Results

3.1 Simulations

Our simulations setup was as follows. We set V = 500, T = 50, S = 10 and create an initial matrix Z in which all values are zero. We then add modules to Z in which all values are 1 and later add noise according to the tested model (binary or normal). To define a new module, we first need to randomly select the rows and columns of each subject s. Time points are selected randomly with w = 1, ${\pi }^{1,1}=0.05,{\pi }^{1|1}=0.6$ and ${\pi }^{1|0}=0.1$. Rows are selected randomly as follows. We first select randomly 20 rows $i_1\dots i_{20}$ for the core module. Then, we add row r to the private module of subject s with probability $p{\prime }_s$ if $r\in \{i_1\dots i_{20}\}$, otherwise r is added with probability $p{\prime }_0$.

Adding random noise to the data depends on the tested model. In the binary case, we randomly replace $Z_{v,t,s}$ with $1-Z_{v,t,s}$, with probability p_w if (v, t, s) belongs to the private module of s and with probability p_o otherwise. In the normal model for each (v, t, s) within the private module of s we select ${\mathrm{ϵ}}_{v,t,s}\sim N(0,{\sigma }_w)$, otherwise we select ${\mathrm{ϵ}}_{v,t,s}\sim N(0,{\sigma }_o)$. We then add the noise by updating $Z_{v,t,s}=Z_{v,t,s}+{\mathrm{ϵ}}_{v,t,s}$. We tested scenarios of a single module with and without subject-specific signals and of multiple modules.

3.2 Case 1: a single core module

In this test, we set $p{\prime }_s=1$ and $p{\prime }_0=0$. This case represents the standard biclustering task because there is no subject-specific signal. Thus, biclustering algorithms are expected to achieve high performance.

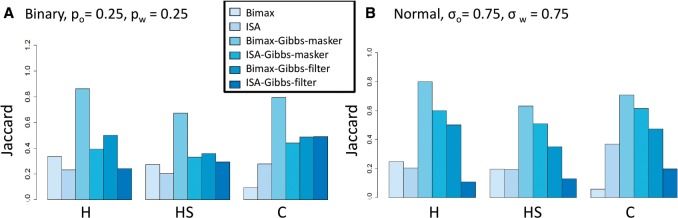
The results are shown in Figure 2A and B. Each algorithm was tested on 10 instances and the average Jaccard score, which quantifies the agreement between the known solution and the algorithm output, is shown. We set high noise levels both in the binary data (Fig. 2A)—$p{\prime }_w=p{\prime }_o=0.25$ and in the normal data (Fig. 2B)—$\sigma {\prime }_w=\sigma {\prime }_o=1$. The Bimax algorithm had a low Jaccard score in most cases, since its output covered only a small part of the true bicluster. Although the false-positive rate was very low (<0.01 both for the bicluster rows and columns), the true-positive rate was low as well (<0.25). ISA performed much better, especially in terms of identifying H and HS. Using TWIGS to improve the solution was beneficial: it was able to keep the high performance of ISA for H and HS and to considerably improve the score of C. It greatly improved the Bimax solution in all criteria. For example, in the normal data, the score of C went up from 0.053 to 0.93. The ISA solution improved from 0.63 to 0.95 using TWIGS. Notably, this improvement was achieved with only 50 sampling iterations, which took less than 7 s on average (over simulation repeats). Thus, this boost in performance was achieved at a low cost of running time. We kept this number of iterations also in subsequent analyses. Note, however, that when the data are much larger (e.g. $\left|T\right|>1000$), the running time could increase to several minutes.

Fig. 2.

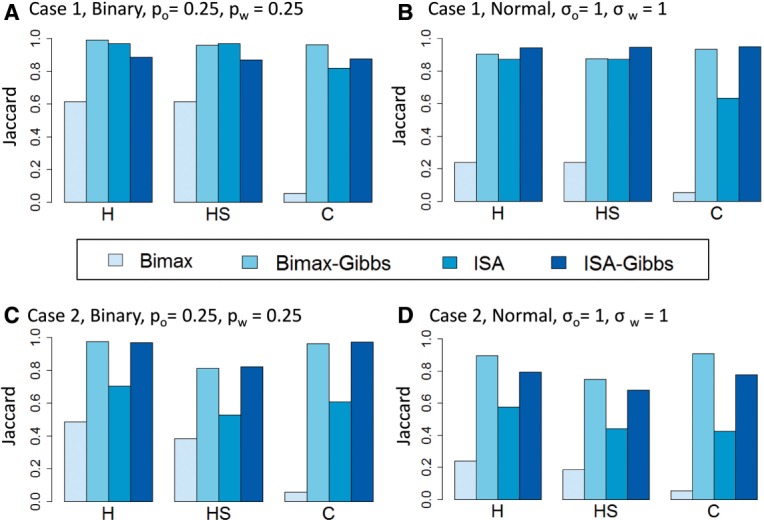
Simulation results for data with a single module. Each bar represents the average over 10 repeats. (A) Case 1: no subject-specific signal. (B) Case 2: with subject-specific signals. The Bimax-Gibbs variant was later chosen as the default TWIGS algorithm

We also tested a binary case in which the noise levels were not symmetric: we set $p{\prime }_w=0.5$ and $p{\prime }_o=0.1$. The results are shown in Supplementary Figure 1. In this case, the Bimax–Gibbs combination reached the top performance in all measurements, with very high scores: 0.92 (H), 0.86 (HS) and 0.93 (C). The performance of both ISA and Bimax was low (all scores were <0.7), indicating that standard algorithms have difficulty in such noise levels.

3.3 Case 2: a core module with subject-specific signal

In this test, we set $p{\prime }_s=0.9$ and $p{\prime }_0=0.01$. Thus, this scenario is different from standard biclustering and triclustering tasks in two ways: (i) not all shared rows are necessarily part of each private module and (ii) each private module is likely to contain additional rows that are not shared among all subjects.

The results (averaged over 10 instances) are shown in Figure 2C and D. The noise levels were $p{\prime }_w=p{\prime }_o=0.25$ in the binary data Fig. 2C) and $\sigma {\prime }_w=\sigma {\prime }_o=1$ in the normal data (Fig. 2D). Similar to Case 1, Bimax had low scores because it typically covered only a small perfect fraction of the module, whereas ISA reached higher performance. However, the performance of ISA was much lower than in Case 1. For example, in the normal data the score of H, which represents the core module rows, dropped from 0.87 in Case 1 to 0.57. This result demonstrates a weakness of standard biclustering algorithms when the data contain subject-specific signal: the algorithms might fail to discover even the shared information. In contrast to ISA and Bimax, TWIGS improved the solution considerably in all measures. For example, the score of H and C was >0.89 when starting with the Bimax solution.

3.4 Case 3: multiple modules

Here, we tested the performance of TWIGS with filter and masker on data with five core modules, each with it own subject-specific signals, using as before $p{\prime }_s=0.9$ and $p{\prime }_0=0.01$. The results are shown in Figure 3. As expected, the results were lower than in the single core module tests. Nonetheless, the results were still high in spite of the high noise levels.

Fig. 3.

Simulation results for data with five core modules. Each bar represents the average over 10 repeats. (A) Binary data. (B) Normal data. The Bimax-Gibbs-masker variant was later chosen as the default TWIGS algorithm

Unlike the previous cases, using masker with Bimax as the base algorithm was much better than all other algorithms. For example, in the binary case (Fig. 3A), it reached scores of 0.86 and 0.8 for H and C respectively, where all other algorithms had scores below 0.6. In the normal data, we observed a sharp decrease in performance when setting the noise levels to ${\sigma }_0=1$ as in the previous sections, see Supplementary Figure 2. With a bit lower noise levels of 0.75, the results were similar to the binary case (Fig. 3B). Interestingly, forcing high mean value in f₁ (i.e. by setting $m_0\ge 1$ and high p₀ constant in the Normal-Gamma model, see Section 2) achieved higher performance scores. For example, setting the mean value to 1.5 improved the score of H from 0.8 to 0.9 and the score of C from 0.71 to 0.77. We discovered that the non-informative variant had some detrimental instances in which some core modules were grouped together (average number of detected modules was 4.2), whereas enforcing high mean for f₁ detected the correct number of core modules.

On the basis of the above results, from this point on, we used the Bimax-Gibbs-masker as the default variant of the TWIGS algorithm.

3.5 Gene expression data

We tested the performance of TWIGS by analyzing transcriptional response of patients to sepsis. Parnell et al. (2013) monitored patients after septic shock. For up to 5 days after sepsis, blood samples were taken daily, and whole blood gene expression was measured using Illumina microarrays. The dataset contained 14 patients for which five profiles, one for each day after sepsis, were available. Our goal was to detect up-regulated biological functions after septic shock. Therefore, for each subject we calculated the log fold change between time points $2,3,4,5$ and the first time point. We binarized the data by setting a threshold of 2 for the fold change (i.e. 1 for the log fold change) and ran masker with Bimax as the base algorithm. See the Supplementary Text for additional analyses using the non-binarized data and for sensitivity analysis of the binarization threshold. We set the minimal size of the detected core module to 10 rows and 10 columns (number of time points from all patients) and f₁ to have ${\pi }^{C1}>0.5$. Using these stop criteria in masker, a single small module of 5 genes was detected over 20 repeats in which we independently and randomly shuffled the values of each row in the input matrix.

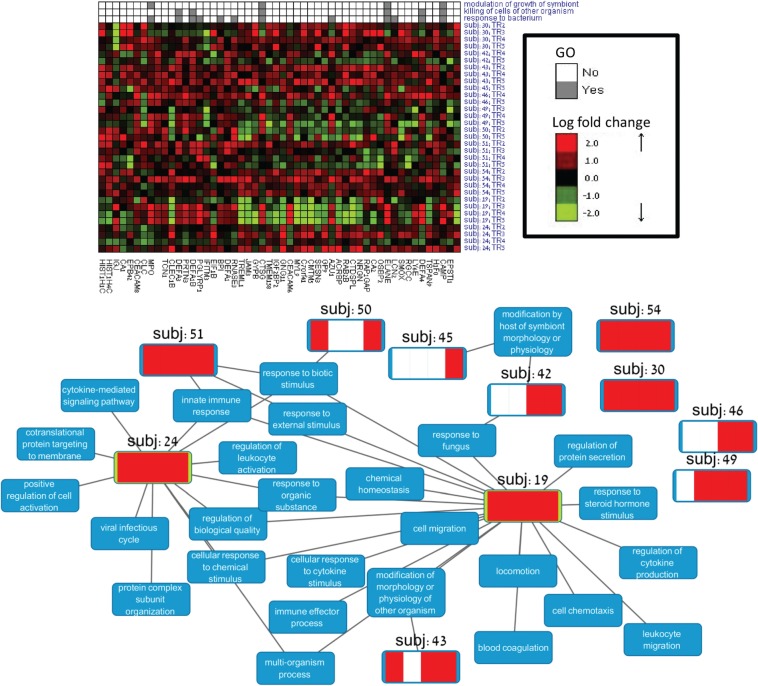
Two core modules were detected on the real expression matrix. The first covered 11 patients and 53 genes. The second covered seven patients and 62 genes. Four patients were represented in both. Distinct private modules were assigned to each subject in each module. Thus, a total of 20 modules (core or private) were detected in the analysis. GO enrichment analysis [using EXPANDER (Ulitsky et al., 2010)] detected significant enrichment (0.05 FDR) in 19 of the modules. The two detected core modules differed in their enriched biological functions. The first was highly enriched with genes related to killing of cells of other organisms ($P=2.7E-11$) and response to bacterium ($P=2.2E-9)$.The second core module was enriched with functions that were more specific to T-cell activity (e.g. regulation of T cell activation $P=4.5E-10$). Thus, TWIGS identified a fuzzy partition of the subjects into two main branches of the immune system and also pointed out the relevant up-regulated genes.

The private modules in the solution were often much larger than the core modules. For example, in the first core module, the private modules of subjects 19 and 24 contained more than 450 genes each. The first core module and the enrichment analysis results of its private modules are shown in Figure 4. See Supplementary Figure 3 for the results of the second core module. Only biological functions that were not significant in the core modules are shown. The figure illustrates how our analysis provides a complementary view to the core modules. That is, although the core modules indicate which biological functions tend to reappear across subjects, the private modules reveal additional enrichments that are sometimes much more specific biologically. For example, the private module of subject 24 was highly enriched with genes related to viral infectious cycle ($P=1.7E-9$). The network also highlights patients without subject-specific unique enrichments (subjects 30, 46, 49 and 50) and two hubs: subjects 24 and 19. Strikingly, out of the 11 patients covered by this core module, these two patients had much larger private modules and they were the only patients that did not survive the septic shock.

Fig. 4.

A module summarizing patient response to sepsis. Top: the first core module heatmap. Bottom: the subject-specific enrichments. The red stripes in each patient’s node represent the time points that were covered by its private module. An edge between a subject and a category (blue node) indicates that the subject-specific module was enriched for that category

3.6 fMRI data

Vaisvaser et al. (2013) collected brain fMRI data from 20 male subjects at rest over 94 time points. In this technique blood flow (BOLD) intensity is measured at every voxel of the brain along time, providing levels of some 100 000 voxels every 2–3 s. The level reflects the activation intensity of the brain voxel. Standard fMRI preprocessing was applied on the raw data as reported in (Vaisvaser et al., 2013). We used a whole brain functional parcellation to transform the data into 517 brain parcels (Craddock et al., 2012). Parcels were masked to include gray matter voxels only using the WFU Pick Atlas Tool (Maldjian et al., 2003; Stamatakis et al., 2010) and 54 parcels that had $\le 5$ gray matter voxels were excluded. For each subject, average BOLD value across all gray matter voxels was calculated within each parcel at each time point. As is standard practice in fMRI analysis (Birn, 2012), to reduce the effect of physiological artifacts and nuisance variables, the whole-brain mean signal, six motion parameters, cerebrospinal fluid and white matter signals were regressed out of the parcel signals. The result is a matrix M_s for each subject s, in which rows are parcels and columns are time points. We standardized the signal of each row in M_s by subtracting the mean and dividing by the standard deviation. This normalization allows us to find relative changes in the activity of brain regions to highlight temporally activated regions (Rana et al., 2013).

We ran TWIGS with the normal model, Bimax as the initial solution finder and masker. With non-informative priors, the algorithm converged to large modules with relatively low mean value (<0.5). As we were interested in highly activated brain regions, we reset the mean of f₁ to a high value: we tested ${\mu }_1=1.5$ and ${\mu }_1=2$. As in the simulations, using such prior improved the results considerably since the non-informative variant tended to merge core modules with high mean value. No module was detected when running the algorithm after randomly and independently shuffling each row of the data matrix (20 repeats).

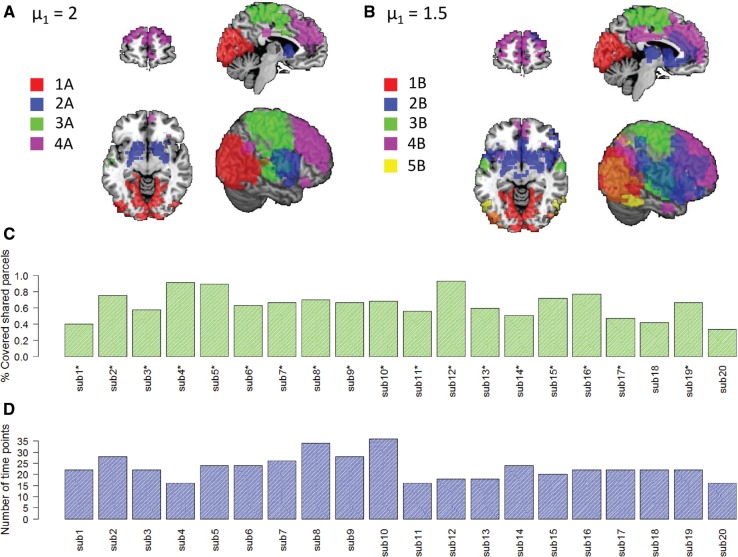
Unlike in the gene expression analysis, each subject participated in each core module. For ${\mu }_1=2$ (Fig. 5A), four core modules were detected (labeled 1A–4A), with an average of 48.5 parcels. For ${\mu }_1=1.5$ (Fig. 5B), five core modules were detected (labeled 1B–5B), with an average of 66.4 parcels. Out of the five core modules detected using ${\mu }_1=1.5$, four had a parallel core module detected using ${\mu }_1=2$. In addition, modules 1A and 1B maintained similar spatial structure and size and so did 3A and 3B. Modules 2A and 4A were larger than their counterparts.

Fig. 5.

Results of the fMRI analysis. (A) The core module rows of the solution with ${\mu }_1=2$. (B) The core module rows of the solution with ${\mu }_1=1.5$. (C, D) Examples of subject-specific statistics. This example shows the results for core module 4B. (C) The percent of core module parcels covered by the private modules. Asterisks indicate subjects whose private module had a significant overlap (hyper-geometric $P\le 0.001$) with the core module. (D) The number of time points in each private module

We evaluated the parcel sets of the identified core modules by comparing them to known functional annotations of the brain (Yeo et al., 2011). The results show that our analysis detected well-known functional modules that are expected to share common activation patterns both during task and at rest. In both solutions, core module 1 was enriched with regions that are involved in visual processing in the occipital lobe of both hemispheres ($q\le E-11$) (Belliveau et al., 1991). Core module 2B was enriched with parcels located within the ventral attention network, which is involved in bottom-up orienting of attention ($q\le 0.02$) (Fox et al., 2006). In both solutions, core module 3 was enriched with parcels located in regions that are involved in sensori-motor processing ($q\le 1E-11$) and in parcels located within regions of the dorsal attention network, which is involved in top-down orienting of attention ($q\le 0.03$) (Fox et al., 2006). Modules 4A and 4B were enriched with parcels located in the default mode network ($q\le 1E-4$), which is composed mainly of midline structures and is involved in self referential functions that include remembering the past as well as planning the future, and the frontoparietal control network, which is responsible for adaptive behavior ($q\le 1E-7$) (Dosenbach et al., 2007). Finally, core module 5B contained 29 parcels and was enriched with regions that are involved in visual processing ($q\le 5E-9$) and with parcels that are located within the dorsal attention network ($q\le 0.001$).

Inspecting the private modules, we observed large heterogeneity in their tendency to overlap with their core module parcels and in the number of time points. Figure 5C and D shows the results for core module 4B. This module is of particular interest as it was enriched with both the default mode network and the frontoparietal control networks. Patterns of co-activation between these two networks have been reported before and suggested to support goal-directed thought processes (Spreng et al., 2010). On average, each private module covered 44.4% of the core module parcels (Fig. 5C) and contained 15.5 time points. In addition, in 18 out of 20 subjects, the overlap between the subject-specific parcels and the core module parcels was significant (hyper-geometric P < 0.001). Other modules had much higher coverage. For example, core module 1B had mean coverage of 64.4% and a larger number of time points (mean 23), see Supplementary Figure 4.

When including the private modules in the enrichment analysis, 15 out of 20 private modules of core module 4B were also enriched with the default mode network. The frontoparietal control network was identified in 12 of the 20 subjects. Although to a much lower extent than in the gene expression analysis, we also detected subject-specific signal. For example, ventral attention enrichment was identified in 4 out of 20 subjects but not in the core module. This suggests a tendency of these four subjects to engage in bottom-up processing (e.g. be more attentive to sensory stimuli) during goal-directed thought processes. These results demonstrate the advantage of our multi-subject analysis: it was able to detect large functional networks that reappear as activated across subjects and even highlight subject-specific activation patterns.

3.7 Comparison to related algorithms

Extant algorithms for three-way data analysis were mainly developed for gene expression data. Triclustering (Zhao and Zaki, 2005) assumes that a module is a subcube created by one subset in each of the three dimensions. This setting is too rigid for simultaneous analysis of responses in many patients. Figures 4 and 5 show that our modules are not triclusters since the time points and gene set of each private module differ under the same core module. Another type of three-way analysis seeks biclusters $<G\prime ,S\prime >$ where $G\prime$ is a set of genes and $S\prime$ is a set of subjects, such that all genes in $G\prime$ manifest a similar time response across all subjects in $S\prime$. Two such algorithms are EDISA (Supper et al., 2007), which seeks high correlation between subjects across time points, and the plaid model of Mankad and Michailidis (2014), which extends (Lazzeroni and Owen, 2002) and seeks up- or down-regulated time responses. Finally, Gerber et al. (2007) simultaneously cluster tissues and genes to produce biclusters, while accounting for three possible time responses for each tissue when introduced to a drug. However, this analysis answers very different questions than TWIGS as it assumes a hierarchical structure of tissue clusters without overlap, whereas we analyze a single tissue over many time points at rest and allow overlapping core modules.

We compared TWIGS to seven methods: ISA (Bergmann et al., 2003), Bimax (Prelic et al., 2006), SAMBA (Tanay et al., 2004), EDISA (Supper et al., 2007), the plaid model (Mankad and Michailidis, 2014), sliding window analysis of fMRI data (Allen et al., 2014) and modularity analysis of fMRI data (Rubinov and Sporns, 2010, 2011). For each method, we tested a wide range of its internal parameters to fine tune it for the tested dataset. The Supplementary Text provides all details; here we give a brief overview.

Our comparison shows that except for modularity analysis (which enforces using all subjects by the method’s definition), extant methods have difficulties in finding modules that cover many subjects. TWIGS provides an almost 2-fold improvement in the ability to find modules that cover many patients. For example, on average, modules identified by EDISA on the sepsis data covered less than five patients compared with nine by TWIGS. The sliding window analysis, which estimates the covariance matrix of each time window and then clusters all windows from all subjects, had an average coverage of less than 10 on the fMRI data, whereas TWIGS covered all 20 subjects. TWIGS was comparable to other methods in enrichment analysis for known biological functions in terms of: (i) the total number of covered functions, (ii) the strength of the detected enrichments and (iii) the fraction of modules with enriched terms. When consolidating scores 1–3 using non-parametric ranking, TWIGS ranked first.

When applying the plaid model to the sepsis data, it tended to find much larger gene sets. However, these modules manifested a very mild up-regulation response compared with the TWIGS modules. The fMRI modularity analysis method of Rubinov and Sporns (2010, 2011) partitioned the brain into clusters, each containing one of our core modules. TWIGS’s subject-specific module augmentations provided additional biological results.

4 Discussion

We presented a novel problem formulation and algorithm for flexible three-way clustering of multi-matrix time course data. We defined a core module as (i) a set of rows that are likely to be active together across a set of subjects and (ii) a set of active time points in each covered subject. In addition, each core module has subject-specific private modules that can contain additional genes and have high overlap with the core module. The set of active time points of a module can vary in size and times among subjects.

Our model is much more flexible than existing models. First, it allows different active time points for each subject, thereby accommodating heterogeneity and asynchrony in the response of different subjects. Second, different subjects can differ in their underlying features (rows) and time points (columns). The row set of a particular subject in a module does not necessarily cover all core module rows. This property was crucial in the analysis of fMRI data, where it allowed discovering core modules that better covered active brain regions. In addition, the row set of a private module can contain additional rows that represent subject-specific signal. This property was crucial in the gene expression case as it allowed discovering patient-specific up-regulated immune processes.

We compared TWIGS to seven other methods and showed that extant methods have difficulties in finding modules that cover many subjects, whereas TWIGS easily finds modules that represent a biological function shared by many subjects. In addition, our method outperformed other methods in terms of enrichment analysis. We employed additional metrics for evaluation in each domain. Other comparison criteria can be used in the future, e.g. test-likelihood or perplexity.

Our current analysis has some limitations that can be addressed by future studies. First, we assume that the data originated from two distributions f₀ and f₁. Other approaches could be considered, such as row-based or column-based additive models (Lazzeroni and Owen, 2002). Second, our basic model deals with only a single module at a time. More complex models and algorithms could be proposed to directly model multiple modules. Finally, additional tests are needed to fully exploit the abilities of the model. For example, we focused only on testing a time window of size 1 to find homogenous highly activated private modules.

Funding

This study was supported in part by the Israel Science Foundation (grant 317/13, to R.S.), the Azrieli Foundation Fellowship and the Edmond J. Safra Center for Bioinformatics at Tel Aviv University (to D.A.). Additional support was provided by the Israeli Centers of Research Excellence (I-COREs) Gene Regulation in Complex Human Disease, Center No. 41/11 (R.S.) and Program in the Cognitive Sciences (to T.H.).

Conflict of Interest: none declared.