A generic methodological framework for studying single cell motility in high-throughput time-lapse data

Abstract

Motivation: Motility is a fundamental cellular attribute, which plays a major part in processes ranging from embryonic development to metastasis. Traditionally, single cell motility is often studied by live cell imaging. Yet, such studies were so far limited to low throughput. To systematically study cell motility at a large scale, we need robust methods to quantify cell trajectories in live cell imaging data.

Results: The primary contribution of this article is to present Motility study Integrated Workflow (MotIW), a generic workflow for the study of single cell motility in high-throughput time-lapse screening data. It is composed of cell tracking, cell trajectory mapping to an original feature space and hit detection according to a new statistical procedure. We show that this workflow is scalable and demonstrates its power by application to simulated data, as well as large-scale live cell imaging data. This application enables the identification of an ontology of cell motility patterns in a fully unsupervised manner.

Availability and implementation: Python code and examples are available online (http://cbio.ensmp.fr/∼aschoenauer/motiw.html)

Contact: thomas.walter@mines-paristech.fr

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

High-throughput (HT) microscopy and high content screening (HCS) are state-of-the-art approaches to investigate many aspects of cellular organization and function, such as protein localization (Glory and Murphy, 2007), spatial transcriptomics (Battich et al., 2013) or drug screening (Perlman et al., 2004).

In particular, when combined with a loss-of-function strategy, these approaches are now widely used to study the molecular basis of biological processes by monitoring the phenotypic consequences of downregulation or overexpression of genes of interest (Pepperkok and Ellenberg, 2006). When performed at a large and ideally genome-wide scale, such screening approaches have become indispensable tools for functional genomics: they have the potential to provide us with a close to complete picture of the proteins involved in the process under study.

Indeed, many large-scale phenotypic screens have been published previously, shedding light on the regulation of such diverse cellular processes as protein secretion (Simpson et al., 2012), endocytosis (Collinet et al., 2010) or cell division (Neumann et al., 2010). Such screens do not only provide lists of candidate genes for further follow-up studies and for computational modeling approaches, they also generate large image databases. Those can turn out to be a precious scientific resource—as a collection of experimental data for punctual queries or as a basis for systematic and potentially integrative computational analysis. Although it has always been a strength in bioinformatics to rely on rich publicly available data sources, the use and re-use of image data is not straightforward. On the one hand, this is due to the lack of standardized data formats (Sommer et al., 2013) and ontologies (Hoehndorf et al., 2012). On the other hand, the computational tools which are necessary to perform such analyses are often not available. As a consequence, studies based on remining existing phenotypic screens have only recently started to appear (Ostaszewski et al., 2012; Pau et al., 2013; Suratanee et al., 2014). We hypothesize that remining these rich phenotypic resources can help to increase our understanding of many basic cellular functions, such as cell motility.

Cell motility plays a key role in many physiological processes including embryonic development or immune response (Friedl and Weigelin, 2008), and is also involved in pathological processes such as fibrosis and metastasis. The latter is dependent on the ability of cancer cells to migrate, both as single cells and collectively (Decaestecker et al., 2007; Yilmaz and Christofori, 2010).

Many in vitro assays have been specifically designed to study cell motility (Decaestecker et al., 2007; Kramer et al., 2013). Examples include semi-automated analysis of single cell traces on bead-coated layers (Naffar-Abu-Amara et al., 2008) and wound healing assays measuring collective cell migration (Simpson et al., 2008).

However, single cell motility studies on live cell imaging data have so far been limited to low-to-medium (Lara et al. 2011) throughput. There are two bottlenecks that currently explain the non-existence of such studies in an HT setup: acquiring large-scale data is expensive, and the relevant computational tools are often either non-existent or not easily scalable.

The contribution of this article is to present MotIW (Motility study Integrated Workflow), and its application to motility gene discovery. A generic methodological framework, MotIW enables to quantitatively study cell motility at single cell resolution in HT time-lapse data in an unsupervised way. It consists of cell tracking, cell trajectory mapping to an original feature space and outlier experiment detection according to a new statistical procedure (Fig. 1). We show the power of our method by applying MotIW to simulated data, which allows us to estimate recall and precision to be expected on real data. We then apply this workflow to a previously published genome-wide screen by RNA interference (RNAi) and live cell imaging, the Mitocheck dataset. Analysis of the screening data reveals the existence of a cell trajectory ontology in the dataset. Without any prior assumption on cell motion, we are able to identify eight types of cell trajectories.

Fig. 1.

Overview of MotIW

The remainder of this article is organized as follows: after a short description of the data and the implementation details in Section 2, we detail MotIW in Sections 3.1–3.3, as well as its application to simulated data in Section 3.4 and the Mitocheck screen in Section 3.5. Section 4 briefly discusses broader perspectives of this workflow.

2 Materials and methods

2.1 A genome-wide time-resolved dataset

We used a previously published genome-wide dataset of time-resolved records of cellular phenotype responses to gene silencing, which were generated for virtually all protein-coding genes (Neumann et al., 2010). It is publicly available at mitocheck.org.

For this, arrays of transfection cocktails containing small interfering RNAs (siRNAs) were spotted directly in live cell-imaging chambers in a 384 format. HeLa cells stably expressing the core histone 2B tagged with green fluorescent protein (GFP) were seeded on top of the arrays, and imaged 18 h after the transfection for 48 h with a time lapse of 30 min (Plan10x, NA 0.4; Olympus). Each microarray contained 8 negative controls (scrambled: not targeting any gene) and 12 positive controls showing different phenotypes. A total of 22 612 protein-coding genes have been targeted by at least 2 siRNAs each, in total 51 767 siRNAs. For each siRNA, there are data from at least 3 technical replicates, which created 182 191 quality controlled time-lapse experiments in total. Because of updates in the genome annotation, some reagents could not be mapped to the current ENSEMBL version. In total, the dataset contains data for 17 816 protein-coding genes in144 909 quality controlled time-lapse experiments.

2.2 Software

We use CellCognition (Held et al., 2010) (cellcognition.org) for segmentation and feature extraction and CPlex (http://www-01.ibm.com/software/commerce/optimization/cplex-optimizer/) for optimization in the tracking procedure. To store, manage and access the screening data, we use a previously published data format CellH5 (Sommer et al., 2013). All scripts are written in the programming language Python 2.7 using SciPy (Jones et al. 2001) and NumPy, and all plots were generated by matplotlib (Hunter 2007).

3 Results

In this section, we present MotIW, our workflow for the automatic and quantitative analysis of single cell motility in video sets from time-lapse microscopy-based screens. Figure 1 summarizes its different steps. Briefly, for each video nuclei are segmented and features are extracted as published previously (Held et al., 2010; Walter et al., 2010). Cells are tracked using a new machine learning-based tracking procedure, described in Section 3.1. The trajectories are then mapped to a feature space described in Section 3.2. Presented in Section 3.3, an original statistical procedure then enables the detection of experiments in which single cell motility is significantly different than that in control movies. Finally, Section 3.4 describes the simulation of trajectories which allows us to validate the performance of the workflow.

3.1 Cell tracking

There exist two main approaches to cell tracking. The deformable model approach relies on identifying and modeling objects on the first frame, and linking them to objects in consecutive frame by updating the models (Zimmer et al., 2002). On the other hand, the object association approach associates preidentified objects in consecutive frames (Lou and Hamprecht, 2011).

Different datasets usually require different object identification approaches. For the sake of modularity, we therefore prefer to keep segmentation and tracking steps independent.

Cell tracking faces several challenges in videos from high content screens like Mitocheck, including high population density in each picture, high phenotypic inter-cell variability and possibly low time resolution between successive images (30 min). Furthermore, the algorithm has to handle apparitions, disparitions, divisions and fusions (this event results from occlusion or segmentation errors). Finally, to be applicable in a screening context, we cannot a priori model cell motion, as such hypotheses are bound to break in the presence of phenotypes. Indeed, the impact of chemical exposure on cell motion is not known. To also avoid dependence on manual parameter tuning, we have extended a non-parametric structured learning approach from Lou and Hamprecht (2011).

We first characterize each cell in each image by a set of 230 object features including geometric, shape and texture features (Held et al., 2010; Walter et al., 2010). The goal of cell tracking in this approach is to match cells in successive images, by assigning them the most likely instant temporal behavior in the set E = {move, appear, disappear, split in 2 or 3, merge at 2 or 3}. All possible matches between cells in consecutive frames are exhaustively considered, subject to distance thresholding. Match features are the following:

• the absolute difference in object features if the event is move, split, merge, the object features otherwise

• the geometrical distance between object at time t, $Ob{j}_{i,t}$, and object at time t + 1, $Ob{j}_{j,t+1}$, if the event is move, split, merge, the minimal distance to the image border otherwise

• the maximal angle between $Ob{j}_{i,t}$ and the elements of $Ob{j}_{j,t+1}$, if the event is a split

• the angle between the main axis of $Ob{j}_{i,t}$ and $Ob{j}_{j,t+1}$ weighted by their average eccentricity, if the event is a move

The optimal object matching $\widehat{z}(t)$ comes down to bi-partite graph matching: it is solved by maximizing a likelihood function L which depends on the weights w of match features and the match features $f_{i,j}^e$, subject to the constraint that all objects are matched in both frames [cf Equation (1)].

$$\widehat{z}(t)=\text{\&}\underset{z(t)}{\mathrm{argmax}}\hspace{0.5em}L(z(t);w)$$ (1)

where

$$\begin{array}{l}L(z(t);w)={\displaystyle \sum _{\begin{array}{c}e\in E\\ Ob{j}_{i,t}\\ Ob{j}_{j,t+1}\end{array}}<}{w}^e,f_{i,j}^e>z_{i,j}^e(t)\\ s.t.\forall i{\displaystyle \sum _{\stackrel{e}{Ob{j}_{j,t+1}}}{z}_{i,j}^e}(t)=1\\ and\forall j{\displaystyle \sum _{\stackrel{e}{Ob{j}_{i,t}}}{z}_{i,j}^e}(t)=1\end{array}$$

The weights w are learned by a support vector machine using annotated trajectories, following the formulation of Lou and Hamprecht (2011). The likelihood maximization, an integer linear programing (ILP) problem, is solved by IBM Cplex.

The extension compared with Lou and Hamprecht (2011) lies in the choice of match features. We also implemented a more efficient computation of match hypotheses using kd-trees. Furthermore, we enabled the tracking model to learn from partial annotations of different experiments. (However, this is not learning from partial annotations in the sense of Lou and Hamprecht (2012). Indeed, in our implementation of Lou and Hamprecht (2011), the user chooses a subset of cells which has to be annotated on all movie frames. In Lou and Hamprecht (2012), the user can choose both a subset of movie frames and a subset of cells (s)he wishes to annotate on those frames.) This permits the user to integrate examples from both control and non-control experiments in the training set, which is crucial to guarantee that the model can efficiently track cells in all conditions. We also added three object division and fusion to E. This is important in a screening context, where aberrant cell divisions may occur. In the future, it could be interesting to couple object segmentation and tracking to correct for missing detections.

To validate MotIW’s cell tracking procedure, we compare it with CellCognition’s constrained nearest-neighbor (CNN) tracking algorithm, and with Jaqaman et al. (2008) as implemented in CellProfiler (Carpenter et al., 2006). The latter approach views tracking as a linear assignment problem (LAP) and uses user-defined costs for performing merges, splits, appearances and disappearances. We have chosen these two approaches for benchmarking, as they are available in popular High Content Screening software.

Our training set consists of ∼32 000 matches, among which 0.5% appear, 0.5% disappear, 1% merge and 2% split. They come from the Mitocheck dataset. Furthermore, they were taken from both control experiments and phenotypic experiments according to Neumann et al. (2010) in order to ensure that the algorithm also works in the presence of phenotypes. The training set was annotated using CellCognition’s CNN tracking algorithm followed by manual correction. As shown in Table 1, MotIW outperforms the other two methods as measured by the average accuracy on the five movement types. As can be seen in Figure 2, they show similar performances on move events and have therefore similar overall (pooled) accuracies. The contribution of the learning approach is most important for the other events, such as cell division, when object matching is less trivial.

Table 1.

Mean recall and precision on all types of matches E (10-fold cross-validation)

Algorithm	Mean recall (%)	Mean precision(%)
CNN	72.7	62.8
Jaqaman et al. (2008)	78.3	73.0
MotIW	91.1	91.5

Fig. 2.

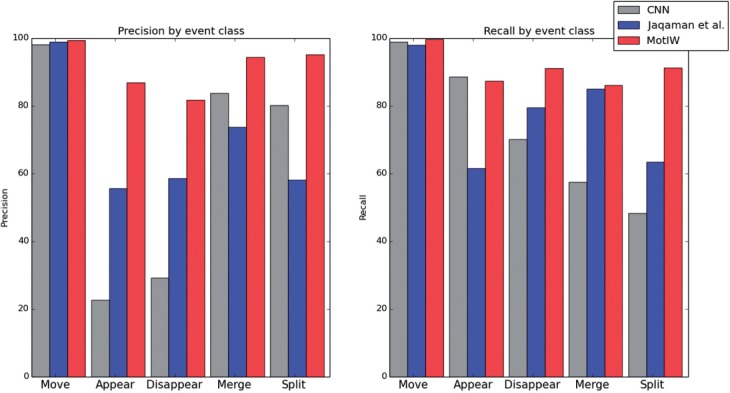
Details of tracking precision and recall according to event types

3.2 Trajectory features

Once cell trajectories are captured, each trajectory is described by a set of 15 features. These features were partly taken from previous publications on quantitative motility analysis, partly newly designed.

Robust and precise features are needed to account for the partial stochasticity of cell migratory behavior. We use three types of features, as detailed in Table 2. Prior to that, trajectories resulting from object fusion and trajectories which are shorter than 10 frames are discarded. This trajectory quality control ensures that cell clusters are not considered, and increases the dataset robustness.

Table 2.

Cell trajectory features and their formulas

Particle motion features
Diffusion coefficient	According to Sbalzarini and Koumoutsakos (2005)
Diffusion adequation	Correlation between MSD(t) and t
Movement type	According to Sbalzarini and Koumoutsakos (2005)
Englobing ball number	See text
Track entropy	See text
Other global features
Convex hull area	—
Effective path length	$L=\left|\right|m_T-m_1|{|}_2$
Effective speed	$L/\sqrt{T}$
Largest move	—
Straightness index	$\sqrt{T}L/P$
Track curvature	See text
Averaged local features
Mean squared displacement (MSD)	$\frac{1}{T-1}{\displaystyle \sum |}|m_t-m_{t-1}|{|}_2^2$
Mean signed turning angle	$\arctan (\frac{\Sigma \sin ({\alpha }_{t+1}-{\alpha }_t)}{\Sigma \cos ({\alpha }_{t+1}-{\alpha }_t)})$

Note: Notations: ${(m_t)}_{t=1\dots T}$, time sequence of cell 2D positions; T, track time duration; P, total track length.

3.2.1 Particle motion features

This group of features encompasses the diffusion coefficient and the movement type, which were in the first place used to study particle motion (see Ferrari et al., 2001; and one of its applications to single particle motion in Biology—Sbalzarini and Koumoutsakos, 2005).

Let us note $<d^p>$ the moment of order p of a particle or a group of particles. For large t, it is proportionate to $t^{{\gamma }_p}$ for most dispersive processes (Ferrari et al., 2001). Assuming that γ_p is proportionate to p (i.e. the particle movement is strongly self-similar), the constant $\gamma ={\gamma }_p/p$ (hereafter the particle’s Movement type) quantifies how directed the particle motion is. If γ is equal to 1, the movement is perfectly directed, whereas if γ is equal to 0.5, it is perfectly diffusive. Between 0.5 and 1, the movement is super-diffusive, whereas below 0.5 it is called sub-diffusive.

Furthermore, assuming $\gamma =0.5$, the constant linking $<d^2>$ [i.e. the mean squared displacement (MSD)] and t can be computed—it is the Diffusion coefficient. The Diffusion adequation is the correlation coefficient between $<d^2>$ and t, hence measuring how well the diffusive model applies to the track at hand.

We have furthermore created two new features to characterize the alternance between periods of diffusive motion and periods of directed motion—the track entropy and the englobing ball number.

It has been observed that cell motion in 2D alternates between diffusive and directed motions (in the absence of any perturbation or chemical gradient). The feature track Entropy was designed to measure how the time sequence of 2D cell positions $m_t=(x_t,y_t)$ distributes in balls of radius r (see also Figure 3). This feature is calculated according to the following procedure, for each track of time duration T:

1. $S=\{1,\dots ,T\}$

2. while $S\ne \left\{\right\}$:i. do $t^{\mathrm{\star }}\leftarrow \text{\&}\underset{S}{\mathrm{argmax}}card(B_r(t))$where $B_r(t)=\left\{i\right|\left|\right|m_i-m_t|{|}_2\le r\text{\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}and}$$min(||m_{i-1}-m_t|{|}_2,\left|\right|m_{i+1}-m_t|{|}_2)\le r\}$ii. do $S\leftarrow S\backslash B_r(t^{\mathrm{\star }})$

3. Compute the track Entropy according to the following formula:

$$Entrop{y}_r=-\frac{1}{T}\sum _{B_r}\frac{card(B_r)}{T}\log (\frac{card(B_r)}{T})$$ (2)

Fig. 3.

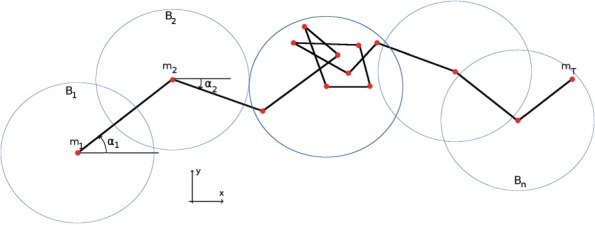
A cell trajectory with notations

The track Entropy measures the entropy of the distribution of track positions in balls of radius r. To deal with cells whose trajectories are concentrated in space, but were not concentrated in time, the constraint is imposed that these balls shall contain only consecutive positions in time.

The englobing Ball number is the number of balls of radius r that contain all track positions. It is normalized by the square root of T to be independent of the track time length T.

Different radii may be relevant for different data (depending on, e.g. the experiment time lapse, the pixel size or the cell type). We chose to use two different radii, $r_1\mathrm{and}{r}_2\mathrm{with}{r}_1<r_2$, to incorporate information about cell trajectories on two different time scales. $r_1\mathrm{and}{r}_2$ were manually chosen, such that for the Mitocheck dataset, the corresponding features are neither constant nor too correlated. They respectively correspond to ∼2.5 and 12 µm. In the following, the features Entropy i and Ball number i correspond to radius r_i.

3.2.2 Other global features

This group of features encompasses further global descriptors of the cell trajectory, such as the track Convex hull area (normalized by the square root of its time length) or the cell Largest move on its trajectory. It also contains the average Track curvature, which we designed as follows for each trajectory: for each position t, an orthogonal regression is performed on $\{(x_i,y_i)|i\in \{t,\dots ,t+{\Delta }_t\}\}$ using orthogonal distance regression (${\Delta }_t=10$). The mean curvature of the trajectory is the average of all regression sums of squares.

3.2.3 Averaged local features

Finally, two features are averaged local features, which are the cell MSD and its Mean signed turning angle.

3.2.4 Feature set evaluation

Track time length is an irrelevant random variable for studying single cell motility, which could bias some features. Therefore, we ensured that they are not significantly correlated with this parameter: the correlation between track time lengths and features is maximal for the Effective space length, where it is equal to ∼30% (on a subset of the Mitocheck dataset, data not shown).

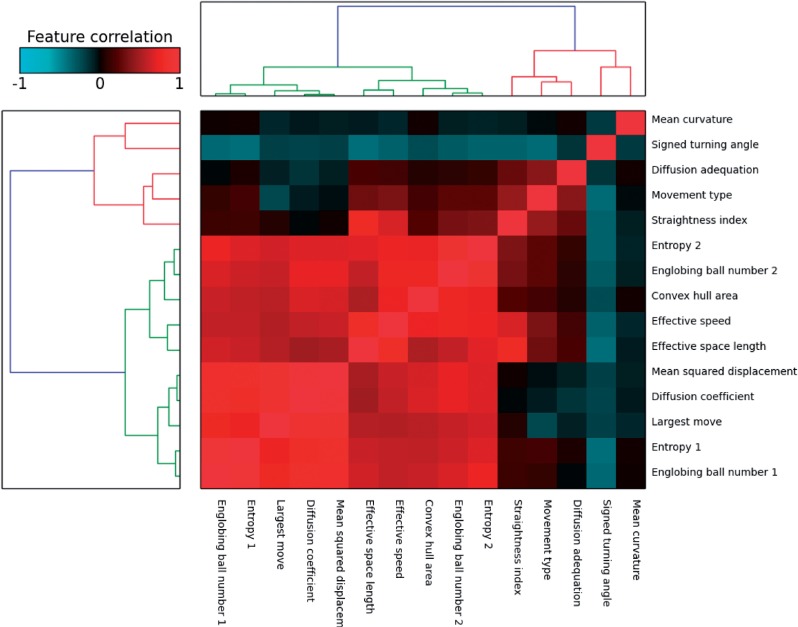
Figure 4 shows the correlation matrix for the extracted features. One group of highly correlated features is visible in the bottom left corner of the heatmap, which encompasses speed-related features. The existence of two feature subgroups within this group can be explained by the following observation: the first group of features, from Ball number 1 to MSD, is linked to cell instantaneous displacements, whereas the second group, from Effective speed to Entropy 2, is linked to its displacements on the whole trajectory.

Fig. 4.

Heatmap showing trajectory feature similarities on a subset of the Mitocheck dataset (1.1 million trajectories coming from detected motility hit experiments according to MotIW). The dengrograms were obtained using the Ward method and the Euclidean distance between feature correlations

The other correlations can as well be explained by feature definitions. As an example, the anti-correlation between Mean signed turning angle and Movement type can be interpreted as follows: a low signed turning angle is indicative of correlated motion, which is super-diffusive and translates into a high Movement type.

Figure 4 indicates that there are less degrees of freedom than features, which was verified by a principal component analysis (PCA). On the same trajectory subset, ∼95% of the variance is explained by the first seven principal components.

3.3 Statistical procedure

HT screening data are organized in batches of experiments which have been performed simultaneously. Each batch includes a set of negative controls, that is, conditions where no effect is expected. Because of a non-negligible batch effect, an experiment can only be compared with controls of the same batch in most of the cases.

Let us consider an experiment i. Following trajectory feature extraction, it can be summarized as a set of Θ feature distributions (Θ = 15). The comparison of these distributions with those of controls from the same batch B_i, using Kolmogorov–Smirnov two-sample test, provides a list of p values ${(p_{\theta })}_{\theta =1\dots \Theta }$.

A final statistic S_i combining the p values of all features is obtained by Fisher’s formula:

$$S_i=-2{\displaystyle \sum _{\theta }l}n(p_{\theta })$$ (3)

As shown in Figure 4, the features are not independent. Therefore, the distribution of this statistic under the null hypothesis does not follow a chi-squared law with $2\Theta$ degrees of freedom. To assess which values of this statistic should be considered as indicative of altered motility, a sample of the distribution of S under the null hypothesis is then computed by comparing the control experiments which were not used in the experiment–control comparisons, with the other controls from the same batch.

In the absence of an explicit form for the null distribution, this sample allows to quantify the intra-batch variations of single cell motility features. The variations can be due to technical artifacts or biological variability. Then, the comparison of the distribution of S statistics obtained from control–experiment comparisons, to the distribution obtained from control–control comparisons, permits the computation of empirical p values. This enables the detection of hit experiments with regard to single cell motility. False discoveries are controlled using the Benjamini–Hochberg procedure (Benjamini and Yekutieli, 2001). This procedure is repeated n times to ensure that the final p value of an experiment i does not depend on the choice of a specific subset of control experiments in its batch. Here is its formalized description:

• 1. Compute a sample of statistic (3) under null hypothesis from control-control comparisons.

• For each batch b,

• For k in $\{1,\dots ,C_b(C_b-1)/2\}$, where C_b is the number of controls of batch b that passed the quality control

  1. Randomly split the control experiments in two groups $A_{b,k}$ of cardinal 2, and $B_{b,k}$ of cardinal $C_b-2$
  2. For each control j of $A_{b,k}$, compute the statistic $S_{b,k,j}^0$ (3) by comparing it with the pooled group of controls $B_{b,k}$

  • 2. Compute statistics from experiment–control comparisons. For computation time feasibility, only n = 5 repetitions corresponding to n splits of the controls set $(A_{b,k},B_{b,k})$ are selected on each batch for experiment–control comparisons.

  1. For each repetition k in $\{1,\dots ,n\}$: For each experiment i belonging to a batch b, compute the statistic $S_{k,i}$(3) by comparing it with the pooled group of controls $B_{b,k}$
  2. Combine distinct iterations: To be conservative, we chose the following approach:

  $$S_i=\underset{k\in \{1\dots n\}}{\max }{S}_{k,i}$$ (4)
• 3. For each experiment i, compute the p value p_i:

  $$p_i=max\left(\frac{card(\{(b,k,j)|S_{b,k,j}^0\ge S_i\})}{card(\{(b,k,j)\})},\frac{1}{card(\{(b,k,j)\})}\right)$$

• 4. For each experiment i, compute the adjusted p value $p_i^{\prime }$ to control the false discovery rate (Benjamini–Hochberg procedure; Benjamini and Yekutieli, 2001)

3.4 Validation on a simulated screen

3.4.1 Screen simulation

To evaluate the performance of our workflow on data for which the ground truth is known, we designed a process to simulate an HT screening experiment.

In a first step, five types of single cell movements were designed, in agreement with qualitative observations from the dataset: random, fast random, curbed directed, flip directed and stop-and-go (Fig. 5).

Fig. 5.

Simulated trajectories: stop-and-go (green), flip directed (red), random (orange), fast random (purple) and curbed directed (blue)

Let $(d_t,{\varphi }_t)$ be the polar coordinates of the difference vector $m_{t-1}-m_t$ of any two consecutive points. For random movement, ${\varphi }_t$ is chosen at random and the distance $d_t=\left|\right|m_t-m_{t-1}|{|}_2$ is drawn from a normal distribution, whose parameters are estimated from the data. The same holds for fast random with increased distance d_t. For the curbed-directed movement type, d_t follows again a normal distribution as for random movement, but the angle is calculated as ${\varphi }_t+\mathrm{ϵ}$ with ${\varphi }_t={\varphi }_{t-1}+\Delta {\varphi }_t$, where $\Delta {\varphi }_t$ and ϵ follow normal distributions, whose parameters are set manually to visually match some observed trajectories.

Flip directed and stop-and-go are two composite types of movement, where the cells alternate between different states. The dwelling times in the two states are random integers with manually fixed ranges (which can be different for the two states) and are drawn independently for each trajectory. Flip-directed movement corresponds to directed movement (${\varphi }_t$ is drawn from a normal distribution) with a 180° flip for every state transition. Finally, stop-and-go movement alternates between slow random movement (where ${\varphi }_t$ is drawn from a uniform distribution) and fast-directed movement (where ${\varphi }_t$ is drawn from a normal distribution).

In a second step, we want to simulate movies (controls and experiments), that is, sets of trajectories. For this, we define five movie types with different proportions of single cell movement types (cf supra). Normal movies account both for control movies and experiments in which cell motility is similar to that of controls. They contain on average 80% of random trajectories, and a mix of the four other trajectory types. This reflects our observation that in real data, experiments and controls typically contain all possible types of cell trajectories and that phenotypes are characterized in a shift in percentage. All other movie types contain (on average) 50–65% random trajectories, the rest being completed according to the movie type. For example, movie type fast is composed of 30% of fast random trajectories, 60% of random trajectories and a mix of the three other trajectory types.

The total number of trajectories in each movie was drawn at random from real data in the following way: first, a batch is randomly chosen in the dataset. Then, we assign a permutation of the real trajectory numbers from the experiments of the picked batch to the simulated positions. In this way, we can include potential batch effects in our simulated data. The number of trajectories of each movement type in each movie is drawn from the corresponding movie type multinomial distribution, where the percentages were defined as described above.

The third step was the simulation of ∼50 000 experimental conditions, which were distributed on 130 plates, and performed in triplicate as in Mitocheck experimental setup (Neumann et al., 2010). For the sake of simplicity, triplicates were supposed to belong to the same movie type. On each plate, between 5% and 15% of the experiments were selected to be other than normal movies.

3.4.2 Application to a simulated screen

Our workflow successfully recognized more than 98% of the experiments, as detailed in Table 3.

Table 3.

Results from the application of MotIW to simulated data

	Recall (%)	Precision (%)
Outlier experiment detection	99.2	98.9
Outlier condition detection	99.5	100.0
Trajectory clustering	91.4 ± 2.1	89.4 ± 4.8

Our simulation pipeline was also used to estimate how useful the trajectory feature set is to capture the differences between different types of trajectory motion. A total of 500 samples of each trajectory type were simulated, and their features extracted. A PCA was performed, after which we retained the eighth first principal components, which explain ∼95% of the dataset variance. Finally, k-means was applied to the dataset with k = 5.

Many simulation parameters (e.g. each track length) are chosen at random, and k-means’ results depend on its initialization: the procedure was therefore repeated 10 times. The results are presented in Table 3. Although distinguishing trajectory types is subject to some errors, it shows that the whole pipeline is robust enough to identify experiments in which cell motility is significantly different. A reasonable accuracy in terms of trajectory types is also obtained.

3.5 Application to the Mitocheck dataset

After evaluating MotIW on simulated data, we then apply it to the whole genome-wide screen Mitocheck (Neumann et al., 2010), which enables us to identify an ontology of 2D cell trajectories.

In the context of the Mitocheck dataset, the identification of an experiment in which cell motility is significantly different from negative controls leads to the identification of genes which might be involved in its mechanisms.

The application of MotIW to the Mitocheck dataset enabled the identification of the experiments which significantly deviate from controls (5%; 7 153 of 144 909). It amounts to 1 180 genes (out of 17 816), some of which are known to be involved in cellular motility, such as RhoA (Ras homolog family, member A) or CDK5 (cyclin-dependent kinase 5).

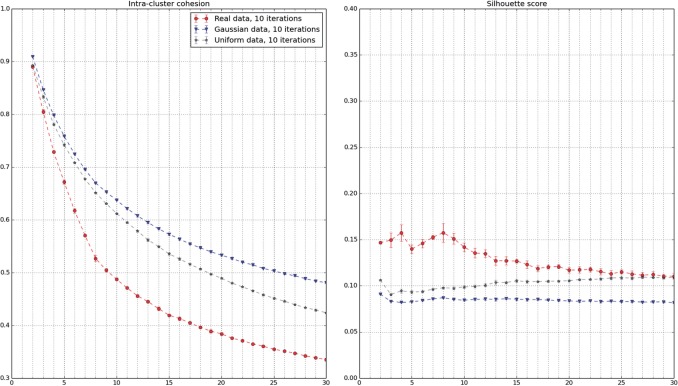
A related question to motility gene discovery is to know whether there exists an ontology of cell trajectories. The approach would be to apply unsupervised clustering methods on the whole trajectory dataset and try to identify a number of motility patterns for which the clustering is of good quality. This is measured by cluster quality indices, which depend on the clustering method (Tan et al., 2005, Chapter 8; Halkidi et al. 2001). As an example, two common indices to evaluate the output of k-means are the intra-cluster cohesion C(k) and the silhouette score S(k). They both compare intra-cluster distances with inter-cluster distances. A slope change in C(k) and a maximum in S(k) are expected at the appropriate number of clusters, if it exists.

This approach did not prove to be successful when applied to pooled trajectories from all experiments, for a wide range of clustering techniques (k-means, Gaussian mixtures models, spectral clustering, fuzzy c-means, kernel k-means—data not shown). It succeeded when all trajectories from the detected experiments were pooled together. Indeed, this small subset contains only experiments which have been selected for being significantly different of controls in terms of single cell motility: it is enriched in rare trajectories. After retaining the first seven principal components (explaining 95% of the variance), k-means was applied to the resulting dataset of ∼1.1 million trajectories.

Figure 6 shows the evolution of intra-cluster cohesion and silhouette score with respect to the number of clusters. It points to k = 8 as being both the best and a good quality clustering on this dataset. Indeed, a break and a maximum are respectively expected in the cluster cohesion and the silhouette score curves at the correct cluster number, if it exists. The cluster characteristics are detailed in Figure 7. Each column in the heatmap corresponds to one cell trajectory, for which the rows show the standard scores of a subset of features.

Fig. 6.

Evaluation of k-means clustering quality as a function of the number of clusters (average and standard deviation on 10 algorithm initializations). The same protocol was applied to a subset of the Mitocheck dataset and two samples of the same dimensions, respectively, drawn from the Uniform and the Normal distributions

Fig. 7.

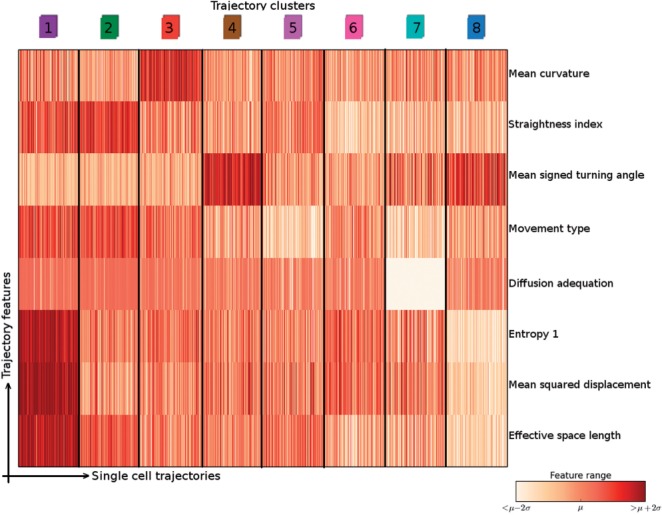
Characterization of our ontology of trajectories. Each column is a single cell trajectory; trajectories are grouped by cluster label. Thousand trajectories were randomly selected per trajectory cluster

In the first place, it shows that single cell information can be retrieved by our statistical procedure, which works at the experiment level. Indeed, a result about single cell motility patterns is obtained from experiments which were selected on the basis of their trajectory feature distributions.

In the second place, it shows that there is more than speed for differentiating trajectory types. For example, clusters 2 and 3 present very similar MSDs and Effective space length. However, trajectory curvatures are different: the features Mean curvature and Straightness index are quite distinct between the two clusters. This can be observed in the Supplementary movie, where cells whose trajectory belongs to cluster 2 (green) are much straighter than those belonging to cluster 3 (red). In this video, cells whose trajectory passed the trajectory quality control have a dot, whose color corresponds to its cluster as indicated in Figure 7.

4 Discussion

This article presents a generic methodological framework for studying single cell motility in a HT setup. It combines single cell tracking, newly designed trajectory features and an original statistical procedure. Furthermore, its output could be used to obtain an ontology of cell motility in an unsupervised manner: cell motion types were inferred from the data without using any prior knowledge. We found that clustering procedures might not scale in the presence of great biological variability, as is typically observed in HT datasets. We suspect that this is due to highly unbalanced classes and large biological variability. Taken together, those effects produce continuous looking datasets. However, applying hit detection with the described statistical procedure prior to clustering solved the problem for our trajectory analysis. It may be a promising procedure to apply to other clustering problems in HCS, such as clustering of nuclear or cellular morphologies.

As cell population migration during metastasis are thought to be led by some leader cell, it is crucial to study single cell motility. The workflow we have presented in this article allows to quantify single cell trajectories. Therefore its application to large-scale datasets will provide useful insights into the molecular regulation of single cell motility, thereby complementing previous studies on collective cell migration.

The application of this workflow is not limited to RNAi data. In a next step, we are going to apply this workflow to newly generated Environmental Toxicology data in order to identify environmentally relevant chemicals which perturb cell motility.