Abstract
Coordination is a taxonomy of how processes change together through time. It depicts the changes of two or more variables in terms of the strength and consistency of their covariation, the directionality of their covariation (i.e., do increases in one variable correspond with increases [in-phase] or decreases [anti-phase] in the other variable), and the timing of their covariation (i.e., do both variables change at the same rate or does one variable change faster than the other). Current methods are able to characterize some, but not all, of these aspects of coordination and provide incomplete information as a result. The current study addresses this limitation by demonstrating that multivariate latent change score models can be used to fully differentiate all possible coordination patterns. Furthermore, one can then expand coordination beyond the two outcome case to test arrangements of underlying coordination mechanisms or patterns. Examples using two simultaneous latent change score models and four simultaneous latent change score models illustrate this approach within the context of adolescents and parents regulating type 1 diabetes.
Keywords: Coordination, Latent Change Score Model, Bidirectional, Structural Equation Modeling, Regulation
Reciprocity, transmission, contagion, synchrony, regulation, coupling, and coordination are just some of the terms that have been used to represent the interplay between two or more variables through time where causal relationships are multidirectional rather than unidirectional (Butler, 2011). Multidirectional relationships are integral to the social sciences. For example, transactional models (Sameroff & Mackenzie, 2003) treat child development as a function of continuous feedback loops between the child and the experiences provided by his or her family and social context. Motor coordination (Kelso, 1995) treats walking and juggling as outcomes of coordinated muscle activity that is made possible by feedback loops between physiological and haptic systems. Likewise, emotion regulation is often argued to be co-regulatory rather than self-regulatory within the contexts of bereavement (Hofer, 1984), dyadic emotion regulation (Butner, Diamond, & Hicks, 2007), and marriage (Gottman, Murray, Swanson, Tyson & Swanson, 2002).
At the root of multidirectional models, the notion is simple: each process moves with another through time and each is able to perturb the other’s natural movement. But the details as to how to capture this simple notion through modeling have varied greatly. Within Structural Equation Modeling, four current approaches embrace dynamical systems logic as a way to understand multidirectional relationships.
Dynamic Factor Models (or Dynamic Factor Analysis) aim to capture temporal and multidirectional relationships simultaneously by modeling time delay (toeplitz) data structures where a single case’s time series data is restructured into leads and lags through time (Browne & Nesselroade, 2005; Ferrer & Nesselroade, 2003; Molenaar, 1985; Nesselroade, 2007; Shirfen, Hooker, Wood, & Nesselroade, 1997). Latent constructs are then utilized to capture the temporal and multidirectional relationships as a function of how the leads and lags move together within and across constructs, with equality constraints through time. Analyses are usually done separately for each time series.
Latent Differential Equation Modeling (or Dynamic Structural Equation Modeling) utilizes the same kind of data structure as Dynamic Factor Models, but specifically applies constraints akin to growth models (usually quadratic growth) to force the estimation of derivatives and the relationships between derivatives (Boker & Nesselroade, 2002). These derivative relationships can then be estimated between simultaneous outcomes to represent multidirectional relationships (Nicholson, Deboeck, Farris, Boker, & Borkowski, 2011) or modeled as a function of emerging from multiple outcomes to imply multidirectionality (Chow, Ram, Boker, Fujita, & Clore, 2005). This approach approximates a continuous time model from the discrete data under an assumption of equally spaced time intervals (Boker et al., 2011; Rotondo, & Boker, 2002).
Continuous Time Models or Stochastic Differential Equation Modeling (sometimes called the Exact Discrete Model) usually utilizes repeated measures data structures (panel data) with a modified form of autoregressive and cross-lagged effects designed to directly extrapolate a continuous time model from discrete data (Oud, 2007; Oud & Jansen, 2000; Oud & Singer, 2008; Voelkle, Oud, Davidov, & Schmidt, 2012). Specifically, it includes an exponential relationship between discrete and continuous portions of the model requiring nonlinear constraints. The Approximate Discrete Model with oversampling provides a good linear approximation (Singer, 2012).
Latent Change Score Modeling (also known as Latent Difference Score Modeling) can be applied to time delay or repeated measures data structures (Grimm, 2012; Ferrer, Hamagami, & McArdle, 2004; McArdle, 2009; McArdle & Hamagami, 2001). Sets of dummy latent variables are used to force the estimation of discrete differences between consecutive time points. These latent discrete differences are then predicted as a function of previous values in time both within and across constructs.
All four techniques hold promise for depicting multidirectional relationships with multiple ways to do so in each circumstance. We seek to extend the current approaches in order to increase interpretability of the multidirectional relationships as it can be difficult to decipher the pattern of results they imply while connecting to theoretical models. We do this by maintaining a description of the pattern generated through time by the multidirectional relationships and the underlying relationships that comprise the pattern. For the purpose of this paper, we restrict our focus to Latent Change Score Modeling. We chose this restriction because Latent Change Score Models can be used with relatively few repeated measurements under an assumption of equivalency of equation across individuals and time.
Our goal is to link substantive theory and statistical models for quantifying multidirectional relationships in a way that optimizes both flexibility and interpretability. In this paper, we focus on coordination as a representation of the inter-relationships among multiple variables through time. Specifically, coordination is a taxonomy of the kinds of patterning one will see through time as a function of multidirectional relationships. The taxonomy is differentiated on qualities of timing between how constructs change together through time (moving together vs. opposing; one to one change vs. some other ratio; strong synchrony vs. weak or no synchrony). Here, we utilize multivariate Latent Change Score Models to parameterize the qualities of coordination that distinguish between the different coordinated patterns.
Our approach treats coordination akin to a third party causer as a way to represent bidirectional relationships. That is, the change in each outcome is treated as manifestations of a shared coordination latent construct. In doing so, we are able to capture the full range of coordination patterns while maintaining interpretations of Latent Change Score Models. By applying theories of coordination to Latent Change Score Models we can also begin to examine coordination in multiple variables simultaneously and test for varying coordinative patterns. To exemplify this approach, we present a model with two simultaneous latent changes and a model with four simultaneous latent changes. This illustration is done in the context of adolescents and parents regulating type I diabetes over two and one half years.
Taxonomy of Coordination
Coordination is most commonly associated with one to one synchrony (also known as phase locking or mode locking) where two or more outcomes move together with equivalent observable changes (first identified by Huygens 1665; as cited in Strogatz, 2003). Perfect one to one synchrony, however, is only one of many coordinated patterns we can observe. Turvey (1990) pointed out that coordination can be placed in a taxonomy that depicts different phase relationships (Kelso, 1995). For example, synchronous patterns may be in-phase such as Huygens’ pendulum clocks that oscillated in exact time with one another and in the movement of legs while hopping, or anti-phase such as how a person’s legs move while walking (i.e., a change in one leg is directly paralleled by an equal change in the other but while one leg is forward, the other is back).
Phase locking need not be one to one. For example, the peddles on a bicycle turn in perfect synchrony with the bicycle wheels, but one can alter the relationship between pedal strokes and wheel revolutions so that when going uphill several peddle cycles equate to one turn of the wheel and when going downhill (in a different gear) one peddle cycle can equate to several turns of the wheel. This relationship depicts the phase locked-ratio – the ratio at which one process changes in comparison to the other process.
Finally, coordinated systems need not be phase-locked at all. For example, when a parent and (smaller) child walk down the street side by side, they may try to establish a lockstep pattern. The parent will have to slow down her stride while the child attempts to match the resultant stride. For brief periods of time they will appear to walk synchronized. Eventually, though, this relationship slips (hence called slippage) and the child might have to take a double or triple step to slide back into that temporary pattern. This pattern of coordination is referred to as entrainment.
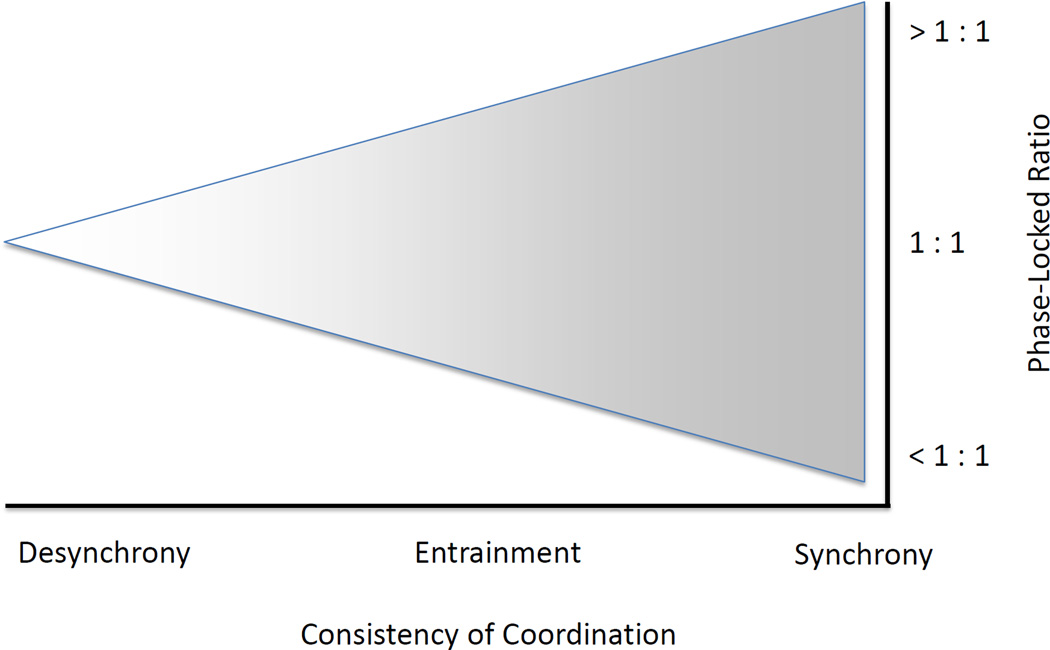
Figure 1 illustrates the range of patterns we include in the spectrum of coordination distinguishable as a function of two dimensions. The left side is labeled desynchrony or the lack of any consistent shared pattern through time (lack of coordination). On the right are the many forms of synchrony. The horizontal axis thus depicts the consistency with which we observe synchronicity. The vertical axis depicts the kind of synchrony we observe (e.g. 2 to 1 anti-phase). In practice, coordination models tend to stabilize on a limited range of phase locked ratios (right side of the cone) in that not all ratios (Treffner & Turvey, 1993) and phasic relationships (i.e., in-phase vs. anti-phase) are as easily maintained (Kelso, 1984).
Figure 1.
Cone showing the theoretical relationship amongst the forms of coordination. This can be depicted as a function of the horizontal axis capturing how synchronized a pattern is observable and the vertical axis capturing the type of synchronous pattern.
From Taxonomy to Model
The two dimensions that depict different coordination patterns can be further differentiated by examining how statistical parameters could constitute these patterns. Specifically, Figure 1 depicts dimensions on which we can differentiate observable patterns from two multidirectional causal variables. However, it does not propose what generates the range of observable patterns within coordination. This requires a model. Von Holst (1937/1973) believed that the full range of coordination could be depicted through the combination of two forces. The maintenance tendency or natural tendency is the pattern each variable would generate if it were in isolation. The magnet effect is the draw for patterns towards synchrony. Specifically the magnet effect is (Von Holst, 1937/1973), “the ‘endeavor’ of one automatism to impose its tempo and a quite specific reciprocal phase relationship upon another” (p.101). When the magnet effect is zero we get two patterns that are unrelated, or desynchrony (the left side of Figure 1). When the magnet effect is nonzero, the pattern moves towards phase-locked relationships (move right on Figure 1). Phase locking occurs when the magnet effect overwhelms the maintenance tendencies entirely (right side of Figure 1). Entrainment occurs when the magnet effect is strong enough relative to the maintenance tendencies to evoke brief periods of phase-locking followed by periods of slippage (moves right in Figure 1, but not to the rightmost side of the cone).
Von Holst’s model does not presume that the magnet effect on each pattern is equal. In his original treatise, this differential pattern of coordination came out as a function of differences in the natural tendencies. More recently, this differential pattern of coordination has been theorized as asymmetrical magnet effects captured by a comparison of the regression paths where one outcome predicts the change in the other outcome through time (Butner & Story, 2010). In other words, current practice is to capture the magnet effect as a pair of coupling relationships. At the extreme end, asymmetric coordination models emulate a unidirectional relationship where only one variable appears to influence the other (Butner, Amazeen, & Mulvey, 2005).
Von Holst’s model for constructing coordination is particularly relevant because it parallels many of the common methods we currently employ to capture multidirectional relationships. For example, Bidirectional Latent Change Score Models (discussed later in this paper) commonly have both the previous values of a construct predict its own changes and values of another construct predict its changes as crossover relationships. The ‘own’ effects can be thought of as the maintenance tendencies and the crossover effects can be thought of as magnet effects. Thus, Von Holst laid down a direct connection between current practices and the taxonomy of coordination.
The problem, as we will demonstrate, is that current implementations of Von Holst’s solution works mathematically, but may falter under statistical estimation due to partialling. Specifically, the maintenance tendencies and magnet effects are estimated as unique effects from one another, but coordination is a model of interdependency and thus the uniqueness of effects is not always easily estimated. The end result is for models designed to estimate the natural tendencies (maintenance tendency) and coupling relationships (magnet effect) fail to differentiate the full range of what coordination is theorized to represent where what we have commonly sacrificed is the notion of synchronous relationships that are other than one to one. Ultimately, we provide an expansion of the current statistical models capable of capturing the full range of coordination patterns while maintaining the ideas generated by Von Holst.
First Order Latent Change Modeling
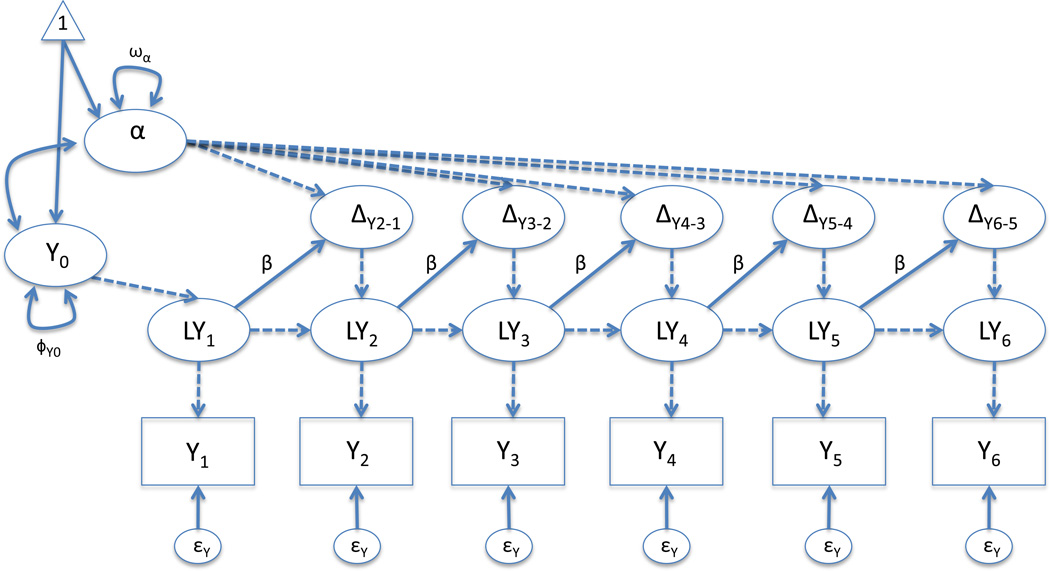
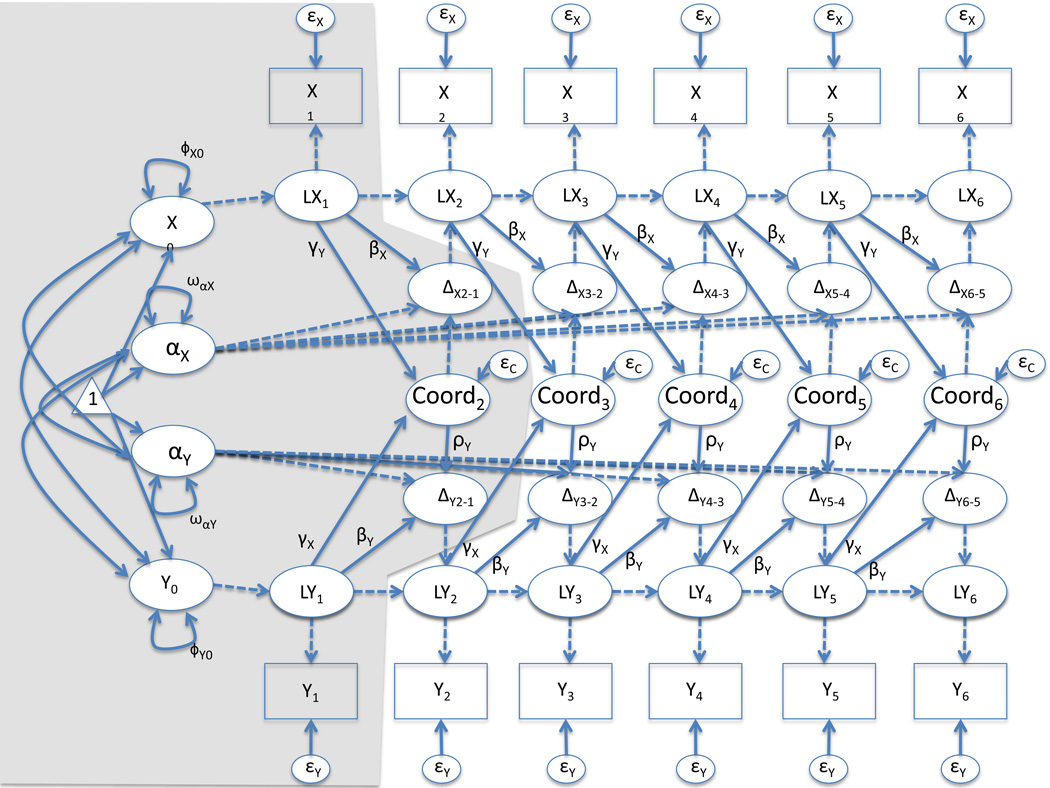
Latent Change Score Models (LCS) are a form of structural equation modeling (SEM) where measurement of outcomes in time are converted into representations of discrete changes where the discrete changes are predicted as a function of earlier values of the outcome (McArdle & Nesselroade, 1994). In SEM, a configuration of latent variables with intercepts and variances fixed to zero and regression weights fixed to one are used to generate latent variables that represent change between two consecutive outcomes. Figure 2 is an example diagram of a LCS model for an outcome measured at 6 points in time where the data are in a repeated measures format. In the measurement part of the model, the complex array of dummy latent variables decomposes observed values of an outcome (Y) as a function of a latent initial value, a latent change in Y between two consecutive time points, and measurement error. In the structural part of the model, the latent change is then treated as the criterion predicted as a function of the previous values of the outcome in time (often labeled beta), along with an intercept (often labeled alpha). We label the latent change factors as (Yt+1 – Yt) to make clear what the latent variables represent.
| (Eq. 1) |
When Y fails to predict the latent change in Y, the intercept captures linear change. When Yt predicts the latent change in Y from time = t to time= t + 1, the intercept becomes the predicted change when Yt is zero. Furthermore, the intercept/linear change can have a random effect in the form of a variance or residual variance (variance in ωα in Figure 2). The coefficient of Y in predicting its own latent change (Beta; β) has been depicted as proportional change (McArdle & Hamagami, 2001). The latent change score model also commonly estimates an average value of Y at time zero, along with a variance component on that initial value (variance in φY0) and error variances on each of the observed Y values (variance in ɛY; equated over time in our presentation). The error variance on each of the observed Y values are errors in measurement while the error in equation (omega; ωα) captures perturbations in change over time.
Figure 2.
Example path diagram of a latent change score model of a single outcome in time measured on six occasions. Measures are assumed to be equally spaced in time. To generate equation 1, all parameters are equated through time. All dashed pathways represent parameters fixed to one. All variances, covariances, and means are shown (thus when not illustrated, they are fixed to zero).
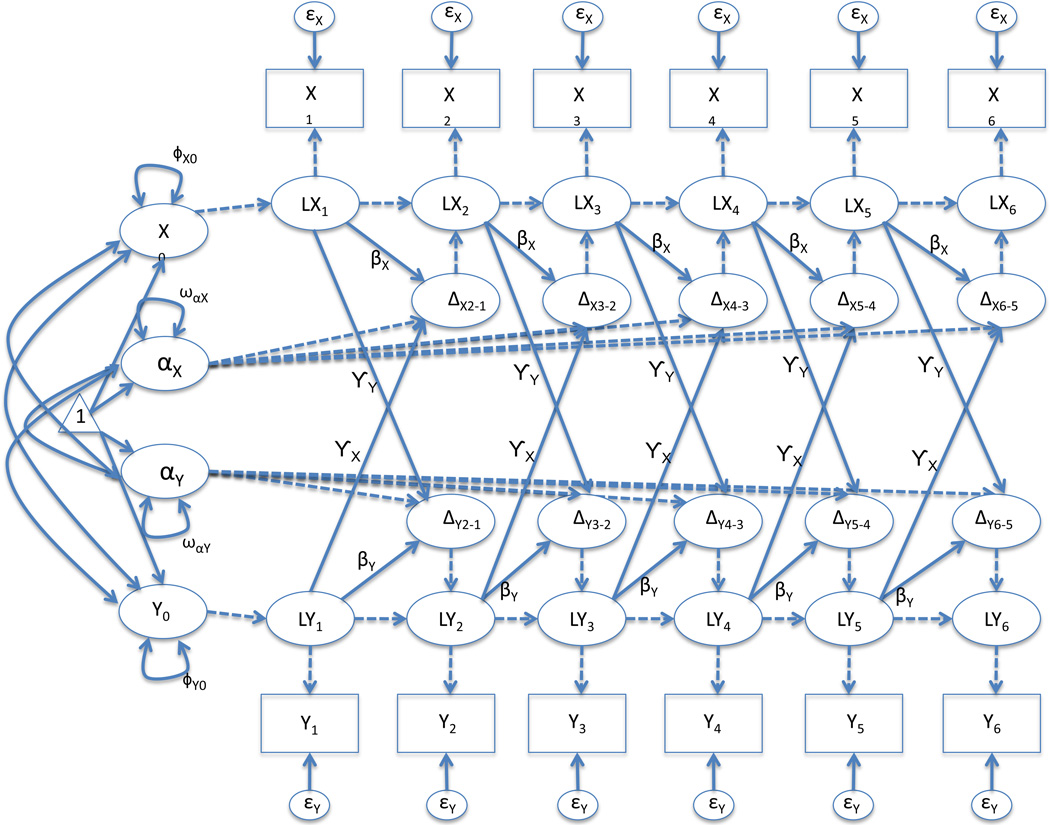
Figure 3 depicts a latent change score model when there are two processes changing in time as a function of a bivariate (dual) latent change score model. This generates two simultaneous equations predicting latent change akin to Von Holst’s decomposition.
| (Eq. 2a) |
| (Eq. 2b) |
The gammas (γ) are known as coupling terms and parallel the notion of the magnet effect. Due to partialling, the betas now take on the meaning of the maintenance tendencies (how each variable uniquely predicts its own change above and beyond any magnet effects).
Figure 3.
Example path diagram of a latent change score model with two outcomes in time measured on six occasions (known as a bivariate latent change score model). This method creates an ambiguity on the interpretation of the various types of coordinated behaviors. To generate equation 2, all parameters are equated through time. All dashed pathways represent parameters fixed to one. All variances, covariances, and means are shown (thus when not illustrated, they are fixed to zero).
Let’s do a little exploring as to how this specific arrangement of maintenance tendencies and magnet effects are able to reproduce the taxonomy of coordination. Desynchrony would occur when both gammas (magnet effects) are essentially zero along with the alphas (intercepts) and betas (maintenance effects) being different across variables. This pattern would occur because each outcome has its own changes and the previous values of the other outcome would be unrelated to change over time. A phase-locked one to one relationship (which also assumes both variables are on the same metric) would result in the identical (i.e. not significantly different) alphas (intercepts) and betas (maintenance tendencies) across X and Y at each of the 6 measurements. However, the gammas would be essentially zero due to partialling (the betas and gammas would be multicolinear). In essence, the only difference between desynchrony and phase locking is in the alphas and betas, not the gammas.
When the data are phase locked in a ratio other than one to one, there are two reasonable possibilities. First the gammas could still be multicolinear with the alphas and betas. However, the alphas and betas will establish the phase relationship and thus be different across X and Y. In this case, non-one to one phase locking and desynchrony are essentially indistinguishable. The second possibility is that non-one to one phase locking will generate distinct gammas and betas across the 6 measurement occasions because the non-constant relationship through time will attenuate the estimates. In this non-one to one phase locked circumstance, the pattern of coefficients would be indistinguishable from entrainment.
When the model is in the realm of entrainment (neither desynchrony nor phase-locking) this model performs substantially better in that both the maintenance tendencies and magnet effects are distinguishable. However, we are essentially collapsing key information in that there is little ability to distinguish the ideal form that the system is being drawn towards in terms of in-phase or anti-phase and phase-locked ratio (i.e. where the pattern exists in the taxonomy represented in Figure 1). An improvement on this approach would be able to isolate desynchrony, phase locking, and entrainment. Furthermore, it would be able to discriminate different phase locked ratios of one to one from two to one, etc and in-phase or anti-phase.
Latent Coordination
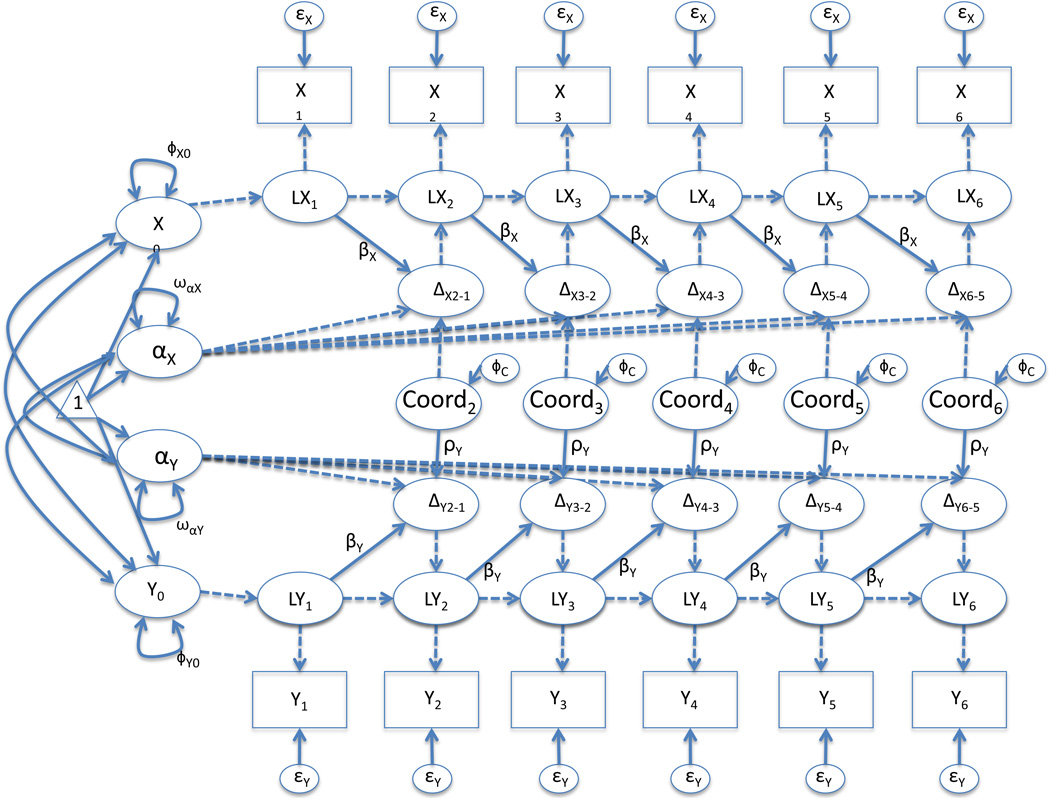
Figure 4 is a slight variation on the bivariate (dual) latent change score equation model that allows for disambiguating non-one-to-one phase locking, entrainment, and desynchrony. In this case, we have defined a series of latent variables (equated over time) as a function of the manifestations from the latent changes in each outcome on their own. We can define this coordination factor using a marker variable strategy where we fix one of the latent changes to have a loading of one and estimate the other. This forms two simultaneous equations.
| (Eq. 3a) |
| (Eq. 3b) |
The loadings (1 and ρ) of the coordination factor on the latent changes in Y and X, respectively, decompose each change into two components. The coordination factor captures the extent to which the two outcomes change together (the horizontal axis on Figure 1). The ratio of the marker variable (fixed to one) and rho establish the phasic ratio of the change occurring between the two change processes (the vertical axis on the right side of Figure 1). A rho of one would indicate a one to one ratio while a rho of 2 would indicate a one to two ratio. The extent to which the model establishes a non-zero variance on the coordination factor and non-zero rhos indicates the extent to which the two processes change together. The variance on the coordination factor is key because it represents how there is variability within (because of equality constraints) and between (because of the panel nature of the data) people in how the changes move together. In our simulation work (discussed in more detail below), even when data is simulated with a non-zero rho but zero variance, both terms still estimate as zero.
Figure 4.
Example path diagram of a two latent change score and one unconditional coordinated factor model. The coordination factor captures the extent to which the changes move together decomposing each change into the shared coordination and the uniqueness for each outcome. The maintenance tendency is then captured by predicting the uniquenesses in change. To generate equation 3, all parameters are equated through time. All dashed pathways represent parameters fixed to one. All variances, covariances, and means are shown (thus when not illustrated, they are fixed to zero).
Since the betas are estimated after controlling for the loadings, they maintain the interpretation of the maintenance tendencies for X and Y respectively. In essence, the coordination factor captures the coordinated portion, while the betas capture the maintenance tendencies. We call this the two latent change score model with one unconditional coordinated factor.
The results from the unconditional coordination model specify the pattern of coordination being observed. If there is zero (non-significant) variance on the coordination factor, the model suggests desynchrony. If there is non-zero (significantly positive) variance in the coordination factor, some degree of synchrony is being observed. If both of the maintenance tendencies are zero (how a variable predicts its own changes, the Betas), then the model implies phase locked behavior because the latent coordination factor has captured the consistent behavior between the two processes leaving only perturbation error in each latent change (which would be unrelated to previous values of the outcomes). Having a non-zero maintenance tendency implies some sort of entrainment instead because there are predictive elements in the changes of each outcome that are not coordinated. The ratio of the loadings (1 and rho) indicate the phase-locked ratio (when phase-locked) or a scaling ratio (when entrained).
Simulations of Coordination
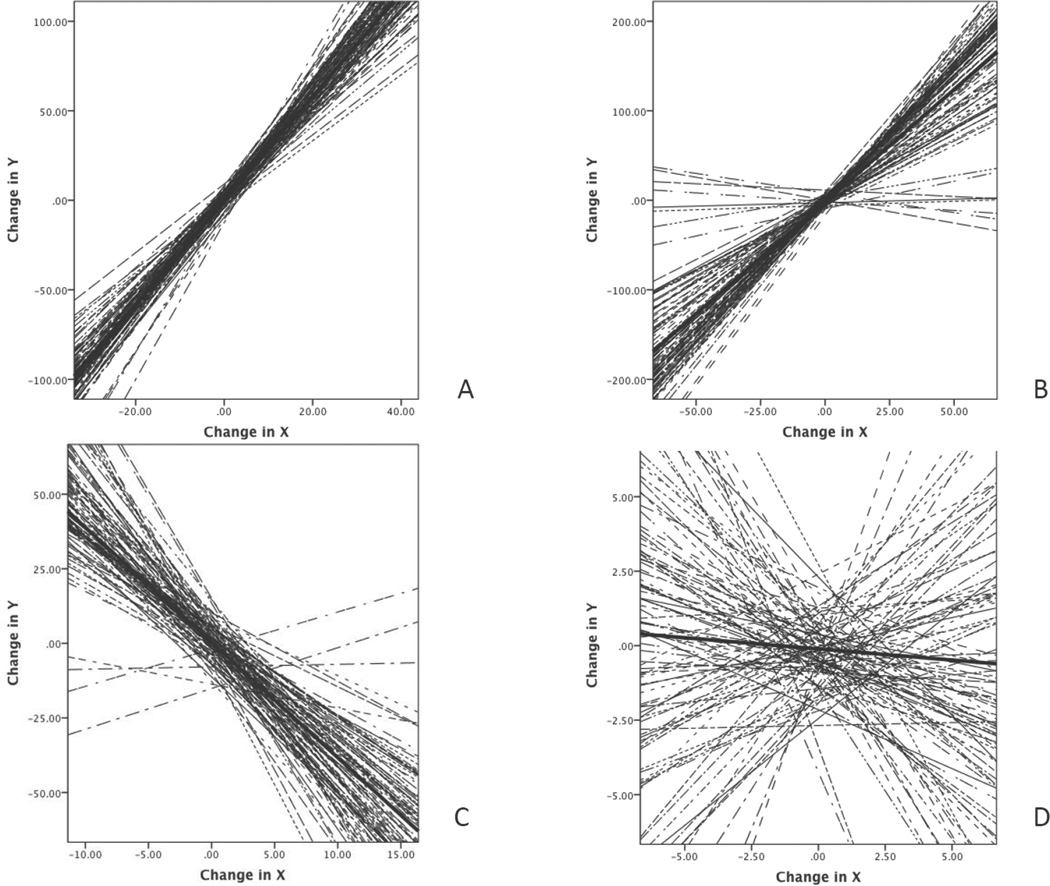
To illustrate these different circumstances, we simulated data in Mplus using the model in Figure 4 varying the existence of the coordination factor, the strength of the maintenance tendencies, and the ratio of loadings. Each illustration is with a sample size of 100 and 6 time points structured in a repeated measures format. Since coordination is depicting how variables change together, we converted the simulated data into differences of adjacent time points and plotted the changes in one variable as a function of the changes in the other variable. We then overlayed a straight least squares slope for each individual (resulting in 100 slopes each a function of 5 pairs of differences per person). This graphing approach allows us to illustrate two key principles. First, it shows how coordination is a function of variables changing together and thus can be shown akin to a scatterplot of the change in one variable as a function of the change in the other. Second, it shows that the combination of panel data structure and equality constraints through time generate a within and between subjects model in the same nature of a growth model where the model itself is within subjects while also capturing between subjects components.
Figure 5A is where we have added a coordination factor with the variance of the factor fixed to be very high (probably beyond what would normally be observed, but it is illustrative). The slope of the average line (b=3) is the ratio of change in the coordination model (ρ=b=3). This occurs because we simulated data to have a loading on the coordination factor equal to 3. The within subject portion is represented by each individual slope. The between subject portion is represented by the consistency/inconsistency of the slopes (in consistency equals between subjects variability). Notice that in this example, most of the slopes are very similar. Thus, in this instance most of the covariation in change occurs within subjects.
Figure 5.
Change plots of simulated data using the bivariate latent change score model with one unconditional coordination factor depicted in figure 4. (A) is a case where variance on the coordination factor was comparatively large and the loading (rho) was 3 – the average slope. (B) ) is the same as (A), but with the addition of maintenance tendencies. As expected, the slopes are more divergent (though the average is still a slope of 3) consistent with entrainment – periods of synchrony and periods of slippage. (C) is a case where the variance on the coordination factor is more reasonable, no maintenance tendencies, but a loading (rho) of −5 to show a 1:5 anti-phase relationship. (D) is a case where there is no variance on the coordination factor and the loading (rho) was near zero .Note that the axis scalings differ across figures to show the difference in simulated data ranges. Since these are least squares slopes, the lines go from positive to negative infinity.
Figure 5b is very similar to 5a except that we changed the average slope and weakened the coordination factor. Specifically it shows coordination variation in a more reasonable range (but no maintenance tendencies), now showing anti-phase behavior with a ratio fixed to −5 (so a slope of negative five). There is now more variation within subjects in that some slopes are essentially zero suggesting inconsistency in the changes over time. There is also more variation between subjects in that there is more variability in the slopes.
Figure 5c is the identical model to 5a with the inclusion of maintenance tendencies. Each process is pulling towards its natural tendency in addition to the coordinated component of behavior creating greater dispersion in the distribution of slopes (between subjects but also partially within subjects). This is consistent with entrainment where there are periods of synchrony and periods of slippage.
Figure 5d is where there is no variance on the latent variable and the loading on the coordination factor (ρ) is close to 0. Notice that there is no coherence within or across individuals as to how the changes move together. This lack of coherence is observable in the average slope being zero and the overall inconsistency in the slopes between subjects.
Adding in Magnet Effects
To generate the concepts depicted by Von Holst (i.e., the maintenance tendencies and magnet effects), we must take the model one step further. Figure 6 does so by adding each previous value of X and Y, respectively, to predict the coordination factor. We call this a two latent change score model with one conditional coordinated factor. In essence, this adds one additional equation to equations 3a and 3b.
| (Eq. 4a) |
| (Eq. 4b) |
| (Eq. 4c) |
The betas maintain their interpretation as the maintenance tendencies as does the rho as the ratio of change. The new equation where coordination is the outcome captures the magnet effects. Specifically, the gammas represent how each variable uniquely influences higher or lower values of coordination. In essence, the coordination factor approach can fully differentiate all the forms of coordination without any ambiguity and is even able to provide phasic information previously thought unavailable in coordination approaches in SEM (Butner & Story, 2010).
Figure 6.
Example predicted time series plots drawn from the conditional coordinated factors model. Predicted trajectories were generated with and without perturbations. The perturbations (taken by varying the intercept as a function of a normal distribution with a mean and variance equal to the intercept factors) carry over from one trajectory to the other such that the coordination keeps the two trajectories in check.
The bivariate (dual) LCS model (Figure 2) and the two LCS with one conditional coordinated factor model (Figure 5) are highly related. It is possible to reconstruct the bivariate LCS results from the conditional coordinated factor model. Specifically, the one conditional coordinated factor model decomposes the original maintenance tendency into two components: the original effect of a variable on its own change and a new indirect effect of a variable onto the coordination factor times the rho between the change of that variable and coordination factor. Summing these together is equivalent to the maintenance tendency estimate from the bivariate LCS model. Thus, anything that can be applied to latent change score models can be applied here by reconstructing the bivariate LCS equations. One such example as generating state space plots (Boker & McArdle, 1995).
The ratio of change or scaling parameter will have some interesting properties. As already mentioned, when phase locked, it will take on the ratio of the phase locking. The sign will also indicate whether the system is in-phase (as one moves up the other moves up) or anti-phase (as one moves up the other moves down). Thus, the scaling parameter is capable of revealing the entire range of phase locked behaviors by combining the sign and the ratio together. One to one phase locking will generate a rho of 1 when in-phase and a rho of −1 when anti-phase.
When entrained (i.e. when there is a non-zero coordination factor variance, non-zero rho, and one or more non-zero maintenance tendencies) the ratio represents the differential scaling of coordination, accounting for the two variables that make-up the system being on entirely different metrics. Given the marker variable strategy, the metric for coordination is defined by the metric of the marker variable. So, the marker variable’s betas and gammas are directly comparable to the betas and gammas of the other variable.
Example of Two LCS Unconditional and Conditional Coordinated Factor Models
To exemplify this approach, we used data from the Adolescents with Diabetes and Parents Together study, which tracked adolescents diagnosed with Type 1 diabetes and their families for two and a half years at six-month intervals for a total of six time points. The objective of the longitudinal study was to understand how developmental changes in mothers’ and fathers’ involvement in diabetes management (described below as maternal and paternal diabetes monitoring), and in the adolescents’ developing self-regulation skills (described below as adolescent self-efficacy for diabetes management and self-control), were associated with diabetes management. In this section, we use the maternal and paternal monitoring data to demonstrate the two LCS unconditional and conditional coordinated factor models. In the subsequent section, we extend coordination beyond the two-outcome case by including adolescent self-efficacy and self-control. Descriptions of methods relevant to demonstrations of both models are now provided. All analyses were conducted in Mplus version 7.
Method
Participants
Participants included 252 adolescents (M age = 12.49 years, SD = 1.53; 53.6% females) diagnosed with type 1 diabetes mellitus recruited from a university/private partnership clinic (85%) and a community-based private practice (15%). Adolescents were between 10 and 14 years of age at study initiation, had diabetes for more than 1 year (M = 4.13 years, SD = 2.98), lived with their mother, and were able to read and write either English or Spanish. Of the qualifying individuals approached, 66% agreed to participate in the study. Most families were Caucasian (91.7%) and middle class; most (63.5%) reported household incomes averaging $50,000 or more annually; 52.4% of mothers and 44% of fathers reported education levels of two years of college or beyond; an average Hollingshead index (1975) value of 41.19 indicated a medium business, minor professional, technical status.
Procedure
This study was approved by the Institutional Review Board; parents gave written informed consent and adolescents gave written assent. Families completed assessments every six months for a period of two and a half years. At each assessment, adolescents completed a set of questionnaires at home, and additional questionnaires and an interview at a laboratory appointment. By time 6, 198 adolescents participated in the study. Common reasons for withdrawing from the study included changes in family circumstances (19%) including the adolescent no longer living with the mother or deaths in the family, families too busy to participate (12%), and study demands (12%). We had no reason to believe these circumstances were a function of non-random missingness and therefore chose to utilize an approach shown to be efficient for data missing at random – Full Information Maximum Likelihood. Given that this model has relationships to growth models (these models default to a pair of latent variable growth models if all predictors fail to predict change) we also benefit from the extent to which prior and future values are able to predict the missing values (Graham, 2009).
Measures
Parental diabetes monitoring
Adolescents completed a diabetes parental monitoring scale developed for this study (see Berg et al., 2008). This scale was based on a general parental monitoring scale (Barber, 1996), and consisted of six items that captured adolescents’ views of their parents’ awareness of their daily activities concerning diabetes management. Adolescents reported how much mothers and how much fathers “really” know about aspects of their diabetes management (e.g., blood glucose readings; how much insulin they’ve taken) using a 1 (doesn’t know) to 5 (knows everything) scale. For this sample, α ≥ .91 at all time points.
Self-efficacy
Adolescents completed the Self-Efficacy for Diabetes Management Scale (Iannotti et al., 2006), reporting their confidence in their ability to manage diabetes across 10 problematic situations (e.g., “How sure are you that you can manage insulin intake when you have eaten more or less than usual). Items were rated from 1 (not at all sure) to 10 (completely sure) and averaged. For this sample, α ≥ .82 at all time points. This measure was only utilized in the second example with four simultaneous latent differences.
Self-control
Adolescents completed a self-control scale that consisted of 11-items designed to tap aspects of the ability to regulate emotions, behaviors, and impulses (Finkenauer, Engels, & Baumeister, 2005). The scale is a shortened version of a 36-item scale created by Tangney, Baumeister, and Boone (2004). Adolescents rated statements about self-control (e.g. “I wish I had more self-discipline”) on a 5-point Likert scale (1= Not at all like me to 5= Very much like me). Finkenauer et al. (2005) reported adequate reliability (α = .67); in the present study reliability was α = .73. Unlike the other scales used in this study, behavioral self-control was only measured in the first four time points (first two years). This measure was only utilized in the second example with four simultaneous latent differences.
Results
Significance is reported at alpha =.05, two-tailed. Data covariances and means along with Mplus syntax can be found at www.psych.utah.edu/~jb4731/coordinated_lcs/. Model fit was evaluated using RMSEA, CFI, and SRMR using criterion depicted by Hui & Bentler (1997; RMSEA <.05 for good, <.08 for acceptable, CFI>.95, SRMR<.05 for good, < .08 for acceptable). Model misfit would suggest an inappropriateness of the coordination model either as a function of the linear equations, equivalency between and within participants, or invariance issues through time. Time was scaled at the measurement occurrences. We first ran the unconditional coordinated factors model where magnet effects were excluded. Model fit was acceptable, Chi-sq (70)=145.514, p<.001, RMSEA 90%Ci: .050<.066<.081, CFI=.956, SRMR=.068. The two equations estimated from this model (using MM for mother’s monitoring and DM for father’s monitoring) are:
| (Eq. 5a) |
| (Eq. 5b) |
The two change processes had significant variation in the coordination factor (var=0.15, z=5.95, p<.001) and significant maintenance tendencies (taken from equations 5a and 5b: −0.36 and −0.40 respectively). The combination of a non-zero (e.g. significant) coordination variance and non-zero maintenance tendencies are consistent with a pattern of coordination within the range of entrainment (in the middle of Figure 1). Using the loadings on the coordination factor, the 1:1.38 ratio (ratio of loadings) are indicative of the ratio of scaling in change between mothers’ and fathers’ monitoring respectively. That is, the coordinated portion of changes in mothers’ monitoring and fathers’ monitoring is in a 1 to 1.38 unit relationship (one unit of change in mothers’ monitoring corresponds to a 1.38 unit change in fathers’ monitoring in terms of coordination; fathers’ monitoring is changing faster relative to mothers’ monitoring). A simple test can be calculated to see if the ratio is different from 1:1, for example, by subtracting the expected value (one) and dividing by the standard error of rho (0.18). In this case it is significantly different from one to one, z=2.06, p=.039. Thus, mothers’ and fathers’ monitoring are not coordinated in a one to one relationship.
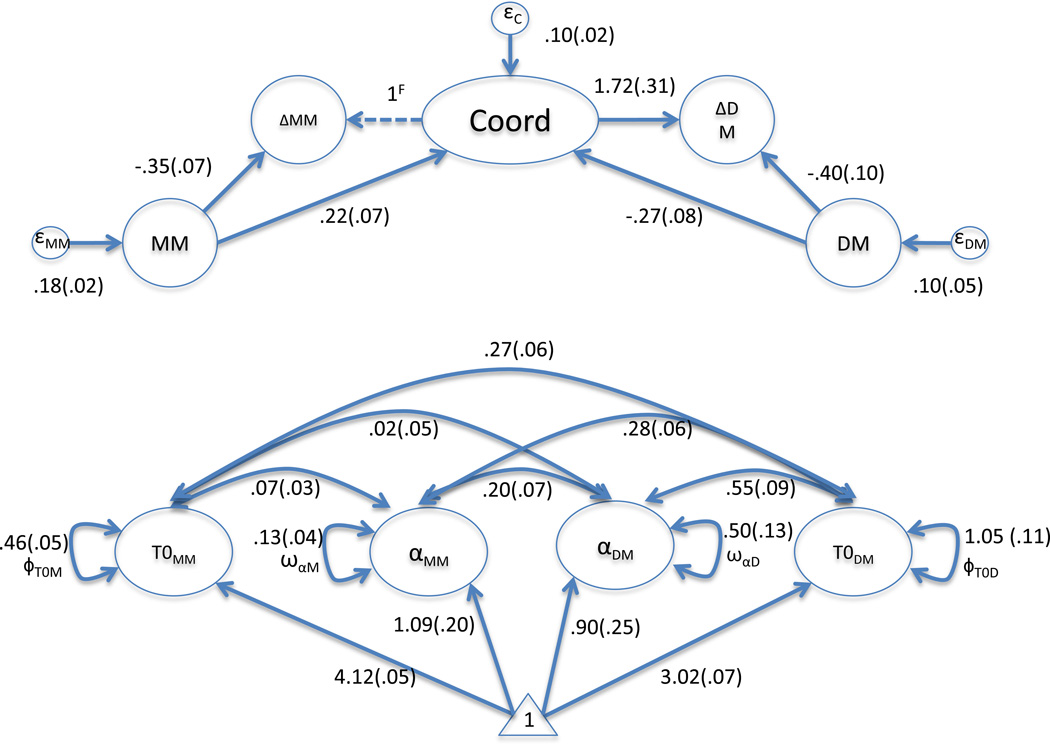
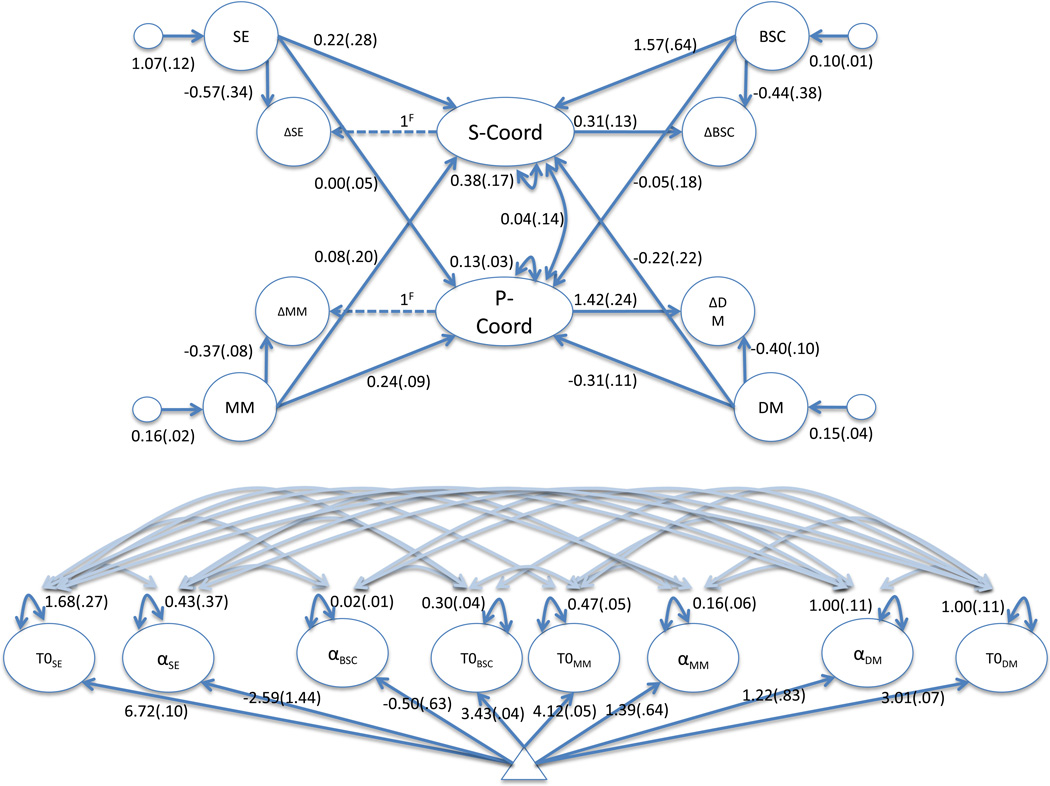
Figure 7 provides a trimmed down graphical representation of the two LCS conditional coordinated factor model where we only show the unique estimated parameters (the rest are fixed or equated to these parameters; it can be thought of as the grey portion of Figure 6 ignoring the generation of a latent node for the observed mother and father monitoring). We generate this trimmed down version of the model because much of the model is equated through time or includes node latent variables to generate the latent change score metrics. Thus, this simplified path diagram highlights the estimated parameters only. Notice that both mothers’ monitoring and fathers’ monitoring predict the coordination factor. In essence, both mother and father drive monitoring coordination, but oppositely such that higher mothers’ monitoring relates to positive change of the coordinated portion of monitoring, while higher fathers’ monitoring relates to negative change of the coordinated portion. This implies a push/pull relationship between mother and father monitoring on the coordinated portion.
Figure 7.
Example path diagram of a two latent change score and one conditional coordinated factor model. The magnet effects are added by having each outcome predict the coordination factor. To generate equation 4, all parameters are equated through time. All dashed pathways represent parameters fixed to one. All variances, covariances, and means are shown (thus when not illustrated, they are fixed to zero). The grey portion are the parameters shown in figure 7 – a trimmed down version that only shows unique parameters.
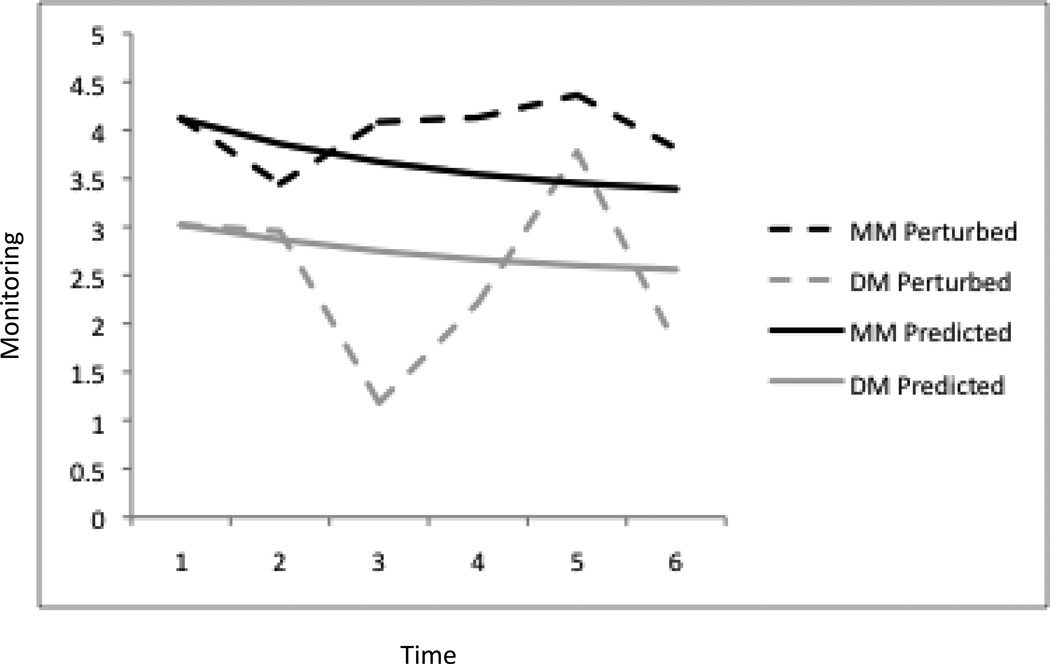
Figure 8 includes an example set of predicted trajectories for both measures simultaneously. To generate these, we took Equations 5a and 5b and inserted the means for the time zero latent variables as the initial values for Mother and Father Monitoring. We then iterated the calculation forward to generate a total of five estimates (six including the initial values). As can be seen in the figure, these predicted slopes are not very illustrative of the coordinated nature. However, coordination should exist in the translation of changes in one outcome carrying over to the other. To illustrate this, we repeated the process, but added perturbations at each time point consistent with the random effects on the alpha factors (i.e. the intercepts at each time point were drawn from a normal distribution with a mean and variance equal to the alpha factors). Consistency in the reactions to the perturbations show the coordinative nature.
Figure 8.
A trimmed down path diagram form of Figure 6 only showing unique parameters (the grey area of Figure 6) using mother and father monitoring as outcomes with six measures in time. This only shows estimated parameters with their standard errors in parentheses.
Beyond Two Processes
There are few examples of coordination models beyond two simultaneous processes. McArdle, Hamagami, Meredith, and Bradway (2000), for example, utilized latent change score models for four outcomes in time to examine the coupling relationships for different facets of intelligence. They allowed for all twelve coupling relationships and provided vector field plots of pairs with significant coupling. They then pulled from investment theory, the cognitive aging literature, and G theory to hypothesize specific combinations of coupling relationships they should and should not expect as an apriori confirmatory testing approach. While the confirmatory approach was fruitful, the overall arrangements of coupling relationships were complex and it was near intractable to identify the coordinative nature of the different intelligence elements and the relationship to the observed trajectories.
We know that many processes can become phase-locked and that coordination has been used to depict everything from the synchronized flashings of fireflies to neuronal firing during an epileptic seizure (Strogatz, 2003). However, little work has been done to understand the underlying principles for how coordination might be organized when it involves more than two variables. For example, we could imagine a series of changing processes that are all coordinated through some sort of central unit or we might imagine each changing process having its own differential impact on other processes or anything in between.
One of the few examples in theorizing about multiple underlying mechanisms comes from Ian Stewart (2002) who theorized a multitude of possible coordination mechanisms that might underlie 4 oscillating processes (e.g. four legs). He argued that each mechanism configuration was capable of different combinations of phase locked behavior. However, Stewart’s thought exercise was under an assumption of phase locking. It is not currently clear how to extend Stewart’s theoretical model to the range of entrainment or how to represent various coordination mechanisms statistically.
Within the new approach for capturing coordination presented in this manuscript, theorizing and testing alternative coordination models suddenly gains some plausibility. For example, a shared or centralized coordination amongst a series of changing outcomes should generate a single latent coordinated factor. In contrast, if there are two different coordination mechanisms, we might expect two coordinated factors with loadings (or rhos in this case) for the relevant changing manifestations. In essence, by changing the factor structure of coordination, we can generate analogs to different underlying mechanisms of coordination.
Additionally, the coordination patterns need not be phase locked to estimate the model. Since it is plausible to have both coordination and a remaining maintenance tendency, it is plausible for the system to be in entrainment, while still being able to compare underlying mechanisms. Thus, the same theoretical apriori rigor of McArdle et al. (2000) can be sought while maintaining comprehension in terms of describing the coordinated structure and its components. The key is in the coordination arrangements: when the organization of coordination factors is nested, they are directly comparable through nested comparison (i.e., χ2 change tests). When not nested, non-nested approaches, such as the AIC and BIC (Bollen, 1989), are plausible for comparing competing models. In every case, the resultant pattern of maintenance tendencies and magnet effects can display the full range of coordination amongst more than two variables.
Example Four Coordinated Latent Changes
To exemplify this approach, we examined whether there was only one coordination mechanism of change in regulatory processes within adolescents with diabetes and their parents or two coordination mechanisms of change. Specifically, in addition to the mother and father monitoring processes examined in the prior example, we utilized two measures that have been traditionally associated with how adolescents self-regulate with respect to diabetes management: the adolescent’s report of self-efficacy and self control.
There are a number of plausible arrangements we might imagine. Coordination may be a unified process in which change in self-regulatory skills of the adolescent is perfectly coordinated with change in parent processes. Such a unified approach to coordination could reflect the long-term coordination of parent and child change processes that contribute to the development of adolescent regulatory skills (Belsky, Fearon, & Bell, 2007). In this case, we would expect only a single coordination factor where the rhos would all be positive. Alternatively, a single coordination factor could arise from a pattern where parents step in when adolescents are unable to regulate on their own and diminish their involvement when they are. This pattern could reflect the sort of scaffolding process described by Vygotsky (1978) and Rogoff (1998), whereby parents provide the support needed for the child to access higher levels of functioning through the zone of proximal development. This pattern of entrainment would again suggest one underlying coordination factor, but the signs on the rhos between the self-regulation measures and the parent-regulation measures would be opposite.
It is also plausible that self-regulation and parent processes coordinate distinctly. That is, we may see two coordination factors, one of the two adolescent self-regulation scales and one of the two parent monitoring scales. This coordinative process could occur in the case when the normative developmental change for one set of processes is not well-coordinated with other developmental pressures. For instance, the cultural pressure in the western world for parental involvement to decline may be ill-timed with developmental pressures for self-regulatory processes. Although traditionally self-regulatory processes are thought to increase during adolescence due to autonomy developments (Steinberg, & Morris, 2001), the protracted development of these self-regulatory skills during adolescence and the current transitional emerging adulthood period (Arnett, 2004) could provide for two different coordinative processes that capture self-regulatory change and parent process change. Importantly, which coordinated factor model we observe tells us nothing about their contribution to regulating diabetes, only that the changes in multiple variables across time function through distinct synchronies or shared synchronies (we would need to add some indicator of regulatory success to link coordination to regulating diabetes).
We conducted models with four simultaneous latent changes testing the unconditional coordinated factors model for one shared coordinated factor and two coordinated factors (one for self-regulation and one for parent regulation). In the two coordinated factors model, the two coordinated factors were allowed to covary. The preferred model was then expanded into the conditional coordinated factors counterpart.
Results
A chi-square difference test between the unconditional one coordinated factors and unconditional two coordinated factors models was significant, χ2(1df)=13.32, p<.001, suggesting that two distinct coordination factors was a better description than only one2. Note that this is identical to a one vs. two factor model comparison, but on the changes. For the self coordination factor, we observed significant variance (var=0.437, z=2.675, p=.007) while the maintenance tendencies for both self-efficacy (beta=0.138, z=1.394, p=.163) and self-control (beta=−0.288, z=−1.213, p=.225) were non-significant. This pattern is consistent with a phase-locked pattern (a coordination factor but no maintenance tendencies).
For the parent coordination factor, we observe results very similar to the two LCS unconditional model presented earlier. As before the variance on the coordination factor is significant (var=.152, z=5.976, p<.001) and we observe significant maintenance tendencies for both mother’s monitoring (beta=−0.355, z=−7.015, p<.001) and father’s monitoring (beta=−0.391, z=−4.731, p<.001). This pattern is consistent with entrainment because the betas and rho are all significant. Also notable is that the scaling ratio was virtually unchanged between the earlier two LCS model and this four LCS model (rho: ratio is 1 Mother’s monitor to 1.332 father’s monitor; no longer significantly different from 1:1, z=1.87, p=.061 but also not significantly different from 1:1.38 observed in the model with only the two parental monitoring scales, z=−0.27, p=.786). It is plausible for these to have changed between the two models because we have essentially altered what is used to define change (all four measures and their correlations vs. just the two parent monitoring measures).
Figure 9 is the simplified model results from the four LCS conditional two coordinated factors model. This model was also an acceptable fit of the data, chi-sq (210df) =302.856, p<.001, RMSEA 90%CI: .031<.042<.052, CFI=.965, SRMR=.059. In total, this model creates six equations in the structural portion of the model, one for each of the outcomes and one for each coordination factor:
| (Eq. 7a) |
| (Eq. 7b) |
| (Eq. 7c) |
| (Eq. 7d) |
| (Eq. 7e) |
| (Eq. 7f) |
Focusing on the magnet effects (predictors of coordination; i.e., gammas), higher levels of the self-coordination factor are associated with higher behavioral self-control (1.57*) but not self-efficacy (.22) nor the potential crossover relationships (.09 or −.22). This pattern suggests that behavioral self-control seems to be functioning as a driver for self-coordination while self-efficacy is more of a barometer, along for the ride. Such results would be consistent with the idea that self-control is a more general resource that affects multiple domains of adolescent functioning (Moffit, Arseneault, Belsky, Dickson, Hancox, Harrington…& Caspi, 2011). As with the earlier two LCS coordinated factors model, both mother (.24) and father monitoring (−.31*) were associated with coordinated change levels with the same pattern as before. In essence, both contribute to coordination.
Figure 9.
Simplified form of the four latent change score and two conditional coordinated factor model with parameter estimates and standard errors on parentheses. Covariances are shown in grey, but values are not given to increase readability.
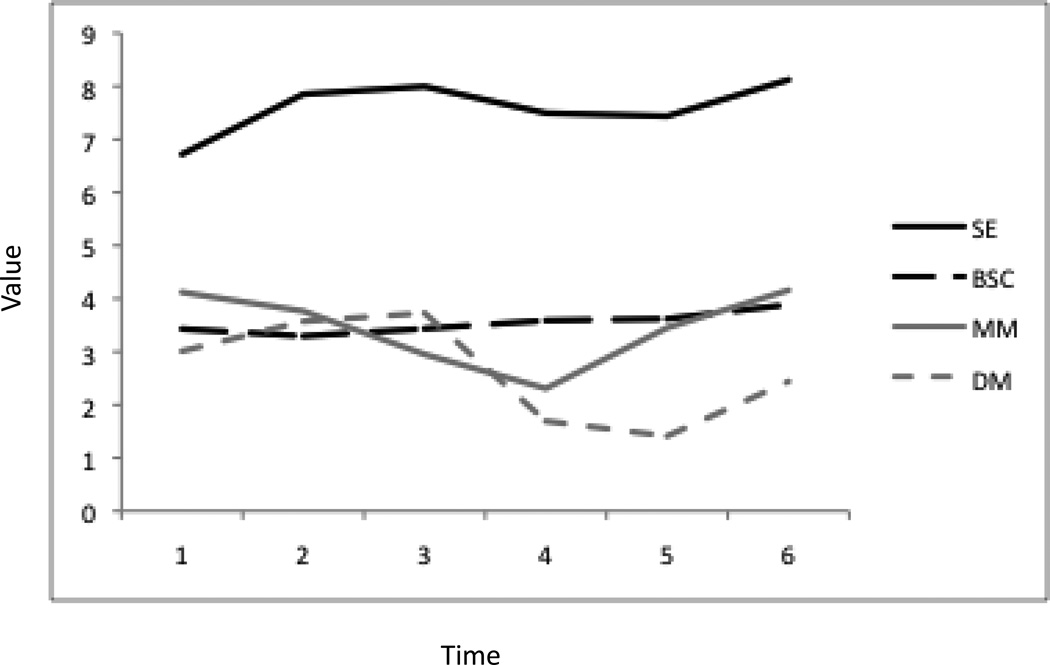
As before, we generated predicted values for each of the six time points, this time using equations 7a–f in conjunction with the mean of the time zero factors and random intercepts drawn from a normal distribution with the mean and variance of the intercept factors. Figure 10 shows that there is greater matching between the two self items over time and greater matching between the two monitoring items over time, consistent with the two dimensional structure.
Figure 10.
Example predicted trajectories for all four variables as a function of the final four process model. All predicted trajectories are with perturbations generated by varying the equation intercepts as a function of the intercept latent variables (intercept replaced with a random number drawn from a normal distribution with a mean and variance equal to the intercept latent variables).
Discussion
In this paper, we presented an expansion on latent change score models where a change in parameters (creating a coordination latent variable) allows the model to differentiate synchronized behavior in a coherent way that distinguishes along dimensions of coordination. When there are only two variables whose change processes are being modeled it generates a two-step procedure:
Run a model building the two latent change scores and estimate a latent variable between the changes, equated through time, using a marker variable strategy. This is the unconditional coordinated factors model. This model can depict what kind of coordination (i.e., desynchrony, entrainment, or phase-locking) is being observed as a function of the maintenance tendencies and the loading on the coordination factor. The extent to which the variance in the coordination factor is non-zero (significant) is the extent to which there is coordination between the two processes within a linear first order change model. If there is no variance on the coordination factor, there is no coordination. When there is variance in the coordination factor, having at least one non-zero maintenance tendency depicts the model in the range of entrainment while maintenance tendencies that are zero (non-significant) suggest phase locking. The loadings for the coordination factor then capture the scaling between the two changes and when phase-locked, capture the phase-locked ratio and phase.
Add in the magnet effects where each variable is allowed to predict the coordination factor. This is the conditional coordinated factors model. These magnet effects detect the sensitivity of higher and lower values in coordination to the processes themselves. Thus they give a sense of the influential nature on coordination (note: higher and lower values of the coordination factor mean higher and lower values of the shared changes [i.e., the phasic relationship], not the existence of or extinction of coordination). A driver-driven system, for example, where one variable essentially forces the other to move with it would appear as a single magnet effect coming from the driver because only previous values of the driver would relate to the future coordinated changes. A mutually driven system would appear as having magnet effects from both variables. A system driven by some other external force would be predicted by neither variable as the changes would not be a function of the previous values.
When there are more than two change processes to be coordinated, the initial step expands into a question of what the arrangement of underlying change processes may be. In our example where we tested one vs. two coordinated factors, we found that two coordinated factors was a better fit. Our logic for this was based on theories of regulation, but this same arrangement could just have easily been sought as a function of measurement. That is, in this circumstance, our results could be explained as adolescents perceiving changes in mothers’ and fathers’ monitoring as some function of the same thing, thus coordinated, but as distinct from changes in the self.
This dual interpretation highlights the meaning of coordination in that, just like any factor model, it is heavily defined by the series of variables that are treated as manifests. Thus, coordination is model specific and subject to all the limitations that occur with latent variable models more generally. Within the context of diabetes regulation examined here, the extent to which parental processes are coordinated with adolescent self-regulatory processes depends on the specific measures of parent processes and self-regulatory skills that are examined. It might be that with a different measure of family processes, one would see a single-factor solution to coordination.
Advantages
One of the model’s major strengths is its flexibility for characterizing the full range of coordinated relationships. The ability to model desynchrony, entrainment, and phase locking using a single set of parameters affords substantial conceptual and statistical benefits. From a conceptual viewpoint, disentangling desynchrony from phase locking may address important substantive questions. For example, if we had discovered desynchrony in our example of family diabetes regulation, it would have implied a lack of coordination within the family system as a whole in parental monitoring of diabetes. While desynchrony would not necessarily imply a dysfunctional approach to monitoring, it is very distinct from a family where mother and father monitor the adolescent’s diabetes in a locked step fashion (i.e., is phase locked with everyone moving in tandem).
Another noteworthy advantage is that the model’s ability to characterize entrainment makes it easier to apply to the kinds of complex processes that are often of interest in psychology and the social sciences. There are very few examples of truly phased locked processes in psychological literature. Instead, many phenomena are depicted in a way consistent with entrainment. For example, emotional contagion is depicted as a convergence of emotions between individuals who spend time together (Hatfield, Caccioppo, & Rapson, 1993). However, it is not seen as a holistic transfer of emotions where one individual ‘clones’ the emotions of another. Instead it is depicted as a subtle phenomenon where a person’s emotions are influenced by the behaviors and emotions of those around the individual (possibly through mimicry). The flexibility of the coordination model for capturing the full range of coordinated relationships implies that fewer assumptions have to be made about the nature of covariation of change and makes the model more robust across a range of circumstances while also having a specificity as to what the model can depict and how it decomposes the data patterns.
The inclusion of a scaling parameter between the changes adds to the flexibility and interpretability of the model. When phase-locked, the scaling parameter captures the observed ratio of change including in-phase vs. anti-phase distinctions. If two outcomes are in a one to two ratio, then rho will come out as either .5 or 2, depending on which variable was treated as the marker variable. Thus, it becomes important to test rho against values other than zero or to report confidence intervals to represent the likely range of phase-locked ratios. Given that rho is merely a scaling parameter, it also accounts for scaling differences in the two outcomes. Thus, when entrained, magnet effects are predicting the same outcome and by choosing which variable is the marker, we can also compare these magnet effects to a given maintenance tendency. In essence, the latent coordination approach resolves many scaling issues inherent in models of 1st order change.
Issues of Estimation
Since coordination is captured through a latent variable logic, issues of identification are paramount. Usually, a two-indicator factor is under identified and thus impossible to estimate unless other parameters provide anchoring information. In the models presented here, this problem is alleviated through equality constraints, forcing the equation to be the same across time (thus each coordination factor is identical). In essence, this forms a degree of measurement invariance, a prerequisite for the study of change (Widaman, Ferrer, & Conger, 2010). However, the pattern of equality constraints utilized here also forces the equation to be invariant across time. Thus, every coordination factor is also equated across time (as are all the terms across time points). Using six time steps then generates six different indicators for each change to be a manifestation of coordination (twelve in total).
The emphasis for identification becomes a function of the number of time points necessary to properly estimate a coordination model. With two latent difference score processes, two time points are enough to make the conditional one coordination factor model fully saturated (just-identified). However, this only gives the latent coordination factor two indicators, which is unstable (unlikely to work). Additionally, this assumes homogenous error variances and no error covariances, which many practitioners commonly free in SEM models over time. Measuring variables beyond two time points allows for over-identification of the model, capturing both misfit due to coordination and misfit due to failure of invariance.
Just because it may be possible to conduct a coordination model with only two time points, the reality is that this may not be coordination. The range of coordination behaviors are describing patterns through time. Arguably, a two time point model lacks the necessary longitudinal structure (Rogosa, 1995) and thus may be capable of depicting data patterns not described here. The notable exception is the Dynamic Factor Analytic data structures (Molenaar and Ram, 2009) that has been used to counter many of these classic problems. Specifically, restructuring a long time series from a single individual/family so that multiple variables represent the leads/lags of a variable or set of variables construct a model invariant through many points in time while being a much simpler model in SEM. These same data structures (aka, Toeplitz, or time delay embedding) can be used with latent change scores reinstating the interpretation of coordination in the two time point model.
Conclusion
In research methods courses, we commonly teach that there are four causal arrangements: a causes b, b causes a, a third party variable causes both, and a and b cause each other in a bidirectional fashion. Previous methods for bidirectional causal estimation try to simultaneously estimate the first two (a causes b and b causes a), with limited success. The approach presented here treats multidirectional causal relationships akin to the unknown third party causer. The distinction seems subtle, but the shift in logic allows us to express and distinguish the full range of coordinated behaviors researchers describe. In essence, coordination may be more like the third party causer than it is a set of unidirectional relationships. And yet it is still distinct from a third party causer: the magnet effects suggest that a and b can appear to be unidirectionally causal under the right methodological circumstance.
This shift also highlights an inherent freedom of measurement we frequently miss. Factor analytic approaches are also known as data reduction approaches, where fewer measures are needed to describe phenomena. Treating coordination as a set of latent variables argues that there is redundancy amongst measures. This redundancy is not the same as what we identify where Ys at a snapshot in time are the outcomes, akin to common factor analytic approaches (though there is a relationship). Instead, it depicts how the changes move together. Knowing that many variables are coordinated tells us that they may be different at any snapshot in time, but their dance through time is linked. Thus, the entire set of coordinated variables may not be necessary to depict the system.
Ultimately, the models presented herein lay the groundwork for interpreting multidirectional relationships both in terms of the patterning in time they generate and components that lead to this pattern. At the same time our approach begins to characterize how we might explore relationships within coordination, in terms of the number and arrangement of coordination factors, without loosing the connection to the overall patternings we observe. This model thus creates new opportunities for the comprehension of these complex models, while also capturing the complexity inherent in coordination patterns.
Acknowledgments
Funding
This study was supported by grant R01 DK063044-01A1 from the National Institute of Diabetes and Digestive Kidney Diseases awarded to Deborah Wiebe (PI) and Cynthia Berg (co-PI). We thank the families who participated, the physicians (Mary Murray, David Donaldson, Rob Lindsay, Carol Foster, Michael Johnson, Marie Simard), staff of the Utah Diabetes Center, Mike T. Swinyard, MC, PC, and additional members of the ADAPT team (Donna Gelfand, Jenni McCabe, Marejka Shaevitz, and Michelle Skinner).
Footnotes
Significant at alpha = .05, two-tailed
Fixed to a value of 1
The unconditional two coordinated factors model and the conditional two coordinated factors model both created out of range values in the implied correlation matrices. This is usually a sign of a problem with the model. However, it is ignorable here. Specifically, the implied correlation matrices require scale invariance for the formulas to properly convert from the estimated values in unstandardized metric to the standardized ones used in correlations. When scale invariance is violated, these formulas are incorrect. This model, through its arrangement of equality constraints, fails invariance implying that tests are not equivalent in standardized metric.Thus, the implied correlation matrix does not represent the model.
References
- Arnett JJ. Emerging adulthood: The winding road from the late teens through the twenties. New York, NY: Oxford University Press; 2004. [Google Scholar]
- Belsky J, Fearon P, Bell B. Parenting, attention, and externalizing problems: testing mediation longitudinally, repeatedly, and reciprocally. Journal of Child Psychology and Psychiatry. 2007;48:1233–1242. doi: 10.1111/j.1469-7610.2007.01807.x. [DOI] [PubMed] [Google Scholar]
- Barber BK. Parental psychological control: Revisiting a neglected construct. Child Development. 1996;67:3296–3319. [PubMed] [Google Scholar]
- Berg CA, Butler JM, Osborn P, King G, Palmer D, Butner J, Murray M, Lindsay R, Donaldson D, Foster C, Swinyard M, Wiebe DJ. The Role of Parental Monitoring in Understanding the Benefits of Parental Acceptance on Adolescent Adherence and Metabolic Control of Type 1 Diabetes. Diabetes Care. 2008;31:678–683. doi: 10.2337/dc07-1678. [DOI] [PubMed] [Google Scholar]
- Boker SM, Cohn JF, Theobald BJ, Matthews I, Mangini M, Spies JR, Brick TR. Something in the way we move: Motion dynamics, not perceived sex, influence head movements in conversation. Journal of Experimental Psychology: Human Perception and Performance. 2011;37(3):874. doi: 10.1037/a0021928. [DOI] [PubMed] [Google Scholar]
- Boker SM, McArdle JJ. A statistical vector field analysis of longitudinal aging data. Experimental Aging Research. 1995;21:77–93. doi: 10.1080/03610739508254269. [DOI] [PubMed] [Google Scholar]
- Boker SM, Nesselroade JR. A method for modeling the intrinsic dynamics of intraindividual variability: Recovering the parameters of simulated oscillators in multi-wave panel data. Multivariate Behavioral Research. 2002;37:127–160. doi: 10.1207/S15327906MBR3701_06. [DOI] [PubMed] [Google Scholar]
- Bollen KA. Structural equations with latent variables. New York, NY: Wiley; 1989. [Google Scholar]
- Browne MW, Nesselroade JR. Representing psychological processes with dynamic factor models: Some promising uses and extensions of ARMA time series models. In: Maydeu–Olivares A, McArdle JJ, editors. Psychometrics: A festschrift to Roderick P. McDonald. Mahwah, NJ: Lawrence Erlbaum Associates; 2005. pp. 415–452. [Google Scholar]
- Butler EA. Temporal interpersonal emotion systems: The “TIES” that form relationships. Personality and Social Psychology Review. 2011;15:367–393. doi: 10.1177/1088868311411164. [DOI] [PubMed] [Google Scholar]
- Butner J, Amazeen P, Mulvey G. Multilevel modeling of two cyclical processes: Extending differential structural equation modeling to coupled systems. Psychological Methods. 2005;10:159–177. doi: 10.1037/1082-989X.10.2.159. [DOI] [PubMed] [Google Scholar]
- Butner J, Diamond LM, Hicks AM. Attachment style and two forms of affect coregulation between romantic partners. Personal Relationships. 2007;14:431–455. [Google Scholar]
- Butner J, Story TN. Oscillators with differential equations. In: Guastello S, Gregson R, editors. Nonlinear Dynamical Systems Analysis for the Behavioral Sciences: Real Data. CRC Press; 2010. [Google Scholar]
- Chow S, Ram N, Boker SM, Fujita F, Clore G. Emotion as a thermostat: representing emotion regulation using a damped oscillator model. Emotion. 2005;5(2):208–225. doi: 10.1037/1528-3542.5.2.208. [DOI] [PubMed] [Google Scholar]
- Ferrer E, Hamagami F, McArdle JJ. Modeling latent growth curves with incomplete data using different types of structural equation modeling and multilevel software. Structural Equation Modeling. 2004;11:452–483. [Google Scholar]
- Ferrer E, Nesselroade JR. Modeling affective processes in dyadic relations via dynamic factor analysis. Emotion. 2003;3:344–360. doi: 10.1037/1528-3542.3.4.344. [DOI] [PubMed] [Google Scholar]
- Finkenauer C, Engels R, Baumeister RF. Parenting behavior and adolescent behavioural and emotional problems: The role of self-control. International Journal of Behavioral Development. 2005;29:58–69. [Google Scholar]
- Gottman JM, Murray JD, Swanson CC, Tyson R, Swanson KR. The mathematics of marriage: Dynamic nonlinear models. Cambridge, MA: MIT Press; 2002. [Google Scholar]
- Graham JW. Missing data analysis: Making it work in the real world. Annual Review of Psychology. 2009;60:549–576. doi: 10.1146/annurev.psych.58.110405.085530. [DOI] [PubMed] [Google Scholar]
- Granger CWJ. Investigating causal relations by econometric models and cross-spectal methods. Econometrica. 1969;37:424–438. [Google Scholar]
- Grimm KJ. Intercept centering and time coding in latent difference score models. Structural Equation Modeling. 2012;19:137–151. doi: 10.1080/10705511.2012.659627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hatfield E, Cacioppo JT, Rapson RL. Emotional contagion. Current Directions in Psychological Science. 1993;2:96–99. [Google Scholar]
- Hofer M. Relationships as regulators: A psycho-biologic perspective on bereavement. Psychosomatic Medicine. 1984;46:183–197. doi: 10.1097/00006842-198405000-00001. [DOI] [PubMed] [Google Scholar]
- Hollingshead AB. Four factor index of social status. New Haven, CT: Department of Sociology, Yale University; 1975. [Google Scholar]
- Hu L, Bentler M. Fit indives in covariance structure modeling: Sensitivity to underparameterized model misspecification. Psychological Methods. 1997;3:424–453. [Google Scholar]
- Iannotti RJ, Schneider S, Nansel TR, Haynie DL, Plotnick LP, Clark LM, et al. Self-efficacy, outcome expectations, and diabetes self-management in adolescents with type 1 diabetes. Journal of Developmental and Behavioral Pediatrics. 2006;27(2):98–105. doi: 10.1097/00004703-200604000-00003. [DOI] [PubMed] [Google Scholar]
- Kelso JAS. Phase transitions and critical behavior in human bimanual coordination. Journal of Physiology: Regulatory, Integrative and Comparative Physiology. 1984;15:R1000–R1004. doi: 10.1152/ajpregu.1984.246.6.R1000. [DOI] [PubMed] [Google Scholar]
- Kelso JAS. Dynamic patterns: The self-organization of brain and behavior. Cambridge, MA: Massachusetts Institute of Technology; 1995. [Google Scholar]
- McArdle JJ. Latent variable modeling of longitudinal data. Annual Review of Psychology. 2009;60:577–605. doi: 10.1146/annurev.psych.60.110707.163612. [DOI] [PubMed] [Google Scholar]
- McArdle JJ, Hamagami F, Meredith W, Bradway KP. Modeling the dynamic hypotheses of Gf-Gc theory using longitudinal life-span data. Learning and Individual Differences. 2000;12:53–79. [Google Scholar]
- McArdle JJ, Hamagami F. Latent difference score structural models for linear dynamic analyses with incomplete longitudinal data. In: Collins LM, Sayer AG, editors. New methods for the analysis of change. Washington, DC: American Psychological Association; 2001. pp. 137–176. [Google Scholar]
- McArdle JJ, Nesselroade JR. Structuring data to study development and change. In: Cohen SH, Reese HW, editors. Life-Span Developmental Psychology: Methodological Innovations. Hillsdale, NJ: Erlbaum; 1994. pp. 223–67. [Google Scholar]
- Moffitt TE, Arseneault L, Belsky D, Dickson N, Hancox RJ, Harrington H, Caspi A. From the Cover: A gradient of childhood self-control predicts health, wealth, and public safety. Proceedings of the National Academy of Sciences. 2011;108(7):2693–2698. doi: 10.1073/pnas.1010076108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molenaar PCM. A dynamic factor analysis model for the analysis of multivariate time series. Multivariate Behavioral Research. 1985;22:329–353. doi: 10.1207/s15327906mbr2203_5. [DOI] [PubMed] [Google Scholar]
- Molenaar PCM, Ram N. Advances in dynamic factor analysis of psychological processes. In: Valsiner J, Molenaar PCM, Lyra M, Chaudhary’s N, editors. Dynamic Process Methodology in the Social and Developmental Sciences. New York, NY: Springer; 2009. pp. 255–268. [Google Scholar]
- Nesselroade JR. Paul B. Baltes (1939–2006) The American Psychologist. 2007;62:696. [Google Scholar]
- Nicholson JS, Deboeck PR, Farris JR, Boker SM, Borkowski JG. Maternal depressive symptomatology and child behavior: Transactional relationship with simultaneous bidirectional coupling. Developmental Psychology. 2011;47:1312–1323. doi: 10.1037/a0023912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oud JHL. Continuous time modeling of reciprocal relationships in the cross- lagged panel design. In: Boker SM, Wenger MJ, editors. Data analytic techniques for dynamical systems. Mahwah, NJ: Lawrence Erlbaum Associates; 2007. pp. 87–129. [Google Scholar]
- Oud JHL, Jansen RARG. Continuous time state space modeling of panel data by means of SEM. Psychometrika. 2000;65:199–215. [Google Scholar]
- Oud JHL, Singer H. Continuous time modeling of panel data: SEM versus filter techniques. Statistica Neerlandica. 2008;62:4–28. [Google Scholar]
- Rogoff B. Cognition as a collaborative process. In: Damon W, editor. Handbook of child psychology, Vol. 2: Cognition, perception, and language. Hoboken, N.J: John Wiley & Sons; 1998. pp. 679–744. [Google Scholar]
- Rogosa DR. Myths and methods: Myths about longitudinal research, plus supplemental questions. In: Gottman JM, editor. In The analysis of change. Hillsdale, New Jersey: Lawrence Erlbaum Associates; 1995. pp. 3–65. [Google Scholar]
- Rotondo JL, Boker SM. Behavioral synchronization in human conversational interaction. Advances in Consciousness Research. 2002;42:151–162. [Google Scholar]
- Sameroff AJ, Mackenzie MJ. Research strategies for capturing transactional models of development: The limits of the possible. Developmental Psychopathology. 2003;15:613–640. doi: 10.1017/s0954579403000312. [DOI] [PubMed] [Google Scholar]
- Shifren K, Hooker KA, Wood PK, Nesselroade JR. The structure and variation of mood in individuals with Parkinson’s Disease: A dynamic factor analysis. Psychology and Aging. 1997;12:328–339. doi: 10.1037//0882-7974.12.2.328. [DOI] [PubMed] [Google Scholar]
- Singer H. SEM modeling with singular moment matrices part II: ML-estimation of sampled stochastic differential equations. Journal of Mathematical Sociology. 2012;36:22–43. [Google Scholar]
- Steinberg L, Morris AS. Adolescent development. Annual Review of Psychology. 2001;52:83–110. doi: 10.1146/annurev.psych.52.1.83. [DOI] [PubMed] [Google Scholar]
- Strogatz SH. Sync: The emerging science of spontaneous order. NY: Hyperion, NY; 2003. [Google Scholar]
- Stewart I. Does god play dice: The new mathematics of chaos. Maldan, MA: Blackwell Publishing; 2002. [Google Scholar]
- Tangney JP, Baumeister RF, Boone AL. High self-control predicts good adjustment, less pathology, better grades, and interpersonal success. Journal of Personality. 2004;72(2):271–324. doi: 10.1111/j.0022-3506.2004.00263.x. [DOI] [PubMed] [Google Scholar]
- Treffner PJ, Turvey MT. Resonance constraints on rhythmic movement. Journal of Experimental Psychology. Human Perception and Performance. 1993;19:1221–1237. [Google Scholar]
- Turvey MT. Coordination. American Psychologist. 1990;45:938–953. doi: 10.1037//0003-066x.45.8.938. [DOI] [PubMed] [Google Scholar]
- Voelkle MC, Oud JHL, Davidov E, Schmidt P. An SEM approach to continuous time modeling of panel data: relating authoritarianism and anomia. Psychological Methods. 2012;17:176–192. doi: 10.1037/a0027543. [DOI] [PubMed] [Google Scholar]
- Von Holst E. On the nature of order in the central nervous system. In: Martin R, editor. The collected papers of Erich von Holst, vol. 1. The behav- ioral physiology of animal and man. Coral Gables, FL: University of Miami Press; 1937, 1973. [Google Scholar]
- Vygotsky LS. Mind in society: The development of higher psychological processes. Cambridge, MA: Harvard University Press; 1978. [Google Scholar]
- Widaman KF, Ferrer E, Conger RD. Factorial invariance within longitudinal structural equation models: Measuring the same construct across time. Child Development Perspectives. 2010;4:10–18. doi: 10.1111/j.1750-8606.2009.00110.x. [DOI] [PMC free article] [PubMed] [Google Scholar]