Building Cell Models and Simulations from Microscope Images

Abstract

The use of fluorescence microscopy has undergone a major revolution over the past twenty years, both with the development of dramatic new technologies and with the widespread adoption of image analysis and machine learning methods. Many open source software tools provide the ability to use these methods in a wide range of studies, and many molecular and cellular phenotypes can now be automatically distinguished. This article presents the next major challenge in microscopy automation, the creation of accurate models of cell organization directly from images, and reviews the progress that has been made towards this challenge.

1. Introduction

Biochemistry and structural biology were revolutionized by the ability to replace rough approximations of molecular shape and interactions, such as “rods,” “sheets,” and “globules” with spatially accurate models of protein structure directly learned from experimental data (such as from X-ray crystallography). Since molecules rarely have only a single structure, this led to probabilistic models for structures and structural transitions. This further enabled a critical advance: the ability to computationally simulate expected behaviors of molecules without requiring further experiments [1].

Cell biology has only begun to appreciate the need for a similar revolution in the way in which cell structure is represented. Currently, an explicit representation of organelle structure is avoided entirely; words, such as Genome Ontology terms, are used to refer to organelles with the assumption of a shared understanding of the structures they display. Communicating that understanding is done by hand-drawn cartoons or example images. Example images may include high-resolution reconstructions for a single organelle or cell, but these are only instances and do not capture the expected variation in that structure. Variation observed in images of a structure may be intrinsic (e.g., endosomes vary in size and shape) or due to measurement noise (e.g., coated vesicles may appear to vary in size or shape due to digital imaging of a low fluorescence signal). By assuming intrinsic variation is small, reconstruction methods have been used on many images to produce refined structures (primarily at the micron level) [2, 3]. However, for most organelles, intrinsic variation is dramatic.

A natural question then becomes how we can represent the structure of cellular components that show significant intrinsic variation in their size or shape. This leads to a larger question: how can we create predictive models that capture variation in the organization of entire cells? In order to enable prediction, such models need to be generative rather than descriptive. The distinction can easily be seen by considering the task of distinguishing pictures of apples from oranges. This can be done using a single feature such as color, combined with the rule that an object is red if and only if it is an apple. However, if the task is to create an apple, knowing that apples are red is not nearly enough. As discussed below, generative models require some choices regarding the completeness or effectiveness of the description.

Automation of descriptive analysis of high resolution/high content cell images has progressed dramatically in the past twenty years [4–8]. The direct creation of generative models from cell images represents the next major challenge in high content analysis. There are a number of reasons why such generative models would be useful. First, as just discussed, they would capture the underlying spatial relationships in a collection of images, that is, they estimate not only the most probable reconstruction of each individual cell or organelle (e.g., removing noise in imaging) but also the modes of variation between individual instances. As such they are well-suited for representing the large collections of images enabled by the development of High Content Screening and Automated Microscopy [9]. Second, models learned separately for different organelles or structures (i.e., from different sets of images) could potentially be combined to synthesize a cell containing all of those organelles in the same cell (assuming that the organelles do not affect each others position or shape). Third, such models could be used to predict the distribution of an organelle in a new cell type (e.g., with a different cell and nuclear arrangement), and those predictions could be rapidly confirmed (or modified) using feature-based approaches without having to build a separate generative model for all organelles in each cell type. Fourth, generative models could provide a better framework for connecting morphology to the mechanisms that produce it, since biochemistry could be directly linked to the parameters of the generative model. Fifth, databases of generative spatial models could provide an important complement to Genome Ontology terms, providing a spatial definition of those terms. Lastly, instances drawn from generative models could be used as the basis for spatially realistic simulations of cellular biochemistry. There are a number of powerful systems for performing such simulations, such as MCell [10], VirtualCell [11], Simmune [12] and SmolDyn [13], but most simulations currently performed with those systems use a very limited number of manually-segmented and manipulated images to provide compartment geometries. Generative models can provide, without manual editing, large numbers of cell geometries with the closed structures that are needed for such simulations.

Some basic criteria for the creation of such generative models of cellular structure and organization have been proposed previously [14]. These were that the models be

1. automated: learnable automatically from images;

2. generative: able to synthesize new, simulated images displaying the specific pattern(s) learned from images;

3. statistically accurate: able to capture pattern variation between cells; and

4. compact: representable by a small number of parameters and communicable with significantly fewer bits than the training images.

As with most modeling efforts, satisfying the latter two criteria requires balancing between the complexity and the completeness of the models (a version of the bias-variance tradeoff [15]). An illustration is the choice of whether to model the shape of an individual organelle (such as a mitochondrion), using an ellipse, which is very compact, or a mesh, which captures every surface irregularity. Converting these representations into generative models differs greatly in the amount of training data required – learning a statistical model of the variation of two or three axis lengths requires far less data than accurately capturing the relationships between hundreds or thousands of minor surface variations.

2. Overview of learning and use of generative models of cell organization

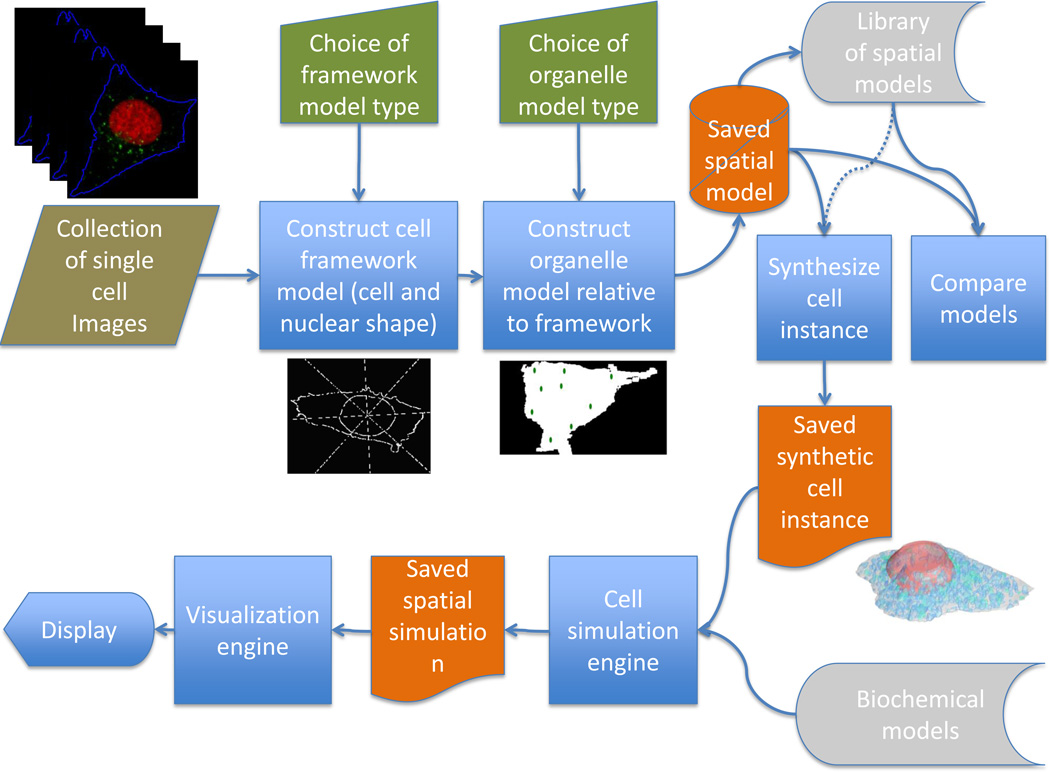
Over a number of years and contributions from a number of participants, the open source CellOrganizer system has been created as a step towards meeting the need for learning and using image-based generative cell models [14, 16–23]. The basic principles of the CellOrganizer pipeline are illustrated in Figure 1, and are generally applicable to efforts in this area. The input is a collection of cell images, most frequently of cells tagged with fluorescent probes specific for one or more proteins or organelles. We begin creation of models from those images by starting with the major geometric components of the eukaryotic cell, the overall cell and nuclear shape as reflected by the positions of the plasma and nuclear membranes. This choice is made not only because these components provide a logical starting point but also because they are easy to define even when specific probes are not include to delineate them. For example, we can get a reasonably good estimate of the plasma membrane position from the autofluorescence in fluorescent channels used to image other proteins; in the rare cases were a nuclear marker is not present, we can frequently make a good estimate of the position of the nuclear membrane from the “hole” present in the pattern of other markers. Having constructed a model of cell and nuclear shape (which we refer to as a framework model), we next construct other models (e.g., for organelles) that are conditional on those shapes.

Figure 1.

Flow chart for creating and using generative models of cell organization.

The parameters of the learned model can then be readily compared with those of other, previously learned models, e.g., for different cell types or conditions. We can also use one or more learned models to synthesize an idealized cell instance free from blur or noise from imaging. This spatial representation of a cell instance can then be used to provide the geometries of compartments for use with biochemical models involving different organelles.

3. Constructing models

We next turn to some specifics on how generative cell models can be created, including general principles of how CellOrganizer creates models from image collections. CellOrganizer is a Matlab package that is accessed by a small number of interface functions that learn models from images or movies, compare models, and synthesize images or movies from models. Control over the operation of those functions is achieved by setting various parameters in a control structure. The starting point for learning a model is a collection of images. Given the many tools available to segment images into individual cell regions and the frequent need to tailor segmentation to a specific collection, CellOrganizer assumes either that input images either contain single cells or that masks are provided to define the region corresponding to each cell. It is called with strings specifying the paths (including optional wildcards specifying subsets of files in those paths) to images of a cytoplasmic or cell boundary marker, a nuclear marker, and any specific organelle markers or tagged proteins. An optional path can be given to provide mask images. The algorithms to be used (and any parameters that they require) are specified through a parameter structure. The primary output is a file containing the learned model of the cellular components and the relationships between them, and additional outputs, such as files containing the model parameters for each cell, can be requested.

An important consideration in constructing cell models is that they can only reflect the properties of the cells in the image collection used for training. Thus, models learned from a collection of fully differentiated cells cannot of course capture behaviors shown by cells during the differentiation process (i.e., they cannot synthesize “green apples” if trained with only images of red ones). Given a collection of images of cells at various stages of differentiation, the model can learn variation in organization associated with that differentiation. Similarly, movies rather than static images are needed as input to learn dynamic behaviors (an example of this is discussed below). However, it should be noted that models learned from static images can with some assumptions be used to simulate dynamics.

3.1. Cell framework models

3.1.1. Nuclear shape models

To illustrate the process, we turn first to modeling the most basic and important components of cells, the nuclear and cell membranes. A number of different approaches have been described for constructing models of either or both of these. While work has been done on constructing generative models of nuclei or cells by hand [24, 25], We will focus here on learning generative models directly from images. Manually constructed models may be oversimplified and may not capture subtle differences between cell populations, and the approach does not scale to the large collections of images available for many cells types. For nuclei, parametric approaches have the advantage discussed above that they are compact and easy to learn. Examples include 2D medial axis models [14] and 3D cylindrical surface models [18]. Models of nuclear shape variation are created using these approaches by estimating the parameters for each nucleus, and then constructing a statistical model of the distribution of those parameters over all nuclei available for training. However, such modeling methods are not suitable when the assumptions underlying them break down, for example, for nuclei with concavities.

A powerful alternative, non-parametric approach is based on performing non-rigid registration of pairs of nuclei [16, 26]. This approach, based on seminal work on large deformation metric mapping [27], measures the amount of change needed to morph one nucleus into another as a measure of the “distance” between them, as illustrated in Figure 2 (thus this approach is referred to as “diffeomorphic”). Once distances are measured for all pairs, a coordinate system is constructed to place all nuclei in a “map” such that similar shapes are placed near each other. The construction of such maps, and how they can be used as generative models, is discussed in section 3.1.3.

Figure 2.

Measuring the distance between two nuclear shapes. The overall difference between two shapes is estimated by gradually morphing one into the other and measuring the overall amount of change needed. The cumulative change (shown below each image) represents a distance between the starting shape and any of the intermediate shapes. From Rohde et al [16].

3.1.2. Cell shape models

Cell shape has also been modeled by a variety of approaches, both descriptive and generative. For example, statistical models of cell shape have been created using descriptive features and used to discover gene perturbations that affect cell shape [28–30]. Work has also been done using eigenshape methods that can be generative [31, 32]. However, these approaches treated cell shape alone and did not consider its relationship to other cell components such as the nucleus. However, to construct realistic cells, we need to have not just the ability to accurately generate cell and nuclear shapes but to be able to generate shapes appropriate for each other and in the proper position and orientation. This can be accomplished by creating two models in which one is dependent upon the other, or by creating a joint model of both components.

3.1.3. Combined models of cell and nuclear shape

The dependent model approach involves learning a nuclear model from available nuclear images, followed by learning a model that captures the relationship between each cell shape and its corresponding nuclear shape. As illustrated in Figure 3a, synthesizing a combined cell and nuclear framework involves randomly choosing a nuclear shape instance from the nuclear model following by providing that instance to the cell shape model and using it to produce an appropriate cell shape. This combination is then passed on to other models that can synthesize organelle distributions that are dependent on both the cell and nuclear shape. The first dependent model of cell and nuclear shape was created for 2D images using a simple ratiometric approach [14] in which the ratio of the distance from the center of the nucleus to the cell boundary and to the nuclear boundary was calculated as a function of the angle from the major axis of the cell. This was later extended to 3D [18]. As with the parametric nuclear models, these ratiometric models are not suitable for complex cell shapes. Regardless of the specific model used, the advantage of the dependent model approach is that a single dependent (cell) model can in principle be applied to instances generated from different types of independent (nuclear) models (and vice versa).

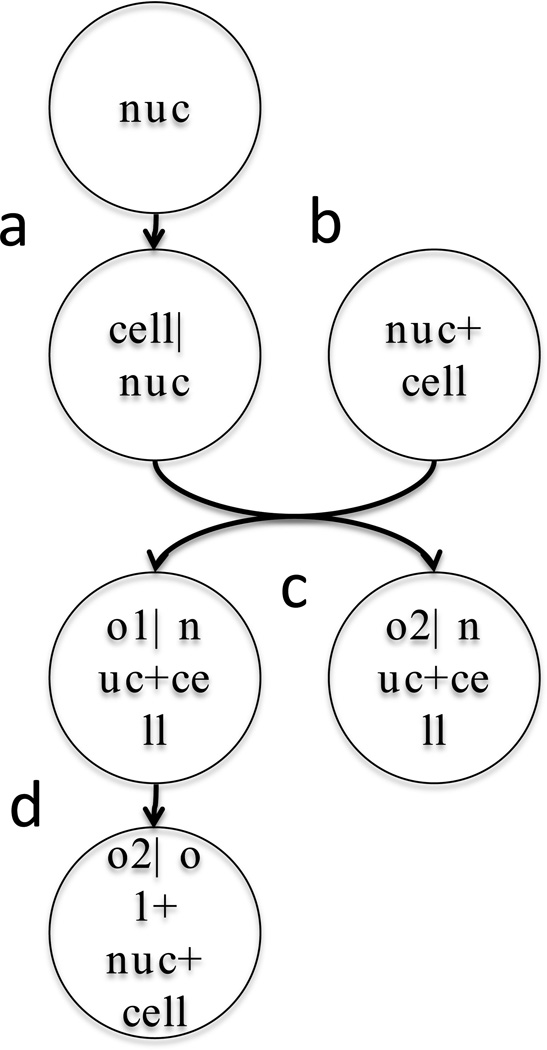
Figure 3.

Example of dependencies between models of cell components. Each circle represents a model, and the text before the vertical bar describes what component(s) it generates and the text after the bar specifies what component(s) it requires to do so. Components are nuclear shape (nuc), cell shape (cell), and organelles (o1, o2).

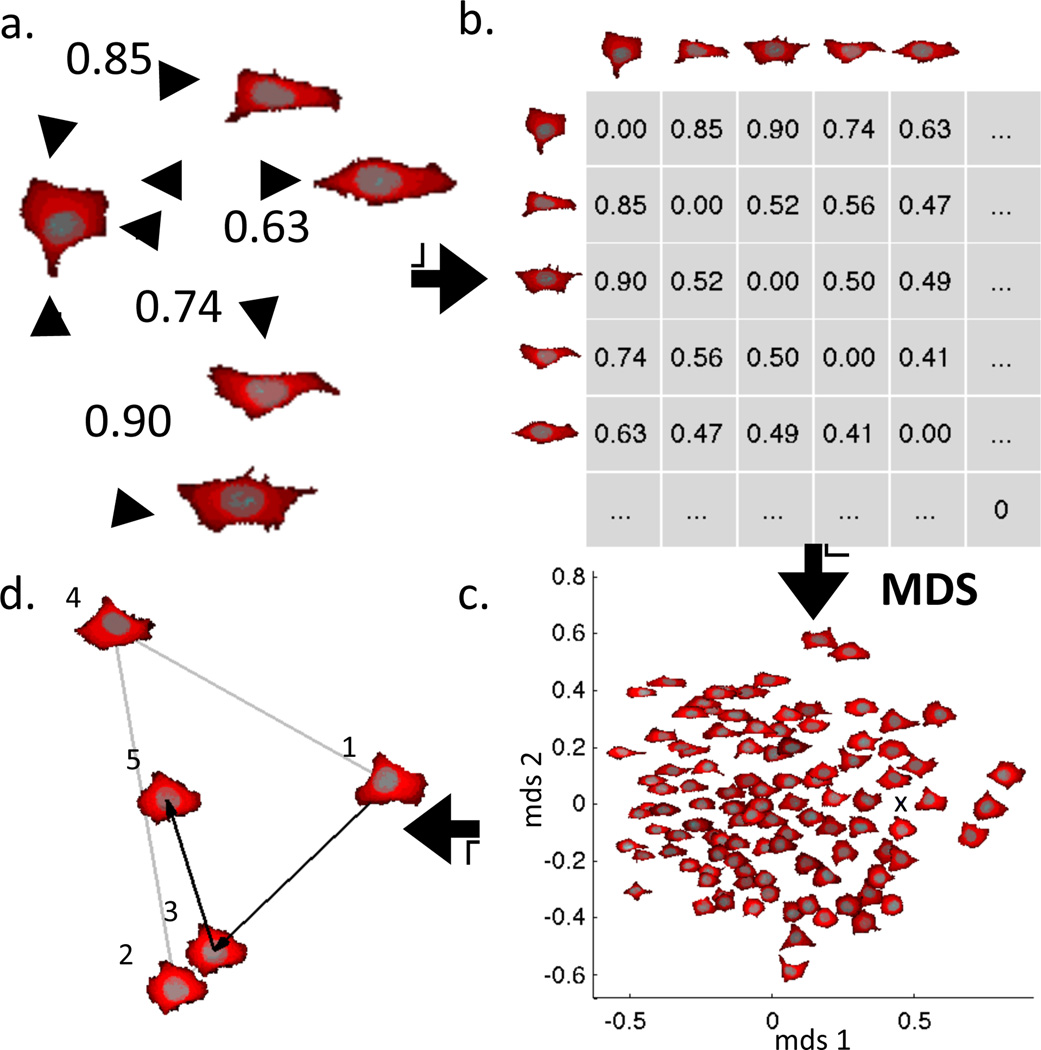
The joint model approach has so far been only been developed using a non-parametric, diffeomorphic approach [33]. An advantage of the diffeomorphic approach is that it can be applied simultaneously to multi-channel images. In the simplest form, the image of the channel corresponding to each component is thresholded or otherwise processed to produce a mask and all pixels in that mask are assigned an index for that component (e.g., nuclear pixels are assigned 2, cytoplasmic pixels are assigned 1, background pixels are assigned 0). Note that in this approach, pixels can only be part of one component (thus cytoplasmic pixels are defined as pixels in the cell shape that are not in the nuclear shape). The process of creating a joint model of cell and nuclear shape is illustrated in Figure 4. The distance between each pair of cells (which measures the “work” required to morph both the nuclear shape and the cell shape) is calculated and stored in a distance matrix (Fig. 4a,b). A map (using two or more dimensions) is then created from that matrix using a method such as multi-dimensional scaling (MDS) that seeks to place each cell in the map such that its distance from each other cell matches as closely as possible the measured distance (Fig. 4c). Optionally, the map (or “shape space”) can be converted into a probability density (e.g., by kernel density estimation). The map (or the matrix that produced it), along with the masks for each of the shapes, forms the generative model. To generate a new shape, a position in the map is randomly chosen, either uniformly or according to the probability density. A shape can then be generated to correspond to the chosen position using the experimentally observed cells that surround that position (Fig. 4d). This is done by (i) projecting a line from cell 3 through the chosen position onto the line between cells 1 and 2, (ii) morphing cell 1 towards cell 2 just as far as the fractional distance from cell 1 to the projected position, and (iii) morphing that shape towards cell 3 to a shape corresponding to its fractional distance.

Figure 4.

Constructing a two-component diffeomorphic shape space map for a collection of cell and nuclear shapes. The distance between each pair of images is calculated (a) and stored in a distance matrix (b). The matrix is used to create a map (c), illustrated in this case using two dimensions (the map is an embedding of the high dimensional shape space into any desired number of dimensions). A shape can be generated for new points in the shape space by interpolation of the nearby shapes (d). In the example, synthesis of the shape at position 5 begins by projecting a line from the cell at position 4 through position 5 until it hits (at position 3) the line connecting positions 1 and 2. A shape corresponding to position 3 is then synthesized by morphing cell 1 into cell 2 just as far as the distance from position 1 to position 3. A shape for position 5 is then found by morphing the shape at position 3 towards position 4. From Johnson et al [33].

It is worth noting that this diffeomorphic approach requires significantly more computation than approaches using descriptive features. For example, the time required to calculate a diffeomorphic distance for a pair of 144 × 144 × 14 voxel 3D image was more than ten times the time required to calculated descriptive features for them [33]. This increased time is due to the need to iteratively solve a differential equation to find the path that morphs each into the other. Another difficulty is that the diffeomorphic approaches scale with the square of the number of cells, while parametric approaches scale linearly.

3.1.4. Dynamic models of cell and nuclear shape

The models discussed so far were built using static images of different cells. Since they capture variation within a population, one can used them to simulate dynamics of cell and nuclear shape under two assumptions: that any cell can adopt shapes similar to any other cell in the population, and that cells adopt new shapes by smooth and random “walks” in the shape space. Associated with the latter assumption can be a subsidiary assumption about the extent of randomness of their paths in the shape space. As cells morph into shapes similar to their neighbors, they can show no preference for which neighbor to morph into, or can show preference based on the density of cells that show particular shapes. In either case, cells are treated as if they are in equilibrium among all shapes in the shape space.

This is often not the case, as cells may be expected to undergo more “directed” shape changes, such as during the cell cycle, differentiation or chemotaxis. If movies of cells are available, a model that captures such directed shape changes can be learned. In the simplest case, pairs of frames from many movies can be used to learn the probability that a cell in a given position in the shape space will move in each direction from that position. Under the assumption that the direction of each movement only depends on the previous position (i.e., that the cell follows a first-order Markov model), a movie with arbitrary temporary resolution and arbitrary length can be synthesized even if only pairs of frames are available (assuming enough pairs are available to make good estimates throughout the shape space). This approach has been applied to learn dynamics shape models for a number of different cultured cell lines [33].

3.2. Models for organelles and other subcellular structures

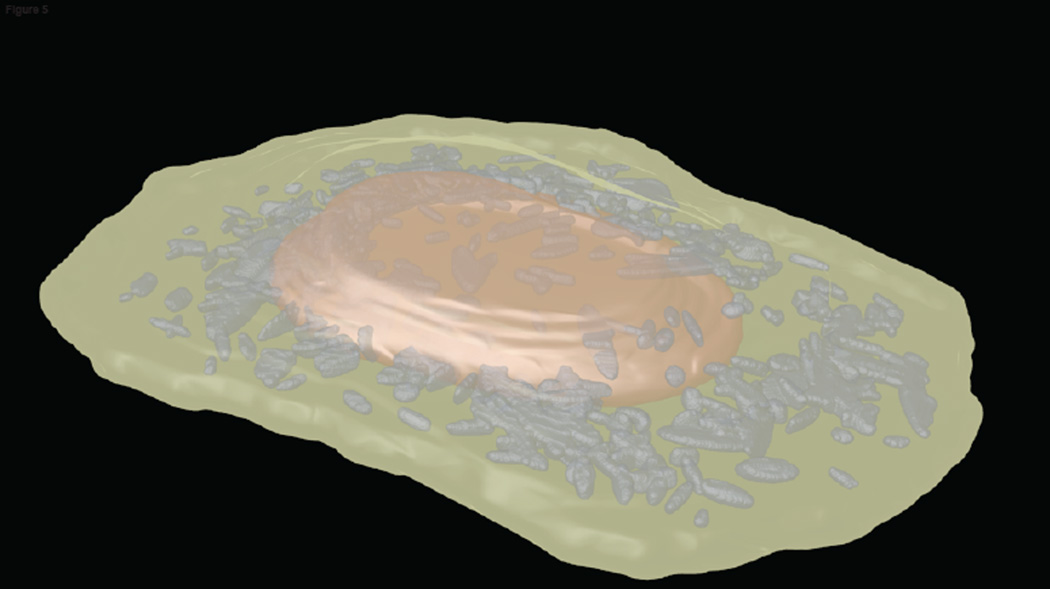
Once the cell framework is defined either through a dependent (Fig. 3a) or a joint (Fig. 3b) model, models for particular organelles can be created relative to it. We first consider those organelles that are punctate, especially those like lysosomes and peroxisomes that are membrane-enclosed. The first task is to process fluorescence images depicting the distribution of proteins contained in these organelles to identify the positions and boundaries of the individual organelles. Assuming that these organelles are roughly ellipsoidal in shape and have a relatively uniform concentration of the tagged protein within the organelle, the contribution of each organelle to the fluorescence intensity of each pixel in an image can be considered to follow a Gaussian distribution. In this case, the task, given an image, becomes to identify the distribution of Gaussian objects most likely to have given rise to that image. This standard Gaussian mixture modeling approach has been used to identify positions and sizes for vesicular organelles, and the results used to produce statistical models of the number of organelles per cell and their variation in size [14, 18]. An example of an image synthesized from such a model is shown in Figure 5.

Figure 5.

Example synthetic image depicting the mitochondrial distribution in a HeLa cell. The image was produced by generating a nuclear shape from a cylindrical surface model, generating a cell shape from the nuclear shape using a ratiometric model, and choosing the number of mitochondria and their sizes from a Gaussian object model. The nuclear volume is shown in red, the cytoplasmic volume in green, and the mitochondria in gray.

An alternative approach is to find the positions of individual organelles using variations on the idea of active contours, piecewise functions with geometric constraints that are fit to images. This approach has been used to model endosomes and analyze virus entry and endosome fusion events [34]. In this case, the boundaries of each organelle need not be ellipsoidal, but converting the boundaries of individual organelles into a generative model has not yet been addressed.

Since subcellular structures vary tremendously in their size, shape and distribution, different approaches are needed for modeling different classes of them. A particularly difficult problem is the modeling of filamentous structures, such as microtubules and microfilaments. While recent progress has been made on algorithms for localizing individual filaments in microscope images [35] and extensive analysis and modeling has been done at the leading edge of cells where individual filaments are easier to follow [36], the tangled web of filaments often seen when viewing whole cells makes the identification of individual filaments quite difficult. The direct approach used for modeling punctate structures, in which the number and distribution of those structures in each cell is available for statistical modeling, is therefore problematic. An alternative is to use indirect or inverse modeling, in which a parametric, generative model for images is constructed, images are generated for different values of the parameters, and the best parameter values are found by comparison of the generated images to acquired images. This approach has been used for constructing generative models of microtubules [17] and to compare those models across different cell types [21].

Much further work is needed to develop modeling approaches for other organelle types, such as cisternal and reticular organelles.

3.3. Learning the relationships between cell components

A critical requirement for cell model learning systems is some means of learning the relationships between different cell components. For example, the localization of organelles or other structures can depend upon cytoskeletal elements such as microtubules; that is, such organelles may normally be in close proximity due to the presence of molecular motors or other microtubule-binding proteins on their surfaces. In this case, building a cell instance containing vesicles and microtubules by synthesizing them independently (Fig. 3c) would be incorrect. The solution is to learn another level of dependency in which an instance of a microtubule is synthesized first (dependent on the cell and nuclear instance) and then the positions (or other aspects) of organelles are chosen using the microtubule distribution as well as the cell and nuclear shape (Fig. 3d). We have recently developed such an approach and used it to show that eleven different classes of punctate or vesicular organelles can be distinguished from each other in part on the basis of the extent to which their localization is dependent upon microtubules [23].

In addition to dependencies between organelle or large macromolecular structures, we must also be concerned with the placement of proteins within organelles and relative to each other. In this regard, we distinguish between colocalization and conditional localization. Either by colocalization analysis from two or more proteins in the same images, or by pattern comparison between separate collections of images for different proteins, we may be able to determine that those proteins are uniformly colocalized in a particular organelle. In this case, positions for those proteins can be randomly distributed within the synthesized instances of that organelle. On the other hand, we may observe that a given protein is distributed in a particular pattern relative to an organelle (such as just on the tips of protuberances or in a single spot on the membrane). This requires learning yet another layer of conditional models that specify where to place a protein relative to instances of that organelle.

In the absence of such models, CellOrganizer currently allows proteins to be placed at random either within or on the boundary of organelles. A much better approach is to consider the geometry of a protein or complex when placing it in a synthetic cell. When concentrations of proteins or organelles are high this can be a significant challenge, but efficient algorithms have been developed to allow placing of diverse components within cell models [37]. An additional consideration is the relative positions of flexible domains within complexes, models for which can be learned through single molecular fluorescence measurements [38].

All of the conditional relationships we have discussed so far have been specified during the model construction based on prior knowledge. An important challenge for the future will be to develop approaches that can learn the dependencies directly.

3.4. Saving models and instances

In CellOrganizer, all of the models for a particular image collection are saved into a single file that include specification of the type of each model (i.e., the algorithm that should be used to generative examples from the model) and the learned parameters of that model. While there are standards for exchanging many types of cell models (e.g., Systems Biology Markup Language, or SBML), including standards for individual instances of cell geometry such as SBML-spatial, there are no current standards for exchanging generative models of cell geometry (this represents a significant future challenge). CellOrganizer therefore saves its models either in the proprietary Matlab binary file format or as XML files with tags for each field. During synthesis of cell instances, models from different files can be combined: the framework model from one cell type can be combined with the lysosome model from another.

4. Comparison of models between conditions

Comparison of cell properties captured from images using numerical features is central to high content screening and analysis. The parameters of generative models also reflect cell properties, and can reveal more interpretable differences than general purpose features such as textures. The parameter values for different models (of the same type) could be compared parameter by parameter to reveal, for example, that models of a particular organelle for two cell types differ only in the average number of that organelle per cell. Alternatively, spatial distributions specified by the parameters of a model (such as a fitted probability distribution that an organelle will occur at different positions in the cell) can be compared between models rather than comparing the parameters themselves (for example, to reveal that an organelle is more likely to be near the nucleus when a particular gene is knocked down than when it is not). Either way, comparisons of models can be used to learn how cell organization changes under different conditions or between cell types; for example, we can learn that a particular drug causes changes only in cell shape but not organelle distributions relative to that shape.

5. Comparing different types of models

The creation of models discussed above seeks to find the best parameters to describe cell instances and the best statistical model to capture the variation in those parameters in the input cell population. The learning process starts from a specification of the particular model to be learned; e.g., a Gaussian object model for vesicle sizes and shapes, logistic regression for vesicle position, and a multivariate Gaussian for variation in parameters across the population. This raises two important issues common to many modeling efforts: how well does the chosen model represent each instance (cell or organelle), and how well does the statistical model capture variation among the instances. The first question can be answered by measuring the residual error, the difference between the original cell and the representation of that cell in the model. For example, a synthetic image can be generated from the representation of each cell and the sum of the squared differences in fluorescence between the synthetic image and the original image can be calculated and normalized for the total fluorescence. This can be done for all cells and, for example, the average error reported. Different model types (e.g., spherical and ellipsoidal Gaussian objects) can be compared on this basis. The second question is more difficult, since we normally wish to assess how well the model predicts which new examples (not used for training) might be found (e.g., by additional imaging) and not just how well the distribution fits the observations we have. This type question is encountered in many modeling contexts, and a full treatment is beyond the scope of this article. A basic principle is to estimate the likelihood of new data given a model using cross-validation. A particular issue is how well the model captures the possibility that there are multiple distinct cell subpopulations. The parametric models in CellOrganizer do not yet deal with this issue, but at least for cell and nuclear shape, the diffeomorphic approaches readily capture multiple subpopulations.

6. Using generated cell instances in cell simulations

As mentioned in the Introduction, an important application of the ability to generate new cell instances is to use them as realistic geometries for cell simulations. To this end, instances generated by CellOrganizer can be saved in SBML-spatial (http://sbml.org/Documents/Specifications/SBML_Level_3/Packages/spatial) so that they can be used by other programs. Many biochemical models exist in repositories such as BioModels (https://www.ebi.ac.uk/biomodels-main), where they are largely in the form of classical compartmental models that assume compartments are well mixed and have only area/volume and perimeter/surface area. Such models (typically stored in SBML) can be combined with a spatial cell instance from CellOrganizer to create a complete specification of initial conditions sufficient to perform simulations of spatiotemporal behavior [39]. Using this approach, we have found that differences in cell geometry can lead to significant differences in the kinetics of cell signaling processes (Sullivan, Tapia, Faeder, and Murphy, in preparation).

7. Conclusions

Learning models of the organization of eukaryotic cells is a complex problem that spans many scales and disciplines. We have focused here on using optical microscope images to identify important factors like the sizes and shapes of cellular components, the numbers of organelles per cell, and the spatial distributions of organelles within cells. In addition to expanding our ability to build such models, a future need will be to incorporate ultrastructural data and molecular dynamics simulation results to identify structures and variation of individual proteins and complexes. Throughout the process, it will be critical to choose appropriate statistical models that adequately capture the interdependence of components. For this we need scalable learning solutions combined with scalable simulation solutions and to be able to rigorously compare different methods for each step and combinations of methods. A further challenge will be to choose appropriate methods for creating simulated cells from the models and visualizing them. Ultimately, data from perturbation studies should allow us to learn how model parameters are linked to specific molecular events.

Highlights.

Generative models of cell organization can be constructed directly from cell images

These models can capture variation from cell to cell and organelle to organelle

Model parameters can provide interpretable basis for comparing different conditions

Models of cell dynamics can be learned from movies of many cells

Generative models can be used to perform spatially-realistic cell simulations