Bayesian Inference for General Gaussian Graphical Models With Application to Multivariate Lattice Data

Abstract

We introduce efficient Markov chain Monte Carlo methods for inference and model determination in multivariate and matrix-variate Gaussian graphical models. Our framework is based on the G-Wishart prior for the precision matrix associated with graphs that can be decomposable or non-decomposable. We extend our sampling algorithms to a novel class of conditionally autoregressive models for sparse estimation in multivariate lattice data, with a special emphasis on the analysis of spatial data. These models embed a great deal of flexibility in estimating both the correlation structure across outcomes and the spatial correlation structure, thereby allowing for adaptive smoothing and spatial autocorrelation parameters. Our methods are illustrated using a simulated example and a real-world application which concerns cancer mortality surveillance. Supplementary materials with computer code and the datasets needed to replicate our numerical results together with additional tables of results are available online.

1. INTRODUCTION

Graphical models (Lauritzen 1996), which encode the conditional independence among variables using a graph, have become a popular tool for sparse estimation in both the statistics and machine learning literatures (Dobra et al. 2004; Meinshausen and Bühlmann 2006; Yuan and Lin 2007; Banerjee, El Ghaoui, and D’Aspremont 2008; Drton and Perlman 2008; Friedman, Hastie, and Tibshirani 2008; Ravikumar, Wainwright, and Lafferty 2010). Implementing model selection approaches in the context of graphical models typically allows a dramatic reduction in the number of parameters under consideration, preventing overfitting and improving predictive capability. In particular, Bayesian approaches to inference in graphical models generate regularized estimators that incorporate model structure uncertainty.

The focus of this article is Bayesian inference in Gaussian graphical models (Dempster 1972) using the G-Wishart prior (Roverato 2002; Atay-Kayis and Massam 2005; Letac and Massam 2007). This class of distributions is extremely attractive since it represents the conjugate family for the precision matrix whose elements associated with edges not in the underlying graph are constrained to be equal to zero. Many recent articles have described various stochastic search methods for Gaussian graphical models (GGMs) with the G-Wishart prior based on marginal likelihoods which, in this case, are given by the ratio of the normalizing constants of the posterior and prior G-Wishart distributions—see the works of Atay-Kayis and Massam (2005), Jones et al. (2005), Carvalho and Scott (2009), Armstrong et al. (2009), Lenkoski and Dobra (2011) and the references therein. Wang and West (2009) proposed a MCMC algorithm for model determination and estimation in matrix-variate GGMs that also involves marginal likelihoods. Although the computation of marginal likelihoods for decomposable graphs is straightforward, similar computations for non-decomposable graphs or matrix-variate GGMs raise significant numerical challenges. This leads to the idea of devising Bayesian model determination methods that avoid the computation of marginal likelihoods.

The contributions of this article are threefold. First, we develop a new Metropolis–Hastings method for sampling from the G-Wishart distribution associated with an arbitrary graph. We discuss our algorithm in the context of the related sampling methods of Wang and Carvalho (2010) and Mitsakakis, Massam, and Escobar (2011), and empirically show that it scales better to graphs with many vertices. Second, we propose novel reversible jump MCMC samplers (Green 1995) for model determination and estimation in multivariate and matrix-variate GGMs. We contrast our approaches with the algorithms of Wong, Carter, and Kohn (2003) and Wang and West (2009) which focus on arbitrary GGMs and matrix-variate GGMs, respectively. Third, we devise a new flexible class of conditionally autoregressive models (CAR) (Besag 1974) for lattice data that rely on our novel sampling algorithms. The link between conditionally autoregressive models and GGMs was originally pointed out by Besag and Kooperberg (1995). However, since typical neighborhood graphs are non-decomposable, fully exploiting this connection within a Bayesian framework requires that we are able to estimate Gaussian graphical models based on general graphs. Our main focus is on applications to multivariate lattice data, where our approach based on matrix-variate GGMs provides a natural approach to create sparse multivariate CAR models.

The organization of the article is as follows. Section 2 formally introduces GGMs and the G-Wishart distribution, along with a description of our novel sampling algorithm for the G-Wishart distribution. Section 3 describes our reversible jump MCMC algorithm for GGMs. This algorithm represents a generalization of the work of Giudici and Green (1999) and is applicable beyond decomposable GGMs. Section 4 discusses inference and model determination in matrix-variate GGMs. Unlike the related framework developed by Wang and West (2009) which involves exclusively decomposable graphs, our sampler operates on the joint distribution of the row and column precision matrices, the row and column conditional independence graphs, and the auxiliary variable that needs to be introduced to solve the underlying non-identifiability problem associated with matrix-variate normal distributions. Section 5 reviews conditional autoregressive priors for lattice data and their connection to GGMs. This section discusses both univariate and multivariate models for continuous and discrete data based on generalized linear models. Section 6 presents two illustrations of our methodology: a simulation study and a cancer mortality mapping model. Finally, Section 7 concludes the article by discussing future directions for our work.

2. GAUSSIAN GRAPHICAL MODELS AND THE G–WISHART DISTRIBUTION

We let X = X_Vp, V_p = {1, 2, …, p}, be a random vector with a p-dimensional multivariate normal distribution N_p(0, K⁻¹). We consider a graph G = (V_p, E), where each vertex i ∈ V corresponds with a random variable X_i and E ⊂ V_p × V_p are undirected edges. Here “undirected” means that (i, j) ∈ E if and only if (j, i) ∈ E. We denote by 𝒢_p the set of all 2^p(p−1)/2 undirected graphs with p vertices. A Gaussian graphical model with conditional independence graph G is constructed by constraining to zero the off-diagonal elements of K that do not correspond with edges in G (Dempster 1972). If (i, j) ∉ E, X_i and X_j are conditionally independent given the remaining variables. The precision matrix K = (K_ij)_1≤i,j≤p is constrained to the cone P_G of symmetric positive definite matrices with off-diagonal entries K_ij = 0 for all (i, j) ∉ E.

We consider the G-Wishart distribution Wis_G(δ, D) with density

$$\mathrm{p}(\mathbf{K}\mid G,\delta ,\mathbf{D})=\frac{1}{I_G(\delta ,\mathbf{D})}{(det\mathbf{K})}^{(\delta -2)/2}exp\left\{-\frac{1}{2}(\mathbf{K},\mathbf{D})\right\},$$ (1)

with respect to the Lebesgue measure on P_G (Roverato 2002; Atay-Kayis and Massam 2005; Letac and Massam 2007). Here 〈A, B〉 = tr(A^TB) denotes the trace inner product. The normalizing constant I_G(δ, D) is finite if δ > 2 and D positive definite (Diaconnis and Ylvisaker 1979). If G is the full graph (E = V_p × V_p), Wis_G(δ, D) is the Wishart distribution Wis_p(δ, D) (Muirhead 2005).

Since our sampling methods rely on perturbing the Cholesky decompositions of the matrix K, we review some key results. We write K ∈ P_G as K = Q^T (Ψ^TΨ)Q where Q = (Q_ij)_{1≤i≤j≤p} and Ψ = (Ψ_ij)_{1≤i≤j≤p} are upper triangular, while D⁻¹ = Q^TQ is the Cholesky decomposition of D⁻¹. We see that K = Φ^TΦ where Φ = ΨQ is the Cholesky decomposition of K. The zero constraints on the off-diagonal elements of K associated with G induce well-defined sets of free elements Φ^ν(G) = {Φ_ij : (i, j) ∈ ν(G)} and Ψ^ν(G) = {Ψ_ij : (i, j) ∈ ν(G)} of the matrices Φ and Ψ—see proposition 2, page 320, and lemma 2, page 326, of the article by Atay-Kayis and Massam (2005). Here ν(G) = ν₌(G) ∪ ν_<(G), ν₌(G) = {(i, i) : i ∈ V_p} and ν_<(G) = {(i, j) : i < j and (i, j) ∈ E}.

We denote by M^ν(G) the set of incomplete triangular matrices whose elements are indexed by ν(G) and whose diagonal elements are strictly positive. Both Φ^ν(G) and Ψ^ν(G) must belong to M^ν(G). The non-free elements of Ψ are determined through the completion operation (Atay-Kayis and Massam 2005, lemma 2) as a function of the free elements Ψ^ν(G). Each element Ψ_ij with i < j and (i, j) ∉ E is a function of the other elements Ψ_i′j′ that precede it in lexicographical order. Roverato (2002) proved that the Jacobian of the transformation that maps K ∈ P_G to Φ^ν(G) ∈ M^ν(G) is $\mathrm{J}(\mathbf{K}\to {\mathbf{\Phi }}^{\nu (G)})=2^p{\prod }_{i=1}^p{\mathrm{\Phi }}_{ii}^{v_i^G+1}$, where $v_j^G=\mid \{j:j<i\text{and}(i,j)\in E\}\mid$. Here |A| denotes the number of elements of the set A. Atay-Kayis and Massam (2005) showed that the Jacobian of the transformation that maps Φ^ν(G) to Ψ^ν(G) is given by $\mathrm{J}({\mathbf{\Phi }}^{\nu (G)}\to {\mathbf{\Psi }}^{\nu (G)})={\prod }_{i=1}^p{Q}_{ii}^{d_i^G+1}$, where $d_i^G=\mid \{j:j>i\text{and}(i,j)\in E\}\mid$. We have det $\mathbf{K}={\prod }_{i=1}^p{\mathrm{\Phi }}_{ii}^2$ and Φ_ii = Ψ_iiQ_ii. It follows that the density of Ψ^ν(G) with respect to the Lebesgue measure on M^ν(G) is

$$\mathrm{p}({\mathbf{\Psi }}^{\nu (G)}\mid \delta ,\mathbf{D})=\frac{2^p}{I_G(\delta ,\mathbf{D})}\prod _{i=1}^p{Q}_{ii}^{v_i^G+d_i^G+\delta }\prod _{i=1}^p{\mathrm{\Psi }}_{ii}^{v_i^G+\delta -1}\times exp\left(-\frac{1}{2}\sum _{i=1}^p\sum _{j=i}^p{\mathrm{\Psi }}_{ij}^2\right).$$ (2)

We note that $v_i^G+d_i^G$ represents the number of neighbors of vertex i in the graph G.

2.1 Existing Methods for Sampling From the G-Wishart Distribution

The problem of sampling from the G-Wishart distribution has received considerable attention in the recent literature. Piccioni (2000) followed by Asci and Piccioni (2007) exploited the theory of regular exponential families with cuts and proposed the block Gibbs sampler algorithm. Their iterative method generates one sample from Wis_G(δ, D) by performing sequential adjustments with respect to submatrices associated with each clique of G. The adjustment with respect to a clique C involves the inversion of a (p − |C|) × (p − |C|) matrix. If G has several cliques involving a small number of vertices but has a large number of vertices p, repeated inversions of high-dimensional matrices must be performed at each iteration. This makes the block Gibbs sampler algorithm impractical for being used in the context of large graphs.

Carvalho, Massam, and West (2007) gave a direct sampling method for Wis_G(δ, D) that works well for decomposable graphs. This algorithm was extended by Wang and Carvalho (2010) to non-decomposable graphs by introducing an accept– reject step as follows. Based on theorem 1, page 328, of the article of Atay-Kayis and Massam (2005), Wang and Carvalho (2010) and Mitsakakis, Massam, and Escobar (2011) wrote the density of Ψ^ν(G) given in (2) as

$$\mathrm{p}({\mathbf{\Psi }}^{\nu (G)}\mid \delta ,\mathbf{D})=\frac{1}{{\mathrm{E}}_h[f({\mathbf{\Psi }}^{\nu (G)})]}f({\mathbf{\Psi }}^{\nu (G)})h({\mathbf{\Psi }}^{\nu (G)}),$$ (3)

where

$$\text{log}f({\mathbf{\Psi }}^{v(G)})=-\frac{1}{2}\sum _{(i,j)\notin v(G),i<j}{\mathrm{\Psi }}_{ij}^2$$

is a function of the non-free elements of Ψ which, in turn, are uniquely determined from the free elements in Ψ^ν(G). Furthermore, h(Ψ^ν(G)) is the product of mutually independent chi-squared and standard normal distributions, that is, ${\mathrm{\Psi }}_{ii}^2-{\chi }_{\delta +v_i^G}^2$ for i ∈ V_p and Ψ_ij ~ N(0, 1) for (i, j) ∈ ν_<(G). The expectation E_h[f (Ψ^ν(G))] is calculated with respect to h(·). Since f(Ψ^ν(G)) ≤ 1 for any Ψ^ν(G) ∈ M^ν(G), we have

$$\mathrm{p}({\mathbf{\Psi }}^{v(G)}\mid \delta ,\mathbf{D})\le Mh({\mathbf{\Psi }}^{v(G)}),$$ (4)

where $M={\mathrm{E}}_h^{-1}[f({\mathbf{\Psi }}^{v(G)})]\ge 1$. From algorithm A.4 of the book by Robert and Casella (2004), an accept–reject method for sampling from Wis_G(δ, D) proceeds by sampling Ψ^ν(G) ~ h(·) and U ~ Uni(0, 1) until U ≤ f(Ψ^ν(G)). The probability of acceptance of a random sample from h(·) as a random sample from Wis_G(δ, D) is

$$Pr(U<f({\mathbf{\Psi }}^{v(G)}))={\mathrm{E}}_h[f({\mathbf{\Psi }}^{v(G)})].$$ (5)

Wang and Carvalho (2010) further decomposed G in its maximal prime subgraphs (Tarjan 1985), applied the accept–reject method for marginal or conditional distributions of Wis_G(δ, D) corresponding with each maximal prime subgraph, and generated a sample from Wis_G(δ, D) by putting together the resulting lower-dimensional sampled matrices.

Mitsakakis, Massam, and Escobar (2011) proposed a Metropolis–Hastings method for sampling from the G-Wishart Wis_G(δ, D) distribution. We denote by K^[s] = Q^T(Ψ^[s])^TΨ^[s]Q the current state of their Markov chain, where (Ψ^[s])^ν(G) ∈ M^ν(G). Mitsakakis, Massam, and Escobar (2011) generated a candidate K′ = Q^T (Ψ′)^TΨ′Q for the next state by sampling (Ψ′)^ν(G) ~ h(·) and determining the non-free elements of Ψ′ from the free sampled elements (Ψ′)^ν(G). The chain moves to K′ with probability

$$min\{f({({\mathbf{\Psi }}^{\prime })}^{v(G)})/f({({\mathbf{\Psi }}^{[s]})}^{v(G)}),1\}.$$ (6)

The inequality (4) implies that this independent chain is uniformly ergodic (Mengersen and Tweedie 1996) and its expected acceptance probability is greater than or equal to E_h[f(Ψ^ν(G))]—see lemma 7.9 in the book by Robert and Casella (2004). Hence, the Markov chain of Mitsakakis, Massam, and Escobar (2011) is more efficient than the method of Wang and Carvalho (2010) when the latter algorithm is employed without graph decompositions or when the graph G has only one maximal prime subgraph. On the other hand, the method of Mitsakakis, Massam, and Escobar (2011) involves changing the values of all free elements Ψ^ν(G) in a single step. As a result, if their Markov chain is currently in a region of high probability, it could potentially have to generate many candidates from h(·) before moving to a new state with comparable or larger probability.

2.2 Our Algorithm for Sampling From the G-Wishart Distribution

We introduce a new Metropolis–Hastings algorithm for sampling from the G-Wishart Wis_G(δ, D) distribution. In contrast to the work of Mitsakakis, Massam, and Escobar (2011), our approach makes use of a proposal distribution that depends on the current state of the chain and leaves all but one of the free elements in Ψ^ν(G) unchanged. The distance between the current and the proposed state is controlled through a Gaussian kernel with a precision parameter σ_m.

We denote by K^[s] = Q^T (Ψ^[s])^TΨ^[s]Q the current state of the chain with (Ψ^[s])^ν(G) ∈ M^ν(G). The next state K^[s+1] = Q^T(Ψ^[s+1])^TΨ^[s+1]Q is obtained by sequentially perturbing the free elements (Ψ^[s])^ν(G). A diagonal element ${\mathrm{\Psi }}_{i_0{i}_0}^{[s]}>0$ is updated by sampling a value γ from a $\mathrm{N}({\mathrm{\Psi }}_{i_0{i}_0}^{[s]},{\sigma }_m^2)$ distribution truncated below at zero. We define the upper triangular matrix Ψ′ such that ${\mathrm{\Psi }}_{ij}^{\prime }={\mathrm{\Psi }}_{ij}^{[s]}$ for (i, j) ∈ ν(G) \ {(i₀, i₀)} and ${\mathrm{\Psi }}_{i_0{i}_0}^{\prime }=\gamma$. The non-free elements of Ψ′ are obtained through the completion operation (Atay-Kayis and Massam 2005, lemma 2) from (Ψ′)^ν(G). The Markov chain moves to K′ = Q^T(Ψ′)^TΨ′Q with probability min{R_m, 1}, where

$$\begin{array}{l}{R}_m=\frac{\mathrm{p}({({\mathbf{\Psi }}^{\prime })}^{v(G)}\mid \delta ,\mathbf{D})}{\mathrm{p}({({\mathbf{\Psi }}^{[s]})}^{v(G)}\mid \delta ,\mathbf{D})}\frac{\mathrm{p}({\mathrm{\Psi }}_{i_0{i}_0}^{[s]}\mid {\mathrm{\Psi }}_{i_0{i}_0}^{\prime })}{\mathrm{p}({\mathrm{\Psi }}_{i_0{i}_0}^{\prime }\mid {\mathrm{\Psi }}_{i_0{i}_0}^{[s]})}\\ =\frac{\phi ({\mathrm{\Psi }}_{i_0{i}_0}^{[s]}/{\sigma }_m)}{\phi ({\mathrm{\Psi }}_{i_0{i}_0}^{\prime }/{\sigma }_m)}{\left(\frac{{\mathrm{\Psi }}_{i_0{i}_0}^{\prime }}{{\mathrm{\Psi }}_{i_0{i}_0}^{[s]}}\right)}^{v_{i_0}^G+\delta -1}{R}_m^{\prime }.\end{array}$$ (7)

Here φ(·) represents the CDF of the standard normal distribution and

$$R_m^{\prime }=exp\left\{-\frac{1}{2}\sum _{i=1}^p\sum _{j=i}^p[{({\mathrm{\Psi }}_{ij}^{\prime })}^2-{({\mathrm{\Psi }}_{ij}^{[s]})}^2]\right\}.$$ (8)

A free off-diagonal element ${\mathrm{\Psi }}_{i_0{j}_0}^{[s]}$ is updated by sampling a value ${\gamma }^{\prime }~\mathrm{N}({\mathrm{\Psi }}_{i_0{j}_0}^{[s]},{\sigma }_m^2)$. We define the upper triangular matrix Ψ′ such that ${\mathrm{\Psi }}_{ij}^{\prime }={\mathrm{\Psi }}_{ij}^{[s]}$ for (i, j) ∈ ν(G) \ {(i₀, j₀)} and ${\mathrm{\Psi }}_{i_0{j}_0}^{\prime }={\gamma }^{\prime }$. The remaining elements of Ψ′ are determined by the completion operation from lemma 2 in the article of Atay-Kayis and Massam (2005) from (Ψ′)^ν(G). The proposal distribution is symmetric $\mathrm{p}({\mathrm{\Psi }}_{i_0{j}_0}^{\prime }\mid {\mathrm{\Psi }}_{i_0{j}_0}^{[s]}=\mathrm{p}({\mathrm{\Psi }}_{i_0{j}_0}^{[s]}\mid {\mathrm{\Psi }}_{i_0{j}_0}^{\prime })$, thus we accept the transition of the chain from K^[s] to K′ = Q^T(Ψ′)^TΨ′Q with probability $min\{R_m^{\prime },1\}$, where $R_m^{\prime }$ is given in Equation (7). Since (Ψ^[s])^ν(G) ∈ M^ν(G), we have (Ψ′)^ν(G) ∈ M^ν(G) which implies K′ ∈ P_G. We denote by K^[s+1] the precision matrix obtained after completing all the updates associated with the free elements indexed by ν(G).

A key computational aspect is related to the dependence of Cholesky decompositions on a particular ordering of the variables involved. Empirically we noticed that the mixing times of Markov chains that make use of our sampling approach can be improved by changing the ordering of the variables in V_p at each iteration. More specifically, a permutation υ is uniformly drawn from the set of all possible permutations ϒ_p of V_p. The row and columns of D are reordered according to υ and a new Cholesky decomposition of D⁻¹ is determined. The set ν(G) and { $d_i^G$: i ∈ V} are recalculated given the ordering of the vertices induced by υ. Although the random shuffling of the ordering of the indices worked well for the particular applications we have considered in this article, we do not have any theoretical justification that explains why it improves the computational efficiency of our sampling approaches.

Our later developments from Section 4 involve sampling K ~ Wis_G(δ, D) subject to the constraint K₁₁ = 1. We have $K_{11}^{[s]}=1\iff {({\mathbf{\Psi }}^{[s]}\mathbf{Q})}_{11}=1\iff {\mathrm{\Psi }}_{11}^{[s]}=1/Q_{11}$. We subsequently obtain the next state K^[s+1] of the Markov chain by perturbing the free elements (Ψ^[s])^{ν(G)\{(1,1)}}. When defining the triangular matrix Ψ′ we set ${\mathrm{\Psi }}_{11}^{\prime }=1/Q_{11}$ which implies that the corresponding candidate matrix K′ has $K_{11}^{\prime }=1$. Thus K^[s+1] also obeys the constraint $K_{11}^{[s+1]}=1$. The random orderings of the variables need to be drawn from the set ${\mathrm{\Upsilon }}_p^{(1,1)}$ of permutations υ ∈ ϒ_p such that υ(1) = 1. This way the (1, 1) element of K always occupies the same position.

2.3 The Scalability of Sampling Methods From the G-Wishart Distribution

Practical applications of our novel framework for analyzing multivariate lattice data from Section 5 involve sampling from G-Wishart distributions associated with arbitrary graphs with tens or possibly hundreds of vertices—see Section 6.2 as well as relevant examples from the works of Elliott et al. (2001), Banerjee, Carlin, and Gelfand (2004), Rue and Held (2005), Lawson (2009), Gelfand et al. (2010). We perform a simulation study to empirically compare the scalability of our approach (DLR) for simulating from G-Wishart distributions with respect to the algorithms of Wang and Carvalho (2010) (WC) and Mitsakakis, Massam, and Escobar (2011) (MME).We consider the cycle graph C_p ∈ 𝒢_p with edges {(i, i + 1) : 1 ≤ i ≤ p − 1} ∪ {(p, 1)} and the matrix A_p ∈ P_Cp such that (A_p)_ii = 1 (1 ≤ i ≤ p), (A_p)_i,i−1 = (A_p)_i−1,i = 0.5 (2 ≤ i ≤ p), and (A_p)_1,p = (A_p)_p,1 = 0.4. We chose C_p because it is the sparsest graph with p vertices and only one maximal prime subgraph, hence no graph decompositions can be performed in the context of the WC algorithm.

We employ the three sampling methods to sample from the G-Wishart Wis_Cp (103, D_p) distribution, where ${\mathbf{D}}_p={\mathbf{I}}_p+100{\mathbf{A}}_p^{-1}$ and I_p is the p-dimensional identity matrix. This is representative of a G-Wishart posterior distribution corresponding with 100 samples from a ${\mathrm{N}}_p(0,A_p^{-1})$ and a G-Wishart prior Wis_Cp (3, I_p). The acceptance probability for generating one sample with the DLR algorithm is defined as the average acceptance probabilities of the updates corresponding with diagonal and off-diagonal free elements in Ψ^ν(G). We calculate Monte Carlo estimates and their standard errors of the acceptance probabilities for our method by running 100 independent chains of length 2500 for each combination (σ_m, p) ∈ {0.1, 0.5, 1, 2} × {4, 6, …, 20}. The same number of chains of the same length have been run with the MME algorithm for p = 4, 6, …, 20. We calculate Monte Carlo estimates of the acceptance probabilities (5) associated with the WC algorithm, that is,

$${\widehat{\mathrm{E}}}_h[f({\mathbf{\Psi }}^{v(C_p)})]=\sum _{s=1}^{2500}f({({\mathbf{\Psi }}^{[s]})}^{v(C_p)}),\text{with}{({\mathbf{\Psi }}^{[s]})}^{v(C_p)}~h(·),s=1,\dots ,2500.$$

The corresponding standard errors were determined by calculating 100 such estimates for each p = 4, 6, …, 20. The results are summarized in Table 1. As we would expect, the acceptance rates for the DLR algorithm decrease as σ_m increases since the proposed jumps in P_Cp become larger. More importantly, for each value of σ_m, the acceptance rates for the DLR algorithm decrease very slowly as the number of vertices p grows. This shows that our Metropolis–Hastings method is likely to retain its efficiency for graphs that involve a large number of vertices. On the other hand, the acceptance rates for the WC algorithm are extremely small even for p = 6 vertices. This implies that a large number of samples from the instrumental distribution h(·) would need to be generated before one sample from Wis_Cp (103, D_p) is obtained. The MME algorithm gives slightly better acceptance rates, but they are still small and are indicative of a simulation method that constantly attempts to make large jumps in areas of low probability of Wis_Cp (103,D_p). Therefore the WC and MME methods might not scale well despite being perfectly valid in theory, hence they cannot be used in the context of the multivariate lattice data models from Section 5. The acceptance rates of the DLR algorithm are a function of the precision parameter σ_m which can be easily adjusted to yield jumps that are not too short but also not too long in the target cone of matrices. This flexibility is key for successfully employing our algorithm for graphs with many vertices.

Table 1.

Monte Carlo estimates and their standard errors (in parentheses) of the acceptance probabilities for our proposed algorithm (DLR) for sampling from the G-Wishart distribution, the Wang and Carvalho (2010) algorithm (WC), and the Mitsakakis, Massam, and Escobar (2011) algorithm (MME)

p	DLR				WC	MME
	σm = 0.1	σm = 0.5	σm = 1	σm =2
4	0.953 (2.0e–3)	0.776 (3.0e–3)	0.600 (3.2e–3)	0.389 (3.8e–3)	0.340 (6.4e–3)	0.473 (1.0e–2)
6	0.947 (2.0e–3)	0.751 (2.4e–3)	0.565 (2.9e–3)	0.356 (2.3e–3)	5.08e–2 (2.2e–3)	0.185 (1.0e–2)
8	0.944 (1.8e–3)	0.740 (2.1e–3)	0.551 (2.3e–3)	0.343 (2.6e–3)	7.94e–3 (7.1e–4)	0.078 (0.9e–2)
10	0.943 (1.7e–3)	0.734 (2.0e–3)	0.543 (2.1e–3)	0.336 (2.1e–3)	1.18e–3 (1.7e–4)	0.035 (8.0e–3)
12	0.942 (1.4e–3)	0.729 (1.8e–3)	0.537 (2.1e–3)	0.331 (2.2e–3)	1.56e–4 (5.1e–5)	0.013 (6.0e–3)
14	0.940 (1.5e–3)	0.725 (1.6e–3)	0.532 (1.8e–3)	0.327 (1.9e–3)	2.27e–5 (1.4e–5)	0.005 (4.0e–3)
16	0.940 (1.3e–3)	0.721 (1.6e–3)	0.527 (1.7e–3)	0.324 (1.7e–3)	2.19e–6 (1.8e–6)	0.002 (3.0e–3)
18	0.939 (1.2e–3)	0.717 (1.4e–3)	0.523 (1.5e–3)	0.321 (1.5e–3)	3.87e–7 (8.0e–7)	0.001 (2.0e–3)
20	0.938 (1.0e–3)	0.714 (1.4e–3)	0.520 (1.6e–3)	0.318 (1.5e–3)	2.08e–8 (3.5e–8)	5.4e–4 (9.0e–4)

It may initially appear that failure to handle graphs with a maximal prime subgraph with 20 vertices is not a major shortcoming of an algorithm that relies on graph decompositions. However, the example we consider in Section 6.2 involves a fixed graphical model whose underlying graph has a maximal prime subgraph with 36 vertices (see the Supplementary Materials). Since this graph is one that is constructed from the neighborhood structure of the United States, we can see the importance of the ability to scale when applying the GGM framework to spatial statistical problems.

3. REVERSIBLE JUMP MCMC SAMPLERS FOR GGMS

The previous section was concerned with sampling from the G-Wishart distribution when the underlying conditional independence graph is fixed. In contrast, this section is concerned with performing Bayesian inference in GGMs, which involves determination of the graph G. Giudici and Green (1999) proposed a reversible jump Markov chain algorithm that is restricted to decomposable graphs and employs a hyper inverse Wishart prior (Dawid and Lauritzen 1993) for the covariance matrix Σ = K⁻¹ = (Σ_ij)_1≤i,j≤p. The efficiency of their approach comes from representing decomposable graphs through their junction trees and from a specification of Σ as an incomplete matrix Γ = (Γ_ij)_1≤i,j≤p such that Σ_ij = Γ_ij if i = j or if (i, j) is an edge in the current graph (i.e., K_ij is not constrained to 0); the remaining elements of Γ are left unspecified but can be uniquely determined using the iterative proportional scaling algorithm (Dempster 1972; Speed and Kiiveri 1986). Brooks, Giudici, and Roberts (2003) presented techniques for calibrating the precision parameter of the normal kernel used by Giudici and Green (1999) to sequentially update the elements of Γ and the edges of the underlying decomposable graph which lead to improved mixing times of the resulting Markov chain. Related work (Scott and Carvalho 2008; Carvalho and Scott 2009; Armstrong et al. 2009) has also focused on decomposable graphs. Graphs of this type have received attention mainly because their special structure is convenient from a computational standpoint. However, decomposability is a serious constraint as it drastically reduces 𝒢_p to a much smaller subset of graphs: the ratio between the number of decomposable graphs and the total number of graphs decreases from 0.95 for p = 4 to 0.12 for p = 8 (Armstrong 2005).

Roverato (2002), Atay-Kayis and Massam (2005), Jones et al. (2005), Dellaportas, Giudici, and Roberts (2003), Moghaddam et al. (2009), Lenkoski and Dobra (2011) explored various methods for numerically calculating marginal likelihoods for non-decomposable graphs. Besides being computationally expensive, stochastic search algorithms that traverse 𝒢_p based on marginal likelihoods output a set of graphs that have the highest posterior probabilities from all the graphs that have been visited, but do not produce estimates of the precision matrix K unless a direct sampling algorithm from the posterior distribution of K given a graph is available. As we have seen in Section 2.3, current direct sampling algorithms (e.g., Wang and Carvalho 2010) might not scale well to graphs with many vertices. Since our key motivation comes from modeling multivariate lattice data (see Section 5), we want to develop a Bayesian method that samples from the joint posterior distribution of precision matrices K ∈ P_G and graphs G ∈ 𝒢_p, thereby performing inference for both K and G. Wong, Carter, and Kohn (2003) developed such a reversible jump Metropolis–Hastings algorithm by decomposing K = TΔT, where $\mathbf{T}=\text{diag}\{K_{11}^{1/2},\dots ,K_{pp}^{1/2}\}$ and Δ = (Δ_ij)_1≤i,j≤p is a correlation matrix with Δ_ii = 1 and Δ_ij = K_ij/(K_iiK_jj)^1/2, for i < j. Their prior specification for K involves independent priors for T_ii and a joint prior for the off-diagonal elements of Δ whose normalizing constant is associated with all the graphs with the same number of edges.

We propose a new reversible jump Markov chain algorithm that is based on a G-Wishart prior for K. While we do not empirically explore the efficiency of our approach with respect to the Wong, Carter, and Kohn (2003) algorithm, we state that the key advantage of our framework lies in its generalization to matrix-variate data—see Section 4.We are unaware of any similar extension of the Wong, Carter, and Kohn (2003) approach. Another benefit of our method with respect to that of Wong, Carter, and Kohn (2003) is related to its flexibility with respect to prior specifications on 𝒢_p—see the discussion below.

We let 𝒟= {x⁽¹⁾, …, x⁽ⁿ⁾} be the observed data of n independent samples from N_p(0, K⁻¹). Given a graph G ∈ 𝒢_p, we assume a G-Wishart prior Wis_G(δ₀, D₀) for the precision matrix K ∈ P_G. We take δ₀ = 3 > 2 and D₀ = I_p. With this choice the prior for K is equivalent with one observed sample, while the observed variables are assumed to be a priori independent of each other. Since the G-Wishart prior for K is conjugate to the likelihood p(𝒟| K), the posterior of K given G is Wis_G(n + δ₀, U + D₀) where $\mathbf{U}={\sum }_{j=1}^n{\mathbf{x}}^{(j)}{({\mathbf{x}}^{(j)})}^T$. We also assume a prior Pr(G) on 𝒢_p. We develop a MCMC algorithm for sampling from the joint posterior distribution

$$\mathrm{p}(\mathbf{K},G\mid \mathcal{D})\propto \mathrm{p}(\mathcal{D}\mid \mathbf{K})\mathrm{p}(\mathbf{K}\mid G,{\delta }_0,{\mathbf{D}}_0)Pr(G),$$

that is well-defined if and only if K ∈ P_G. We sequentially update the precision matrix given the current graph and the edges of the graph given the current precision matrix—see Appendix A. The addition or deletion of an edge involves a change in the dimensionality of the parameter space since the corresponding element of K becomes free or constrained to zero, hence we make use of the reversible jump MCMC methodology of Green (1995). The graph update step also requires the calculation of the normalizing constants of the G-Wishart priors corresponding with the current and the candidate graph. To this end, we make use of the Monte Carlo method of Atay-Kayis and Massam (2005) which converges very fast when computing I_G(δ, D) [see Equation (1)] even for large graphs when δ is small and D is set to the identity matrix (Lenkoski and Dobra 2011).

Our framework accommodates any prior probabilities Pr(G) on the set of graphs 𝒢_p which is a significant advantage with respect to the covariance selection prior from Wong, Carter, and Kohn (2003). Indeed, the prior in the work of Wong, Carter, and Kohn (2003) induces fixed probabilities for each graph and does not allow the possibility of further modifying these probabilities according to prior beliefs. A usual choice is the uniform prior Pr(G) = 2^−m with $m=\left(\begin{array}{c}p\\ 2\end{array}\right)$, but this prior is biased toward middle-size graphs and gives small probabilities to sparse graphs and to graphs that are almost complete. Here the size of a graph G is defined as the number of edges in G and is denoted by size(G) ∈ {0, 1, …, m}. Dobra et al. (2004) and Jones et al. (2005) assumed that the probability of inclusion of any edge in G is constant and equal to ψ ∈ (0, 1), which leads to the prior

$$Pr(G)\propto {\psi }^{\text{size}(G)}{(1-\psi )}^{m-\text{size}(G)}.$$ (9)

Sparser graphs can be favored with prior (9) by choosing a small value for ψ. Since ψ could be difficult to elicit in some applications, Carvalho and Scott (2009) integrated out ψ from (9) by assuming a conjugate beta distribution Beta(a, b), which leads to the prior

$$Pr(G)\propto B(a+\text{size}(G),b+m-\text{size}(G))/B(a,b),$$ (10)

where B(·, ·) is the beta function. From the work of Scott and Berger (2006) it follows that prior (10) has an automatic multiplicity correction for testing the inclusion of spurious edges. Armstrong et al. (2009) suggested a hierarchical prior on 𝒢_p (the size-based prior) that gives equal probability to the size of a graph and equal probability to graphs of each size, that is,

$$\begin{array}{l}Pr(G)=Pr(\text{size}(G))Pr(G\mid \text{size}(G))\\ =\frac{1}{m+1}{\left(\begin{array}{c}m\\ \text{size}(G)\end{array}\right)}^{-1},\end{array}$$ (11)

which is also obtained by setting a = b = 1 in (10). We note that the expected size of a graph under size-based prior is m/2, which is also the expected size of a graph under the uniform prior on 𝒢_p.

4. REVERSIBLE JUMP MCMC SAMPLER FOR MATRIX–VARIATE GGMS

We extend our framework to the case when the observed data 𝒟 = {x⁽¹⁾, …, x⁽ⁿ⁾} are associated with a p_R × p_C random matrix X = (X_ij) that follows a matrix-variate normal distribution

$$\text{vec}(\mathbf{X})\mid {\mathbf{K}}_R,{\mathbf{K}}_C~{\mathbf{N}}_{p_R{p}_C}(\mathbf{0},{[{\mathbf{K}}_C\otimes {\mathbf{K}}_R]}^{-1}),$$

with probability distribution function (Gupta and Nagar 2000):

$$\mathrm{p}(\mathbf{X}\mid {\mathbf{K}}_R,{\mathbf{K}}_C)={(2\pi )}^{-p_R{p}_C/2}{(det{\mathbf{K}}_R)}^{p_C/2}{(det{\mathbf{K}}_C)}^{p_R/2}\times exp\left\{-\frac{1}{2}\text{tr}[{\mathbf{K}}_R\mathbf{X}{\mathbf{K}}_C{\mathbf{X}}^T]\right\}.$$ (12)

Here K_R is a p_R ×p_R row precision matrix and K_C is a p_C × p_C column precision matrix. Furthermore, we assume that K_R ∈ P_GR and K_C ∈ P_GC where G_R = (V_pR, E_R) and G_C = (V_pC, E_C) are two graphs with p_R and p_C vertices, respectively. We consider the rows X_1*, …, X_pR* and the columns X_*1, …, X_*pC of the random matrix X. From theorem 2.3.12 of the book by Gupta and Nagar (2000) we have ${\mathbf{X}}_{i\ast }^T~{\mathrm{N}}_{pc}(\mathbf{0},{({\mathbf{K}}_R^{-1})}_{ii}{\mathbf{K}}_C^{-1})$ and ${\mathbf{X}}_{\ast j}~{\mathrm{N}}_{p_R}(\mathbf{0},{({\mathbf{K}}_C^{-1})}_{jj}{\mathbf{K}}_R^{-1})$. The graphs G_R and G_C define graphical models for the rows and columns of X (Wang and West 2009):

$$\begin{array}{l}{\mathbf{X}}_{i_1\ast }⫫{\mathbf{X}}_{i_2\ast }\mid {\mathbf{X}}_{(V_{p_R}\backslash \{i_1,i_2\})\ast }\\ \iff {({\mathbf{K}}_R)}_{i_1{i}_2}={({\mathbf{K}}_R)}_{i_2{i}_1}=0\\ \iff (i_1,i_2)\notin E_R\text{and}\\ {{\mathbf{X}}_{\ast }}_{j_1}⫫{\mathbf{X}}_{\ast j_2}\mid {\mathbf{X}}_{(V_{p_C}\backslash \{j_1,j_2\})\ast }\\ \iff {({\mathbf{K}}_C)}_{j_1{j}_2}={({\mathbf{K}}_R)}_{j_2{j}_1}=0\\ \iff (j_1,j_2)\notin E_C.\end{array}$$ (13)

Any prior specification for K_R and K_C must take into account the fact that the two precision matrices are not uniquely identified from their Kronecker product which means that, for any z > 0, (z⁻¹K_R) ⊗ (zK_C) = K_R ⊗ K_C represents the same precision matrix for vec(X)—see Equation (12). We follow the idea laid out in the article of Wang and West (2009) and impose the constraint (K_C)₁₁ = 1.We define a prior for K_C through parameter expansion by assuming a G-Wishart prior Wis_GC (δ_C, D_C) for the matrix zK_C with z > 0, δ_C > 2, and D_C ∈ P_GC. It is immediate to see that the Jacobian of the transformation from zK_C to (z, K_C) is J((zK_C)→(z, K_C)) = z^{|ν(G_C)|−1}. It follows that our joint prior for (z, K_C) is given by

$$\mathrm{p}(z,{\mathbf{K}}_C\mid G_C,{\delta }_C,{\mathbf{D}}_C)=\frac{1}{I_{G_C}({\delta }_C,{\mathbf{D}}_C)}{(det{\mathbf{K}}_C)}^{({\delta }_C-2)/2}\times exp\left\{-\frac{1}{2}\langle {\mathbf{K}}_C,z{\mathbf{D}}_C\rangle \right\}{z}^{p_C({\delta }_C-2)/2+\mid v(G_C)\mid -1}.$$

The elements of K_R ∈ P_GR are not subject to any additional constraints, hence we assume a G-Wishart prior Wis_GR (δ_R, D_R) for K_R. We take δ_C = δ_R = 3, D_C = I_pC, and D_R = I_pR. We complete our prior specification by choosing two priors Pr(G_C) and Pr(G_R) for the row and column graphs, where G_R ∈ 𝒢_pR and G_C ∈ 𝒢_pC—see our discussion from Section 3.

We perform Bayesian inference for matrix-variate GGMs by developing a MCMC algorithm for sampling from the joint posterior distribution of the row and column precision matrices, the row and column graphs, and the auxiliary variable z:

$$\mathrm{p}({\mathbf{K}}_R,z,{\mathbf{K}}_C,G_R,G_C\mid \mathcal{D})\propto \mathrm{p}(\mathcal{D}\mid {\mathbf{K}}_R,{\mathbf{K}}_C)\mathrm{p}({\mathbf{K}}_R\mid G_R,{\delta }_R,{\mathbf{D}}_R)\times \mathrm{p}(z,{\mathbf{K}}_C\mid G_C,{\delta }_C,{\mathbf{D}}_C)Pr(G_C)Pr(G_R),$$ (14)

that is defined for K_R ∈ P_GR, K_C ∈ P_GC with (K_C)₁₁ = 1 and z > 0. Equation (14) is written as

$$\begin{array}{l}\mathrm{p}({\mathbf{K}}_R,z,{\mathbf{K}}_C,G_R,G_C\mid \mathcal{D})\\ \propto z^{p_C({\delta }_C-2)/2+\mid v(G_C)\mid -1}\\ \times {(det{\mathbf{K}}_R)}^{({np}_C+{\delta }_R-2)/2}{(det{\mathbf{K}}_C)}^{({np}_R+{\delta }_C-2)/2}\\ \times exp\left\{-\frac{1}{2}\text{tr}\left[\sum _{j=1}^n{\mathbf{K}}_R{\mathbf{x}}^{(j)}{\mathbf{K}}_C{\left({\mathbf{x}}^{(j)}\right)}^T+{\mathbf{K}}_R{\mathbf{D}}_R+{\mathbf{K}}_C(z{\mathbf{D}}_C)\right]\right\}\\ \times Pr(G_C)Pr(G_R).\end{array}$$ (15)

The details of our sampling scheme are presented in Appendix B. Updating the row and column precision matrices involves sampling from their corresponding G-Wishart conditional distributions using the Metropolis–Hastings approach from Section 2.2, while updating z involves sampling from its gamma full conditional. The updates of the row and column graphs involve changes in the dimension of the parameter space and require a reversible jump step (Green 1995).

It is relevant to discuss how our MCMC sampler from Appendix B is different from the methodology proposed by Wang and West (2009). First of all, Wang and West (2009) allowed only decomposable row and column graphs which makes their framework inappropriate for modeling multivariate lattice data where the graph representing the neighborhood structure of the regions involved is typically not decomposable. Second of all, they proposed a Markov chain sampler for the marginal distribution associated with (G_R, G_C) of the joint posterior distribution (15):

$$Pr(G_R,G_C\mid \mathcal{D})\propto \mathrm{p}(\mathcal{D}\mid G_R,G_C)Pr(G_C)Pr(G_R),$$ (16)

which involves the marginal likelihood

$$\mathrm{p}(\mathcal{D}\mid G_R,G_C)=\int \mathrm{p}(\mathcal{D}\mid {\mathbf{K}}_R,{\mathbf{K}}_C)\mathrm{p}({\mathbf{K}}_R\mid G_R,{\delta }_R,{\mathbf{D}}_R)\times \mathrm{p}(z,{\mathbf{K}}_C\mid G_C,{\delta }_C,{\mathbf{D}}_C)d{\mathbf{K}}_{R}d{\mathbf{K}}_{C}dz.$$ (17)

Wang and West (2009) employed the candidate’s formula (Besag 1989; Chib 1990) to approximate the marginal likelihood (17). They sampled from (16) by sequentially updating the row and column graphs. The update of the row graph proceeds by sampling a candidate $G_R^{\prime }$ from an instrumental distribution $\pi (G_R^{\prime }\mid G_R)$ and accepting it with Metropolis–Hastings probability

$$min\left\{\frac{\mathrm{p}(\mathcal{D}\mid G_R^{\prime },G_C)Pr(G_R^{\prime })\pi (G_R\mid G_R^{\prime })}{\mathrm{p}(\mathcal{D}\mid G_R,G_C)Pr(G_R)\pi (G_R^{\prime }\mid G_R)},1\right\}.$$ (18)

The update of the column graph is done in a similar manner. Therefore resampling G_R or G_C requires the computation of a new marginal likelihood (17) which entails a considerable computational effort even for graphs with a small number of vertices. We avoid the computation of marginal likelihoods by sampling from the joint distribution (15) in which the row and column precision matrices have not been integrated out. Sampling from the joint marginal distribution (16) seems appealing because it involves the reduced space of row and column graphs. However, the numerical difficulties associated with repeated calculations of marginal likelihoods (17) outweigh the benefits of working in a smaller space. We empirically compare the efficiency of our inference approach for matrix-variate GGMs with the work of Wang and West (2009) in Section 6.1.

5. BAYESIAN HIERARCHICAL MODELS FOR MULTIVARIATE LATTICE DATA

Conditional autoregressive (CAR) models (Besag 1974; Mardia 1988) are routinely used in spatial statistics to model lattice data. In the case of a single observed outcome in each region, the data are associated with a vector X = (X₁, …, X_pR)^T where X_i corresponds to region i. The zero-centered CAR model is implicitly defined by the set of full conditional distributions

$$X_i\mid \{X_j:j\ne i\}~\mathrm{N}\left(\sum _{j\ne i}{b}_{ij}{X}_j,{\mathrm{\lambda }}_i^2\right),i=1,\dots ,p_R.$$ (19)

Therefore, CAR models are just two-dimensional Gaussian Markov random fields. According to Brook’s (1964) theorem, this set of full-conditional distributions implies that the joint distribution for X satisfies

$$\mathrm{p}(\mathbf{X}\mid \mathbf{\lambda })\propto exp\{-\frac{1}{2}{\mathbf{X}}^T{\mathbf{\Lambda }}^{-1}(\mathbf{I}-\mathbf{B})\mathbf{X}\},$$

where $\mathbf{\Lambda }=\text{diag}\{{\mathrm{\lambda }}_1^2,\dots ,{\mathrm{\lambda }}_{p_R}^2\}$ and B is a p_R × p_R matrix such that B = (b_ij) and b_ii = 0. In order for Λ⁻¹(I−B) to be a symmetric matrix we require that $b_{ij}{\mathrm{\lambda }}_j^2=b_{ji}{\mathrm{\lambda }}_i^2$ for i ≠ j; therefore the matrix B and vector λ must be carefully chosen. A popular approach is to begin by constructing a symmetric proximity matrix W= (w_ij), and then set b_ij = w_ij/w_i+ and ${\mathrm{\lambda }}_i^2={\tau }^2/w_{i+}$ where w_i+ = Σ_j w_ij and τ² > 0. In that case, Λ⁻¹(I − B) = τ⁻²(E_W −W), where E_W = diag{w₁₊, …, w_pR+}. The proximity matrix W is often constructed by first specifying a neighborhood structure for the geographical areas under study; for example, when modeling state or county level data it is often assumed that two geographical units are neighbors if they share a common border. This neighborhood structure can be summarized in a graph G_R ∈ 𝒢_pR whose vertices correspond to geographical areas, while its edges are associated with areas that are considered neighbors of each other. The proximity matrix W is subsequently specified as

$$w_{ij}=\{\begin{array}{ll}1,\hfill & \text{if}j\in {\partial }_{G_R}(i)\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}$$ (20)

where ∂_GR(i) denotes the set of vertices that are linked by an edge in the graph G_R with the vertex i.

Specifying the joint precision matrix for X using the proximity matrix derived from the neighborhood structure is very natural; essentially, it implies that observations collected on regions that are not neighbors are conditionally independent from each other given the rest. However, note that the specification in (20) implies that (E_W − W)1_pR = 0 and therefore the joint distribution on X is improper. Here 1_l is the column vector of length l with all elements equal to 1. Proper CAR models (Cressie 1973; Sun et al. 2000; Gelfand and Vounatsou 2003) can be obtained by including a spatial autocorrelation parameter ρ, so that

$$X_i\mid \{X_j:j\ne i\}~\mathrm{N}\left(\rho \sum _{j\ne i}\frac{w_{ij}}{w_{i+}}{X}_j,\frac{{\tau }^2}{w_{i+}}\right).$$ (21)

The joint distribution on X is then multivariate normal ${\mathrm{N}}_{p_R}(\mathbf{0},{\mathbf{V}}_{\mathbf{W}}^{-1}({\tau }^{-2},\rho ))$ where V_W(τ⁻², ρ) = τ⁻²(E_W − ρW) ∈ P_GR. This distribution is proper as long as ρ is between the reciprocals of the minimum and maximum eigenvalues for W. In particular, note that taking ρ = 0 leads to independent random effects.

In the spirit of Besag and Kooperberg (1995), an alternative but related approach to the construction of models for lattice data is to let X ~ N_pR (0, K⁻¹) and assign K a G-Wishart prior Wis_GR(δ_R, (δ_R − 2)D_R), where ${\mathbf{D}}_R={\mathbf{V}}_{\mathbf{W}}^{-1}({\tau }^{-2},\rho )$. The mode of Wis_GR (δ_R, (δ_R − 2)D_R) is the unique matrix K = (K_ij) ∈ P_GR that satisfies the relations

$$\begin{array}{l}\hfill {({\mathbf{K}}^{-1})}_{ij}={({\mathbf{D}}_R)}_{ij},\text{if}j\in {\partial }_{G_R}(i),\text{and}\\ \hfill K_{ij}=0,\text{if}j\notin {\partial }_{G_R}(i).\end{array}$$ (22)

The matrix ${\mathbf{D}}_R^{-1}={\mathbf{V}}_{\mathbf{W}}({\tau }^{-2},\rho )$ verifies the system (22), hence it is the mode of Wis_GR(δ_R, (δ_R − 2)D_R). As such, the mode of the prior for K_R induces the same prior specification for X as (21). It is easy to see that, conditional on K_R ∈ P_GR, we have

$$X_i\mid \{X_j:j\ne i\}~\mathrm{N}\left(-\sum _{j\in {\partial }_{G_R}(i)}\frac{K_{ij}}{K_{ii}}{X}_j,\frac{1}{K_{ii}}\right).$$ (23)

Hence, by modeling X using a Gaussian graphical model and restricting the precision matrix K to belong to the cone P_GR, we are inducing a mixture of CAR priors on X where the priors on

$$b_{ij}=\{\begin{array}{ll}-K_{ij}/K_{ii},\hfill & \text{if}j\in {\partial }_{G_R}(i)\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}$$

and ${\mathrm{\lambda }}_i^2=1/K_{ii}$ [see Equation (19)] are induced by the G-Wishart prior Wis_GR (δ_R, (δ_R − 2)D_R).

The specification of CAR models through G-Wishart priors solves the impropriety problem of intrinsic CAR models and preserves the computational advantages derived from standard CAR specifications while providing greater flexibility. Indeed, the prior is trivially proper because the matrix K ∈ P_GR is invertible by construction. The computational advantages are preserved because the full conditional distributions for each X_i can be easily computed for any matrix K without the need to perform matrix inversion, and they depend only on a small subset of neighbors {X_j:j ∈ ∂_GR(i)}. Additional flexibility is provided because the weights b_ij for j ∈ ∂_GR (i) and smoothing parameters ${\mathrm{\lambda }}_i^2$ are being estimated from the data rather than being assumed fixed, allowing for adaptive spatial smoothing. Our approach provides what can be considered as a nonparametric alternative to the parametric estimates of the proximity matrix of Cressie and Chan (1989).

A similar approach can be used to construct proper multivariate conditional autoregressive (MCAR) models (Mardia 1988; Gelfand and Vounatsou 2003). In this case, we are interested in modeling a p_R × p_C matrix X = (X_ij) where X_ij denotes the value of the jth outcome in region i. We let X follow a matrix-variate normal distribution with row precision matrix K_R capturing the spatial structure in the data (which, as in univariate CAR models, is restricted to the cone P_GR defined by the neighborhood graph G_R), and column precision matrix K_C, which controls the multivariate dependencies across outcomes. It can be easily shown that the row vector X_i* of X depends only on the row vectors associated with those regions that are neighbors with i—see also Equation (13):

$${\mathbf{X}}_{i\ast }^T\mid \{{\mathbf{X}}_{j\ast }^T:j\ne i\}~{\mathrm{N}}_{p_C}\left(-\sum _{j\in {\partial }_{G_R}(i)}\frac{{({\mathbf{K}}_R)}_{ij}}{{({\mathbf{K}}_R)}_{ii}}{\mathbf{X}}_{j\ast }^T,\frac{1}{{({\mathbf{K}}_R)}_{ii}}{\mathbf{K}}_C^{-1}\right).$$

Given the matrix-variate GGMs framework from Section 4, we can model the conditional independence relationships across outcomes through a column graph G_C ∈ 𝒢_pC and require K_C ∈ P_GC As opposed to the neighborhood graph G_R which is known and considered fixed, the graph G_C is typically unknown and needs to be inferred from the data.

The matrix-variate GGM formulation for spatial models can also be used as part of more complex hierarchical models. Indeed, CAR and MCAR models are most often used as a prior for the random effects of a generalized linear model (GLM) to account for residual spatial structure not accounted for by covariates. When no covariates are available, the model can be interpreted as a spatial smoother where the spatial covariance matrix controls the level of spatial smoothing in the underlying (latent) surface. Similarly, MCAR models can be used to construct multivariate spatial GLMs. More specifically, consider the p_R × p_C matrix Y = (Y_ij) of discrete or continuous outcomes, and let Y_ij ~ h_j(·|η_ij) where h_j is a probability mass or probability density function that belongs to the exponential family with location parameter η_ij. The spatial GLM is then defined through the linear predictor

$$g^{-1}({\eta }_{ij})={\mu }_j+X_{ij}+{\mathbf{Z}}_{ij}{\mathit{\beta }}_j,$$ (24)

where g(·) is the link function, μ_j is an outcome-specific intercept, X_ij is a zero-centered spatial random effect associated with location i, Z_ij is a matrix of observed covariates for outcome j at location i, and β_j is the vector of fixed effects associated with outcome j. As an example, by choosing y_ij ~ Poi(η_ij), g⁻¹(·) = log(·) we obtain a multivariate spatial log-linear model for count data, which is often used for disease mapping in epidemiology (see Section 6.2). We further assign a matrix-variate normal distribution for X with independent G-Wishart priors for K_R and zK_C, where z > 0 is an auxiliary variable needed to impose the identifiability constraint (K_C)₁₁ = 1:

$$\begin{array}{ll}\hfill {\mathbf{K}}_R\mid {\delta }_R,{\mathbf{D}}_R& ~{\text{Wis}}_{G_R}({\delta }_R,({\delta }_R-2){\mathbf{D}}_R),\hfill \\ \hfill (z{\mathbf{K}}_C)\mid {\delta }_C,{\mathbf{D}}_C& ~{\text{Wis}}_{G_C}({\delta }_C,{\mathbf{D}}_C).\hfill \end{array}$$ (25)

Prior elicitation for this class of spatial models is relatively straightforward. Indeed, elicitation of the matrix D_R = (E_W − ρW)⁻¹ requires only the elicitation of the neighborhood matrix W which also defines the neighborhood graph G_R, along with reasonable values for the spatial autocorrelation parameter ρ. In particular, in the application we discuss in Section 6.2 we assume that, a priori, there is a strong degree of positive spatial association, and choose a prior for ρ that gives higher probabilities to values close to 1 (Gelfand and Vounatsou 2003):

$$\rho ~\text{Uni}(\{0,0.05,0.1,\dots ,0.8,0.82,\dots ,0.90,0.91,\dots ,0.99\}).$$ (26)

In the case of MCAR models, it is common to assume that the prior value for the conditional covariance between variables is zero, which leads to choosing D_C from the G-Wishart prior for zK_C to be a diagonal matrix. We note that the scale parameter τ² is no longer identifiable in the context of the joint prior (25), hence it is then sensible to pick D_C = I_pC .

At this point, a word of caution about the interpretation of the models seems appropriate. The graphs G_R = (V_pR, E_R) and G_C = (V_pC, E_C) induce conditional independence relationships associated with the rows and columns of the random-effects matrix X—see Equation (13). Similar conditional independence relationships hold for the rows and columns of the matrix of location parameters η = (η_ij), but these extend to the observed outcomes Y only if its entries are continuous (for a more thorough discussion, see the Supplementary Materials). Hence, the reader must be careful when interpreting the results of these models when binary or count data are involved; in these cases, any statement about conditional independence needs to be circumscribed to the location parameters η.

6. ILLUSTRATIONS

6.1 Simulation Study

We empirically compare the reversible jump MCMC sampler for matrix-variate GGMs proposed in Section 4 (RJ-DLR) with the methodology of Wang and West (2009) (WW). We consider the row graph Ḡ_R = (V_pR, Ē_R) with p_R = 5 vertices and with edges Ē_R = {(1, i) : 1 < i ≤ 5} ∪ {(2, 3), (3, 4), (4, 5), (2, 5)}. We take the column graph Ḡ_C to be the cycle graph with p_C = 10 vertices (see Section 2.3). We note that both the row and column graphs are non-decomposable, with Ḡ_R being relatively dense and with Ḡ_C being relatively sparse. We define the row and column precision matrices K̄_R ∈ P_ḠR and K̄_C ∈ P_ḠC to have diagonal elements equal to 1 and nonzero off-diagonal elements equal with 0.4. We generate 100 datasets each comprising n = 100 observations sampled from the 5 × 10 matrix-variate normal distribution p(·|K̄_R, K̄_C)—see Equation (12).

For each dataset we attempted to recover the edges of Ḡ_R and Ḡ_C with the RJ-DLR and the WW algorithms. The two MCMC samplers were run for 10,000 iterations with a burn-in of 1000 iterations. We implemented the RJ-DLR algorithm in R and C++ (code available as Supplemental Material). We used the code developed by Wang and West (2009) for their method. In the RJ-DLR algorithm we set σ_m,R = σ_m,C = σ_g,R = σ_g,C = 0.5, which yields average rejection rates on Metropolis–Hastings updates of about 0.3 for both K̄_C and K̄_R. We assumed independent uniform priors for the row and column graphs.

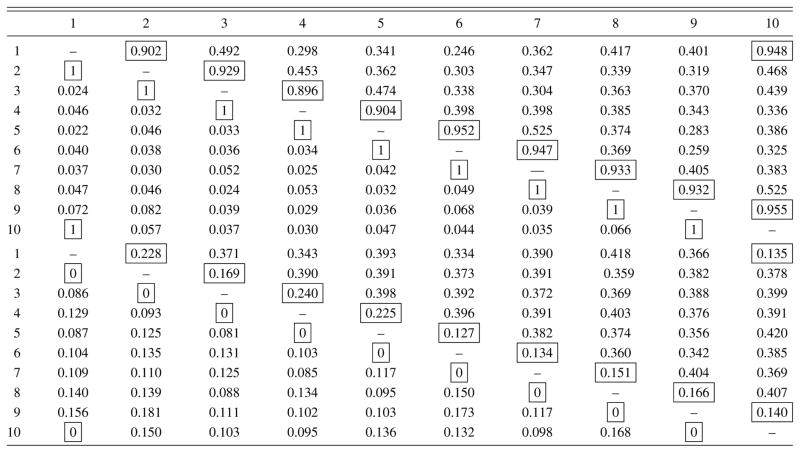
Tables 2 and 3 show the average posterior edge inclusion probabilities for Ḡ_R and Ḡ_C. Our RJ-DLR method recovers the structure of both graphs very well: the edges that belong to each graph receive posterior inclusion probabilities of 1, while the edges that are absent from each graph receive posterior inclusion probabilities below 0.1. The ability of the RJ-DLR algorithm to recover the structures of a dense row graph and of a sparse column graph is quite encouraging since the uniform priors for the row and column graphs favored middle-size graphs.

Table 2.

Average estimates (left panel) and their standard errors (right panel) of posterior edge inclusion probabilities for the row graph Ḡ_R obtained using the RJ-DLR algorithm (below diagonal) and the WW algorithm (above diagonal). The boxes identify the edges that are in Ḡ_R

Table 3.

Average estimates (upper panel) and their standard errors (lower panel) of posterior edge inclusion probabilities for the column graph Ḡ_C obtained using the RJ-DLR algorithm (below diagonal) and the WW algorithm (above diagonal). The boxes identify the edges that are in Ḡ_C

The WW method shows diminished performance in recovering graphical structures. Edges (1, 4), (1, 5), and (2, 5), which are actually in Ḡ_R, are given average inclusion probabilities of only 0.7. Edge (1, 3), which is in Ḡ_R, receives a very low inclusion probability, while edge (2, 4), which is not in Ḡ_R, is given a high inclusion probability. The WW algorithm includes edges that are in the column graph with relatively high probabilities (typically above 0.9). However, edges that do not belong to Ḡ_C also appear to be included quite often, with an average inclusion probability between 0.3 and 0.4. These tables also show a large standard deviation of edge inclusion probabilities across the 100 datasets using the WW method. The decreased performance of the WW algorithm versus our own RJ-DLR algorithm is likely attributable to the fact that Wang and West (2009) accounted only for decomposable graphs in their framework, which may be poor at approximating the non-decomposable graphs considered in this example.

6.2 Mapping Cancer Mortality in the United States

Accurate and timely counts of cancer mortality are very useful in the cancer surveillance community for purposes of efficient resource allocation and planning. Estimation of current and future cancer mortality broken down by geographic area (state) and tumor has been discussed in a number of recent articles, including those by Tiwari et al. (2004), Ghosh and Tiwari (2007), Ghosh et al. (2007), and Ghosh, Ghosh, and Tiwari (2008). This section considers a multivariate spatial model on state-level cancer mortality rates in the United States for 2000. These mortality data are based on death certificates that are filed by certifying physicians. They are collected and maintained by the National Center for Health Statistics (http://www.cdc.gov/nchs) as part of the National Vital Statistics System. The data are available from the Surveillance, Epidemiology, and End Results (SEER) program of the National Cancer Institute (http://seer.cancer.gov/seerstat).

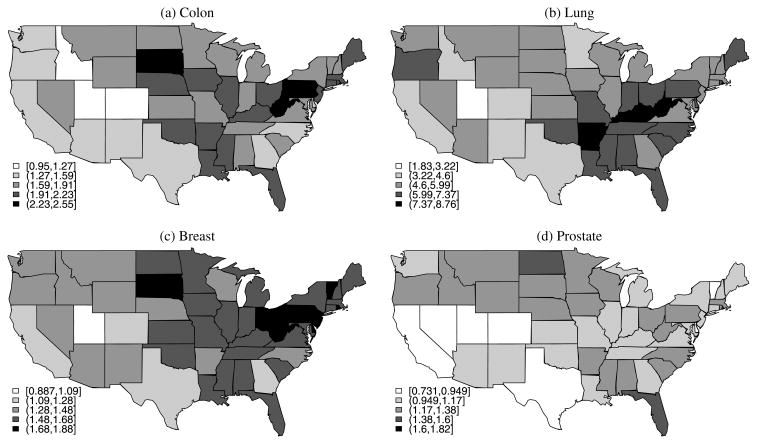
The data we analyze consist of mortality counts for 11 types of tumors recorded in the 48 continental states plus the District of Columbia. Since mortality counts below 25 are often deemed unreliable in the cancer surveillance community, we treated them as missing. Along with mortality counts, we obtained population counts in order to model death risk. Figure 1 shows raw mortality rates for four of the most common types of tumors (colon, lung, breast, and prostate). Although the pattern is slightly different for each of these cancers, a number of striking similarities are present; for example, Colorado appears to be a state with low mortality for all of these common cancers, while West Virginia, Pennsylvania, and Florida present relatively high mortality rates.

Figure 1.

Mortality rates (per 10,000 habitants) in the 48 continental states and the D.C. area corresponding to four common cancers during 2000.

We consider modeling these data using Poisson multivariate log-linear models with spatial random effects. More concretely, we let Y_ij be the number of deaths in state i = 1, …, p_R = 49 for tumor type j = 1, …, p_C = 11. We set

$$Y_{ij}\mid {\eta }_{ij}~\text{Poi}({\eta }_{ij}),log({\eta }_{ij})=log(m_i)+{\mu }_j+X_{ij}.$$ (27)

Here m_i is the population of state i, μ_j is the intercept for tumor type j, and X_ij is a zero-mean spatial random effect associated with location i and tumor j. We denote X̃_ij = μ_j + X_ij. We further model X̃ = (X̃_ij) with a matrix-variate normal prior:

$$\text{vec}(\stackrel{\sim }{\mathbf{X}})\mid \mathit{\mu },{\mathbf{K}}_R,{\mathbf{K}}_C~{\mathrm{N}}_{p_R{p}_C}(\text{vec}\{{({\mathbf{1}}_{p_R}{\mathit{\mu }}^T)}^T\},{[{\mathbf{K}}_C\otimes {\mathbf{K}}_R]}^{-1}),$$ (28)

where μ = (μ₁, …, μ_pC)^T.

We consider four models in total. The first two models we consider (GGM-U and GGM-S) are based on the sparse models for multivariate aerial data described in Section 5, and differ only in terms of the prior assigned on the space of graphs [GGM-U uses a uniform prior, while GGM-S uses the size-based prior from Equation (11)]. Hence, the joint prior for the row and column precision matrices is given in (25) for both models. The column graph G_C is unknown and allowed to vary in 𝒢₁₁. The row graph G_R is fixed and derived from the incidence matrix W corresponding with the neighborhood structure of the U.S. states. More explicitly, each state is associated with a vertex in G_R. Two states are linked by an edge in G_R if they share a common border. The Supplementary Materials describe the neighborhood structure of G_R and provide its decomposition into maximal prime subgraphs. What is interesting about the graph G_R, and relevant in light of the results of Section 2.3, is that its decomposition yields 13 maximal prime subgraphs. Most of these prime components are complete and only contain two or three vertices; however, one maximal prime subgraph has 36 vertices (states), making G_R non-decomposable with a sizable maximal prime subgraph. The degrees of freedom for the G-Wishart priors are set as δ_R = δ_C = 3, while the centering matrices are chosen as D_C = I_pC and D_R = (E_W − ρW)⁻¹.

The third model, which we call model FULL, is obtained by keeping the column graph G_C fixed to the full graph. This is equivalent to replacing the G-Wishart prior for (zK_C) from Equation (25) with a Wishart prior Wis_pC (δ_C, D_C). Finally, model MCAR is obtained from model FULL by substituting the G-Wishart prior for K_R from Equation (25) with K_R = E_W − ρW. The resulting prior distribution for the spatial random effects X̃ in model MCAR is precisely the MCAR(ρ, Σ) prior of Gelfand and Vounatsou (2003). In all cases, we complete the model specification by choosing the prior from Equation (26) for the spatial autocorrelation parameter ρ and a multivariate normal prior for the mean rates vector μ ~ N_pC (μ₀, Ω⁻¹) where μ₀ = μ₀1_pC and Ω = ω⁻²I_pC. We set μ₀ to be the median log incidence rate across all cancers and regions, and ω to be twice the interquartile range in raw log incidence rates.

Posterior inferences for models GGM-U and GGM-S are obtained by extending the sampling algorithm from Appendix B; details are presented in the Supplemental Materials. MCMC samplers for models FULL and MCAR are similarly derived in a straightforward manner. Missing counts were sampled from their corresponding predictive distributions. We monitored the chains to ensure convergence for each model. We set σ_m,R = σ_g,R = 0.2 and σ_m,C = σ_g,C = 0.5, which achieved rejection rates of roughly 0.3 when updating elements of both K_R or K_C. Furthermore, the average acceptance rate of a reversible jump move for the column graph G_C was around 0.22 for both GGM-U and GGM-S.

To assess the out-of-sample predictive performance of the four models, we performed a 10-fold cross-validation exercise. The exercise was run by randomly dividing the non-missing counts (those above 25) in ten bins. For each bin j, we used the samples from the other nine bins as data and treated the samples from bin j as missing. In this comparison, the MCMC sampler for each of the four models was run ten times for 160,000 iterations and the first half of the run was discarded as burn-in. In the sequel, we denote the predicted counts for model ℳ ∈ {GGM-U, GGM-S, FULL, MCAR} by $Y_{ij}^{cv}(\mathcal{M})$. We employ the goodness-of-fit (mean squared error of the posterior predictive mean or MSE) and the variability/penalty (mean predictive error or VAR) terms of Gelfand and Ghosh (1998), that is,

$$\begin{array}{l}\text{MSE}(\mathcal{M})=\frac{1}{\mid \{(i,j):Y_{ij}\ge 25\}\mid }\times \sum _{\{(i,j):Y_{ij}\ge 25\}}{({\mathrm{E}}_{\mathcal{M}}[Y_{ij}^{cv}(\mathcal{M})]-Y_{ij})}^2,\\ \text{VAR}(\mathcal{M})=\frac{1}{\mid \{(i,j):Y_{ij}\ge 25\}\mid }\sum _{\{(i,j):Y_{ij}\ge 25\}}{\text{Var}}_{\mathcal{M}}[Y_{ij}^{cv}(\mathcal{M})],\end{array}$$

to compare the predictive mean and variance of the four models. We also calculated the ranked probability score (RPS) (discussed by Czado, Gneiting, and Held 2009 in the context of count data), which measures the accuracy of the entire predictive distribution. The results, which are summarized in Table 4, reveal an interesting progression in the out-of-sample predictive performance of the four methods. Under either the MSE, VAR, or the RPS criteria, model MCAR performs considerably worse than model FULL, which in turn is outperformed by both models GGM-U and GGM-S. Also, the effect of the choice of prior on the column graph space appears negligible as GGM-U and GGM-S have roughly the same predictive performance. It is noteworthy to mention that the improvement in the RPS in the sequence of models MCAR, FULL, GGM-U, and GGM-S comes both because of a better prediction of the means as well as because the predictive distributions become sharper—see the article by Gneiting and Raftery (2007) for a discussion of the trade-off between sharpness and calibration in the formation of predictive distributions. The dramatic improvement in predictive performance that results from moving from model MCAR to model FULL is the result of using the G-Wishart distribution to allow greater flexibility in the spatial interactions over the CAR specification suggested by Gelfand and Vounatsou (2003). On the other hand, the additional gain yielded by the use of models GGM-U or GGM-S versus model FULL would seem to come from the increased parsimony of the GGM models.

Table 4.

Ten-fold cross-validation predictive scores in the U.S. cancer mortality example. Model GGM-S is best with respect to fit (MSE) and ranked probability score (RPS), while model GGM-U is best with respect to variability (VAR) of the out-of-sample predicted counts

Model	MSE	VAR	RPS
GGM-U	17,379.9	23,685.2	62.1
GGM-S	16,979.8	24,361.1	61.8
FULL	18,959.6	24,530.4	63.2
MCAR	19,211.1	47,568.7	76.7

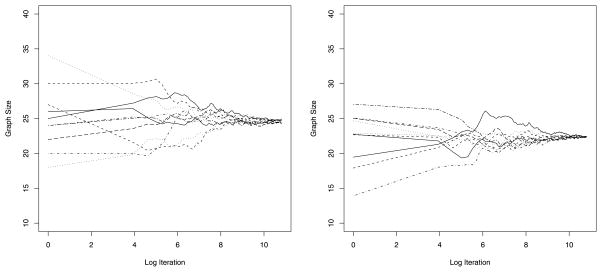
We also conducted an in-sample comparison of the four models. For each model, we ran ten Markov chains for 160,000 iterations and discarded the first half as burn-in based; Figure 2 is indicative of the performance of the MCMC sampler we employed. These runs used the entire dataset (with the exception of counts below 25, which are still treated as missing), rather than the cross-validation datasets. The Supplemental Materials give detailed tables of fitted values and 95% credible intervals for all counts in the dataset obtained using each of the four models. Table 5 summarizes these results by presenting the empirical coverage rates and the average lengths of these in-sample 95% credible intervals for each of the four models. We see that the methods based on the G-Wishart priors for the spatial component (GGM-U, GGM-S, FULL) have very similar coverage probabilities that are close to the nominal 95%. These three models also tend to have relatively short credible intervals, with GGM-U and GGM-S presenting the smallest (and almost identical) values. In contrast, model MCAR returns credible intervals that are too wide, containing 99% of all observed values. As with the out-of-sample exercise, these results suggest that both the additional flexibility in modeling the spatial dependence and the sharper estimates of the dependence across cancer types provided by the matrix-variate GGMs are key to prevent overfitting.

Figure 2.

Convergence plot of the average size of the column graph G_C by log iteration for model GGM-U (left panel) and model GGM-S (right panel).

Table 5.

Nominal coverage rates and mean length of the in-sample 95% credible intervals for the U.S. cancer mortality example obtained using the four Poisson multivariate log-linear models

Model	Coverage rate	Mean length
GGM-U	0.960	65.464
GGM-S	0.964	65.474
FULL	0.964	65.885
MCAR	0.990	69.239

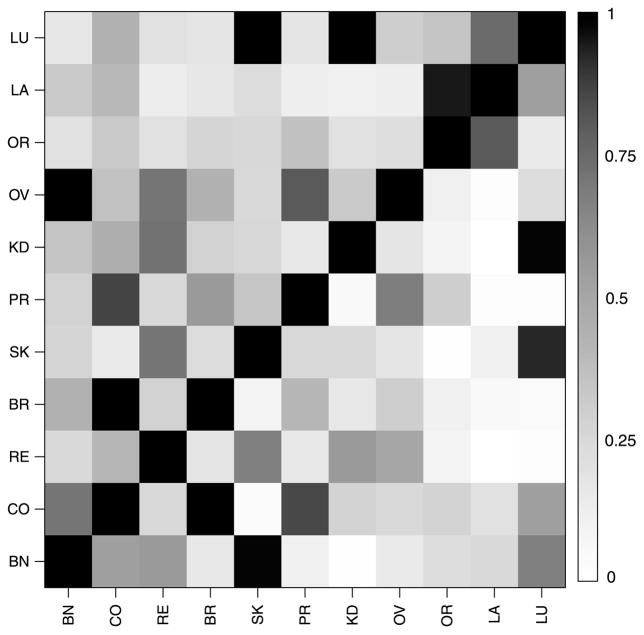
Finally, we compare the estimates of the column graph G_C under GGM-U and GGM-S to assess the sensitivity of the model to the prior on graph space. Figure 3 shows a heatmap of the posterior edge inclusion probabilities in the column graph G_C, with the lower triangle corresponding to GGM-U and the upper triangle to GGM-S. Overall there is substantial coherence in terms of the effects of the uniform and size-based priors on 𝒢₁₁ on the frequency on which edges are added or deleted from the column graph. From the left panel of Figure 2 we see that the average size of the column graph G_C in GGM-U is 24.8 edges while the right panel shows that the average graph size in model GGM-S is 22.5 edges. Both of these numbers are quite close to 27.5—the average graph size under the uniform prior and the size-based prior on 𝒢₁₁. This suggests that there is little sensitivity to the prior in terms of graph selection.

Figure 3.

Edge inclusion probabilities for model GGM-U (lower triangle) and model GGM-S (upper triangle) in the U.S. cancer mortality example. The acronyms used are explained in the Supplementary Materials.

7. DISCUSSION

In this article we have developed and illustrated a surprisingly powerful computational approach for multivariate and matrix-variate GGMs that scales well to problems with a moderate number of variables. Convergence seems to be achieved quickly (usually within the first 5000 iterations) and acceptance rates are within reasonable ranges and can be easily controlled. In the context of the sparse multivariate models for aerial data discussed in Section 5 the running times, although longer than for conventional MCAR models, are still short enough to make routine implementation feasible (e.g., in the cancer surveillance example from Section 6.2, about 22 hours on a dual-core 2.8 GHz computer running Linux). However, computations can still be quite challenging when the number of units in the lattice is very high. We plan to explore more efficient implementations that exploit the sparse structure of the Cholesky decompositions of precision matrices induced by GGMs.

We believe that our application to the construction of spatial models for lattice data makes for particularly appealing illustrations. On one hand, the U.S. cancer mortality example we have considered suggests that the additional flexibility in the spatial correlation structure provided by our approach is necessary to accurately model some spatial datasets. Indeed, our approach allows for “nonstationary” CAR models, where the spatial autocorrelation and spatial smoothing parameters vary spatially. On the other hand, to the best of our knowledge, we are unaware of any approach in the literature to construct and estimate potentially sparse MCAR, particularly under a Bayesian approach. In addition to providing insights into the mechanisms underlying the data generation process, the model offers drastically improved predictive performance and sharper estimation of model parameters.

SUPPLEMENTARY MATERIALS

Code

Computer code to run all routines discussed in this article, as well as the U.S. cancer mortality data. (DLR-archive.tar.gz.zip, GNU zipped tar file)

Results

Theoretical results related to conditional independence relationships in sparse latent Gaussian processes; the description of the MCMC algorithm used to fit the sparse multivariate spatial Poisson count model from Section 6.2; tables describing the U.S. cancer mortality data, the graphical model constructed from the neighborhood structure of the United States, as well as fitted values and 95% credible intervals for the models considered in the article in Section 6.2. (DLR-supplement.pdf, PDF file)

APPENDIX A: DETAILS OF THE REVERSIBLE JUMP MCMC SAMPLER FOR GGMS

The MCMC algorithm from Section 3 sequentially updates the elements of the precision matrix and the edges of the underlying graph as follows. We denote the current state of the chain by (K^[s], G^[s]), K^[s] ∈ P_G^[s]. Its next state (K^[s+1], G^[s+1]), K^[s+1] ∈ P_G^[s+1], is generated by sequentially performing the following two steps. We make use of two strictly positive precision parameters σ_m and σ_g that remain fixed at some suitable small values. We assume that the ordering of the variables has been changed according to a permutation υ selected at random from the uniform distribution on ϒ_p. We denote by (U + D₀)⁻¹ = (Q^*)^TQ^* the Cholesky decomposition of (U + D₀)⁻¹, where the rows and columns of this matrix have been permuted according to υ.

We denote by ${\text{nbd}}_p^{+}(G)$ the graphs that can be obtained by adding an edge to a graph G ∈ 𝒢_p and by ${\text{nbd}}_p^{-}(G)$ the graphs that are obtained by deleting an edge from G. We call the one-edge-way set of graphs ${\text{nbd}}_p(G)={\text{nbd}}_p^{+}(G)\cup {\text{nbd}}_p^{-}(G)$ the neighborhood of G in 𝒢_p. These neighborhoods connect any two graphs in 𝒢_p through a sequence of graphs such that two consecutive graphs in this sequence are each others’ neighbors.

Step 1: Resample the graph

We sample a candidate graph G′ ∈ nbd_p(G^[s]) from the proposal

$$q(G^{\prime }\mid G^{[s]})=\frac{1}{2}\text{Uni}({\text{nbd}}_p^{+}(G^{[s]}))+\frac{1}{2}\text{Uni}({\text{nbd}}_p^{-}(G^{[s]})),$$ (A.1)

where Uni(A) represents the uniform distribution on the discrete set A. The distribution (A.1) gives an equal probability of proposing to delete an edge from the current graph and of proposing to add an edge to the current graph. We favor (A.1) over the more usual proposal distribution Uni(nbd_p(G^[s])) that is employed, for example, by Madigan and York (1995). If G^[s] contains a very large or a very small number of edges, the probability of proposing a move that adds or, respectively, deletes an edge from G^[s] is extremely small when sampling from Uni(nbd_p(G^[s])), which could lead to poor mixing in the resulting Markov chain.

We assume that the candidate G′ sampled from (A.1) is obtained by adding the edge (i₀, j₀), i₀ < j₀, to G^[s]. Since $G^{\prime }\in {\text{nbd}}_p^{+}(G^{[s]})$ we have $G^{[s]}\in {\text{nbd}}_p^{-}(G^{\prime })$. We consider the decomposition of the current precision matrix K^[s] = (Q^*)^T ((Ψ^[s])^T Ψ^[s])Q^* with (Ψ^[s])^ν(G[s]) ∈ M^ν(G[s]). Since the vertex i₀ has one additional neighbor in G′, we have $d_{i_0}^{G^{\prime }}=d_{i_0}^{G^{[s]}},d_{j_0}^{G^{\prime }}=d_{j_0}^{G^{[s]}}+1,v_{i_0}^{G^{\prime }}=v_{i_0}^{G^{[s]}}+1,v_{j_0}^{G^{\prime }}=v_{j_0}^{G^{[s]}}$, and ν(G′) = ν(G^[s]) ∪ {(i₀, j₀)}. We define an upper triangular matrix Ψ′ such that ${\mathrm{\Psi }}_{ij}^{\prime }={\mathrm{\Psi }}_{ij}^{[s]}$ for (i, j) ∈ ν(G^[s]). We sample $\gamma ~\mathrm{N}({\mathrm{\Psi }}_{i_0{j}_0}^{[s]},{\sigma }_g^2)$ and set ${\mathrm{\Psi }}_{i_0{j}_0}^{\prime }=\gamma$. The rest of the elements of Ψ′ are determined from (Ψ′)^ν(G′) through the completion operation. The value of the free element ${\mathrm{\Psi }}_{i_0{j}_0}^{\prime }$ was set by perturbing the non-free element ${\mathrm{\Psi }}_{i_0{j}_0}^{[s]}$. The other free elements of Ψ′ and Ψ^[s] coincide.

We take K′ = (Q^*)^T ((Ψ′)^T Ψ′)Q^*. Since (Ψ′)^ν(G′) ∈ M^ν(G′), we have K′ ∈ P_G′. The dimensionality of the parameter space increases by 1 as we move from (K^[s], G^[s]) to (K′, G′). Since (Ψ′)^ν(G[s]) = (Ψ^[s])^ν(G[s]), the Jacobian of the transformation from ((Ψ^[s])^ν(G[s]), γ) to (Ψ′)^ν(G′) is equal to 1. Moreover, Ψ^[s] and Ψ′ have the same diagonal elements, hence $det{\mathbf{K}}^{[s]}={\prod }_{i=1}^p{(Q_{ii}^{\ast }{\mathrm{\Psi }}_{ii}^{[s]})}^2=det{\mathbf{K}}^{\prime }$. The Markov chain moves to (K′, G′) with probability $min\{R_g^{+},1\}$ where $R_g^{+}$ is given by Green (1995)

$$R_g^{+}={\sigma }_g\sqrt{2\pi }{Q}_{i_0{i}_0}^{\ast }{Q}_{j_0{j}_0}^{\ast }{\mathrm{\Psi }}_{i_0{i}_0}^{[s]}\frac{I_{G^{[s]}}({\delta }_0,{\mathbf{D}}_0)}{I_{G^{\prime }}({\delta }_0,{\mathbf{D}}_0)}\frac{Pr(G^{\prime })}{Pr(G^{[s]})}\frac{\mid {\text{nbd}}_p^{+}(G^{[s]})\mid }{\mid {\text{nbd}}_p^{-}(G^{\prime })\mid }\times exp\left\{-\frac{1}{2}\left[\langle {\mathbf{K}}^{\prime }-{\mathbf{K}}^{[s]},\mathbf{U}+{\mathbf{D}}_0\rangle -\frac{{({\mathrm{\Psi }}_{i_0{j}_0}^{\prime }-{\mathrm{\Psi }}_{i_0{j}_0}^{[s]})}^2}{{\sigma }_g^2}\right]\right\}.$$ (A.2)

Otherwise the chain stays at (K^[s], G^[s]).

Next we assume that the candidate G′ is obtained by deleting the edge (i₀, j₀) from G^[s]. We have $d_{i_0}^{G^{\prime }}=d_{i_0}^{G^{[s]}},d_{j_0}^{G^{\prime }}=d_{j_0}^{G^{[s]}}-1,v_{i_0}^{G^{\prime }}=v_{i_0}^{G^{[s]}}-1,v_{j_0}^{G^{\prime }}=v_{j_0}^{G^{[s]}}$, and ν(G′) = ν(G^[s])\{(i₀, j₀)}. We define an upper triangular matrix Ψ′ such that ${\mathrm{\Psi }}_{ij}^{\prime }={\mathrm{\Psi }}_{ij}^{[s]}$ for (i, j) ∈ ν(G′). The rest of the elements of Ψ′ are determined through completion. The free element ${\mathrm{\Psi }}_{i_0{j}_0}^{[s]}$ becomes non-free in Ψ′, hence the parameter space decreases by 1 as we move from (Ψ^[s])^ν(G[s]) to (Ψ′)^ν(G′) ∈ M^ν(G′). As before, we take K′= (Q^*)^T ((Ψ′)^T Ψ′)Q^*. The acceptance probability of the transition from (K^[s], G^[s]) to (K′, G′) is $min\{R_g^{-},1\}$ where

$$\begin{array}{l}{R}_g^{-}={({\sigma }_g\sqrt{2\pi }{Q}_{i_0{i}_0}^{\ast }{Q}_{j_0{j}_0}^{\ast }{\mathrm{\Psi }}_{i_0{i}_0}^{[s]})}^{-1}\\ \times \frac{I_{G^{[s]}}({\delta }_0,{\mathbf{D}}_0)}{I_{G^{\prime }}({\delta }_0,{\mathbf{D}}_0)}\frac{Pr(G^{\prime })}{Pr(G^{[s]})}\frac{\mid {\text{nbd}}_p^{-}(G^{[s]})\mid }{\mid {\text{nbd}}_p^{+}(G^{\prime })\mid }\\ \times exp\left\{-\frac{1}{2}\left[\langle {\mathbf{K}}^{\prime }-{\mathbf{K}}^{[s]},\mathbf{U}+{\mathbf{D}}_0\rangle +\frac{{({\mathrm{\Psi }}_{i_0{j}_0}^{\prime }-{\mathrm{\Psi }}_{i_0{j}_0}^{[s]})}^2}{{\sigma }_g^2}\right]\right\}.\end{array}$$ (A.3)

We denote by (K^[s+1/2], G^[s+1]), K^[s+1/2] ∈ G^[s+1], the state of the chain at the end of this step.

Step 2: Resample the precision matrix

Given the updated graph G^[s+1], we update the precision matrix K^[s+1/2] = (Q^*)^T × (Ψ^s+1/2)^T Ψ^s+1/2Q^* by sequentially perturbing the free elements (Ψ^[s+1/2])^ν(G[s+1]). For each such element, we perform one iteration of the Metropolis–Hastings algorithm from Section 2.2 with δ = n + δ₀, D = U + D₀, and Q = Q^*. The standard deviation of the normal proposals is σ_m. We denote by K^[s+1] ∈ P_G^[s+1] the precision matrix obtained after all the updates have been performed.

APPENDIX B: DETAILS OF THE REVERSIBLE JUMP MCMC SAMPLER FOR MATRIX-VARIATE GGMS

Our sampling scheme from the joint posterior distribution (15) is composed of the following five steps that explain the transition of the Markov chain from its current state ( ${\mathbf{K}}_R^{[s]},{\mathbf{K}}_C^{[s]},G_R^{[s]}$, z^[s]) to its next state ( ${\mathbf{K}}_R^{[s+1]},{\mathbf{K}}_C^{[s+1]},G_R^{[s+1]}$, z^[s+1]). We use four strictly positive precision parameters σ_m,R, σ_m,C, σ_g,R, and σ_g,C.

Step 1: Resample the row graph

We denote $n_R^{\ast }={np}_C$ and ${\mathbf{U}}_R^{\ast }={\sum }_{j=1}^n{\mathbf{x}}^{(j)}{\mathbf{K}}_C^{[s]}{({\mathbf{x}}^{(j)})}^T$. We generate a random permutation υ_R ∈ ϒ_pR of the row indices V_pR and reorder the row and columns of the matrix ${\mathbf{U}}_R^{\ast }+{\mathbf{D}}_R$ according to υ_R. We determine the Cholesky decomposition ${({\mathbf{U}}_R^{\ast }+{\mathbf{D}}_R)}^{-1}={({\mathbf{Q}}_R^{\ast })}^T{\mathbf{Q}}_R^{\ast }$. We proceed as described in Step 1 of Appendix A. Given the notations from Appendix A, we take p = p_R, $n=n_R^{\ast },\mathbf{U}={\mathbf{U}}_R^{\ast }$, δ₀ = δ_R, D₀ = D_R, and σ_g = σ_g,R. We denote the updated row precision matrix and graph by $({\mathbf{K}}_R^{[s+1/2]},G_R^{[s+1]}),{\mathbf{K}}_R^{[s+1/2]}\in {\mathrm{P}}_{G_R^{[s+1]}}$.

Step 2: Resample the row precision matrix

We denote $n_R^{\ast }={np}_C$ and ${\mathbf{U}}_R^{\ast }={\sum }_{j=1}^n{\mathbf{x}}^{(j)}{\mathbf{K}}_C^{[s]}{({\mathbf{x}}^{(j)})}^T$. We determine the Cholesky decomposition ${({\mathbf{U}}_R^{\ast }+{\mathbf{D}}_R)}^{-1}={({\mathbf{Q}}_R^{\ast })}^T{\mathbf{Q}}_R^{\ast }$ after permuting the row and columns of ${\mathbf{U}}_R^{\ast }+{\mathbf{D}}_R$ according to a random ordering in ϒ_pR.. The conditional distribution of ${\mathbf{K}}_R\in {\mathrm{P}}_{G_R^{[s+1]}}$ is G-Wishart ${\text{Wis}}_{G_R^{[s+1]}}(n_R^{\ast }+{\delta }_R,{\mathbf{U}}_R^{\ast }+{\mathbf{D}}_R)$. We make the transition from ${\mathbf{K}}_R^{[s+1/2]}$ to ${\mathbf{K}}_R^{[s+1]}\in {\mathrm{P}}_{G_R^{[s+1]}}$ using Metropolis–Hastings updates described in Section 2.2. Given the notations we used in that section, we take p = p_R, $\delta =n_R^{\ast }+{\delta }_R,\mathbf{D}={\mathbf{U}}_R^{\ast }+{\mathbf{D}}_R,\mathbf{Q}={\mathbf{Q}}_R^{\ast }$, and σ_m = σ_m,R.

Step 3: Resample the column graph

We denote $n_C^{\ast }={np}_R$ and ${\mathbf{U}}_C^{\ast }={\sum }_{j=1}^n{({\mathbf{x}}^{(j)})}^T{\mathbf{K}}_R^{[s+1]}{\mathbf{x}}^{(j)}$. We sample a candidate column graph $G_C^{\prime }\in {\text{nbd}}_{p_C}(G_C^{[s]})$ from the proposal

$$q(G_C^{\prime }\mid G_C^{[s]},z^{[s]})=\frac{1}{2}\frac{{(z^{[s]})}^{\mid v(G_C^{\prime })\mid }}{{\sum }_{G_C^{″}\in {\text{nbd}}_{p_C}^{+}(G_C^{[s]})}{(z^{[s]})}^{\mid v(G_C^{″})\mid }}{\mathbf{1}}_{\{G_C^{\prime }\in {\text{nbd}}_{p_C}^{+}(G_C^{[s]})\}}+\frac{1}{2}\frac{{(z^{[s]})}^{\mid v(G_C^{\prime })\mid }}{{\sum }_{G_C^{″}\in {\text{nbd}}_{p_C}^{-}(G_C^{[s]})}{(z^{[s]})}^{\mid v(G_C^{″})\mid }}{\mathbf{1}}_{\{G_C^{\prime }\in {\text{nbd}}_{p_C}^{-}(G_C^{[s]})\}},$$ (B.1)

where 1_A is equal to 1 if A is true and is 0 otherwise. The proposal (B.1) gives an equal probability that the candidate graph is obtained by adding or deleting an edge from the current graph.

We assume that $G_C^{\prime }$ is obtained by adding the edge (i₀, j₀) to $G_C^{[s]}$. We generate a random permutation ${\upsilon }_C\in {\mathrm{\Upsilon }}_{p_C}^{(1,1)}$ of the row indices V_pC and reorder the row and columns of the matrix ${\mathbf{U}}_C^{\ast }+z^{[s]}{\mathbf{D}}_C$ according to υ_C. The permutation υ_C is such that υ_C(1) = 1, hence the (1, 1) element of ${\mathbf{K}}_C^{[s]}$ remains in the same position. We determine the Cholesky decomposition ${({\mathbf{U}}_C^{\ast }+z^{[s]}{\mathbf{D}}_C)}^{-1}={({\mathbf{Q}}_C^{\ast })}^T{\mathbf{Q}}_C^{\ast }$ of ${({\mathbf{U}}_C^{\ast }+z^{[s]}{\mathbf{D}}_C)}^{-1}$. We consider the decomposition of the column precision matrix ${\mathbf{K}}_C^{[s]}={({\mathbf{Q}}_C^{\ast })}^T{({\mathbf{\Psi }}_C^{[s]})}^T{\mathbf{\Psi }}_C^{[s]}{\mathbf{Q}}_C^{\ast }$ with ${({\mathbf{\Psi }}_C^{[s]})}^{v(G_C^{[s]})}\in {\mathrm{M}}^{v(G_C^{[s]})}$. We define an upper triangular matrix ${\mathbf{\Psi }}_C^{\prime }$ such that ${({\mathbf{\Psi }}_C^{\prime })}_{ij}={({\mathbf{\Psi }}_C^{[s]})}_{ij}$ for $(i,j)\in v(G_C^{[s]})$. We sample $\gamma ~\mathrm{N}({({\mathbf{\Psi }}_C^{[s]})}_{i_0{j}_0},{\sigma }_{g,C}^2)$ and set ${({\mathbf{\Psi }}_C^{\prime })}_{i_0{j}_0}=\gamma$. The rest of the elements of ${\mathbf{\Psi }}_C^{\prime }$ are determined from ${({\mathbf{\Psi }}_C^{\prime })}^{v(G_C^{\prime })}$ through the completion operation (Atay-Kayis and Massam 2005, lemma 2). We consider the candidate column precision matrix

$${\mathbf{K}}_C^{\prime }={({\mathbf{Q}}_C^{\ast })}^T{({\mathbf{\Psi }}_C^{\prime })}^T{\mathbf{\Psi }}_C^{\prime }{\mathbf{Q}}_C^{\ast }.$$ (B.2)

We know that ${\mathbf{K}}_C^{[s]}\in {\mathrm{P}}_{G_C^{[s]}}$ must satisfy ${({\mathbf{K}}_C^{[s]})}_{11}=1$. The last equality implies ${({\mathbf{\Psi }}_C^{[s]})}_{11}=1/{({\mathbf{Q}}_C^{\ast })}_{11}$, hence ${({\mathbf{\Psi }}_C^{\prime })}_{11}=1/{({\mathbf{Q}}_C^{\ast })}_{11}$. Therefore we have ${\mathbf{K}}_C^{\prime }\in {\mathrm{P}}_{G_C^{\prime }}$ and ${({\mathbf{K}}_C^{\prime })}_{11}=1$.

We make the transition from ( ${\mathbf{K}}_C^{[s]},G_C^{[s]}$) to ( ${\mathbf{K}}_C^{\prime },G_C^{\prime }$) with probability $min\{R_C^{+},1\}$ where

$$\begin{array}{l}{R}_C^{+}={\sigma }_{g,C}\sqrt{2\pi }{({\mathbf{Q}}_C^{\ast })}_{i_0{i}_0}{({\mathbf{Q}}_C^{\ast })}_{j_0{j}_0}{({\mathbf{\Psi }}_C^{[s]})}_{i_0{i}_0}\\ \times \frac{I_{G_C^{[s]}}[{\delta }_C,{\mathbf{D}}_C]}{I_{G_C^{\prime }}({\delta }_C,{\mathbf{D}}_C)}\frac{Pr(G_C^{\prime })}{Pr(G_C^{[s]})}\frac{{\sum }_{G_C^{″}\in {\text{nbd}}_{p_C}^{+}(G_C^{[s]})}{(z^{[s]})}^{\mid v(G_C^{″})\mid }}{{\sum }_{G_C^{″}\in {\text{nbd}}_{p_C}^{-}(G_C^{\prime })}{(z^{[s]})}^{\mid v(G_C^{″})\mid }}\\ \times exp\left\{-\frac{1}{2}\left[\langle {\mathbf{K}}_C^{\prime }-{\mathbf{K}}_C^{[s]},{\mathbf{U}}_C^{\ast }+z^{[s]}{\mathbf{D}}_C\rangle -\frac{{({({\mathrm{\Psi }}_C^{\prime })}_{i_0{j}_0}-{({\mathrm{\Psi }}_C^{[s]})}_{i_0{j}_0})}^2}{{\sigma }_{g,C}^2}\right]\right\}.\end{array}$$ (B.3)

Next we assume that $G_C^{\prime }$ is obtained by deleting the edge (i₀, j₀) from $G_C^{[s]}$. We define an upper triangular matrix ${\mathbf{\Psi }}_C^{\prime }$ such that ${({\mathbf{\Psi }}_C^{\prime })}_{ij}={({\mathbf{\Psi }}_C^{[s]})}_{ij}$ for $(i,j)\in v(G_C^{\prime })$. The candidate ${\mathbf{K}}_C^{\prime }$ is obtained from ${\mathbf{\Psi }}_C^{\prime }$ as in Equation (B.2). We make the transition from ( ${\mathbf{K}}_C^{[s]},G_C^{[s]}$) to ( ${\mathbf{K}}_C^{\prime },G_C^{\prime }$) with probability $min\{R_C^{-},1\}$ where

$$\begin{array}{l}{R}_C^{-}={\{{\sigma }_{g,C}\sqrt{2\pi }{({\mathbf{Q}}_C^{\ast })}_{i_0{i}_0}{({\mathbf{Q}}_C^{\ast })}_{j_0{j}_0}{({\mathbf{\Psi }}_C^{[s]})}_{i_0{i}_0}\}}^{-1}\\ \times \frac{I_{G_C^{[s]}}({\delta }_C,{\mathbf{D}}_C)}{I_{G_C^{\prime }}({\delta }_C,{\mathbf{D}}_C)}\frac{Pr(G_C^{\prime })}{Pr(G_C^{[s]})}\frac{{\sum }_{G_C^{″}\in {\text{nbd}}_{p_C}^{-}(G_C^{[s]})}{(z^{[s]})}^{\mid v(G_C^{″})\mid }}{{\sum }_{G_C^{″}\in {\text{nbd}}_{p_C}^{+}(G_C^{\prime })}{(z^{[s]})}^{\mid v(G_C^{″})\mid }}\\ \times exp\left\{-\frac{1}{2}\left[\langle {\mathbf{K}}_C^{\prime }-{\mathbf{K}}_C^{[s]},{\mathbf{U}}_C^{\ast }+z^{[s]}{\mathbf{D}}_C\rangle +\frac{{({({\mathrm{\Psi }}_C^{\prime })}_{i_0{j}_0}-{({\mathrm{\Psi }}_C^{[s]})}_{i_0{j}_0})}^2}{{\sigma }_{g,C}^2}\right]\right\}.\end{array}$$ (B.4)

We denote the updated column precision matrix and graph by ( ${\mathbf{K}}_C^{[s+1/2]},G_C^{[s+1]}$).

Step 4: Resample the column precision matrix

We denote $n_C^{\ast }={np}_R$ and ${\mathbf{U}}_C^{\ast }={\sum }_{j=1}^n{({\mathbf{x}}^{(j)})}^T{\mathbf{K}}_R^{[s+1]}{\mathbf{x}}^{(j)}$. We determine the Cholesky decomposition ${({\mathbf{U}}_C^{\ast }+z^{[s]}{\mathbf{D}}_C)}^{-1}={({\mathbf{Q}}_C^{\ast })}^T{\mathbf{Q}}_C^{\ast }$ after permuting the row and columns of ${\mathbf{U}}_C^{\ast }+z^{[s]}{\mathbf{D}}_C$ according to a random ordering in ${\mathrm{\Upsilon }}_{p_C}^{(1,1)}$. The conditional distribution of ${\mathbf{K}}_C\in {\mathrm{P}}_{G_C^{[s+1]}}$ with (K_C)₁₁ = 1 is G-Wishart ${\text{Wis}}_{G_C^{[s+1]}}(n_C^{\ast }+{\delta }_C,{\mathbf{U}}_C^{\ast }+z^{[s]}{\mathbf{D}}_C)$. We make the transition from ${\mathbf{K}}_C^{[s+1/2]}$ to ${\mathbf{K}}_C^{[s+1]}\in {\mathrm{P}}_{G_C^{[s+1]}}$ using the Metropolis–Hastings updates from Section 2.2. Given the notations we used in that section, we take p = p_C, $\delta =n_C^{\ast }+{\delta }_C,\mathbf{D}={\mathbf{U}}_C^{\ast }+z^{[s]}{\mathbf{D}}_C,\mathbf{Q}={\mathbf{Q}}_C^{\ast }$, and σ_m = σ_m,C. The constraint (K_C)₁₁ = 1 is accommodated as described at the end of Section 2.2.

Step 5: Resample the auxiliary variable

The conditional distribution of z > 0 is

$$\text{Gamma}\left(\frac{p_C({\delta }_C-2)}{2}+\mid v(G_C^{[s+1]})\mid ,\frac{1}{2}\text{tr}({\mathbf{K}}_C^{[s+1]}{\mathbf{D}}_C)\right).$$ (B.5)

Here Gamma(α, β) has density f(x|α, β) ∝ β^αx^α−1 exp(−βx). We sample z^[s+1] from (B.5).