Polarizable Atomic Multipole Solutes in a Generalized Kirkwood Continuum

Abstract

The generalized Born (GB) model of continuum electrostatics is an analytic approximation to the Poisson equation useful for predicting the electrostatic component of the solvation free energy for solutes ranging in size from small organic molecules to large macromolecular complexes. This work presents a new continuum electrostatics model based on Kirkwood’s analytic result for the electrostatic component of the solvation free energy for a solute with arbitrary charge distribution.¹ Unlike GB, which is limited to monopoles, our generalized Kirkwood (GK) model can treat solute electrostatics represented by any combination of permanent and induced atomic multipole moments of arbitrary degree. Here we apply the GK model to the newly developed Atomic Multipole Optimized Energetics for Biomolecular Applications (AMOEBA) force field, which includes permanent atomic multipoles through the quadrupole and treats polarization via induced dipoles. A derivation of the GK gradient is presented, which enables energy minimization or molecular dynamics of an AMOEBA solute within a GK continuum. For a series of 55 proteins, GK electrostatic solvation free energies are compared to the Polarizable Multipole Poisson-Boltzmann (PMPB) model² and yield a mean unsigned relative difference of 0.9%. Additionally, the reaction field of GK compares well to that of the PMPB model, as shown by a mean unsigned relative difference of 2.7% in predicting the total solvated dipole moment for each protein in this test set. The CPU time needed for GK relative to vacuum AMOEBA calculations is approximately a factor of three, making it suitable for applications that require significant sampling of configuration space.

1. INTRODUCTION

The solvent environment influences the structure and behavior of solutes within it. For example, the scaling of the radius of gyration of a polymer with chain length in dilute aqueous solution can be predicted by considering whether solvent molecules prefer interactions amongst themselves to those with the polymer.³ This scaling law serves to emphasize that rigorous results can be obtained without treating the solvent in explicit atomic detail. Here we present an analytic model of the electrostatic interactions between a solute represented by polarizable atomic multipoles and a continuum environment characterized by its permittivity, dispensing with the expense of representing explicit solvent molecules.

Our approach can be traced to work presented by Born in 1920 to describe the electrostatic solvation energy of a charged, spherical ion in terms of macroscopic continuum theory.⁴ In 1934, Kirkwood extended this approach to a spherical particle with arbitrary electrostatic multipole moments with application to the study of zwitterions, which have a large dipole moment.¹ More recently, Kong and Ponder revisited Kirkwood’s theory to allow analytic treatment of off-center point multipoles.⁵ For a single spherical particle in isolation, therefore, the theoretical foundations to enable use of macroscopic continuum theory have already been established.

However, a general analytic solution to the Poisson equation for an arbitrarily spaced collection of spherical dielectric particles embedded in solvent is tenable only via approximations. For example, the generalization of Born’s method to a collection of monopoles began to be considered in the 1990’s by a number of groups including Schaefer et al.^6,7, Hawkins et al.^8,9, Still et al.^10,11, Feig et al.^12,13 and Onufriev et al.^14–18. This generalized Born (GB) approach is intended to approximate the numerical solution of the Poisson equation for realistic molecular geometries and monopole charge distributions.^19–22 Given highly accurate self-energies, GB has been shown to be remarkably quantitative.^{13,14,16,23,24} The goal of the present work is to extend the ideas underlying GB to more accurate charge distributions, specifically to the treatment of polarizable atomic multipoles, which might be termed generalized Kirkwood (GK) by analogy.

In order to further motivate the present work, we recall the electrostatic solvation energy is a key component of an implicit solvent model, which typically also includes apolar contributions due to cavitation and dispersion.^11,25,26 Given a solute potential and implicit solvent, a broad range of physical properties can be predicted, including conformational preferences such as radius of gyration, binding energies and pK_as.²⁴ Recent work by a number of groups to explicitly include higher order permanent moments and polarization within the functional form of empirical force field electrostatics may improve the quality of theoretical predictions based on implicit solvent approaches.^27–32 However, this step forward can only be realized if the improved detail of the molecular mechanics electrostatic model is propagated through to the reaction potential.

For an excellent introduction to the fundamentals of GB theory, including treatment of salt effects, we recommend the review by Bashford and Case.³³ Feig and Brooks present a review of recent improvements in GB methodology as well as novel applications.¹² Assuming this level of familiarity, we immediately outline the key components of GB that need to be further generalized in order to incorporate polarizable atomic multipoles.

1.1 Effective radii and the self-energy

Definition of the “perfect” effective radius a_i for site i under the GB approximation¹⁶ guarantees an exact self-energy. It is based on the following equality

$$a_i=\frac{1}{2}(\frac{1}{{\epsilon }_s}-\frac{1}{{\epsilon }_h})\frac{{q_i}^2}{\mathrm{\Delta }{\mathrm{W}}_{\mathit{\text{self}},i}^{\mathit{\text{Poisson}}}}$$ (1)

where the factor of ½ accounts for the cost of polarizing the continuum, q_i is a partial charge, ε_h is the permittivity of a homogeneous reference state and ε_s is the permittivity of the solvent. The self-energy $\mathrm{\Delta }{\mathrm{W}}_{\mathit{\text{self}},i}^{\mathit{\text{Poisson}}}$ can be determined to high precision numerically. In this manner, the self-energy for each fixed partial charge of a solute is mapped onto the Born equation.⁴ Alternatively, an analytic solution for the self-energy in terms of an energy density is possible after making the Coulomb field approximation

$$\mathrm{\Delta }{\mathrm{W}}_{\mathit{\text{self}},i}^{GB}=\frac{1}{2}(\frac{1}{{\epsilon }_s}-\frac{1}{{\epsilon }_h})\frac{q_i^2}{4\pi }\underset{\mathit{\text{solvent}}}{\int }\frac{1}{r^4}dV$$ (2)

although other methods will be elaborated below. Substituting for $\mathrm{\Delta }{\mathrm{W}}_{\mathit{\text{self}},i}^{\mathit{\text{Poisson}}}$ in Eq. (1) with $\mathrm{\Delta }{\mathrm{W}}_{\mathit{\text{self}},i}^{GB}$ from Eq. (2) and changing the limits of integration for convenience it can be shown that each effective Born radius is³³

$$a_i={(\frac{1}{r_i}-\frac{1}{4\pi }\underset{\mathit{\text{solute}},r>r_i}{\int }\frac{1}{r^4}dV)}^{-1}$$ (3)

where the integration over the solute does not include the region within the atomic radius r_i. A number of analytic methods have been developed for determining this integral, notably the pairwise descreening method of Hawkins, Cramer and Truhlar that we will refer to as HCT^8,9, a method by Qiu et al. that assumes constant energy density within each descreening atom¹¹, and more recently a parameter free approach by Gallicchio et al.³⁴ Although effective radii determine the reaction potential at atomic centers, we note that the electrostatic solvation energy of a polarizable atomic multipole also depends on its higher order gradients.

After computing effective radii, the total self-energy of a solute within GB is

$$\mathrm{\Delta }{\mathrm{W}}_{\mathit{\text{self}}}^{GB}=\frac{1}{2}(\frac{1}{{\epsilon }_s}-\frac{1}{{\epsilon }_h})\sum _i\frac{q_i^2}{a_i}.$$ (4)

For permanent multipoles, the self-energy of higher order components must be considered. Furthermore, if the solute is polarizable, self-consistent induced moments elicit a reaction potential that leads to an additional contribution to the electrostatic solvation free energy. We will avoid decomposing the polarization energy into self-energy and cross-term contributions, since it is inherently many-body and therefore any partitioning is somewhat artificial.

1.2 Cross-term energy

An analytic continuum electrostatics model designed to match results from the Poisson equation must also include an estimate of the pairwise cross-term energy between all multipole pairs. Given effective radii, the GB cross-term energy for fixed partial charges is given by

$$\mathrm{\Delta }{\mathrm{W}}_{\mathit{\text{cross}}}^{GB}=\frac{1}{2}(\frac{1}{{\epsilon }_s}-\frac{1}{{\epsilon }_h})\sum _i\sum _{j\ne i}\frac{q_i{q}_j}{f}$$ (5)

where the empirical generalizing function f usually takes the form¹⁰

$$f=\sqrt{r_{ij}+a_i{a}_j{e}^{-r_{ij}/c_f{a}_i{a}_j}}$$ (6)

where r_ij is the distance between sites i and j and the tuning parameter c_f is chosen in the range 2–8. As r_ij goes to zero, the Born formula is recovered, such that the self-energy is simply a special case of the cross-term energy. Derivation of a general form for the pairwise cross-term energy between two multipole components will be presented, which is similar in spirit to GB in that the limiting cases of superimposition and wide separation for a pair of solvated multipoles are reproduced. The accuracy of the proposed interpolation at intermediate separations will be investigated via a series of tests ranging from simple systems consisting of only two sites up to the electrostatic solvation energy and dipole moment of proteins.

Our tests of GK rely on the Polarizable Multipole Poisson-Boltzmann (PMPB) model² as a standard of accuracy, which has been implemented for solutes described by the Atomic Multipole Optimized Energetics for Biomolecular Applications (AMOEBA) force field.^35–37 In our previous work, excellent agreement was seen in the electrostatic response of proteins solvated by the PMPB continuum when compared to ensemble average explicit water simulations, indicating that at the length scale of proteins treatment of solvent as a continuum is valid. As an alternative to numerical PMPB electrostatics, the analytic GK formulation for the AMOEBA force field is orders of magnitude more efficient.

The description of GK will be subdivided into four sections. First, determination of the self-energy for a permanent multipole will be considered. Second, we will propose a functional form for the cross-term energy between arbitrary degree multipole moments. Third, given the underlying GK theory, we continue on to the derivation of the electrostatic solvation energy and gradient in the specific case of solutes described by the AMOEBA force field. Finally, we apply the GK continuum model to a series of proteins and compare their electrostatic solvation free energy and total dipole moment to analogous calculations with the PMPB continuum.

2 MULTIPOLE SELF-ENERGY

We begin by reiterating that the self-energy of a multipole depends on not only the reaction potential at atomic centers, but on the reaction field, the reaction field gradient, and so on. Unlike GB, the perfect effective radius is not enough information to guarantee the higher order features of the reaction potential are correct, unless the multipole site happens to be at the center of a spherical cavity. Two methods have been investigated to describe the self-energy of a permanent atomic multipole. The first method reduces to the Coulomb-field approximation (CFA) for a monopole and requires knowledge of the analytic solution for the field in solvent based on a multipole at the center of a spherical dielectric cavity. We term this the solvent field approximation (SFA), as it is consistent with the CFA, but requires more information.¹ A second approach makes use of Grycuk’s method for determining effective radii based on the reaction potential of an off-center charge within a spherical solute.³⁸ We refer to this approach as the reaction potential approximation (RPA).

Before detailing the SFA and RPA methods, a brief introduction to the electrostatic energy of a dielectric media will be given. The work required to assemble a fixed charge distribution in a linearly polarizable medium^33,39,40 can be formulated by a volume integral of the product of the charge density ρ(r) with the potential ϕ(r) or by the scalar product of the electric field E with the electric displacement D

$$W=\frac{1}{2}\underset{V}{\int }\rho (r)\varphi (r)dV=\frac{1}{8\pi }\underset{V}{\int }\mathbf{E}·\mathbf{D}dV$$ (7)

where the displacement is proportional to the electric field in regions of constant permittivity ε

$$\mathbf{D}=\epsilon \mathbf{E}.$$ (8)

For our purposes, the system of interest is composed of a solute with a different permittivity than the solvent. The electrostatic free energy of this system relative to a homogeneous reference state is^33,39

$$\mathrm{\Delta }G=\frac{1}{8\pi }\underset{V}{\int }(\mathbf{E}·\mathbf{D}-{\mathbf{E}}_h·{\mathbf{D}}_h)dV$$ (9)

where in the homogeneous case the field is Coulombic and can be defined relative to the vacuum field as E_h = E_vac/ε_h using the homogeneous permittivity ε_h. The homogeneous displacement is simply D_h = E_vac. A less intuitive, but equivalent definition of the electrostatic free energy given in Eq. (9) is^33,39

$$\mathrm{\Delta }G=\frac{1}{8\pi }\underset{V}{\int }(\mathbf{E}·{\mathbf{D}}_h-\mathbf{D}·{\mathbf{E}}_h)dV.$$ (10)

This expression can be subdivided into integrals over the solute and solvent volumes as

$$\mathrm{\Delta }G=\frac{1}{8\pi }\underset{\mathit{\text{solute}}}{\int }(\mathbf{E}·{\mathbf{D}}_h-\mathbf{D}·{\mathbf{E}}_h)dV+\frac{1}{8\pi }\underset{\mathit{\text{solvent}}}{\int }(\mathbf{E}·{\mathbf{D}}_h-\mathbf{D}·{\mathbf{E}}_h)dV.$$ (11)

In both the homogeneous and mixed permittivity states the solute retains the homogeneous permittivity. By using the relationships for the homogeneous field and displacement described above it can be seen that the integral over the solute vanishes

$$\mathrm{\Delta }G=\frac{1}{8\pi }\underset{\mathit{\text{solute}}}{\int }(\mathbf{E}·{\mathbf{E}}_{\mathit{\text{vac}}}-{\epsilon }_h\mathbf{E}·{\mathbf{E}}_{\mathit{\text{vac}}}/{\epsilon }_h)dV+\frac{1}{8\pi }\underset{\mathit{\text{solvent}}}{\int }({\mathbf{E}}_s·{\mathbf{E}}_{\mathit{\text{vac}}}-{\epsilon }_s{\mathbf{E}}_s·{\mathbf{E}}_{\mathit{\text{vac}}}/{\epsilon }_h)dV$$ (12)

to leave only the integral over the solvent

$$\mathrm{\Delta }G=\frac{1}{8\pi }(1-\frac{{\epsilon }_s}{{\epsilon }_h})\underset{\mathit{\text{solvent}}}{\int }({\mathbf{E}}_s·{\mathbf{E}}_{\mathit{\text{vac}}})dV.$$ (13)

Having made no assumptions to this point, the remaining challenge can be simplified to defining the field within the solvent E_s for the mixed permittivity case. This is the starting point for the SFA. In general, the solvent field does not have an exact analytic form for a union of spheres. However, many molecular systems of interest are globular, and therefore an approximation based on the assumption of a spherical solute is not only qualitatively reasonable, but in many cases quantitative.

2.1 Solvent field approximation

The SFA is similar to the CFA, but is based on evaluating Eq. (13) using Kirkwood’s solution for the field outside a spherical solute with a central multipole moment^1,41

$${\mathbf{E}}_s=\sum _{l=0}^{\infty }\frac{(2l+1){\epsilon }_h}{(l+1){\epsilon }_s+l{\epsilon }_h}{\mathbf{E}}_{\mathit{\text{vac}}}^{(l)}$$ (14)

where ${\mathbf{E}}_{\mathit{\text{vac}}}^{(l)}$ is the vacuum field due to all multipole moments of degree l, defined using either irregular spherical harmonics or Cartesian tensors. Throughout the current work we neglect salt effects, although their addition to a future GK formulation is straightforward. This definition of the self-energy is equivalent to the CFA for a monopole and becomes approximate for off-center multipole sites or for non-spherical solute geometries.

Under the SFA, the self-energy of a permanent multipole site i is given by

$$\mathrm{\Delta }{G}_i^{SFA}=\frac{1}{8\pi }(1-\frac{{\epsilon }_s}{{\epsilon }_h})\underset{\mathit{\text{solvent}}}{\int }{\mathbf{E}}_{\mathit{\text{vac}},i}·\sum _{l=0}^{\infty }\left(\frac{(2l+1){\epsilon }_h}{(l+1){\epsilon }_s+l{\epsilon }_h}{\mathbf{E}}_{\mathit{\text{vac}},i}^{(l)}\right)dV.$$ (15)

It is possible to invert the integration domain by adding and subtracting an integral over the solute region outside the radius R_i of atom i to Eq. (15) giving

$$\mathrm{\Delta }{G}_i^{SFA}=\frac{1}{8\pi }(1-\frac{{\epsilon }_s}{{\epsilon }_h})\underset{r>R_i}{\int }{\mathbf{E}}_{\mathit{\text{vac}},i}·\sum _{l=0}^{\infty }\left(\frac{(2l+1){\epsilon }_h}{(l+1){\epsilon }_s+l{\epsilon }_h}{\mathbf{E}}_{\mathit{\text{vac}},i}^{(l)}\right)dV-\frac{1}{8\pi }(1-\frac{{\epsilon }_s}{{\epsilon }_h})\underset{\underset{r>R_i}{\mathit{\text{solute}},}}{\int }{\mathbf{E}}_{\mathit{\text{vac}},i}·\sum _{l=0}^{\infty }\left(\frac{(2l+1){\epsilon }_h}{(l+1){\epsilon }_s+l{\epsilon }_h}{\mathbf{E}}_{\mathit{\text{vac}},i}^{(l)}\right)dV.$$ (16)

The first integral is the solvation energy of a lone multipole $\mathrm{\Delta }{G}_i^M$ and the second represents the effect of descreening sites. Substituting $\mathrm{\Delta }{G}_i^M$ into Eq. (16) gives

$$\mathrm{\Delta }{G}_i^{SFA}=\mathrm{\Delta }{G}_i^M-\frac{1}{8\pi }(1-\frac{{\epsilon }_s}{{\epsilon }_h})\underset{\underset{r>R_i}{\mathit{\text{solute}},}}{\int }{\mathbf{E}}_{\mathit{\text{vac}},i}·\sum _{l=0}^{\infty }\left(\frac{(2l+1){\epsilon }_h}{(l+1){\epsilon }_s+l{\epsilon }_h}{\mathbf{E}}_{\mathit{\text{vac}},i}^{(l)}\right)dV$$ (17)

where

$$\mathrm{\Delta }{G}_i^M=\frac{1}{2}[c_0\frac{q_i^2}{a_i}+c_1\frac{{\mu }_{i,\alpha }^2}{a_i^3}+c_2\frac{2}{3}\frac{{\mathrm{\Theta }}_{i,\alpha \beta }^2}{a_i^5}]$$ (18)

and

$$c_l=\frac{1}{{\epsilon }_h}\frac{(l+1)({\epsilon }_h-{\epsilon }_s)}{(l+1){\epsilon }_s+l{\epsilon }_h}.$$ (19)

In Eq. (18) we have assumed the Einstein convention for summation over Greek subscripts α and β which can take the value x, y, or z. The descreening integral in Eq. (17), which we will refer to as I_i, can be decomposed into a sum of pairwise integrals I_ij^8,9

$$I_i(r_{ij},R_i,R_j)=\sum _{j\ne i}\int \underset{0}{\overset{{\xi }_{ij}}{\int }}\underset{0}{\overset{2\pi }{\int }}{\mathbf{E}}_{\mathit{\text{vac}},i}·\sum _{l=0}^{\infty }\left(\frac{(2l+1){\epsilon }_h}{(l+1){\epsilon }_s+l{\epsilon }_h}{\mathbf{E}}_{\mathit{\text{vac}},i}^{(l)}\right)r^2\text{ sin }\theta d\varphi d\theta \mathit{\text{dr}}=\sum _{j\ne i}{I}_{ij}(r_{ij},R_i,R_j)$$ (20)

where ξ_ij is the angle formed between the pairwise axis and any ray that begins at the center of atom i and passes through the circle of intersection between the integration shell and atom j

$${\xi }_{ij}={\text{cos}}^{-1}\left(\frac{r_{ij}^2-R_j^2+r^2}{2r_{ij}r}\right)$$ (21)

where r_ij is the distance between atoms i and j, R_j is the radius of atom j and r is the radial integration variable. The integration limits for the radial coordinate depend on what extent atoms i and j intersect, and therefore the solution to Eq. (20) is presented as an indefinite integral that is to be evaluated at limits described below. Typically the radius of the descreening atom is scaled down to prevent over counting due to atomic overlap, although parameter free approaches are being explored.³⁴ Specifically, R_j is replaced with sR_j where the HCT scale factor s is a parameter between 0 and 1 fit to reproduce PMPB results (see section 2.3 below).

Unlike the field due to a partial charge, the field due to a multipole of arbitrary order has an angular dependence. Our approach has been to represent the field using a spherical harmonic basis, rather than Cartesian tensors, to determine the analytic solution to Eq. (20) through quadrupole order. Additionally, it is assumed that the positive z-axis of the multipole frame is directed towards the center of the descreening atom. This imposes symmetry that greatly reduces the number of non-vanishing terms in the solution, but requires rotation of multipole moments for each pairwise descreening interaction.

A complex definition of spherical harmonics is commonly used in the formulation of quantum mechanics, however this work uses the following real form

$$Y_l^{(m)}(\theta ,\varphi )=\{\begin{array}{cc}{(-1)}^m\sqrt{2}\sqrt{\frac{(l-m)!}{(l+m)!}}{P}_l^{(m)}(\text{cos }\theta )\text{cos }m\varphi \hfill & \hfill m>0\hfill \\ \hfill \sqrt{\frac{(l-m)!}{(l+m)!}}{P}_l^{(m)}(\text{cos }\theta )\hfill & \hfill m=0\hfill \\ {(-1)}^{|m|}\sqrt{2}\sqrt{\frac{(l-|m|)!}{(l+|m|)!}}{P}_l^{(|m|)}(\text{cos }\theta )\text{sin}|m|\varphi \hfill & \hfill m<0\hfill \end{array}$$ (22)

where $Y_l^{(m)}(\theta ,\varphi )$ is of degree l ≥ 0 and order |m| ≤ l, $P_l^{(m)}$ are the associated Legendre polynomials, the polar angle ranges from 0 ≤ θ ≤ π and the azimuth ranges from 0 ≤ φ ≤ 2π. We chose to use the Racah normalization, which has the property that $Y_l^{(0)}(0,0)=1$. In combination with our choice of phase factors, this ensures formulas for the conversion between Cartesian multipole moments and those consistent with this definition of real spherical harmonics are identical to the conversions commonly used for complex spherical harmonics. The conversion formulas through quadrupole degree are given in Table A-1 of the Supporting Information.⁴²

The potential due to a unit magnitude multipole moment ${\mathrm{\Phi }}_l^{(m)}(r,\theta ,\varphi )$ is obtained by multiplication of the real spherical harmonics by a radial factor of 1/r^l+1 to give

$${\mathrm{\Phi }}_l^{(m)}(r,\theta ,\varphi )=\frac{Y_l^{(m)}(\theta ,\varphi )}{r^{l+1}}$$ (23)

and are listed in Table A-2 through quadrupole order. The unit field can then be calculated as the negative gradient of the unit potential

$${\mathbf{E}}_l^{(m)}=-\nabla {\mathrm{\Phi }}_l^{(m)}(r,\theta ,\varphi )=-\frac{\partial {\mathrm{\Phi }}_l^{(m)}(r,\theta ,\varphi )}{\partial r}\hat{\mathbf{r}}-\frac{1}{r}\frac{\partial {\mathrm{\Phi }}_l^{(m)}(r,\theta ,\varphi )}{\partial \theta }\hat{\mathit{\theta }}-\frac{1}{r\text{ sin }\theta }\frac{\partial {\mathrm{\Phi }}_l^{(m)}(r,\theta ,\varphi )}{\partial \varphi }\hat{\mathit{\varphi }}.$$ (24)

The field for 9 multipole components through degree 2, which are listed in Table A-3 of the Supporting Information, lead to 36 scalar products that must be integrated via Eq. (20) to determine the descreening energy due to atom j. However, due to the symmetry of the integration domain only 14 scalar products lead to non-zero integrals, and these are listed in Table A-4. The integration results are given in Table 1, showing 11 unique terms and 3 duplicates. Schaeffer et al. originally presented the same result for a monopole^6,7, and the higher order formulas are presented here for the first time. If the descreening angle ξ_ij is π as a result of atom j completely engulfing atom i, then the indefinite integrals simplify to those given in Table 2. This situation can occur for hydrogen atoms bonded to a heavy atom, for example, or in more artificial structures where one still wishes to have a continuous potential.

Table 1.

Indefinite integrals for pairwise descreening of multipoles through quadrupole

(l, m)1	(l, m)2	D(l, m)i, (l, m)i (rij, Rj)
(0, 0)	(0, 0)	$-(2\text{ ln}(r)r^2+4r_{ij}r-r_{ij}^2+R_j^2)/16r_{ij}{r}^2$
	(1, 0)	$-(4r^4\text{ ln}(r)+4r_{ij}^2{r}^2+4r^2{R}_j^2-r_{ij}^4+2r_{ij}^2{R}_j^2-R_j^4)/64r^4{r}_{ij}^2$
	(2, 0)	$-(12r^6\text{ ln}(r)+6r_{ij}^2{r}^4+18r^4{R}_j^2+3r^2{r}_{ij}^4+6r^2{r}_{ij}^2{R}_j^2-9r^2{R}_j^4-2r_{ij}^6+6r_{ij}^4{R}_j^2-6r_{ij}^2{R}_j^4+2R_j^6)/256r_{ij}^3{r}^6$
(1, 0)	(1, 0)	$-(12r^6\text{ ln}(r)-42r_{ij}^2{r}^4+18r^4{R}_j^2+64r^3{r}_{ij}^3-21r^2{r}_{ij}^4+30r^2{r}_{ij}^2{R}_j^2-9r^2{R}_j^4-2r_{ij}^6+6r_{ij}^4{R}_j^2-6r_{ij}^2{R}_j^4+2R_j^6)/384r^6{r}_{ij}^3$
	(2, 0)	$-(24r^8\text{ ln}(r)-48r^6{r}_{ij}^2+48r^6{R}_j^2+60r_{ij}^4{r}^4+72r_{ij}^2{r}^4{R}_j^2-36r^4{R}_j^4-16r^2{r}_{ij}^6+48r^2{r}_{ij}^4{R}_j^2-48r^2{r}_{ij}^2{R}_j^4+16r^2{R}_j^6-3r_{ij}^8+12r_{ij}^6{R}_j^2-18r_{ij}^4{R}_j^4+12r_{ij}^2{R}_j^6-3R_j^8)/1024r^8{r}_{ij}^4$
(1, 1) (1, −1)	(1, 1) (1, −1)	$(12r^6\text{ ln}(r)+102r_{ij}^2{r}^4+18r^4{R}_j^2-128r^3{r}_{ij}^3+51r^2{r}_{ij}^4-42r^2{r}_{ij}^2{R}_j^2-9r^2{R}_j^4-2r_{ij}^6+6r_{ij}^4{R}_j^2-6r_{ij}^2{R}_j^4+2R_j^6)/768r^6{r}_{ij}^3$
	(2, 1) (2, −1)	$\sqrt{3}(24r^8\text{ ln}(r)+96r^6{r}_{ij}^2+48r^6{R}_j^2-84r_{ij}^4{r}^4-72r_{ij}^2{r}^4{R}_j^2-36r^4{R}_j^4+32r^2{r}_{ij}^6-48r^2{r}_{ij}^4{R}_j^2+16r^2{R}_j^6-3r_{ij}^8+12r_{ij}^6{R}_j^2-18r_{ij}^4{R}_j^4+12r_{ij}^2{R}_j^6-3R_j^8)/3072r^8{r}_{ij}^4$
(2, 0)	(2, 0)	$-3(120r^{10}\text{ ln}(r)-140r^8{r}_{ij}^2+300r^8{R}_j^2-540r^6{r}_{ij}^4+360r^6{r}_{ij}^2{R}_j^2-300r^6{R}_j^4+1024r^5{r}_{ij}^5-360r^4{r}_{ij}^6+600r^4{r}_{ij}^4{R}_j^2-440r^4{r}_{jj}^2{R}_j^4+200r^4{R}_j^6-35r^2{r}_{ij}^8+180r^2{r}_{ij}^6{R}_j^2-330r^2{r}_{ij}^4{R}_j^4+260r^2{r}_{ij}^2{R}_j^6-75r^2{R}_j^8-12r_{ij}^{10}+60r_{ij}^8{R}_j^2-120r_{ij}^6{R}_j^4+120r_{ij}^4{R}_j^6-60r_{ij}^2{R}_j^8+12R_j^{10})/20480r^{10}{r}_{ij}^5$
(2, 1) (2, −1)	(2, 1) (2, −1)	$(120r^{10}\text{ ln}(r)+180r^8{r}_{ij}^2+300r^8{R}_j^2+900r^6{r}_{ij}^4-120r^6{r}_{ij}^2{R}_j^2-300r^6{R}_j^4-1536r^5{r}_{ij}^5+600r^4{r}_{ij}^6-680r^4{r}_{ij}^4{R}_j^2-120r^4{r}_{ij}^2{R}_j^4+200r^4{R}_j^6+45r^2{r}_{ij}^8-60r^2{r}_{ij}^6{R}_j^2-90r^2{r}_{ij}^4{R}_j^4+180r^2{r}_{ij}^2{R}_j^6-75r^2{R}_j^8-12r_{ij}^{10}+60r_{ij}^8{R}_j^2-120r_{ij}^6{R}_j^4+120r_{ij}^4{R}_j^6-60r_{ij}^2{R}_j^8+12R_j^{10})/10240r^{10}{r}_{ij}^5$
(2, 2) (2, −2)	(2, 2) (2, −1)	$-(120r^{10}\text{ ln}(r)+1140r^8{r}_{ij}^2+300r^8{R}_j^2-4380r^6{r}_{ij}^4-1560r^6{r}_{ij}^2{R}_j^2-300r^6{R}_j^4+6144r^5{r}_{ij}^5-2920r^4{r}_{ij}^6+1880r^4{r}_{ij}^4{R}_j^2+840r^4{r}_{ij}^2{R}_j^4+200r^4{R}_j^6+285r^2{r}_{ij}^8-780r^2{r}_{ij}^6{R}_j^2+630r^2{r}_{ij}^4{R}_j^4-60r^2{r}_{ij}^2{R}_j^6-75r^2{R}_j^8-12r_{ij}^{10}+60r_{ij}^8{R}_j^2-120r_{ij}^6{R}_j^4+120r_{ij}^4{R}_j^6-60r_{ij}^2{R}_j^8+12R_j^{10})/40960r^{10}{r}_{ij}^5$

Table 2.

Indefinite integrals for pairwise descreening of multipoles through quadrupole when ξ_ij = π.

li	Dli
0	$-\frac{1}{2r}$
1	$-\frac{1}{3r^3}$
2	$-\frac{3}{10r^5}$

We note that after performing the integral no angular dependence remains. Therefore, although the derivation is based on spherical harmonics, our solution is equally useful for Cartesian tensors by using the conversion formulas in Table A-1. We can now define the pairwise descreening integral for a permanent atomic multipole at site i being descreened by site j under the SFA as

$$I_{ij}(r_{ij},R_i,R_j)=\sum _{l_i=0}^n\frac{(2l_i+1){\epsilon }_h}{(l_i+1){\epsilon }_s+l_i{\epsilon }_h}\sum _{m_i=-l_i}^{l_i}{Q}_{l_i}^{(m_i)}\sum _{l_j=0}^n\sum _{m_j=-l_j}^{l_i}{Q}_{l_j}^{(m_j)}{D}_{{(l,m)}_j,{(l,m)}_j}(r_{ij},R_i,R_j)$$ (25)

where $Q_{l_i}^{(m_i)}$ is the magnitude of a spherical harmonic of site i, $Q_{l_j}^{(m_j)}$ is the magnitude of a spherical harmonic of site j and D_{(l, m)i, (l, m)j} (r_ij, R_i, R_j) is given by

$$D_{{(l,m)}_i,{(l,m)}_j}(r_{ij},R_i,R_j)=\{\begin{array}{c}{\delta }_{(l_1,l_2)}{\delta }_{(m_1,m_2)}{D}_{l_i}{|}_{r=R_i}^{r=R_j-r_{ij}}+D_{{(l,m)}_i,{(l,m)}_j}(r_{ij},R_j){|}_{r=R_j-r_{ij}}^{r=r_{ij}+R_j}\hspace{1em}{R}_j-r_{ij}>R_i\hfill \\ \hfill \text{Case }1:\text{Engulfment by the descreener}\hfill \\ D_{{(l,m)}_i,{(l,m)}_j}(r_{ij},R_j){|}_{r=R_i}^{r=r_{ij}+R_j}\hspace{1em}\begin{array}{c}{R}_j-r_{ij}<=R_i\hfill \\ r_{ij}<R_i+R_j\hfill \end{array}.\hfill \\ \hfill \text{Case }2:\text{Partial overlap}\hfill \\ D_{{(l,m)}_i,{(l,m)}_j}(r_{ij},R_j){|}_{r=r_{ij}-R_j}^{r=r_{ij}+R_j}\hspace{1em}{r}_{ij}>R_i+R_j\hfill \\ \hfill \text{Case }3:\text{No overlap}\hfill \end{array}$$ (26)

Radial limits are detailed for three cases including engulfment by the descreener, partial overlap and no overlap. These limits are applied in conjunction with the indefinite integrals D_{(l, m)i, (l, m)j} (r_ij, R_j) and D_li listed in Table 1 and Table 2, respectively. We note that the Kronecker delta functions δ specify that the engulfment integrals between orthogonal spherical harmonics vanish. In our implementation of Eq. (25), the magnitudes of the spherical harmonic moments are found via conversion from AMOEBA traceless Cartesian multipoles.

2.2 Reaction potential approximation

An alternative to the CFA for determining effective radii based on the analytic solution for the reaction potential of an off-center charge within a spherical dielectric cavity^1,43 has been proposed by Grycuk³⁸. We briefly outline this RPA method and its application to the self-energy of a permanent multipole.

The reaction potential at r due to an off-center charge at r₀ inside a spherical dielectric cavity of permittivity ε_h surrounded by solvent with permittivity ε_s is given by

$$\mathrm{\Phi }(\mathbf{r})=\frac{q}{a{\epsilon }_h}\sum _{l=0}^{\infty }\frac{(l+1)({\epsilon }_h-{\epsilon }_s)}{(l+1){\epsilon }_s+l{\epsilon }_h}{\left(\frac{r{r}_0}{a^2}\right)}^l{P}_l(\text{cos }\theta )$$ (27)

where a is the cavity radius, q is the magnitude of the charge and P_l is the Legendre polynomial of degree l whose argument is the cosine of the angle θ between r and r₀.^1,43 The self-energy of a charge based on Eq. (27) is

$$W(d)=\frac{1}{2}\frac{q^2}{a{\epsilon }_h}\sum _{l=0}^{\infty }\frac{(l+1)({\epsilon }_h-{\epsilon }_s)}{(l+1){\epsilon }_s+l{\epsilon }_h}{\left(\frac{d^2}{a^2}\right)}^l{P}_l(1)$$ (28)

where d is used to specify the distance between the multipole site and the center of the sphere. For d=0, all asymmetric self-interactions vanish, for example the charge with a dipole component, but for off-center multipole sites these interactions are generally nonzero.⁵ Noting that P_l (1) = 1 for all l, the summation in Eq. (28) can be reduced to a closed form if the factor (l+1) can be canceled by setting lε_h in the denominator to (l+1)ε_h or to 0, giving quantities that are more positive W₊ (d) or more negative W₋ (d) than the true self-energy, respectively

$$W_{+}(d)=\frac{1}{2}\frac{({\epsilon }_h-{\epsilon }_s)}{{\epsilon }_s{\epsilon }_h+{{\epsilon }_h}^2}\frac{q^2}{a}\sum _{l=0}^{\infty }{\left(\frac{d^2}{a^2}\right)}^l=\frac{1}{2}\frac{({\epsilon }_h-{\epsilon }_s)}{({\epsilon }_s{\epsilon }_h+{{\epsilon }_h}^2)}{q}^2\frac{a}{(a^2-d^2)}.$$ (29)

$$W_{-}(d)=\frac{1}{2}(\frac{1}{{\epsilon }_s}-\frac{1}{{\epsilon }_h})\frac{q^2}{a}\sum _{l=0}^{\infty }{\left(\frac{d^2}{a^2}\right)}^l=\frac{1}{2}(\frac{1}{{\epsilon }_s}-\frac{1}{{\epsilon }_h})q^2\frac{a}{(a^2-d^2)}$$

Both the upper and lower bound approach the true self-energy if ε_s □ ε_h allowing the simpler form to be used as an approximation

$$W(d)\approx W\_(d)$$ (30)

As shown by Grycuk, it is possible to calculate the factor a_r = a/(a² − d²), which is equivalent to the inverse of an effective radius, as

$$a_r={\left(\frac{3}{4\pi }\underset{ex}{\int }\frac{1}{r^{\prime 6}}dV\right)}^{1/3}.$$ (31)

This expression can be motivated by the analytic solution for a spherical geometry

$$\underset{ex}{\int }\frac{1}{r^{\prime 6}}dV=2\pi \underset{a}{\overset{\infty }{\int }}\underset{0}{\overset{\pi }{\int }}\frac{r^2\text{ sin }\theta }{{(r^2+d^2-2dr\text{ cos }\theta )}^3}d\theta dr=\frac{4\pi }{3}\frac{a^3}{{(a^2-d^2)}^3}$$ (32)

As d approaches zero, the multipole site approaches the center of the dielectric sphere such that a_r equals the radius of the sphere a. In practice this integral is evaluated using the pairwise descreening approach described in the previous section for the SFA and elsewhere.^8,9,38 After determining effective radii, the self-energy for each permanent atomic multipole under the RPA is evaluated via Eq. (18).

2.3 Self-energy accuracy

We now demonstrate that for a series of proteins the RPA is superior to the SFA, which is consistent with findings for fixed partial charge models.^38,44 The perfect self-energy and perfect effective radii for all permanent atomic multipole sites in five proteins structures retrieved from the Protein Databank⁴⁵, including 1CRN⁴⁶, 1ENH⁴⁷, 1FSV⁴⁸, 1PGB⁴⁹ and 1VII⁵⁰, were determined using the PMPB model.² The grid size for all calculations was 257×257×257 using a grid spacing of 0.31 Å to give approximately 10 Å of continuum solvent between the low dielectric boundary and the grid boundary. The Bondi radii set (H 1.2, C 1.7, N 1.55, O 1.52, S 1.8) was used to define a step-function solute-solvent boundary with the solute dielectric set to unity and that of the solvent to 78.3.⁵¹ Multiple Debye-Hückel boundary conditions were used to complete the definition of the Dirichlet problem. We also tried larger grids, up to 353×353×353, and therefore smaller grid spacing, which leads to the PMPB electrostatic solvation energy increasing by less than 2%. We opted for efficiency, since the important conclusion of this section, that the RPA is superior to the SFA, is not altered.

The SFA was fit using nonlinear optimization to determine one HCT scale factor per atomic number that minimized the RMS percent error in the permanent atomic multipole self-energies against numerical PMPB results for 3,032 data points. As discussed previously, these HCT parameters scale down the radius of the descreening atom to prevent over counting due to atomic overlap. This lead to a mean unsigned relative difference (MURD) between the perfect self-energy for each multipole site and the SFA self-energy of 5.5%. However, using only a single scale factor (0.568), rather than one per atomic number, increased the MURD by just 0.4 to 5.9%.

Similarly, the RPA was fit using nonlinear optimization to determine a second set of scale factors to minimize the RMS percent difference between analytic effective radii and perfect effective radii. The achieved MURD in the effective radii was 1.1%. Alternatively, using a single scale factor (0.690) increased the MUPD by only 0.2% to 1.3%. Therefore, given the negligible improvements of using one HCT parameter per atomic number, we prefer implementations of the SFA and RPA that are each based on a single parameter.

The total analytic self-energy for each protein is compared to the total computed by summing the numerical permanent multipole self-energies as shown in Table 3. Fitting of a single HCT parameter for each method as described above eliminated the systematic error for both the SFA and RPA. However, the mean unsigned percent difference of the RPA (0.5) is smaller than that of the SFA (0.8). Considering that the RPA is more efficient and more accurate than the SFA, it is our preferred method to compute effective radii and permanent multipole self-energies.

Table 3.

Shown is a comparison of the performance of the SFA and RPA in determining the perfect self-energy (kcal/mole) for a series of five folded proteins. Optimization of a single HCT scale factor for each method removes systematic error as shown by the mean signed percent differences. However, the mean RPA unsigned percent difference of 0.5 is smaller than that of the SFA.

	Self-Energy			Signed % Difference		Unsigned % Difference
	PMPB	SFA	RPA	SFA	RPA	SFA	RPA
CRN	−8141	−8191	−8196	−0.6	−0.7	0.6	0.7
ENH	−11919	−11852	−11878	0.6	0.3	0.6	0.3
FSV	−6254	−6341	−6287	−1.4	−0.5	1.4	0.5
PGB	−11794	−11743	−11803	0.4	−0.1	0.4	0.1
VII	−7206	−7132	−7133	1.0	1.0	1.0	1.0
Mean				0.0	0.0	0.8	0.5

3 MULTIPOLE CROSS-TERM ENERGY

There are two concepts needed to extend the GB cross-term to the interaction between two arbitrary multipole components. First, we describe the simplest possible definition for the reaction potential of any multipole component in the presence of a second multipole site, where an effective radius characterizes each site. Second, using this auxiliary definition of the reaction potential for each site, we formulate the cross-term energy in a consistent fashion. The electrostatic solvation free energy for the interaction between multipole components will be reproduced in the limiting cases of superimposition and wide separation.

3.1 Generalized Kirkwood auxiliary reaction potential

The generalized Kirkwood auxiliary reaction potential is a building block for defining the interaction energy and its gradients for any pair of multipole components. It is motivated by noting that the only difference between the analytic solution for the reaction potential inside and outside of a spherical solute with central multipole is exchange of the solute radius a in the former case with separation distance r_ij in the latter, where r_ij = (x_j − x_i, y_j − y_i, z_j − z_i).^1,41 For example, substitution for f in Eq. (33) below by a or r_ij gives the analytic formulas for the reaction potential inside and outside of the dielectric boundary, respectively.

Rather than using radial factors of $1/r_{ij}^{l+1}$ as was done earlier in defining the unit vacuum potential in terms of real spherical harmonics, the factor $r_{ij}^l/f^{2l+1}$ is used to define the unit GK auxiliary reaction potential $A_l^{(m)}$ for a multipole component of degree l and order m,

$$A_l^{(m)}({\mathbf{r}}_{ij},a_i,a_j,\theta ,\varphi )=c_l\frac{r_{ij}^l}{f^{2l+1}}{Y}_l^{(m)}(\theta ,\varphi )$$ (33)

where f is the generalizing function defined in Eq. (6) and c_l is a function of the permittivity inside and outside the solute defined in Eq. (19). We note that for $r_{ij}^2\gg a_i{a}_j,r_{ij}^l/f^{2l+1}$ approaches $1/r_{ij}^{l+1}$ to give the reaction potential in solvent. When r_ij = 0 and therefore a_i = a_j = a, then $r_{ij}^l/f^{2l+1}$ simplifies to $r_{ij}^l/a^{2l+1}$ to give the reaction potential at the center of the two concentric atoms. In this case the reaction potential is nonzero only for the monopole.

A definition in terms of Cartesian tensors is possible by first taking successive gradients of 1/r_ij and then substituting for factors of r_ij in the denominator with factors of f. For example, neglecting the ij subscript, the vacuum tensors are⁴²

$$T=\frac{1}{r}$$

$$T_{\alpha }={\nabla }_{\alpha }\frac{1}{r}=-\frac{r_{\alpha }}{r^3}$$

$$T_{\alpha \beta }={\nabla }_{\alpha }{\nabla }_{\beta }\frac{1}{r}=\frac{3r_{\alpha }{r}_{\beta }}{r^5}-\frac{{\delta }_{\alpha \beta }}{r^3}$$

$$T_{\alpha \beta \gamma }={\nabla }_{\alpha }{\nabla }_{\beta }{\nabla }_{\gamma }\frac{1}{r}=-\frac{15r_{\alpha }{r}_{\beta }{r}_{\gamma }}{r^7}+\frac{3(r_{\alpha }{\delta }_{\beta \gamma }+r_{\beta }{\delta }_{\alpha \gamma }+r_{\gamma }{\delta }_{\alpha \beta })}{r^5}$$ (34)

$$T_{\alpha \beta \gamma \delta }={\nabla }_{\alpha }{\nabla }_{\beta }{\nabla }_{\gamma }{\nabla }_{\delta }\frac{1}{r}=\frac{105r_{\alpha }{r}_{\beta }{r}_{\gamma }{r}_{\delta }}{r^9}-\frac{15(r_{\alpha }{r}_{\beta }{\delta }_{\gamma \delta }+r_{\alpha }{r}_{\gamma }{\delta }_{\beta \delta }+r_{\alpha }{r}_{\delta }{\delta }_{\beta \gamma }+r_{\beta }{r}_{\gamma }{\delta }_{\alpha \delta }+r_{\beta }{r}_{\delta }{\delta }_{\alpha \gamma }+r_{\gamma }{r}_{\delta }{\delta }_{\alpha \beta })}{r^7}+\frac{3({\delta }_{\alpha \beta }{\delta }_{\gamma \delta }+{\delta }_{\alpha \gamma }{\delta }_{\beta \delta }+{\delta }_{\alpha \delta }{\delta }_{\beta \gamma })}{r^5}$$

where α, β, γ and δ can take the values x, y, or z and the Kronecker delta function is unity if its subscripts are equal, but zero otherwise. Applying the substitution gives

$$A=c_0\frac{1}{f}$$

$$A_{\alpha }=-c_1\frac{r_{\alpha }}{f^3}$$

$$A_{\alpha \beta }=c_2\frac{3r_{\alpha }{r}_{\beta }}{f^5}$$ (35)

$$A_{\alpha \beta \gamma }=-c_3\frac{15r_{\alpha }{r}_{\beta }{r}_{\gamma }}{f^7}$$

$$A_{\alpha \beta \gamma \delta }=c_4\frac{105r_{\alpha }{r}_{\beta }{r}_{\gamma }{r}_{\delta }}{f^9}$$

and represent the GK auxiliary reaction potential tensors. We have removed terms that require summing over a trace by requiring use of traceless multipoles. Unlike the vacuum case, the GK auxiliary reaction potential tensor of degree l is not simply a gradient of a degree l−1 tensor.

The total auxiliary reaction potential due to multipole i, up to quadrupole order, at site j is

$${\varphi }^{(i)}({\mathbf{r}}_{ij},a_i,a_j)=q_{i}A-{\mu }_{i,\alpha }{A}_{\alpha }+\frac{1}{3}{\mathrm{\Theta }}_{i,\alpha \beta }{A}_{\alpha \beta }$$ (36)

where the Einstein convention for repeated summation over Greek subscripts is implied. The total auxiliary potential due to multipole j, up to quadrupole order, at site i is given by

$${\varphi }^{(j)}({\mathbf{r}}_{ji},a_i,a_j)=q_{j}A-{\mu }_{j,\alpha }{A}_{\alpha }+\frac{1}{3}{\mathrm{\Theta }}_{j,\alpha \beta }{A}_{\alpha \beta }$$ (37)

where r_ji is defined from site j to site i.

3.2 Generalized Kirkwood cross-term

Given the auxiliary reaction potentials, we define the auxiliary cross-term energy using Eq. (36) to be

$$U^{(i)}({\mathbf{r}}_{ij},a_i,a_j)=\frac{1}{2}(q_j{\varphi }^{(i)}+{\mu }_{j,\gamma }{\nabla }_{\gamma }{\varphi }^{(i)}+\frac{1}{3}{\mathrm{\Theta }}_{j,\gamma \delta }{\nabla }_{\gamma }{\nabla }_{\delta }{\varphi }^{(i)})$$ (38)

such that substituting for ϕ⁽ⁱ⁾ gives

$$U^{(i)}({\mathbf{r}}_{ij},a_i,a_j)=\frac{1}{2}\left[q_j\right(q_{i}A-{\mu }_{i,\alpha }{A}_{\alpha }+\frac{1}{3}{\mathrm{\Theta }}_{i,\alpha \beta }{A}_{\alpha \beta })+{\mu }_{j,\gamma }{\nabla }_{\gamma }(q_{i}A-{\mu }_{i,\alpha }{A}_{\alpha }+\frac{1}{3}{\mathrm{\Theta }}_{i,\alpha \beta }{A}_{\alpha \beta })+\frac{1}{3}{\mathrm{\Theta }}_{j,\gamma \delta }{\nabla }_{\gamma }{\nabla }_{\delta }(q_{i}A-{\mu }_{i,\alpha }{A}_{\alpha }+\frac{1}{3}{\mathrm{\Theta }}_{i,\alpha \beta }{A}_{\alpha \beta }\left)\right]$$ (39)

while the auxiliary cross-term energy using Eq. (37) is

$$U^{(j)}({\mathbf{r}}_{ji},a_i,a_j)=\frac{1}{2}(q_i{\varphi }^{(j)}+{\mu }_{i,\gamma }{\nabla }_{\gamma }{\varphi }^{(j)}+\frac{1}{3}{\mathrm{\Theta }}_{i,\gamma \delta }{\nabla }_{\gamma }{\nabla }_{\delta }{\varphi }^{(j)})$$ (40)

such that substituting for ϕ^(j) gives

$$U^{(j)}({\mathbf{r}}_{ji},a_i,a_j)=\frac{1}{2}\left[q_i\right(q_{j}A-{\mu }_{j,\alpha }{A}_{\alpha }+\frac{1}{3}{\mathrm{\Theta }}_{j,\alpha \beta }{A}_{\alpha \beta })+{\mu }_{i,\gamma }{\nabla }_{\gamma }(q_{j}A-{\mu }_{j,\alpha }{A}_{\alpha }+\frac{1}{3}{\mathrm{\Theta }}_{j,\alpha \beta }{A}_{\alpha \beta })+\frac{1}{3}{\mathrm{\Theta }}_{i,\gamma \delta }{\nabla }_{\gamma }{\nabla }_{\delta }(q_{j}A-{\mu }_{j,\alpha }{A}_{\alpha }+\frac{1}{3}{\mathrm{\Theta }}_{j,\alpha \beta }{A}_{\alpha \beta }\left)\right]$$ (41)

In the case of superimposition, either U⁽ⁱ⁾ or U^(j) exactly reproduces the correct self-energies. In the case of wide separation, both ϕ⁽ⁱ⁾ and ϕ^(j) neglect the bending of field lines near the spherical dielectric cavity surrounding site j and site i, respectively. The density of field lines in the case of wide separation is not an issue for a fixed partial charge interaction, although neglect of this effect introduces an error of less than 1% for dipole interactions in the case of a solute with unit permittivity in water.

Gradients of the auxiliary reaction potential can easily be obtained, although it is important to note that

$${\nabla }_{\alpha }A\ne A_{\alpha }.$$ (42)

Namely, ∇_αA includes a factor of $(1-e^{-r_{ij}^2/c_f{a}_i{a}_j}/c_f)$ relative to A_α such that equality is only achieved for r_ij equal to zero or infinity. This subtle point implies, not surprisingly, the auxiliary reaction potential is too simple for intermediate r_ij. An important consequence is that U⁽ⁱ⁾ ≠ U^(j). A consistent model requires that the α-component of the potential gradient at site j of a unit charge at site i should equal the potential at site i of the dipole’s unit magnitude α-component at site j. This reciprocity condition is a well-known property of linear dielectric continuums.⁴⁰ We note that in practice ∇_αA ≈ A_α and therefore we simply take the average of the energies to obtain a consistent interaction model.

$$\mathrm{\Delta }{G}_{ij}=\frac{1}{2}(U^{(i)}+U^{(j)})$$ (43)

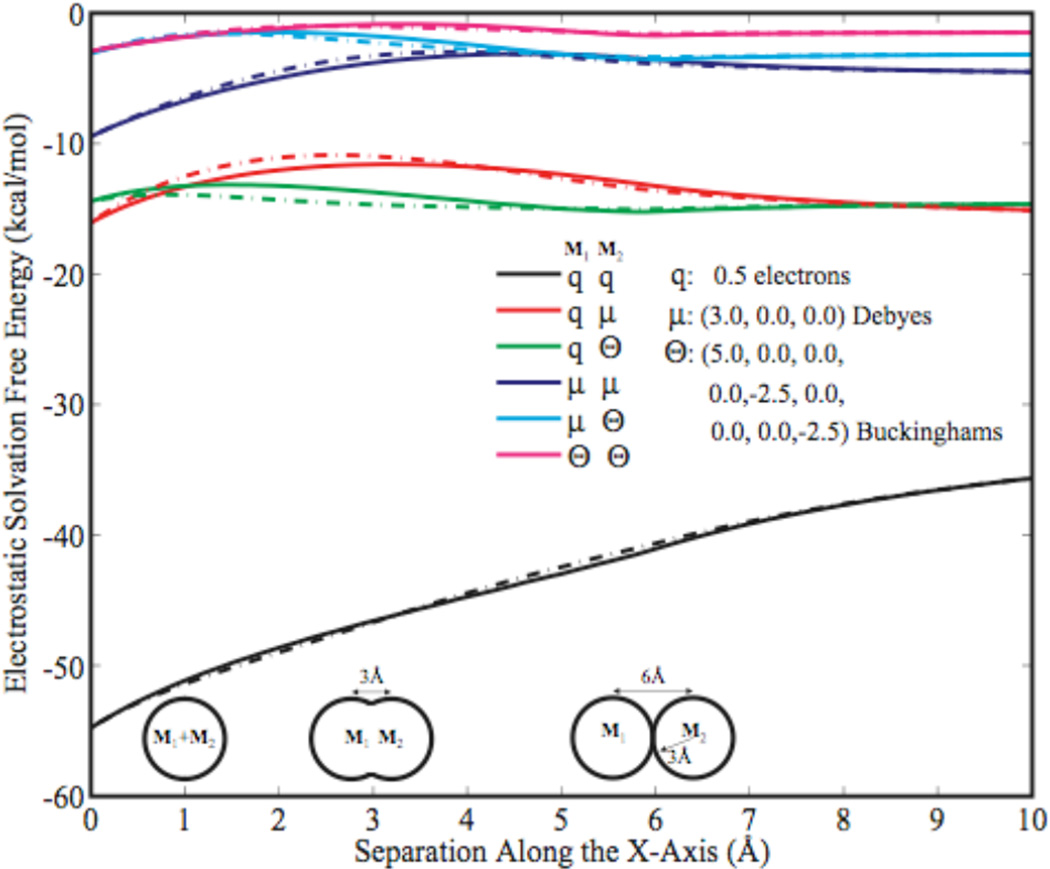
The qualitative behavior of the GK cross-term formulation for multipole permutations through quadrupole degree is seen in Figure (1). The system is composed of two spheres, each with a radius of 3.0 Å and unit permittivity, in a solvent with permittivity 78.3. The total electrostatic solvation energy was evaluated using the PMPB and GK models. In the case of superimposition, the GK value is exact. When the two spheres are widely separated, GK asymptotes to the PMPB results for all permutations. For intermediate separations, the behavior is promising, but not exact.

Figure 1.

The solvation energy for a system composed two spheres, each with a radius of 3 Å and permittivity of 1, and a variety of multipole combinations are computed as a function of separation along the x-axis using numerical Poisson solutions (solid lines) and generalized Kirkwood (dashed lines). The solvent permittivity was 78.3. The limiting cases of wide separation and superimposition are reproduced in all cases, while intermediate separations are seen to be a reasonable approximation.

4 AMOEBA SOLUTES UNDER GENERALIZED KIRKWOOD

4.1 Electrostatic solvation free energy

Derivation of the electrostatic solvation free energy for an AMOEBA solute^35–37 within the GK continuum resembles the derivation of the PMPB electrostatic solvation free energy.² Each permanent atomic multipole site can be considered as a vector of coefficients including charge, dipole and quadrupole components

$${\mathbf{M}}_i={[q_i,d_{i,x},d_{i,y},d_{i,z},{\mathrm{\Theta }}_{i,xx},{\mathrm{\Theta }}_{i,xy},{\mathrm{\Theta }}_{i,xz},\dots ,{\mathrm{\Theta }}_{i,zz}]}^t$$ (44)

where the superscript t denotes the transpose. The interaction potential energy between two sites i and j separated by the distance r_ij in a homogeneous permittivity ε_h can then be represented in tensor notation as

$$\mathrm{U}\left({\mathbf{r}}_{ij}\right)={\mathbf{M}}_i^t{\mathbf{T}}_{ij}{\mathbf{M}}_j={\left[\begin{array}{c}\hfill q_i\hfill \\ \hfill d_{i,x}\hfill \\ \hfill d_{i,y}\hfill \\ \hfill d_{i,z}\hfill \\ \hfill {\mathrm{\Theta }}_{i,xx}\hfill \\ \hfill ⋮\hfill \end{array}\right]}^t\left[\begin{array}{ccccc}\hfill 1\hfill & \hfill \frac{\partial }{\partial x_j}\hfill & \hfill \frac{\partial }{\partial y_j}\hfill & \hfill \frac{\partial }{\partial z_j}\hfill & \hfill \cdots \hfill \\ \hfill \frac{\partial }{\partial x_i}\hfill & \hfill \frac{{\partial }^2}{\partial x_i\partial x_j}\hfill & \hfill \frac{{\partial }^2}{\partial x_i\partial y_j}\hfill & \hfill \frac{{\partial }^2}{\partial x_i\partial z_j}\hfill & \hfill \cdots \hfill \\ \hfill \frac{\partial }{\partial y_i}\hfill & \hfill \frac{{\partial }^2}{\partial y_i\partial x_j}\hfill & \hfill \frac{{\partial }^2}{\partial y_i\partial y_j}\hfill & \hfill \frac{{\partial }^2}{\partial y_i\partial z_j}\hfill & \hfill \cdots \hfill \\ \hfill \frac{\partial }{\partial z_i}\hfill & \hfill \frac{{\partial }^2}{\partial z_i\partial x_j}\hfill & \hfill \frac{{\partial }^2}{\partial z_i\partial y_j}\hfill & \hfill \frac{{\partial }^2}{\partial z_i\partial z_j}\hfill & \hfill \cdots \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill \end{array}\right]\frac{1}{{\epsilon }_h{r}_{ij}}\left[\begin{array}{c}\hfill q_j\hfill \\ \hfill d_{j,x}\hfill \\ \hfill d_{j,y}\hfill \\ \hfill d_{j,z}\hfill \\ \hfill {\mathrm{\Theta }}_{j,xx}\hfill \\ \hfill ⋮\hfill \end{array}\right]$$ (45)

Similarly, the GK energy for two multipoles (self or cross-term) is given by

$$\mathrm{\Delta }{G}_{ij}({\mathbf{r}}_{ij},a_i,a_j)=\frac{1}{2}{\mathbf{M}}_i^t{\mathbf{K}}_{ij}{\mathbf{M}}_j$$ (46)

where the factor of ½ accounts for the cost of charging the continuum and the GK interaction matrix K_ij depends on the coordinates of all atoms via the effective radii a_i and a_j. As introduced above, GK requires averaging of the auxiliary reaction potentials and their respective gradients to obtain a consistent interaction matrix

$${\mathbf{K}}_{ij}=\frac{1}{2}[{\mathbf{K}}^{(i)}+{\mathbf{K}}^{(j)}]$$

$${\mathbf{K}}^{(i)}({\mathbf{r}}_{ij},a_i,a_j)=\left[\begin{array}{ccccc}\hfill A\hfill & \hfill \frac{\partial A}{\partial x}\hfill & \hfill \frac{\partial A}{\partial y}\hfill & \hfill \frac{\partial A}{\partial z}\hfill & \hfill \cdots \hfill \\ \hfill A_x\hfill & \hfill \frac{\partial A_x}{\partial x}\hfill & \hfill \frac{\partial A_x}{\partial y}\hfill & \hfill \frac{\partial A_x}{\partial z}\hfill & \hfill \cdots \hfill \\ \hfill A_y\hfill & \hfill \frac{\partial A_y}{\partial x}\hfill & \hfill \frac{\partial A_y}{\partial y}\hfill & \hfill \frac{\partial A_y}{\partial z}\hfill & \hfill \cdots \hfill \\ \hfill A_z\hfill & \hfill \frac{\partial A_z}{\partial x}\hfill & \hfill \frac{\partial A_z}{\partial y}\hfill & \hfill \frac{\partial A_z}{\partial z}\hfill & \hfill \cdots \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill \end{array}\right]$$ (47)

$${\mathbf{K}}^{(j)}({\mathbf{r}}_{ji},a_i,a_j)={\left({\mathbf{K}}^{(i)}\right({\mathbf{r}}_{ji},a_i,a_j\left)\right)}^t$$

Each site may also be polarizable, such that an induced dipole is formed in vacuum ${\mathit{\mu }}_i^v$ proportional to the strength of the local field

$${\mathit{\mu }}_i^v={\alpha }_i{\mathbf{E}}_i^v={\alpha }_i(\sum _{j\ne i}{\mathbf{T}}_{d,ij}^{(1)}{\mathbf{M}}_j+\sum _{k\ne i}{\mathbf{T}}_{ik}^{(11)}{\mathit{\mu }}_k)$$ (48)

Here α_i is an isotropic atomic polarizability and ${\mathbf{E}}_i^v$ is the total vacuum field, which can be decomposed into contributions from permanent multipole sites and induced dipoles, and the summations run over all multipole sites. The interaction tensors ${\mathbf{T}}_{d,ij}^{(1)}$ and ${\mathbf{T}}_{ik}^{(11)}$ are, respectively,

$${\mathbf{T}}_{d,ij}^{(1)}=\left[\begin{array}{ccccc}\hfill \frac{\partial }{\partial x_i}\hfill & \hfill \frac{{\partial }^2}{\partial x_i\partial x_j}\hfill & \hfill \frac{{\partial }^2}{\partial x_i\partial y_j}\hfill & \hfill \frac{{\partial }^2}{\partial x_i\partial z_j}\hfill & \hfill \cdots \hfill \\ \hfill \frac{\partial }{\partial y_i}\hfill & \hfill \frac{{\partial }^2}{\partial y_i\partial x_j}\hfill & \hfill \frac{{\partial }^2}{\partial y_i\partial y_j}\hfill & \hfill \frac{{\partial }^2}{\partial y_i\partial z_j}\hfill & \hfill \cdots \hfill \\ \hfill \frac{\partial }{\partial z_i}\hfill & \hfill \frac{{\partial }^2}{\partial z_i\partial x_j}\hfill & \hfill \frac{{\partial }^2}{\partial z_i\partial y_j}\hfill & \hfill \frac{{\partial }^2}{\partial z_i\partial z_j}\hfill & \hfill \cdots \hfill \end{array}\right]\frac{1}{{\epsilon }_h{r}_{ij}}$$ (49)

and

$${\mathbf{T}}_{ik}^{(11)}=\left[\begin{array}{ccc}\hfill \frac{{\partial }^2}{\partial x_i\partial x_k}\hfill & \hfill \frac{{\partial }^2}{\partial x_i\partial y_k}\hfill & \hfill \frac{{\partial }^2}{\partial x_i\partial z_k}\hfill \\ \hfill \frac{{\partial }^2}{\partial y_i\partial x_k}\hfill & \hfill \frac{{\partial }^2}{\partial y_i\partial y_k}\hfill & \hfill \frac{{\partial }^2}{\partial y_i\partial z_k}\hfill \\ \hfill \frac{{\partial }^2}{\partial z_i\partial x_k}\hfill & \hfill \frac{{\partial }^2}{\partial z_i\partial y_k}\hfill & \hfill \frac{{\partial }^2}{\partial z_i\partial z_k}\hfill \end{array}\right]\frac{1}{{\epsilon }_h{r}_{ik}}$$ (50)

where the d in ${\mathbf{T}}_{d,ij}^{(1)}$ denotes that masking rules for the AMOEBA group-based polarization model are applied. Upon adding the GK reaction field due to the permanent multipoles and induced dipoles, the self-consistent induced dipoles are proportional to the self-consistent reaction field

$${\mathit{\mu }}_i={\alpha }_i{\mathbf{E}}_i={\alpha }_i\left[\sum _j\right[(1-{\delta }_{ij}){\mathbf{T}}_{d,ij}^{(1)}+{\mathbf{K}}_{ij}^{(1)}]{\mathbf{M}}_j+\sum _k[(1-{\delta }_{ik}){\mathbf{T}}_{ik}^{(11)}+{\mathbf{K}}_{ik}^{(11)}\left]{\mathit{\mu }}_k\right]$$ (51)

where the sums now include self-contributions to the reaction field, but exclude Coulomb self-interactions via Kronecker delta functions. The GK interaction matrices ${\mathbf{K}}_{ij}^{(1)}$ and ${\mathbf{K}}_{ik}^{(11)}$ are, respectively,

$${\mathbf{K}}_{ij}^{(1)}=\frac{1}{2}\left({\mathbf{K}}_{ij}^{(1,i)}\right({\mathbf{r}}_{ij},a_i,a_j)+{\mathbf{K}}_{ij}^{(1,j)}({\mathbf{r}}_{ji},a_i,a_j\left)\right)$$ (52)

where

$${\mathbf{K}}_{ij}^{(1,i)}({\mathbf{r}}_{ij},a_i,a_j)=\left[\begin{array}{ccccc}\hfill A_x\hfill & \hfill \frac{\partial A_x}{\partial x}\hfill & \hfill \frac{\partial A_x}{\partial y}\hfill & \hfill \frac{\partial A_x}{\partial z}\hfill & \hfill \cdots \hfill \\ \hfill A_y\hfill & \hfill \frac{\partial A_y}{\partial x}\hfill & \hfill \frac{\partial A_y}{\partial y}\hfill & \hfill \frac{\partial A_y}{\partial z}\hfill & \hfill \cdots \hfill \\ \hfill A_z\hfill & \hfill \frac{\partial A_z}{\partial x}\hfill & \hfill \frac{\partial A_z}{\partial y}\hfill & \hfill \frac{\partial A_z}{\partial z}\hfill & \hfill \cdots \hfill \end{array}\right]$$ (53)

$${\mathbf{K}}_{ij}^{(1,j)}({\mathbf{r}}_{ji},a_i,a_j)=\left[\begin{array}{ccccc}\hfill \frac{\partial A}{\partial x}\hfill & \hfill \frac{\partial A_x}{\partial x}\hfill & \hfill \frac{\partial A_y}{\partial x}\hfill & \hfill \frac{\partial A_z}{\partial x}\hfill & \hfill \cdots \hfill \\ \hfill \frac{\partial A}{\partial y}\hfill & \hfill \frac{\partial A_x}{\partial y}\hfill & \hfill \frac{\partial A_y}{\partial y}\hfill & \hfill \frac{\partial A_z}{\partial y}\hfill & \hfill \cdots \hfill \\ \hfill \frac{\partial A}{\partial z}\hfill & \hfill \frac{\partial A_x}{\partial z}\hfill & \hfill \frac{\partial A_y}{\partial z}\hfill & \hfill \frac{\partial A_z}{\partial z}\hfill & \hfill \cdots \hfill \end{array}\right]$$ (54)

and

$${\mathbf{K}}_{ik}^{(11)}=\left[\begin{array}{ccc}\hfill \frac{\partial A_x}{\partial x}\hfill & \hfill \frac{\partial A_x}{\partial y}\hfill & \hfill \frac{\partial A_x}{\partial z}\hfill \\ \hfill \frac{\partial A_y}{\partial x}\hfill & \hfill \frac{\partial A_y}{\partial y}\hfill & \hfill \frac{\partial A_y}{\partial z}\hfill \\ \hfill \frac{\partial A_z}{\partial x}\hfill & \hfill \frac{\partial A_z}{\partial y}\hfill & \hfill \frac{\partial A_z}{\partial z}\hfill \end{array}\right]$$ (55)

where averaging cancels for the matrix ${\mathbf{K}}_{ik}^{(11)}$ that produces the field at site i due to the induced dipole at site k as a result of symmetry.

The linear system of equations, both for the vacuum and solvated systems, can be solved via a number of approaches, including direct matrix inversion or iterative schemes such as successive over-relaxation (SOR). The total vacuum electrostatic energy ${\mathrm{U}}_{\text{elec}}^{\mathrm{v}}$ includes pairwise permanent multipole interactions and many-body polarization

$${\mathrm{U}}_{\text{elec}}^{\mathrm{v}}=\frac{1}{2}[{\mathbf{M}}^t\mathbf{T}-{\left({\mathit{\mu }}^{\mathrm{v}}\right)}^t{\mathbf{T}}_{\mathrm{p}}^{(1)}]\mathbf{M}$$ (56)

where the factor of ½ avoids double-counting of permanent multipole interactions in the first term and accounts for the cost of polarizing the system in the second term. Furthermore, M is a column vector of 13N multipole components

$$\mathbf{M}=\left[\begin{array}{c}\hfill {\mathbf{M}}_1\hfill \\ \hfill {\mathbf{M}}_2\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{M}}_{\mathrm{N}}\hfill \end{array}\right]$$ (57)

T is a N × N supermatrix with T_ij off-diagonal elements

$$\mathbf{T}=\left[\begin{array}{cccc}\hfill 0\hfill & \hfill {\mathbf{T}}_{12}\hfill & \hfill {\mathbf{T}}_{13}\hfill & \hfill \cdots \hfill \\ \hfill {\mathbf{T}}_{21}\hfill & \hfill 0\hfill & \hfill {\mathbf{T}}_{23}\hfill & \hfill \cdots \hfill \\ \hfill {\mathbf{T}}_{31}\hfill & \hfill {\mathbf{T}}_{32}\hfill & \hfill 0\hfill & \hfill \cdots \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill \end{array}\right]$$ (58)

μ^v is a 3N column vector of converged induced dipole components in vacuum

$${\mathit{\mu }}^{\mathrm{v}}=\left[\begin{array}{c}\hfill {\mu }_{1,x}^v\hfill \\ \hfill {\mu }_{1,y}^v\hfill \\ \hfill {\mu }_{1,z}^v\hfill \\ \hfill ⋮\hfill \\ \hfill {\mu }_{N,z}^v\hfill \end{array}\right]$$ (59)

and ${\mathbf{T}}_{\mathrm{p}}^{(1)}$ is a 3N × 13N supermatrix with ${\mathbf{T}}_{\mathrm{p},ij}^{(1)}$ as off-diagonal elements

$${\mathbf{T}}_{\mathrm{p}}^{(1)}=\left[\begin{array}{cccc}\hfill 0\hfill & \hfill {\mathbf{T}}_{\mathrm{p},12}^{(1)}\hfill & \hfill {\mathbf{T}}_{\mathrm{p},13}^{(1)}\hfill & \hfill \cdots \hfill \\ \hfill {\mathbf{T}}_{\mathrm{p},21}^{(1)}\hfill & \hfill 0\hfill & \hfill {\mathbf{T}}_{\mathrm{p},23}^{(1)}\hfill & \hfill \cdots \hfill \\ \hfill {\mathbf{T}}_{\mathrm{p},31}^{(1)}\hfill & \hfill {\mathbf{T}}_{\mathrm{p},32}^{(1)}\hfill & \hfill 0\hfill & \hfill \cdots \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill \end{array}\right].$$ (60)

The subscript p denotes a tensor matrix that operates on the permanent multipoles to produce the electric field in which the polarization energy is evaluated, while the subscript d is used to specify an analogous tensor matrix that produces the field that induces dipoles. The differences between the two are masking rules that leave out 1–2, 1–3, and 1–4 interactions in the former case and use the AMOEBA group based polarization scheme for the later.³⁵

For the solvated system, the total electrostatic energy is similar to the vacuum case

$${\mathrm{U}}_{\text{elec}}=\frac{1}{2}\left[{\mathbf{M}}^t\right(\mathbf{T}+\mathbf{K})-{\mathit{\mu }}^t({\mathbf{T}}_{\mathrm{p}}^{(1)}+{\mathbf{K}}^{(1)}\left)\right]\mathbf{M}$$ (61)

where the GK matrices are

$$\mathbf{K}=\left[\begin{array}{cccc}\hfill {\mathbf{K}}_{11}\hfill & \hfill {\mathbf{K}}_{12}\hfill & \hfill {\mathbf{K}}_{13}\hfill & \hfill \cdots \hfill \\ \hfill {\mathbf{K}}_{21}\hfill & \hfill {\mathbf{K}}_{22}\hfill & \hfill {\mathbf{K}}_{23}\hfill & \hfill \cdots \hfill \\ \hfill {\mathbf{K}}_{31}\hfill & \hfill {\mathbf{K}}_{32}\hfill & \hfill {\mathbf{K}}_{33}\hfill & \hfill \cdots \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill \end{array}\right]$$ (62)

and

$${\mathbf{K}}^{(1)}=\left[\begin{array}{cccc}\hfill {\mathbf{K}}_{11}^{(1)}\hfill & \hfill {\mathbf{K}}_{12}^{(1)}\hfill & \hfill {\mathbf{K}}_{13}^{(1)}\hfill & \hfill \cdots \hfill \\ \hfill {\mathbf{K}}_{21}^{(1)}\hfill & \hfill {\mathbf{K}}_{22}^{(1)}\hfill & \hfill {\mathbf{K}}_{23}^{(1)}\hfill & \hfill \cdots \hfill \\ \hfill {\mathbf{K}}_{31}^{(1)}\hfill & \hfill {\mathbf{K}}_{32}^{(1)}\hfill & \hfill {\mathbf{K}}_{33}^{(1)}\hfill & \hfill \cdots \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill \end{array}\right]$$ (63)

The total electrostatic solvation free energy is determined as the difference between the vacuum electrostatic energy and total electrostatic energy in solvent as

$${\mathrm{U}}_{\text{solv}}=\frac{1}{2}({\mathbf{M}}^t\mathbf{K}-{\mathit{\mu }}^{\mathrm{\Delta }}{\mathbf{T}}_{\mathrm{p}}^{(1)}-\mathit{\mu }{\mathbf{K}}^{(1)})\mathbf{M}$$ (64)

where μ^Δ represents the change in the induced dipoles upon solvation

$${\mathit{\mu }}^{\mathrm{\Delta }}=\mathit{\mu }-{\mathit{\mu }}^{\mathrm{v}}.$$ (65)

4.2 Permanent multipole energy gradient

The permanent multipole electrostatic solvation energy gradient between sites i and j only depends on the gradient of the GK interaction tensor

$$\frac{\partial {\mathbf{K}}_{ij}}{\partial r_{i,\mathrm{\sigma }}}=\frac{1}{2}[{(\frac{\partial {\mathbf{K}}^{(i)}}{\partial r_{i,\mathrm{\sigma }}}+\frac{\partial {\mathbf{K}}^{(j)}}{\partial r_{i,\mathrm{\sigma }}})}_{a_i,a_j}+(\frac{\partial {\mathbf{K}}^{(i)}}{\partial a_i}+\frac{\partial {\mathbf{K}}^{(j)}}{\partial a_i})\frac{\partial a_i}{\partial r_{i,\mathrm{\sigma }}}+(\frac{\partial {\mathbf{K}}^{(i)}}{\partial a_j}+\frac{\partial {\mathbf{K}}^{(j)}}{\partial a_j}\left)\frac{\partial a_j}{\partial r_{i,\mathrm{\sigma }}}\right]$$ (66)

and subscript a_i and a_j denote keeping the effective radii fixed in this case. Generation of the GK interaction tensors that make up $\frac{\partial {\mathbf{K}}^{(i)}}{\partial r_{i,\sigma }},\frac{\partial {\mathbf{K}}^{(i)}}{\partial a_i},\frac{\partial {\mathbf{K}}^{(i)}}{\partial a_j},\frac{\partial {\mathbf{K}}^{(j)}}{\partial r_{i,\sigma }},\frac{\partial {\mathbf{K}}^{(j)}}{\partial a_i}$ and $\frac{\partial {\mathbf{K}}^{(j)}}{\partial a_j}$ are described in Appendix B of the Supporting Information. The derivatives of the effective radii with respect to an atomic displacement follow from the pairwise descreening implementation of the RPA and will not be discussed here.^8,9,38 We also point out that there is a torque on the permanent dipoles due to the permanent reaction field and also on the permanent quadrupoles due to the permanent reaction field gradient. All torques, including contributions from the polarization energy gradient discussed below, are converted to forces on adjacent atoms that define the local coordinate frame of the multipole.

4.3 Polarization energy gradient

The polarization energy gradient when using either the “direct” or “mutual” polarization models within the GK continuum will now be derived. The definition of the starting point for the iterative convergence of the self-consistent reaction field (SCRF) is the total “direct” field E_direct at each polarizable site. This field is the sum of the permanent atomic multipoles (PAM) intramolecular field

$${\mathbf{E}}_{\mathrm{d}}={\mathbf{T}}_{\mathrm{d}}^{(1)}\mathbf{M}$$ (67)

where ${\mathbf{T}}_{\mathrm{d}}^{(1)}$ is analogous to the tensor matrix defined in deriving the AMOEBA vacuum energy in Eq. (56), and the PAM GK reaction field

$${\mathbf{E}}_{\mathrm{R}\mathrm{F}}={\mathbf{K}}^{(1)}\mathbf{M}$$ (68)

The product of the direct field E_direct with a vector of atomic polarizabilities determines the initial induced dipoles μ_direct

$${\mathit{\mu }}_{\text{direct}}=\mathit{\alpha }{\mathbf{E}}_{\text{direct}}=\mathit{\alpha }({\mathbf{T}}_{\mathrm{d}}^{(1)}+{\mathbf{K}}^{(1)})\mathbf{M}$$ (69)

At this point the induced dipoles do not act upon each other nor do they elicit a reaction field. This is defined as the direct model of polarization.

In contrast to the direct polarization model, the total SCRF E has two additional contributions due to the induced dipoles and their reaction field,

$$\mathbf{E}=({\mathbf{T}}_{\mathrm{d}}^{(1)}+{\mathbf{K}}^{(1)})\mathbf{M}+({\mathbf{T}}^{(11)}+{\mathbf{K}}^{(11)})\mathit{\mu }$$ (70)

for a sum of 4 contributions. The induced dipoles

$$\mathit{\mu }=\mathit{\alpha }\left[\right({\mathbf{T}}_{\mathrm{d}}^{(1)}+{\mathbf{K}}^{(1)})\mathbf{M}+({\mathbf{T}}^{(11)}+{\mathbf{K}}^{(11)}\left)\mathit{\mu }\right]$$ (71)

can be solved for in an iterative fashion using successive over-relaxation (SOR) to accelerate convergence.⁵² Alternatively, the induced dipoles can be solved for directly as a mechanism for deriving the polarization energy gradient with respect to an atomic displacement. Moving all terms containing the induced dipoles to the LHS allows their isolation

$$({\mathit{\alpha }}^{-1}-{\mathbf{T}}^{(11)}-{\mathbf{K}}^{(11)})\mathit{\mu }=({\mathbf{T}}_{\mathrm{d}}^{(1)}+{\mathbf{K}}^{(1)})\mathbf{M}$$ (72)

For convenience, a matrix C is defined as

$$\mathbf{C}={\mathit{\alpha }}^{-1}-{\mathbf{T}}^{(11)}-{\mathbf{K}}^{(11)}$$ (73)

which is substituted into Eq. (72) above to show the induced dipoles are a linear function of the PAM M, directly via the intramolecular interaction tensor ${\mathbf{T}}_{\mathrm{d}}^{(1)}$ that implicitly contains the AMOEBA group based polarization scheme, and also through their reaction field

$$\mathit{\mu }={\mathbf{C}}^{-1}({\mathbf{T}}_{\mathrm{d}}^{(1)}+{\mathbf{K}}^{(1)})\mathbf{M}={\mathbf{C}}^{-1}({\mathbf{E}}_{\mathrm{d}}+{\mathbf{E}}_{\mathrm{R}\mathrm{F}})$$ (74)

The polarization energy can now be described in terms the permanent reaction field and solute field E_p

$${\mathrm{U}}_{\mu }=-\frac{1}{2}{({\mathbf{E}}_{\mathrm{p}}+{\mathbf{E}}_{\mathrm{R}\mathrm{F}})}^t\mathit{\mu }$$ (75)

To find the polarization energy gradient, we wish to avoid terms that rely on the change in induced dipoles with respect to an atomic displacement. Therefore, the induced dipoles in Eq. (75) are substituted for using Eq. (74) to yield

$${\mathrm{U}}_{\mu }=-\frac{1}{2}{({\mathbf{E}}_{\mathrm{p}}+{\mathbf{E}}_{\mathrm{R}\mathrm{F}})}^t{\mathbf{C}}^{-1}({\mathbf{E}}_{\mathrm{d}}+{\mathbf{E}}_{\mathrm{R}\mathrm{F}})$$ (76)

By the chain rule, the polarization energy gradient is

$$\frac{\partial {\mathrm{U}}_{\mu }}{\partial r_{i,\mathrm{\sigma }}}=-\frac{1}{2}\left[{(\frac{\partial {\mathbf{E}}_{\mathrm{p}}}{\partial r_{i,\mathrm{\sigma }}}+\frac{\partial {\mathbf{E}}_{\mathrm{R}\mathrm{F}}}{\partial r_{i,\mathrm{\sigma }}})}^t{\mathbf{C}}^{-1}\right({\mathbf{E}}_{\mathrm{d}}+{\mathbf{E}}_{\mathrm{R}\mathrm{F}})+{({\mathbf{E}}_{\mathrm{p}}+{\mathbf{E}}_{\mathrm{R}\mathrm{F}})}^t\frac{\partial {\mathbf{C}}^{-1}}{\partial r_{i,\mathrm{\sigma }}}({\mathbf{E}}_{\mathrm{d}}+{\mathbf{E}}_{\mathrm{R}\mathrm{F}})+{({\mathbf{E}}_{\mathrm{p}}+{\mathbf{E}}_{\mathrm{R}\mathrm{F}})}^t{\mathbf{C}}^{-1}(\frac{\partial {\mathbf{E}}_{\mathrm{d}}}{\partial r_{i,\mathrm{\sigma }}}+\frac{\partial {\mathbf{E}}_{\mathrm{R}\mathrm{F}}}{\partial r_{i,\mathrm{\sigma }}}\left)\right]$$ (77)

For convenience a mathematical quantity ν is defined, which is similar to μ, as

$$\mathit{\nu }=({\mathbf{E}}_{\mathrm{p}}+{\mathbf{E}}_{\mathrm{R}\mathrm{F}}){\mathbf{C}}^{-1}$$ (78)

We can now greatly simplify Eq. (77) above using Eqs. (74) and (78) along with the identity $\frac{\partial {\mathbf{C}}^{-1}}{\partial r_{i,\sigma }}=-{\mathbf{C}}^{-1}\frac{\partial \mathbf{C}}{\partial r_{i,\sigma }}{\mathbf{C}}^{-1}$ to give

$$\frac{\partial {\mathrm{U}}_{\mu }}{\partial r_{i,\mathrm{\sigma }}}=-\frac{1}{2}[{\left(\frac{\partial {\mathbf{E}}_{\mathrm{p}}}{\partial r_{i,\mathrm{\sigma }}}\right)}^t\mathit{\mu }+{\mathit{\nu }}^t\frac{\partial {\mathbf{E}}_{\mathrm{d}}}{\partial r_{i,\mathrm{\sigma }}}+{\left(\frac{\partial {\mathbf{E}}_{\mathrm{R}\mathrm{F}}}{\partial r_{i,\mathrm{\sigma }}}\right)}^t\mathit{\mu }+{\mathit{\nu }}^t\frac{\partial {\mathbf{E}}_{\mathrm{R}\mathrm{F}}}{\partial r_{i,\mathrm{\sigma }}}-{\mathit{\nu }}^t\frac{\partial \mathbf{C}}{\partial r_{i,\mathrm{\sigma }}}\mathit{\mu }]$$ (79)

Under the direct polarization model, C is an identity matrix whose derivative is zero, and therefore Eq. (79) simplifies to

$$\frac{\partial {\mathrm{U}}_{{\mu }_{\text{direct}}}}{\partial r_{i,\mathrm{\sigma }}}=-\frac{1}{2}[{\left(\frac{\partial {\mathbf{E}}_{\mathrm{p}}}{\partial r_{i,\mathrm{\sigma }}}\right)}^t\mathit{\mu }+{\mathit{\nu }}^t\frac{\partial {\mathbf{E}}_{\mathrm{d}}}{\partial r_{i,\mathrm{\sigma }}}+{\left(\frac{\partial {\mathbf{E}}_{\mathrm{R}\mathrm{F}}}{\partial r_{i,\mathrm{\sigma }}}\right)}^t\mathit{\mu }+{\mathit{\nu }}^t\frac{\partial {\mathbf{E}}_{\mathrm{R}\mathrm{F}}}{\partial r_{i,\mathrm{\sigma }}}]$$ (80)

The first two terms on the RHS appear in the polarization energy gradient even in the absence of a continuum reaction field and are described elsewhere.³⁵ The third and fourth terms are specific to GK and can be combined. We require the derivative of the GK reaction field due to permanent multipoles with respect to movement of any atom

$$\frac{\partial {\mathbf{E}}_{\mathrm{R}\mathrm{F}}}{\partial r_{i,\mathrm{\sigma }}}=\frac{\partial {\mathbf{K}}^{(1)}}{\partial r_{i,\mathrm{\sigma }}}\mathbf{M}$$ (81)

It is therefore sufficient to describe the gradient of any ${\mathbf{K}}_{ij}^{(1)}$ sub-matrix of K⁽¹⁾ as

$$\frac{\partial {\mathbf{K}}_{ij}^{(1)}}{\partial r_{i,\mathrm{\sigma }}}=\frac{1}{2}[{(\frac{\partial {\mathbf{K}}_{ij}^{(1,i)}}{\partial r_{i,\mathrm{\sigma }}}+\frac{\partial {\mathbf{K}}_{ij}^{(1,j)}}{\partial r_{i,\mathrm{\sigma }}})}_{a_i,a_j}+(\frac{\partial {\mathbf{K}}_{ij}^{(1,i)}}{\partial a_i}+\frac{\partial {\mathbf{K}}_{ij}^{(1,j)}}{\partial a_i})\frac{\partial a_i}{\partial r_{i,\mathrm{\sigma }}}+(\frac{\partial {\mathbf{K}}_{ij}^{(1,i)}}{\partial a_j}+\frac{\partial {\mathbf{K}}_{ij}^{(1,j)}}{\partial a_j}\left)\frac{\partial a_j}{\partial r_{i,\mathrm{\sigma }}}\right]$$ (82)

The tensors that make up $\frac{\partial {\mathbf{K}}_{ij}^{(1,i)}}{\partial r_{i,\sigma }},\frac{\partial {\mathbf{K}}_{ij}^{(1,i)}}{\partial a_i},\frac{\partial {\mathbf{K}}_{ij}^{(1,i)}}{\partial a_j},\frac{\partial {\mathbf{K}}_{ij}^{(1,j)}}{\partial r_{i,\sigma }},\frac{\partial {\mathbf{K}}_{ij}^{(1.j)}}{\partial a_i}$ and $\frac{\partial {\mathbf{K}}_{ij}^{(1,j)}}{\partial a_j}$ are described in Appendix B. In this case there is a torque on the permanent dipoles and quadrupoles due to the reaction field and reaction field gradient of (μ + ν)/2, respectively.

The full mutual polarization gradient has an additional term compared to the direct polarization gradient, in addition to the implicit difference due to the induced dipoles being converged self-consistently. Specifically, the derivative of the matrix C leads to two terms

$${\mathit{\nu }}^t\frac{\partial \mathbf{C}}{\partial r_{i,\mathrm{\sigma }}}\mathit{\mu }=-{\mathit{\nu }}^t(\frac{\partial {\mathbf{T}}^{(11)}}{\partial r_{i,\mathrm{\sigma }}}+\frac{\partial {\mathbf{K}}^{(11)}}{\partial r_{i,\mathrm{\sigma }}})\mathit{\mu }$$ (83)

The first term on the RHS occurs in vacuum and is described elsewhere³⁵, however, the final term is specific to GK. The gradient of one sub-matrix of the $\frac{\partial {\mathbf{K}}^{(11)}}{\partial r_{i,\sigma }}$ supermatrix is

$$\frac{\partial {\mathbf{K}}_{ij}^{(11)}}{\partial r_{i,\mathrm{\sigma }}}={\left(\frac{\partial {\mathbf{K}}_{ij}^{(11)}}{\partial r_{i,\mathrm{\sigma }}}\right)}_{a_i,a_j}+\frac{\partial {\mathbf{K}}_{ij}^{(11)}}{\partial a_i}\frac{\partial a_i}{\partial r_{i,\mathrm{\sigma }}}+\frac{\partial {\mathbf{K}}_{ij}^{(11)}}{\partial a_j}\frac{\partial a_j}{\partial r_{i,\mathrm{\sigma }}}$$ (84)

The expression for the gradient of ${\mathbf{K}}_{ij}^{(11)}$ is simpler than those for the other GK interaction matrices because it is symmetric.

The veracity of the AMOEBA/GK energy gradients was checked using finite-differences of the energy, optimization of proteins to an RMS convergence criterion of 10⁻⁴ kcal/mole/Å and constant energy molecular dynamics. For example, at a mean temperature of 300 K the protein 1ETL showed a mean total energy of −361.20 kcal/mole with a standard deviation of just 0.25 kcal/mole over 1 nsec. The simulation started with a total energy of −361.25 and finished at −365.28 kcal/mole.

5 VALIDATION AND APPLICATION

GK is an approximation to the Poisson solution that extends GB to arbitrary order polarizable atomic multipoles. Here we test GK by comparing to numerical PMPB solutions in the limit of using a van der Waals definition of the solute-solvent interface parameterized using the Bondi radii set.⁵¹ Specifically, the electrostatic solvation free energy and total solvated dipole moment for a series of 55 proteins was compared using the PMPB and GK continuums. This test set based on PDB entries⁴⁵ was recently proposed by Tjong and Zhou for studying the accuracy of analytic solvation models and is characterized by structures with less than 10% sequence identity, resolution better than 1.0 Å and less than 250 residues.⁴⁴ Amino acids with missing side-chains were changed to alanine if the C_β carbon was present and glycine if not. The TINKER⁵³ pdbxyz program added missing hydrogen atoms. Histidine residues were made neutral with the δ-nitrogren protonated. All structures were optimized in vacuum to an RMS gradient of 5.0 kcal/mole/Å, with the goal being to remove bad contacts. The average heavy atom RMS distance from the crystal structure was 0.07 Å after optimization.

5.1 Electrostatic solvation free energy of proteins

Previous studies have shown that given accurate effective radii, GB predicts the electrostatic solvation energy of proteins to a mean unsigned relative difference of approximately 1% relative to numerical Poisson calculations.¹⁶ In this section we investigate whether it is reasonable to expect similar performance from GK by comparing the electrostatic solvation free energy for a series of folded proteins to values computed using the PMPB model.

The PMPB calculations used a grid spacing of 0.31 Å and at least 10 Å between the edge of the solute-solvent boundary and the grid boundary. A finer grid spacing of 0.23 Å was also tried, which lowered the PMPB energy by approximately 2%, but did not change the quality of the agreement between the two models. The interior of the protein was assigned a permittivity of 1.0 while the solvent was set to 78.3. The induced dipoles were deemed to have converged at a tolerance of 0.01 RMS Debye. Converging to a tighter tolerance of 10⁻⁶ RMS Debye only changed the electrostatic solvation free energy by 0.1% relative to the loser criteria, and was therefore deemed unnecessary. The constant in generalizing function c_f was optimized by hand to eliminate systematic error, which was found to occur at a value of 2.455.

The results are shown in Table 4. The mean signed relative difference is 0.0% a result of tuning the cross-term parameter. The mean unsigned relative difference is 0.9%, which is comparable to the most accurate GB methods.^{13,15,17,34,44,54} We anticipate using a different cross-term parameter when optimizing GK to reproduce PMPB calculations based on a molecular surface definition.

Table 4.

The electrostatic solvation free energy (kcal/mole) for 55 proteins within the PMPB and GK continuum models. The number of atoms and total charge of each protein is listed along with the signed and unsigned relative difference of the GK model to PMPB.

			Energy		% Difference
	Natoms	Q	PMPB	GK	Signed	Unsigned
1A6M	2435	2	−2831	−2765	2.3	2.3
1AHO	936	0	−1161	−1158	0.3	0.3
1BYI	3383	−4	−3861	−3873	−0.3	0.3
1C75	985	−6	−1733	−1742	−0.5	0.5
1C7K	1927	−5	−2523	−2481	1.7	1.7
1CEX	2867	1	−3161	−3212	−1.6	1.6
1EB6	2566	−15	−5044	−5042	0.1	0.1
1EJG	642	0	−580	−614	−6.0	6.0
1ETL	140	−1	−246	−247	−0.5	0.5
1EXR	2240	−25	−8656	−8620	0.4	0.4
1F94	967	2	−1240	−1226	1.1	1.1
1F9Y	2535	−5	−2964	−2968	−0.2	0.2
1G4I	1842	−1	−2356	−2345	0.5	0.5
1G66	2794	−2	−2826	−2824	0.1	0.1
1GQV	2135	7	−2708	−2723	−0.6	0.6
1HJE	175	1	−264	−269	−2.0	2.0
1IQZ	1171	−17	−4663	−4729	−1.4	1.4
1IUA	1207	−1	−1400	−1419	−1.4	1.4
1J0P	1597	8	−2975	−2934	1.4	1.4
1K4I	3253	−6	−4085	−4099	−0.3	0.3
1KTH	885	0	−1469	−1448	1.4	1.4
1L9L	1226	11	−3182	−3150	1.0	1.0
1M1Q	1236	−4	−2084	−2077	0.3	0.3
1NLS	3564	−7	−4743	−4756	−0.3	0.3
1NWZ	1912	−6	−2768	−2760	0.3	0.3
1OD3	1893	−3	−2105	−2104	0.0	0.0
1OK0	1076	−5	−1578	−1571	0.5	0.5
1P9G	519	4	−814	−817	−0.4	0.4
1PQ7	3065	4	−2946	−2942	0.1	0.1
1R6J	1230	0	−1486	−1477	0.6	0.6
1SSX	2755	8	−3000	−2980	0.7	0.7
1TG0	1029	−12	−3017	−3014	0.1	0.1
1TQG	1660	−7	−2920	−2900	0.7	0.7
1TT8	2676	1	−2762	−2758	0.1	0.1
1U2H	1495	2	−2038	−2002	1.8	1.8
1UCS	997	0	−1027	−1042	−1.4	1.4
1UFY	1911	0	−2130	−2145	−0.7	0.7
1UNQ	1947	−1	−3217	−3155	1.9	1.9
1VB0	913	3	−1246	−1232	1.1	1.1
1VBW	1056	8	−1931	−1927	0.2	0.2
1W0N	1756	−5	−2380	−2356	1.0	1.0
1WY3	560	1	−750	−747	0.3	0.3
1X6Z	1720	−1	−2170	−2198	−1.3	1.3
1X8Q	2815	−1	−3739	−3714	0.7	0.7
1XMK	1268	1	−1723	−1724	0.0	0.0
1YK4	774	−8	−1893	−1920	−1.4	1.4
1ZZK	1243	1	−1730	−1699	1.8	1.8
2A6Z	3430	−3	−4203	−4186	0.4	0.4
2BF9	560	−2	−933	−940	−0.8	0.8
2CHH	1624	−3	−2128	−2131	−0.1	0.1
2CWS	3400	−3	−3651	−3616	1.0	1.0
2ERL	567	−6	−1178	−1179	0.0	0.0
2FDN	731	−8	−1746	−1796	−2.9	2.9
2FWH	1830	−6	−2495	−2502	−0.3	0.3
3LZT	1960	8	−2754	−2723	1.1	1.1
Mean	1692	−1.9	−2458	−2454	0.0	0.9

5.2 Dipole moment of solvated proteins

The change in dipole moment as a function of environment for a polarizable solute is a relevant observable in terms of validating GK because it indicates whether or not the reaction field strength is consistent. The PMPB calculations are exactly equivalent to those described in the previous section. Furthermore, the same constant was used in the GK cross-term. In Table 5 it is observed that the total dipole moment of proteins within the GK continuum achieve a mean signed relative difference of −2.7% and a mean unsigned percent difference of 2.7%. This indicates a small, but systematic underestimation of the reaction field. In all cases, for both PMPB and GK models, the reaction field factor was greater than one, except for 1P9G. In this case, the vacuum dipole moment decreased from 18 to 15 and 13 Debye in the PMPB and GK models, respectively. Overall, the mean reaction field factor for the 55 proteins was 1.28 in the PMPB model and 1.24 in GK.

Table 5.

The total dipole moment (Debye) for 55 proteins in vacuum and within the PMPB and GK continuum models. The signed and unsigned relative difference of the GK model to PMPB is given along with their reaction field factors.

	Dipole Moment			% Difference		Reaction Field Factor
	Vacuum	PMPB	GK	Signed	Unsigned	PMPB	GK
1A6M	191.5	252.1	242.6	−3.7	3.7	1.32	1.27
1AHO	119.3	143.6	142.6	−0.7	0.7	1.20	1.20
1BYI	295.8	357.4	343.1	−4.0	4.0	1.21	1.16
1C75	125.0	167.2	165.7	−0.9	0.9	1.34	1.33
1C7K	229.3	310.3	302.7	−2.4	2.4	1.35	1.32
1CEX	451.0	599.7	574.3	−4.2	4.2	1.33	1.27
1EB6	217.9	281.0	274.6	−2.3	2.3	1.29	1.26
1EJG	37.4	49.0	48.9	−0.3	0.3	1.31	1.31
1ETL	29.3	42.9	41.2	−3.8	3.8	1.46	1.41
1EXR	352.5	395.6	384.2	−2.9	2.9	1.12	1.09
1F94	90.7	116.7	113.0	−3.2	3.2	1.29	1.25
1F9Y	138.4	166.0	161.9	−2.5	2.5	1.20	1.17
1G4I	87.9	102.1	97.9	−4.1	4.1	1.16	1.11
1G66	226.5	279.9	273.5	−2.3	2.3	1.24	1.21
1GQV	314.6	394.5	385.2	−2.4	2.4	1.25	1.22
1HJE	48.3	61.2	60.4	−1.4	1.4	1.27	1.25
1IQZ	86.1	110.7	107.2	−3.1	3.1	1.29	1.25
1IUA	107.5	146.1	141.5	−3.2	3.2	1.36	1.32
1J0P	105.2	148.7	142.3	−4.3	4.3	1.41	1.35
1K4I	130.1	163.0	159.6	−2.1	2.1	1.25	1.23
1KTH	117.1	152.1	148.9	−2.1	2.1	1.30	1.27
1L9L	422.8	525.9	517.0	−1.7	1.7	1.24	1.22
1M1Q	261.7	318.1	311.2	−2.2	2.2	1.22	1.19
1NLS	244.9	331.8	313.0	−5.7	5.7	1.35	1.28
1NWZ	83.2	130.2	126.9	−2.5	2.5	1.56	1.53
1OD3	115.2	165.9	160.9	−3.0	3.0	1.44	1.40
1OK0	149.4	193.7	189.1	−2.4	2.4	1.30	1.27
1P9G	17.7	14.6	13.0	−10.7	10.7	0.82	0.74
1PQ7	46.4	49.6	49.1	−1.1	1.1	1.07	1.06
1R6J	86.8	108.8	106.7	−1.9	1.9	1.25	1.23
1SSX	66.0	93.8	89.9	−4.2	4.2	1.42	1.36
1TG0	236.9	316.8	311.1	−1.8	1.8	1.34	1.31
1TQG	355.4	489.5	477.3	−2.5	2.5	1.38	1.34
1TT8	339.6	450.3	434.3	−3.6	3.6	1.33	1.28
1U2H	157.1	206.0	200.6	−2.6	2.6	1.31	1.28
1UCS	111.1	133.0	132.9	0.0	0.0	1.20	1.20
1UFY	94.0	105.9	102.3	−3.4	3.4	1.13	1.09
1UNQ	601.1	735.2	718.8	−2.2	2.2	1.22	1.20
1VB0	132.2	158.2	155.0	−2.0	2.0	1.20	1.17
1VBW	94.4	117.0	114.0	−2.6	2.6	1.24	1.21
1W0N	114.9	155.4	150.0	−3.5	3.5	1.35	1.31
1WY3	63.7	96.4	93.6	−3.0	3.0	1.51	1.47
1X6Z	294.2	366.7	355.9	−2.9	2.9	1.25	1.21
1X8Q	183.8	244.2	237.6	−2.7	2.7	1.33	1.29
1XMK	272.8	356.1	347.0	−2.6	2.6	1.31	1.27
1YK4	66.1	83.7	83.6	−0.2	0.2	1.27	1.26
1ZZK	195.2	246.5	241.6	−2.0	2.0	1.26	1.24
2A6Z	84.1	105.0	101.4	−3.4	3.4	1.25	1.21
2BF9	255.7	290.6	288.4	−0.7	0.7	1.14	1.13
2CHH	267.4	335.7	329.2	−1.9	1.9	1.26	1.23
2CWS	168.6	220.5	211.0	−4.3	4.3	1.31	1.25
2ERL	81.2	108.1	105.6	−2.3	2.3	1.33	1.30
2FDN	78.3	93.2	93.4	0.3	0.3	1.19	1.19
2FWH	104.9	146.3	142.9	−2.3	2.3	1.39	1.36
3LZT	178.5	214.6	209.8	−2.3	2.3	1.20	1.18
Mean	173.2	220.9	215.0	−2.7	2.7	1.28	1.24

6 CONCLUSIONS

Over the course of the past several years GB has been shown to be capable of capturing the electrostatic response of the solvent environment to solutes. It has been successfully applied to molecular dynamics simulations, scoring protein conformations and the prediction of binding affinities.²⁴ However, GB models are generally limited to use with fixed atomic partial charge electrostatic representations. Applications of recent interest, including high-resolution homology modeling, design of protein-protein interactions and design of proteins with enzymatic activity may require improved accuracy in force field electrostatics.^28,29,55 We suggest that the AMOEBA force field coupled with the GK continuum model is a promising improvement.

There are two main differences between GB and GK. First, the GK self-energy of a permanent multipole site depends on Kirkwood’s solution for the electrostatic solvation energy of a spherical particle with arbitrary charge distribution, which is reduced to Born’s formula in the case of a monopole. Second, the GK cross-term is formulated by averaging a simple auxiliary potential for each multipole site, which reduces to the GB cross-term for monopole interactions.

We have implemented GK for the AMOEBA force field, including energy gradients, within the TINKER package.⁵³ The model was tested against numerical PMPB calculations of the electrostatic solvation free energy for a series of 55 diverse proteins and showed a mean unsigned relative difference of 0.9%. The fidelity of the reaction field of GK relative to PMPB can be inferred from the total solvated dipole moment of each protein, which showed GK to have a mean unsigned relative difference of 2.7%.

The next step in the implementation of GK for AMOEBA solutes will be parameterization of a complete implicit solvent model by addition of an apolar term.²⁶ The overall model will be parameterized against small molecules solvation free energies, which has been a successful approach in the past.^{9,10,25,56,57} Alternatively, the electrostatic, dispersion and cavitation components of solvation can be matched to explicit solvent free energy perturbation results.^58–61

GK may be useful for developing new continuum models based on electron densities derived from electronic structure calculations. For example, Cramer and Truhlar have successfully employed GB in their SMX series of solvation models.^8,9,62,63 GK would also offer an analytic alternative to the numerical distributed multipole solvation model of Rinaldi et al.^64,65

Further improvements in both the PMPB and GK continuum electrostatics models may depend on reconciling deficiencies that emerge in treating local, specific molecular interactions. For example, both the Clausius-Mossotti⁴⁰ and Onsager⁶⁶ theories for the permittivity of a liquid break down for substances that “associate”, such as water. Here association is defined as short range ordering that leads to correlations in the orientations and positions of neighboring groups, such as hydrogen bonding pairs. Formalisms introduced by Kirkwood⁶⁷ and Fröhlich⁶⁸ include a correction factor to explicitly account for this deviation from continuum behavior. More recently, Rick and Berne showed that no parameterization of the dielectric boundary for a water molecule in liquid water could simultaneously fit the electrostatic free energy and reaction potential to within 20%, mainly due to nonlinear electrostriction.⁶⁹ This effect, inherent in both numerical and analytic continuum electrostatic models, may be a limiting factor in the accuracy of current implicit solvation models.