A double classification tree search algorithm for index SNP selection

Abstract

Background

In population-based studies, it is generally recognized that single nucleotide polymorphism (SNP) markers are not independent. Rather, they are carried by haplotypes, groups of SNPs that tend to be coinherited. It is thus possible to choose a much smaller number of SNPs to use as indices for identifying haplotypes or haplotype blocks in genetic association studies. We refer to these characteristic SNPs as index SNPs. In order to reduce costs and work, a minimum number of index SNPs that can distinguish all SNP and haplotype patterns should be chosen. Unfortunately, this is an NP-complete problem, requiring brute force algorithms that are not feasible for large data sets.

Results

We have developed a double classification tree search algorithm to generate index SNPs that can distinguish all SNP and haplotype patterns. This algorithm runs very rapidly and generates very good, though not necessarily minimum, sets of index SNPs, as is to be expected for such NP-complete problems.

Conclusions

A new algorithm for index SNP selection has been developed. A webserver for index SNP selection is available at

http://cognia.cu-genome.org/cgi-bin/genome/snpIndex.cgi/

Background

Because SNPs are often coinherited as components of a haplotype, they can be highly correlated. Because of this, it is theoretically possible to choose a much smaller number of SNPs to be used as an index set in identifying haplotype or SNP patterns. Johnson and his collaborators [1] have referred to such characteristic SNPs as haplotype tagging SNPs (htSNPs). Bafna et al. [2] refer to them as informative SNPs, using the language of probability theory. We prefer the use of the more general "index SNPs" to indicate not only haplotype but any SNP patterns. The use of index SNPs can reduce the work in SNP-based genotyping research. Clayton [3] provides computer software for htSNP selection. In his program, he uses five as the default maximum htSNP number and implements a brute force search algorithm to browse over subsets of SNP numbers up to a given maximum, choosing the subset according to predetermined criteria. However, if a large number of index SNPs is required, this algorithm fails. Similarly, Sebastiani and his collaborators [4] have developed a program called BEST (Best Enumeration of SNP Tags); again, use of this program is not feasible with very large sets of SNPs. In the HapScope project, Zhang et al. [5] have developed two programs for selection of index SNPs: BFA, a brute force algorithm and GPA, a greedy partition algorithm. We have re-formulated the index SNP selection problem and developed a new greedy algorithm for index SNP selection based on a double classification tree search algorithm similar to the double search algorithm we previously developed for physical mapping [6]. This is not an enumeration algorithm. It runs rapidly and generates very reasonable results, though not guaranteeing generation of a minimum set, as is expected by the NP-complete nature of problem. The NP-complete property has been proved by Bafna et al [2]. For the reader's convenience, we have attached a brief proof as an appendix.

Algorithm

Classification tree search algorithm for SNP generation

We use a classification tree for partitioning SNP patterns. We choose SNPs as classifiers in constructing classification trees. For example, assume we have a set of SNP patterns or haplotype patterns (henceforth, we will use the terms "SNP patterns" and "haplotype patterns" interchangeably) as shown in Table 1. Note that these are not stretches of contiguous sequence; only the SNP positions are indicated.

Table 1.

A data sample to show the algorithm.

Haplotype1	ACAGATG
Haplotype2	ACGAATG
Haplotype3	ATGGGTG
Haplotype4	GTAAGTG
Haplotype5	GTGGGCA
Haplotype6	GTAGACA
Haplotype7	ATAAGCA
Haplotype8	GTGGACA

We can generate a classification tree as shown in Figure 1.

Figure 1.

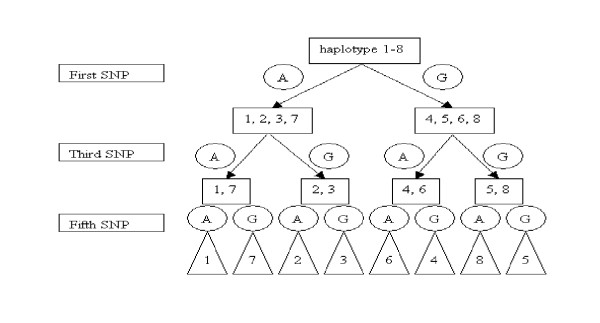
Classification tree search algorithm for the data in Table 1.

Three SNPs (the first, the third, and the fifth) have been chosen as classifiers. The three SNPs can be used to identify the haplotypes. In other words, the three SNPs can be used as index SNPs for the whole set of SNP patterns. In this example, a group of three SNPs is the minimum set of SNPs to distinguish the haplotypes, i.e., the tree has a minimum height of three. It is easy to appreciate that there is no classification tree for the above haplotype set with a height less then three. We propose here a greedy algorithm to generate a classification tree with a "good" height, but no guarantee that it is the minimum height. Our algorithm can be divided into two phases: a greedy phase to choose the classifiers and a tree-building phase to divide the haplotype patterns into the subtrees. A classification tree will be built by recurrently switching from greedy phase to tree building phase until all leaves of the tree have only one haplotype pattern. It is the purpose of our greedy method to choose a classifier from among the SNPs based on its possessing the smallest maximum sized subtree compared to those of the SNPs that have not yet been used as classifiers. If more than one SNP generates smallest maximum subtrees of the same height, we then examine the second maximum subtrees. If they are also the same size, we check the third, and so on. If all classifiers have smallest maximum subtrees of the same size, we can choose any one of them. In the above example, the first SNP has 4 as the maximum size of its subtrees. In contrast, the second SNP has 6 as the maximum size of its subtrees, so it would be rejected. The algorithm is described in Figure 2.

Figure 2.

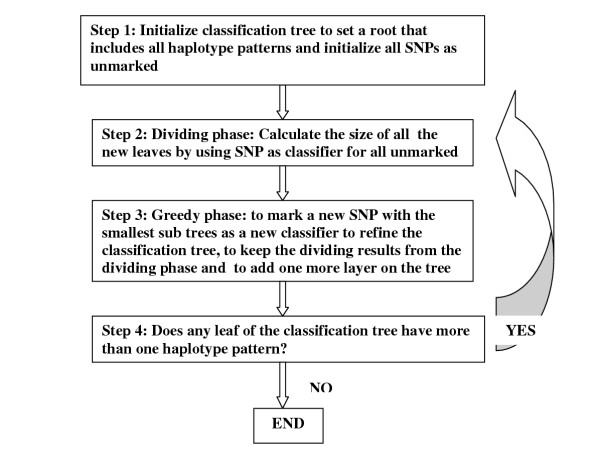
Flow chart of the algorithm.

This algorithm runs very fast. Let the number of SNPs be N and the number of haplotype patterns be M. The major calculation is on the loop of step 2 and step 3. Since the loop can run no more than the number of SNPs: N, step 2 needs less than O(NM) operations. Step 3 needs less than O(NM) operations also. The total complexity of this algorithm is below the order of O(N²M).

Properties of classifiers

We outline some fundamental properties for a set of classifiers. We denote a set of classifiers as a complete set if and only if the set of classifiers can distinguish haplotypes. If no proper subset of a complete set is a complete set, we will call it minimal complete set. The smallest minimal complete set will be called the minimum complete set.

(1) The whole SNP set for the group of haplotypes is a complete set.

(2) For SNPs with only two variations (the major and the minor), the size of a complete set of classifiers cannot be less than log₂ N where N is the number of haplotypes.

(3) Any complete set of classifiers can be used to build up a classification tree. If the complete set is a minimal set, the height of the tree is equal to the number of classifiers in the set.

(4) The classification tree algorithm generates a complete set.

A double classification tree search algorithm

Our goal is to generate a minimum index SNP set. But one run of the above greedy classification tree search algorithm is insufficient to attain this objective. This can be demonstrated by examining the set of SNP data presented in Table 2.

Table 2.

A data sample to show the second round search is needed.

	1	2	3	4	5
A	1	1	1	1	1
B	1	1	1	1	0
C	1	1	1	0	1
D	0	1	1	0	0
E	1	1	0	1	1
F	1	1	0	1	0
G	0	1	0	0	1
H	0	1	0	0	0
I	1	0	1	1	1
J	0	0	1	1	0
K	0	0	1	0	1
L	0	0	0	1	1

Using the previously described classification tree search algorithm:

SNP 1 splits the 12 patterns into groups of 6 and 6;

SNP 2 splits the 12 patterns into groups of 8 and 4;

SNP 3 splits the 12 patterns into groups of 7 and 5;

SNP 4 splits the 12 patterns into groups of 7 and 5;

SNP 5 splits the 12 patterns into groups of 7 and 5.

Based on the algorithm, we choose SNP 1 first as classifier. But no set of four SNPs containing SNP 1 suffice to distinguish all 12 patterns:

SNPs 1, 2, 3, 4 cannot distinguish A from B;

SNPs 1, 2, 3, 5 cannot distinguish A from C;

SNPs 1, 2, 4, 5 cannot distinguish A from E;

SNPs 1, 3, 4, 5 cannot distinguish A from I.

Hence, the algorithm will have to choose all five SNPs to distinguish all the patterns. But SNPs 2, 3, 4, 5 will distinguish these patterns, and clearly that is a minimal set. We have been trapped by SNP 1. In order to avoid such a trap, a second round tree search is needed. For the second round search, we force the last classifier of the first round to be used as the first classifier in the second round. The same rule is followed for choosing the second classifier, and so on. By the double search algorithm, in the first search we may generate classifiers in the order: SNP1, SNP5, SNP3, SNP4, and SNP2; in the second search we will generate in order: SNP2, SNP3, SNP4, and SNP5.

Index SNP selection with constraints

Sometimes it is necessary to select some important and interesting SNPs as the index SNPs. In that case, we can use those SNPs as classifiers first in building up the trees. Then the greedy algorithm is used to choose additional classifiers. On our webserver, the user can provide a list for those SNPs that definitely should be included.

Discussion

The index SNP selection problem is a very important and practical problem. Since it is an NP-complete problem, there is no polynomial algorithm so far for an exact solution. Brute force algorithms have been developed that are useful for small sets of data. In contrast, the double search algorithm is good for both small and large data sets. This algorithm gives a quite reasonable solution but is not guaranteed to generate the minimum index set. Given the NP-complete nature of the problem, it may be possible to develop different approximation algorithms in the future.

We have compared our algorithm with other methods for a set of real data downloaded from UW-FHCRC Variation Discovery Resource (SeattleSNPs) [8]. There are 40 SNPs in this data set (see Figure 3). By our program, 10 index SNPs were selected from left to right numbered 1, 10, 13, 14, 15, 20, 21, 27, 29, and 36. This is a minimum index SNP set. We tried to run Best [4]. After one night, we cancelled the process without any results.

Figure 3.

A test data set was downloaded from UW-FHCRC Variation Discovery Resource (SeattleSNPs). On the top of this table are the locations of the SNPs. For example, the first SNP is located on the 31st base. The last figure on every haplotype is the frequency. For example haplotype one (hap1) has frequency 1087. By our program, 10 index SNPs were selected from left to right numbered 1, 10, 13, 14, 15, 20, 21, 27, 29, and 36. The locations are in bold type. This is a minimum index SNP set. We tried to run the Best program. After one night, we cancelled the process without any results.

This program is designed for haplotype data. It can be extended for genotype data. It is our strategy to select a minimum set of index SNPs after a small set of data has been genotyped and haplotypes have been generated. Then the selected minimum index SNPs will be used to genotype the whole sample set.

This program is limited to deal with biallelic SNP. The non-biallelic case and the missing data case can be developed using a SNP pattern extension.

Authors' contributions

PZ developed the new double search algorithms. HS implemented the web-server. RU provided a brief proof for the NP-completeness. All authors read and approved the final manuscript.

Appendix: A brief proof of the N-P completeness

We reduce the following NP-complete problem known as the minimum test set problem [7] to the minimum index SNP set problem:

Input

Collection C of subsets of a finite set S, positive integer k ≤ C.

Question

Is there a subcollection C' ⊆ C with C' ≤ k such that for each pair of distinct elements u, v ∈ S, there is some set c ∈ C' that contains exactly one of u and v?

Let C = {c₁, ..., c_n} and S = {s₁, ..., s_m}. We then construct a set of SNPs as follows;

(1) the number of SNPs is n (the number of the size of C),

(2) the number of SNP patterns is m (the number of the size of S),

(3) the ith letter of the jth SNP pattern is '1' if s_j ∈ c_i, otherwise '0'.

Intuitively, the jth SNP pattern describes if the element s_j ∈ S is in each subset c_i or not.

The reduction can be done in linear time, and the solution of the minimum index SNP set problem directly gives the solution of the minimum test set problem.