Breast cancer risk prediction using clinical models and 77 independent risk-associated SNPs for women aged under 50 years: Australian Breast Cancer Family Registry

Abstract

Background

The extent to which clinical breast cancer risk prediction models can be improved by including information on known susceptibility single nucleotide polymorphisms (SNPs) is not known.

Methods

Using 750 cases and 405 controls from the population-based Australian Breast Cancer Family Registry who were younger than 50 years at diagnosis and recruitment, respectively, Caucasian and not BRCA1 or BRCA2 mutation carriers, we derived absolute 5-year risks of breast cancer using the BOADICEA, BRCAPRO, BCRAT, and IBIS risk prediction models and combined these with a risk score based on 77 independent risk-associated SNPs. We used logistic regression to estimate the odds ratio per adjusted standard deviation for log-transformed age-adjusted 5-year risks. Discrimination was assessed by the area under the receiver operating characteristic curve (AUC). Calibration was assessed using the Hosmer–Lemeshow goodness-of-fit test. We also constructed reclassification tables and calculated the net reclassification improvement.

Results

The odds ratios for BOADICEA, BRCAPRO, BCRAT, and IBIS were 1.80, 1.75, 1.67, and 1.30, respectively. When combined with the SNP-based score, the corresponding odds ratios were 1.96, 1.89, 1.80, and 1.52. The corresponding AUCs were 0.66, 0.65, 0.64, and 0.57 for the risk prediction models, and 0.70, 0.69, 0.66, and 0.63 when combined with the SNP-based score.

Conclusions

By combining a 77 SNP-based score with clinical models, the AUC for predicting breast cancer before age 50 years improved by >20%.

Impact

Our estimates of the increased performance of clinical risk prediction models from including genetic information could be used to inform targeted screening and prevention.

Introduction

Information from breast cancer risk prediction models is important at the population level to aid decisions on the cost-effective use of limited resources for screening and prevention. It is also useful at the individual level to help women make decisions on screening or prevention tailored to their specific circumstances (1–3). Commonly used breast cancer risk prediction models include: BOADICEA (4, 5) and BRCAPRO (6–8), both of which are based on pedigree data for breast and ovarian cancer; BCRAT (9, 10), which is based on established risk factors and first-degree family history of breast cancer; and IBIS (11), which is based on established risk factors and first-degree and second-degree family history of breast cancer. There have been several prospective validation studies of these models across different age distributions and geographic locations with varied results (12–16). Risk prediction models need to be well calibrated to provide accurate information on the proportion of the population that will develop the disease, and they also need sufficient discriminatory accuracy to be clinically useful. Reclassification tables can be used to quantify the proportion of women that moves into, or out of, clinically important risk categories (17).

Since 2007, genome-wide association studies have identified many single nucleotide polymorphisms (SNPs) that are each associated with a small increment in breast cancer risk. While no single SNP is causal or informative on its own, considering the combined associations of these SNPs has the potential to improve estimates of individual breast cancer risk, as has been recently shown by the Breast Cancer Association Consortium (18).

Modelling and empirical studies have quantified how much the area under the receiver operating characteristic curve (AUC) for BCRAT can be increased by including 7 SNPs (19–21) or 10 SNPs (22). Other analyses have shown how the classification of women into high-risk groups is improved by including 7 SNPs (19, 20, 23) or 15 SNPs (24) to BCRAT. Analyses of 18 SNPs (25) and simulations of 67 SNPs (25, 26) have demonstrated improvement in the ability of IBIS to discriminate women at high risk of breast cancer, while the addition of 76 SNPs and a measure of mammographic density has been shown to increase the AUC for the Breast Cancer Surveillance consortium risk prediction model (27).

Recently, 77 SNPs have been identified that are independently associated with breast cancer and a combined risk score with an AUC of 0.622 (95% CI 0.619, 0.627) and accounts for 14% of the familial aggregation of breast cancer (18). This large multi-center study, however, did not include information on family history and other risk factors, so the clinical utility of the current best SNP-based risk prediction has yet to be formally addressed.

We previously investigated combining the BCRAT risk prediction model with a risk score based on 7 SNPs (19). We now investigate the extent to which risk estimates obtained from BOADICEA, BRCAPRO, BCRAT, and IBIS can be improved, in terms of their calibration and discriminatory accuracy, by combination with a risk score based on the previously identified 77 SNPs (18).

Materials and Methods

Sample

We studied cases and controls from the population-based component of the Australian site of the Breast Cancer Family Registry (ABCFR), which has been described in detail previously (28–30). Cases and controls were recruited during 1992 to 1999, and were adult women living in metropolitan Sydney or Melbourne. Cases were identified from the population-complete cancer registries in New South Wales and Victoria, and included all women aged less than 40 years and a random sample of women aged 40 to 59 years at diagnosis of a histologically confirmed first primary invasive breast cancer. Controls were selected from the electoral roll (to which registration is compulsory for Australian citizens) using proportional random sampling based on the expected age distribution of the cases. All cases and controls completed an interviewer-administered questionnaire that asked about established and putative risk factors for breast cancer and details of cancer diagnoses concerning themselves and their first-degree and second-degree adult relatives. Participants were also asked to provide a blood sample.

The ABCFR recruited 1,223 cases and 805 controls who were aged under 50 years at diagnosis and recruitment, respectively. Of these, 905 (74%) cases and 490 (61%) controls provided a blood sample, and genotyping was performed by the Collaborative Oncological Gene-Environment Study for the 750 cases and 405 controls who were Caucasian and not known to be carriers of mutations in BRCA1 or BCRA2. Estrogen receptor (ER) and progesterone receptor (PR) status was available for 416 (55%) of the cases. For BCRAT, risk score calculations were limited to the 568 cases and 280 controls aged 35 years or older at diagnosis and recruitment, respectively. Genotyping was performed by the Collaborative Oncological Gene–Environment Study (www.cogseu.org) using a custom Illumina iSelect array (31). The 77 SNPs used in this study were those used by Mavaddat et al. (18).

Ethics approval for the study was granted by the human research ethics committees of the University of Melbourne, the Victorian Cancer Council and the New South Wales Cancer Council.

Risk Prediction Models

We calculated the 5-year absolute risk of invasive breast cancer at baseline using four risk prediction models: BOADICEA (4, 5), BRCAPRO (6–8), BCRAT (9, 10), and IBIS (11). For cases, we ignored personal breast cancer diagnosis in the risk calculations. For BOADICEA and BRCAPRO, unknown age at cancer diagnosis for relatives was changed to the earliest of either age at last follow-up or 70 years. For BCRAT, we did not have information on biopsies or atypical hyperplasia, so these variables were coded as unknown. In accordance with BCRAT’s design, its application was restricted to women aged 35 years or older (9, 10). For IBIS, we did not have information on hyperplasia or lobular carcinoma in situ; these and unknown ages were coded as missing. The risk factors based on these risk prediction models were the age-adjusted log 5-year risks.

SNP-Based Risk Score

Using the approach of Mealiffe et al. (20), we calculated a SNP-based (relative) risk score using previously published estimates of the odds ratio (OR) per allele and risk allele frequency (p) (18) assuming independent and additive risks on the log OR scale. For each SNP, we calculated the unscaled population average risk as μ = (1 – p)² + 2p(1 – p)OR + p²OR². Adjusted risk values (with a population average risk equal to 1) were calculated as 1/μ, OR/μ and OR²/μ for the three genotypes defined by number of risk alleles (0, 1, or 2). The overall SNP-based risk score was then calculated by multiplying the adjusted risk values for each of the 77 SNPs (19).

Combined Risk Prediction Model and SNP-Based Risk Scores

For each of BOADICEA, BRCAPRO, BCRAT and IBIS, we calculated a combined risk score by multiplying the SNP-based risk score by the model’s predicted 5-year absolute risk of breast cancer. As for the risk prediction model scores, the risk factors were the age-adjusted log 5-year risks.

Statistical Analysis

The model risk scores, the SNP-based score based on the published estimates, and the combined risk scores were log transformed for all analyses. We used Pearson correlation to test for associations between the model risk scores, the SNP-based score and the combined risk scores.

We used logistic regression to fit the individual and combined risk and SNP-based scores – adjusted for age using the controls – to estimate risk associations, in terms of the OR per standard deviation of the age-adjusted log 5-year predicted risk, while adjusting for age group due to the sampling strategy (32). Model calibration was assessed using the Hosmer–Lemeshow goodness-of-fit test, which compares the expected and observed numbers of cases and controls within groups that were defined by deciles of risk. Discrimination between cases and controls was measured using the AUCs of the risk scores.

As in Mealiffe et al. (20), we categorized 5-year absolute risks as low risk (<1.5%), intermediate risk (≥1.5% and <2.0%) and high risk (≥2.0%) and constructed reclassification tables for each of the risk prediction models as a cross-tabulation of the classification of the risk score from the original model with the risk score from the combined model. The net reclassification improvement statistic was calculated as P(up|case) – P(down|case) + P(down|control) – P(up|control), where up refers to moving to a higher risk category and down refers to moving to a lower risk category.

Stata Release 13 (33) was used for all statistical analyses; all statistical tests were two sided, and P values less than 0.05 were considered nominally statistically significant.

Results

Table 1 shows the characteristics of the study participants. For cases, the mean 5-year risk of breast cancer was 1.04% (SD 1.73%) from BOADICEA, 1.10% (SD 1.93%) from BRCAPRO, and 1.19% (SD 2.51%) from IBIS. For controls, the mean 5-year risk of breast cancer was 0.52% (SD 0.51%) from BOADICEA, 0.55% (SD 0.69%) from BRCAPRO, and 0.62% (SD 0.67%) from IBIS. BCRAT is only applicable to women aged 35 years or older, and for these women, the mean BCRAT 5-year risk of breast cancer was 0.76% (SD 0.34%) for cases and 0.66% (SD 0.31%) for controls The mean SNP-based score was 1.30 (SD 0.61) for cases and 1.08 (SD 0.50) for controls. Supplementary Table 1 shows the genotype distributions and the minor allele frequencies for cases and controls for each of the 77 SNPs as well as the OR per allele (adjusted for age group).

Table 1.

Characteristics of cases and controls

	Cases		Controls
	N	(%)	N	(%)
Age (years)
20–34	182	(24.3)	125	(30.9)
35–39	285	(38.0)	142	(35.1)
40–44	128	(17.1)	77	(19.0)
45–49	155	(20.7)	61	(15.1)
Any first-degree relative with breast cancer
No	661	(88.1)	379	(93.6)
Yes	89	(11.9)	26	(6.4)
Age at menarche (years)
<12	148	(19.7)	66	(16.3)
12	148	(19.7)	98	(24.2)
13	231	(30.8)	113	(27.9)
≥14	218	(29.1)	128	(31.6)
Missing	5	(0.7)	0	(0.0)
Age at first live birth (years)
<20	50	(6.7)	31	(7.7)
20–24	162	(21.6)	86	(21.2)
25–29	225	(30.0)	109	(26.9)
≥30	128	(17.1)	64	(15.8)
No live birth	185	(24.7)	115	(28.4)
Estrogen receptor status
Negative	155	(20.7)
Positive	261	(34.8)
Missing	334	(44.5)
Progesterone receptor status
Negative	118	(15.7)
Positive	298	(39.7)
Missing	334	(44.5)

The SNP-based score was not correlated with the risk scores of any of the risk prediction models: BOADICEA (r = 0.01; 95% CI −0.05, 0.07; P = 0.7), BRCAPRO (r = −0.02; 95% CI −0.08, 0.04; P = 0.5), BCRAT (r = 0.01; 95% CI −0.06, 0.08; P = 0.8), and IBIS (r = 0.02; 95% CI −0.04, 0.07; P = 0.6). For women aged 35 years or older, the BCRAT risk score was modestly correlated with the risk scores for BOADICEA (r = 0.32; 95% CI 0.25, 0.38; P < 0.001), BRCAPRO (r = 0.21; 95% CI 0.14, 0.27; P < 0.001), and IBIS (r = 0.29; 95% CI 0.23, 0.35; P < 0.001). For all women, there were strong correlations between the risk scores for BOADICEA and BRCAPRO (r = 0.93; 95% CI 0.92, 0.94; P < 0.001), BOADICEA and IBIS (r = 0.94; 95% CI 0.93, 0.95; P < 0.001), and BRCAPRO and IBIS (r = 0.86; 95% CI 0.84, 0.87; P < 0.001).

The 5-year risk predictions were all correlated with age: BOADICEA (r = 0.17; 95% CI 0.11, 0.22; P < 0.001), BRCAPRO (r = 0.16; 95% CI 0.10, 0.21; P < 0.001), BCRAT (r = 0.68; 95% CI 0.64, 0.71; P < 0.001), and IBIS (r = 0.14; 95% CI 0.08, 0.19; P < 0.001). The risk prediction models combined with the SNP-based score were all correlated with age: BOADICEA (r = 0.14; 95% CI 0.08, 0.19; P < 0.001), BRCAPRO (r = 0.14; 95% CI 0.09, 0.20; P < 0.001), BCRAT (r = 0.43; 95% CI 0.38, 0.49; P < 0.001), and IBIS (r = 0.10; 95% CI 0.04, 0.16; P < 0.001). The SNP-based score was not correlated with age (r = 0.02; 95% CI −0.036, 0.079; P = 0.5).

Table 2 shows the OR per age-adjusted standard deviation of the risk factors, 95% CI, and chi-square statistic for the Hosmer–Lemeshow goodness-of-fit test for each of the log-transformed risk scores, SNP-based risk score and combined risk scores. The OR for each combined risk score was higher than both the SNP-based score and the model risk score alone. The OR was greatest for the combined BOADICEA and SNP-based score, followed by the combined BRCAPRO and SNP-based score. The OR was least for the IBIS risk score. Using the Hosmer–Lemeshow goodness-of-fit test, while there was evidence that the BOADICEA risk score alone did not give a good fit, there was no evidence that any of the combined risk scores gave a poor fit to the data.

Table 2.

Age group-adjusted odds ratios per age-adjusted standard deviation, with corresponding 95% confidence intervals, and the Hosmer–Lemeshow goodness-of-fit chi-square for log-transformed risk scores

Log-transformed risk score	OR*	(95% CI)	P	χ2†	P
SNP-based	1.46	(1.29, 1.64)	2.4 × 10−16	11.4	0.2
BOADICEA	1.8	(1.57, 2.07)	2.6 × 10−12	20	0.01
BOADICEA and SNP-based	1.96	(1.71, 2.24)	8.3 × 10−11	9.9	0.3
BRCAPRO	1.75	(1.52, 2.02)	5.7 × 10−7	14.4	0.1
BRCAPRO and SNP-based	1.89	(1.66, 2.16)	5.6 × 10−10	8.9	0.4
BCRAT	1.67	(1.43, 1.95)	4.1 × 10−23	7.7	0.5
BCRAT and SNP-based	1.8	(1.55, 2.10)	5.5 × 10−21	7	0.5
IBIS	1.3	(1.16, 1.45)	3.0 × 10−14	7.9	0.4
IBIS and SNP-based	1.52	(1.35, 1.71)	2.6 × 10−12	7.2	0.5

^*adjusted for age group;

^†Hosmer–Lemeshow goodness-of-fit test using 10 groups (8 degrees of freedom) Abbreviations: OR, odds ratio; CI, confidence interval

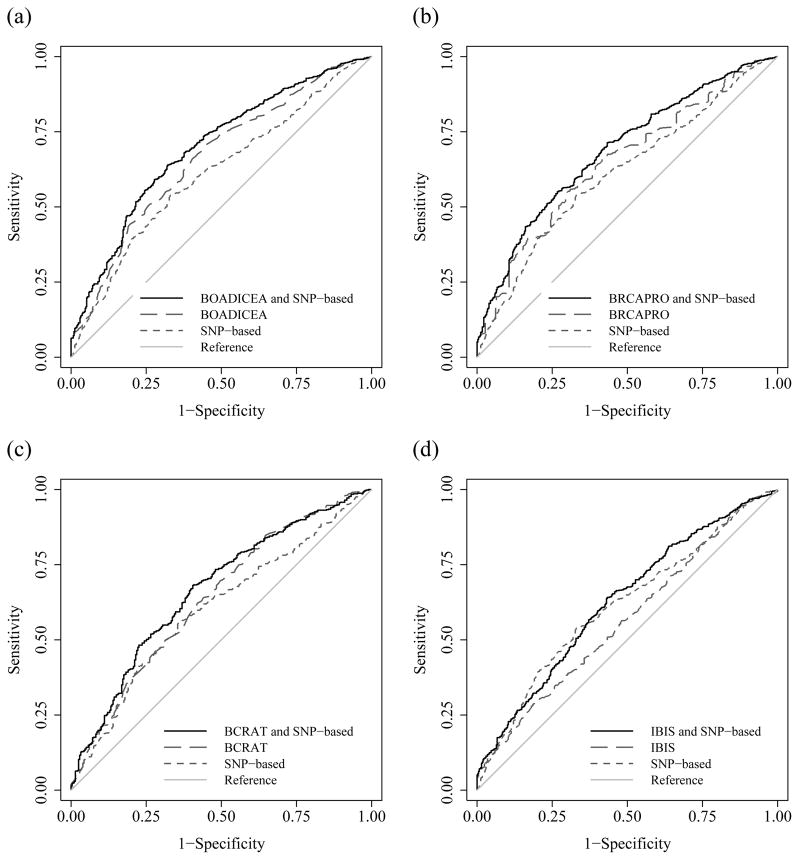
Table 3 shows that, using the AUC criteria, for each of the four risk prediction models the combined risk score gave greater discrimination than both the SNP-based score and the corresponding model risk score. The BOADICEA and SNP combined risk score had the highest AUC, followed by the combined BRCAPRO and SNP-based score, while the IBIS risk score had the lowest AUC. When including the SNP-based score compared with the risk prediction model alone, compared with the baseline of 0.5, the AUC was 25%, 27%, 21%, and 86% higher for the BOADICEA, BRCAPRO, BCRAT, and IBIS models, respectively. Figure 1 shows, for each of the risk prediction models, the receiver operating characteristic curves for the risk prediction model, the SNP-based score and the combined risk score. The combined risk scores increased the AUC for BOADICEA (P = 0.01), BRCAPRO (P = 0.004) and IBIS (P < 0.001), but not for BCRAT (P = 0.2).

Table 3.

Area under the receiver operating characteristic curve for the log-transformed risk scores

Log-transformed risk score	AUC	(95% CI)
SNP-based	0.61	(0.58, 0.65)
BOADICEA	0.66	(0.63, 0.70)
BOADICEA and SNP-based	0.70	(0.67, 0.73)
BRCAPRO	0.65	(0.62, 0.68)
BRCAPRO and SNP-based	0.69	(0.66, 0.72)
BCRAT	0.64	(0.60, 0.68)
BCRAT and SNP-based	0.67	(0.63, 0.70)
IBIS	0.57	(0.53, 0.60)
IBIS and SNP-based	0.63	(0.59, 0.66)

^*adjusted for age group

Abbreviations: AUC, area under the receiver operating characteristic curve; CI, confidence interval

Figure 1.

AUCs for the risk prediction model, SNP-based, and combined model and SNP-based risk scores for (a) BOACICEA, (b) BRCAPRO, (c) BCRAT, and (d) IBIS.

The AUC for the SNP-based score was higher (P = 0.01) for ER positive disease (AUC = 0.65; 95% CI 0.61, 0.69) than for ER negative disease (AUC = 0.56; 95% CI 0.51, 0.61). Similarly, the AUC for the SNP-based score was higher (P = 0.02) for PR positive disease (AUC = 0.64; 95% CI 0.60, 0.68) than for PR negative disease (AUC = 0.56; 95% CI 0.50, 0.62). For the IBIS risk score, the AUC was marginally higher (P = 0.05) for PR negative disease (AUC = 0.64; 95% CI 0.59, 0.70) than for PR positive disease (AUC = 0.57; 95% CI 0.53, 0.62). For the combined BCRAT and SNP-based score, the AUC was marginally higher (P = 0.05) for ER positive disease (AUC = 0.70; 95% CI 0.65, 0.75) than for ER negative disease (AUC = 0.62; 95% CI 0.56, 0.68). For all other risk scores, there was no difference in AUC by ER or PR disease status (data not shown; all P > 0.1).

For each of the four models, the risk scores and the combined risk scores were classified as low risk (1.5%), intermediate risk (≥1.5% and <2.0%), and high risk (≥2.0%), as shown in Table 4, which also shows the percentage of cases and controls moving into higher and lower risk categories. For each of the models, there was a statistically significant net reclassification improvement (all P < 0.05).

Table 4.

Predicted 5-year breast cancer risk for cases and controls according to the risk models and their corresponding combined risk scores

Risk scores	Combined risk score
	Cases					Controls
	<1.5%	≥1.5% and <2.0%	≥2.0%	Up	Down	<1.5%	≥1.5% and <2.0%	≥2.0%	Up	Down	NRI (95% CI)
BOADICEA				9.1%	13.1%				4.7%	1.0%	0.040 (0.007, 0.073)
<1.5%	614	33	24			377	13	4
≥1.5% and <2.0%	7	3	11			2	3	2
≥2.0%	1	2	55			1	1	2
BRCAPRO				10.7%	0%				4.7%	0.2%	0.063 (0.030, 0.094)
<1.5%	616	50	30			382	15	4
≥1.5% and <2.0%	0	0	0			1	0	0
≥2.0%	0	0	52			0	0	3
BCRAT				14.1%	1.4%				6.8%	0.7%	0.066 (0.019, 0.110)
<1.5%	471	45	24			256	13	4
≥1.5% and <2.0%	8	7	11			2	3	2
≥2.0%	0	0	2			0	0	0
IBIS				10.7%	1.1%				6.2%	1.7%	0.052 (0.015, 0.088)
<1.5%	595	44	23			363	18	4
≥1.5% and <2.0%	5	4	13			4	2	3
≥2.0%	2	1	63			1	2	8

Abbreviations: CI, confidence interval; NRI, net reclassification improvement

Note: Up is a change to a higher risk category and down is a change to a lower risk category.

Discussion

For all four clinical risk prediction models, BOADICEA, BRCAPRO, BCRAT and IBIS models, the OR was higher for the combined risk scores than for the models alone, and the AUC was increased by at least 20% when the model risk score was combined with the SNP-based score. We found that the SNP-based score gave greater discrimination for predicting ER positive and PR positive disease, even when combined with the risk prediction scores.

The SNP-based score was not correlated with the risk factors derived from the risk prediction models. This might seem surprising given that the BOADICEA and BRCAPRO risk scores are based on family history and the 77 SNPs explain a non-trivial proportion of breast cancer risk overall (18), but the studies from which the 77 SNPs were discovered were dominated by later onset disease. The issue of SNPs and early-onset disease, for which familial factors are stronger risk factors, remains relatively unexplored. New genome-wide association studies based on early-onset cases in the discovery phase could help rectify this situation and allow even better risk prediction models for young women.

Using SNPs might potentially be better able to improve risk prediction models than using other risk factors for breast cancer (2). For example, perhaps because of the correlation between the mammographic density risk factor and the risk factors involved in the BCRAT model, the inclusion of mammographic density resulted in only a modest improvement in AUC for BCRAT (34, 35).

For each of the risk prediction models, combining with the SNP-based score resulted in about 10% of cases moving into a higher risk category and less than 2% of controls moving into a lower risk category, which is similar to results from a much larger cohort study examining the effect of combining a risk score based on 67 SNPs with the IBIS model (25).

The odds ratio per adjusted standard deviation (OPERA) assesses the ability of a risk factor to discriminate between cases and controls on a population basis (32). It builds on the fact that the estimated risk gradient for a risk factor is its change when holding constant all other factors that have been controlled for. That is why we have fitted the age-adjusted risk scores. If the OR is the risk gradient on a given scale, then OPERA = OR^s, where s is the estimated standard deviation of the risk factor in the population after adjusting for all other factors, and s can be estimated using the control sample.

In this study, the SNP-based score did not vary with the age of controls, but the 5-year risk predictions were strongly associated with age when based on the models alone and when combined with the SNP-based score. Following the OPERA concept, we have presented the ORs in Table 2 in terms of the standard deviations of the age-adjusted risk scores, and this allows comparison of risk gradients across the different risk measures.

The estimated OR for the log SNP-based score alone was 1.46, which is similar to the estimate of 1.55 reported by Mavaddat et al. (18). Based on the OPERA concept, the combinations of the SNP-based score with the 5-year risk predictions from BOADICEA, BRCAPRO, and BCRAT are among the other strongest known risk factors for breast cancer; mammographic density adjusted for age and body mass index typically has an OPERA of about 1.4 (32) and epigenome-wide methylation has been reported to have an OPERA of 1.5 (36). Therefore, the new risk prediction scores that we have derived are now the strongest known means for differentiating women with and without breast cancer, at least for disease diagnosed before age 50 years. In interpreting our risk estimates, note that about half of our cases were younger than 40 years at diagnosis. Familial risk is more important for young women, and for early onset disease, and as such, risk scores based on BOADICEA, BRCAPRO, and SNPs are expected to be more discriminatory.

The four breast cancer risk prediction models investigated here differ in their use of phenotypic information. BOADICEA (4, 5) and BRCAPRO (6–8) both use pedigree-based data, while IBIS (11) uses a combination of pedigrees and established risk factors and BCRAT (9, 10) uses established risk factors with no information about pedigree structure. IBIS (alone or combined with the SNP-based score) has a smaller OR than the other risk prediction models. This may be because IBIS was developed using data from predominately postmenopausal women and is intended for use with high-risk populations (37), while the other models are designed to be used for women unselected for risk factors, as in this study.

A potential weakness of our study was the missing values for the models’ risk score calculations. However, given the key issue we are addressing is how much the addition of the SNP score increases the predictive ability of the models, this should not induce a substantive bias in our estimates of increased predictive performance. We used the approach of multiplying the SNP-based score by the risk factor based on a clinical model so as to be able to compare our findings with those of previous studies (19, 20). We also fitted models along the traditional line in which the SNP-based score and the (virtually independent) risk factor are separate entities (data not shown). When we did this, the estimates for each factor were virtually unchanged. The log likelihoods of the two approaches were generally similar, especially for the BOADICEA and BRCAPRO models. Therefore, our conclusions about the improvements in prediction are robust to the analytic approach.

These risk prediction models are likely to perform better when more SNPs and risk-associated genes are discovered. There could be up to 1,000 more independent SNPs that are associated with risk of breast cancer (31) that could be included in risk prediction models. Analytic approaches that extract more information from genotyping data by, for example, considering pathways or SNP–SNP interactions, might produce better SNP-based risk prediction scores.

Given the multiplicative risk model that underlies epidemiology and now SNP-based genetic risk scores, the distribution of risk for women in the population would appear to be, at least to a good approximation, log normal. To explain the increased risk associated with having an affected family member, it must have a large variance such that the risk for women in the upper quartile is at least 20 times that for women in the lower quartile (38). This study has shown that, by using risk models based on SNPs and family history, substantial proportions of this variance is being explained and there is the ability to differentiate between women at low risk (much less than population average risk) as well as those at increased risk across a very wide range. This opens up the possibility of precision prevention and screening and enables genomic information to substantially lower the impact of breast cancer (39).

In conclusion, we have quantified the extent to which breast cancer risk prediction for women under the age of 50 years is improved by including a risk score based on 77 known susceptibility SNPs. Our estimates of the performance of risk prediction models that combine clinical and genetic information could be used to inform targeted screening and prevention.