Statistical Considerations for a Trial of Ebola Virus Disease Therapeutics

Abstract

The 2014 West African outbreak of Ebola virus ravaged Liberia, Sierra Leone, and Guinea, causing hemorrhagic fever and death. The need to identify effective therapeutics was acute. The usual drug development paradigm of phase I, followed by phase II, and then phase III trials would take too long. These and other factors led to the design of a clinical trial of Ebola virus disease therapeutics that differs from more conventional clinical trial designs. This manuscript describes the Ebola virus disease medical countermeasures (EVD MCM) trial design and the thinking behind it.

Introduction

Ebola viruses cause hemorrhagic fever and are associated with high case fatality rates. Although Ebola virus is not new, the 2014 West African outbreak was much worse than previous outbreaks in terms of geographic range and number of patients affected. It was clear that the usual drug development process of conducting phase I dose finding trials, phase II preliminary efficacy trials, and then phase III definitive trials needed to be accelerated. In fact, the situation was so dire that a debate arose about whether randomized controlled trials of vaccines or therapeutics were ethical.^[1–3] Many clinicians felt obligated to offer their patients experimental treatments. The resulting potpourri of outcome data on different treatments was difficult to interpret. For example, one treatment might be chosen as first line therapy while another might be reserved for the sickest patients because of a preconceived notion, whether correct or incorrect, that it is best. Desperately needed was a randomized controlled trial with frequent monitoring to allow early stopping if one arm clearly shows superiority over the other. This manuscript describes the design and statistical considerations for such a trial.

The design of the EVD MCM trial currently underway (approximately 60 patients were randomized as of the writing of this manuscript) was influenced by several factors. The mortality rate could change over time because of improvements to supportive care, changes in the virus, characteristics of the infected patients, etc. This emphasizes the need to have concurrently randomized controls. Given ethical concerns surrounding a randomized controlled trial for EVD MCM, the control must use the best standard of care available at the given site. Using an experimental treatment as control is problematic because if experimental treatments 1 and 2 show no difference, were they both effective, both ineffective, or both harmful? Even if experimental arm 2 is superior to arm 1, arm 2 could be no better, or even worse, than best standard of care. Another factor influencing the design is that, although there are multiple candidate therapies, one (Zmapp), a mixture of 3 monoclonal antibodies, stood out in terms of supportive pre-clinical data. Therefore, the initial randomization is to Zmapp plus optimized standard of care (oSOC) versus oSOC alone. Circumstances might warrant later inclusion of other agents. For example, there was uncertainty about the availability of Zmapp. If the supply of Zmapp is interrupted for a prolonged period, randomization will be to the next most promising agent versus oSOC during the lull. Another therapeutic could also be introduced into the trial if Zmapp is shown to be effective. In that case Zmapp would likely become part of the new oSOC, to be compared to oSOC plus a new experimental therapy. In any case, each therapeutic is compared only to control patients randomized during the same period. Because information is lacking about factors predicting disease severity and death, only two stratification factors are used: cycle threshold (< 22 versus ≥ 22), which is an indicator of the amount of virus in the body, and location of treatment. Because of the high expected mortality rate, 28-day mortality is the primary outcome. This will be analyzed using a test of proportions rather than a logrank test. The rationale is that a logrank test could be highly statistically significant under scenarios for which treatment should not be considered successful. For example, suppose that nearly everyone dies within 28 days in both arms, but the first Zmapp death occurs after the last oSOC death. The hazard ratio and p-value will both be tiny, but the treatment should not be considered successful if nearly everyone dies in both arms. Nonetheless, a secondary analysis on survival will be conducted to see if results are consistent.

treatment delays death by a matter of days, which would not be a meaningful improvement.

Flexibility and Overview of Barely Bayesian Design

The EVD MCM trial requires more flexibility than a traditional clinical trial. Traditional trials are based on control of the type I error rate, a quantity that is difficult to calculate in a flexible trial in which the design may change as a result of internal (e.g., outcome results) and external (e.g., drug supply) forces. Even in a traditional two-arm trial with a fixed number of patients, unplanned changes can make it difficult to compute type I error rate. For instance, a data and safety monitoring board (DSMB) may decide not to stop even though the pre-specified monitoring boundary is crossed. Calculation of the actual type I error rate is problematic in this situation. Some have argued that one should treat such an interim analysis as though no alpha had been spent, but that assumes there was no chance of stopping the trial. The truth is that if results had been dramatic enough, the trial would have stopped at that analysis. Therein lies a shortcoming of type I error rate: to properly calculate it, we must know how we would have acted if other results had been observed. We need to know whether more extreme results would have caused us to stop. It is not possible to rigorously calculate the type I error rate even in this simple setting. Our setting of an Ebola virus disease treatment trial requires even greater flexibility. For instance, the treatment supply may become scarce, the number of available patients may dwindle, and newer promising agents may become available. It may be very difficult to compute the type 1 error rate in the presence of major, midstream design changes.

We use an alternative analysis we dub “barely Bayesian.” We formulate our prior uncertainty about the 28-day mortality probabilities in the two arms using independent uniform prior distributions on [0, 1]. After observing data, we update these noninformative priors to posterior distributions. This is very easy because the uniform prior is a beta (1, 1) distribution, and the beta is a conjugate prior for the binomial distribution. A beta (1, 1) prior distribution likens our prior opinion to observing 2 people, 1 of whom died. This is consistent with our best guess of 0.5 for the probability of death, but with substantial uncertainty about the guess. The posterior distribution after observing x deaths and n – x survivals in a given arm is beta (1 + x, 1 + n – x):

$$g(p|x)=\{\frac{\mathrm{\Gamma }(n+2)}{\mathrm{\Gamma }(x+1)\mathrm{\Gamma }(n-x+1)}\}{p}^x{(1-p)}^{n-x}=\{\frac{(n+1)!}{x!(n-x)!}{p}^x{(1-p)}^{n-x}\}.$$

It is as if we augmented our observed numbers (x, n–x) of deaths and survivals with our prior opinion corresponding to (1, 1). We then use the posterior distributions in arms A and B to compute the posterior probability that p_A < p_B, which is (see appendix)

$$P(p_A<p_B|x_A,x_B)=\sum _{k=x_A+1}^{n_A+1}\frac{\left(\begin{array}{c}{n}_A+1\\ k\end{array}\right)\left(\begin{array}{c}{n}_B+1\\ x_B\end{array}\right)(n_B-x_B+1)}{\left(\begin{array}{c}{n}_A+n_B+2\\ k+x_B\end{array}\right)(n_A+n_B-k-x_B+2)}.$$ (1)

This posterior probability is analogous to one minus a p-value; large values suggest a treatment benefit. But unlike a p-value, the posterior probability does not depend on what action we would have taken if other results had been observed. The scenario described above in which a monitoring boundary is crossed but the DSMB recommends continuation causes no problems. We simply compute the posterior probability that p_A < p_B given all data, including the interim analysis at which the boundary was not followed. Likewise, if other changes are made, we still use the posterior probability that p_A < p_B to make decisions about the treatment effect.

Another advantage of the Bayesian paradigm is that it easily facilitates inference for both absolute and relative treatment effects. A classical statistical analysis of a binary outcome like 28-day mortality is often based on Fisher's exact test. The parameter corresponding to Fisher's exact test is the odds ratio, which estimates a relative, rather than absolute treatment effect. If we want to describe the uncertainty about the absolute effect, we must either have a large sample size or use a different test statistic. For example, we could use Barnard's unconditional procedure to generate a confidence interval for the absolute difference, but it does not necessarily match the conclusion from Fisher's exact test.^[4] For example, suppose that after 3 patients per arm, all 3 die in one arm and all 3 survive in another. The confidence interval associated with Barnard's test, (0.08, 1), excludes 0, but the two-tailed p-value from Fisher's exact test is 0.1. One could apply melded confidence intervals, but they can be quite conservative^[5]. With the Bayesian methodology described above, the test declares superiority of arm A to Arm B precisely when the posterior probability that p_A < p_B exceeds a given threshold. We can then compute a Bayesian credible interval of likely values for either the absolute effect, p_A–p_B, or the relative effect, p_A/p_B. Either interval will be consistent with the test in the sense that the test of treatment effect will be significant precisely when the credible interval for p_A – p_B excludes 0, which happens precisely when the credible interval for p_A/p_B excludes 1.

Two potential disadvantages of Bayesian methodology are: 1) conclusions depend on the prior distribution chosen, and 2) the type 1 error rate could be inflated to an unacceptable level. Concern over the first point is why we selected a non-informative prior distribution that is quickly over-shadowed by actual data. This can be seen in the above formulation whereby the prior distribution on the mortality probability p in a given arm corresponds to only 2 observations. Moreover, use of the same prior distribution in each arm pushes things toward the null hypothesis. These facts, coupled with conservative interim boundaries, mitigate concern over the second potential disadvantage of Bayesian methodology, namely the potential for substantially inflated type 1 error rate. We will show the error rate can be inflated, but only to a degree that we consider acceptable under the circumstances of an Ebola epidemic.

Monitoring

Monitoring for Efficacy

Aggressive early monitoring is needed because little to no human data exist for potential ebolavirus therapeutics, and because of high expected mortality. We would like to be able to stop quite early if the experimental arm has either unforseen harm or convincing benefit. On the other hand, aggressive early monitoring inflates the type 1 error rate if it is not accounted for.^[6–7] We stop for benefit at an interim analysis only if the posterior probability that arm A is superior to arm B is 99.9% or higher. This is similar in spirit to the Haybittle-Peto classical monitoring boundary requiring a p-value of 0.001 to stop for benefit at an interim analysis.^[8] If the trial proceeds to the end, arm A is declared superior if the posterior probability that p_A < p_B is 97.5% or higher.

The earliest time at which the boundary can be crossed is after 6 patients per arm; if all 6 survive in arm A and all 6 die in Arm B, the posterior probability that A is better, from equation (1), is 0.9997. We therefore monitor beginning with 6 per arm and after each additional observation up to 20 per arm in case there is overwhelming efficacy early. After that, we monitor after each additional 20 per arm until the target of 100 per arm is reached. Table 1 shows boundaries for between 6 and 12 patients per arm. For example, the fourth column shows boundaries for 9 patients per arm. Arm A is declared superior to arm B if the numbers of deaths in arms A and B are (0, 7), (0, 8), (0, 9), (1, 8), (1, 9), or (2, 9). At the end of the trial, with 100 per arm, the z-score to declare arm A superior to arm B is very close to 1.96. That is, the conclusion using the barely Bayesian approach is nearly identical to that of a z-test of proportions at one-tailed α of 0.025.

Table 1.

Barely Bayesian boundaries for numbers per arm given in top row. Boundaries in parentheses are numbers of deaths in arms (A,B) to declare A superior, with + indicating that number or greater.

6	7	8	9	10	11	12
(0, 6)	(0, 6+)	(0, 7+)	(0, 7+)	(0, 7+)	(0, 7+)	(0, 7+)
	(1, 7)	(1, 8)	(1, 8+)	(1, 8+)	(1, 9+)	(1, 9+)
			(2, 9)	(2, 9+)	(2, 10+)	(2, 10+)
				(3, 10)	(3, 11)	(3, 11+)
					(4, 11)	(4, 12)
						(5, 12)

Comparison with Other Test Statistics and Boundaries

Two interesting contrasts of the barely Bayesian method with other methods are comparing different tests at a given level of evidence (e.g., 0.001 or 0.025), and comparing monitoring boundaries that “spend” alpha differently. We first compare the barely Bayesian test with Fisher's exact test at an early interim analysis using a level of evidence corresponding roughly to α = 0.001. Fisher's exact test conditions on the marginal totals of the 2×2 table summarizing the number of deaths and survivals in the two arms, and sums the probabilities of all tables that are consistent with these marginals and are at least as extreme as the observed table. We would like to be able to stop and declare benefit if one arm is clearly superior to another, but with few patients assigned to each arm, the number of tables consistent with the observed marginals could be quite small. This means that with Fisher's exact test, we may not be able to achieve a p-value less than 0.001; i.e., we cannot reject the null hypothesis. For instance, even if no one dies in arm A and everyone dies in arm B, it is impossible for Fisher's exact test to reach a one-tailed p-value of 0.001 or less unless there are 7 people per arm. As noted in the preceding section, the barely Bayesian method yields a 99.97% posterior probability that the mortality rate is lower in arm A than in arm B if 0 of 6 and 6 of 6 patients die in arms A and B. Therefore, the boundary is crossed with only 6 per arm instead of the 7 required by Fisher's exact test. Other scenarios showing very favorable early results also lead to a definitive conclusion with the barely Bayesian method, but not with Fisher's exact test. For example, the barely Bayesian method reaches a definitive finding with 7 per arm if all 7 survive and 1 of 7 survive in arms A and B, whereas the one-tailed Fisher's exact p-value of 0.002 does not meet the required level of 0.001.

One alternative method is Barnard's test, which does not condition on the total number of deaths.^[4] We calculate the null probability of each table with the given sample sizes that is at least as extreme as the observed table. This probability depends on the common mortality probability p, so we must maximize over p. Because the number of possible tables is greater than with Fisher's exact test, the null distribution is finer, and we can find an attainable alpha level closer to 0.001. Moreover, when one arm has strikingly good results and the other arm has strikingly bad results, Barnard's test declares a treatment difference when Fisher's exact test does not. For instance, suppose 0 of n and n of n patients die in arms A and B. Whether we use Barnard's test or Fisher's exact test, there is only one table as extreme, namely itself. The probability of that table, without conditioning on the total number of deaths, is pⁿ(1 – p)ⁿ = {p(1 – p)}ⁿ. For Barnard's test we maximize this expression over p. The maximimum of {p(1 – p)}ⁿ occurs at p = 1/2, with maximum value (1/4)ⁿ. Therefore, if 0 out of 5 and 5 out of 5 die in arms A and B, the one-tailed p-value is (1/4)⁵ < 0.001. That is, Barnard's test can lead to a boundary crossing with only 5 per arm.

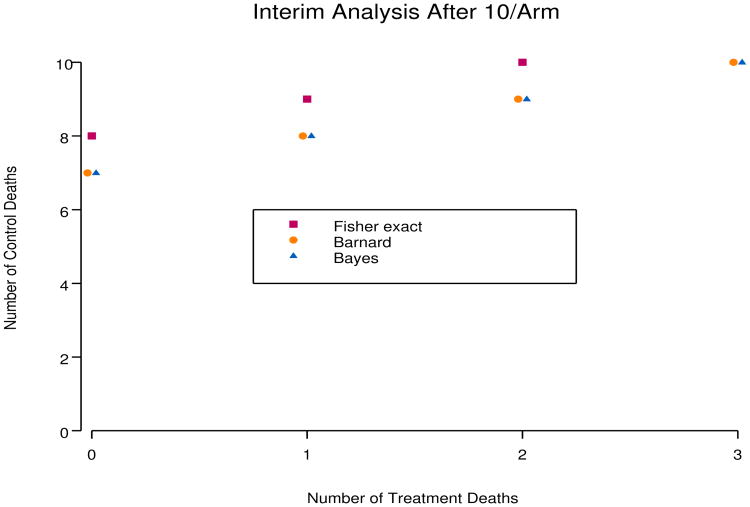
The Bayesian method is quite close to Barnard's method. Figure 1 shows that the rejection regions for the barely Bayesian and Barnard methods are identical for sample sizes of 10 per arm, while the rejection region for Fisher's exact test at level 0.001 is more conservative. With larger sample sizes, rejection regions for the three methods become indistinguishable, and credible intervals for p_T – p_C are very close to confidence intervals using Barnard's test. For the very small sample size case, if no one dies in arm A and everyone dies in arm B, the numbers per arm required for Barnard's test, the Bayesian method, and Fisher's exact test are 5, 6, and 7, respectively.

Figure 1.

Comparison of rejection regions with 10/arm. If the number of deaths in the control arm is greater than or equal to the boundary value, treatment is declared beneficial.

The other comparison of interest involves the rate of spending of type 1 error rate over information time. Traditional monitoring methods spend very little alpha early in the trial. The advantage is that the boundary at the end of the trial is close to what it would have been with no interim monitoring, but a disadvantage is that the early boundaries may be virtually impossible to cross. For example, consider the spending function analog of the O'Brien-Fleming boundary.^[9–10] Even if everyone dies in the oSOC arm and no one dies in the experimental arm, the boundary is not crossed until there are 15 patients per arm (although less drastic modifications have been proposed.^[11] There is an ethical imperative to stop before results are that overwhelming. On the other hand, if we lower early boundaries too much, the final boundary may have to be dramatically increased to prevent unacceptable inflation of the type 1 error rate. This leads to a reduction in power. An example is the Pocock boundary, which Pocock himself now recommends against.^[12] We must therefore find a compromise that both challenges and navigates the perilous torrent of aggressive early monitoring.

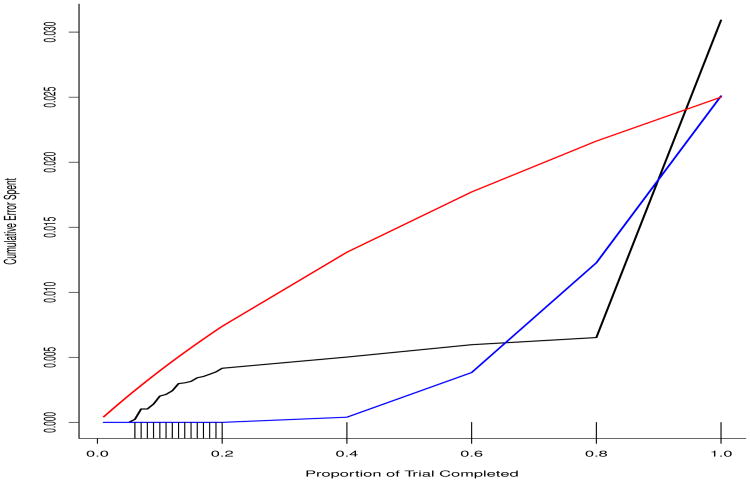
Figure 2 shows that the barely Bayesian approach is a compromise between the very conservative spending of the O'Brien-Fleming-like spending function (blue curve) and the liberal spending of the Pocock-like spending function (red curve). The black curve representing the barely Bayesian method spends more early than does O'Brien-Fleming, but less than Pocock. Much later in the trial, the barely Bayesian and O'Brien-Fleming spending functions cross, but then cross again, so that the barely Bayesian method ends up the highest. However, it should be stressed that the Bayesian method does not control the type 1 error rate at the 0.025 level.

Figure 2.

The rate of spending of type 1 error rate of the barely Bayesian method (black curve) compared to the O'Brien-Fleming (blue curve) and Pocock (red curve) methods for the monitoring schedule depicted as hash marks on the x-axis.

Credible Intervals

Estimation in the Bayesian paradigm is straightforward using the posterior distributions of p_A and p_B given the observed numbers x_A and x_B of deaths by day 28 in arms A and B among those randomized at least 28 days prior to the analysis date. From these posterior distributions, we compute the posterior distribution of the treatment effect measure. For instance, the posterior distribution function H(θ | x_A, x_B) and density function h(θ | x_A, x_B) of θ = p_A – p_B are

$$H(\theta |x_A,x_B)={\int }_0^1{G}_A(\theta +p|x_A)g_B(p|x_B)dp$$ (2)

$$h(\theta |x_A,x_B)={\int }_0^1{g}_A(\theta +p|x_A)g_B(p|x_B)dp,$$ (3)

where g_A(p | x_A) and G_A(p|) denote the beta posterior density and distribution functions of p_A given x_A, and similarly for g_B(p | x_B) and G_B(p | x_B). One can use numerical integration to evaluate the above expressions. An alternative is to use the double sum expression for the density derived in the appendix. To be consistent with the monitoring plan, we use 99.8% two-tailed credible intervals at an interim analysis because that corresponds to a one-tailed level of 0.001. The final analysis uses a 95% two-tailed credible interval.

Inference on the relative risk is also straightforward. The posterior distribution function H(λ | x_A, x_B) and density function h(λ, x_A, x_B) for λ = p_A/p_B given x_A and x_B are

$$H(\mathrm{\lambda }|x_A,x_B)={\int }_0^1{G}_A(\mathrm{\lambda }p|x_A)g_B(p|x_B)dp$$ (4)

$$h(\mathrm{\lambda }|x_A,x_B)={\int }_0^{1}p{g}_A(\mathrm{\lambda }p|x_A)g_B(p|x_B)dp.$$ (5)

The appendix derives expressions for the distribution and density functions involving single finite sums.

Hypothetical Data at Interim Analyses

We illustrate the use of the barely Bayesian methodology with two hypothetical interim analyses, one after 6 patients per arm, and the other after 12 in arm A and 11 in arm B.

Suppose that the numbers of deaths by 28 days in arms A and B at the first interim analysis with 6 per arm are x_A = 1 and x_B = 3. The posterior distributions of p_A and p_B are beta (1+1, 1+5) = (2, 6) and beta (1+3, 1+3) = (4, 4), respectively. The posterior probability that arm A has a lower mortality probability than arm B is obtained using equation (1):

$$P(p_A<p_B|1,3)=\sum _{k=2}^7\frac{\left(\begin{array}{c}7\\ k\end{array}\right)\left(\begin{array}{c}7\\ 3\end{array}\right)(4)}{\left(\begin{array}{c}14\\ k+3\end{array}\right)(11-k)}=0.867.$$

This posterior probability seems fairly high, but it is not close to the level of 0.999 required to stop early. We estimate the absolute difference p_A – p_B by the median of its posterior distribution: equating (2) to 0.5 and solving for θ yields −0.26. This is very close to the posterior mean of p_A – p_B, which is 2/(2 + 6) – 4/(4 + 4) = −0.25. The 99.8% credible interval for θ = p_A – p_B, obtained by equating (2) to 0.001 and 0.999 and solving for θ, is (−0.82, 0.45). We can also estimate the relative risk λ = p_A/p_B: p_A/p_B is estimated by 0.47, 99.8% credible interval: (0.01,4.48).

At the second analysis with n_A = 12 and n_B = 11, suppose there are 2 deaths in arm A and 5 in arm B. The posterior credible intervals and probabilities that arm A is superior are:

1. p_A – p_B = −0.25, 99.8% credible interval: (−0.72,0.30)

2. p_A/p_B = 0.44, 99.8% credible interval: (0.03, 2.70).

3. Posterior probability that arm A is better: 0.923.

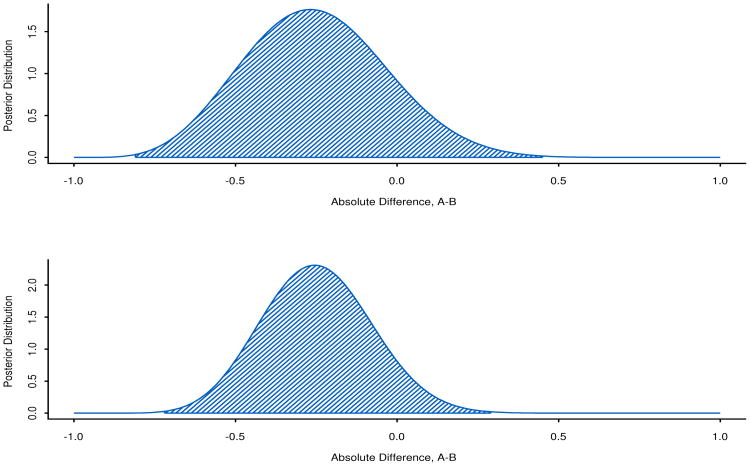
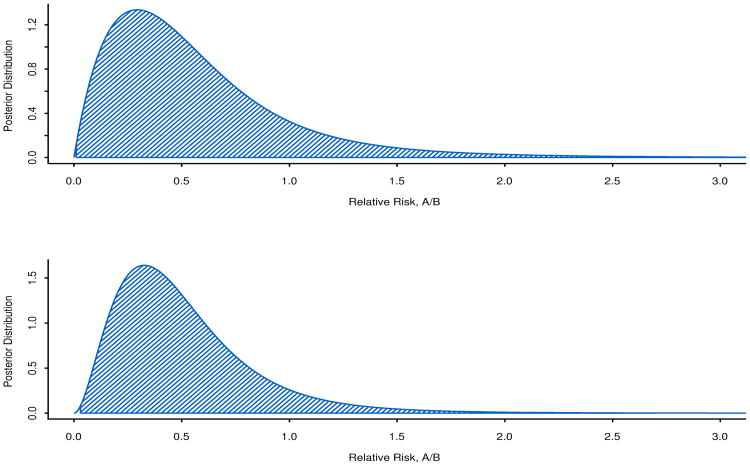
Graphs of the posterior distribution functions, together with 99.8% credible intervals, are shown in Figures 3 and 4. These are useful because they visually depict the increase in information through greater peakedness of the posterior distribution of the parameter with 23 people compared to 12 people.

Figure 3.

Differences in 28-day mortality probabilities, p_A – p_B, at the first hypothetical analysis with n_A = n_B = 6 and the second hypothetical analysis with n_A = 12, n_B = 11. The 99.8% credible intervals are shaded.

Figure 4.

Ratio of 28-day mortality probabilities, p_A/p_B, at the first hypothetical analysis with n_A = n_B = 6 and the second hypothetical analysis with n_A = 12, n_B = 11. The 99.8% credible intervals are shaded.

An Intriguing Connection to Fisher's Exact Test

The barely Bayesian method is always more powerful than Fisher's exact test, as the following connection shows. Earlier we stated that the posterior probability that p_A < p_B is analogous to one minus a p-value. It turns out that there is more than just an analogy. The proof of the following result is in the appendix.

Theorem 1

For independent uniform prior distributions on p_A and p_B, the posterior probability that p_A < p_B is 1 – p_val, where p_val is the one-tailed p-value from Fisher's exact test after adding a non-event to arm A and an event to arm B.

This characterization of the barely Bayesian method gives it the appearance of cheating. But another way to view the method is as an attempt to correct the overly conservative Fisher's exact test. When the sample sizes are small, Fisher's exact test can be very conservative, and adding a control death and a treatment survival is a correction. When the sample sizes are large, the correction is very small and the barely Bayesian procedure is asymptotically equivalent to Fisher's exact test.

It is clear from Theorem 1 that the barely Bayesian method is always more powerful than Fisher”s exact test, albeit at the cost of a somewhat inflated type 1 error rate. Figure 5 shows the comparison of cumulative probability of declaring a treatment benefit by different times for the barely Bayesian and Fisher's exact methods. Cumulative power is always higher for the barely Bayesian method.

Figure 5.

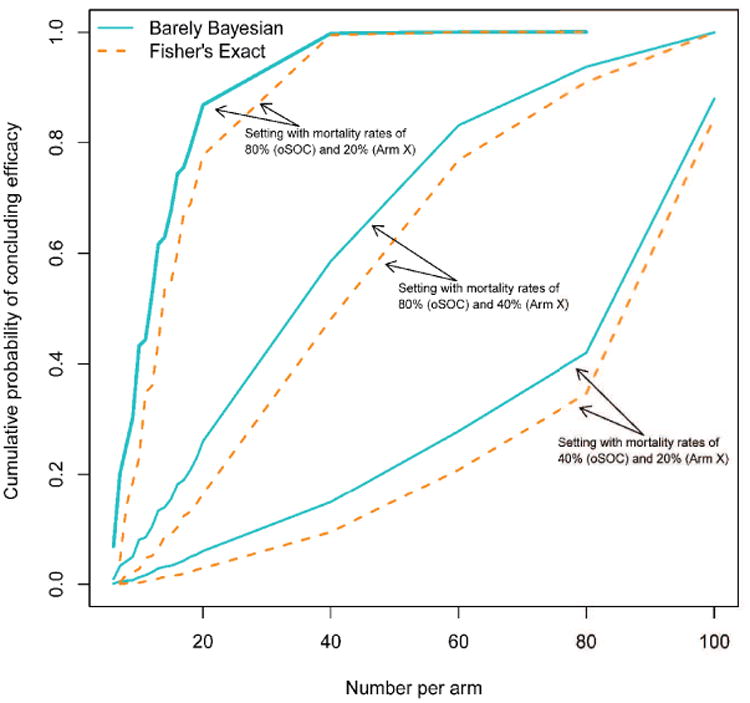
Cumulative power by different times in the trial for the barely Bayesian method compared to Fisher's exact test coupled with the Haybittle-Peto procedure.

Futility and Curtailment for External Reasons

A subset of the steering committee blinded to outcome data will make recommendations concerning stopping one or more treatments for external reasons, such as the epidemic ending. If this occurs, we will compute 95% (not 99.8%) credible intervals at that time. This is analogous to spending all unused alpha at the time the study is terminated. Such a procedure could be abused if the termination recommendation were instead made by a group with access to outcome data by arm. The concern would be that if one saw strong results that did not meet the 99.8% threshold, one could still declare a significant result by declaring the trial over and using a less stringent level of 95%.

In addition to stopping for external reasons, the trial could stop for futility. The conditional probability of reaching a significant result at the end of the trial will be calculated given the current results by arm. This conditional power calculation will be made only after 40% of the trial is completed. Consideration for stopping for futility will be given if the conditional power, computed under the original assumption of a 50% mortality reduction, is less than 0.20.

A sensitivity Analysis Incorporating Partial Followup

As argued earlier, analysis of proportions of deaths by 28 days is preferred to survival methods, but analysis of proportions is less efficient because it ignores information from partial followup.^[13] One way to ameliorate this problem is to conduct a sensitivity analysis of the patients with less than 28 days of followup. For instance, suppose that an interim analysis using only patients with 28-day followup produces a result that crosses, or is close to, a boundary. For people with less than 28 days of followup, consider all possible outcomes. For instance, suppose there are 5 people with less than 28 days of followup, 2 in oSOC and 3 in Zmapp. There are 2⁵ possible 5-tuples corresponding to 28-day survival/death for each of 5 people. For each possible 5-tuple, recompute the test statistic and see whether the boundary is crossed. Compute the probability of the 5-tuple using the conditional 28-day mortality probabilities given survival so far. For instance, for a patient with 10 days of followup, compute the conditional probability of death by day 28 given survival to day 10. One could use either arm-specific or overall conditional probabilities in this calculation. Sum the probabilities of all 5-tuples leading to crossing of the boundary. This “conditional power” estimates the probability of exceeding the boundary if we had 28-day mortality on everyone. High conditional power provides confidence that the answer will not change once everyone has the full 28 days of followup.

Discussion

A randomized controlled trial in Ebola disease is needed to efficiently determine whether one or more experimental therapies are beneficial. Such a trial must have adaptive features to react to both internal and external conditions. We have presented a design that attempts to balance efficiency, rigor, and flexibility. The design leads to a small increase in the type 1 error rate, but gains power over more standard methods. The degree of inflation of type 1 error rate is considered acceptable under the circumstances of an Ebola outbreak. Although motivated by Bayesian thinking, boundaries are similar to the Haybittle-Peto boundary applied to Barnard's test. In adaptive settings such as this, it is very convenient to think in terms of posterior probabilities instead of p-values. The Bayesian framework also easily facilitates estimation of either relative or absolute effects in a way that matches the conclusion of the statistical test. The flexibility afforded by this design allows changing to a new standard of care if data confirms efficacy of a study agent. The primary analysis after such a change would involve concurrently enrolled participants. Although the current decline in cases in West Africa makes it difficult to demonstrate effectiveness of multiple agents, such flexibility may be useful in future studies of therapeutics of emerging infectious diseases. Indeed, we recommend the barely Bayesian design in other serious epidemics with similar circumstances.

Appendix: Derivation of Formulas

Posterior probability that arm A is superior to arm B

(i.e., p_A < p_B)

$$\begin{array}{c}P(p_A<p_B|x_A,x_B)={\int }_0^1{G}_A(p|x_A)g_B(p|x_B)dp\\ ={\int }_0^1\sum _{k=x_A+1}^{n_A+1}\left(\begin{array}{c}{n}_A+1\\ k\end{array}\right)p^k{(1-p)}^{n_A+1-k}\frac{\mathrm{\Gamma }(n_B+2)p^{x_B}{(1-p)}^{n_B-x_B}}{\mathrm{\Gamma }(x_B+1)\mathrm{\Gamma }(n_B+1-x_B)}dp\\ =\sum _{k=x_A+1}^{n_A+1}\left(\begin{array}{c}{n}_A+1\\ k\end{array}\right)\frac{\mathrm{\Gamma }(n_B+2)}{\mathrm{\Gamma }(x_B+1)\mathrm{\Gamma }(n_B+1-x_B)}{\int }_0^1{p}^{k+x_B}{(1-p)}^{n_A+n_B-x_B-k+1}dp\\ =\sum _{k=x_A+1}^{n_A+1}\left(\begin{array}{c}{n}_A+1\\ k\end{array}\right)\frac{(n_B+1)!}{x_B!(n_B-x_B)!}\frac{\mathrm{\Gamma }(k+x_B+1)\mathrm{\Gamma }(n_A+n_B-x_B-k+2)}{\mathrm{\Gamma }(n_A+n_B+3)}\\ =\sum _{k=x_A+1}^{n_A+1}\frac{\left(\begin{array}{c}{n}_A+1\\ k\end{array}\right)\left(\begin{array}{c}{n}_B+1\\ x_B\end{array}\right)(n_B-x_B+1)}{\left(\begin{array}{c}{n}_A+n_B+2\\ x_B+k\end{array}\right)(n_A+n_B-x_B-k+2)}.\end{array}$$

Posterior Distribution/Density of Relative Risk

Assume λ ≤ 1

$$H(\mathrm{\lambda }|x_A,x_B)=Pr(p_A/p_B\le \mathrm{\lambda }|x_A,x_B)={\int }_0^{1}P(p_A\le {\mathrm{\lambda }}_p|x_A)g_B(p|x_B)dp={\int }_0^1{G}_A(\mathrm{\lambda }p|x_A)g_B(p|x_B)dp.$$

Now differentiate with respect to λ to obtain the density:

$$\begin{array}{c}h(\mathrm{\lambda }|x_A,x_B)={\int }_0^{1}p{g}_A({\mathrm{\lambda }}_p|x_A)g_B(p|x_B)dp\\ ={\int }_0^1\frac{(n_B+1)!(n_A+1)!p^{x_B+1}{(1-p)}^{n_B-x_B}{(\mathrm{\lambda }p)}^{x_A}{(1-\mathrm{\lambda }p)}^{n_A-x_A}}{x_B!(n_B-x_B)!x_A!(n_A-x_A)!}dp\\ =\frac{(n_B+1)!(n_A+1)!{\mathrm{\lambda }}^{x_A}}{x_B!x_A!(n_B-x_B)!(n_A-x_A)!}{\int }_0^1{p}^{x_B+x_A+1}{(1-p)}^{n_B-x_B}{(1-\mathrm{\lambda }p)}^{n_A-x_A}dp\\ =\frac{(n_B+1)!(n_A+1)!{\mathrm{\lambda }}^{x_A}}{x_B!x_A!(n_B-x_B)!(n_A-x_A)!}{\int }_0^1{p}^{x_B+x_A+1}{(1-p)}^{n_B-x_B}\sum _{k=0}^{n_A-x_A}(\begin{array}{c}{n}_A-x_A\\ k\end{array}){(1)}^k{(-\mathrm{\lambda }p)}^{n_A-x_A-k}dp\\ =\frac{(n_B+1)!(n_A+1)!}{x_B!x_A(n_B-x_B)!(n_A-x_A)!}\sum _{k=0}^{n_A-x_A}\left(\begin{array}{c}{n}_A-x_A\\ k\end{array}\right){(-1)}^{n_A-x_A-k}{\mathrm{\lambda }}^{n_A-k}{\int }_0^1{p}^{x_B+1+n_A-k}{(1-p)}^{n_B-x_B}dp\\ =\frac{(n_B+1)!(n_A+1)!}{x_B!x_A!(n_A-x_A)!}\sum _{k=0}^{n_A-x_A}\frac{(n_A-k+x_B+1)!}{(n_B+n_A-k+2)!}\left(\begin{array}{c}{n}_A-x_A\\ k\end{array}\right){(-1)}^{n_A-x_A-k}{\mathrm{\lambda }}^{n_A-k}.\end{array}$$

To obtain the distribution function, integrate over λ:

$$H(\mathrm{\lambda }|x_A,x_B)=\frac{(n_B+1)!(n_A+1)!}{x_B!x_A!(n_A-x_A)!}\sum _{k=0}^{n_A-x_A}\frac{(n_A-k+x_B+1)!}{(n_A-k+1)(n_B+n_A-k+2)!}(\begin{array}{c}{n}_A-x_A\\ k\end{array}){(-1)}^{n_A-x_A-k}{\mathrm{\lambda }}^{n_A-k+1}.$$

For λ > 1

Reverse the roles of A and B and replace λ by 1/λ in the distribution function:

$$H(\mathrm{\lambda }|x_A,x_B)=1-\frac{(n_A+1)!(n_B+1)!}{x_A!x_B!(n_B-x_B)!}\sum _{k=0}^{n_B-x_B}\frac{(n_B-k+x_A+1)!}{(n_B-k+1)(n_A+n_B-k+2)!}(\begin{array}{c}{n}_B-x_B\\ k\end{array}){(-1)}^{n_B-x_B-k}{(1/\mathrm{\lambda })}^{n_B-k+1}.$$

Differentiate with respect to λ to get the density:

$$h(\mathrm{\lambda }|x_A,x_B)=\frac{(n_A+1)!(n_B+1)!}{x_A!x_B!(n_B-x_B)!}\sum _{k=0}^{n_B-x_B}\frac{(n_B-k+x_A+1)!(n_B-k+1)}{(n_B-k+1)(n_A+n_B-k+2)!}(\begin{array}{c}{n}_B-x_B\\ k\end{array}){(-1)}^{n_B-x_B-k}{\mathrm{\lambda }}^{-(n_B-k+2)}.$$

Posterior Distribution/Density for Absolute Effect

The posterior distribution function and density for the difference in mortality probabilities, p_A – p_B, given x_A deaths out of n_A in arm A and x_B deaths out of n_B in arm B, are slightly more complicated:

$$\begin{array}{c}H(\theta |x_A,x_B)=P(p_A-p_B\le \theta |x_A,x_B)={\int }_0^1{G}_A(\theta +p|x_A)g_B(p|x_B)dp\text{and}\\ h(\theta |x_A,x_B)=\frac{dH(\theta |x_A,x_B)}{d\theta }={\int }_0^1{g}_A(\theta +p|x_A)g_B(p|x_B)dp={\int }_0^{1-\theta }{g}_A(\theta +p|x_A)g_B(p|x_B)dp.\end{array}$$

We can simplify h(θ | x_A, x_B) for nonnegative θ as follows. h(θ | x_A, x_B)

$$\begin{array}{c}h(\theta |x_A,x_B)\\ =\frac{(n_B+1)!(n_A+1)!}{x_B!x_A!(n_B-x_B)!(n_A-x_A)!}{\int }_0^{1-\theta }{p}^{x_B}{(1-p)}^{n_B-x_B}{(\theta +p)}^{x_A}{(1-\theta -p)}^{n_A-x_A}dp\\ =c{\int }_0^{1-\theta }\sum _{i=0}^{x_A}\sum _{j=0}^{n_A-x_A}{\theta }^i{p}^{x_A-i}\left(\begin{array}{c}{x}_A\\ i\end{array}\right){(1-p)}^j{(-\theta )}^{n_A-x_A-j}\left(\begin{array}{c}{n}_A-x_A\\ j\end{array}\right)p^{x_B}{(1-p)}^{n_B-x_B}dp\\ =c{\int }_0^{1-\theta }\sum _{i=0}^{x_A}\sum _{j=0}^{n_A-x_A}\left(\begin{array}{c}{x}_A\\ i\end{array}\right)\left(\begin{array}{c}{n}_A-x_A\\ j\end{array}\right){(-1)}^{n_A-x_A-j}{\theta }^{n_A-x_A+i-j}{p}^{x_B+x_A-i}{(1-p)}^{n_B-x_B+j}dp\\ =c\sum _{i=0}^{x_A}\sum _{j=0}^{n_A-x_A}\left(\begin{array}{c}{x}_A\\ i\end{array}\right)\left(\begin{array}{c}{n}_A-x_A\\ j\end{array}\right){(-1)}^{n_A-x_A-j}{\theta }^{n_A-x_A+i-j}{\int }_0^{1-\theta }{p}^{x_B+x_A-i}{(1-p)}^{n_B-x_B+j}dp\\ =c\sum _{i=0}^{x_A}\sum _{j=0}^{n_A-x_A}\left(\begin{array}{c}{x}_A\\ i\end{array}\right)\left(\begin{array}{c}{n}_A-x_A\\ j\end{array}\right)\frac{(x_B+x_A-i)!(n_B-x_B+j)!}{(n_B+x_A-i+j+1)!}{(-1)}^{n_A-x_A-j}{\theta }^{n_A-x_A+i-j}{B}_{\gamma ,\eta }(1-\theta ).\end{array}$$

Where

$$\begin{array}{ccc}c=\frac{(n_B+1)!(n_A+1)!}{x_B!x_A!(n_B-x_B)!(n_A-x_A)!},& \gamma =x_B+x_A-i+1,& \eta =n_B-x_B+j+1\end{array}$$ (6)

and B_a,b(·) is the beta-distribution function with parameters a and b.

For negative θ, write H(θ | x_A, x_B) as P(p_A – p_B ≤ θ | x_A, x_B) = 1 – P(p_B – p_A ≤ −θ | x_A, x_B). Now differentiate with respect to θ to obtain

$$c\sum _{i=0}^{x_B}\sum _{j=0}^{n_B-x_B}\left(\begin{array}{c}{x}_B\\ i\end{array}\right)\left(\begin{array}{c}{n}_B-x_B\\ j\end{array}\right)\frac{(x_A+x_B-i)!(n_A-x_A+j)!}{(n_A+x_B-i+j+1)!}{(-1)}^i{\theta }^{n_B-x_B+i-j}{B}_{\gamma ,\varphi }(1+\theta ).$$

Here, c and γ are as given in (6) and

$$\varphi =n_A-x_A+j+1.$$

Proof of Theorem 1

Consider a bin with n_A + 1 and n_B + 1 amber and blue balls, respectively. Continue drawing balls until x_B + 1 blue ones are selected, and let K be the number of amber balls drawn before reaching x_B + 1 blue balls. Then P(K = k) = P(C∩D), where C is the event that among the first k + x_B balls selected, exactly k are amber and x_B are blue, and D is the event that the (k + x_B + 1)st ball is blue. The probability of C is $\left(\begin{array}{c}{n}_A+1\\ k\end{array}\right)\left(\begin{array}{c}{n}_B+1\\ x_B\end{array}\right)/\left(\begin{array}{c}{n}_A+n_B+2\\ k+x_B\end{array}\right)$. The conditional probability of D given C is (n_B + 1 − x_B)/{n_A + n_B + 2 − (k + x_B)} = (n_B − x_B + 1)/(n_A + n_B − k − x_B + 2). Therefore, P(C⋂D) = P(C)P(D | C), which is the summand of (1). Therefore, (1) is the probability that K is at least x_A + 1, which is equivalent to the event that among the first x_A + x_B + 1 balls, there are at most x_B blue balls. Thus, (1) is

$$\sum _{i=0}^{x_B}\frac{\left(\begin{array}{c}{n}_B+1\\ i\end{array}\right)\left(\begin{array}{c}{n}_A+1\\ x_A+x_B+1-i\end{array}\right)}{\left(\begin{array}{c}{n}_A+n_B+2\\ x_A+x_B+1\end{array}\right)}=1-\sum _{i=x_B+1}^{n_B+1}\frac{\left(\begin{array}{c}{n}_B+1\\ i\end{array}\right)\left(\begin{array}{c}{n}_A+1\\ x_A+x_B+1-i\end{array}\right)}{\left(\begin{array}{c}{n}_A+n_B+2\\ x_A+x_B+1\end{array}\right)}.$$