Predicting effects of noncoding variants with deep learning–based sequence model

Abstract

Identifying functional effects of noncoding variants is a major challenge in human genetics. To predict the noncoding-variant effects de novo from sequence, we developed a deep learning–based algorithmic framework, DeepSEA (http://deepsea.princeton.edu/), that directly learns a regulatory sequence code from large-scale chromatin-profiling data, enabling prediction of chromatin effects of sequence alterations with single-nucleotide sensitivity. We further used this capability to improve prioritization of functional variants including expression quantitative trait loci (eQTLs) and disease-associated variants.

Noncoding genomic variations constitute the majority of disease and other trait-associated single-nucleotide polymorphisms (SNPs)¹, but characterizing their functional effects remains a challenge. Recent progress on prioritizing functional noncoding variants has been made by integrating evolutionary conservation and genomic and chromatin annotations at the position of interest^2–4. Such approaches are valuable for prioritizing sequence variants; however, current methods except for a parallel work⁵ have not been able to extract and utilize regulatory sequence information de novo for noncoding-variant function prediction, which requires precise allele-specific prediction with single-nucleotide sensitivity. In fact, no previous approach predicts functional effects of noncoding variants from only genomic sequence, and no method has been demonstrated to predict with single-nucleotide sensitivity the effects of noncoding variants on transcription factor (TF) binding, DNA accessibility and histone marks of sequences.

A quantitative model accurately estimating binding of chromatin proteins and histone marks from DNA sequence with single-nucleotide sensitivity is key to this challenge. This is especially true because although motifs have been used for variant detection with limited success, they show substantially less predictive power than evolutionary features and chromatin annotation^2,3. Furthermore, multiple sources of evidence indicate that in vivo TF binding depends upon sequence beyond traditionally defined motifs. For example, TF binding can be influenced by cofactor binding sequences, chromatin accessibility and structural flexibility of binding-site DNA⁶. DNase I–hypersensitive sites (DHSs) and histone marks are expected to have even more complex underlying mechanisms involving multiple chromatin proteins^7,8. Therefore, accurate sequence-based prediction of chromatin features requires a flexible quantitative model capable of modeling such complex dependencies—and those predictions may then be used to estimate functional effects of noncoding variants.

To address this fundamental problem, here we developed a fully sequence-based algorithmic framework, DeepSEA (deep learning–based sequence analyzer), for noncoding-variant effect prediction. We first directly learn regulatory sequence code from genomic sequence by learning to simultaneously predict large-scale chromatin-profiling data, including TF binding, DNase I sensitivity and histone-mark profiles (Fig. 1). This predictive model is central for estimating noncoding-variant effects on chromatin. We introduce three major features in our deep learning–based model: integrating sequence information from a wide sequence context, learning sequence code at multiple spatial scales with a hierarchical architecture, and multitask joint learning of diverse chromatin factors sharing predictive features. To train the model, we compiled a diverse compendium of genome-wide chromatin profiles from the Encyclopedia of DNA Elements (ENCODE) and Roadmap Epigenomics projects^9,10, including 690 TF binding profiles for 160 different TFs, 125 DHS profiles and 104 histone-mark profiles (Supplementary Table 1). In total, 521.6 Mbp of the genome (17%) were found to be bound by at least one measured TF and were used as a regulatory information–rich and challenging set for training our DeepSEA regulatory code model (Online Methods).

Figure 1.

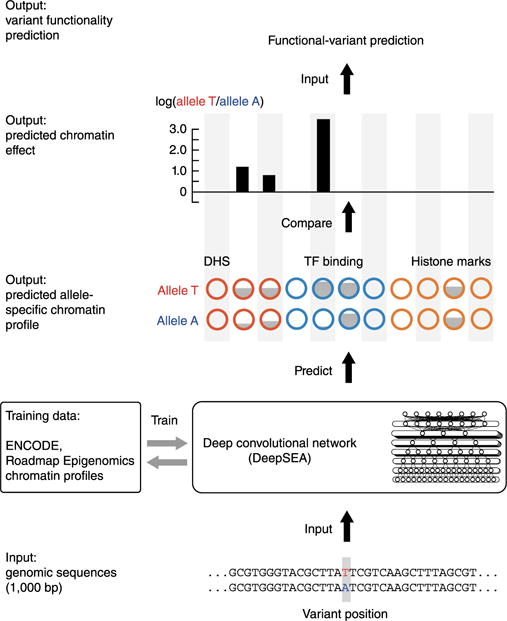
Schematic overview of the DeepSEA pipeline, a strategy for predicting chromatin effects of noncoding variants.

Integrating wider sequence context is critical because sequence surrounding the variant position determines the regulatory properties of the variant and thus is important for understanding functional effects of noncoding variants. Whereas previous studies for TF binding prediction have focused on small sequence windows directly associated with the binding sites^11,12, we found increasing the context sequence size to 1 kbp substantially improved performance of our model (Supplementary Fig. 1). The multilayer hierarchically structured model allows us to scale to such long sequence input and learn sequence dependencies at multiple scales.

We share learned predictive sequence features across all chromatin profile predictors with a multitask model. In addition to greatly increasing computational efficiency, this multitask architecture allows predictive strength to be shared across a wide range of chromatin feature profiles for TF binding, DHSs and histone marks. For example, a sequence feature that is effective for recognizing binding of a specific TF can be simultaneously used by another predictor for a physically interacting TF.

Next we evaluated how well DeepSEA can predict chromatin features from holdout genomic sequences (Fig. 2a and Supplementary Table 2). We found that DeepSEA predicted chromatin features with high accuracy, including TF binding sites, for which the median area under the curve (AUC) was 0.958. This surpassed the performance of the current best method for chromatin immunoprecipitation–based TF binding prediction—gapped k-mer support vector machine (gkm-SVM¹², also used by Lee et al.⁵)—applied on our data set for nearly all TFs (median AUC = 0.896) (Supplementary Fig. 2 and Online Methods). Our method also enabled high-performance sequence-based prediction of both DHSs (median AUC = 0.923) and histone modifications (median AUC = 0.856).

Figure 2.

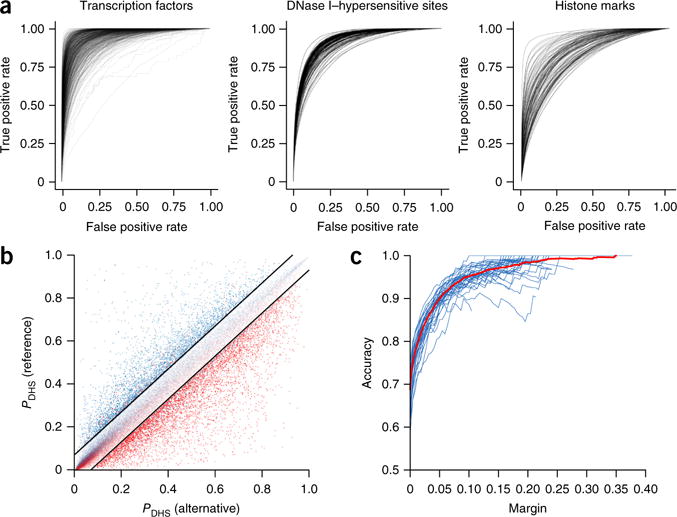
The deep-learning model accurately predicts chromatin features from sequence with single-nucleotide sensitivity. (a) Receiver operating characteristic (ROC) curves for each TF (left), DNase-seq (center) and histone-mark (right) profile prediction. Chromatin features with at least 50 test-positive samples were used. (b) DeepSEA predictions for DNase I–sensitive alleles of 57,407 allelically imbalanced variants from the digital genomic footprinting (DGF) DNase-seq data for 35 different cell types. The y and x axes show, respectively, for a variant, the predicted probabilities that the sequences carrying the reference allele and the alternative allele are DHSs within the corresponding cell type. The red and blue dots represent, respectively, the experimentally determined alternative allele–biased and reference allele–biased variants as determined by DGF data. The black lines indicate the margin, or the threshold of predicted probability differences between the two alleles for classifying high-confidence predictions (margin = 0.07 for this plot). (c) Accuracy. Each blue line indicates the performance for a different cell type, and the red line shows the overall performance on allelically imbalanced variants for all 35 cell types.

Sequence elements informative of chromatin feature prediction for any sequence can be identified through the ‘in silico saturated mutagenesis’ approach (Online Methods). Through computational mutation scanning along all potential single-nucleotide substitutions, the approach analyzes the effects of each base substitution on chromatin feature predictions, thereby identifying which sequence features are most informative for a specific chromatin effect prediction (Supplementary Fig. 3).

To enable systematical evaluation of the predicted chromatin effects of single-nucleotide alteration in noncoding sequence, we devised a high-throughput data–based evaluation protocol using allelic imbalance information from digital genomic footprinting (DGF) DNase-seq data on ENCODE cell lines¹³. Allelic imbalance—when one allele is observed in DNase-seq data significantly more often than the other allele at a heterozygous site for a single-cell-type sample—indicates different DNase I sensitivities of the two alleles. The pipeline identified 57,407 allelically imbalanced SNPs from 35 cell types with DHS predictors in DeepSEA (28,918 reference allele–biased variants, 28,489 alternative allele–biased variants; Supplementary Table 3 and Online Methods). We used these allelically imbalanced SNPs as the standards for evaluating the DHS prediction in DeepSEA at single-nucleotide sensitivity.

The DeepSEA model accurately predicted the more DNase I–sensitive allele with the DHS classifier for the corresponding cell type, even though the model was trained on only the reference genome and not on the variant data—a result supporting highly accurate prediction of the effect of even a single-nucleotide change (Fig. 2b,c). Moreover, the accuracy robustly increased as we retained only high-confidence predictions by raising the threshold of absolute predicted probability difference (Fig. 2c and Supplementary Table 4). For example, for confidently predicted allelically imbalanced SNPs with probability difference greater than 0.1 (6,726 variants), the model achieved >95% accuracy. On a smaller-scale evaluation, with histone-mark QTLs identified from Yoruba lymphoblastoid cells, we similarly observed that the confidently predicted allelically imbalanced SNPs were highly consistent with estimated QTL effects (Supplementary Fig. 4). Thus our model is capable of delivering high-confidence prediction of chromatin effect of genomic variants on the basis of genomic sequence alone.

Furthermore, our model could accurately predict the effect of individual SNPs on TF binding with the DeepSEA TF binding classifiers, as demonstrated for several SNPs with experimentally validated known effects on TF binding. For the breast cancer risk locus SNP rs4784227 (ref. 14), we identified the increased affinity of FOXA1 as the strongest effect of C-to-T alteration consistently in all five cell types for which we have learned predictors for FOXA1. For an SNP associated with the inherited blood disorder α thalassemia¹⁵, the model predicted that the alteration of T to C creates a binding site for GATA1. For an isolated pancreatic agenesis mutation¹⁶, we predicted the deleterious effect to FOXA2 binding with A-to-G alteration.

Finally, we extended DeepSEA to prioritize functional SNPs on the basis of the predicted chromatin effect signals. This is, to our knowledge, the first approach for prioritization of functional variants using de novo regulatory sequence information. DeepSEA allows us to produce classifiers with superior performance in predicting trait-associated variants from population genetics studies (for example, disease-associated genome-wide association study (GWAS) SNPs) without relying on any annotation information by combining de novo sequence-based chromatin effect predictions with evolutionary conservation information.

Specifically, we trained boosted logistic regression classifiers for predicting Human Gene Mutation Database (HGMD) annotated noncoding regulatory mutations¹⁷, noncoding eQTLs from the GRASP (Genome-Wide Repository of Associations between SNPs and Phenotypes) database¹ and noncoding trait-associated SNPs identified in GWAS studies from the US National Human Genome Research Institute’s GWAS Catalog¹⁸ on the basis of predicted chromatin effects and evolutionary features (Supplementary Fig. 5). For negative ‘nonfunctional’ variant standards, we used 1000 Genomes Project SNPs¹⁹ with controlled minor allele frequency distribution in 1000 Genomes population (Supplementary Tables 5 and 6).

The performance of DeepSEA functional predictors surpassed that of previous methods in prioritizing HGMD regulatory mutations, eQTLs and GWAS phenotype-associated SNPs, as evaluated on several groups of control SNPs that were matched with positive SNPs at different distance scales (Fig. 3 and Supplementary Fig. 6). DeepSEA outperformed previous methods even though no additional annotation information beyond the sequence was used as input, whereas the methods we compared against utilized additional chromatin and genomic annotations (Fig. 3). Furthermore, DeepSEA was capable of discriminating even against non-trait-associated SNPs located close to trait-associated SNPs, a challenging task for existing methods. We analyzed predictive power of each individual feature (Supplementary Table 7) and tested DeepSEA’s performance while only using either predicted chromatin effect or evolutionary conservation scores (Supplementary Fig. 7). DeepSEA models were accurate even when only chromatin effect predictions were used as input, and adding evolutionary conservation information (also used by all other methods) provided a further performance improvement to DeepSEA-based classifiers. Interestingly, DeepSEA chromatin predictions were more informative for common noncoding variants such as eQTLs and trait-associated (GWAS) variants, whereas the evolutionary conservation information was more informative for noncoding mutations from HGMD, which are more likely to be deleterious and under significant purifying selection.

Figure 3.

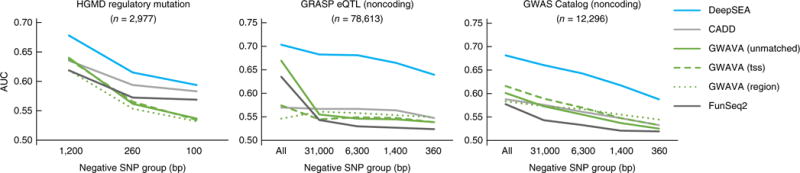
Sequence-based prioritization of functional noncoding variants. Comparison of DeepSEA to other methods for prioritizing functionally annotated variants including HGMD annotated regulatory mutations, noncoding GRASP eQTLs and noncoding GWAS Catalog SNPs against noncoding 1000 Genomes Project SNPs (across multiple negative-variant groups with different scales of distances to the positive SNPs). The x axes show the average distances of negative-variant groups to a nearest positive variant. The “All” negative-variant groups are randomly selected negative 1000 Genomes SNPs. Because GWAVA was trained on the HGMD regulatory mutations, we filtered out GWAVA training positive-variant examples and closely located variants (within 2,000 bp) in evaluating its performance on HGMD regulatory mutations. Model performance is measured with area under the receiver operating characteristic curves (AUC).

Our method’s capability of making de novo predictions based on the exact sequence-change information also allowed us to predict the effects of insertions or deletions (indels). Evaluated on HGMD indels, the model trained with HGMD SNPs could prioritize HGMD indels against nearby control 1000 Genomes indels with high accuracy, without any training on indels (Supplementary Fig. 8).

We expect DeepSEA to help unveil the regulatory information in the vast and currently poorly understood noncoding genomic regions and contribute to understanding the potential functions of complex disease or trait-associated SNPs. The approach can be readily adapted, and likely further improved, as knowledge of functional variants increases, providing additional training data.

METHODS

Methods and any associated references are available in the online version of the paper.

ONLINE METHODS

Model design and training

A deep convolutional network is a type of multilayer neural network. As is typical in a deep neural network, the model is organized by a sequential layer-by-layer structure executing a sequence of functional transformations. Each layer consists of a number of computational units called neurons. Each neuron receives input from a set of previous-layer neurons or input data and outputs a single value. All neurons in a layer together constitute an internal feature representation or output of that layer.

The deep convolutional network model features sequential alternating convolution and pooling layers that extract sequence features at different spatial scales, followed by one fully connected layer that integrates information from the full-length sequence and a sigmoid output layer that computes probability output for each individual chromatin factor feature. Each layer of the deep convolutional network executes a linear transformation of the output from the previous layer by multiplying a weight matrix, followed by a nonlinear transformation. The weight matrix is learned during training to minimize predictive errors.

The basic layer types in our model are convolution layer, pooling layer and fully connected layer. A convolution layer computes output by one-dimensional convolution operation with a specified number of kernels (weight matrices), and all convolution operation outputs are then transformed by the rectified linear activation function (ReLU), which sets values below 0 to 0. In the first convolution layer, each kernel can be considered as a position weight matrix (PWM), and the convolution operation is equivalent to computing the PWM scores with a moving window with step size 1 on the sequence. In higher-level convolution layers, each convolution kernel is a PWM over the output of the previous layer. More formally, a convolution layer computes

$$\text{convolution}{(X)}_{\text{ik}}=\text{ReLU}\left({\displaystyle \sum _{m=0}^{M-1}{\displaystyle \sum _{n=0}^{N-1}{W}_{mn}^k{X}_{i+m,n}}}\right)$$

where X is the input, i is the index of the output position and k is the index of kernels. Each convolution kernel W^k is an M × N weight matrix with M being the window size and N being the number of input channels (for the first convolution layer N equals 4, for higher-level convolution layers N equals the number of kernels in the previous convolution layer). ReLU represents the rectified linear function

$$\text{ReLU}\left(x\right)=\{\begin{array}{l}x\\ 0\end{array}\begin{array}{c}\text{if}x\ge 0\\ \text{if}x<0\end{array}$$

A pooling layer computes the maximum value in a window of spatially adjacent convolution layer outputs for each kernel, with a step size equal to the size of the pooling window so it reduces the size of the output and allows learning sequence features at a higher spatial scale in the next convolution layer. More formally, the pooling operation is defined as

$$\text{pooling}{(X)}_{\text{ik}}=max(\{X_{iM,k},X_{\left(iM+1\right),k},\dots ,X_{\left(iM+M-1\right),k}\})$$

where X is the input, i is the index for output position, k is the index of kernels and M is the pooling window size.

DeepSEA uses three convolution layers with 320, 480 and 960 kernels, respectively (for detailed specifications see Supplementary Note). Higher-level convolution layers receive input from larger spatial ranges and are capable of representing more complex patterns than the lower layers.

On top of the third convolution layer we added a fully connected layer in which all neurons receive input from all outputs of the previous layer, integrating information from the full length of 1,000 bp. This fully connected layer computes ReLU(WX), where X is the input and W is the weight matrix for the fully connected layer.

The last layer, the sigmoid output layer, makes predictions for each of the 919 chromatin features (125 DNase features, 690 TF features, 104 histone features) and scales predictions to the 0–1 range by the sigmoid function

$$\text{Sigmoid}\left(x\right)=\frac{1}{1+e^{-x}}$$

Therefore, the sigmoid output layer computes Sigmoid(WX), where X is the input and W is the weight matrix for the sigmoid output layer. Notably, all the predictors in the output layer share the same set of input from the previous layer, thus allowing sharing predictive sequence features across all chromatin feature predictors.

Training of the DeepSEA model

To train the model, we minimized the objective function, which is defined as the sum of negative log likelihood (NLL) and regularization terms for controlling overfitting. Specifically,

$$\begin{array}{c}\text{objective}=\text{NLL}+{\lambda }_1\Vert W{\Vert }_2^2+{\lambda }_2\Vert H^{-1}{\Vert }_1\\ \text{NLL}=-{\displaystyle \sum _s{\displaystyle \sum _t\log \left(Y_t^s{f}_t\left(X^s\right)+\left(1-Y_t^s\right)\left(1-f_t\left(X^s\right)\right)\right)}}\end{array}$$

where s indicates index of training samples and t indicates index of chromatin features. $Y_t^s$ indicates 0,1 label for sample s, chromatin feature t. f_t(X^s) represents the predicted probability output of the model for chromatin feature t given input X^s. We used a combination of multiple regularization techniques typical for training deep neural networks. L2 regularization term $\Vert W{\Vert }_2^2$ is defined to be the sum of squares of all the weight matrix entries. ‖H⁻¹‖₁ is defined to be the L1 norm of all the output values of the last layer (fully connected layer) before the output layer. Additionally, the optimization is subjected to regularization constraints that for any layer m and neuron n, $\Vert W_m^n{\Vert }_2\le {\lambda }_3$ or the L2 norm of weights for any neuron must not be larger than a specified value. Values of all the regularization parameters λ₁, λ₂, λ₃ as well as other hyperparameters are provided in the Supplementary Note.

Derivatives of the objective function with respect to the model parameters were computed by standard backpropagation algorithm. We optimized the objective function using stochastic gradient descent with momentum. We applied dropout training, which randomly set a proportion of neurons to a value of 0 at the specified layers in each training step to further regularize the model.

Our implementation utilizes the Torch7 library (https://github.com/torch/torch7). Tesla K20m GPU was used for training the model.

Data for training DeepSEA

Training labels were computed from uniformly processed ENCODE and Roadmap Epigenomics data releases. The full list of all chromatin profile files we used are provided in Supplementary Table 1.

To prepare the input for the deep convolutional network model, we split the genome into 200-bp bins. For each bin we computed the label for all 919 chromatin features; a chromatin feature was labeled 1 if more than half of the 200-bp bin is in the peak region and 0 otherwise.

We focused on the set of 200-bp bins with at least one TF binding event, resulting in 521,636,200 bp of sequences (17% of whole genome), which was used for training and evaluating chromatin feature prediction performance. (Variant analyses were not restricted to this region.)

Each training sample consists of a 1,000-bp sequence from the human GRCh37 reference genome centered on each 200-bp bin and is paired with a label vector for 919 chromatin features. The 1,000-bp DNA sequence is represented by a 1,000 × 4 binary matrix, with columns corresponding to A, G, C and T. The 400-bp flanking regions at the two sides provide extra contextual information to the model.

Training and testing sets were split by chromosomes and strictly nonoverlapping. Chromosome 8 and 9 were excluded from training to test chromatin feature prediction performances, and the rest of the autosomes were used for training and validation. 4,000 samples on chromosome 7 spanning the genomic coordinates 30,508,751–35,296,850 were used as the validation set. All hyperparameters were selected on the basis of log likelihood of the validation set data. The validation set data was not used for training or testing.

For evaluating performance on the test set, we used area under the receiver operating characteristic curve (AUC). The predicted probability for each sequence was computed as the average of the probability predictions for the forward and complementary sequence pairs.

The GRCh37/hg19 genome assembly was used for all analyses in this study.

TF prediction comparison with gkm-SVM

The gkm-SVM 1.1 software was downloaded from http://www.beerlab.org/gkmsvm/downloads/gkmsvm-1.1.tar.gz. The gkm-SVM models were trained for each individual chromatin factor feature with the maximum number of mismatches set to 3 and default parameters as described in Ghandi et al.¹². For many chromatin features with a large amount of binding regions, the gkm-SVM software is not scalable to using all binding sites because of the requirement of computing a full kernel matrix. We thus randomly selected 5,000 positive sequences and an equal amount of negative sequences if the number of total positives is larger than 5,000 as in Ghandi et al.¹². Unlike DeepSEA, gkm-SVM is not optimized for integrating information from sequence contexts as large as the 1,000-bp window DeepSEA used. (The average length of sequences in the original gkm-SVM publication was about 300 bp.) Therefore, we trained two sets of gkm-SVM classifiers, one on 1,000-bp sequences (similar to DeepSEA) and one on the center 300-bp sequences (similar to the original gkm-SVM publication), and we compared DeepSEA’s performance with the better-performing gkm-SVM results (using 300 bp).

In silico saturated mutagenesis for analyzing predictive sequence features

To discover informative sequence features within any sequence, we performed computational mutation scanning to assess the effect of mutating every base of the input sequence (3,000 substitutions on a 1,000 bp sequence) on chromatin feature predictions. The effect of a base substitution on a specific chromatin feature prediction was measured by log₂ fold change of odds or

$${\log }_2\left(\frac{P_0}{1-P_0}\right)-{\log }_2\left(\frac{P_1}{1-P_1}\right)$$

where P₀ represents the probability predicted for the original sequence and P₁ represents the probability predicted for the mutated sequence. This method for context-specific sequence feature analysis fully utilizes the DeepSEA’s capability of using flanking sequence context information.

Evaluation of the single-nucleotide sensitivity of chromatin feature prediction

Alignment files of ENCODE digital genomic footprinting (DGF) data were downloaded from http://hgdownload.cse.ucsc.edu/goldenPath/hg19/encodeDCC/wgEncodeUwDgf/.

Variants were called with VarScan 2 (ref. 20) using default settings on DGF samples with at least 200 million total mapped reads. We then filtered the called variants to retain only variants with at least 20 reads supporting existence of each of the alleles and at least 100 reads in total. We further removed samples with flat allele frequency distributions, which indicate aneuploidy or low data quality as allele frequency distribution for normal diploid samples is expected to peak at ~0.5. Specifically, we removed samples with kurtosis of allele frequency distribution lower than 0. Called variants with alternative allele frequency <0.2 were excluded when calculating kurtosis.

To detect allelically imbalanced variants, we ran Fisher’s exact test to compute the P value under the null hypothesis of two alleles being equal. Variants with P <0.01 and reference allele frequency larger than 0.7 or less than 0.4 were retained for downstream analysis. This pipeline found roughly the same amount of reference allele–biased and alternative allele–biased variants. The DeepSEA predictions for the reference and alternative alleles were made by the DHS predictor for the same cell type as the DGF samples.

Histone QTLs identified from the Yoruba lymphoblastoid cell lines were obtained from McVicker et al.²¹. We used SNPs identified at FDR <0.1 level. Two histone marks, H3K27ac and H3K4me3, have more than ten SNPs each in this data set and are thus suitable for evaluation. The DeepSEA predictions for the reference and alternative alleles were made by the H3K4me3 and H3K27ac predictors for the Monocytes-CD14+_RO01746 cell line.

Functional SNP prioritization

For positive standards we used single-nucleotide substitution variants annotated as regulatory mutations in the HGMD professional version 2014.4 (ref. 17), eQTL data from the GRASP 2.0.0.0 database with a P-value cutoff of 1 × 10⁻¹⁰ (ref. 1) and GWAS SNPs downloaded from the NHGRI GWAS Catalog on 17 July 2014 (ref. 18). Coding variants were filtered on the basis of the UCSC build hg19 knownGene track²².

For negative standards, we created several sets of negative SNPs with different distances to positive standard SNPs. Negative standards for HGMD regulatory mutations were created by finding, for each variant in the positive standard, the closest 1000 Genomes SNPs in the full set, 25% random subset and 5% random subset of 1000 Genomes SNPs with minor allele frequency greater than 0.01. The maximum distance allowed in each group was 400 bp, 1,000 bp and 6,000 bp, and the mean distances were approximately 100 bp, 260 bp and 1,200 bp, respectively. For negative standards of eQTLs and GWAS SNPs, similarly we created negative standards by finding, for each positive standard variant, the closest 1000 Genomes SNPs in the full set, 20%, 4% and 0.8% random subset of 1000 Genomes SNPs, with minor allele frequency distribution matched with the positive standards. The maximum distances allowed in each group were 2 kbp, 8 kbp, 30 kbp and 150 kbp, and the mean distances were approximately 360 bp, 1,400 bp, 6,300 bp and 31 kbp, respectively. In addition, for eQTLs and GWAS SNPs, we also randomly selected 1,000,000 noncoding 1000 Genomes SNPs with minor allele frequency distribution matched with the eQTL or GWAS positive standards. All negative SNPs were further filtered to remove coding variants and overlap with positive standard variants. To avoid overestimating performance in cross validation, if multiple SNPs were colocated, we retained only one SNP.

To compute predicted chromatin effects of variants using the DeepSEA model, for each SNP, we obtained the 1,000-bp sequence centered on that variant based on the reference genome (specifically, the sequence is chosen so that the variant was located at the 500th nucleotide). Then we constructed a pair of sequences carrying either the reference or alternative allele at the variant position.

To compute features for each positive and negative standard SNP, based on the chromatin feature predictions for every pair of sequences carrying a reference and an alternative allele, respectively, we computed 2 × 919 predicted chromatin effect features, which are the absolute differences between probability values

$$\left|P\left(\text{reference}\right)-P\left(\text{alternative}\right)\right|$$

and the relative log fold changes of odds

$$\left|\log \frac{P\left(\text{reference}\right)}{1-P\left(\text{reference}\right)}-\log \frac{P\left(\text{alternative}\right)}{1-P\left(\text{alternative}\right)}\right|$$

The predicted chromatin effect features were computed for both forward and complementary sequences and then averaged.

In addition, we computed four evolutionary conservation features for the variant base position. Specifically, we included base-level PhastCons²³ scores for primates (excluding human), PhyloP²⁴ scores for primates (excluding human), and GERP++^25,26 neutral evolution and rejected substitution scores. The evolutionary conservation feature scores were downloaded from http://cadd.gs.washington.edu/. The missing values were imputed as in Kircher et al.³.

For each of the three variant types, HGMD single-nucleotide substitution regulatory mutations, eQTLs and GWAS SNPs, we trained a regularized logistic regression model, using the XGBoost implementation (https://github.com/tqchen/xgboost). The HGMD regulatory mutation model was trained with L1 regularization parameter 20 and L2 regularization parameter 2,000 for ten iterations. eQTL and GWAS SNP models were trained with L1 regularization parameter 0 and L2 regularization parameter 10 for 100 iterations. Step-size shrinkage parameter eta was set to 0.1 in all cases. All features were standardized to mean 0 and variance 1 before training. Unequal positive and negative training sample sizes were balanced with sample weights.

The performance of each model was estimated by tenfold cross-validation. We showed the performance when the HGMD model was trained with 1,200-bp average distance 1000 Genomes negative SNP group and eQTL and GWAS models were trained on the random 1000 Genomes negatives SNP group, and tested on all negative sets. To avoid overestimating performances due to local effects, cross-validation folds were contiguous regions of the chromosomes.

For evaluating HGMD regulatory mutation model performance on HGMD indels, we obtained HGMD annotated noncoding small insertion or deletion variants (<50 bp) with genomic coordinate information from the HGMD professional version 2014.4 (ref. 17). We similarly constructed negative standards by identifying the closest 1000 Genomes indels in the full set, 25% random subset and 5% random subset of 1000 Genomes indels with minor allele frequency greater than 0.01. The maximum distance allowed in each negative indel group was 7,000 bp, 21,000 bp and 80,000 bp, and the mean distances were approximately 1,200 bp, 5,100 bp and 24,000 bp, respectively. Negative SNPs were further filtered to remove coding variants and overlap with positive standard variants. To compute the chromatin effects of indels, we similarly obtained the 1,000-bp sequence centered on each indel based on the reference genome. If the insertion or deletion changed the total length of sequence, we truncated or extended the sequence to 1,000 bp evenly on both ends.

For comparison with existing approaches, we computed the CADD C-scores, GWAVA output probabilities, and FunSeq2 noncoding scores for the same sets of positive and negative variants. For evaluating performance of GWAVA, which was trained on HGMD regulatory mutations, we excluded the GWAVA training set variants and variants located within 2 kbp of GWAVA training set variants to avoid test-set contamination. The GWAVA software was downloaded from http://www.sanger.ac.uk/resources/software/gwava/. For CADD, we ran the analysis using the CADD webserver v1.0 (http://cadd.gs.washington.edu/). For Funseq2, the software was downloaded from http://info.gersteinlab.org/Funseq2; we ran the analysis with the default settings, and the “noncoding score” output was used.

DeepSEA functional significance score

The functional significance score is computed on the basis of DeepSEA chromatin effect predictions and evolutionary information–derived scores. Specifically, the DeepSEA functional significance score for a variant is defined as the product of the geometric mean E value for predicted chromatin effects and the geometric mean E value for evolutionary conservation features.

E values measure significance for each individual chromatin feature and evolutionary information–derived score. Specifically, for each predicted chromatin feature of a variant, we computed the E value as the proportion of 1000 Genomes SNPs¹⁹ with higher predicted chromatin effect magnitude on the same chromatin feature. The magnitude of the predicted chromatin effect on a chromatin feature for a variant is computed as the product of the absolute difference between probability values and the relative log fold change of odds. For each evolutionary conservation score, the E-value is the proportion of 1000 Genomes SNPs with higher score.

1,000,000 randomly selected 1000 Genomes SNPs were used for computing the empirical background distributions for the 919 predicted chromatin effect features and the four evolutionary information–derived scores.

Functional significance scores were evaluated with the same evaluation standards as used in the functional variant prioritization models.