Synthesis of a cycloidal mechanism of the prosthetic ankle

Introduction

Most prosthetic feet are designed to mimic shock absorption and push-off (Gitter et al., 1991). Such materials as tibreglass and carbon graphite in Seattle Foot, Flex-Foot, Carbon Copy II, so-called Energy Storing (ES) prosthetic feet, enable a greater portion of energy of the “falling” body to be accumulated and released before plantar flexion (Bartkus et al., 1994). The ES feet provide some amount of eversion/inversion as well in the Genesis Foot, Seattle-Light, and Dual Ankle Springs (DAS).

Certain positive outcomes of using ES feet have been reported, e.g. improved ankle range of motion and gait symmetry (Wagner et al., 1987); a smaller number of skin problems like abrasions compared to the “conventional” SACH foot (Alaranta et al., 1994). The amputees preferred ES feet as transmitting Jess shock and having greater damping properties (Wirta et al., 1991).

Nevertheless, ES feet have not shown sufficient improvement in overall performance (Childress et al., 1974; Torbum et al., 1990; Lehmann et al., 1993) in comparison with the conventional SACH foot (Goh et al., 1984). No significant differences in frequency of stump pain were observed (Aiaranta et al., 1994). No improvements have been found in such amputee gait characteristics such as the performance of the existing knee in trans-tibial patients (Edelstein, 1990). During the early stance, the patient's knee bends notably less than normal because the prosthetic foot, either conventional, or ES does not produce the controlled plantar flexion obtained naturally by eccentric contraction of dorsiflexors. Knee flexion is also less than normal during late stance.

The author believes, that the reason for this is that both SACH and ES feet have a similar mechanical outcome in the dorsiflexion phase, namely, the moment of resistance to dorsiflexion, and this characteristic does not mimic the moment of resistance to dorsiflexion in normal gait.

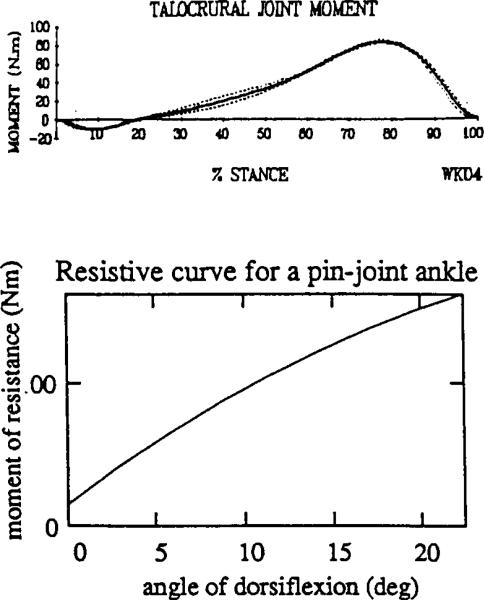
The moment of resistance (resistive curve) to dorsiflexion in a normal ankle typically has a concave downwards shape shown in Figure 1a (Scott and Winter, 1991). The beginning of dorsiflexion during regular level gait occurs with practically no resistance from plantar flexor muscles. Then, resistance slowly increases as the dorsiflexion progresses, while at the end of dorsiflexion the resistance rapidly increases nonlinearly. In contrast with this concave shape of resistive curve seen in the normal ankle, existing prostheses demonstrate a convex shape of their resistive curves (Fig. 1b).

Fig. 1.

(a). Moment of resistance (resistive curve) to dorsiflexion in the ankle during normal walking (from Scott and Winter (1991), with kind permission from Elsevier Science Ltd., Kidlington OX5 1GB, UK.

(b). Typical resistive curve in the current prosthetic ankle unit either of bending or pin-joint type. The curve is shown from the vertical position of the shank; M₀ is an initial moment to be applied to start the articulation.

If one agrees that a concave resistive curve in the prosthetic ankle is beneficial for an amputee's gait and wants to build an initially compliant prosthesis, the conflict between compliance and durability must first be overcome. Mechanically there are two basic structures employed in the ES foot design. The first is an L-shaped leaf spring (Seattle Foot, Flex-Foot, Carbon Copy II). The second is a multi-bar linkage with elastic elements (Genesis Foot, DAS, College Park Foot). Both types of mechanisms have similar resistive curves (Fig. 1b) with at least non-concave shape (convex or linear). Both types of mechanisms provide an initial moment of resistance M₀ which must be applied to a tibial component of the prosthesis to deviate from a vertical position and to articulate the ankle. As this analysis indicates, the initial resistive moment M₀ cannot be made zero in both kinds of mechanisms. In a mechanism based on the L-shaped leaf spring, for example, the structure acts simultaneously as a resistor to deflection and as a feature for load bearing. If a designer intends to lower M₀ he is at risk of losing durability.

The purpose of this work was to synthesise a mechanism of a prosthetic foot with more natural moment of resistance in the dorsiflexion phase.

Method

Biomechanical aim of the design

The moment of resistance to dorsiflexion in the normal ankle during level gait has been chosen as a biomechanical aim in the design of a new prosthetic ankle. During dorsiflexion in normal walking and running, a period of almost free mobility in the ankle joint is followed by a period of almost total fixation. This phenomenon is referred to as a deceleration during dorsiflexion (Winter, 1979), and is explained as a means to slow down the movement of the body's centre of mass and facilitate heel lift. The EMG pattern of the foot plantar flexors supports this statement both for walking (Crenna and Frigo, 1991) and running (Reber et al., 1993). A normal pattern of the foot plantar flexors’ performance (EMG signal versus stance events) correlates to the moment of resistance in the ankle. The mostly concave shape of the curve in the dorsiflexion period of stance suggests that initiation of dorsiflexion does not face a large amount of resistance from the foot plantar flexors. This resistance rapidly increases nonlinearly to the end of the dorsiflexion period, which results in deceleration of articulation of the ankle and lifting of the heel. The maximal value for the moment around the talocrural joint (articulation of the ankle in sagittal plane) is averaged from 80 to 120 Nm. A similar concave nonlinear pattern is seen in the subtalar joint (frontal articulation) with the maximal moment of resistance of 23-25 Nm (Scott and Winter, 1991).

Dorsiflexion period is followed by the rapid plantar flexion which occurs during late stance until “toe-off.” It is well documented that during the plantar flexion, foot flexor muscles generate much less power than at the end of dorsiflexion period when the heel has to be raised (Perry, 1992). This means that the major loss in performance of foot flexor muscles after trans-tibial amputation, affects not the plantar flexion, but the preceding dorsiflexion. It opens consequently a possibility to mimic the performance of the lost muscles by a passive elastic system “charge-release”, where “charge” corresponds to dorsiflexion and “release” corresponds to the following plantar flexion. One can say that the level of approximation of the prosthetic foot/ankle performance to those demonstrated by the real foot/ankle, depends on how well a “charge-release” mechanism is designed. The power released and the resistive curve, are two typical characteristics of any “charge-release” mechanism. Both characteristics can be used as targets in a synthesis of a new mechanism. Power released in the plantar flexion period in the real ankle, was chosen as a target in designing most ES feet (Gitter et al., 1991). While that “release” goal was achieved for plantar flexion, not enough attention has been paid to the “charge” component, namely, to the resistive curve in the dorsiflexion period. Indeed, in all ES feet on the market, the charge during dorsiflexion is provided by activation of bending or compression of elastic elements. The analysis shows that thes types of mechanisms have non-concave (convex or linear) pattern (Fig. 1b), opposite to the concave pattern seen in the real ankle. Thus, the beginning of dorsiflexion in bending type designs results in greater resistance, than in the biological prototype. This is also true for structures like Genesis and SACH feet, employing compression/extension. The term “rigid” will be used in relation to those prosthetic ankles, in which the resistive curve has a convex shape, and does not match the design target to be reached by the present simulation.

Disadvantages of a “rigid” prosthetic ankle

It is hypothesised here that a low initial compliance of the prosthetic ankle has at least two negative consequences on an amputee's performance.

• The first consequence of a “rigid” ankle is a decrease in range of motion (ROM) in the existing knee of a trans-tibial amputee during the stance phase of locomotion. The knee activity (flexion/extension) during stance phase has been known as a “third determinant of normal gait” (of six) (Saunders et al., 1953). This mechanism contributes shock absorption after heel strike, and decreases energy consumption by lowering the maximum elevation of the centre of gravity of the body in mid-stance. The average ROM in the trans-tibial amputated limb knee joint is approximately one half that of normals (7° versus 15° in norm) and even more notably decreased in trans-femoral patients (Zuniga et al., 1972; Breaky, 1976). However, in transtibial patients there is no anatomical basis for reduced flexion of the existing knee. This leads to the suggestion that presently available “rigid” foot and ankle prostheses are responsible for the decreased ROM in the existing knee.

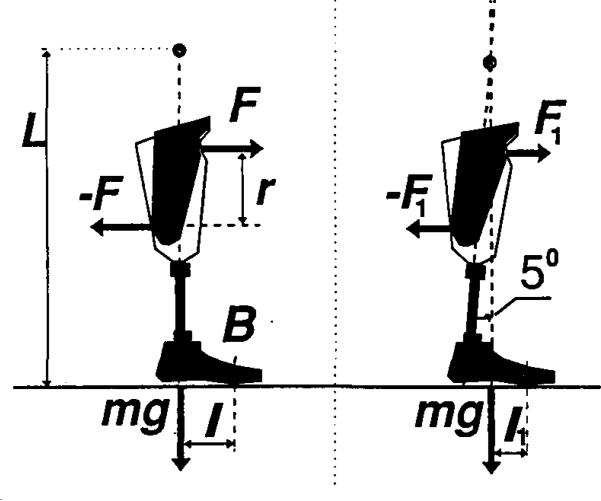
• The second consequence of a “rigid” ankle is an excessive pressure applied to the stump from the socket. Assuming that fit and alignment are optimal, the ultimate mechanical cause of excessive pressures on the stump is the resistance of the prosthesis in the process of its deformation or its resistive curve. The deformation of the prosthesis is provided by the forces and moments generated by stump and ground reactions in combination with the internal resistive characteristics of the joints of the prosthesis. Analysis of the classical Radcliffe's diagrams of moments from the socket affecting an amputee's stump during the gait cycle (Radcliffe, 1962), shows that these moments can be substantially decreased if resistance in the ankle joint is reduced. The rationale for that conclusion can be seen in (Fig.2), which is a modification of Radcliffe's diagram (1962). Two types of ankle joints are considered: completely solid with no articulation (Fig. 2a), and partially solid with initial compliance at 5° (Fig. 2b). In both cases, the prostheses are forced to perform roll-over around metatarsal zone B, the so-called “third rocker” (Perry, 1962). The confirmation in (Fig. 2a) has a vertical initial position of the shank, and the patient's stump produces the couple of forces, whose normal components are F,-F. The couple F,-F acts on the socket and provides the moment M_B=rF about the point B of application of ground reactions in the metatarsal zone, where r is a distance between parallel lines of action F and -F. The moment M_B results in a heel lift of the prosthetic foot. The force of gravity mg with centre of mass elevated at L, gives a moment M_g=mgl about the point B, where l is a distance from the projection of the force of gravity on a horizontal plane to the centre of a metatarsal joint B. The moment M_g acts in the opposite direction relative to the M_B and the heel could be lifted when M_B becomes greater than M_g:

  $$M_B>M_g.$$ (1)

Fig. 2.

(a). A minimal force couple F,-F provided by a stump, which tends to bend the metatarsal area (the point B) of a prosthetic foot when the moment M_B=rF becomes greater than the moment M_g=mgl of the force of gravity. The elevation of the centre of mass m is L.

(b). Decreased moment's Mg arm l₁ when free deflection is allowed in the ankle up to 5° of dorsiflexion and corresponding couple F₁,-F₁

Ground reaction forces in the configuration presented in (Fig. 2) when the heel is just lifted, are applied to the metatarsal area through the point B. Their moments around point B yield zero, and do not contribute to the condition of heel-off (1). The feet with solid ankle (Fig. 2a) provide heel-off with a leg position close to vertical, when the l has its maximal value. If the prosthetic ankle has a greater initial compliance to allow heel-off at 5° of dorsiflexion (Fig. 2b) it would give a new lever arm l₁ for the force of gravity:

$$l_1=l-L\sin (5°).$$ (2)

Averaged anthropometric data (McConville et al., 1980) for elevation L of the male adult's centre of gravity, suggest L = 1 m; and for the length l of the portion of the foot hom ankle to metatarsal joints: l = 0.2 m. Due to (2), we have l₁ almost half l. Therefore, the moment M_B1 which lifts the heel, and consequently forces F₁,-F₁ could be approximately half of M_B and F,-F correspondingly. In accordance with Newton's third law, forces of the same magnitude act on the stump from the socket. Hence, the longer heel off can be delayed due to greater ankle compliance (more dorsiflexed ankle al the moment of heel-off), the less pressure would be applied to the patients’ stump. The tendency of facilitating rollover by pennitting more dorsiflexion before heel-off, has however a natural limitation. When the maximal angle of dorsiflexion exceeds a maximal normal value (13°-15°), as in the Flex-Fool with (19.8°±3.3°) (Torbum et al., 1990), the force of gravity acts anterior to the metatarsal joint projection, and the moment of the force of gravity acts in the same direction as the bending moment from the stump. This results in an excessive delay in heel-off, which leads to an excessive lowering of the centre of mass due to the continuing second rocker (Perry, 1992). To compensate for this lowering of the centre of mass, some additional movements of the body segments are needed. Amputees might associate this with discomfort. Thus, excessive compliance of the ankle zone in the Flex-Foot at the later dorsiflexion phase could be a reason why amputees, when they had a choice, showed a preference for other energy storing feet in the study by Torbum et al. (1990).

The importance of reducing normal and shear stresses on the stump in a prosthetic socket has been widely discussed in the lierature, and experimental and model studies have been conducted (Sanders et al., 1993; Vannah and Childress, 1993). Stress magnitude ranges have been reported: up to 205 kPa for normal stress and 54 kPa for shear stress with the highest stresses on the posteroproximal or lateral sites of the stump. Waveforms of stresses were double-peaked, with the first and greater peak 25-40% into stance. This timing of the first peak of the stresses corresponds to the initiation of the dorsiflexion phase, which is affected by the level of the ankle joint compliance. However, there has been no discussion on the connection of these measurements to the design of prosthetic feet.

Even more important would be a reduction of normal and shear stresses on the stump in the perspective of direct skeletal attachment for leg prostheses (Eriksson and Brånemark, 1994). It seems reasonable to suggest that a terminal device (foot prosthesis) which produces less moment to a connector with bone will better prolong a sound “connector-bone” attachment.

Mathematical model of a new rolling ankle

A new rolling joint prosthetic foot and ankle (RJA) with self-adjustable rigidities in the hinges has been invented (Pitkin, l994a). A mathematical modeling of the prosthetic cam rolling ankle joint has been conducted to determine the design parameters, which provide the match with the biomechanical aim. Limitations: a) the model represents not the real ankle joint, but a mechanism which simulates one characteristic of the real ankle, namely, its resistive curve or moment of resistance to dorsiflexion in level walking; b) the mechanism is “passive”, i.e. no powered elements are included; c) the mechanism comprises two solids with the capability of relative rolling without slip; d) the solids are connected by an elastic extension tie with linear characteristics. Assumptions and theoretical basis: a) the higher-pair (cycloidal) mechanism is adequate for the simulation and practical purposes; b) the passive mechanism with linear elastic tie is able to produce the resistive curve of concave shape seen in the real ankle controlled by muscles; c) the mechanism is simple enough to be prototyped; d) rolling without slip can be technically provided.

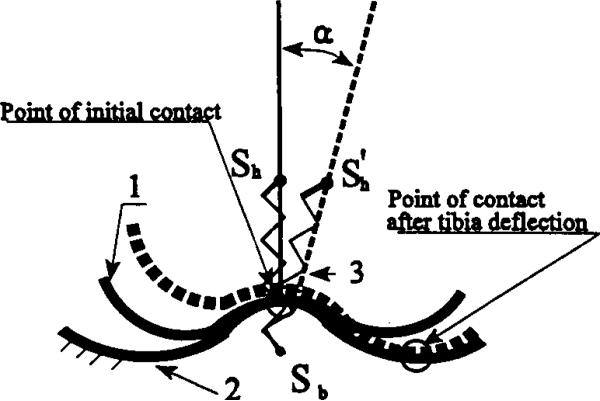
The input of the model is the tibia articulation angle α (Fig. 3). The mathematical model describes the design by a set of geometrical (contacting surfaces) and mechanical (elastic element) parameters, which determine the model's output. The output of the model is the moment M(α) of resistance to the tibia articulation measured about the articulation angle α. This moment is generated by the extension spring 3 when the tibial component rolls component 1 along the rear-midfoot component 2. The moment M(α) is calculated against the instantaneous point of a contact between curved surfaces of the tibial and the rear-midfoot components.

Fig. 3.

Basic design of a new Rolling Joint Prosthetic Foot and Ankle (RJA): 1- tibial component; 2 - rear-midfoot component; 3 - extension spring generating the moment of resistance to deflection when the tibial component rolls along the rear-midfoot component.

The contacting surfaces are analytically simulated by the combinations of circular arcs (Figs. 4 and 5), and constructed from the equations developed. A similar method was developed and published elsewhere (Pitkin, 1975) to describe the nonlinear relationship between vertical load applied through the shank to the real foot and elongation of the foot (Wright and Rennels, 1964).

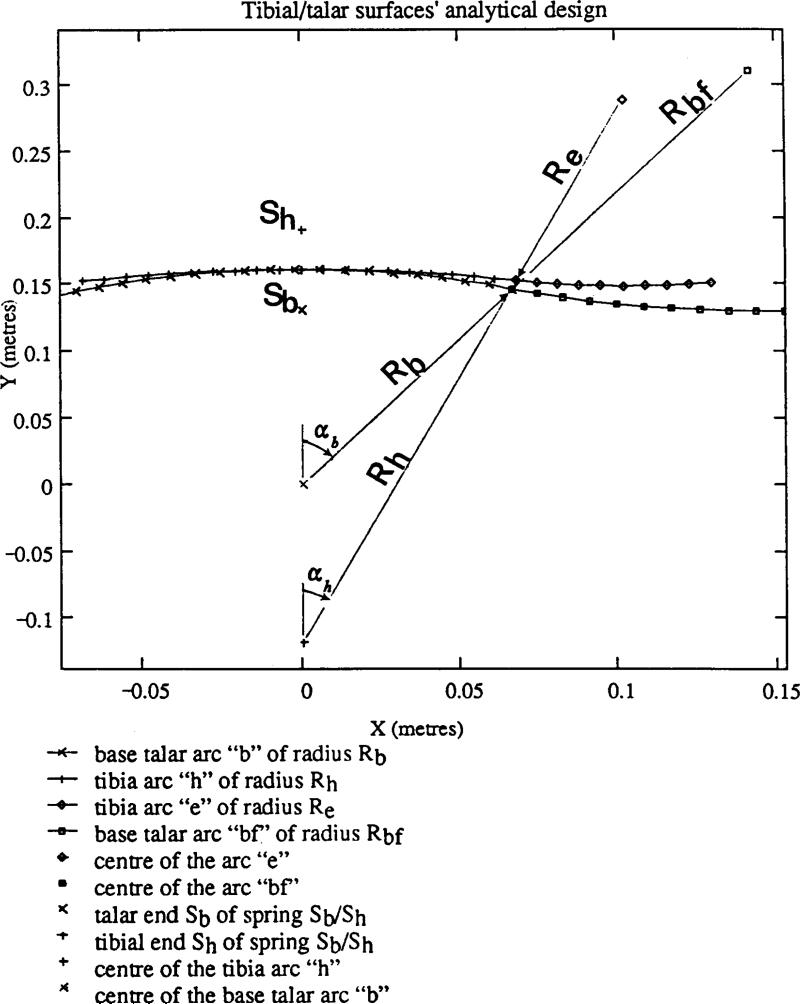
Fig. 4.

Analytical design of the contacting surfaces. Tibial surface is built accordingly to the equations 3-4; the talar surface of the rear-midfoot component (Fig 3, 1-2) is built by the equations 5-6

Fig. 5.

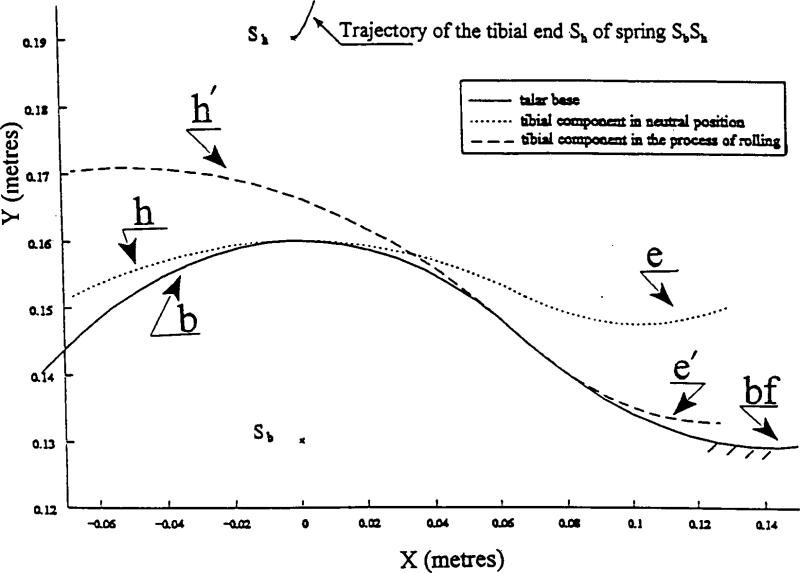
Analytical representation of the cycloidal motion (rolling without slippage) of the tibial component along the talar surface of the rear-midfoot component. A trajectory of the tibial end (point S_h) of the connecting spring (see Fig.3.3) is defined by the equations 7-8.

The talar surface of the rear-midfoot is simulated by the arc b of the circle of radius R_b, which will be a base wheel of the cycloidal motion and whose centre O_b coincides with the origin of the absolute coordinate system (Fig. 4). The base arc b is given by the parametric equation

$$\begin{array}{cc}\hfill x\left(t\right)=& R_b\cos \left(t\right),\hfill \\ \hfill y\left(t\right)=& R_b\sin \left(t\right);t=(-{\alpha }_b;{\alpha }_b).\hfill \end{array}$$ (3)

where angle α_b determines the possible range of motion (rolling with contact between arc b and arc h) in the artificial ankle. Fore part of the arc b is connected to the convex arc bf of radius R_bf The coordinates of the arc centre are R_bfx = (R_b + R_bf)sin(α_hR_h/R_b); R_bfy = R_b + R_bf)cos(α_hR_h/R_b). The equation of the arc bf is:

$$\begin{array}{cc}\hfill x\left(t\right)=& R_{bfx}+R_{bf}\cos \left(t\right),\hfill \\ \hfill y\left(t\right)=& R_{bfy}+R_{bf}\sin \left(t\right);t=(\frac{\pi }{2}-{\alpha }_h;3\frac{\pi }{2}-{\alpha }_h),\hfill \end{array}$$ (4)

where the angle α_h is determined through the angle α_b by the condition of rolling of one arc along another without slip: α_bR_b = α_hR_h.

The tibial surface comprises the middle arc h of radius R_h and and two even sided arcs e of radii R_e (left arc is not shown). The arc h is located in the centre of the tibial component, and has the equation

$$\begin{array}{cc}\hfill x\left(t\right)=& R_h\cos \left(t\right),\hfill \\ \hfill y\left(t\right)=& (R_b-R_h)+R_h\sin \left(t\right);t=(-{\alpha }_h;{\alpha }_h).\hfill \end{array}$$ (5)

Right sided arc e has equation

$$\begin{array}{cc}\hfill x\left(t\right)=& (R_h+R_e)\sin \left({\alpha }_h\right)+R_e\cos \left(t\right),\hfill \\ \hfill y\left(t\right)=& (R_b-R_h)+(R_h+R_e)\cos \left({\alpha }_h\right)+R_e\sin \left(t\right).\hfill \end{array}$$ (6)

Equations 3-6 are plotted in Figure 4 using the MathCad PLUS 5.0 software (MathSoft Inc., Cambridge, MA, USA). Figure 4 displays the contacting surfaces of the tibial and rear-midfoot components in the initial neutral position. Both tibial and rear-midfoot components are connected by the linear elastic spring with rigidity μ and initial length l₀ Points of attachment of the spring to the rear-midfoot and tibial components have coordinates Sb = (0;R_b-a_b) and S_h = (0;R_b+a_h) correspondingly. The tibial component rolls clockwise along the rear-midfoot component. The middle arc h generates an inverted hypotrochoidal trajectory of the tibial end of the spring (point S_h), which has the equation.

$$\begin{array}{cc}\hfill x_{ih}\left(\alpha \right)=& (R_b-R_h)\sin \left(\frac{R_h}{R_b}\alpha \right)+(R_h+{\alpha }_h)\sin \left((\frac{R_h}{R_b}-1)\alpha \right),\hfill \\ \hfill y_{ih}\left(\alpha \right)=& (R_b-R_h)\cos \left(\frac{R_h}{R_b}\alpha \right)+(R_h+{\alpha }_h)\cos \left((\frac{R_h}{R_b}-1)\alpha \right),\hfill \end{array}$$ (7)

where a = (π/2 – α_hR_b/R_h; π/2 + α_h(2-R_b/R_h)) is the current angle of dorsiflexion.

When rolling progresses and arc e becomes involved in a contact with the arc bf, a trajectory of the point S_h is described by the equation of a regular hypotrochoid:

$$\begin{array}{cc}\hfill x_{rh}\left(\alpha \right)=& R_{bfx}-(R_{bf}-{\mathrm{R}}_{\mathrm{e}})\sin ({\alpha }_b-\frac{R_{\mathrm{e}}}{R_{bf}}\alpha )-a_e\sin ((1-\frac{R_{\mathrm{e}}}{R_{bf}})\alpha +\beta +{\alpha }_b),\hfill \\ \hfill y_{rh}\left(\alpha \right)=& R_{bfy}-(R_{bf}-{\mathrm{R}}_{\mathrm{e}})\cos ({\alpha }_b-\frac{R_{\mathrm{e}}}{R_{bf}}\alpha )-a_e\cos ((1-\frac{R_{\mathrm{e}}}{R_{bf}})\alpha +\beta +{\alpha }_b),\hfill \end{array}$$ (8)

where a_e = ((R_h + R_e)² + (R_h + a_e)² − 2(R_h R_e) (R_h + a_e)cos(α_h))^−1/2; α_eR_e = α_bfR_bf is a condition of rolling of the arc e along the arc bf without slip; and β = asin((R_h + a_h)sin(α_h/a_e). A combination of the arc b with the arc bf has been a new development of the initial design RJF (Pitlcin, 1995), in which the arc e continued epytrochoidal rolling along the base arc b. The current addition has resulted in better prevention against slip of the tibial component along the talar component, and in better approximation to the targeted resistive curve at the end of the dorsiflexion phase.

Both trajectories of the inverted and regular hypotrochoids for the point S_h are plotted in Figure 5. This shows also the middle arcs b and h; the right arcs e and bf in initial neutral position along with an intermediate position e′ - bf′ of the tibial contacting surface. The talar end of spring (point S_b) belongs to the base wheel and does not move. Parameters R_b, R_h, R_e, R_bf, α_h, μ, a_h and a_b detemtine dimensions and mechanical outcome (moment M(α) of resistance to dorsiflexion) of the ankle unit. The particular values of parameters for the plots in Figure 5 were: αh = π/16; R_h = 0.28 m; R_b = 0.16 m; R_e = 0.14m; R_bf = 0.18 m; μ = 3×10⁵ N/m; a_b = a_h = 0.03m. This set of the model's parameters, as can be seen further, provides a desired match to the biomechanical target and is acceptable from the technological point of view. An analytical dependence M(α) comprises two dependencies: M_ih(α) and M_rh(α) which correspond to the consecutive inverted and regular hypotroichoidal parts of the trajectory of the tibial end S_b of the spring:

$$\begin{array}{cc}\hfill M_{ih}\left(\alpha \right)=& (T_0+\mu \Delta l_{ih}\left(\alpha \right))L_{ih}\left(\alpha \right),\hfill \\ \hfill M_{rh}\left(\alpha \right)=& (T_0+\mu \Delta l_{rh}\left(\alpha \right))L_{rh}\left(\alpha \right),\hfill \end{array}$$ (9)

where elongations Δl_ih(α) and Δl_rh(α) of the spring in two consecutive rollings, generating inverted and regular hypotrochoids for the tibial end S_b of the spring are:

$$\begin{array}{cc}\hfill \Delta l_{ih}\left(\alpha \right)=& \sqrt{x_{ih}{\left(\alpha \right)}^2+{((R_b-a_b)-y_{ih}\left(\alpha \right))}^2}-(a_b+a_h),\hfill \\ \hfill \Delta l_{rh}\left(\alpha \right)=& \sqrt{x_{rh}{\left(\alpha \right)}^2+{((R_b-a_b)-y_{rh}\left(\alpha \right))}^2}-(a_b+a_h),\hfill \end{array}$$

and corresponding instantaneous lever arms L_ih(α) and L_rh(α) are:

$$\begin{array}{cc}\hfill L_{ih}\left(\alpha \right)=& \mid \frac{R_b{x}_{ih}\left(\alpha \right)\cos \left(\frac{R_h}{R_b}\right)}{\Delta l_{ir}\left(\alpha \right)+(a_b+a_h)}+\frac{R_b((R_b-a_h)-y_{ih}\left(\alpha \right))\sin \left(\frac{R_h}{R_b}\right)}{\Delta l_{ir}\left(\alpha \right)+(a_b+a_h)}-\frac{(R_b-a_h)x_{ih}\left(\alpha \right)}{\Delta l_{ir}\left(\alpha \right)+(a_b+a_h)}\mid ,\hfill \\ \hfill L_{ir}\left(\alpha \right)=& \mid \frac{Y_{cbf}{x}_{rh}\left(\alpha \right)+X_{cbf}((R_b-a_h)-y_{rh}\left(\alpha \right))}{\Delta l_{rh}\left(\alpha \right)+(a_b+a_h)}-\frac{(R_b-a_h)x_{rh}\left(\alpha \right)}{\Delta l_{rh}\left(\alpha \right)+(a_b+a_h)}\mid ,\hfill \end{array}$$

with substitutions:

$$\begin{array}{cc}\hfill X_{cbf}\left(\alpha \right)=& (R_b+R_{bf})\sin \left({\alpha }_h\frac{R_h}{R_b}\right)-R_{bf}\sin ({\alpha }_h\frac{R_h}{R_b}-\frac{R_e}{R_{bf}}\alpha ),\hfill \\ \hfill Y_{cbf}\left(\alpha \right)=& (R_b+R_{bf})\cos \left({\alpha }_h\frac{R_h}{R_b}\right)-R_{bf}\cos ({\alpha }_h\frac{R_h}{R_b}-\frac{R_e}{R_{bf}}\alpha ).\hfill \end{array}$$

T₀ in (9) is an initial tension of the spring S_bS_h, necessary for durability and integrity of the whole ankle-foot assembly. It is important that the value of T₀ does not affect an initial zero-value of the moment M_ih(α) (M_ih(0) = 0), since L(0) = 0.

The analytical representation of the contacting surfaces (equations 3-6) and the outcome function M(α) (equation 9) permits the synthesising of a mechanism, which mimics the resistive curve in the real ankle.

Synthesis of the cycloidal mechanism of RJA

Hartenberger and Denavit (1964) define the synthesis of a mechanism as the detennination of the parameters that will yield an approximation to a desired function between the input and output. The synthesis could be approached by geometric and algebraic methods. Algebraic methods are based on displacement equations, i.e. equations relating the input and output variables of a mechanism in terms of its fixed parameters. In this work the algebraic approach is used with equations (9). These equations link the displacement of the tibial end of the connecting spring with the moment of resistance to the related ankle articulation.

The problem of “four accuracy points” synthesis of a planar joint (Freudenstein and Sandor, 1959) must be considered. The cam-rolling joint is a higher-pair linkage such that to four given positions of the tibial member, defined by dorsiflexion angles α₁, α₂, α₃ and a₄ there correspond four prescribed values of the moment M(α): M₁(α₁), M₂(α₂), M₃(α₃) and M₄(α₄). A substitution of these values to the left of the equation (9) yields a system of four equations with respect to the design parameters. This approach permitted the determination of four design parameters that solve the problem of synthesis of the mechanism. The other parameters may be fixed or chosen for any specific reasons. Those reasons could be, for example, performance requirements and technological limitations. The performance requirements are stability, spatial mobility, shock absorption, and self-controlled rigidity. The technological limitations are durability, mass, and dimensional fit to the cosmetic shell.

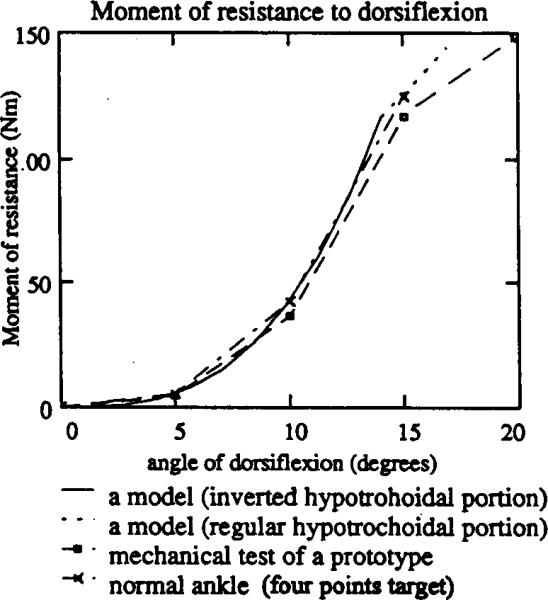
The contacting surfaces of the prosthetic ankle mechanism in the RJA were synthesised using the MathCad PLUS 5.0 software. The four points of accuracy: M₁(0)=0; M₂(5)=5.3 Nm; M₃(10)=42.2 Nm; M₄(l5)=124.1 Nm (Fig. 6) were a reasonable approximation to the resistive curves of the real ankle. To get that approximation, a joint moment curve M(t) on a time base (Fig. 1a) measured and calculated by Scott and Winter (1991), was combined with a typical ankle angle dependence α(t) from (Perry, 1992, p.53) also against time. Numerical exclusion of time has yielded a dependence M(α), shown in Figure 6, which appears to be a typical sagittal resistive curve of the real ankle joint. The synthesis procedure yielded the following geometrical characteristics of a mechanism: R_h = 0.28 m; R_b = 0.16 m; R_e = 0.14m; R_bf = 0.18 m, while the remaining model's parameters were chosen from the technological considerations as α_h = π/16; μ = 3×l0⁵ N/m; a_b = a_h = 0.03m.

Fig. 6.

The resistive curves for the biomechanical target that is a typical normal gait pattern in the ankle joint (Fig. 1 (b)), for the RJA prototype and for the mathematical model (equation (9)). The curve of the RJA (mechanical tests) is in a reasonable agreement with the mathematical model, and with the nonlinear moment of resistance in the real ankle.

The samples of the RJA were manufactured by the Ohio Willow Wood Co., Mt. Sterling Ohio, USA, following these findings (Fig. 7). The rear-midfoot member is coated with polyurethane to get a layer of high friction to provide rolling of contacting surfaces without slip. The tibial member is mounted on the rear-midfoot and has an additional S-shaped member, compared to Figure 3. This member provides the vertical shock absorption and affects the tension of the middle elastic bands when compression of the S-shaped member changes the distance between the hooks and the bottom of the rear-midfoot. The first peak of the vertical component of the ground reastion force decreases the initial tension in the bands. It eases the initiation of the mobility in the ankle joint during the first third of dorsiflexion, and makes the dependence “moment-deflection” more similar to the norm. An additional elastic O-ring in the rear is provided which is loose during most of the midstance. It contributes to the moment of resistance to dorsiflexion at the final stage of midstance, prior to heel-off, and increases the frontal stability of the entire assembly.

Fig. 7.

The sample manufactured by The Ohio Willow Wood Co., Mt. Sterling, OH, USA. Besides the basic design (see Fig. 3), the tibial component has the S-shaped member for better vertical shock absorption, and an elastic loose O-ring in the rear for better frontal stability

Two principal requirements have been fulfilled in this design: relatively free articulation in the artificial ankle joint at the beginning of dorsiflexion, and nonlinearly increased resistive counterforces at the end of the dorsiflexion phase.

Results

Verification of the model and mechanical tests

Mechanical tests of the RJA prototypes were conducted by the Ohio Willow Wood Company. The tests included verification of the mathematical model and comparison of the resistive curves of the RJA prototype and some feet and ankle units in the market.

The existing prostheses were Carbon Copy II Symes with regular toe resistance and fixed ankle; Carbon Copy II Symes with Endolite Multiflex Ankle; Carbon Copy II Symes with DAS MARS ankle unit 1401: Carbon Copy II Symes with DAS MARS ankle unit 1402. All feet except RJA were 26 em long. The RJA is 15 em in length. Each foot and ankle unit was mounted to an Interlaken servohydraulic test frame at angles of 0, 5, 15 and 20 degrees, and loaded using displacement control (0.3 mm/second) until a given load or position was reached. The amount of displacement at each angle increased significantly.

In Figure 6 there are three resistive curves which relate to the biomechanical target, to the RJA prototype and to the mathematical model (equation (9)). The curve of the RJA is in reasonable agreement with the mathematical model, and with the nonlinear moment of resistance in the real ankle (Fig. 1b). The other result is that by easily acquiring a foot flat position, the RJA would seem to provide greater stability throughout the stance period. The ease with which foot-flat is achieved may be controlled by varying the geometry of the foot and the elasticity of the RJA's elastic bands.

Pilot gait study

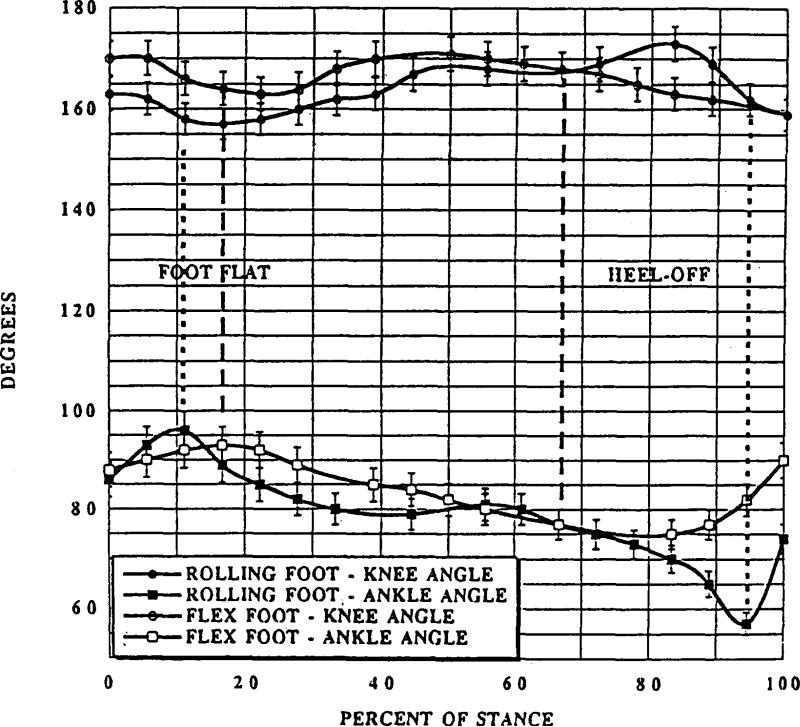
One subject, a male bilateral traumatic trans-tibial amputee, 27 years of age, wearing Flex-Feet, was involved in the pilot biomechanical gait study. In the experiment, knee and ankle angles were measured during the stance phase of level walking. The RJA was attached to the left prosthetic socket, and the Flex-Foot was attached to the right socket. Parallel use of the new and existing designs gave the subject and investigators quick feedback and data for a pilot comparison of the gait parameters. The subject was accustomed to using both prosthetic feet. He walked down a 10m runway at a comfortable speed of 1.3 m/s±10%. A high speed video camera mounted perpendicular to the runway at hip height was used to film the subject's gait. The video data were digitised manually at a frequency of 50 Hz using the computer interfaced system LabVIEW, In Figure 8 an increased ROM in the knee during the first half of the stance period 15°±1.2° for the RJA versus 6°±0.6° for the Flex-Foot is presented. Times of foot-flat and heel-off are shown. In addition, an increase in the ankle plantar flexion with the RJA immediately after heel strike is shown. This effect of the rolling joint foot and ankle on existing knee performance seems to be normalising.

Fig. 8.

Knee (existing) and ankle (prosthetic) angles in the RJA and Flex-Foot.

In addition, the subject felt that the stress on his stump was lower when he used the RJA prototype than when he used the Flex-Foot (Pitkin, 1994b).

Two additional subjects have qualitatively tested the RJF prototypes at the OWW site in November 1994. They also reported lowering of stress at their stumps, and pointed on high rotational compliance as a benefit of the new prosthesis.

Discussion

A mechanism of the angle of dorsiflexion adjustment in the normal is controlled by calf muscles and lost by trans-tibial amputees along with plantar flexion. Many attempts have been made to improve plantar flexion of the prosthetic foot (Hittenberger, 1986; Phillips, 1989: Kristinsson, 1992; Colwell, 1994). However, the amputee's perfomiance might be of greater normality if more attention was given to emulating normality dorsiflexion.

The moment of resistance to deflection (resistive curve) in the ankle joint during the stance period of gait is considered in this study as a determinant or mechanical outcome of normal dorsiflexion. The pattern of that mechanical outcome is nonlinear with low resistance to deflection in the ankle at the beginning of dorsiflexion and rapidly increasing resistance prior to the heel-off (Crenna and Frigo, 1991; Scott and Winter, 1991). In the contrast with this concave pattern, prosthetic foot and ankle units in the market and in the patent literature available, demonstrate convex dependence “moment-angle” with the higher slope at the beginning of dorsiflexion and the lower slope at its end.

The mechanical outcome of the real ankle was taken as an aim for prosthetic design, and synthesis of a cam rolling mechanism with higher-pair connection was provided. The newly developed rolling joint prosthetic foot and ankle (RJA) (Pitkin, 1994a; 1995) shows nonlinear mechanical outcome (moment of resistance to deflection) in the dorsiflexion phase, similar to the biological prototype.

Two positive consequences of using the rolling joint prosthetic foot and ankle prototype have been found in the pilot biomechanical study on a bilateral trans-tibial amputee wearing Flex-Feet. The first is a better performance of the subject's sound knee joint. The average range of motion in the amputated limb knee joint is approximately half the normal in transtibial patients (7° versus 15° in norm) and even more notably decreased in trans-femoral patients (Breakey, 1976; Zuniga et al., 1972), In the case of trans-femoral amputee gait, the lowering of the knee range of motion is directly affected by the prosthesis knee design, which has to substitute the lost knee joint functions. However, in trans-tibial patients there is no anatomical basis for reduced flexion of the existing knee in stance. A pilot gait study of the subject with trans-tibial bilateral amputations has proved an increased range of motion in the knee (15° versus 6°) with the RJA in comparison with the Flex-Foot (Fig. 8).

The second positive consequence of using the rolling joint prosthetic foot and ankle prototype was the subject's feeling of easiness in the beginning of tlexion in the ankle during the first third of the stance period. A smooth transfer to the area of the metatarsals took place at the end of the second third of stance, and the heel of the RJA was lifted. One should recognise that it is not exclusively the magnitude of the stress that causes skin breakdown. The combination of such parameters as magnitude, frequency, and loading in other directions, tissue conditions, etc., may all simultaneously contribute to skin breakdown (Radcliffe and Foort, 1961; Sanders et al., 1993). The reduction of normal and shear stresses on the stump would be even more important in the perspective of direct skeletal attachment for leg prostheses (Eriksson and Brånemark, 1994).

There might be a concern that the RJF docs not mimic the resistive curve of the ankle at different walking speeds and under conscious control of the amputee. A mathematical model of a mechanism developed is not “sensitive” to the speed of amhulation, since the nonlinear resistive curve was intentionally provided by a linear elastic tie included in a rolling structure. However, the design of the RJF has an ability to respond to speed and correlated load changes. The distance between points of attachment of the elastic tie (and consequently the resistive curve) depends not only on the angle of dorsiflexion as in the mathematical model, but also on vertical loads from the prosthetic tibial connector (Fig. 6). This additional component of the moment of resistance might become a means for self-adjustment of the prosthesis to changes m speed. Further research and prototyping work is required to establish this.

Conclusions

1. The technique of synthesis of a cycloidal prosthesis mechanism with a given outcome has been developed, which would be useful for the design of prosthetic devices.

2. Further investigation m cam rolling (cydoidal) prosthetic joint design and usage should he conducted, since a more biological output appears possible.