Forward-in-Time, Spatially Explicit Modeling Software to Simulate Genetic Lineages Under Selection

Abstract

SELECTOR is a software package for studying the evolution of multiallelic genes under balancing or positive selection while simulating complex evolutionary scenarios that integrate demographic growth and migration in a spatially explicit population framework. Parameters can be varied both in space and time to account for geographical, environmental, and cultural heterogeneity. SELECTOR can be used within an approximate Bayesian computation estimation framework. We first describe the principles of SELECTOR and validate the algorithms by comparing its outputs for simple models with theoretical expectations. Then, we show how it can be used to investigate genetic differentiation of loci under balancing selection in interconnected demes with spatially heterogeneous gene flow. We identify situations in which balancing selection reduces genetic differentiation between population groups compared with neutrality and explain conflicting outcomes observed for human leukocyte antigen loci. These results and three previously published applications demonstrate that SELECTOR is efficient and robust for building insight into human settlement history and evolution.

Introduction

Analysis of current genetic diversity enables inferences regarding the evolution of species. However, factors affecting genetic diversity (eg, demography, migration, genetic drift, and natural selection) interact to such an extent that they are challenging to disentangle, and distinct situations may lead to similar outcomes. Genetic data consequently require specific analytical tools. In this context, computer simulation is a powerful approach to investigate the joint effects of these various processes, since it allows simulation of complex scenarios. Although more complexity does not necessarily equal more realism,¹ computer simulation has been shown to be an invaluable tool for understanding the evolutionary processes that might otherwise remain undetected.^2–4

Until recently, spatially explicit simulations have been used mostly for the study of selectively neutral loci.⁵ A few studies have investigated the effects of positive or negative selection in a spatially explicit context,^6,7 but none of these have considered multiallelic loci under balancing selection, the main characteristics of the major histocompatibility complex (MHC). Moreover, the interaction of balancing selection and population structure has been shown to be complex.^8,9 Three types of balancing selection models have been proposed to explain the high diversity of MHC lineages as follows: (1) heterozygote advantage (HA),¹⁰ (2) rare allele advantage (RAA),¹¹ and (3) fluctuating selection over space and time (FS).¹² The relative role and contribution of these three nonmutually exclusive models in the evolution of MHC is intensely debated.^12–15 Even though a spatial model with constant negative frequency-dependent selection (FDS) coefficients on specific human leukocyte antigen (HLA) alleles has previously been implemented,¹⁶ this framework is not flexible enough to test the alternative models aforementioned. HA and RAA selection have also been modeled,^17–20 sometimes including sexual selection through disassortative mating,²¹ but without any spatial component. The island model²² has been used to integrate space and selection in order to assess the effects of migration on genetic differentiation when selection is at play,^8,9,23,24 but this is not, strictly speaking, a spatially explicit model.

The study of the human MHC, namely, HLA, has great potential to unravel human evolution and settlement,^25–30 as large worldwide databases are available for several genes.³¹ However, a spatially explicit computer simulation framework capable of taking HLA characteristics into account has not been previously available. In this context, we developed a new computer simulation program called SELECTOR. The originality of SELECTOR lies in the simulation of both population spatial demography and balancing selection at a multiallelic genetic locus. In particular, it merges three main evolutionary processes as follows: (1) population spatial structure and migration, (2) genetic drift, and (3) natural selection (balancing or positive). In SELECTOR, selection may either be uniform over the whole simulated geographic area or vary with latitude and/or longitude. Moreover, SELECTOR allows the user to perform model comparison and parameter estimation, as it can easily be integrated in an approximate Bayesian computation (ABC) estimation framework such as ABCtoolbox.³² In the work presented here, we describe the main principles of SELECTOR, validate the algorithms using simple models for which theoretical expectations can be computed, and finally illustrate its use through a specific application.

Program Implementation

SELECTOR can be used to simulate complex evolutionary models by taking into account demographic variation of population sizes over space and time, as well as the effect of selection at a given genetic locus. SELECTOR simulates the genes of diploid individuals, generation after generation (ie, forward in time) within a two-dimensional stepping-stone framework.³³ The whole population is subdivided into numerous subunits called demes, where each deme has its own spatial coordinates and can exchange migrants with neighboring demes at each generation. Demographic increase in population within each deme follows a logistic growth model to account for competition for resources among the members of each deme.³⁴ Demographic parameters such as migration, growth rates and carrying capacity can be modified independently in each deme at different periods of time during the simulation. A wide variety of demographic scenarios, including a succession of demographic events, can thus be tested. Even though the demographic and migration algorithms in SELECTOR are derived from those implemented in the program SPLATCHE (model no. 1: even number of migrant, SPLATCHE user manual, p. 21,³⁵) SELECTOR simulates forward in time all the individuals and genes in the entire population and does not use a backward coalescent algorithm³⁶ to reconstruct the genetic diversity of samples. This full forward approach has the major advantage of allowing the user to consider various types of natural selection on genetic lineages.

Demographic model

Each deme has its own demographic characteristics and is regulated independently using a logistic growth model as follows:

$$N_i(t)=N_i(t-1)\left(1+r_i\frac{K_i-N_i(t-1)}{K_i}\right)$$ (1)

where N_i(t) and N_i(t − 1) are the number of individuals belonging to the current deme i at generation t and t − 1, respectively, r_i is the growth rate by generation (the rapidity at which the population density increases or decreases), and K_i is the carrying capacity (the maximum number of individuals sustained by the resources of the deme). If r_i = 0, the population does not grow, while if r_i = 1, it doubles during the earliest phase of growth, then the increase slows down because of intrademe competition $\left(\frac{K_i-N_i(t-1)}{K_i}\right)$. If K_i = 0, the deme is not activated, which means that it cannot be occupied at any time (no growth, no immigration) even if some individuals are added into it at the beginning of the simulation.

Migration model

In every deme, the number of emigrants E from deme i at each generation t and in each direction j is computed as

$$E_{ij}(t)=\left[\frac{m_{ij}{N}_i(t)}{B_i}+z_{ij}(t-1)\right]$$ (2)

where m_ij is the migration rate in that direction (from i to j), N_i(t) is the number of individuals in the current deme i at generation t, B_i is the number of neighbors (with K > 0) of the current deme i, and z_ij is the remaining fractional part of migration from preceding generations (refer the user’s manual for a numerical example). E_ij is an integer (number of individuals) and equal among all neighboring demes, so that the remaining fractional part from E_ij (i in direction j) is kept in memory for the next generation and computed as

$$z_{ij}(t)=\left(\frac{m_{ij}{N}_i(t)}{B_i}+z_{ij}(t-1)\right)-E_{ij}(t)$$ (3)

Note that in SELECTOR, Nm defines the amount of emigration from one deme because it can be set independently for each deme using the parameters K and m. However, in a homogeneous area and at demographic equilibrium (ie, when N = K), the number of immigrants is equal to the number of emigrants. In SELECTOR, it is possible to modify the migration rate between any pair of demes. This refers to the routes in the SELECTOR user’s manual.³⁷ Note that a deme with K = 0 is never considered as a target of migration and cannot receive immigrants.

Demographic processes

The order of demographic events is as follows:

1. Demographic regulation occurs in every deme i using Equation 1 leading to N_i(t).

2. The number of emigrants E_ij(t) in all directions j is computed in every deme i using Equations 2 and 3 and the total number of emigrants is computed as $E_i={\displaystyle \sum _1^{B_i}{E}_{ij}(t)}$.

3. The number of immigrants in each deme i is computed as $I_i={\displaystyle \sum _1^{B_i}{E}_{ij}(t)}$.

4. The density in every deme i is updated with the sum of emigrants and immigrants as

$${N^{\prime }}_i(t)=N_i(t)-E_i+I_i$$ (4)

Note that the number of simulated generations must be either defined by the user, assuming that the generation time is known, or estimated for the organism under study, or a prior distribution may be defined in order to take into account uncertainty regarding the generation time.

Simulated genetic data

SELECTOR simulates the allele frequency trajectories in demes through the effects of genetic drift, migration, demographic variation, and selection. To achieve this, it records the two allelic variants of a given genetic locus for each simulated diploid individual. These variants are simply coded “ax” where x varies between 1 and n_max, the maximum number of allelic variants in the system (defined by the user as input parameters). At the beginning of a simulation, alleles taken from a list from 1 to n_max are randomly distributed in the first generation of individuals belonging to the source population(s). All alleles have the same probability 1/n_max of being drawn. This implies that initial allele frequencies vary among source populations, if there are more than one, and among independent simulations because different subsets of alleles are randomly drawn from the ancestral genetic pool of n_max alleles for each source and each simulation. Some alleles may not be represented in the source population(s), and this probability is inversely proportional to the initial population size. If the size of the source population is large, then the variation of initial genetic diversity among simulations is reduced. All source populations can either be constituted from the same or from different ancestral allelic pools (identical or different lists of alleles, respectively). The number of alleles can increase during the simulation if the mutation rate parameter is > 0, so that each new allele appearing by mutation increments ax by 1. Refer the SELECTOR user’s manual for more details.³⁷ SELECTOR outputs either allele frequencies for the whole deme or for a sample of n individuals drawn randomly from the deme in a format directly usable by ARLEQUIN.³⁸ The data output can then be used to compute various indices of genetic diversity and structure.

Transmission of gametes

Within each deme, the transmission of genes from one generation to the next is based on a Wright–Fisher’s model.^22,39 For each individual at generation t, two alleles are drawn randomly from two different individuals at generation t − 1.

Effect of selection

Three different models of selection are implemented in SELECTOR. When selection applies (selection coefficient s > 0), the transmission of gametes from one generation to the next in each deme is modified as described here.

Symmetric overdominant selection (SOS), also called HA, simulates overdominant balancing selection, where all heterozygotes have the same selective advantage (fitness) over homozygotes.^10,40 If the new genotype is heterozygote, it is accepted with the probability P = 1. If the new genotype is homozygote, it is either kept with the probability P = 1 − s, where s is the selection coefficient against homozygotes, or a new pair of alleles is drawn.

Frequency dependent selection (FDS), also called RAA, simulates a selection in favor of alleles that are less frequent in the population. A new allele a_i is accepted with a probability P = 1 − f(a_i) ^* s, where f(a_i) is the current frequency of the allele a_i in the deme and s is the selection coefficient against frequent alleles. If f(a_i) tends to 0, then the probability of keeping a_i is close to 1, while if f(a_i) tends to 1, then this probability is close to 1 – s. If the allele is not retained, then a new one is drawn.

Dominant positive selection (DPS) simulates positive selection for one specific allele a₁ among n_max alleles. Individuals who do not carry the selected allele have a fitness equal to 1 − s, whereas the carriers have a fitness of 1.⁴¹ If the new genotype has the selected allele, in a homozygote or heterozygote state, it is accepted with the probability P = 1. If the genotype does not have the selected allele, it is kept with the probability P = 1 − s, or a new genotype is drawn.

Program Validation

In order to validate the algorithm of allele transmission implemented in SELECTOR, we performed a series of simulations for which theoretical expectations can be analytically computed.

Evolution of allele frequencies within a single deme

In a single deme of size N individuals, we simulated the evolution of n_a alleles during t generations, in the absence of selection. Then, we computed the heterozygosity H_t within the deme and compared it with the expected heterozygosity given by the formula $H_t=H_0{\left(1-\frac{1}{2N}\right)}^t$,⁴² where H₀ is the initial density at time 0. Here, the parameters K = N and r = 0 apply, since the population size is constant (ie, size is equal to carrying capacity).

We varied all three parameters (K, r, and n_a) in eight independent combinations and performed 1,000 simulations for each combination. Average $\overline{H_t}$ and standard deviation over these 1,000 simulations have been computed and compared with the expected H_t (Table 1).

Table 1.

Comparison between simulated $({\overline{H}}_t)$ and expected (H_t) heterozygosity in a deme for various combinations of parameters n_a, H₀, t, and N.

SIMULATED WITH SELECTOR					EXPECTED Ht	DIFFERENCE
na	H0	t	N	${\overline{H}}_t$
2	0.5	100	100	0.304 ± 0.18	0.303	0.001
2	0.5	1000	100	0.003 ± 0.03	0.003	0.000
2	0.5	100	1000	0.475 ± 0.03	0.476	0.003
2	0.5	1000	1000	0.300 ± 0.18	0.303	0.003
10	0.9	100	100	0.539 ± 0.16	0.545	0.006
10	0.9	1000	100	0.007 ± 0.05	0.006	0.001
10	0.9	100	1000	0.857 ± 0.02	0.856	0.001
10	0.9	1000	1000	0.550 ± 0.17	0.546	0.004

When comparing the simulated heterozygosity to the one expected theoretically under identical conditions (number of generations, deme size, and initial heterozygosity), we found that the average over 1,000 simulations was very close to the expected heterozygosity, differing by ≤0.6% in all cases. The small differences can be explained by the stochasticity of allele transmission in SELECTOR (see standard deviation), while the expected value is deterministic.

Evolution of allele frequencies within a series of interconnected demes

We assessed the validity of the migration algorithm by modeling four interconnected demes in a 2 × 2 stepping-stone area, in the absence of selection. At the beginning of the simulation, each deme had one specific allele with 100% frequency (a₁ in deme 1, a₂ in deme 2, etc.). We simulated 500 generations with a migration rate m = 0.01 between each pair of demes, and large deme size (10,000 diploid individuals) in order to minimize the effect of genetic drift. We then recorded the evolution of allele frequencies in the first deme and compared them with the frequencies theoretically expected with the formula $p_t=\overline{p}+{\left(1+m\right)}^t\left(p_0-\overline{p}\right)$ where p_t is the frequency expected at time t in a deme when the initial frequency of the allele in that deme is p₀ and the average frequency of that allele over all demes is $\overline{p}$. This formula generates the expected allele frequencies for an island model with large deme size so that genetic drift can be neglected.⁴³ Completion of 100 simulations of this model typically takes ~8 minutes 30 seconds in a single node from a Linux server.

Figure 1A shows that the evolution of allele frequencies through time within a deme converges toward an equilibrium frequency of 25% for all four alleles, as expected theoretically. The differences between the theoretical and the simulated curves are due to the differences between the two models: the theoretical curves have been obtained for a deterministic island model with an infinite size, while the simulated curves have been generated by a stochastic stepping-stone model with a finite (but large) size. Figure 1A shows that the frequency of allele a₁ (blue curve), which was fixed in deme 1 at the beginning of the simulation, decreases, while the frequency of allele a₄ (yellow curve), initially fixed in deme 4 without any direct connection with deme 1, takes longer to reach equilibrium compared with the two alleles fixed in the neighboring demes, 2 and 3, which directly exchange migrants. The orange and green curves represent a₂ and a₃, respectively.

Figure 1.

Comparison between simulated frequencies (sim, solid lines) and frequencies expected theoretically (exp, dotted lines). (A) Evolution of allele frequencies in the absence of selection within four interconnected demes. (B) Evolution of two alleles within a single deme under the effect of DPS on allele a₁. (C) Evolution of two alleles within a single deme under the effect of SOS and FDS. (D) Schematic representation of the grid of demes where simulations are performed for the theoretical application. Each color represents one group of demes (blue, red, green, and yellow). Dark demes represent demes where genetic sampling is done. Migration between adjacent demes from different groups occurs at rate m_inter and is symbolized by black arrows, while gray arrows symbolize migration between adjacent demes from the same group, which occurs at rate m_intra. For the sake of clarity, only a few arrows are represented but migration occurs between all pairs of demes.

Evolution of allele frequencies under DPS

In a single deme of size N = 10,000 (again to avoid too rapid genetic drift), we simulated the evolution of the frequencies of two alleles, a₁ and a₂, where a₁ is under positive selection (DPS). The fitness of the various genotypes is computed as w_a1a1 = 1, w_a1a2 = 1, and w_a2a2 = 1 − s, where s is the selection coefficient. The initial frequency of both alleles at time t₀ is 0.5, but a₁ is positively selected (s = 0.1) for 100 generations. We compared the simulated frequencies with those computed using the classical equation of allele frequencies in diploids under selection for survivorship.⁴³

Figure 1B shows that the frequency of the allele a₁ under positive selection increases gradually through time, in accordance with theoretical expectations. The small variation is explained by the stochasticity of the simulated algorithm. The result of a single simulation is displayed. Completing 100 simulations of this model typically takes ~30 seconds in a single node from a Linux server.

Evolution of allele frequencies under overdominant selection

We further simulated the evolution of allele frequencies in a biallelic system (n_a = 2) where heterozygotes are favored compared with homozygotes (SOS: w_a1a1 = 1 − s, w_a1a2 = 1, and w_a2a2 = 1 − s) in a single deme of size N = 10,000. The initial frequencies of alleles a₁ and a₂ are 0.1 and 0.9, respectively, and we simulated selection for 200 generations when s = 0.1. We also simulated the evolution of these frequencies with the same parameters but using FDS. Then, we compared the simulated frequencies with those computed using the classical equation of allele frequencies in diploids under selection for survivorship.⁴³ Completing 100 simulations of this model typically takes ~60 seconds in a single node from a Linux server.

Figure 1C shows that the frequencies of the two alleles converge to an equilibrium frequency of 0.5 if the size of the population is large enough to neglect drift, for both balancing selection models (SOS or FDS), as expected from theory.

Application

The interaction of balancing selection and population structure is challenging to study.⁹ It has, for example, been shown that genes under balancing selection are less sensitive to population subdivision than neutral ones and are thus expected to show limited differentiation among demes compared with neutral genes under the same demographic conditions.^8,23,44 However, this conflicts with most observations,^15,45 with some exceptions.⁴⁶ In human populations, discordant results have been obtained; some studies have not found any reduction of interpopulation differentiation,^44,47 while others have found some low interpopulation or intercontinental differentiation for almost all HLA loci, except DPB1.^48–50 Because Schierup et al.²³ theoretically showed that the reduction of genetic differentiation under balancing selection, compared to neutrality, is more pronounced when gene flow between demes is low, with almost no difference when gene flow is large, we believe that spatial gene flow heterogeneity between demes may explain these contrasting HLA results.

We tested this hypothesis by assessing the effects of heterogeneous gene flow between populations on measures of genetic differentiation under balancing selection. We used SELECTOR to simulate the evolution of allele frequencies in interconnected demes, when SOS is at play. Thus, we designed a virtual square area made up of 256 demes (16 × 16 demes, Fig. 1D). This area was divided into four identical groups of demes (square area of 64 demes each, Fig. 1D) connected by a migration rate m_inter, while the rate between demes of the same group is m_intra. We performed several tens of thousands of simulations, varying input parameters such as K (carrying capacity), r (growth rate), m_intra (migration rate between each pair of neighboring demes belonging to the same group), m_inter (migration rate between each pair of neighboring demes belonging to different groups), n_a (number of alleles), and s (coefficient of selection against homozygotes). Either all the demes were fully occupied at carrying capacity during the whole simulation (constant population size) or they were populated after a population expansion from one single deme, where this deme was located in group A and the initial population size starting the population expansion was 50 individuals. Population density within demes increased logistically at rate r (0.5 for all simulations) until it reached K (two choices, either 50 or 500). Migration occurred at rate m = 0.2 (20% of individuals belonging to each deme spread over the neighboring demes at each generation), even when demes had reached demographic equilibrium (carrying capacity). Genetic isolation between groups was not complete, and gene transfers could occur at a reduced migration rate (either by 40, 20, or 10 folds). We simulated a locus with 20 different lineages associated with symmetrical HA, with a selection coefficient between 0 (no selection) and 0.2 (very strong selection), and we randomly drew eight samples of 100 genes in each group of demes, at regular spatial intervals (dark colored demes in Fig. 1D).

We measured genetic differentiation at the end of each simulation by computing the indices F_CT, F_SC, and F_ST based on allele frequencies through an Analysis of molecular variance (AMOVA),⁵¹ the average pairwise genetic distances D_intra between samples within the four groups of demes, and the average pairwise genetic distances D_inter between samples belonging to different groups. We used the coancestry coefficient as a measure of genetic distance.⁵² We also used multidimensional scaling analyses (MDS) to visualize pairwise genetic distances between the subsets of data.^53,54

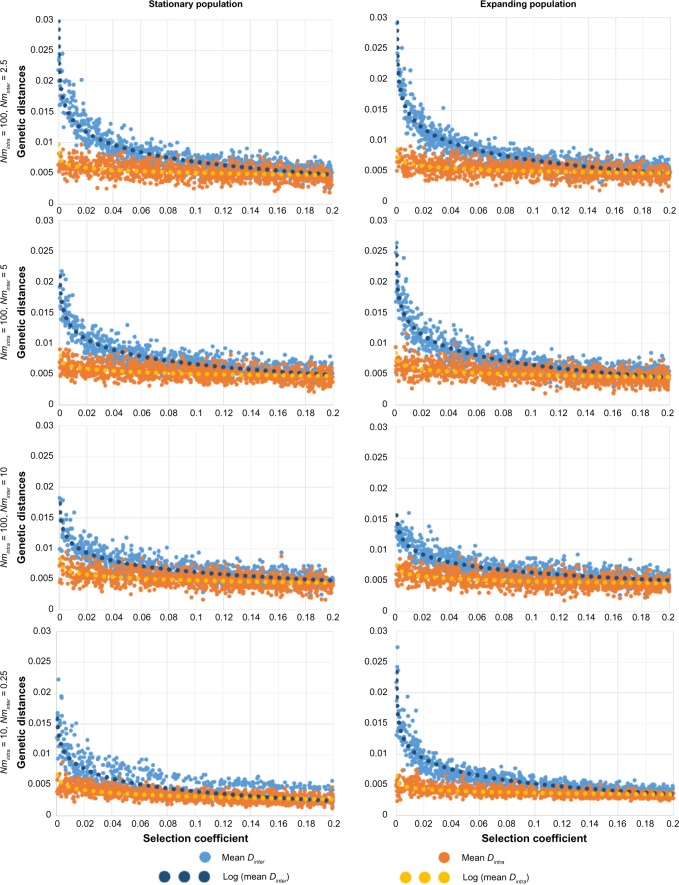
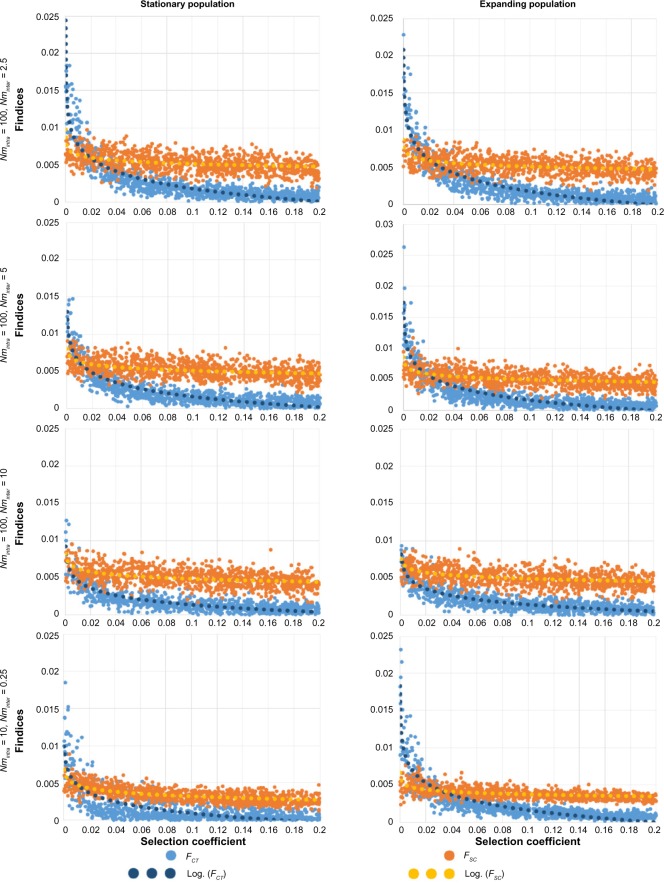
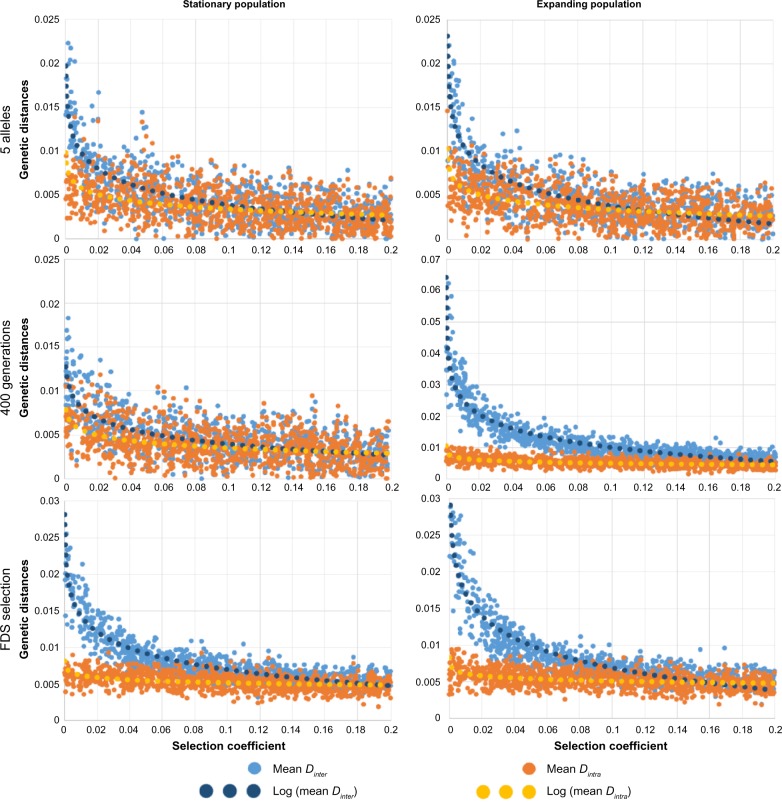
Our results show that, as theoretically expected,^8,23,44 genetic differentiation between demes is globally reduced under balancing selection compared with neutrality (Figs. 2 and 3). They also support previous results, suggesting that this reduction is generally less pronounced when gene flow is high (increasing Nm_inter from line 1 to line 3 in Figs. 2 and 3). In addition, our results reveal new patterns of population differentiation that emerge when mixing various gene flow intensities in a spatially structured population. When gene flow between groups of populations is reduced compared with within groups (Nm_inter <Nm_intra), we observe that the average genetic distance D_inter between groups tend to be much more affected by selection than the intragroup average genetic distance D_intra (Fig. 2). When balancing selection increases, then D_inter gradually decreases until reaching D_intra (sometimes even becoming smaller, Fig. 4), thereby diluting the signal of genetic isolation. This can also be seen when looking at fixation indices, the F_CT being much more affected by balancing selection than the F_SC. F_CT may even become smaller than F_SC if balancing selection is relatively strong (Fig. 3). This effect is more pronounced in an expanding population compared with a stationary one and less pronounced when the number of alleles is lower or the time frame is shorter (Fig. 4, line 1 and line 2). This effect is consistently observed through parameter values and the choice of balancing selection models (FDS instead of SOS, Fig. 4, line 3).

Figure 2.

Pairwise F_ST within population groups (in orange) and between population groups (in blue) for 1,000 simulations and varying selection coefficients (symmetric HA). Dotted lines represent logarithmic regression lines. The left column shows the results for a stationary population, while the right column shows the results for an expanding population. Nm_inter increases from line 1 to line 3 and K is changed from 500 to 50 in line 4, compared to line 1 while all the other parameters remain identical (n_a = 20 alleles, r = 0.5, and m = 0.2).

Figure 3.

F_CT (in orange) and F_SC (in blue) values for 1,000 simulations and varying selection coefficients (symmetric HA). Dotted lines represent logarithmic regression lines. The left column shows the results for a stationary population, while the right column shows the results for an expanding population. Nm_inter increases from line 1 to line 3 and K is changed from 500 to 50 in line 4, compared to line 1 while all the other parameters remain identical (n_a = 20 alleles, r = 0.5, and m = 0.2).

Figure 4.

Pairwise F_ST within population groups (in red) and between population groups (in blue) for 1,000 simulations and varying selection coefficients (symmetric HA). Dotted lines represent logarithmic regression lines. The left column shows the results for a stationary population, while the right column shows the results for an expanding population. All simulations have been obtained with the parameters Nm_intra = 100, Nm_inter = 2.5 as in the first line of Figure 2. Only five alleles have been set in the first line (instead of 20 in Figure 2), 400 generations in the second line (instead of 2,000), and the FDS model for balancing selection in the third line (instead of SOS). Note the differences in the scale of the Y-axis in various graphs.

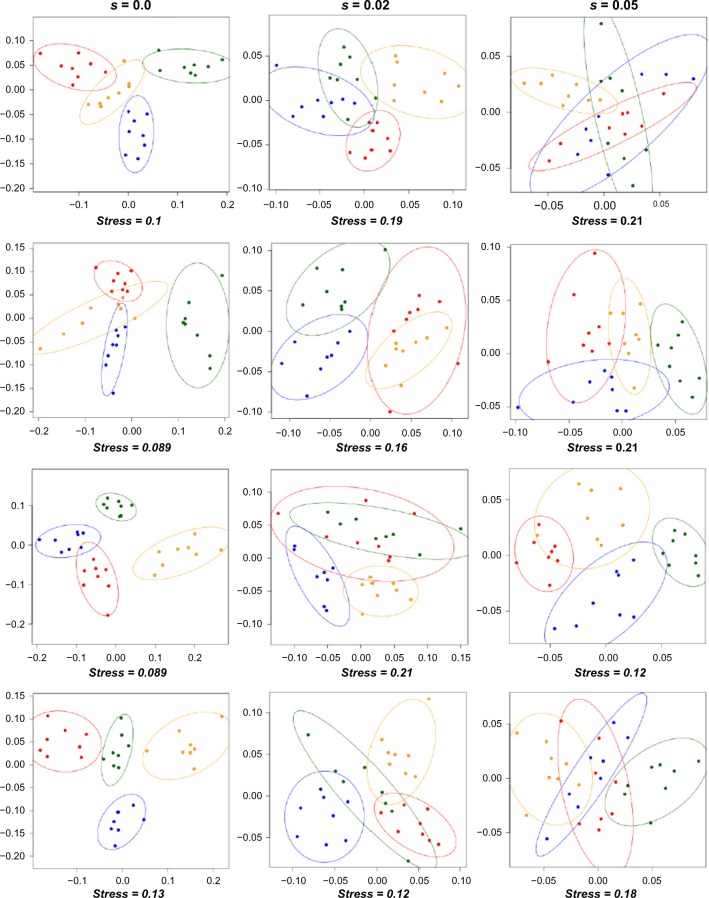
When balancing selection occurs, genetic distances between populations that are not spatially isolated are only slightly reduced compared with neutral expectations, whereas genetic distances between spatially isolated populations are strongly reduced (ie, they are inversely proportional to the gene flow across the geographical barrier). This effect translates into a distortion of the graphical representation of the genetic relationships between populations. For instance, Figure 5 shows 12 examples (randomly taken) of MDS performed on the simulated population samples, with s = 0.0, 0.02, or 0.05. In the absence of selection (s = 0.0), the genetic differentiation between geographic groups of populations is clearly visible in most of the cases, reflecting the strong barrier to gene flow between them (N_minter = Nm_intra/40). In contrast, when selection is at play (s > 0.0), genetic differentiation between geographic groups vanishes and the groups tend to overlap on the MDS. This effect increases with selection, and there is almost no genetic differentiation between the four groups of demes when balancing selection is strong (s = 0.05), despite a strong reduction of gene flow between them. Inversely, the genetic differentiation between populations within the geographic groups is almost independent of the amount of balancing selection and does not change much with or without the action of selection. This is due to the fact that the effect of migration is stronger than that of selection within groups, while it is the opposite between groups.

Figure 5.

Examples of MDS obtained in three series of independent simulations. The four MDS on the left pane have been generated from simulations without selection (s = 0%), while the four on the middle have been generated with a coefficient of balancing selection s = 2% and the four on the right pane with a coefficient of balancing selection s = 5%. Each dot represents one sample and each color (red, blue, yellow, and green) a group of eight samples located in the same area (color code is identical to Figure 1D). In all, 90% confidence limits for ellipses around the centroid of each group are displayed using the ordiellipse function of the VEGAN package in R.

Here, we used SELECTOR to investigate patterns of genetic differentiation between spatially distributed populations, accounting for isolation by distance,⁵⁵ where gene flow is not uniform (accounting for partial barriers to migration, such as mountains, rivers, or seas). These two condition properties constitute one of the novelties of SELECTOR compared with previous approaches. In a virtual square area subdivided into four groups of demes separated by a partial barrier to migration, we simulated the evolution of allele frequencies in populations (demes) during 2,000 generations and we recorded indices of genetic differentiation such as genetic distances D and fixation indices F_SC and F_CT. Our results confirm that genetic differentiation between demes is globally reduced under balancing selection compared with neutrality (Figs. 2–4). This could be explained by two factors: (1) under overdominance, the demes tend to share the same set of alleles, as rare alleles entering a deme have a higher fitness than alleles already present and (2) overdominant selection tends to increase within-deme diversity relative to the total diversity because alleles are kept at more equal frequency than for neutral alleles. Our results also confirm that the difference between overdominant selection and neutrality is more pronounced when gene flow is reduced, because a strong gene flow aids the mixing of alleles between demes and thus tends to erase the effect of balancing selection. More strikingly, new patterns of population differentiation emerge when mixing various gene flow intensities in a spatially structured population (Figs. 2 and 3). When a partial barrier to gene flow exists between geographic groups (Nm_inter < Nm_intra, eg, separation between two different continents), the average genetic distance D_inter between groups tends to be more affected by selection than the intragroup average genetic distance D_intra. Consequently, when significant genetic differentiation is detected through the analysis of neutral loci, this differentiation may not leave any signal on loci under balancing selection. But when looking at populations not separated by a barrier (belonging to the same continent), no differences are found between the two types of loci. Our results are robust to the parameters of the model as long as Nm_inter remains smaller than Nm_intra (Fig. 4).

Discussion

The rapid development of computational techniques has led to studies of new aspects of genetic evolution. In particular, simulation approaches permit exploration of realistic evolutionary scenarios that are too complex to be studied analytically, and these approaches have the power to integrate models affected by various processes (including genetic, environmental, cultural, and demographic processes). In this context, we present SELECTOR, a program that simulates genetic lineages under selection in a spatially explicit population framework. SELECTOR was primarily adapted to HLA loci because of the large worldwide datasets available for these genes and the need of a simulation program able to take into consideration their specific characteristics (multiple alleles and overdominant balancing selection) in a population genetic framework. We have validated the algorithms of SELECTOR by showing that its outputs are those expected theoretically in simple situations, but the power of SELECTOR resides in the simulation of more complex scenarios for which expectations cannot be computed analytically.^30,56,57 While SELECTOR has primarily been designed to investigate the joint effects of selection and demography on HLA markers, as exemplified in the study by Di et al.³⁰, it has also been applied to assess the effects of restricted gene flow on selected and neutral loci.⁵⁷ SELECTOR can also be used to test comparable evolutionary hypotheses on other markers, such as lactase persistence.⁵⁶

Here, we used SELECTOR to investigate patterns of genetic differentiation that could explain contrasting outcomes obtained on HLA data, for which some studies show a reduced interpopulation differentiation compared with neutral loci,^48–50 while others show no difference.^44,47 Our results suggest that, if gene flow is high between populations, the effect of balancing selection is negligible compared with that of demography.^30,47 In contrast, when gene flow is reduced among populations, such as where there is a partial or strong geographic barrier, the effect of selection is visible, as is the case for the Strait of Gibraltar.⁵⁷ The same logic may also explain why in the study by Sanchez-Mazas,⁵⁰ the variance of components among continents is significantly reduced (t-test: P-value = 0.036, Table 2) between HLA under putative balancing selection (HLA-A, -B, -C, -DRB1, -DQA1, and -DQB1) compared with nearly neutral loci (HLA-DPB1, DNA markers, and STR), while the variance components between populations within continents is not (t-test: P-value = 0.337, Table 2). Indeed, smaller Nm between continents would allow for balancing selection to be detected, while larger Nm within continents would not. This question deserves to be investigated further through additional quantitative analyses.

Table 2.

Hierarchical analysis of genetic variance showing the variance components (%) taken from the study by Sanchez-Mazas.⁵⁰

LOCUS	NUMBER OF POPULATIONS	WITHIN POPULATIONS	AMONG POPULATIONS WITHIN CONTINENTS	AMONG CONTINENTS
HLA-A	81	88.5	6.2	5.3
HLA-C	59	92	4.1	3.9
HLA-B	69	92.5	4.3	3.2
HLA-DRB1	91	91.3	5.1	3.6
HLA-DQA1	46	88.3	4.6	7.1
HLA-DQB1	69	89.3	5.4	5.3
HLA-DPB1a	49	84	6.3	9.7
DNA markersa	14	84.4	4.7	10.8
STRa	52	87.6	3.1	9.2

Note:

^aLoci considered as evolving nearly neutrally.

Here, we mainly used a model of overdominant selection as a first approximation to the mode of balancing selection acting on HLA loci, which explains the maintenance of numerous alleles.¹¹ Interestingly, these results do not differ significantly when either a model of HA (SOS) or a model of RAA (FDS, Fig. 4) is applied. However, the patterns of selective pressure may have been more complex, resulting from a combination of the following: (1) overdominant and positive selection at some alleles in response to the presence of specific pathogens⁵⁸; and/or (2) variability through space due to various pathogen environments⁵⁹; and/or (3) variable through time due to climatic variation. New selection models, such as divergent allele advantage²⁰ or selection varying in time and space,¹⁵ and more detailed relationships between selection, demography, and environment could be the next improvements of SELECTOR. Indeed, one of the interests of the simulation approach is that models can be improved and carefully investigated to assess specific combinations of parameter values and processes that may bring deeper understanding of observed patterns of genetic diversity. Another improvement of our approach would be the incorporation of molecular or multilocus data to analyze genomic information.

SELECTOR has been inspired by the program SPLATCHE,³⁵ and both programs have similar basic demographic processes. The major difference between the two processes is that the forward-in-time process implemented in SELECTOR, while being computationally more demanding than SPLATCHE’s backward-in-time coalescent approach, allows incorporating natural selection processes, while SPLATCHE simulates neutral loci only. However, the similarity between the two programs renders their respective outputs easily comparable, and they can consequently be used to associate genetic patterns of selected genes, such as HLA, to neutral molecular markers.⁵⁷ The evolution of allele frequencies in all demes can be obtained in a simple tabulated text format that is easily readable. In addition, final allele frequencies in a series of samples specified by the user are output in ARLEQUIN format (currently 3.5).³⁸ and can thus be easily analyzed to compute various intra- or interpopulation genetic statistics. SELECTOR has been developed in C++, which makes it computationally efficient and particularly suitable for research purposes. Thanks to its Linux version, SELECTOR may be incorporated through a bash pipeline into the ABC approach,⁶⁰ such as with ABCtoolbox,³² in order to estimate parameters and formally compare models. This powerful method permits assessment of the relative probabilities of contrasting evolutionary scenarios, as well as estimation of the best parameter values.^30,56,57 Input parameters of SELECTOR can be directly drawn from prior distributions defined by the user (see SELECTOR user manual)³⁷ and summary statistics computed from the output using ARLEQUIN. Since it is an approximation technique, ABC avoids the calculation of a likelihood function, and thus allows evaluation of complex evolutionary scenarios that would otherwise be intractable by full likelihood approaches. Even though ABC requires a large number of simulations, which depend on the number of parameters to be estimated and on the prior ranges used,^61–63 it has been shown to outperform approximate maximum-likelihood approaches.⁶⁴ We believe that SELECTOR provides a versatile and computationally efficient framework to investigate such scenarios.

When compared with other forward-in-time simulation approaches, SELECTOR allows simulating (1) various natural selection mechanisms (not available in SPLATCHE), (2) spatially explicit scenarios, in comparison with “simuPOP,”⁶⁵ and (3) more than three populations with sophisticated patterns of gene flow between populations and subpopulations, in comparison with “dadi”.⁶⁶ SELECTOR is also more research oriented, being faster than dadi or simuPOP since it is written in C++, which is compiled into a binary executable file, instead of interpreted Python.

Conclusion

Here, we have presented the simulation program SELECTOR and demonstrated that it is a powerful and robust tool for investigating the combined effects of selection and demography on the genetic variability of MHC loci.^30,57 Moreover, its versatility makes it invaluable for tackling other evolutionary questions and gaining insights into the genetic evolution of human beings and other organisms. SELECTOR is freely available for research and teaching purposes at http://ua.unige.ch/en/agp/tools/selector/.

Availability and Requirements

SELECTOR is written in C++, runs on MS windows or Linux, and is freely available for academic purposes at http://ua.unige.ch/en/agp/tools/selector/.