Unbiased diffusion in two-dimensional channels with corrugated walls

Abstract

This paper deals with diffusion of point particles in linearly corrugated two-dimensional channels. Such geometry allows one to obtain an approximate analytical expression that gives the particle effective diffusivity as a function of the geometric parameters of the channel. To establish its accuracy and the range of applicability, the expression is tested against Brownian dynamics simulation results. The test shows that the expression works very well for long channel periods, but fails when the period is not long enough compared to the minimum width of the channel. To fix this deficiency, we propose a simple empirical correction to the analytical expression. The resulting corrected expression for the effective diffusivity is in excellent agreement with the simulation results for all values of the channel period.

I. INTRODUCTION

The key quantity that characterizes the speed of unbiased diffusive transport of point Brownian particles in quasi-one-dimensional systems with periodically varying geometric constraints (two-dimensional channels and three-dimensional tubes) is the effective diffusivity. This quantity, denoted by D_eff, describes the mean square displacement of the particle along the channel/tube axis at long times, when the displacement significantly exceeds the system period l,

$${\displaystyle \overline{\mathrm{\Delta }{x}^2\left(t\right)}=2D_{\mathit{eff}}t>>l^2,t\to \infty ,}$$ (1.1)

where Δx(t) is the particle displacement along the axis in time t, and the bar above Δx²(t) denotes the averaging over realizations of the particle trajectory. The effective diffusivity determines the long-time behavior not only of the second moment of the displacement, but also of the displacement probability density given by the effective particle propagator G_eff (Δx, t),

$${\displaystyle G_{\mathit{eff}}\hspace{0.17em}(\mathrm{\Delta }x,t)=\frac{1}{\sqrt{4\pi D_{\mathit{eff}}t}}{e}^{-\mathrm{\Delta }{x}^2/\left(4D_{\mathit{eff}}t\right)},t\to \infty .}$$ (1.2)

The goal of the theory is to establish a connection between the effective diffusivity and the system geometry, which is a very challenging task. Analytical expressions, giving D_eff in terms of the geometric parameters of the system, have been derived only for a few two-dimensional and three-dimensional periodic systems. Here we show how to obtain an expression for D_eff in a linearly corrugated two-dimensional channel schematically illustrated in Fig. 1 and then check the predictions of this expression against Brownian dynamics simulations.

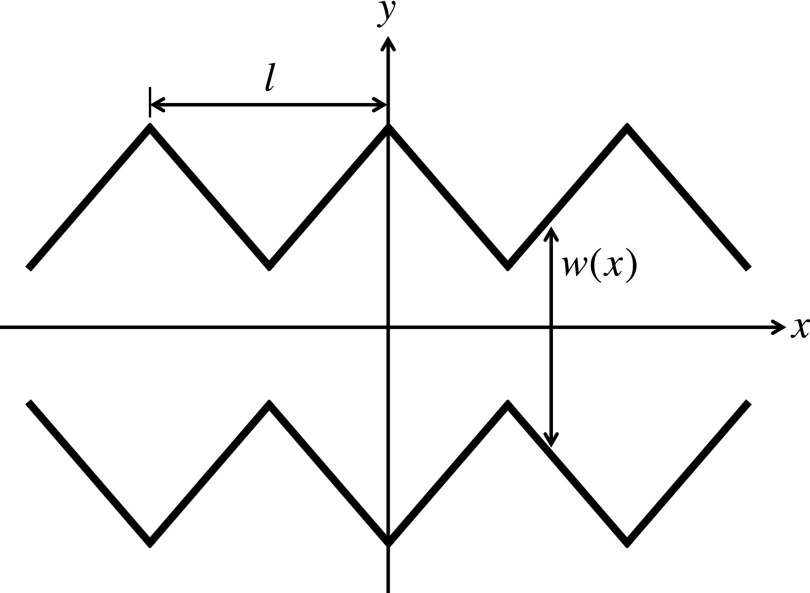
FIG. 1.

Schematic representation of a linearly corrugated two-dimensional channel of period l and position-dependent width w(x).

The outline of this paper is as follows. In Section II, we first introduce an effective one-dimensional description of the particle motion along the channel axis in terms of the modified Fick-Jacobs equation.¹ Second, we use the Lifson-Jackson formula² to find D_eff as a function of the geometric parameters of the channel. While the second step is exact, the first is an approximation.³ To test the accuracy of the obtained expression for D_eff and to establish the range of its applicability, in Section III we compare the effective diffusivity predicted theoretically with that obtained from Brownian dynamics simulations. While the agreement is excellent for sufficiently long channel periods, for short periods we find a systematic discrepancy between the theoretical predictions and simulations results. This deficiency is fixed by an empirical correction to the obtained expression for the effective diffusivity. Some concluding remarks, including a discussion of similarities and differences between the two-dimensional linearly corrugated channel and its three-dimensional counterpart, linearly corrugated tube, are made in Section IV.

II. THEORY

Consider a point Brownian particle diffusing in a two-dimensional periodic channel with linearly corrugated walls shown in Fig. 1. We choose the coordinate system so that its x-axis coincides with the channel centerline. The particle motion in the y direction, orthogonal to the centerline, is limited by the reflecting channel walls, |y| < w(x)/2, where w(x) is the position-dependent width of the channel. The channel width is a periodic function of x, w(x + l) = w(x), given by

$${\displaystyle w\left(x\right)/2=a+\lambda (l/2-|x\left|\right),\left|x\right|\le l/2,}$$ (2.1)

where a and l are the minimum half-width of the channel and its period, respectively, and λ ≥ 0 is one half of the absolute value of the width variation rate.

The starting point of our analysis is the modified Fick-Jacobs equation derived by Zwanzig,¹ which provides an approximate one-dimensional description of particle diffusion in the x direction. Denoting the particle propagator (the Green’s function) by G(x, t|x₀), where x and x₀ are the particle x coordinates at time t and at t = 0, respectively, the modified Fick-Jacobs equation can be written as

$${\displaystyle \frac{\partial G}{\partial t}=\frac{\partial }{\partial x}\left[D\left(x\right)w\left(x\right)\frac{\partial }{\partial x}\left(\frac{G}{w\left(x\right)}\right)\right],}$$ (2.2)

where D(x) is the effective position-dependent diffusivity of the particle. The applicability of the effective one-dimensional description of diffusion in two-dimensional channels of varying width in terms of the modified Fick-Jacobs equation is studied in detail in Ref. 4. As shown in this work, Eq. (2.2) is applicable when the width variation rate does not exceed unity, λ ≤ 1, and D(x) is given by either the Reguera-Rubi⁵ (RR) or Kalinay-Percus⁶ (KP) formulas,

$${\displaystyle D_{\mathit{RR}}\left(x\right)=\frac{1}{{\left(1+w^{\prime }{\left(x\right)}^2/4\right)}^{1/3}}{D}_0}$$ (2.3)

and

$${\displaystyle D_{\mathit{KP}}\left(x\right)=\frac{arctan\left(w^{\prime }\left(x\right)/2\right)}{w^{\prime }\left(x\right)/2}{D}_0,}$$ (2.4)

where D₀ is the particle diffusivity in space with no constraints. Note that alternative derivations of the KP expression for D(x), Eq. (2.4), were given by Martens et al.⁷ and Dagdug and co-authors.⁸ In these studies the result was obtained using different formalisms which also differ from the formalism used by Kalinay and Percus in their derivation.

When w(x) and D(x) in Eq. (2.2) are periodic functions, one can find the effective diffusivity by the Lifson-Jackson formula,²

$${\displaystyle D_{\mathit{eff}}=\frac{1}{〈w\left(x\right)〉〈1/\left(D\left(x\right)w\left(x\right)\right)〉},}$$ (2.5)

where the angular brackets denote averaging over the period: $〈f\left(x\right)〉=(1/l){\int }_0^{l}f\left(x\right)dx$. The position-dependent diffusivity, D(x), is a function of the absolute value of the local width variation rate, $\left|dw\left(x\right)/dx\right|$.¹ For linearly corrugated channels, according to Eq. (2.1), this quantity is a constant, $\left|dw\left(x\right)/dx\right|=2\lambda$, and, therefore, D(x) is a constant. Denoting this constant diffusivity by D_λ, we can write Eq. (2.5) as

$${\displaystyle D_{\mathit{eff}}=\frac{1}{〈w\left(x\right)〉〈1/w\left(x\right)〉}{D}_{\lambda }.}$$ (2.6)

Substituting here w(x) given in Eq. (2.1) and performing averaging of w(x) and 1/w(x) over the period, we arrive at

$${\displaystyle D_{\mathit{eff}}=\frac{\lambda l/\left(2a\right)}{\left[1+\lambda l/\left(4a\right)\right]ln\left[1+\lambda l/\left(2a\right)\right]}{D}_{\lambda }.}$$ (2.7)

Here D_λ is given by one of the expressions for the position-dependent diffusivity in Eqs. (2.3) and (2.4), which in the case under consideration take the forms

$${\displaystyle D_{\lambda ,\hspace{0.17em}\mathit{RR}}=\frac{1}{{\left(1+{\lambda }^2\right)}^{1/3}}{D}_0}$$ (2.8)

and

$${\displaystyle D_{\lambda ,\hspace{0.17em}\mathit{KP}}=\frac{arctan\left(\lambda \right)}{\lambda }{D}_0.}$$ (2.9)

The expressions in Eqs. (2.7)-(2.9) give the effective diffusivity as a function of the dimensionless geometric parameters of the channel λ and l/a. Similar result for D_eff is reported in Ref. 9 that deals with the effective diffusion of active swimmers.

Note that, although the expressions in Eqs. (2.8) and (2.9) look quite different, they lead to very close values of the diffusivity D_λ. Their ratio,

$${\displaystyle \frac{D_{\lambda ,\hspace{0.17em}\mathit{RR}}}{D_{\lambda ,\hspace{0.17em}\mathit{KP}}}=\frac{\lambda }{{\left(1+{\lambda }^2\right)}^{1/3}arctan\left(\lambda \right)},}$$ (2.10)

is tabulated in Table I. One can see that the ratio very slowly increases with λ from unity at λ = 0 (channel of constant width) to its maximum value at λ = 1, where the ratio approximately is 1.01. Since D_λ, RR and D_λ, KP are so close to each other, it does not matter which of the two expressions is used in Eq. (2.7).

TABLE I.

The diffusivity ratio in Eq. (2.10) as a function of λ.

λ	0.2	0.4	0.6	0.8	1.0
Dλ, RR/Dλ, KP	1.000 03	1.000 48	1.002 09	1.005 39	1.010 57

According to Eq. (2.7) the effective diffusivity, considered as a function of the channel period l at a fixed value of λ, monotonically decreases and tends to zero, as the channel period increases and tends to infinity. This happens because, as l increases, diffusing particles spend more and more time in the wide parts of the channel, and transitions between neighboring wide parts become more and more infrequent.

The decrease of the effective diffusivity can also be rationalized using the concept of the entropy potential, U_ent(x), defined as

$${\displaystyle U_{\mathit{ent}}\left(x\right)=-k_{B}Tln\left(w\left(x\right)/w\left(0\right)\right),}$$ (2.11)

where k_B and T are the Boltzmann constant and absolute temperature. As follows from Eq. (2.11), U_ent(x) is a periodic function of x, U_ent(x + l) = U_ent(x), which has minima in the wide sections of the channel and maxima in the narrow sections, located, respectively, at x = nl and x = (n + 1/2) l, n = 0, ± 1, ± 2, …, (see Fig. 1). As l increases, the wells of the entropy potential deepen. This is the reason why the interwell transitions become more and more infrequent, leading to the decrease of the effective diffusivity.

III. COMPARISON WITH THE SIMULATION RESULTS

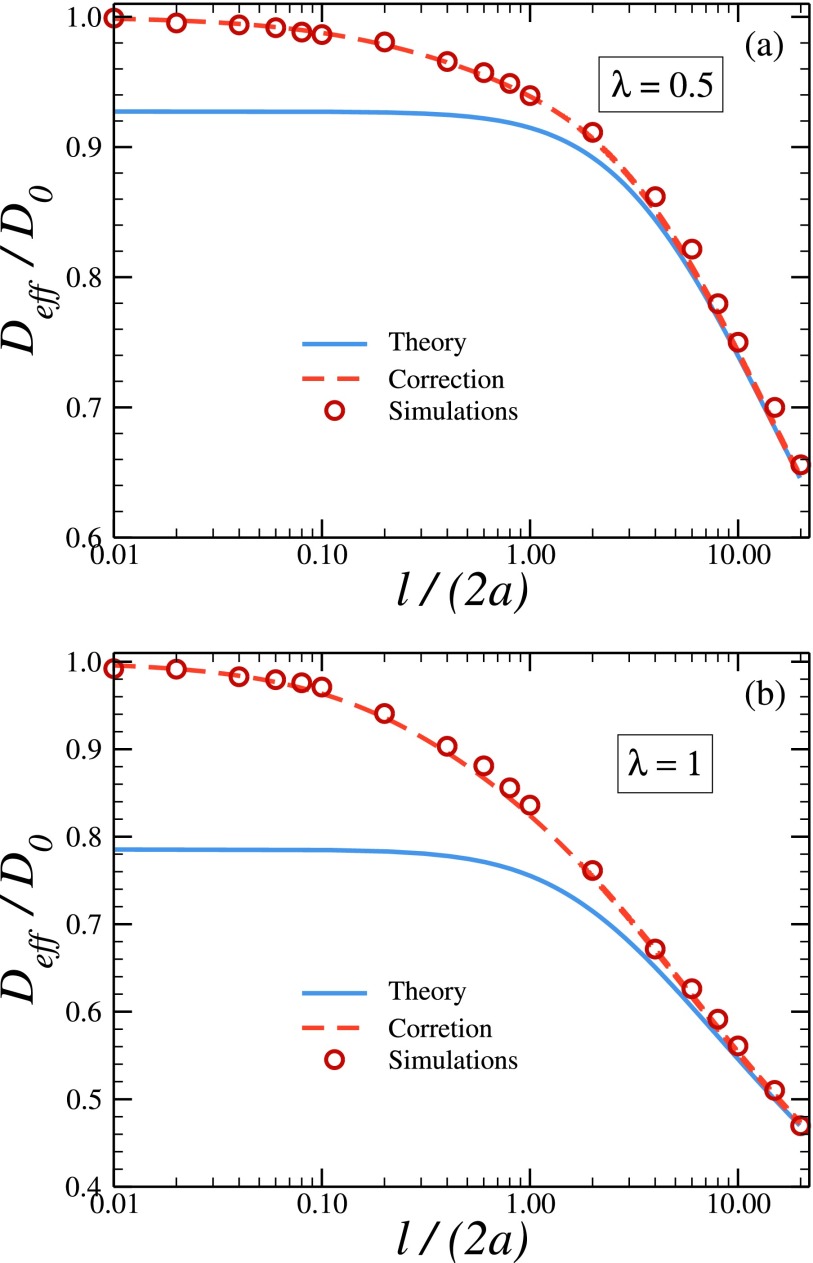
To test the accuracy of the approximate expression for the effective diffusivity in Eq. (2.7) and to establish the range of its applicability as a function of the channel period l, we compare theoretically predicted values of D_eff with the values obtained from Brownian dynamics simulations. This is done in Fig. 2, where the solid curves show the l-dependences of the effective diffusivity predicted by Eq. (2.7) with D_λ given by the KP formula in Eq. (2.9), and symbols give the values of D_eff obtained from the simulations. Panels (a) and (b) represent the results at λ = 0.5 and λ = 1.0, respectively. As mentioned earlier, D_λ, RR in Eq. (2.8) and D_λ, KP in Eq. (2.9) are very close (see Table I), so that the theoretical dependences drawn using D_λ, RR and D_λ, KP are practically indistinguishable. Comparison shows that the accuracy of the theoretical predictions increases with the channel period. For the width variation rate of λ = 1.0, the relative error of the theoretical predictions does not exceed 5% at l = 4a and is less than 1% at l ≥ 8a. For the smaller width variation rate the relative error is even smaller. Thus, Eqs. (2.7)-(2.9) reliably predict the effective diffusivity when l ≥ 4a and λ ≤ 1.0.

FIG. 2.

Effective diffusivity, D_eff, normalized to D₀, as a function of the ratio l/a at λ = 0.5 (a) and λ = 1.0 (b). Solid curves are the theoretically predicted dependences drawn using Eq. (2.7) with D_λ given by the KP formula in Eq. (2.9). Symbols are the normalized values of the effective diffusivity obtained from Brownian dynamics simulations. Dashed curves are drawn using Eq. (2.7) with D_λ replaced by D_λ,γ given in Eq. (3.2), where D_λ is given by the KP formula in Eq. (2.9).

In Fig. 2 one can also see that the theory fails to predict the behavior of the effective diffusivity as l → 0. In this limit, according to Eq. (2.7), D_eff → D_λ, whereas the simulations show that D_eff → D₀, which is larger than D_λ. The reason why the theory fails is that the one-dimensional description in terms of the modified Fick-Jacobs equation is not applicable in this limiting case. Indeed, as l → 0, the amplitude of the channel width variation, 2λl, becomes much smaller than the minimum channel width, meaning that the particles diffuse in the channel with practically flat walls.

As follows from the analysis presented in Ref. 4, most of the particles do not collide with the walls while travelling the channel period if the condition that the period is longer than the doubled minimum width of the channel, l ≥ 4a, is not met. As a consequence, the modified Fick-Jackobs equation is not applicable in such a case. To construct an expression that describes the effective diffusivity over the entire range of the channel period, including small l, where the expression in Eq. (2.7) fails, we introduce a dimensionless parameter, γ,

$${\displaystyle \gamma =\frac{l/a}{1+l/a}=\frac{l}{a+l},}$$ (3.1)

which increases from zero to unity as the period increases from zero to infinity. We use this parameter to define the diffusivity D_λ,γ,

$${\displaystyle D_{\lambda ,\gamma }=D_0-\gamma \left(D_0-D_{\lambda }\right),}$$ (3.2)

which decreases from D₀ to D_λ as γ goes from zero to unity. Replacing D_λ in Eq. (2.7) by D_λ,γ, we obtain an expression for D_eff, which is in perfect agreement with our simulation results over the entire range of the channel period, as illustrated in Fig. 2. As before, D_λ in Eq. (3.2) is given by either RR or KP formulas in Eqs. (2.8) and (2.9).

IV. CONCLUDING REMARKS

The derivation of the expression for the effective diffusivity in Eq. (2.7) is based on the approximate one-dimensional description of diffusion along the channel axis by the modified Fick-Jackobs equation. This one-dimensional description fails when the period of the channel is not large enough, compared to the minimum channel width. As a consequence, Eq. (2.7) underestimates the effective diffusivity for channels with short periods (Fig. 2). Replacing in Eq. (2.7) D_λ by D_λ,γ given by Eq. (3.2), we obtain an expression which is in perfect agreement with the effective diffusivities found from Brownian dynamics simulations for all values of the channel period (Fig. 2).

A channel with linearly corrugated walls has an important property—position-dependent diffusivity D(x) in such a channel is a constant, D_λ. This allowed us to simplify the general expression for D_eff in Eq. (2.5) and to write the effective diffusivity in the form given in Eq. (2.6). Using the entropy potential, Eq. (2.11), the latter can be written as

$${\displaystyle D_{\mathit{eff}}=\frac{1}{〈e^{-\beta U_{\mathit{ent}}\left(x\right)}〉〈e^{\beta U_{\mathit{ent}}\left(x\right)}〉}{D}_{\lambda },}$$ (4.1)

where $\beta =1/\left(k_{B}T\right)$. This expression gives D_eff as a product of a λ-dependent scaling factor D_λ and a dimensionless factor ${\left(〈e^{-\beta U_{\mathit{ent}}\left(x\right)}〉〈e^{\beta U_{\mathit{ent}}\left(x\right)}〉\right)}^{-1}$, which is completely determined by the entropy potential (i.e., by the channel geometry). Such presentation of D_eff is universal in the sense that it is equally applicable to linearly corrugated tubes in three dimensions. Although both D_λ and the entropy potential in three dimensions differ from their two-dimensional counterparts, the expression for D_eff in Eq. (4.1) remains unchanged.

The radius r(x) of a linearly corrugated three-dimensional tube of period l, r(x + l) = r(x), can be written in the form similar to w(x)/2 in Eq. (2.1),

$${\displaystyle r\left(x\right)=a+\lambda (l/2-|x\left|\right),\left|x\right|\le l/2,}$$ (4.2)

where a is the minimum tube radius, and the tube cross section at the origin, x = 0, has the maximum radius, r(0) = a + λl/2 = r_max. The entropy potential in this case is given by

$${\displaystyle U_{\mathit{ent}}\left(x\right)=-k_{B}Tln(A\left(x\right)/A\left(0\right))=-2k_{B}Tln(r\left(x\right)/r\left(0\right)),}$$ (4.3)

where A(x) = πr²(x) is the position-dependent cross-sectional area of the tube. Using U_ent(x) in Eq. (4.3), we can write Eq. (4.1) in the form

$${\displaystyle D_{\mathit{eff}}=\frac{1}{〈r^2\left(x\right)〉〈1/r^2\left(x\right)〉}{D}_{\lambda },}$$ (4.4)

which is the three-dimensional analog of Eq. (2.6). Performing the averaging of r²(x) and 1/r²(x) over the period, we obtain

$${\displaystyle D_{\mathit{eff}}=\frac{1+\lambda l/\left(2a\right)}{1+\lambda l/\left(2a\right)+{\left[\lambda l/\left(2a\right)\right]}^2/3}{D}_{\lambda }.}$$ (4.5)

This result for the effective diffusivity with D_λ given by the corresponding RR formula, $D_{\lambda }=D_0/\sqrt{1+{\lambda }^2}$,⁵ has been obtained in Ref. 10. Note that the effective diffusivity in Eq. (4.5), as its two-dimensional counterpart, fails when the period is smaller or comparable with the minimum tube radius.¹⁰ It turns out that this failure is also fixed by the replacement D_λ in Eq. (4.5) by D_λ,γ given by an expression similar to that in Eq. (3.2) that accounts for the changing probability of collision with the tube wall during the time required for the particle to pass the corrugation period.

Expressions in Eqs. (2.7) and (4.5) show how the effective diffusivities for the two-dimensional linearly corrugated channel and three-dimensional linearly corrugated tube depend on the dimensionless geometric parameters l/a and λ. The difference between the two expressions is most pronounced in the large-l asymptotic behaviors of the two effective diffusivities. In the two-dimensional case, Eq. (2.7) shows that D_eff vanishes, as l → ∞, as 1/ln(l), whereas its three-dimensional counterpart, according to Eq. (4.5), approaches zero in this limiting case as 1/l. This difference in the asymptotic behavior is due to the difference in the entropy potentials.

To compare the influence of the entropy potential on the effective diffusivity in two and three dimensions, consider the effective diffusivity scaled by D_λ,

$${\displaystyle \frac{D_{\mathit{eff}}}{D_{\lambda }}=\frac{1}{〈e^{-\beta U_{\mathit{ent}}\left(x\right)}〉〈e^{\beta U_{\mathit{ent}}\left(x\right)}〉},}$$ (4.6)

which depends only on the entropy potential. According to Eqs. (2.7) and (4.5), the ratio D_eff/D_λ in two (2d) and three (3d) dimensions is given by

$${\displaystyle \frac{D_{\mathit{eff}}}{D_{\lambda }}=\left\{\begin{array}{lc}\frac{\lambda l/\left(2a\right)}{\left[1+\lambda l/\left(4a\right)\right]ln\left[1+\lambda l/\left(2a\right)\right]},\hfill & \hfill 2d\hfill \\ \frac{1+\lambda l/\left(2a\right)}{1+\lambda l/\left(2a\right)+{\left[\lambda l/\left(2a\right)\right]}^2/3},\hfill & \hfill 3d\hfill \end{array}\right..}$$ (4.7)

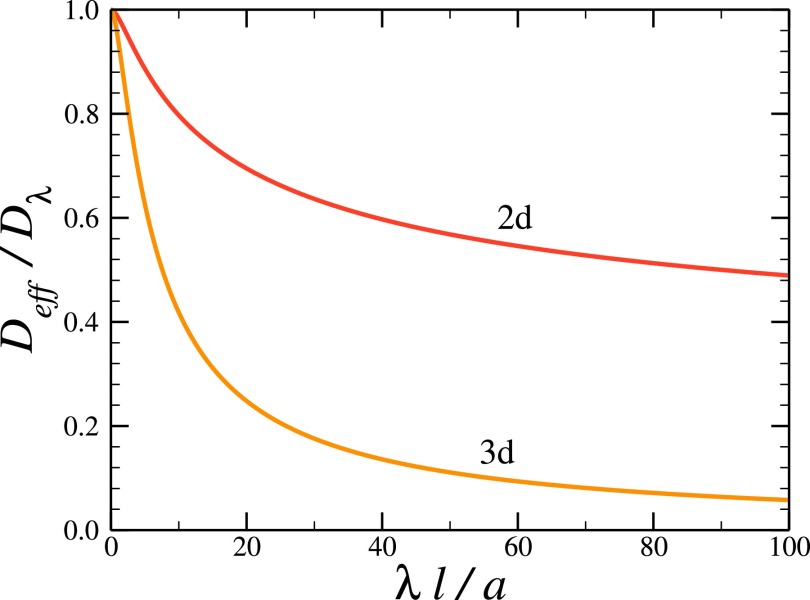
The decrease of this ratio with the increase of λl/a is illustrated in Fig. 3. One can see that in three dimensions the influence of the entropy potential on the ratio D_eff/D_λ is stronger than in two dimensions.

FIG. 3.

The ratio D_eff/D_λ, given in Eq. (4.7), as a function of the ratio λl/a in two and three dimensions.

To rationalize this observation, we note that according to Eqs. (2.11) and (4.3) the two entropy potentials are

$${\displaystyle U_{\mathit{ent}}^{\left(2d\right)}\left(x\right)=-k_{B}Tln\frac{a+\lambda (l/2-|x\left|\right)}{a+\lambda l/2},\left|x\right|\le l/2}$$ (4.8)

and

$${\displaystyle U_{\mathit{ent}}^{\left(3d\right)}\left(x\right)=-2k_{B}Tln\frac{a+\lambda \left(l/2-\left|x\right|\right)}{a+\lambda l/2},\left|x\right|\le l/2.}$$ (4.9)

Thus, the three-dimensional entropy potential is double its two-dimensional counterpart, $U_{\mathit{ent}}^{\left(3d\right)}\left(x\right)=2U_{\mathit{ent}}^{\left(2d\right)}\left(x\right)$. This is the reason why the effect of the entropy potential on the ratio D_eff/D_λ in three dimensions is stronger than in two dimensions.